Mass Preserving Registration for Heart MR Images

Abstract

This paper presents a new algorithm for non-rigid registration between two doubly-connected regions. Our algorithm is based on harmonic analysis and the theory of optimal mass transport. It assumes an underlining continuum model, in which the total amount of mass is exactly preserved during the transformation of tissues. We use a finite element approach to numerically implement the algorithm.

1 Introduction

Image registration is the process of generating a common geometric frame of reference between two or more image datasets. This technique is especially useful in the context of medical image processing. A successful registration technique allows for the integration of pre-operative information with intra-operative imaging to improve image-guided surgery and therapy. For example, in brain surgery where craniotomy is performed, the ventricles in the brain may be compressed due to pressure changes. A surgical plan based on pre-surgical images must therefore be updated accordingly to reflect these shape deformations. There have been numerous algorithms proposed for non-rigid registration. See [9] for a detailed review and the references therein. Our method employs optimal mass transport, and therefore belongs to the category of warping algorithms based on continuum and fluid mechanics. The approach may be formulated as an energy minimization problem. We should point out that our methodology may not be suitable under circumstances where the mass preservation assumption is invalid, such as the matching of two different perspective projections of a spatial object.

In the work of [5,11], an algorithm was presented for finding an optimal warping function between two simply-connected domains, or more specifically two rectangular regions. The assumption was that the mass is preserved at all points in the image domain. However, this is not always the case. Sometimes, the mass preserving (MP) assumption is valid only in parts of the two images. The specific example we have in mind concerns two magnetic resonance (MR) images of the heart taken at different times in the cardiac cycle, but corresponding to the same spatial position. Indeed, during the cycle, the MP assumption is valid in the myocardium, but not in the ventricles where the volume of blood varies from time point to time point. With this key example in mind, we will derive an algorithm for extending previous approaches to two doubly-connected domains, based on harmonic analysis and a Finite Element Method (FEM). Here, we treat image intensity as tissue mass density, due to the fact that in MR images intensity is related to proton density, thus related to mass density. After registration, image intensity (mass density) can change, but the total amount of mass (mass density times area or the integral of intensity) preserves.

We now outline the contents of this paper. In Section 2, we give a brief review of the optimal mass transport problem and a general gradient descent solution. In Section 3, we summarize the approach for finding an optimal MP mapping between two doubly-connected domains. In Section 4, we illustrate the proposed algorithm using a pair of heart MR images. Finally, in Section 5, we summarize the contribution of this paper and discuss some possible future research directions.

2 Background on Optimal Mass Transport

The Monge-Kantorovich Problem (MKP) is concerned with the optimal way of moving certain amount of mass from one domain into another. The total amount of mass remains constant in this process. It has been widely studied in various fields such as econometrics, fluid dynamics, transportation, and image retrieval [7]; see [6] and the references therein. In this paper, we will consider only 2D problems. Accordingly, let Ω₀ and Ω₁ be domains of R², having smooth boundaries. On each domain Ω_i, we assume that there exists a positive mass density function μ_i, i = 0, 1. It is further assumed that the same total amount of mass is associated with the two domains.

We will be considering a class of diffeomorphisms u from Ω₀ to Ω₁ which satisfy the “Jacobian equation” in the form of

$${\mu }_0=\mid Du\mid {\mu }_1\circ u,$$ (1)

where |Du| is the determinant of the Jacobian of u, and ∘ represents the composition of functions. Equation (1) is an infinitesimal form of the mass preservation (MP) constraint. We are interested in finding an MP mapping u which differs minimally from the identity. To this end, we introduce the L² Kantorovich–Wasserstein penalty functional on u ∈ MP, defined as:

$$M[u]:={\int }_{{\mathrm{\Omega }}_0}{\left|\right|u(x)-x\left|\right|}^2{\mu }_0(x)dx$$ (2

This functional places a penalty on the distance the map u moves each bit of material, weighted by the material’s mass. The resulting distribution of material is constrained to be the given density μ₁. The “optimal” mapping ũ is the one that minimizes functional (2), and is the “cheapest” way of transporting mass from one domain into the other. An energy term penalizing intensity change can also be added, please refer to [5].

Theoretical results [2,3] show that there is a unique minimizer ũ ∈ MP, and that this minimizer is characterized as being the gradient of a convex function w, i.e., ũ = ∇w. There have been a number of algorithms proposed for solving this problem, e.g. linear programming [6], which is the most popular one. However, the linear programming approach has a high computational complexity. In the method presented here, we use a gradient descent approach to solve for the optimal transport problem, based on the equivalent problem of polar factorization. Here we will briefly describe the procedure; for mathematical details we refer the reader to [5].

The first step of the method is to construct an initial MP mapping. For two rectangular regions, the initial mapping can be found by solving a family of 1D problems unsing simple numerical integration. Assume the two domains have shapes of Ω₀ = [0, A₀] × [0, B₀] and Ω₁ = [0, A₁] × [0, B₁], respectively. Assume further that the initial mass preserving mapping has the form of u⁰(x, y) = (a(x), b(x, y)). Since both μ₀ and μ₁ are positive everywhere, it is easy to solve u⁰ = (a(x), b(x, y)) from the following equations:

$$\begin{array}{l}{\int }_0^{a(x)}{\int }_0^{B_1}{\mu }_1(\eta ,y)\mathit{dyd}\eta ={\int }_0^x{\int }_0^{B_0}{\mu }_0(\eta ,y)\mathit{dyd}\eta \\ a^{\prime }(x){\int }_0^{b(x,y)}{\mu }_1(a(x),\rho )d\rho ={\int }_0^y{\mu }_0(x,\rho )d\rho .\end{array}$$ (3)

The second step is to find the minimizer ũ of the energy functional (2), using an iterative approach. In [5], it is shown that the evolution of u should have the following form in order to satisfy the mass preserving constraint:

$$u_t=\frac{2}{{\mu }_0}Du{\nabla }^{\perp }{\mathrm{\Delta }}^{-1}\text{div}[{(u-\underset{\_}{id})}^{\perp }],$$ (4)

where ⊥ rotates a vector by π/2 in the counterclockwise direction, Δ⁻¹ denotes the inverse of Laplacian, and id stands for the identity map. It can be shown that the optimal mapping ũ is a curl-free vector field [5].

3 Mass-Preserving Registration Between Two Doubly-Connected Domains

In the previous section, we briefly described the approach for solving the transport problem between two rectangular regions. However, this approach cannot be applied on doubly-connected regions (i.e. an annular region) without some modifications. The main difficulty comes from the construction of an initial MP mapping u⁰ between two irregular doubly-connected domains. In this section, we present an algorithm which constructs such a mapping by using harmonic parametrization. In this approach, the two domains are first harmonically parameterized, then the initial MP mapping u⁰ is constructed by solving a 1D transport problem along one harmonic coordinate, followed by a family of 1D transport problems along the other harmonic coordinate.

3.1 Harmonic Parametrization

Here we sketch the steps for constructing an analytic function f^h = u^h + iv^h for the harmonic parametrization. Similar techniques have been applied for measuring tissue thickness [10], for colon surface visualization [4], and for parametrization of ventricular regions of the heart [8].

Assume we have a triangulated doubly-connected domain Σ, which has an inner boundary denoted by σ₀ and an outer boundary denoted by σ₁ as shown in Figure 1. First, we want to construct u^h, which is the real part of f. It is assumed that u^h satisfies

Fig. 1.

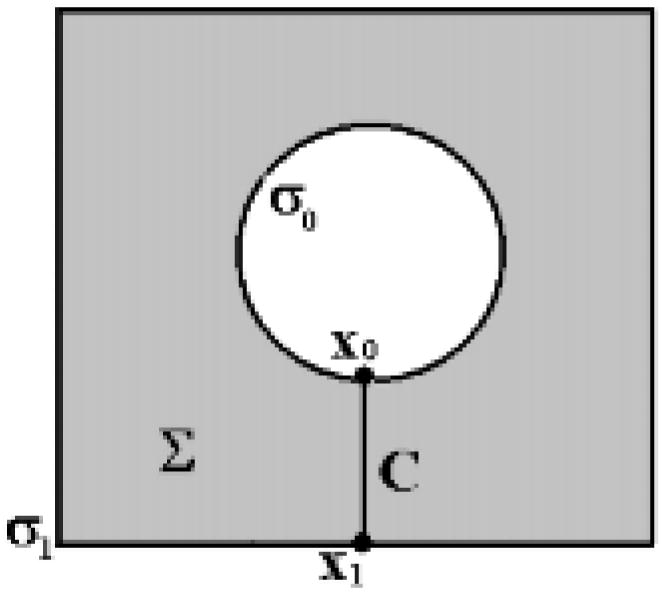
A doubly-connected domain Σ with two boundaries

$$\begin{array}{c}\mathrm{\Delta }{u}^h=0\\ \text{with}{u}^h({\sigma }_0)=0\text{and}{u}^h({\sigma }_1)=1\end{array}$$ (5)

The Laplace equation can be solved by using standard FEM techniques [4]. A cut C is then found from σ₀ to σ₁ by following the gradient of u^h from an arbitrary point x₀ ∈ σ₀ to another point x₁ ∈ σ₁. The cut C and two original boundaries σ₀ and σ₁ form a new closed and oriented boundary B for the domain,

$$B:x_0\stackrel{{\sigma }_0}{\to }{x}_0\stackrel{C}{\to }{x}_1\stackrel{{\sigma }_1}{\to }{x}_1\stackrel{-C}{\to }{x}_0$$

The boundary condition of the imaginary part v^h can be then prescribed by,

$$v^h(\zeta )={\int }_{{\zeta }_0}^{\zeta }\frac{\partial v}{\partial s}ds={\int }_{{\zeta }_0}^{\zeta }\frac{\partial u}{\partial n}ds$$

according to the Cauchy-Riemann equations. Inside the cut surface, v^h is found as the solution of Laplace’s equation Δv^h = 0.

Once the analytic function f^h = u^h + iv^h is constructed, a curvilinear harmonic polar coordinate system is defined by taking u^h as one coordinate axis and v^h as the other. The coordinate u^h can be thought of as a curvilinear “radius” and v^h as the “angle”. By scaling u^h and v^h by a constant, v^h can be made to run from 0 to 2π. Figure 2 shows such a parametrization on a heart MR image without involving the ventricle area.

Fig. 2.

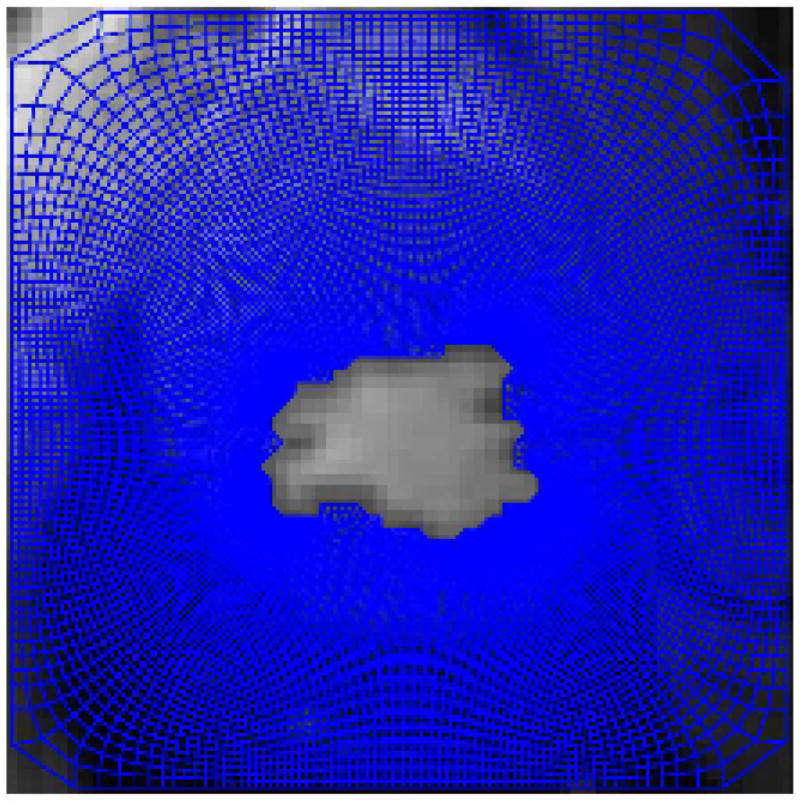
Harmonic parametrization of a heart image

3.2 Finding the Initial Mapping u⁰

By performing harmonic parametrization, the first doubly-connected domain (Ω₀, μ₀) is cut and mapped onto a rectangular region ( ${\mathrm{\Omega }}_0^h,{\mu }_0^h$) via a harmonic (conformal) mapping $f_0^h=u_0^h+{iv}_0^h$. If we define the mass density ${\mu }_0^h$ by

$${\mu }_0^h={\mid D{f}_0^h\mid }^{-1}{\mu }_0,$$ (6)

then the mapping from Ω₀ to ${\mathrm{\Omega }}_0^h$ is mass-preserving. Similarly, the second doubly-connected domain (Ω₁, μ₁) is mapped onto another rectangular region ( ${\mathrm{\Omega }}_1^h,{\mu }_1^h$) via $f_1^h=u_1^h+{iv}_1^h$. Here, ${\mu }_1^h$ is taken to be

$${\mu }_1^h={\mid D{f}_1^h\mid }^{-1}{\mu }_1.$$ (7)

The remaining task is to find an MP mapping from ( ${\mathrm{\Omega }}_0^h,{\mu }_0^h$) to ( ${\mathrm{\Omega }}_1^h,{\mu }_1^h$). Since Ω₀ and Ω₁ are now rectangular regions, we can use the algorithm presented in Section 2 to find an initial MP mapping u_init between them. This process can be illustrated by the following diagram.

The resulting initial mapping u⁰ is the composition of $f_0^h$, u_init and ${(f_1^h)}^{-1}$, so that

$$u^0={(f_1^h)}^{-1}\circ u_{\text{init}}\circ f_0^h.$$ (8)

Compositions of MP mappings and inverses of MP mappings are also MP mappings. Thus u⁰ is and MP mapping, since $f_0^h,f_1^h$ and u_init are.

3.3 Finding the Minimizer ũ

The equation we use to evolve u is the same as for rectangular regions. The finite element method (FEM) is used to solve the Poisson equation (the Δ⁻¹ part of equation (4)) on a triangulated irregular domain.

In the evolution equation of u (equation (4)), we use an upwinding scheme for computing Du. For all other derivatives, we use a Least Mean Square (LMS) method to numerically implement the spatial derivatives. For example, assume that a given point (x₀, y₀) has N neighbors (x_i, y_i), i = 1…N, and a function Φ is defined such that Φ (x_i, y_i) = Φ_i for i = 0…N. It is easy to show that the derivatives of Φ should satisfy

$$\left(\begin{array}{c}{\mathrm{\Phi }}_x\\ {\mathrm{\Phi }}_y\end{array}\right)={(A^{T}A)}^{-1}{A}^T\left(\begin{array}{c}{\mathrm{\Phi }}_1-{\mathrm{\Phi }}_0\\ \cdots \\ {\mathrm{\Phi }}_N-{\mathrm{\Phi }}_0\end{array}\right),$$ (9)

where A is the position difference matrix given by

$$A=\left(\begin{array}{c}{x}_1-x_0,y_1-y_0\\ \cdots \\ x_N-x_0,y_N-y_0\end{array}\right).$$ (10)

A time step was chosen as in [5] to make the algorithm stable.

4 Example

We illustrate the procedure outlined above on two 256 × 256 MR images of the heart acquired on a GE scanner. Referring to Figure 3, we show the diastolic (Figure 3(a)) and systolic (Figure 3(b)) time points of the cardiac cycle.

Fig. 3.

Two heart MR images and their segmentation results

The black regions in Figure 3 (c) and (d) are two multi-connected domains, corresponding to the heart muscle and other tissues in which we use image intensity as the mass density. Uniform mass densities could also be used, in which case mass preservation becomes a simple area preservation constraint. These regions were chosen as natural candidates to apply an MP deformation (in contrast to the left ventricle in which the change is too drastic to sensibly apply the procedure). Harmonic parametrization is first done on each domain (as shown in Figure 2 for the diastolic image), and an FEM-based L² MKP is then solved between the two domains to find the correspondence. Figure 4 shows the deformed grid. We can also create a morphing video to show the deformation of the first image into the second. Figure 5 shows some key frames in the video.

Fig. 4.

The deformed grid on the systolic heart image

Fig. 5.

Morphing movie for two heart images in Figure 3

5 Conclusions

In this note, we extended the methodology for applying MP registration [5] to a pair of doubly-connected domains. For an L² version of the problem, a gradient descent algorithm is proposed to solve the problem iteratively. Harmonic analysis is employed in this approach for constructing an initial MP mapping. If the radius of the inner boundary is small enough, the inner boundary can be considered as a single landmark. In this sense, we have solved for MP registration on two domains with a pair of corresponding landmarks. This technique can also be extended into multi-connected domains (corresponding to multiple landmarks).

In the present work, the pure L² Kantorovich-Wasserstein functional is proposed as the similarity measure. A modified energy functional penalizing the intensity change can also be implemented [12]. Other types of distance measures, e.g. minimizers of the Dirichlet energy integral, can also be combined with a mass preservation constraint [1]. We plan to implement these ideas in some future work.