Bursting synchronization dynamics of pancreatic β-cells with electrical and chemical coupling

Abstract

Based on bifurcation analysis, the synchronization behaviors of two identical pancreatic β-cells connected by electrical and chemical coupling are investigated, respectively. Various firing patterns are produced in coupled cells when a single cell exhibits tonic spiking or square-wave bursting individually, irrespectively of what the cells are connected by electrical or chemical coupling. On the one hand, cells can burst synchronously for both weak electrical and chemical coupling when an isolated cell exhibits tonic spiking itself. In particular, for electrically coupled cells, under the variation of the coupling strength there exist complex transition processes of synchronous firing patterns such as “fold/limit cycle” type of bursting, then anti-phase continuous spiking, followed by the “fold/torus” type of bursting, and finally in-phase tonic spiking. On the other hand, it is shown that when the individual cell exhibits square-wave bursting, suitable coupling strength can make the electrically coupled system generate “fold/Hopf” bursting via “fold/fold” hysteresis loop; whereas, the chemically coupled cells generate “fold/subHopf” bursting. Especially, chemically coupled bursters can exhibit inverse period-adding bursting sequence. Fast–slow dynamics analysis is applied to explore the generation mechanism of these bursting oscillations. The above analysis of bursting types and the transition may provide us with better insight into understanding the role of coupling in the dynamic behaviors of pancreatic β-cells.

Introduction

Pancreatic β-cells located in islets of Langerhans in the pancreas are responsible for the synthesis and secretion of insulin in response to a glucose challenge. Like nerve and endocrine cells, pancreatic β-cells are electrically excitable (Ashcroft and Rorsman 1989) and the electrical firing patterns typically come in the form of bursting, characterized by an active phase of fast spiking followed by a quiescent phase without spiking (Dean and Mathews 1970). It is well-known that bursting can be exhibited by a wide range of nerve and endocrine cells, and it is likely one of the most important and distinctive patterns in dynamic behaviors. Bursting activity is also important for pancreatic β-cells because it leads to oscillations in the intracellular free Ca²⁺ concentration, which in turn leads to oscillations in insulin secretion (Ravier et al. 1999).

There is strong evidence that impaired insulin secretion is the initial and main genetic factor predisposing to Type II diabetes (Bergsten 2000). Insulin secretion is a complex multicellular process, which depends on interactions between β-cells within an islet as well as on the interactions between islets in the pancreas (Krasimira et al. 2006). In order to observe an overall oscillatory insulin profile, it is necessary to understand the collective behavior of β-cells. Eelectrical coupling through gap junctions and chemical coupling through chemical synapse have been suggested to be exists in regulating basal insulin release (Calabrese et al. 2000; Rorsman et al. 1989; Salehi et al. 2005). Evidence for electrical coupling via gap junctions between islet cells has previously been provided by electron microscopy, recordings of membrane potential and currents using sharp intracellular electrodes (Zhang et al. 2008; Orci et al. 1975; Meissner 1976).

Synchronization, as an emerging phenomenon of a population of dynamically interacting units (Arenas et al. 2008; Wang and Jiao 2006; Wang and Zhang 2003; Zhang et al. 2010), has been extensively studied both in coupled cells (Wang et al. 2011;Marek and Stuchl 1975) or complex networks (Gomez-Gardenes et al. 2007; Volman et al. 2011; Sun et al. 2011). It has been demonstrated that the electrical activity of two electrically coupled β-cells can exhibit different forms of synchronous activities, both in vivo (Valdeolmillos et al. 1996) and in vitro (Eddlestone et al. 1984). Numerical simulations have been used to examine the role of the electrical coupling strength in synchronous behaviors within intact islets. Based on a minimal but representative model of bursting electrical activity in the pancreatic β-cell, Sherman and Rinzel considered an idealized case of pairs of identical cells, and showed that they can be converted from tonic spiking to bursting by weak electrical coupling (Sherman and Rinzel 1991, 1992). Later, Sherman further gave the bifurcation analysis of a coupled pair of identical bursters by extending the theory of bursting for square-wave bursters from single cell to coupled cells (Sherman 1994). Using the same method, the normal form analysis of coupled bursters was primarily presented in (De Vries and Sherman 1998). The importance of the bifurcation structure for the synchronization of coupled cells has also been studied in (Perc and Marhl 2004a, b).

Although the minimal model explains the minimum conditions needed for generating bursting oscillations, it doesn’t involve the ATP-sensitive K⁺ current. Given that this ionic current does exist and plays an important role in pancreatic β-cells, the minimal model was extended by including the ATP-sensitive K⁺ current to get the modified model, proposed by De Vries and Sherman (2000). In this paper, it was shown that weak electrical coupling can still induce synchronous bursting oscillations in cells,which are incapable of bursting individually, and the coupled system will return to the in-phase (IP) spiking state eventually under strong electrical coupling. However, how the synchronous bursting changes during the transition process is still not clear. Here we show that under moderate electrical coupling strength, two regular firing patterns can be produced in the intermediate process, that is, the anti-phase (AP) spiking firing pattern and another completely different bursting synchrony, respectively. We also show that weak electrical coupling can make the two-coupled cells transit to burst synchronization with “fold/Hopf” bursting via the “fold/fold” hysteresis loop while the isolated single cell only exhibits “fold/homoclinic” type of bursting.

As mentioned above, electrical coupling has been well studied in the pancreatic islets, and is believed to account for signal synchronization of islet cells; in contrast, the influence of chemical coupling on islet synchronization and its physiological response are less concerned. It was known that neurons communicate through synapses more often than gap junctions and neuronal network with chemical coupling can be successful in producing important biological rhythms (Rubin and Terman 2002). Chemical coupling also exists in pancreatic β-cells. The existence of diffusible chemical coupling in pancreatic β-cells has been presented in that changes in the flow rate appear due to the period of oscillation of cells (Cunningham et al. 1996; Kennedy et al. 2002). Here, we investigate the effects of chemical coupling on the two chemically coupled β-cells. In particular, when the single cell exhibits continuous spiking, the chemically coupled system can exhibit burst synchronization, and the bursting types of which are similar to the electrical coupling case. However, the bifurcation mechanism is totally different. In addition, when the single cell exhibits “fold/homoclinic” type of bursting, the coupled system generates the inverse period-adding bursting sequence in a certain range of the coupling strength. Moreover, with strong chemical coupling strength, the two-cell model can generate complete burst synchronization with “fold/subHopf” type of bursting.

This paper is organized as follows. In “Dynamics of electrically coupled cells” and “Dynamics of chemically coupled cells”, we show how the coupling strength affects the synchronization firing behaviors of two coupled β-cells connected by electrical and chemical couplings, respectively. “Conclusion” deals with a discussion of the results. In the “Appendix”, we include the isolated single model and a description for the generation mechanism of continuous spiking and the “fold/homoclinic” bursting of the individual cell.

Dynamics of electrically coupled cells

The main goal of the paper is to analyze what will happen in synchronization behaviors of the coupled pancreatic β-cells when an individual cell exhibits either tonic spiking or “fold/homoclinic” bursting, which is shown in the “Appendix”. In order to well understand the effects of coupling strength on the dynamics of the coupled system, fast–slow dynamics analysis is extended to a pair of coupled identical cells. The results are presented in “Dynamics of electrically coupled cells” and “Dynamics of chemically coupled cells” according to the types of electrical and chemical coupling, respectively. Each section will be divided into two subsections depending on the dynamical behavior of the individual cell.

To incorporate the electrical coupling of two identical pancreatic β-cells via gap junctions, the variables v, n and s are indexed by the cell number and a coupling term is added to the first equation as follows:

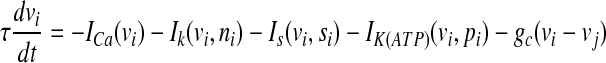1

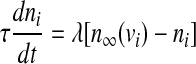2

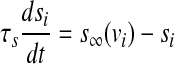3

where 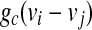represents the coupling term, and g_c is the coupling strength independent of v₁ and v₂. The values of fixed parameters used in this paper are listed in Table 1.

Table 1.

Parameter values

gCa = 3.6	vCa = 20 mV	vm = −20 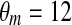mV	mV	τ = 20 ms
gK = 10	vK = −75 mV	vn = −17 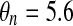mV	mV	λ = 0.8
gK(ATP) = 1.2	p = 0.5	vs = −22 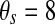mV	mV	τs = 20,000 ms
gs = 2 or 4

Two coupled spiking cells

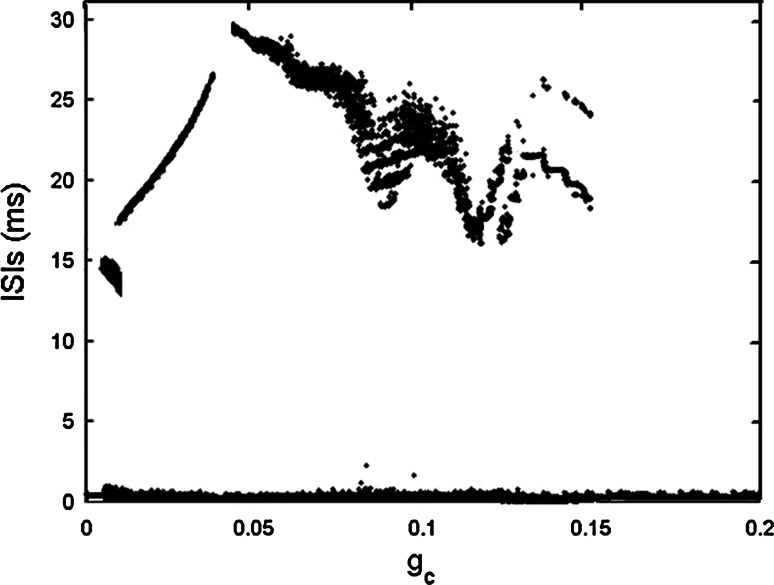
When g_s = 2, the single cell exhibits continuous spiking (see Fig. 14a in the “Appendix”). It is pointed out that weak electrical coupling can induce synchronous bursting oscillations in coupled cells that are incapable of bursting alone. The strong coupling can make the cells revert to spiking again (De Vries and Sherman 2000), which also can be seen clearly from Fig. 1, where the bifurcation diagram of ISIs versus g_c is illustrated.

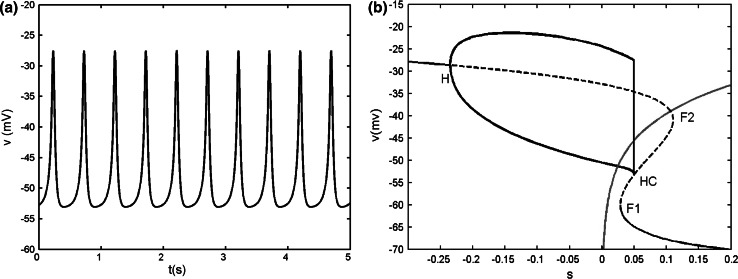
Fig. 14.

a Time series of the single model with g_s = 2. b Bifurcation diagram of the fast subsystem of [Eqs. (8), (9)]. H refers to the supHopf bifurcation, F1 and F2 refer to the fold bifurcations, HC refers to the homoclinic bifurcation. The C shaped curve represents the maximum and minimum values of periodic solutions originated from H. The phase plot of the whole system is also superposed on the (v, s) plane. The red line is the s-nullcline. (Color figure online)

Fig. 1.

Bifurcation diagram of ISIs versus the electrical coupling strength g_c in the two electrically coupled cells

Here we can find that between the two extreme cases, there exist other synchronous activities during the transition process. If only regular firing patterns are concerned, it can be seen that with g_c increasing, the continuous spiking transits to regular bursting firstly, and then experiences spiking in a certain range of g_c. Soon afterwards, the coupled system transits to bursting again, and if the coupling strength is strong enough, it finally returns to spiking again. Four typical cases of the electrical coupling strengths are chosen as representatives to understand the whole transition process.

The case of g_c = 0.01

Now the two-cell model generates synchronous bursting (see Fig. 2), and the spikes within burst are anti-phase (see Fig. 3a). The two-coupled cells achieving bursting synchronization have s₁ 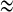 s₂ for the slow variable. In order to study the bifurcation structure for the fast subsystem of the coupled system, that is, Eqs. (1), (2), we can treat s₁ (or s₂) as the bifurcation parameter (Sherman and Rinzel 1991, 1992; Sherman 1994; Sherman et al. 1988; De Vries and Sherman 2000; Perc and Marhl 2004a, b). Owing to the fact of achieving synchronization in the coupled system, there must exist some function relation between v₁ and v₂. Hence, we can only choose v₁(or v₂) as the state variable of the synchronously coupled cells.

Fig. 2.

Two electrically coupled cells with g_s = 2, g_c = 0.01. a Time series of the variable v₁. b Time series of the variable v₂

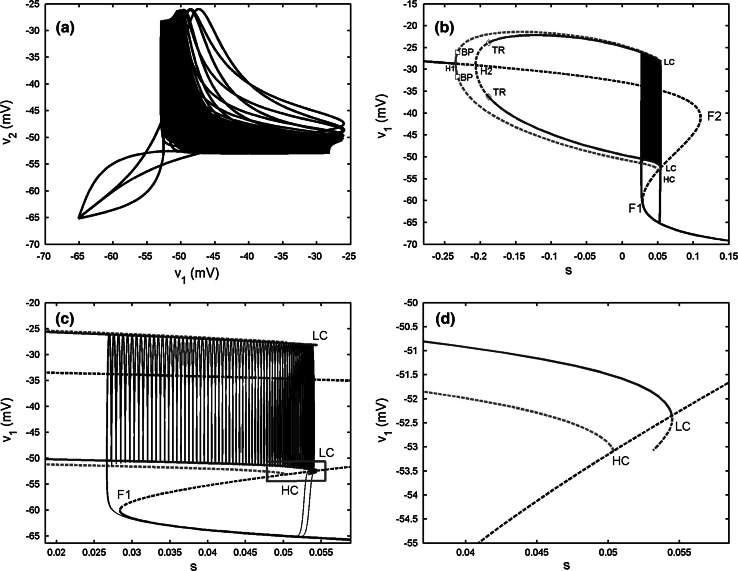
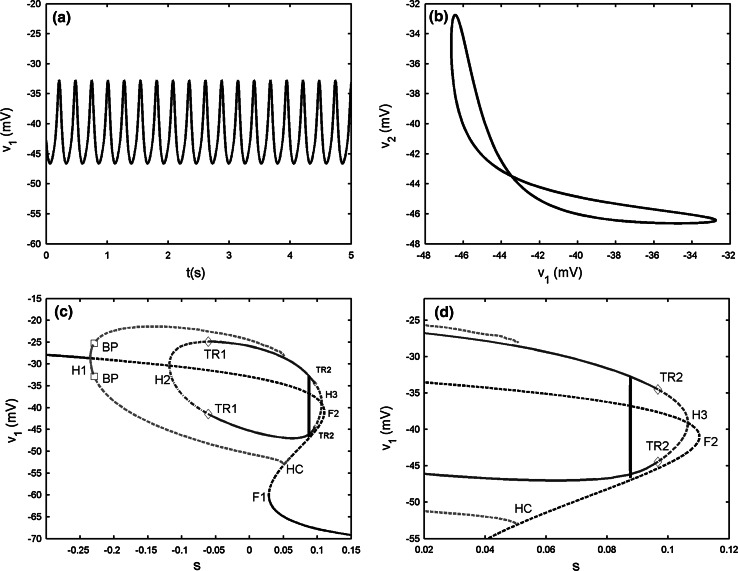
Fig. 3.

Two electrically coupled cells with g_s = 2, g_c = 0.01. a The projection of the coupled system on (v₁, v₂) plane. b Bifurcation diagram for the fast subsystem of two-cell model [Eqs. (1), (2)] with s = s₁ = s₂ taken as the bifurcation parameter. H1 and H2 refer to the supHopf bifurcations, BP refers to the pitchfork of periodic bifurcations labeled by open squares, TR refers the torus bifurcation labeled by diamonds, F1 and F2 refer to the fold bifurcations, HC refers to the homoclinic bifurcation, LC refers to the fold limit cycle bifurcation. The red and blue lines represent IP and AP branches, respectively. c The enlargement of the bistability region in b. The phase plot of the whole system is also included. d The magnification of the rectangular area in c. (Color figure online)

The bifurcation of the fast subsystem with respect to the slow variable s₁ is presented in Fig. 3b. For clarity, only the pertinent solution branches are included. It is seen that the steady state is the same as that in the single cell. But, on the upper branch there are two supHopf bifurcations instead of only one. The periodic branch originated from the left Hopf bifurcation point H1, corresponding to the synchronous IP bursting solutions (marked by red color in figures) of the coupled system, is detected at the same parameter value as that of the single cell. The IP branch is initially stable, but loses stability via the pitchfork of periodic bifurcation (BP). A branch of synchronized AP bursting solutions (marked by blue color in figures) emerges from the second supHopf bifurcation H2. It is unstable initially, but becomes stable via the torus bifurcation (TR) up to the fold limit cycle bifurcation (LC). Moreover, AP has smaller amplitude than IP, as a result, the termination of the AP branch lies to the right of that of the IP branch. Thus there exists bistability between the steady state on the lower branch of the Z shaped curve and the periodic AP solution on the AP branch, which gives rise to the bursting oscillation.

In order to better understand the bursting pattern, we start to explain the system behavior at the silent phase of bursting. It is seen that the trajectory moves left along the lower branch of the Z shaped curve until it meets the fold bifurcation F1. Then the system enters the active phase without the supHopf bifurcation H1 participated in the trajectory and there is no IP solution. Instead, the trajectory mainly lingers on the AP branch during the active phase, which indicates that the two cells are AP synchronized. The active phase of trajectory ends with the fold LC, where the stable periodic solution becomes unstable (see Fig. 3d), and then the trajectory returns to the bottom branch, restarting the cycle. According to the classification scheme of bursting mechanisms given in (Izhikevich 2000), this type of bursting belongs to the “fold/fold limit cycle” bursting. It marks the beginning of the complex transition process.

The case of g_c = 0.04

In this case, the synchronization of AP continuous spiking is shown in Fig. 4a, b. It is clearly observed that the amplitude of spiking becomes smaller than that of individual cell (see Fig. 14a in the “Appendix”). Fast–slow dynamics analysis is applied to explore the dynamical behavior of this phenomenon as shown in Fig. 4c. Compared with Fig. 3b, the Zshaped curve persists with the left supHopf bifurcation H1 being unchanged, and the IP branch also ends with the homoclinic bifurcation HC. However, now the upper branch of the Z shaped curve has three supHopf bifurcation points together, that is, H1 at s = −0.235, H2 at s = −0.1183 and H3 at s = 0.1056, respectively. Moreover, two periodic branches originating from the points H2 and H3 are connected together to form a closed loop, which is separated from the middle branch and represents the AP branch, as seen in Fig. 4c. In addition, the fast subsystem has extra TRs labeled as TR2 in the right side of AP branch. It is noted that the trajectory locates on the AP branch totally so that the coupled system exhibits AP continuous spiking. It is noticed that the amplitude is very small, only about 10 mv, which is not very practical in a real neural system. It is interesting to explore essence of this phenomenon in the present systems studied in the future.

Fig. 4.

Two electrically coupled cells with g_s = 2, g_c = 0.04. a Time series of the variable v₁. b The projection on (v₁, v₂) plane. c Fast–slow dynamics analysis of the fast subsystem. H1, H2 and H3 refer to the supHopf bifurcations, TR1 and TR2 refer to the torus bifurcations in the AP branch, F1 and F2 refer to the fold bifurcations, HC refers to the homoclinic bifurcation. d The magnification of the region near the right knee of the Z shaped curve in c

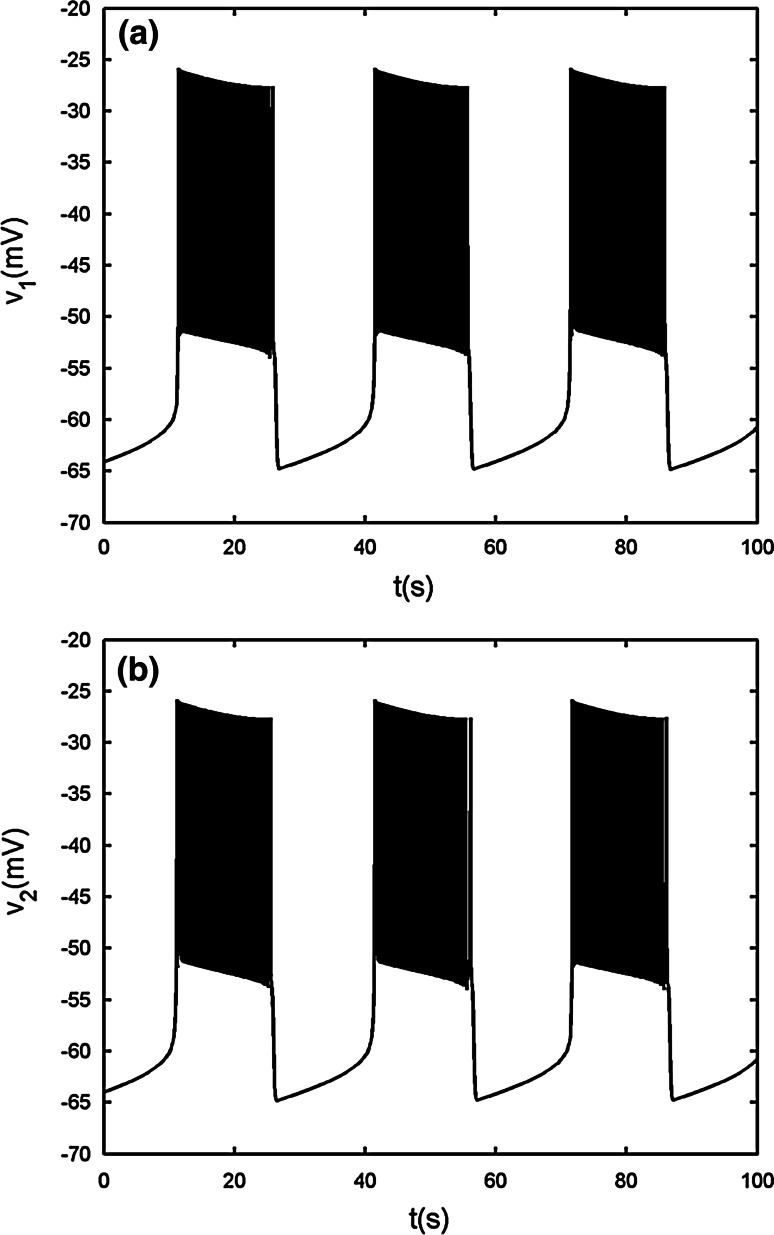
The case of g_c = 0.0435

As the first case with g_c = 0.01, the electrically coupled system exhibits bursting synchronization with the spikes being AP (see Fig. 5a, b). Compared with Fig. 2, it is seen that the burst period of the variable v₁ becomes much bigger with g_c increasing, and at the same time the spike amplitude is decreased. Fast–slow dynamics analysis is illustrated in Fig. 5c. The bifurcation structure of the fast subsystem is very similar to Fig. 4c. Hence, the details about the bifurcation diagram are omitted here. Like the first case, there exists bistability between the stable nodes on the lower branch and the stable AP branch up to the second TR TR2. Moreover, the AP branch, which starts from the second supHopf bifurcation H₂ at s = −0.1089 and terminates at the third supHopf bifurcation H₃ at s = 0.1054, is far from the IP branch originating from the left point H₁ at s = −0.235. Therefore, it can be seen clearly that during the active phase the two cells are synchronized IP at first, and then transit to AP synchronization very quickly. The disappearance of the silent phase and active phase depends on the fold bifurcation F1 and the TR TR2, respectively. Thus, this type of bursting pattern is classified as “fold/torus” type. Compared with previous results, Cases 2 and 3 are new phenomena.

Fig. 5.

Two electrically coupled cells with g_s = 2, g_c = 0.0435. a Time series of the variable v₁. b The projection on (v₁, v₂) plane. c Fast–slow dynamics analysis of the fast subsystem. The description of the lines and points is the same as that in Fig. 4c. d The magnification of the bistability region in c

The case of g_c = 0.15

The two-coupled cells achieve complete spiking synchronization (see Fig. 6a, b). Compared with the former cases, the upper branch of the Z shaped curve has only one supHopf bifurcation H1. Hence, the IP branch only exists while the AP branch disappears. Moreover, there are three pitchforks of BPs on the IP branch, labeled as BP1, BP2 and BP3, respectively. The stable IP branch becomes unstable via the first pitchfork of BP BP1 until the second pitchfork of BP BP2 is reached, and then it is stable and reverts to be unstable again via the third pitchfork of BP BP3. The bifurcations BP2 and BP3 are close together, the local enlargement of the neighborhood near the two points is given in Fig. 6d to distinguish them. It is seen that the spiking solution is totally located in the region between the two bifurcations BP2 and BP3. Thus, the two cells behave identically. It must be pointed out that even though the shape of the bifurcation diagram of the two-coupled cells is almost the same as that of the single cell, and the dynamical behavior of the variable v₁ (or v₂) is also nearly unchanged as mentioned above. However, the detailed bifurcation structure of the fast subsystem is actually different, especially for the existence of three pitchforks of BPs. This case is the last situation we listed in the paper when two continuous spiking cells are electrically coupled.

Fig. 6.

Two electrically coupled cells with g_s = 2, g_c = 0.15. a Time series of the variable v₁. b The projection on (v₁, v₂) plane. c Fast–slow dynamics analysis of the fast subsystem. BP1, BP2 and BP3 refer to the pitchfork of periodic bifurcations. d The magnification of the region between the bifurcations BP2 and BP3 in c. The subfigure in the right upper corner is the magnification of the region near the point HC

At last, we point out that if the coupling strength is larger than the critical value g_c = 0.2, the electrically coupled system still produce complete spiking synchronization and the bifurcation structure of the fast subsystem is identical to that of the single cell.

Two coupled bursters

In the above statement, it is shown that weak electrical coupling can make continuous spiking transit to bursting. Actually, the single system and electrically coupled system with proper coupling strength, both of which can be able to generate bursting on their own, while the generation mechanism for bursting may be different with details described below.

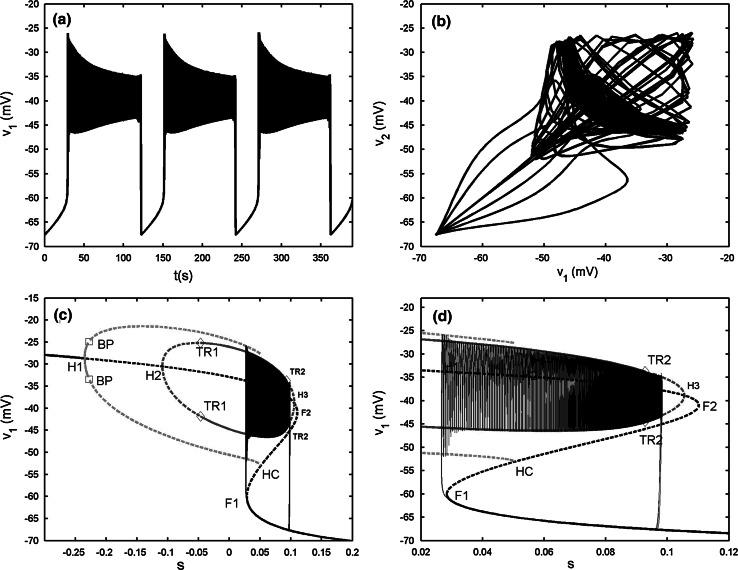
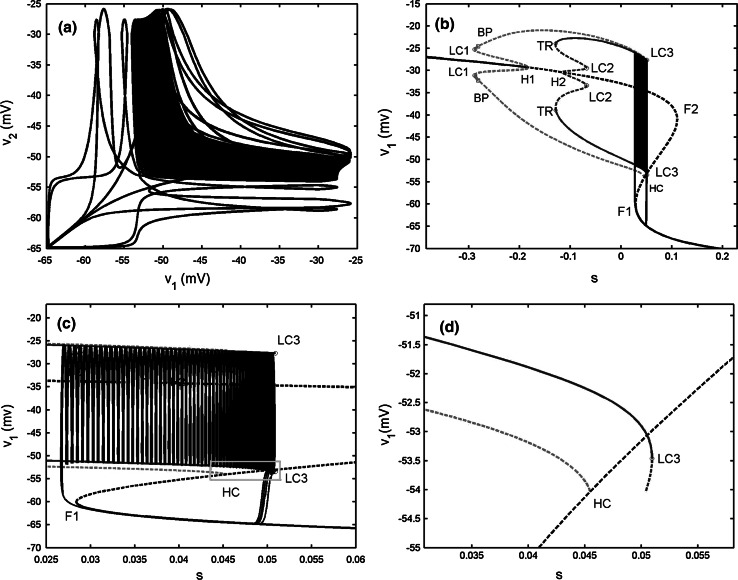
When g_s = 4, as illustrated in Fig. 15a in the “Appendix”, the isolated single cell exhibits “fold/homoclinic” type of bursting. The two-cell model with the electrical coupling strength g_c = 0.05 generates the synchronized bursting, but the spikes are anti-phased (see Fig. 7b). Compared with the original single model, it is observed that weak electrical coupling makes the burst period become longer, about 50 s. The bifurcation diagram is given in Fig. 7c. It is noticed that the bifurcation structure of the fast subsystem for the coupled system is almost the same as that of Fig. 5c. However, the bursting trajectory with the projection on (v₁, s₁) plane is quite different. During the active phase of bursting, the trajectory has a short stay in oscillating between the maximum and minimum of the IP branches firstly, thus it has some big spikes at the beginning of the active phase. Afterwards it starts to wrap towards the stable periodic branch emerged from the second Hopf bifurcation H2. The trajectory experiences the third Hopf bifurcation H3, and then spirals the stable focus originating from H₃ with amplitude decaying as shown in Fig. 7d. Finally, the upper resting state transits to the lower stable branch via the fold bifurcation F2, and initiates the silent phase of bursting. According to the classification of bursting, this type of bursting belongs to the “fold/Hopf” bifurcation via “fold/fold” hysteresis type.

Fig. 15.

a Time series of the single model with g_s = 4. b Bifurcation diagram of the fast subsystem. The description of the lines and points is the same as that in Fig. 14b

Fig. 7.

Two electrically coupled cells with g_s = 4, g_c = 0.05. a Time series of the variable v₁. b The projection on (v₁, v₂) plane. c Fast–slow dynamics analysis of the fast subsystem. The description of the lines and points is the same as that in Fig. 6c. d The magnification of the bistability region in c

Dynamics of chemically coupled cells

In this section, we consider two coupled pancreatic β-cells with chemical synaptic coupling,

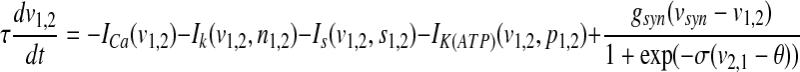4

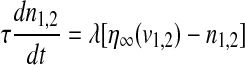5

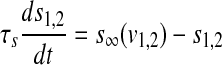6

where the subscript 1 (or 2) represents cell 1 (or 2), g_syn is the synaptic coupling strength, and v_syn is the synaptic reversal potential that determines the type of synapses, which is dependent on the type of synaptic transmitter released from a presynaptic cell and its receptors. The coupling becomes excitatory (or inhibitory) for v_syn > v_c (or v_syn < v_c), where v_c is the equilibrium potential for single cell. Here we choose v_syn = −15 mv, thus the coupling system is on the excitatory regime. 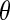is the synaptic threshold, above which the postsynaptic cell can be affected by the presynaptic one, and it is fixed at −30 mv; The 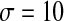represents a constant rate for the onset of excitation. The values of other parameters referred in the equations are the same as the single cell which can be found in Table 1.

Two coupled spiking cells

When g_s = 2, it is known that the single cell exhibits tonic spiking (see Fig. 14a in the “Appendix”). The purpose of this part is to show that two chemically coupled cells with moderate coupling strength can also generate bursting oscillations but with less cases of firing pattern, compared with the results for electrical coupling in “Two coupled spiking cells”.

The case of g_syn = 0.03

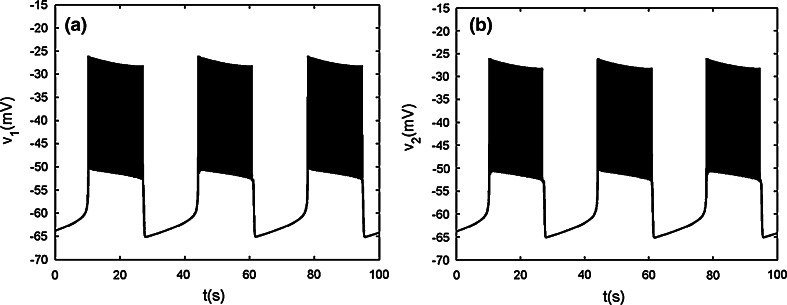
In such case, the dynamics of the two-coupled cells are bursting synchronization (see Fig. 8) with AP spiking inside bursts (see Fig. 9a). As the cases referred in the electrical coupling, the slow variables s₁ 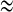 s₂ is also available. Thus fast–slow dynamics analysis can also be applied to the chemically coupled system. The fast subsystem is consisted of Eqs. (4), (5) with the slow variable s = s₁ = s₂ taken as the bifurcation parameter. It is noticed that the Z shaped curve of the fast subsystem is identical to that of the single cell. Especially, the twofold bifurcations F1 and F2 are detected at the same parameter values as the individual cell. Similar to Fig. 3b, the upper branch of the Z shaped curve also has two supHopf bifurcations H1 and H2. However, the left Hopf bifurcation H1 is taken at a different value at s = −0.1815, indicating that this is distinct from the electrical coupling cases. The IP branch originating from the H1 point becomes stable via the fold LC LC1 up to the pitchfork of BP. The AP branch emerging from the second Hopf bifurcation H2 changes stability via the TR, while it passes through the fold LC LC2 with the stability unchanged in this process. As s decreases, the silent phase of bursting corresponding to the lower stable branch of the Z shaped curve transits to the spiking state corresponding to the stable limit cycle around the upper branch of the Z shaped curve via the fold bifurcation F1. Then the trajectory starts to wrap towards the stable AP branch, thus within each burst the spikes are completely anti-phased. After a time interval, the AP branch becomes unstable via the fold LC LC3 as shown in Fig. 9d. Hence the trajectory jumps to the lower rest state to complete one loop. In a word, the generation mechanism of this type of bursting is similar to that of Fig. 3b. This bursting also belongs to the “fold/fold limit cycle” type; whereas the bifurcation structure of the fast subsystem is very different.

Fig. 8.

Two chemically coupled cells with g_s = 2, g_syn = 0.05. a Time series of the variable v₁. b Time series of the variable v₂

Fig. 9.

Two chemically coupled cells with g_s = 2, g_syn = 0.05. a The projection on (v₁, v₂) plane. b Bifurcation diagram for the fast subsystem of two-cell model [Eqs. (4), (5)] with s = s₁ = s₂ taken as the bifurcation parameter. LC1, LC2 and LC3 refer to the fold limit cycle bifurcations, respectively. The description of the lines and other points is the same as that in Fig. 3b. c The enlargement of the bistability region in b. d The magnification of the rectangular area in c

The case of g_syn = 0.13

With this coupling strength, the coupled system is still in bursting synchronization. Thus, it experiences different firing patterns (see Fig. 10a) due to the changes of the AP branch. In Fig. 10c, the unstable AP branch emerged from the second Hopf bifurcation H2 at s = −0.1081 becomes stable directly via the TR without the participation of the fold LC as that in Fig. 9b. Moreover, the AP branch is still unstable when the trajectory jumps to the upper branch via the fold bifurcation F1. Hence, the trajectory oscillates along the IP branch at the beginning, which causes the early stage of the active phase. As time is evolving, the trajectory is attracted by the stable limit cycle that results from the TR. Thereby, the AP synchronization starts until the fold LC LC2 is reached. Hence, compared with Fig. 8, this type of bursting can also be classified as “fold/fold limit cycle” type, while the firing pattern has some difference.

Fig. 10.

Two chemically coupled cells with g_s = 2, g_syn = 0.13. a Time series of the variable v₁. b The projection on (v₁, v₂) plane. c Fast–slow dynamics analysis of the chemically coupled system. The description of the lines and the points is the same as that in Fig. 9b. d The enlargement of the bistability region in c

Two coupled bursters

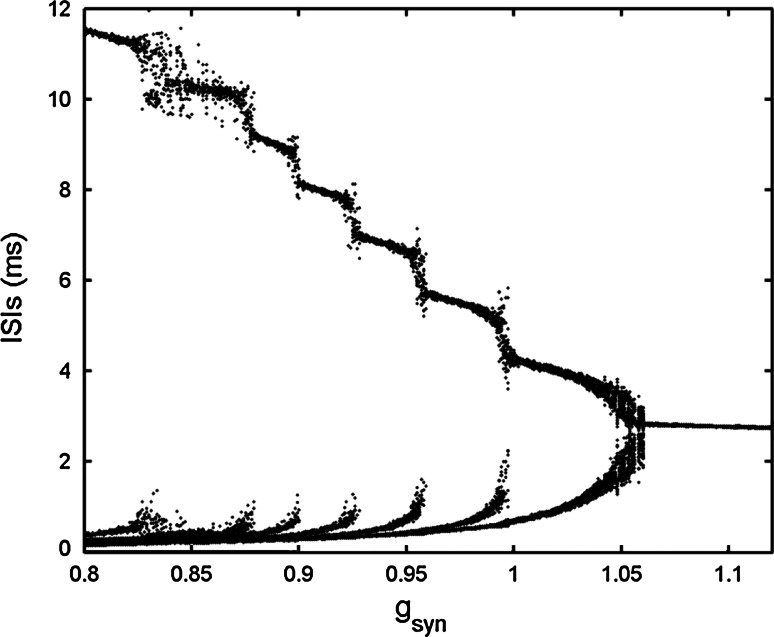
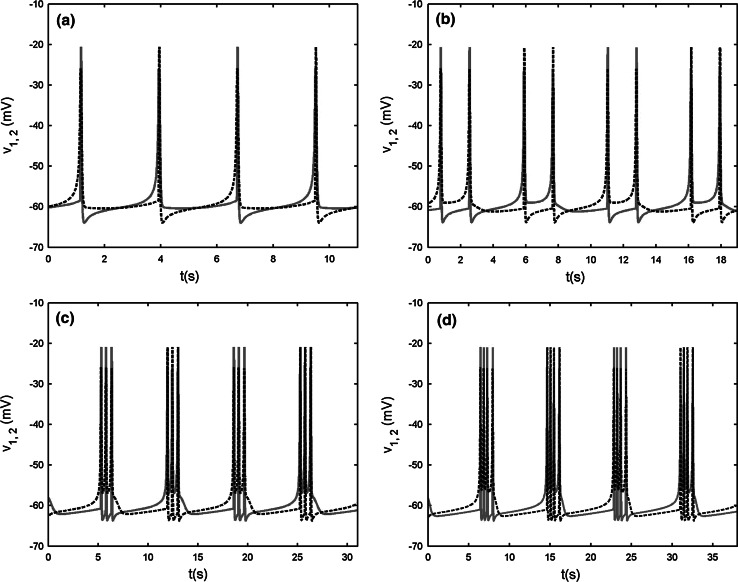
When g_s = 4, the single cell produces square-wave bursting (see Fig. 15a in the “Appendix”). The bifurcation structure of ISIs of two chemically coupled pancreatic β-cells is given in Fig. 11, in which the chemical coupling strength is varied to hunt different firing patterns. It can be seen that with increasing g_syn, an inverse period-adding firing sequence can be evidently observed. For the sake of clearness, Fig. 12 only shows the time courses of inverse-adding firing sequence from period −1 to 4, where g_syn is chosen as 1.1, 1.05, 0.97 and 0.95, respectively. It is noted that the two-coupled system can exhibit “compound bursting”, that is, the bursting rhythm consists of two kinds of sub-bursting with different spike amplitudes. For convenience, we refer to the sub-bursting with larger amplitude as sub-bursting 1, and the other as sub-bursting 2. It is seen that both the number of spikes and the width of sub-bursting 1 and 2 are almost equal. Moreover, two cells are in AP synchronization. In other words, when one cell happens to be in the active phase of sub-bursting 1, the other cell just experiences the active phase of sub-bursting 2, and then vice verse. From Fig. 12 it is seen that when g_syn = 1.1 both sub-bursting 1 and 2 have only one spike in a burst. When g_syn is decreased to 1.05, 0.97 and 0.95, respectively, the number of spikes in a burst is increased to 2, 3, 4 continuously. This clearly claims the existence of the inverse period-adding sequence.

Fig. 11.

Bifurcation diagram of ISIs versus the chemical coupling strength g_syn in the two chemically coupled cells

Fig. 12.

Time courses of the membrane potentials of the period-adding firing sequence from period −1 to 4 with g_syn = 1.1, 1.05, 0.97 and 0.95, respectively. The red solid lines and the black dashed lines represent the time courses for the variable v₁ and v₂, respectively. (Color figure online)

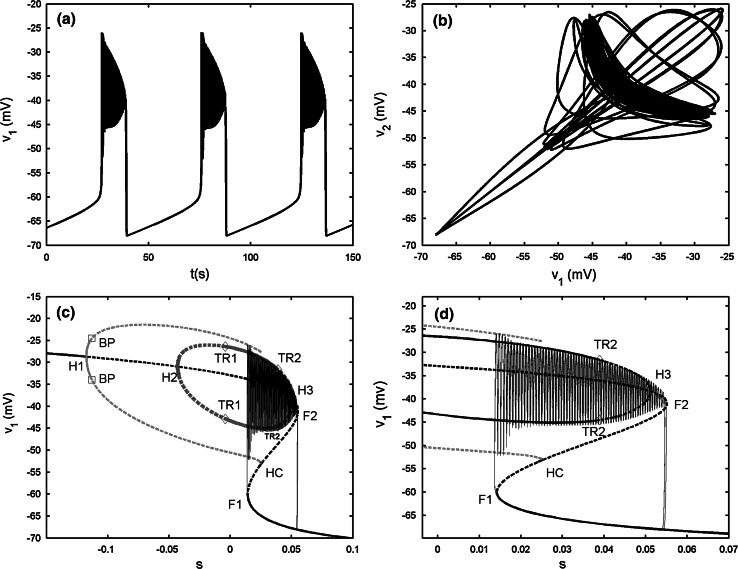
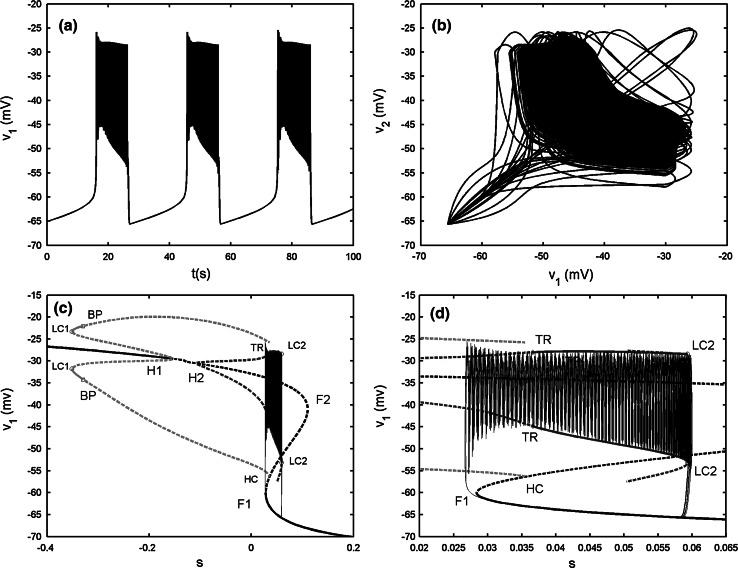
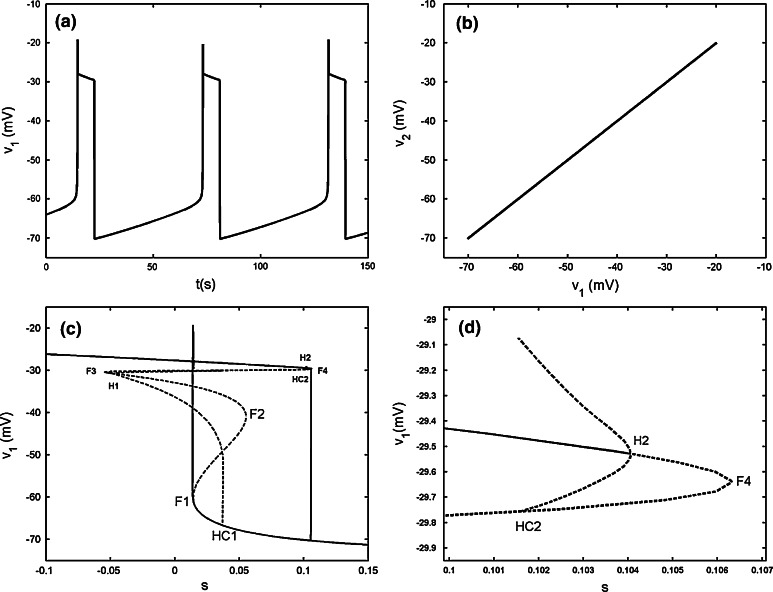
When the chemical coupling strength is increased to g_syn = 2.4, the two cells can realize complete bursting synchronization (see Fig. 13a, b). Hence s₁ = s₂ holds strictly Fast–slow dynamics analysis can be used to explain the generation mechanism of this type of bursting. The stationary branch is not Z shaped curve, but it has fourfold bifurcations instead. The curve of equilibria of the fast subsystem can be divided into three parts, that is, the upper, middle and lower parts, respectively. The middle part is connected by fold bifurcations F3 and F4, and it is composed of the saddles of the fast subsystem. The upper part is that above the middle part and is composed of foci of the fast subsystem. The remainder is named as the lower part, which is coincident with the Z shaped curve of the single cell before (see Fig. 13c). Therefore, the upper part, the middle part and the lower sub-branches of the lower part have the same meaning as before and are composed of foci, saddle and node, respectively. Here we notice that although the steady states both on the middle part and the middle sub-branch of the lower part are saddles, but their eigenvalues have different characters. The saddle on the middle part has three negative eigenvalues and one positive eigenvalue, while the saddle on the middle sub-branch of the lower part has two negative eigenvalues and two positive ones, respectively. Thus, both of which are double roots. The silent phase of bursting ends with the fold bifurcation F1, and then the trajectory is attracted by the stable foci in the upper part to start bursting. With s increasing, the stable focus in the upper part becomes unstable via the subHopf bifurcation H2 (see Fig. 13d), and these results in the transition to the silent phase of bursting. Thus the coupled system is capable of the “fold/subHopf” type of bursting. It is noticed that there exists a subHopf bifurcation H1 in the upper sub-branch of the lower part but it does not influence the shape of bursting pattern.

Fig. 13.

Two chemically coupled cells with g_s = 4, g_syn = 2.4. a Time series of the variable v₁. b The projection on (v₁, v₂) plane. c Fast–slow dynamics analysis of the chemically coupled system. The solid and dashed lines represent the stable and unstable states, respectively. F1–F4 are the fold bifurcations, respectively. H1 and H2 refer to the subHopf bifurcations. HC1 and HC2 refer to the homoclinic bifurcations. d The enlargement of the region near the point H2

Conclusion

In summary, the effects of electrical and chemical coupling on synchronization behaviors of coupled pancreatic β-cells are investigated by extending the fast–slow dynamics analysis from single cell to the coupled cells. For two electrically coupled cells, when an isolated cell exhibits continuous spiking individually, with the coupling strength increasing, there exists synchronization transition with at least four different synchronous states, including two kinds of bursting synchronization with totally different bifurcation structure of the fast subsystem, and another two synchronous spiking regimes with continuous AP and IP rhythms, respectively. For the model used in this paper, these results explain the role of the electrical coupling in more detail comparing to the previous results. For two chemically coupled cells, two spiking cells can transit to bursting under weak chemical coupling condition. Moreover, an interesting inverse period-adding bursting sequence in the coupled cells is found when the isolated cell exhibits square-wave bursting. In addition, the two coupled cells with proper chemical coupling strength can produce the “fold/subHopf” type of bursting. Our bifurcation analysis is based on the assumption that the slow variables of two cells s₁ 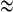 s₂. Thus s = s₁ = s₂ could be taken as the bifurcation parameter. In fact, this assumption is valid mostly except the inverse period-adding bursting sequence occurring in the chemically coupled cells. The latter case is worthy of the further research.

Appendix

See Figs. 14 and 15.

The model for a single pancreatic β-cell is described by the following equations:

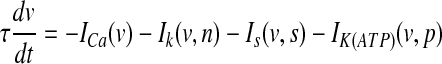7

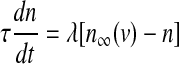8

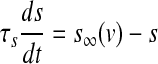9

Three variables in this system are: the membrane potential (v), the delayed rectifier activation (n), and a very slow variable s which has been postulated to be the intracellular Ca²⁺ (Sherman et al. 1988). The s equation is a Ca²⁺-balance equation.

Equation (7) is the current balance equation that determines the membrane potential v and is composed of four ionic currents, which are defined by

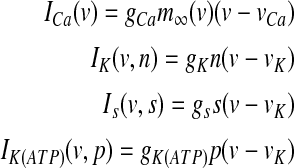with the constant conductance g_Ca, g_K, g_s and g_K(ATP) and the reversal potentials v_Ca, v_K for Ca²⁺ and K⁺ ions, respectively. I_Ca is assumed to respond instantaneously to a change in membrane potential with the steady state function 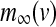, while the dynamics for I_K is governed by the gating variable n via Eq. (2), where τ is the activation time constant for the delayed rectifier K⁺ channel, and 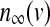is the equilibrium function for the activation variable n. In the expression of I_K(ATP), p is the fraction of the open K(ATP) channels. The dynamics for I_s is similar to that of I_K. But comparing with τ, the time constant τ_s becomes much bigger.

The equilibrium functions 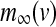, 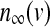and 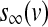have the general expression given by 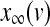as follows:

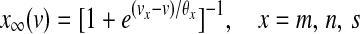Since τ_s >> τ, s responds on a much slower time scale than v and n. Thus Eqs. (7)–(9) construct a system with both slow and fast scales. The fast subsystem is composed of Eqs. (7) and (8), in which the slow variable s is considered as the bifurcation parameter. The trajectory of the whole system is then superimposed on the bifurcation diagram of the fast subsystem to explain the dynamical behavior of the model; this is the fast–slow dynamics analysis (Rinzel 1987).

All the parameters are listed in Table 1. Depending on the value of the parameter g_s, the system either undergoes a spiking solution or generates bursting oscillations. Both of which can be explained by using fast–slow dynamics analysis. The details of the two typical cases are explained as follows.

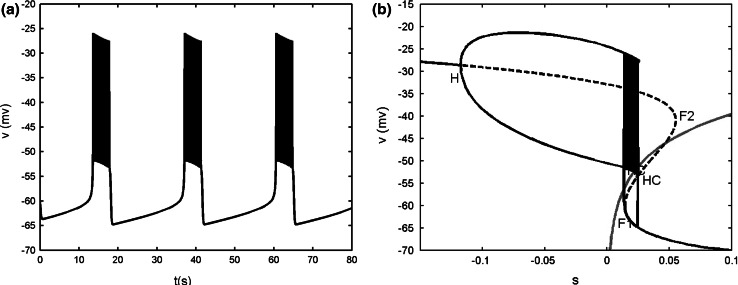
When g_s = 2, the single cell gives continuous spiking (see Fig. 14a). The bifurcation diagram of the fast subsystem with respect to the slow variable s is plotted in Fig. 14b. The equilibrium points form a Z shaped curve in (v, s) plane. The Z shaped curve is made up of the upper, middle and the lower branch. With the increase of s, the stable foci on the upper branch become unstable via a supHopf bifurcation H at s = −0.235. A branch of stable limit cycle oscillations emerges from the H point, and it terminates at homoclinic bifurcation HC. The middle and lower branches are composed of saddles and stable nodes, respectively. The s-nullcline is also superimposed onto the bifurcation diagram. The dynamics of the full system can be understood by using the Z shaped curve and the s-nullcline together. It is seen that the s-nullcline intersects the periodic branch and the intersection sufficiently deeps into the periodic branch, so that the system produces continuous spiking (Terman 1992).

When g_s = 4, the single cell exhibits a typical bursting oscillation (see Fig. 15a). Fast–slow dynamics analysis is illustrated in Fig. 15b. It is noticed that g_s is not involved in the slow subsystem. Hence, it has no effect on the s-nullcline. Compared with Fig. 14b, it is seen that the s-nullcline still intersects with the periodic branch, and at this time the intersection is near the end of the periodic branch. If the variable s varied very slowly, this would result in continuous spiking. However, s does not vary such slow actually in this case so that the bursting can be produced (Terman 1992). Moreover, for values of s between the left knee of the Z shaped curve and the homoclinic bifurcation, there is bistablility between the stable node state on the lower branch, which corresponds to the silent phase of bursting, and the stable limit cycle oscillation corresponding to the active phase of bursting. The silent phase disappears via the fold bifurcation F1, and the active phase ends with the homoclinic bifurcation HC. Since this type of bursting depends on passing through both fold and homoclinic bifurcations, it is called as “fold/homoclinic” bursting (Perc and Marhl 2003). It is also known as “square-wave” bursting, due to the fact that the active phase spikes rise from a plateau (Rinzel 1987).