Abstract
Detection and identification of nanoparticles is of growing interest in atmospheric monitoring, medicine and semiconductor manufacturing. While elastic light scattering with interferometric detection provides good sensitivity to single particles, active optical components prevent scalability realistic sizes for deployment in the field or clinic. Here we report on a simple phase-sensitive nanoparticle detection scheme with no active optical elements. Two measurements are taken simultaneously, allowing amplitude and phase to be decoupled. We demonstrate detection of 25 nm Au particles in liquid in Δt ~ 1 ms with a signal-to-noise ratio of 37. Such performance makes it possible to detect nanoscale contaminants or larger proteins in real time without the need of artificial labeling.
1. Introduction
Detection and identification of nanoparticles is of growing interest. Atmospheric nanoparticles affect climate change [1–3] and human health [4, 5], and detecting nanoparticles in solution is of interest in biodefense [6], and in medicine as cancer-fighting agents or drug delivery units [7–9]. In all of these applications, good sensitivity to low particle concentrations is essential. Information can be lost through averaging over large ensembles of particles, so the ability to interrogate single particles is advantageous. Elastic light scattering is a label-free detection method that provides information about particle size and material.
A small particle in solution can be modeled as a dipole scatterer, so that an incident field E0 and scattered field Es are related by the particle’s polarizabilty α [10], i.e.
| (1) |
where k = 2π/λ is the wavenumber expressed in terms of the wavelength λ. The polarizability contains size and material information, since
| (2) |
Here, R is the radius of the particle and ε0 is the permittivity of free space. The dielectric constants of the particle and medium (solution) are denoted by εp and εm respectively, and are functions of the frequency of light, ω. If intensity is measured instead of electric field, the relationships in equations 1 and 2 give rise to a (kR)6 dependence, preventing the detection of small particles. This problem can be overcome with inferferometric detection. Interfering Es with a reference Er results in a detected intensity
| (3) |
where φ represents the relative phase between the fields. The term 2|Es||Er|cos (φ) depends on (kR)3 instead of (kR)6, and contains an amplification by the reference field. Unfortunately, if the phase φ is unknown, it is impossible to extract |Es|. Several methods exist to remove the phase dependence, including heterodyne interferometry [11] and phase-shifting interferometry [12–14]. In the former, the interference of a signal with a frequency-shifted reference beam produces a beat frequency Δω at which the intensity signal is demodulated, effectively decoupling amplitude and phase. In the latter, known phase offsets are introduced, and linearly independent intensity measurements are taken either sequentially or simultaneously, from which |Es| can be determined [15, 16]. In this paper we present a variation of phase-shifting interferometry for particle detection. It is simpler than heterodyne interferometry, and requires only two detectors that perform simultaneous measurements, unlike traditional phase shifting interferometry. This allows for detection bandwidths greater than 1kHz, which is necessary for many particle detection applications. We test the system with immobilized particles, and then with particles in solution. One of the main advantages of the dual-phase system lies in its scalability to portable dimensions, which is essential for biodefense applications in particular. To that end, we demonstrate the use of a numerical aperture increasing lens (NAIL) for illumination and detection [17]. NAILs provide high NA while taking up very little space, allowing the possibility of scalability.
2. Dual-Phase Interferometry
Standard (homodyne) interferometry renders a signal that is proportional to the last term in equation 3, which is a result of both phase variations (φ) and amplitude variations (|Es|). The inability to decouple these two variations limits particle detection applications. In order to measure amplitude and phase of the scattered field independently, we have developed a dual-phase interferometer, illustrated in Fig. 1. By controlling the polarization state of the signal and reference beams, two simultaneous orthogonal measurements are performed to decouple amplitude and phase. In essence, we add a known phase offset δi to the reference beam, such that equation 3 becomes
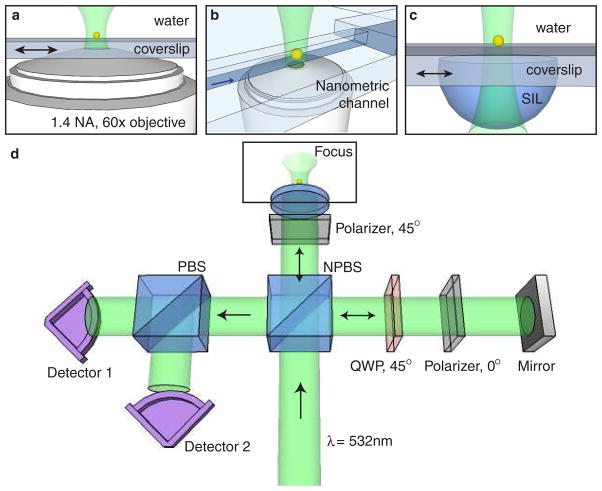
Fig. 1.
The dual-phase detection apparatus. (a) Configuration for immobilized particles. A 1.4 NA oil-immersion objective is used to focus light on a particle, and the particle is scanned through the focus. (b) Nanoscale channel configuration. Particles in solution are loaded into reservoirs at the ends of a 15 μm channel of cross-section 500 nm by 400 nm, and a microscope objective focuses light on the channel. The black arrow indicates the direction of electro-osmotic flow. (c) Numerical aperture increasing lens (NAIL) configuration. A NAIL is water-bonded to a coverslip, and is used to focus light on an immobilized particle, which is scanned through the focus. (d) Schematic of dual-phase interferometer. A linear polarizer sets the polarization state of the signal beam to 45°, and a combination of a polarizer and quarter-wave plate (QWP) set the reference polarization to be circular. After reference and signal are combined with a non-polarizing beamsplitter (NPBS), a polarizing beam-splitter (PBS) sends the two orthogonal polarization states to detectors. The difference in relative phase between signal and reference at the two detectors is π/2.
| (4) |
and we are left with three unknown quantities: |Es|, |Er| and φ. Much of the literature on phase-shifting interferometry discusses ways to make three or more intensity measurements of the form of equation 4 in order to uniquely determine |Es|. In contrast, we first measure the non-interferometric reference “background” |Er|2, and then make two measurements with different δi simultaneously in the presence of a particle, allowing for high detection bandwidths and only two detectors. While almost any phase offsets will work, our strategy is to measure two intensities I1 and I2 with phase offsets δ1 = 0 and δ2 = −π/2 such that
| (5) |
| (6) |
We do this by combining a linearly polarized signal with a circularly polarized reference beam, and separating orthogonal polarizations with a polarizing beamsplitter. The relative phase between signal and reference differs by π/2 between the two detectors, each of which record intensities at 50k samples per second. This choice of δ1 and δ2 leads to a somewhat simpler algebra. In many cases, the signal strength is small (i.e. |Es| ≪ |Er|), and the non-interferometric offset in I1 and I2 is simply the measured intensity in the absence of a particle. If this assumption is violated, we can use a measurement of |Er|2 along with equations 5 and 6 to uniquely determine the background |Er| and the value of interest |Es|. We define the quantities
| (7) |
| (8) |
We can then easily extract the amplitude or phase of the interferometric part of the signal by taking the modulus or argument of IX and IY, i.e.
| (9) |
| (10) |
The reference intensity |Er|2 can be measured at any time in the absence of a particle, and is subtracted in real time. Each particle event thus appears as a ~ 1 ms peak in the intensity time series, and we take as our signal the modulus of the two intensity measurements, as in equation 9. Either the peak maximum or peak area can be used as a measure of the particle’s polarizability.
If |Es|2 is too large to be neglected, the modulus and argument of IX and IY will not give the correct amplitude and phase. Instead, equations 5 and 6 must be combined to eliminate φ, so that the signal intensity is given by
| (11) |
Measurement and subtraction of the background as in equation 7 and 8 can be accomplished in several ways. In the simplest case, the non-interferometric signal is constant and equal to the reference intensity, so its value can be subtracted from every intensity measurement on each detector. In some cases there is a small spurious reflection from the glass-water interface on the nanometric channels for coverslip, which gives rise to a time-varying background. The recorded intensity on one detector becomes
| (12) |
where the angles φ, φsb and φrb represent the relative phases among the three beams. The sum |Er|2 + |Eb|2 + 2|Er||Eb|cos (φrb) can be viewed as a offset in the I1 vs. I2 plane that is constant or slowly varying compared to the particle’s transit time. The combined background can then be determined at each particle event as an extrapolation of the values around the event. Possible methods include averaging a small neighborhood around the event, or fitting the background to a slowly varying curve and subtracting the fit. For all data included in this letter, a third-order spline was used to fit the background in the neighborhood of each event. The term |Es||Eb|cos (φsb) represents the interference of two weak fields and can generally be neglected, so that equation 12 reduces to the simpler case of equation 3, and the above analysis is still valid. A stronger spurious reflection would lead to a phase-dependent error in the measurement of |Es|. Since the particles traverse the focus in ~ 1 ms, a high-pass filter with cutoff < 1 kHz may be applied to each detector signal after background subtraction to further reduce noise if necessary.
3. Experiment and Results
3.A. Immobilized Particles
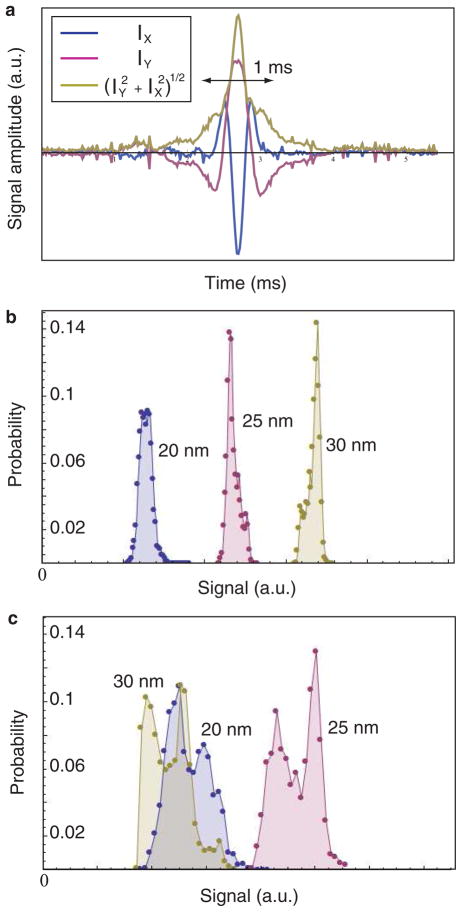
To demonstrate the sensitivity and precision of the dual-phase detection scheme, we first examine a particle immobilized on a glass surface and immersed in water, as illustrated in Fig. 1(a). Fig. 2(a) shows a time series of the recorded intensity on each detector for a single such detection event. Accumulating 3000 such events and recording the area under each peak results in the histograms of Fig. 2(b), which shows data for Au particles of 20 nm, 25 nm and 30 nm radii. In Fig. 2(c) we instead construct a histogram of values obtained from a single detector (i.e. I1 − |Er|2) for the same data set. This is analogous to homodyne detection, in which phase variations in the interferometer are unaccounted for. A comparison of these histograms demonstrates the intractability of phase-coupled interferometric detection. All of the peaks are wider, with the peak corresponding to the largest particle overlapping with the other peaks due to a particularly large variation of phase during the experiment. We conclude from these data that the dual-phase detection scheme successfully decouples amplitude and phase.
Fig. 2.
Immobilized particle detection using dual-phase interferometry. (a) Time series of a detection event for a 30 nm radius immobilized Au particle in water. The event time is determined by the particle speed and the size of the laser focus, and the time resolution is determined by the data acquisition speed (50k samples/sec). (b), (c) Histograms of signals for 20 nm (blue), 25 nm (pink) and 30 nm (yellow) radius Au nanoparticles immobilized on glass and immersed in water. In (a), the dual-phase scheme is used, and the signal is the area under the particle event peak. In (c), the intensity from a single detector is taken after background subtraction for the same data set, and the histogram is constructed from the maxima of the peaks, imitating homodyne interferometry. The inherent phase dependence leads to wider peaks, and happens to give a smaller apparent signal from the largest particle in this case. Scott’s choice was used to determine bin widths for all histograms.
3.B. Particles in Solution
In order to detect single particles in solution, we use nanoscale channels fabricated by photolithography. The fabrication of nanoscale channels is discussed in detail elsewhere [11,18]. A solution containing 25 nm Au particles is driven through the channel using electro-osmotic flow, so that particles pass through a laser focus in the center of the channel. Two new uncertainties are introduced in this configuration. First, the particle’s path is now only approximately known; it may move through the focus by different trajectories, so the particle intensity signature will not be identical for each transit. Second, the solution contains particles of a manufacturer-specified range of sizes, in contrast to the above experiment performed on a single particle. We again create a histogram using 3000 detection events, illustrated in Fig. 3(b). This histogram is wider than in the immobilized particle case due to the distribution of particles and trajectory uncertainties.
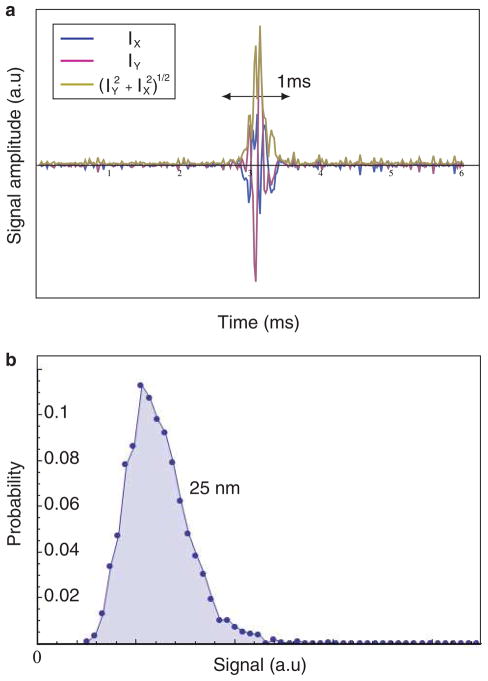
Fig. 3.
Particle detection in nanoscale channels. (a) Background-subtracted time series of a particle detection event for a 25 nm radius Au particle in the nanoscale channel configuration from Fig. 1(b). (b) Histogram of signals from 3000 such events. Scott’s choice was used to determine bin widths for the histogram.
3.C. Numerical Aperture Increasing Lens
The advantages of the dual-phase system over other phase-sensitive nanoparticle detection methods include its simplicity and scalability. The apparatus includes no active optical elements, and no electronics beyond the detectors and data acquisition hardware. In comparison to heterodyne detection, a dual-phase system may be designed with shorter path lengths and better control over reference intensity, since it does not require frequency shifting by AOMs. For applications that require a small footprint, nearly every element of the system is scalable, with the exception of the oil-immersion microscope objective. To demonstrate a feasible alternative, we use a numerical aperture increasing lens (NAIL) bonded to a microscope coverslip in combination with an air objective for illumination of an immobilized particle, as illustrated in Fig. 1(c).
The radius r and thickness D of the NAIL is chosen to fulfil the aplanatic condition D = r(1 + 1/n) − X when bonded to a coverslip of thickness X. The NAIL is made of fused silica so that the refrective index n = 1.45 matches that of the coverslip and nanofluidic channel material and back-reflections are eliminated. The numerical aperture of the objective/NAIL system is given by NA = NAobj * n2, where NAobj is the NA of the air objective by itself. In our case, NAobj = 0.4, so NA ≈ 0.8, giving a resolution improvement of approximately 2. To save space, such performance could be acheived by using a well designed aspheric lens instead of an air objective. If necessary, the NA could be improved to the theoretical maximum of NA ≈ 2 by using a higher NA air objective.
Figure 4(a) shows a typical time trace of a particle detetion event. Since the numerical aperture of the objective/NAIL system is lower than the oil-immersion objective, the SNR is ~ 12, somewhat lower than that obtained with the oil-immersion objective. Nevertheless, we demonstrate sensitivity to 50 nm Au nanoparticles, and the ability of the system to decouple amplitude and phase is not affected. We note that an air objective is not necessary for use in combination with the NAIL, and that a well designed aspheric lens will give comparable results. A histogram of 3000 particle detection events is shown in Fig. 4(b). The lower NA of the NAIL in comparison to an oil-immersion microscope objective contributes to the wider histogram as compared to the immobilized case.
Fig. 4.
Particle detection using NAIL. (a) Background-subtracted time series of a particle detection event for a 50 nm radius Au particle using the NAIL configuration from Fig. 1(c). (b) Histogram of signals from 3000 such events. Scott’s choice was used to determine bin widths for the histogram.
4. Conclusion
While the dual-phase system was developed for particle detection, it could be used in any interferometry application in which one field point is sampled at a time. For example, the sample could be raster scanned through a laser focus as in confocal microscopy or near-field microscopy. In this case, amplitude and phase of the scattered signal would be used to create images of the optical properties of the sample. We believe that the dual-phase system is promising for any single-field-point sensing application in which sensitivity to small signals in crucial, and in which scalability is necessary.
Acknowledgments
This work was supported by DARPA (grant W31P4Q-08-1-0005), and NIH (grant AI085543). The authors thank Anirban Mitra and John Lesoine for the fabrication of nanometric channels.
References
- 1.Menon S, Hansen J, Nazarenko L, Luo Y. Climate effects of black carbon aerosols in china and india. Science. 2002;297:2250–2253. doi: 10.1126/science.1075159. [DOI] [PubMed] [Google Scholar]
- 2.Kaufman YJ, Koren I. Smoke and pollution aerosol effect on cloud cover. Science. 2006;313:655–658. doi: 10.1126/science.1126232. [DOI] [PubMed] [Google Scholar]
- 3.Ramanathan V, Carmichael G. Global and regional climate changes due to black carbon. Nature Geosc. 2008;1:221–227. [Google Scholar]
- 4.Holgate ST, Samet JM, Koren HS, Maynard RL, editors. Air Pollution and Health. Academic Press; San Diego: 1999. [Google Scholar]
- 5.Somers CM, McCarry BE, Malek F, Quinn JS. Reduction of particulate air pollution lowers the risk of heritable mutations in mice. Science. 2004;304:1008–1010. doi: 10.1126/science.1095815. [DOI] [PubMed] [Google Scholar]
- 6.Hillman MR. Overview: cause and prevention in biowarfare and bioterrorism. Vaccine. 2002;20:3055–3067. doi: 10.1016/s0264-410x(02)00300-6. [DOI] [PubMed] [Google Scholar]
- 7.Yezhelyev MV, Gao X, Xing Y, Al-Hajj A, Nie S, O’Regan RM. Emerging use of nanoparticles in diagnosis and treatment of breast cancer. Lancet Oncol. 2006;7:657–667. doi: 10.1016/S1470-2045(06)70793-8. [DOI] [PubMed] [Google Scholar]
- 8.Loo C, Lin A, Hirsch L, Lee MH, Barton J, Halas N, West J, Drezek R. Nanoshell-enabled photonics-based imaging and therapy of cancer. Technol Cancer Res Treat. 2004;3:33–40. doi: 10.1177/153303460400300104. [DOI] [PubMed] [Google Scholar]
- 9.Vollmer F, Arnold S. Whispering-gallery-mode biosensing: label-free detection down to single molecules. Nature Methods. 2008;5:591–596. doi: 10.1038/nmeth.1221. [DOI] [PubMed] [Google Scholar]
- 10.Novotny L, Hecht B. Principles of Nano-Optics. Cambridge University Press; Cambridge: 2006. p. 404. [Google Scholar]
- 11.Mitra A, Deutsch B, Ignatovich F, Dykes C, Novotny L. Nano-optofluidic detection of single viruses and nanoparticles. ACS Nano. 2010;4:1305–1312. doi: 10.1021/nn901889v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bruning JH, Herriott DR, Gallagher DP, Gallagher DP, White AD, Brangaccio DJ. Digital wavefront measuring interferometer for testing optical surfaces and lenses. Applied Optics. 1974;13:2693–2703. doi: 10.1364/AO.13.002693. [DOI] [PubMed] [Google Scholar]
- 13.Bruning J. Phase measurement interferometry. In: Malacara D, editor. Optical Shop Testing. Wiley; NY: 1987. p. 414. [Google Scholar]
- 14.Surrel Y. Phase stepping: a new self-calibrating algorithm. Applied Optics. 1993;32:3598–3600. doi: 10.1364/AO.32.003598. [DOI] [PubMed] [Google Scholar]
- 15.Creath K. Phase measurement interferometry techniques. In: Wolf E, editor. Progress in Optics. Vol. 26. North Holland; Amsterdam: 1988. pp. 349–393. [Google Scholar]
- 16.Millerd J, Brock N, Hayes J, Kimbrough B, Novak M, North-Morris M, Wyand JC. Modern approaches in phase measuring technology. Proc SPIE. 2004;5856:14. [Google Scholar]
- 17.Ippolito SB, Goldberg BB, Ünlü MS. Theoretical analysis of numerical aperture increasing lens microscopy. J Appl Phys. 2005;97:053105. [Google Scholar]
- 18.Ignatovich FV, Novotny L. Experimental study of nanoparticle detection by optical gradient forces. Rev Sci Instr. 2003;74:5231–5235. [Google Scholar]