A Rate Code for Sound Azimuth in Monkey Auditory Cortex: Implications for Human Neuroimaging Studies

Abstract

Is sound location represented in the auditory cortex of humans and monkeys? Human neuroimaging experiments have had only mixed success at demonstrating sound location sensitivity in primary auditory cortex. This is in apparent conflict with studies in monkeys and other animals, in which single-unit recording studies have found stronger evidence for spatial sensitivity. Does this apparent discrepancy reflect a difference between humans and animals, or does it reflect differences in the sensitivity of the methods used for assessing the representation of sound location? The sensitivity of imaging methods such as functional magnetic resonance imaging depends on the following two key aspects of the underlying neuronal population: (1) what kind of spatial sensitivity individual neurons exhibit and (2) whether neurons with similar response preferences are clustered within the brain.

To address this question, we conducted a single-unit recording study in monkeys. We investigated the nature of spatial sensitivity in individual auditory cortical neurons to determine whether they have receptive fields (place code) or monotonic (rate code) sensitivity to sound azimuth. Second, we tested how strongly the population of neurons favors contralateral locations. We report here that the majority of neurons show predominantly monotonic azimuthal sensitivity, forming a rate code for sound azimuth, but that at the population level the degree of contralaterality is modest. This suggests that the weakness of the evidence for spatial sensitivity in human neuroimaging studies of auditory cortex may be attributable to limited lateralization at the population level, despite what may be considerable spatial sensitivity in individual neurons.

Introduction

For humans, the role of primary auditory cortex in processing information about sound location is uncertain. Although lesions that include auditory cortex can impair sound localization in both animals and humans (Sanchez-Longo and Forster, 1958; Jenkins and Masterton, 1982; Thompson and Cortez, 1983; Hefner and Heffner, 1986; Zatorre and Penhune, 2001; Smith et al., 2004; King et al., 2007), human neuroimaging studies have had mixed success at identifying differential patterns of activation as a function of sound location. For monaural sounds, activation is stronger in the contralateral than in the ipsilateral primary auditory cortex (Woldorff et al., 1999; Petkov et al., 2004; Krumbholz et al., 2005a), but no contralateral preference has been found for more realistic binaural stimuli (Woldorff et al., 1999; Brunetti et al., 2005; Krumbholz et al., 2005b; Zimmer and Macaluso, 2005; Zimmer et al., 2006). Similar mixed results have occurred for other metrics of spatial sensitivity: one study found that, when stimuli were presented from a larger range of space, the area of activation in primary auditory cortex was larger (Brunetti et al., 2005), and one study using a similar strategy did not (Zatorre et al., 2002).

These mixed results could be accounted for in one of two ways. First, if individual auditory cortical neurons generally use a rate code for encoding sound location [i.e., they respond monotonically as a function of (e.g.) azimuth] and if contralaterally preferring and ipsilaterally preferring neurons are intermingled, then little spatial sensitivity would be evident in the aggregate activity of a large population of neurons. We term this the “scrambled rate code” hypothesis. Second, if auditory cortical neurons have spatial receptive fields, but if neurons with receptive fields in the left and right hemifields are intermingled with each other, this too will diminish the effect of sound location on the aggregate activity. This we call the “scrambled place code” hypothesis. Either of these possibilities might produce the observed pattern of human neuroimaging results.

Single-unit recording studies in animals have shown that auditory cortical neurons are sensitive to sound location (for review, see King et al., 2007 and Discussion), but they have not clearly differentiated between these two possible coding formats using statistical methods. Accordingly, we analyzed the spatial sensitivity in primary auditory cortex of monkeys to determine (1) what type of spatial sensitivity do individual neurons show [i.e., do neurons have receptive fields consistent with a place code for sound location, or instead do they show monotonic sensitivity to sound azimuth, as is the case earlier in the auditory pathway (Groh et al., 2003)] and (2) how strong is the population bias in favor of contralateral locations (i.e., how scrambled is the code)?

Our results suggest that the spatial sensitivity of auditory cortical neurons most closely resembles a scrambled rate code. At the population level, the contralateral bias was weak, providing an explanation for why human neuroimaging studies do not always detect spatial signals. Together with our previous study in the primate inferior colliculus (IC) (Groh et al., 2003), the emerging picture is that the monkey auditory pathway uses a rate code, not a place code, for representing sound location. This is fundamentally different from the coding format in the visual and somatosensory pathways, in which spatial receptive fields and hence place codes predominate. The difference in coding format poses an unresolved problem for the integration of information across sensory modalities.

Materials and Methods

General procedures.

Three adult rhesus monkeys (two females and one male) served as subjects for these experiments. The Institutional Animal Care and Use Committee at Dartmouth College approved all procedures. Animals underwent an initial surgery to implant a head post for restraining the head and a scleral eye coil for monitoring eye position at a 500 Hz sample rate (Robinson, 1972; Judge et al., 1980). All surgical procedures were performed under isoflurane inhalant anesthesia, using aseptic techniques. The animals were then trained using positive reinforcement to maintain fixation on a visual stimulus directly in front of them while a sound was presented from a loudspeaker in a random location. The experiments were conducted in a single-walled sound attenuation chamber (IAC, Bronx, NY) lined with sound absorbent foam (3 inch Sonex One) to reduce echoes. Experiments were conducted in darkness.

Recording methods.

A cylinder was implanted using stereotaxic techniques to allow access to the left auditory cortex in one female monkey (G) and the right auditory cortex in the other female (monkey C) and male (monkey E) using a straight vertical approach (Pfingst and O'Connor, 1980). We used standard recording techniques: electrical potentials were amplified and action potentials were detected using a dual window discriminator (Bak Electronics, Germantown, MD). The time of occurrence of action potentials was stored for off-line analysis.

Experimental paradigms and stimuli.

Each trial began with a 500 ms period of fixation on a central light-emitting diode, followed by a 500 ms sound presented from loudspeakers on the horizontal meridian, in the frontal hemisphere. Speakers were distributed on the horizontal meridian from −90° ipsilateral location to the recording site to +90° contralateral side, with 0° being center in front of the monkey. Speakers were spaced 5° apart in the central 40° (i.e., between −20 and 20°, inclusive) and at locations ±90, ±70, ±50, and ±30°. Auditory stimuli consisted of broadband noise [500 Hz to 18 kHz, mean across speakers, 50.2 SD 0.38 dB sound pressure level (SPL)]. In some sessions, trials were randomly interleaved with trials for a different study in which fixation was followed by a visual or combined visual-auditory stimulus; data from these trials are not included here. The average number of trials per speaker location per neuron was 18.3 (SD 3.2). Animals received liquid reinforcement for maintaining fixation throughout the trial. The liquid was delivered via a solenoid valve that made a minimally audible clicking sound.

At the end of the testing for spatial sensitivity, frequency response functions were assessed in 86 neurons (of monkey E). Tones (500 ms; 400 Hz to 12 kHz in quarter octave increments; 50 dB SPL) were presented from the most contralateral loudspeaker. No task performance was required for these trials.

Data analysis.

Unless otherwise specified, our metric of neural activity consisted of the number of action potentials that occurred during the stimulus presentation (500 ms). Neurons were considered auditory if their discharge rate in response to the stimulus differed significantly from their responses during the preceding 500 ms of spontaneous activity (two-tailed paired t test, p < 0.05). For this test, all sound locations were pooled together because this proved to be the most inclusive criterion, with 119 of 167 recorded neurons meeting the criterion. When the t test was conducted on the responses for each sound location separately, 108 neurons met criterion for significance (with Bonferroni's corrected p values); 103 neurons met the criterion for significance using both methods.

We also conducted an analysis of whether the spatial sensitivity during the initial transient response (0–100 ms after stimulus onset) versus the later sustained period (100–500 ms after stimulus onset) were similar (Table 1).

Table 1.

Results of curve fitting for different time periods of the response

	Time period
	Full (0–500 ms)					Transient (0–100 ms)			Sustained (100–500 ms)
	n	% of total (n = 119)	% of fits (n = 91)	And ANOVA?	% of total (n = 119)	n	% of total (n = 119)	% of fits (n = 59)	n	% of total (n = 119)	% of fits (n = 90)
A. Total sigmoid	79	66.4	86.8	75	63.0	49	41.2	83.1	80	67.2	88.9
B. Total Gaussian	88	73.9	96.7	76	63.9	56	47.1	94.9	88	73.9	97.8
C. Sigmoid and Gaussian	76	63.9	83.5	72	60.5	46	38.7	78.0	78	65.5	86.7
D. Sigmoid and/or Gaussian	91	76.5	100.0	79	66.4	59	49.6	100.0	90	75.6	100.0
E. Total ANOVA	80	67.2

Sigmoidal and Gaussian curves were fit to the responses as a function of sound location using a nonlinear least-squares regression method. The column labeled ″% of fits″ gives the fraction of the total population of cells fit by at least one function (p < 0.05) (i.e., line A, B, or C divided by line D). The results of the ANOVA for the full time period are provided for comparison.

Our statistical analyses consisted chiefly of ANOVA and sigmoidal and Gaussian curve fitting. The sigmoidal and Gaussian curve fitting was accomplished using Matlab (MathWorks, Natick, MA) and the “lsqnonlin” function, which involves an iterative search to minimize the least-squares error of the function.

Latencies.

Latency was calculated in two ways. First, for a conservative estimate of the overall response latency for each neuron, we used a method based on the peristimulus time histogram (PSTH) of the responses to all the sound locations. We calculated the time from sound onset until the first bin of a PSTH exceeded the mean bin height of the baseline by 3 SDs. PSTHs were constructed with 3 ms bins (Groh et al., 2003). The mean response latency of the neurons in our sample was 50.2 ms, which is on the long end of the range of latencies in previous reports involving tonal stimuli near the characteristic frequency (Recanzone et al., 1993, 1999, 2000; Fu et al., 2004; Kajikawa et al., 2005).

We used a different measure of response latency for an analysis of the relationship between latency and sound location (see Fig. 8). Here, we needed a measure of latency that could be calculated on the neural responses for each sound location for each neuron. The PSTH measure becomes noisy when the number of trials used to construct the PSTH is reduced. Accordingly, for this analysis we used first spike latency. First-spike latency can be a noisier measure of response latency than the PSTH-based method described above, and will be biased toward underestimating the true response latency in neurons with spontaneous activity, but offers the advantage of providing a measure of response latency on each individual trial. The underestimation bias is not a problem when the issue involves a comparison between the response latencies for different stimulus conditions (in this case, different sound locations). The mean response latency based on the first-spike latency was 27.8 ms for the neurons in the sample (i.e., shorter than the answer obtained with the PSTH-based method, but more in keeping with the latencies reported in other studies).

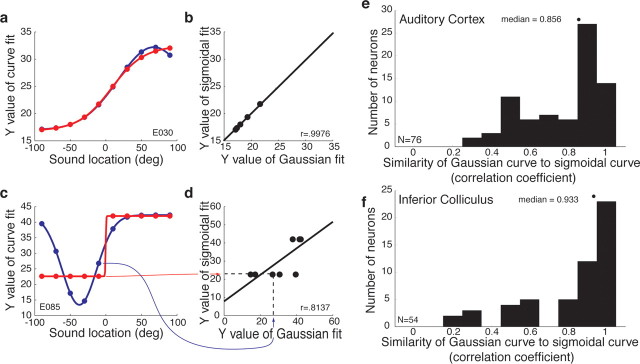
Figure 8.

The similarity of the sigmoidal and Gaussian curves across the neural population in auditory cortex and the IC. a, c, Gaussian and sigmoidal curve fits for two example neurons (same neurons as shown in Figs. 1b,h, 4b,h). We evaluated these curves at 1° intervals across the range of tested locations (data points shown are for 20° intervals, for simplicity of presentation). b, d, We then regressed the sigmoidal and Gaussian curve values against each other and calculated the correlation coefficient. The red and blue arrows track one pair of data points in c to the corresponding data point in d. e, f, Distribution of correlation coefficients in auditory cortex (e) and the IC (f). The medians of these distributions were 0.856 for auditory cortex and 0.933 for the IC.

Location of recordings.

The locations of our recording penetrations were identified using magnetic resonance imaging (MRI) at the Dartmouth College Brain Imaging Center (GE 1.5 T scanner, three-dimensional T1-weighted gradient echo pulse sequence, 5 inch receive-only surface coil; GE Medical Systems, Milwaukee, WI). One or more tungsten electrodes were inserted just above the dura for the scan; these electrodes were readily visible in the images and served as reference points for the reconstruction of the recording locations. In accordance with the boundaries of the core auditory cortex identified in the literature (for details, see Werner-Reiss et al., 2003), we limited our recording locations to those ≥5 mm rostral from the caudal end of the supratemporal plane, ≥2 mm from the medial end of the supratemporal plane in the region caudal to the insula/circular sulcus, and ≥2 mm from the lateral edge of the supratemporal plane. In the region adjacent to the insula/circular sulcus, recording locations were restricted to those within the supratemporal plane rather than dipping down onto the lower/outer bank of the circular sulcus. All recording sites were well caudal of the RT region of core, and consisted of sites mainly in putative A1 but potentially in R as well.

Results

Spatial sensitivity and contralateral bias

We recorded the responses of 119 auditory neurons (paired t test of sound-evoked activity compared with baseline firing, p < 0.05) in the core auditory cortex of three rhesus monkeys. Of these, 80 (67.2%) were spatially sensitive according to an ANOVA (p < 0.05) (Table 1). Eight example neurons are presented in Figure 1. The top panel for each neuron displays the activity in the form of a raster plot with the raster lines sorted by sound location, with contralateral locations at the top of the raster. The bottom panel shows PSTHs with sound location indicated by color. All of these neurons were determined to be spatially sensitive according to the ANOVA, and were chosen for display based on the strength of their spatial sensitivity according to the curve-fitting analysis that is described in later sections of Results.

Figure 1.

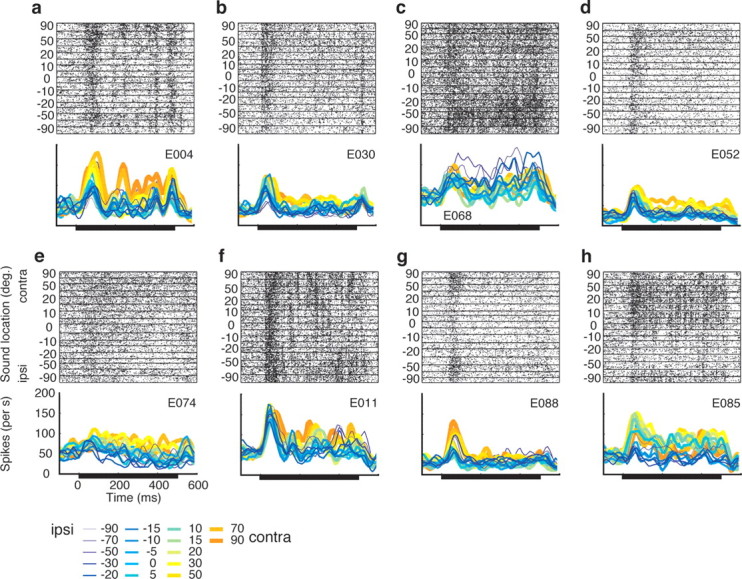
Responses of auditory cortical neurons as a function of sound location. This figure shows the eight neurons that had the highest correlation coefficients in the curve fitting analysis described in Results (see Representational format). Each panel shows a raster plot with the rows organized according to the location of the sound (y-axis). Beneath the raster plots are the corresponding PSTHs [10 ms bins, smoothed with a 5-point triangular filter $\left(\frac{1}{9},\frac{2}{9},\frac{1}{3},\frac{2}{9},\frac{1}{9}\right)$], with the responses for different sound locations indicated in different colors. ipsi, Ipsilateral; contra, contralateral.

There is considerable variability in the specific spatial profile of these individual neurons. Most responded to nearly every tested sound location. Several were biased in favor of contralateral locations (a, b, d, e), some in favor of ipsilateral locations (c), and others had more complicated response patterns (g, h). It is not clear whether a technique that assessed the pooled activity of these neurons [such as functional MRI (fMRI) or positron emission tomography (PET)] would detect differences in activation as a function of sound location. To address this question quantitatively, we conducted a series of population analyses designed to paint a portrait of the aggregate activity of the units in our sample.

Figure 2a shows the “point image” of activity of the neurons in our sample as a function of sound location. The data shown illustrate the average level of activity across the entire neural population as a function of sound location. The activity of each individual neuron for each sound location was expressed as a fraction of its maximum response. This plot confirms that there is a bias in the overall level of activity in favor of contralateral locations, but this bias is surprisingly small, corresponding to an ∼8% difference in net activity across the population for ipsilateral versus contralateral locations. The overall pattern of results is very similar when the neural population responses are averaged in raw form without normalization, and also involves an ∼8% difference in net activity (Fig. 2b).

Figure 2.

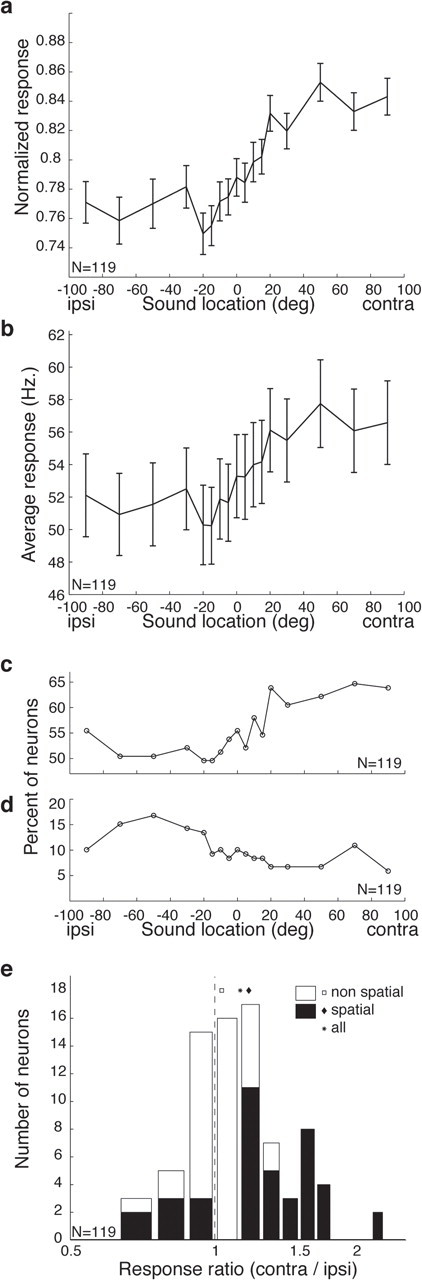
The neural population is biased in favor of contralateral locations. a, Averaged responses of the population of all recorded neurons (n = 119) as a function of sound location. The responses of each neuron were normalized as a fraction of its largest evoked response before averaging. b, Average responses of the neural population without normalization. c, Percentage of neurons showing statistically significant excitatory responses as a function of sound location (two-tailed t test, p < 0.05). d, Percentage of neurons showing statistically significant inhibitory responses as a function of sound location (two-tailed t test, p < 0.05). e, Histogram of ratio of contralateral to ipsilateral responses across the population. The distribution is significantly biased in favor contralateral locations, both for the subset of neurons that showed spatial sensitivity (ANOVA, p < 0.05) as well as for the population as a whole (two-tailed t test on log₁₀[mean(contralateral response)/mean(ipsilateral response)], p < 0.001). ipsi, Ipsilateral; contra, contralateral. Error bars indicate SEM.

Figure 2c shows a similar pattern using a different metric: the percentage of neurons showing a statistically significant excitatory response as a function of sound location. The proportion of neurons showing a statistically significant response ranges from ∼50 to ∼65%, with the larger proportion occurring for more contralateral locations. When inhibitory responses are considered (Fig. 2d), the pattern is reversed appropriately; the proportion of neurons inhibited by sound is higher for ipsilateral (∼15%) than for contralateral (∼8%) sounds.

Figure 2e shows the difference between the response evoked at the farthest contralateral and the farthest ipsilateral sound location, expressed as a proportion of whichever of those responses was greater. The distribution of difference scores is significantly biased in favor of the contralateral side (p < 0.0001), but the effect size is modest: the mean ratio of the responses to contralateral versus ipsilateral sounds was 1.13:1 for all neurons, or 1.18:1 when just sound location-sensitive neurons (as defined by the ANOVA) were included.

In short, these different measures of population activity all suggest that the difference in activation to be expected from presenting lateralized sounds should be on the order of 8–15%.

Representational format: background, statistical considerations, and simulations

The above analyses assess the overall pattern of activation to be predicted from pooling together all the neurons in core auditory cortex on one side of the brain and demonstrate that, in general, neurons slightly prefer contralateral to ipsilateral sounds. But what is the format of this representation? The answer to this question is of profound importance for the coding of auditory space generally, as well as having implications for neuroimaging studies.

Two classes of possibilities exist: sound location might be rate coded, with individual neurons responding with monotonically increasing functions for more contralateral sound locations, or sound location might be place coded, with individual neurons having circumscribed receptive fields tiling the contralateral hemifield. In the visual and somatosensory systems, place codes are the rule because the physical configuration of the peripheral sensory structures create this kind of representation: the optics of the eye ensure that photoreceptors have circumscribed receptive fields, and somatosensory receptors in the skin respond only to mechanical stimuli applied to that location on the skin. In the auditory system, sound location must be computed based on interaural timing and level difference cues as well as spectral cues. What format is used for the resulting representation is a matter for empirical investigations, rather than something that can be deduced from first principles (Porter and Groh, 2006).

Both types of coding format could produce a bias for the contralateral sphere such as that revealed in the preceding analyses, but might produce rather different patterns of activation in an imaging study. In an orderly topographic place code, the physical site of activation will vary with the location of the sound, but the overall level of activity will not vary. In a rate code, the level of activity will vary with sound location, but the site of activity should be stable. Comparison of the total activity in left auditory cortex versus right auditory cortex could yield differences in activation for eccentric sounds for either type of code, and a more fine-grained investigation would be needed to differentiate between them. At present, the spatial resolution of imaging studies probably do not permit distinguishing between these possibilities, but because advances in technology may make this possible in the future, it is worth considering the question at the single-unit level.

Although distinguishing a place code from a rate code may seem straightforward, in practice there is no single statistical criterion for distinguishing between these two types of representation. One logical approach is to compare Gaussian and sigmoidal curve fitting, as we have done previously for both sound location and eye position in the IC (Groh et al., 2003; Porter et al., 2006). The rationale and somewhat counterintuitive predicted results for place and rate codes are illustrated in Figure 3. The place code (Fig. 3a) is simulated with a series of Gaussian functions varying in the location of the peak (as well as height and tuning width). The rate code (Fig. 3b) is simulated with a series of sigmoidal functions, also varying in inflection point, slope, and height.

Figure 3.

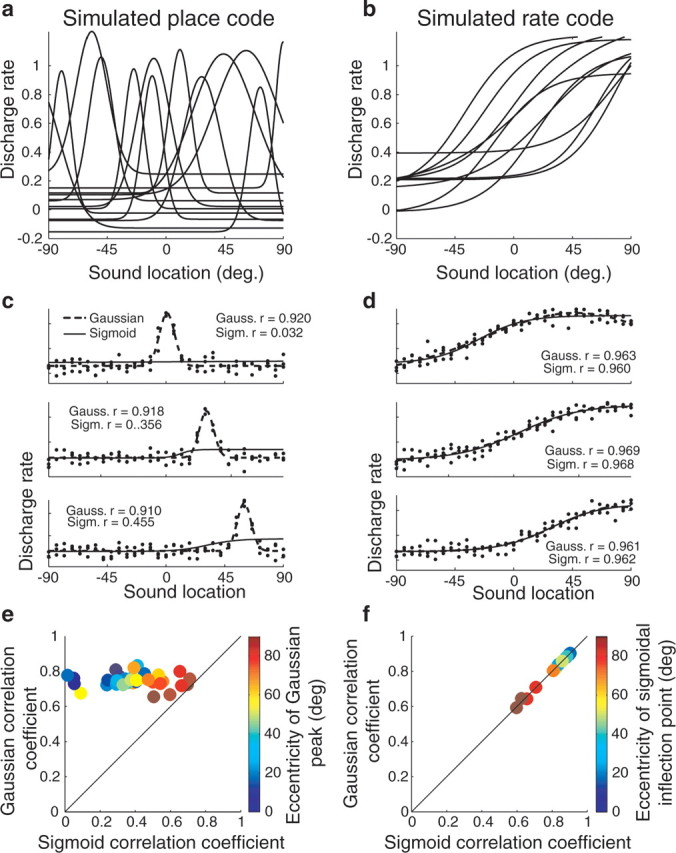
Simulations of place and rate codes and how Gaussian and sigmoidal curve fits would appear for each representational format. a, A series of Gaussian curves, varying in peak location, tuning width, and peak and floor heights. A population of Gaussian-tuned neurons in which the peaks span the range of possible spatial locations would indicate the existence of a place code for space. b, A series of sigmoidal curves. Monotonic tuning, such as a sigmoid, would indicate the existence of a rate code. Although the curves shown here vary in their inflection points and other parameters, this is not a formal requirement of a rate code. c, Simulation of three Gaussian-tuned neurons. The simulated responses of each neuron were constructed by first choosing the parameters of a Gaussian (referred to as the “known,” or underlying, Gaussian function). The underlying Gaussian for the neuron in the top panel had a peak at 0°. Then, responses on individual trials for specific sound locations were simulated by calculating the value of the underlying Gaussian at that sound location and adding normally distributed random noise, to simulate the naturally occurring variability in neural responses. Then, both Gaussian and sigmoidal curve fits were calculated for these simulated raw data. The resulting curves, together with their correlation coefficients, are plotted on each panel. d, Simulation of three sigmoidal neurons. Here, sigmoidal curves were used as the underlying functions that, when combined with noise, generated the raw simulated responses on individual trials. Again, both Gaussian and sigmoidal functions were then fit to the resulting simulated responses. e, Population plot of the correlation coefficients of Gaussian and sigmoidal curves for a population of individual neurons whose underlying tuning functions were Gaussian. Gaussian curves were always successful at fitting such response patterns; sigmoidal functions became increasingly successful as the eccentricity (i.e., the absolute value of the azimuthal location) of the Gaussian peak increased. f, Population plot of the correlation coefficients of Gaussian and sigmoidal curves for a population of individual neurons whose underlying tuning functions were sigmoidal. Both Gaussian and sigmoidal curves were successful at fitting such response patterns. The correlation coefficients for both curve fits decreased as the eccentricity of the inflection point of the underlying sigmoidal function increased. Gauss., Gaussian; Sigm., sigmoid.

Although it might seem that a Gaussian function would always provide the best fit to a neuron whose tuning function is truly Gaussian in shape, and that a sigmoid would always provide the best fit to a neuron whose tuning function is truly sigmoidal in shape, this is only partially correct. In fact, for a neuron whose “true” response pattern is Gaussian, a Gaussian function will provide a better fit than a sigmoid, but both may be statistically significant. And for a neuron whose response pattern is really sigmoidal, both Gaussian and sigmoidal functions can be equally successful at fitting the responses.

The predictions for Gaussian-tuned neurons are illustrated in Figure 3c. Responses on individual trials were simulated by adding noise (drawn from a normal distribution) to the responses predicted from a known Gaussian function. Then, we found the Gaussian and sigmoidal functions that produced the best fits to the simulated responses. The resulting curves and their associated correlation coefficients for three simulated neurons are illustrated in each panel. When the neuron is tuned to a central location (top panel), only the Gaussian provides a statistically significant fit. However, as soon as the peak of the tuning of the neuron is offset from the center (middle and bottom panels), then the sigmoidal function also becomes successful at providing a statistically significant fit, although the correlation coefficient values are much lower.

Figure 3e illustrates this pattern across a population of simulated neurons, showing a plot of the correlation coefficients for the Gaussian functions versus those of the sigmoidal functions, with the color of the data point corresponding to the eccentricity of the peak of the Gaussian. All the data points lie above the line of unity slope, indicating that the Gaussians provide a better fit than the sigmoids, but as the eccentricity increases the data points move closer to the unity slope line reflecting the increased success of sigmoidal functions at capturing the response patterns.

The predicted pattern for neurons with underlying sigmoidal functions is illustrated in Figure 3, d and f. The responses on individual trials for three neurons with sigmoidal response patterns with inflection points of varying eccentricity were simulated in the same manner as for the Gaussian neurons. Again, both sigmoids and Gaussians were fit to the simulated data. For all three neurons, both sigmoidal and Gaussian curve fits were successful. In fact, the sigmoidal and Gaussian curve fits were equally successful (the correlation coefficient values were essentially identical) and the resulting curves were indistinguishable from each other in shape, so much so that the sigmoidal curves (thin lines) are covered up by the Gaussian curves (thick lines) for two of the three neurons shown.

The results for this population of simulated neurons are shown in Figure 3f, again with a plot of the Gaussian versus the sigmoidal correlation coefficient. The results lie along the line of unity slope, indicating that sigmoids and Gaussians were equally good at providing a fit to the data. As the eccentricity of the inflection points increased, both types of fits account for less of the variance, but the effect was similar for both Gaussians and sigmoids. We conducted additional simulations manipulating the parameters of the sigmoidal function used to generate the simulated responses, and found that only when the slope of the underlying sigmoidal function was steep (approaching a step function) did the sigmoidal functions provide a better fit than Gaussians (results not shown).

In short, when the underlying response pattern is nonmonotonic, a nonmonotonic function such as a Gaussian will usually provide a better fit than a monotonic function. However, the converse is not true: when the underlying response pattern is monotonic, both monotonic and nonmonotonic functions may be able to provide an equally good fit to the responses. The reason for this is that a nonmonotonic function such as a Gaussian has a monotonic half, so that it has the potential to provide a successful fit to monotonic data. Accordingly, in evaluating the representational format of real neural data, we applied both Gaussian and sigmoidal curve fitting, and we were interested in several aspects of the results: (1) Do both curves provide statistically significant fits? (2) Does the Gaussian account for more of the variance than the sigmoid, or are both about equally good? (3) When Gaussians fit the data, do they do so because they are nonmonotonic or is only a monotonic half of the Gaussian actually used? (4) How similar is the shape of the sigmoidal and Gaussian curves, when they both provide statistically significant fits? Together, the answers to these questions can provide a quantitative assessment of whether a representation more closely resembles a place code or a rate code.

Representational format: neurons

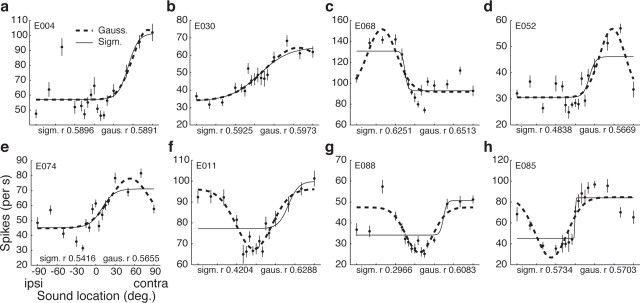
Ninety-one of the 119 neurons (76.5%) were fit by at least one type of curve. The results of this curve fitting analysis are shown for eight individual neurons in Figure 4 (the same neurons as those shown in Fig. 1; these neurons had the eight highest correlation coefficients in the curve fitting analysis). A variety of patterns are evident. Some neurons were about equally well fit by both the Gaussian and the sigmoidal curve, and the two curves were quite similar to each other (a, b). For other neurons, the Gaussian and the sigmoid captured about an equal amount of the variance but the two curves that accomplished this were dissimilar in shape (h). Some neurons were better fit by the Gaussian than the sigmoid (c–g). Some Gaussian functions had peaks (a–e), and others had troughs (f–h).

Figure 4.

Sigmoid and Gaussian curve fits of response versus sound location for the eight neurons displayed in Figure 1. The individual data points shown are the mean responses for each sound location; error bars are SEs. These means are shown for illustration purposes; the curve fits were calculated based on the raw data. All of the illustrated fits are significant p < 0.05. ipsi, Ipsilateral; contra, contralateral; sigm., sigmoid; gaus., Gaussian.

Across the population, 76 of 119 neurons (63.9%) were fit by both the sigmoidal and the Gaussian functions, and an additional 15 were fit by one or the other (Fig. 5a) (total number of fits, 91 of 119 or 76.5%). That these curves were generally appropriate ways to capture the spatial sensitivity of auditory cortical neurons is apparent from the good correspondence between the curve fits and the ANOVA as a measure of spatial sensitivity (Table 1): 79 of the 80 neurons dubbed spatially sensitive by ANOVA were also fit by at least one function.

Figure 5.

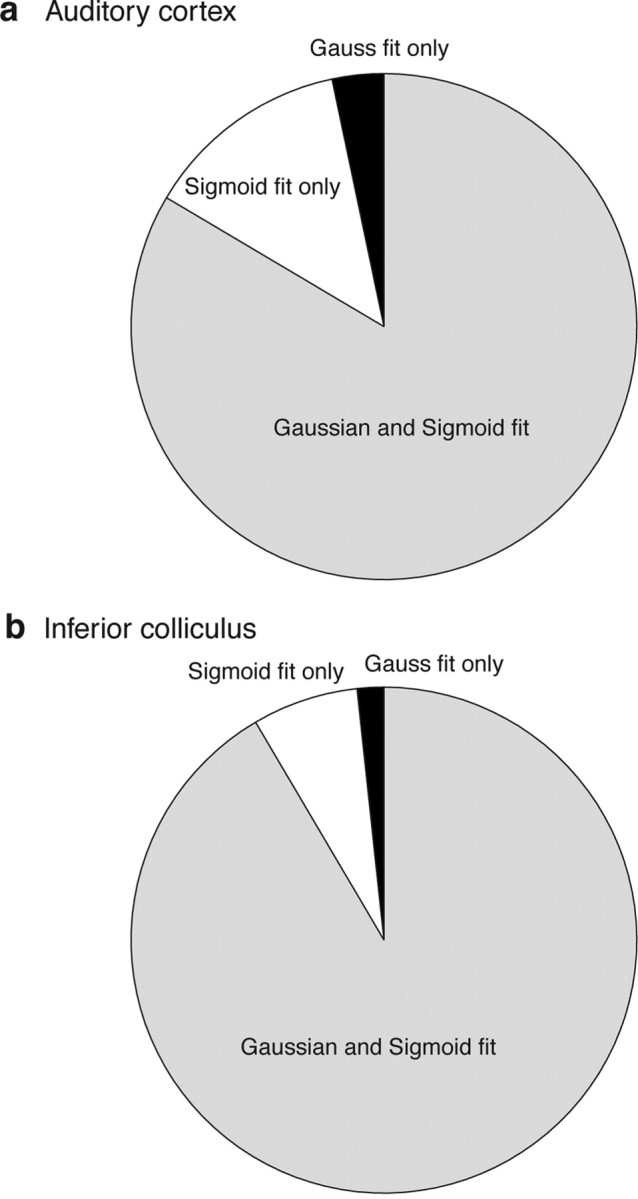
a, Diagram summarizing the breakdown of Gaussian and sigmoidal fits for the auditory cortical neurons with significant curve fits (p < 0.05; 91 of 119 neurons included on chart). b, Similar results for the IC, based on our previous work (Groh et al., 2003). The chart includes 59 of 99 total neurons.

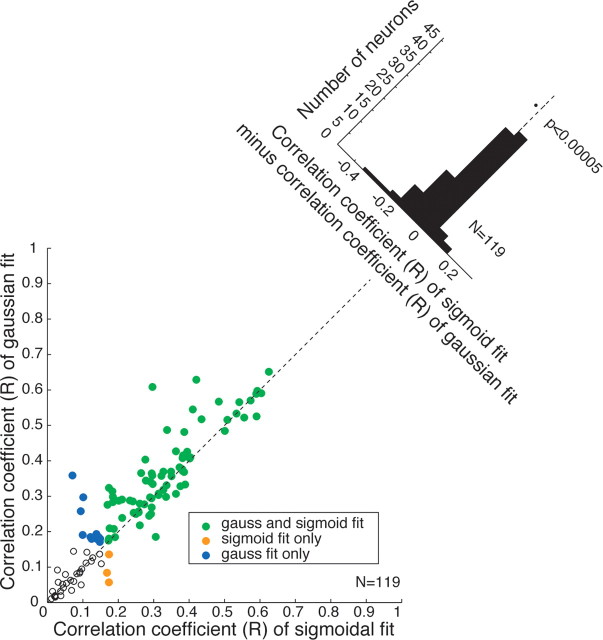
The fact that most neurons could be fit by either a sigmoidal or a Gaussian function using standard statistical criteria would seem to suggest a primarily monotonic or rate code, but it is important to compare the quality and similarity of the two fits. Figure 6 compares the quality of the two fits, by plotting the correlation coefficient of the Gaussian versus that of the sigmoidal fit. If Gaussian functions are better than sigmoids, the data should lie above the line of slope 1, although both fits might be statistically significant. Most of the data lie along the slope 1, with a slight but statistically significant bias for the Gaussian fits to be superior to the sigmoids, as illustrated by the tilted histogram at the top right corner of the plot.

Figure 6.

Comparison of the goodness of fit for Gaussian versus sigmoidal functions. The correlation coefficient (r) of the Gaussian fit is plotted versus that of sigmoidal fit for each neuron, with the color and symbol type indicating whether the curve fit was statistically significant for either, both, or neither function type. The tilted inset summarizes the data in a histogram. The x-axis shows the difference between the Gaussian and sigmoidal correlation coefficients. The dotted line reference is at 0. The mean of this distribution is significantly different from 0, favoring the Gaussian functions (t test, p < 0.00005).

Thus, the majority of neurons could be successfully fit by either a Gaussian or a sigmoidal curve, with the Gaussian curve providing only a slightly better fit, on average. This pattern of findings suggests that the average auditory cortical neuron encodes sound location in a predominantly monotonic manner that is more consistent with a rate coding of location, but with some peaks or troughs, like a bumpy road up a hill.

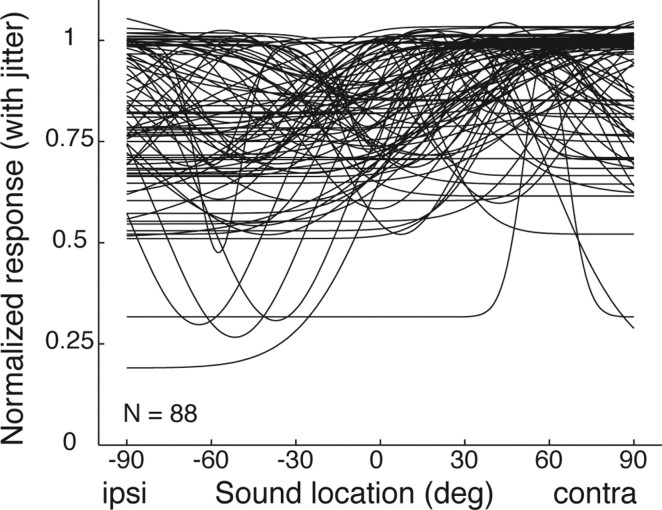
What is the overall shape of the Gaussian functions? Are they in fact reasonably monotonic, as would be expected from the similarity of the Gaussian and sigmoidal correlation coefficients? Figure 7 shows the family of Gaussian curves that successfully fit the response patterns of individual neurons. The curves are very broad, confirming that these Gaussians are effectively monotonic within the range of existing sound locations. This figure also confirms several of the earlier points concerning laterality. The contralateral bias is modest but apparent: the peaks tend to be located on the contralateral side; “troughed” Gaussian functions have their valleys on the ipsilateral side. Most of the Gaussian functions have a “floor” at a value of >50% of the peak height, consistent with the neurons responding to sounds at ipsilateral as well as contralateral locations.

Figure 7.

The family of statistically significant Gaussian curve fits across the population. The curves are normalized to the same peak height, with a small amount of jitter (randomly drawn from a normal distribution with a mean of 0 and a SD of 0.02) added in the vertical dimension so that the curves do not lie exactly on top of one another. ipsi, Ipsilateral; contra, contralateral.

On the whole, the pattern of results concerning representational format is similar to our previous observations in the IC (Fig. 4b) (Groh et al., 2003), except that the “bumpiness” (i.e., the tendency of the response function to show local maxima or minima at locations other than at the farthest contralateral or ipsilateral locations) appears to be greater in the auditory cortex than in the IC. For example, neurons such as those in Figure 4, c–h, which had considerable differences between the shapes of the sigmoidal and Gaussian curve fits, were more obvious in the auditory cortex than the IC. To evaluate this quantitatively, we conducted a more sensitive comparison of the Gaussian and sigmoidal curve fits in both the auditory cortex and IC. Our goal was to quantify the similarity in the shape of the Gaussian and sigmoidal curves that fit the data to each other.

Figure 8 illustrates how we did this. We first evaluated the Gaussian and sigmoidal curve fits for each neuron across the range of tested locations, as illustrated for two example neurons in Figure 8, a and c (same neurons as shown in Figs. 1b,h, 4b,h). The Gaussian and sigmoidal curve fits for the neuron in Fig. 8a were so similar as to be almost identical to each other, whereas the curve fits for the neuron in Fig. 8c were similar but not identical. We then regressed the evaluated points of the Gaussian and sigmoidal curve fits against one another (Fig. 8b,d) to determine the correlation coefficient between the two curves. The red and blue arrows in Figure 8, c and d, track one of the evaluated sets of points from one graph to the other. If the Gaussian and sigmoidal curves match each other in shape exactly, the correlation coefficient will have a value of 1, with less similar curves having values between 0 and 1. The neuron in Figure 8, a and b, has a correlation coefficient of 0.9976, whereas the neuron in Figure 8, c and d, has a correlation coefficient of 0.8137.

Figure 8, e and f, shows the results of this analysis across the population for both auditory cortex and the IC. Gaussian and sigmoidal curve fits showed slightly better correspondence with each other in the IC (median correlation coefficient, 0.933) than in auditory cortex (mean correlation coefficient, 0.856). This pattern confirms quantitatively that the representation for sound location in auditory cortex is slightly more “bumpy” than that in the IC, although both are still predominantly monotonic.

Latency of response and sound location

Previous studies in auditory cortex of cats have shown that response latency varies with sound location, and have suggested that temporal information might be used as part of the code for sound location (Middlebrooks et al., 1994, 1998; Brugge et al., 1996, 1998, 2001; Eggermont, 1998; Eggermont and Mossop, 1998; Xu et al., 1998; Brugge and Reale, 2000; Furukawa et al., 2000; Jenison et al., 2001; Furukawa and Middlebrooks, 2002; Reale et al., 2003; Stecker and Middlebrooks, 2003; Stecker et al., 2005b). We confirmed that first spike latency varies with sound location in primate auditory cortex as well. Figure 9a shows the average first spike latency as a function of sound location. A linear regression through these average values shows a statistically significant effect at the population level. Figure 9b shows a population histogram of the slopes of similar regression lines fit to each individual cell. This distribution of individual values is also significantly different from zero (mean, −0.0198; t test, p < 0.05), indicating that on average the neurons respond sooner to contralateral sounds than to ipsilateral sounds.

Figure 9.

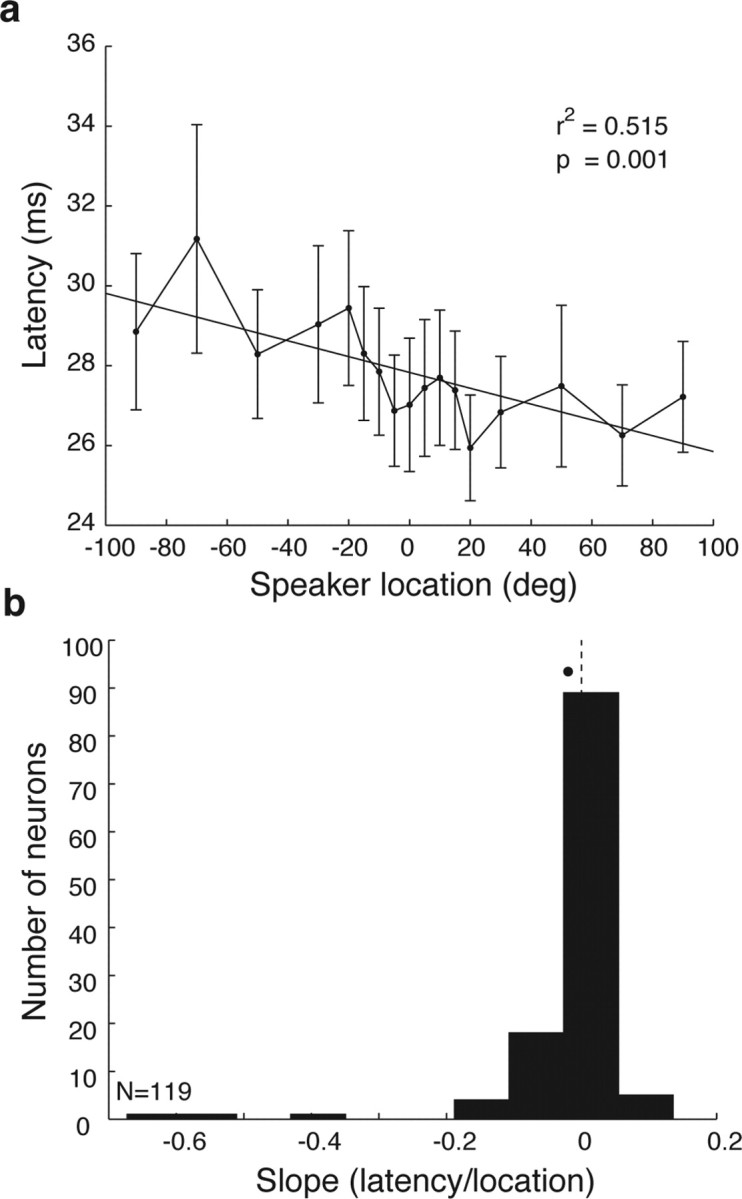
Response latency as a function of sound location. a, Mean latency as a function of sound location across the population. Error bars indicate SEM. b, The distribution of slopes of regression lines capturing the latency as a function of sound location across the population of individual neurons. The average slope was −0.23 ms/°.

Time period of the response and sound location sensitivity

As can be seen in Figure 1, the responses of auditory cortical neurons to steady sounds nevertheless vary in time. Steinschneider and Fishman (2004) have recently demonstrated that both earlier and later components of the response are sensitive to sound location. We assessed whether spatial sensitivity varied in different temporal epochs of the response in our data set. We divided the response into an initial transient period (0–100 ms after sound onset) and a later sustained period (100–500 ms), and compared the spatial sensitivity during these subepochs to the spatial sensitivity during the whole response period (0–500 ms) (Table 1). The general pattern of results was very similar in all three epochs, with the pattern of sensitivity during the 100–500 ms epoch being especially close to that for the entire 0–500 ms epoch. Among neurons with statistically significant curve fits, most were fitted by both sigmoid and Gaussian fits (whole response, 76 of 91 or 83.5%; transient, 46 of 59 or 78.0%; sustained, 78 of 90 or 86.7%). The incidence of statistically significant spatial sensitivity was lower in the transient 0–100 ms epoch, but this is likely attributable to the higher variability associated with assessing a neural response during such a short period of time, and thus the reduced likelihood of achieving statistical significance, and does not appear to be attributable to any fundamental difference in the activity patterns early versus late after sound onset.

Discussion

Representational format

The main finding of this study is that monkey auditory cortical neurons, like IC neurons, seem to use a rate code for representing sound location. Most sound-sensitive neurons respond better the closer the sound is to the axis of the ears, on the contralateral side for the majority of neurons and the ipsilateral side for the remainder. The format of the representation for sound location is similar in the monkey IC (Groh et al., 2003), although the rate code in auditory cortex is less smooth and more “bumpy” than that in the IC. In fact, no quantitative investigation has as yet yielded evidence for a place code for sound location in the monkey brain, although numerous candidate brain areas remain to be explored (e.g., intraparietal cortex, superior colliculus).

That auditory cortex may use a rate code for representing sound location is a major difference compared with the primary cortices for the other two spatial senses, vision and touch, for which place codes for stimulus location are the rule. This means that a transformation of representational format might be needed before signals from auditory cortex could converge with spatial signals in the visual or somatosensory pathways. We previously suggested several potential models for translating signals from either a place code to a rate code (Groh, 2001) or vice versa (Groh et al., 2003; Porter and Groh, 2006). It will be of interest to assess the representation at subsequent stages of processing such as intraparietal cortex to determine whether such a transformation is accomplished as signals progress along the pathway. One possibility is that a rate-to-place transformation is accomplished gradually, which could account for the “bumpiness” of the rate code in auditory cortex: the auditory cortical code might constitute an intermediate state in a gradual transition from a rate code in the IC to a place code at a subsequent stage of processing.

Relationship to previous neurophysiological studies

Our study provides a statistically based framework for evaluating whether candidate neural populations are more consistent with place or rate codes. A statistical test is very useful because neural responses can be very variable, so it is not always obvious from inspecting the average responses of a neuron whether small differences in responsiveness at adjacent locations are really meaningful.

Although the methods used here have not been previously used in auditory cortex, a number of previous studies in monkeys and other animals have evaluated the spatial sensitivity of auditory cortical neurons using other means (Middlebrooks and Pettigrew, 1981; Rajan et al., 1990a,b; Brugge et al., 1994, 1996, 1998, 2001; Clarey et al., 1994, 1995; Middlebrooks et al., 1994, 1998; Barone et al., 1996; Eggermont and Mossop, 1998; Xu et al., 1998; Brugge and Reale, 2000; Furukawa et al., 2000; Recanzone, 2000; Furukawa and Middlebrooks, 2002; Stecker and Middlebrooks, 2003; Stecker et al., 2003, 2005a,b; Mrsic-Flogel et al., 2005; Woods et al., 2006). These studies have provided numerous clues about auditory cortical spatial sensitivity that are more consistent with a rate code than a place code: neurons tend to exhibit broad spatial tuning (Recanzone, 2000; Mickey and Middlebrooks, 2003; Woods et al., 2006); many neurons show “hemifield” sensitivity (Middlebrooks and Pettigrew, 1981); few neurons have circumscribed receptive fields in frontal space (Rajan et al., 1990a); and (for studies involving sampling in 360°), the distribution of “best” areas tends to be centered on the interaural axes of the ears (Woods et al., 2006).

The lack of evidence for a place code has been noted by many of these previous studies, and other types of codes have been sought. One such possibility has been that spike timing information might encode sound location (Middlebrooks et al., 1994). Evidence that first spike latency and/or the temporal pattern of the response varies with sound location has been reported in cats and ferrets (Middlebrooks et al., 1994, 1998, 2002; Brugge et al., 1996, 1998, 2001; Eggermont, 1998; Eggermont and Mossop, 1998; Xu et al., 1998; Brugge and Reale, 2000; Furukawa et al., 2000; Jenison et al., 2001; Furukawa and Middlebrooks, 2002; Reale et al., 2003; Stecker and Middlebrooks, 2003; Mrsic-Flogel et al., 2005; Stecker et al., 2005b). This has also been shown to be true for awake cats (Mickey and Middlebrooks, 2003). In monkey, however, Woods and Recanzone (2006) have argued that first spike latency is only a very noisy signal of sound location. Our study confirms that first spike latency is, on average, correlated with sound location, but supports Woods and Recanzone's view that the correlation may be a weak one in monkeys.

Relationship to human neuroimaging studies

Most evoked potential and neuroimaging experiments in humans measure the pooled activity of large populations of neurons. In contrast, single- and multiple-unit recording experiments in animals assess the activity of individual or small groups of neurons separately. Such studies provide fine-grained spatial and temporal information regarding neural activity, and have the potential to make predictions for the outcome of studies that assess pooled activity. However, such predictions require that (1) a uniform or at least overlapping set of stimulus conditions be used for the study of each neuron, and (2) quantitative population analyses generate a portrait of the pattern of activity across the data set. In this study, we conducted such analyses to facilitate the comparison of single-unit and neuroimaging results, especially with regard to the contralaterality of the representation of auditory space in auditory cortex.

We found a modest contralateral bias in the population of active neurons. The size of this bias, on the order of 8–15%, provides an account for why it has been difficult to observe a contralateral bias in the level of activation in human primary auditory cortex with imaging studies (Woldorff et al., 1999; Zatorre et al., 2002; Petkov et al., 2004; Brunetti et al., 2005; Krumbholz et al., 2005a,b; Zimmer and Macaluso, 2005; Zimmer et al., 2006): the modest size of the effect may be pushing the limits of the sensitivity of imaging methods. This is a valuable insight because it reassures that the difficulty in identifying a contralateral bias in human auditory cortex is to be expected from primate single-unit data, and does not necessarily constitute evidence that human auditory cortex is performing a different function or is organized differently than its counterpart in close animal relatives.

Representational format and neuroimaging

Place codes and rate codes should in principle produce very different patterns of activity in an fMRI, PET, or ERP (event-related potential) study. If sound location is indeed encoded monotonically in human auditory cortical neurons, and if this organization is lateralized so that the neurons in each hemisphere usually have increasing activity for more contralateral sound locations, this should produce a blood oxygen level-dependent (BOLD) signal that is monotonically related to the azimuthal location, assuming a straightforward linkage between neural activity and the hemodynamic response (Rees et al., 2000; Logothetis et al., 2001; Rainer et al., 2001; Kayser et al., 2004; Nir et al., 2007; Viswanathan and Freeman, 2007).^a Such a pattern of responses would be especially easily detected using a general linear model regressing the BOLD signal in an auditory cortical region of interest (ROI) against sound azimuth. The predicted picture with a place code is less clear, and depends in part on how the receptive fields are organized topographically and whether the receptive fields sample acoustic space evenly (i.e., every location in space recruits about the same number of auditory neurons). If the receptive fields in one hemisphere favor the contralateral hemifield, then there should be a corresponding lateralization to the BOLD signal from auditory cortical ROIs. If the space in that hemifield is evenly sampled by the neurons contained in the ROI, then a regression of the BOLD signal against sound azimuth for locations within a hemifield might identify little or no relationship: the shift in the active population would still be contained within the ROI and would produce no difference in the overall metabolic demands of that volume of tissue. If there is a finer-grained topographical organization, then the site of activation in auditory cortex should shift with changes in sound location. In an fMRI experiment, the “best” voxels should shift, provided that the spatial grain of the map is adequate to produce a spatially varying BOLD signal, that the scanner can sample the tissue finely enough to detect these shifts, and that the shifts are not smeared through the use of a large averaging kernel during data analysis.

In short, detecting differences in neural activity because of sound location poses certain challenges for imaging experiments, even when the responses of individual neurons are highly modulated by sound location. In monkeys, most individual neurons are modulated by sound location, but the nature of the responses (monotonic sensitivity to sound azimuth) combined with the way that the population is organized (only somewhat lateralized) would tend to make it difficult to observe spatial sensitivity using methods that measure the pooled activity of a large population of neurons. These findings suggest that the reason human imaging and evoked potential experiments have found only weak evidence for spatial sensitivity in human auditory cortex could be attributable to the limited power of these methods at detecting the activity of small populations of neurons, and should not be construed as evidence that human auditory cortex is not involved in spatial hearing.

Does the visual fixation stimulus affect auditory spatial sensitivity?

In the current study, we used a visual fixation stimulus to control eye position. The reason for this design is that changes in eye position can produce changes in activity in auditory cortical neurons (Werner-Reiss et al., 2003; Fu et al., 2004; Woods et al., 2006). At the same time, visual stimuli can themselves influence the responses of auditory cortical neurons (Ghazanfar et al., 2005) as well as neurons in other areas of the auditory pathway (Porter et al., 2007). Thus, it will be of interest to investigate further whether the presence of a visual stimulus alters spatial sensitivity of auditory cortical neurons, above and beyond any associated effect of eye position. Our present experiments do not answer this question, but some insights pertinent to this issue were obtained in our previous study of eye position sensitivity in auditory cortical neurons (Werner-Reiss et al., 2003). In that experiment, visual fixation and sound location were independently varied, with sampling of eight to nine visual fixations and sound locations spanning the central 35–48° of space. Thus, the visual fixation and sound locations were coincident in space on approximately one of eight or one of nine of the trials. We found no tendency for the congruency of visual fixation and auditory stimulus locations to systematically produce enhanced responses (Werner-Reiss et al., 2003, their supplemental information). Of course, in that study, as in this one, there was a substantial difference in the time of onset of the visual stimulus and the auditory stimulus (500 ms or more). It is certainly possible, and perhaps even likely, that temporally coincident visual and auditory stimuli might interact with each other in ways that were not apparent in either the present or our previous study. Given that the normal sensory environment includes multiple visual stimuli spanning the entire visual scene, and given the apparent discrepancy in coding format between the visual and auditory pathways, studies of the impact of visual stimuli on auditory spatial sensitivity will be of great interest in the future.