Bending of short DNA helices

Abstract

In their recent Science paper, Vafabakhsh and Ha claim that DNA duplexes at the range of 100 bp experience anomalous flexibility, much greater than the flexibility of large DNA molecules.¹ However, careful reevaluation of their data leads to the conclusion that the presented data do not warrant the authors’ claim.

It has been commonly accepted over the past few decades that DNA bending occurs by small changes of the angles between the planes of adjacent base pairs and can be quantitatively described by the wormlike chain (WLC) model. In 2004 this view was challenged by Cloutier and Widom (C&W) who claimed that the cyclization of short DNA fragments, around 100 bp in length, occurred by about 1,000 times more efficient than the WLC model predicted.² They suggested that sharp kinks of the type proposed by Crick and Klug³ could be responsible for very efficient cyclization of short DNA fragments. Theoretical analysis confirmed that such disruptions of the helical structure should increase the probability of looping for sufficiently short DNA fragments.^4-6 Thus, the question is not “if” but “when”: how short must the DNA circle be to include sharp bends of DNA axis? C&W claimed that the cutoff length exceeds 130 bp.

It turned out that C&W did not determine the cutoff length correctly. They measured the rate of the ligase-assisted cyclization of small DNA fragments with short sticky ends. The rate was used to calculate so-called j-factor, the equilibrium concentration of one end of the fragment in the vicinity of the other end. This method allows an accurate determination of the j-factor if certain conditions are met^7,8. In particular, the rate of ligation of the joined sticky ends has to be much lower than the rate of their dissociation. It appeared that this condition was not met in C&W experiments: they used a way too high ligase concentration and this resulted in the great overestimation of the fragments’ j-factor, as the later experiments showed.⁶ Under a proper ligase concentration the measured j-factors of 106–128 bp-long DNA fragments perfectly fitted the theoretical predictions based on the WLC model.⁶ Du et al. concluded that in the absence of torsional stress DNA circles consisting of 100 bp or longer do not contain structural disruptions.⁶ Later Demurtas et al. have arrived at the same conclusion based on direct observation of the shapes of DNA minicircles by cryo-EM.⁹

It proved to be too difficult to determine the j-factor for even shorter fragments by the ligase method because under permissive ligase concentrations very few circles are formed before the ligase loses its activity. To investigate the presence of structural disruptions in even smaller DNA circles Du et al. probed the structure of such covalently closed circles by the single strand-specific endonucleases.¹⁰ By this approach, it was found that the disruptions appear in torsionally unstressed circles when their length is somewhere between 73 and 84 bp. However, the calculations show that the disruptions should not essentially affect the j-factors of torsionally unstressed DNA fragments larger than 60 bp.¹¹

In their recent paper we are commenting on, Vafabakhsh and Ha (V&H) challenge this conclusion.¹ They monitor cyclization of short DNA fragments via joining long sticky ends, of 8–10 nucleotides. Joining such sticky ends at room temperature makes rather stable DNA circles even without ligation. This allows V&H to avoid ligation and to use single-molecule FRET to monitor cyclization of the fragments and to determine their j-factor in the range of 67–106 bp. They conclude that the obtained j-factors are a few orders of magnitude larger than the theoretical predictions based on the WLC model, i.e essentially confirm the conclusion made by C&W², which has been overturned by the data based on ligase, single strand-specific nuclease and cryo-EM assays.^6,9,10 The contradiction between V&H’s data and the data in refs ^{6, 9} and ¹⁰ can be easily resolved, however. First of all, joining of such long sticky ends does not require the alignment of the duplex ends, since long single-stranded sticky ends are very flexible and can form a double-stranded segment at any mutual orientation of the duplex ends (Fig. 1). The contour length of the single-stranded DNA counted per nucleotide is twice of the length of the double helix per base pair, so the joining of the long sticky ends can occur when the duplex ends are separated by a few nm. This means that the experimental data have to be compared with the theoretical prediction for the j-factor of DNA fragments with arbitrary orientation of the duplex ends and 3–5 nm capture radius, r_c.

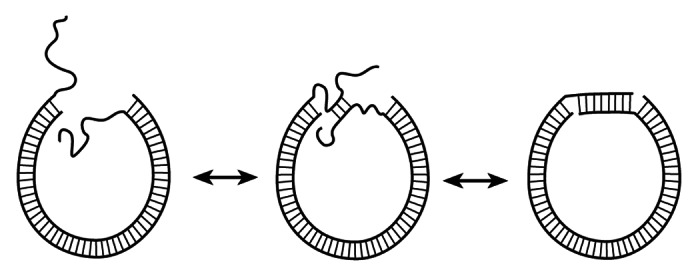
Figure 1. Cyclization of DNA fragments with long sticky ends. The ends of the duplex can have any mutual orientation during their joining due to the high bending flexibility and unrestricted torsional freedom of the sticky ends.

The corresponding theoretical curve is shown in Figure 3F of the V&H paper (dotted line) and in a slightly corrected form in our Figure 2. Clearly, the discrepancy between the dashed/dotted curves and the experimental data is not striking. The cyclization mechanism shown in Figure 1 means that the j-factor must not oscillate, since formation of a stable helical segment by the long sticky ends occurs under any torsional orientation of the duplex ends. Therefore, what V&H considered as an indication of the j-factor oscillations (experimental points in the vicinity of 100 bp) actually indicates the scattering of the measured values. This conclusion is supported by the fact that the apparent maximum of the measured j-factor at 100 bp corresponds to the DNA fragment with a semi-integer number of the helix turns (9.5 turns), where the oscillating j-factor has to be in a local minimum rather than in a maximum. Thus, the actual accuracy of the j-factor determination in V&H experiments was about an order of magnitude, while the apparent discrepancy between the WLC-based theoretical predictions and the measured results is 1–2 orders of magnitude.

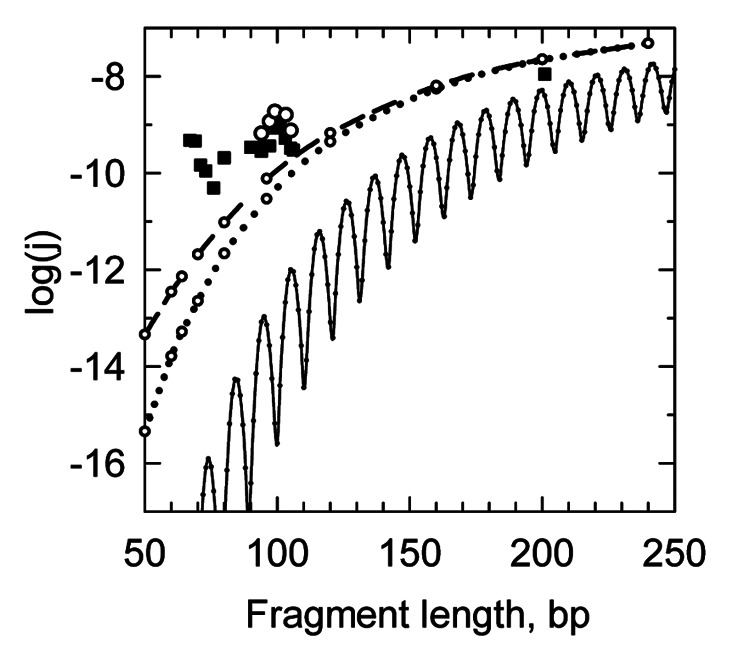
Figure 2. The j-factors of short DNA fragments. The dashed and dotted lines correspond to the calculated j-factors for arbitrary angles between the duplex ends and capture radius, r_c, of 3 nm (dotted line) and 5 nm (dashed line). The points correspond to the experimental data shown in Figure 3E of V&H. The thin black line corresponds to the j-factor that accounts for axial and torsional orientations of the fragment ends. All calculated curves correspond to DNA persistence length of 48 nm. The calculations were made as described in ref. 12.

There could be several reasons why the measured j-factor values are still higher than the predicted ones. Sequence errors and chemical flaws in the synthetic oligos, and errors due to annealing the final duplexes from several synthetic oligos could be major sources of imperfect duplexes, in our opinion. Such imperfect duplexes could carry mismatches, bulge loops, internal nicks and single-stranded gaps that serve as hinges. The authors failed to perform necessary quality control of the final dsDNAs products obtained via annealing of synthetic oligos to exclude such a possibility. Moreover, such quality control performed by Du et al. (see supporting material of ref. 10) indicated that duplexes in minicircles obtained via direct annealing of synthetic oligos were not perfect since they exhibited an incomplete digestion by restriction endonucleases. That is why in their experiments Du et al. used cloning to obtain perfect DNA duplexes for making minicircles.¹⁰ Very similar observation about quality of the duplexes obtained via hybridization of synthetic oligos are reported by Seeman’s lab.¹³ They have found that the DNAs produced from PCR do not exhibit these deficiencies.¹³ Although in case of experiments of V&H the preparation of matched duplexes by cloning or PCR would be more difficult since they need dye molecules attached to DNA ends, it is still very much achievable. For instance, one can obtain matched duplexes without dyes by cloning or PCR and then use short synthetic adapters carrying dyes to attach them to the perfect duplexes’ termini. They could not tether such molecules to the surface but they still could encapsulate them into phospholipid vesicles, as they did in some of their expriments.¹ In the absence of additional experiments with duplexes obtained by cloning or PCR, it seems reasonable to assume that minicirles obtained via direct annealing of synthetic oligos carry unligated nicks, gaps, mismatches and bulges that serve as hinges, reducing DNA bending rigidity and increasing the j-factor to unpredictable levels.

Another observation by V&H that the dependence of the cyclization rate on the fragment size is relatively weak, is also in a semi-quantitative agreement with the theoretical prediction for the loose boundary conditions (see Fig. 2).

We conclude that V&H have failed to present convincing evidences that the WLC model is not valid for torsionally unstressed DNA minicircles in the range of 100 bp.

The authors thank Ned Seeman for a fruitful discussion of the issues raised in the commentary.

Vafabakhsh R, Ha T. Extreme bendability of DNA less than 100 base pairs long revealed by single-molecule cyclization. Science. 2012;337:1097–101. doi: 10.1126/science.1224139.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.