Discriminating preictal and interictal states in patients with temporal lobe epilepsy using wavelet analysis of intracerebral EEG

Abstract

Objective

Identification of consistent distinguishing features between preictal and interictal periods in the EEG is an essential step towards performing seizure prediction. We propose a novel method to separate preictal and interictal states based on the analysis of the high frequency activity of intracerebral EEGs in patients with mesial temporal lobe epilepsy.

Methods

Wavelet energy and entropy were computed in sliding window fashion from preictal and interictal epochs. A comparison of their organization in a 2 dimensional space was carried out using three features quantifying the similarities between their underlying states and a reference state. A discriminant analysis was then used in the features space to classify epochs. Performance was assessed based on sensitivity and false positive rates and validation was performed using a bootstrapping approach.

Results

Preictal and interictal epochs were discriminable in most patients on a subset of channels that were found to be close or within the seizure onset zone.

Conclusions

Preictal and interictal states were separable using measures of similarity with the reference state. Discriminability varies with frequency bands.

Significance

This method is useful to discriminate preictal from interictal states in intracerebral EEGs and could be useful for seizure prediction.

1. Introduction

A fundamental question about epilepsy is how seizures are generated and if they are predictable. The answer is often related to the investigation of pre-seizure periods for clinical and physiological changes that may explain the mechanisms leading to a seizure and potentially anticipate its occurrence. Studies of scalp and intracranial EEGs have demonstrated the existence of a preictal state using linear and nonlinear methods to detect temporal and spatiotemporal dynamic changes in the seconds to hours preceding seizures. Early work (Viglione and Walsh, 1975) showed a gradual change of EEG patterns in the minutes before seizure onset in a few samples. Further studies were carried out mainly with spectral analysis in an attempt to identify seizure precursors (Wieser and Preictal, 1989; Duckrow and Spencer, 1992; Osorio et al., 1998; Salant et al., 1998). Characteristic changes were found in the seconds preceding onset. Other groups reported changes in spike activity in the pre-seizure periods (Siegel et al., 1982; Lange et al., 1983). These findings were not confirmed (Gotman and Marciani, 1985; Gotman and Koffler, 1989). Starting in the early 1990s, studies reported evidence that a preictal state is detectable with methods derived from nonlinear dynamics theory applied to EEG signals. Iasemidis et al. (1990) used the largest Lyapunov exponent as a measure of chaoticity from intracranial EEGs. Seizures were hypothesized to be transitional states between less ordered and more ordered states. Martinerie and Adam (1998) reported a decrease in spatio-temporal complexity during preictal periods, measured by the correlation density. Le Van Quyen et al. (1999, 2000) showed a decrease in the dynamical similarity index and a change in phase synchronization in intracranial recordings, minutes before a seizure.

Despite encouraging results, these studies lacked validation on controlled interictal data. Statistical significance and specificity in particular, could not be assessed. This issue was tackled in the late 1990s with controlled studies carrying out statistical validation. Mormann et al. (2000) reported differences in the degree of synchronization between interictal and preictal recordings using mean phase coherence. Results with high sensitivity rates were reported by Lehnertz and Elger (1998) using correlation dimension, Le Van Quyen et al. (2001) using similarity index, Iasemidis et al. (2001) using the largest Lyapunov exponent, Litt et al. (2001) and Gigola et al. (2004) using accumulated signal energy and by Mormann et al. (2003a,b) using phase synchronization.

The optimistic results from these studies were challenged by some groups who raised the problem of high in-sample optimization and inability to generalize the results on unselected data. Carried out on unseen and more extended data sets, results from several studies (Iasemidis et al., 1990; Lehnertz and Elger, 1998; Le Van Quyen et al., 2001; Litt et al., 2001) were non-reproducible, emphasizing the need for statistical validation (Mormann et al., 2007).

Recent research on high frequency intracranial EEG shows increasing evidence that High Frequency Oscillations (HFOs) could be biomarkers of the seizure onset region (Jirsch et al., 2006; Jacobs et al., 2008; Khosravani et al., 2009) and play an important role in epileptogenicity (Jacobs et al., 2009a, 2010). Zijlmans et al. (2011) found an increase in the rate of HFOs in the 10 s before seizure on-set. Though this change is not sufficiently long to be considered in the seizure prediction context, it could be useful in early seizure detection (Osorio et al., 1998). Longer preictal periods up to 15 min have been investigated by Jacobs et al. (2009b) who found no systematic preictal change in the rate of HFOs, suggesting that these patterns may not be good indicators of the preictal state. However, high frequencies may play a role in seizure initiation and could be analyzed for seizure precursors.

Some studies have proposed seizure prediction approaches based on wavelet analysis of scalp and intracranial EEG sampled at 256 Hz (Mirowski et al., 2009; Indic and Narayanan, 2011) and 500 Hz (Wang et al., 2011). In this study we propose a new approach to discriminate between preictal and interictal states, as a first step towards seizure prediction. We explore the high frequency content (50 to 450 Hz) of intracranial EEG data of selected segments from preictal and interictal periods. We analyze these segments by means of a continuous wavelet transform and quantify the dynamics of the preictal and interictal states in a space defined by wavelet entropy and energy. A reference state is defined in this space and hypothesized to be an attractor (Milnor, 1985) for all impending seizures of a given patient. Features are calculated and assessed for their ability to distinguish preictal from interictal states in out-of-sample data sets using discriminant analysis based classification methods. A bootstrapping statistical validation approach is used to validate the results.

2. Materials and methods

2.1. Materials

Six patients with implanted electrodes, chosen randomly from a set of patients diagnosed with mesial temporal lobe epilepsy and admitted in the Montreal Neurological Institute for investigation between 2004 and 2009, were selected. EEG epochs from prolonged day and night recordings filtered at 500 Hz and sampled at 2000 Hz were extracted. Up to 8 preictal epochs lasting ~22 min each and 10 interictal epochs remote from the seizures lasting ~66 min each were selected for each patient. Selected clinical and subclinical seizures (for preictal data) were at least 2 h apart to minimize postictal dynamics. This criterion resulted in the exclusion of 24 seizures in one patient and 1 seizure in another from a total of 63 clinical and subclinical seizures. Interictal epochs were at least 4 h from any seizure and 1 h from each other. Seizure onsets were determined by an experienced neurologist. In total, 670 min of preictal data and 3723 min of interictal data were analyzed. Three bipolar channels from the 4 deepest contacts of each multi-contact electrode were analyzed. Electrodes were implanted bilaterally in the amygdala, hippocampus and parahippocampus. These structures of the mesial temporal lobe are suspected to be the seizure onset zone. We hypothesize that recordings from areas within or close to the seizure onset zone carry a better discrimination power between preictal and interictal dynamics. Depending on the number of electrodes implanted and the areas targeted, up to 18 EEG channels (3 × 6) were analyzed for each patient. A summary of electrode implantation, EEG epochs selected and seizure onset is given in Table 1. We hereafter denote Xi (i = 1,2,3) a bipolar channel X(i)−X(i + 1) generated by electrode contacts X(i) and X(i + 1), where X is the electrode name and X(1) the deepest contact. For example RH1 denotes the bipolar channel RH(1)–RH(2) generated by the deepest contact RH(1) and the adjacent contact RH(2).

Table 1.

EEG dataset and seizure onset summary.

Patient No.	Age gender	Duration of implantation (days)	No. of seizures (no. of subclinical seizures)	No. of seizures recorded at 2000 Hz (no. of subclinical seizures)	No. of interictal EEG epochs selected (tot. duration in min)	No. of preictal EEG epochs selected (tot. duration in min)a	Selected electrodes	Seizure onset
1	40F	7	7 (0)	4 (0)	9 (477)	4 (66)	RA, RH, RP	Medial structures of right temporal lobe
2	29M	10	8 (0)	8 (0)	10 (662)	8 (147)	RA, RH, RP, LA, LH	Most seizures had onset in right MTL
3	42F	15	34 (31)	6 (3)	10 (665)	8 (163)	RA, RH, RP, LA, LH, LP	Right temporal predominanceb
4	46M	19	25 (14)	6 (2)	10 (659)	8 (126)	RA, RH, RP, LA, LH, LP	Right hippocampusc
5	44F	11	14 (1)	6 (0)	10 (666)	6 (116)	RA, RH, RP, LA, LH, LP	Bilateral independent epileptiform generatorsd
6	40F	13	56 (40)	16 (12)	9 (594)	4 (52)	RA, RH, RP, LA, LH, LP	Focal onset in the left posterior hippocampuse
Total			144 (86)	46 (17)	58 (3723)	38 (670)

(R = right, L = Left, A = Amygdala, H = Hippocampus, P = Parahippocampus).

^aSome seizures were excluded from the analysis because they did not meet the 2 h. separation criteria.

^bBilateral temporal epileptic generators in both mesial temporal lobes independently. Right-sided generator appears to be much more important.

^cPreponderance of the right temporal lobe to generate seizures, mostly in the hippocampus. Hippocampal areas and amygdale were also involved.

^d Interictal discharges more prominent on the left, more confined to the hippocampus and parahippocampus. Right diffuse interictal discharges involving H, PH, and A areas and temporal neo-cortex. 12 of 14 seizures originated from the left MTL structures.

^eDepth electrode LP.

2.2. Overview of the method and definitions

Using preictal and interictal epochs from each patient EEG, the purpose is to discriminate preictal and interictal states. Each epoch is analyzed in a sliding window using wavelet transform whereby energy and entropy are calculated (see Section 2.3). The analysis is performed independently in 4 frequency bands between 50 and 450 Hz with a bandwidth of 100 Hz.

We introduce a 2-dimensional space S where wavelet energy and entropy are the co-ordinates. In this plane, an EEG epoch is represented by an energy and entropy profile, namely the sequence of points in S calculated in each window of the epoch. To compare the states underlying preictal and interictal EEG epochs, we introduce a reference state represented in S by a disk D (Fig. 1) and we define three features that characterize the energy and entropy profile of any EEG epoch with respect to this disk (see Section 2.4).

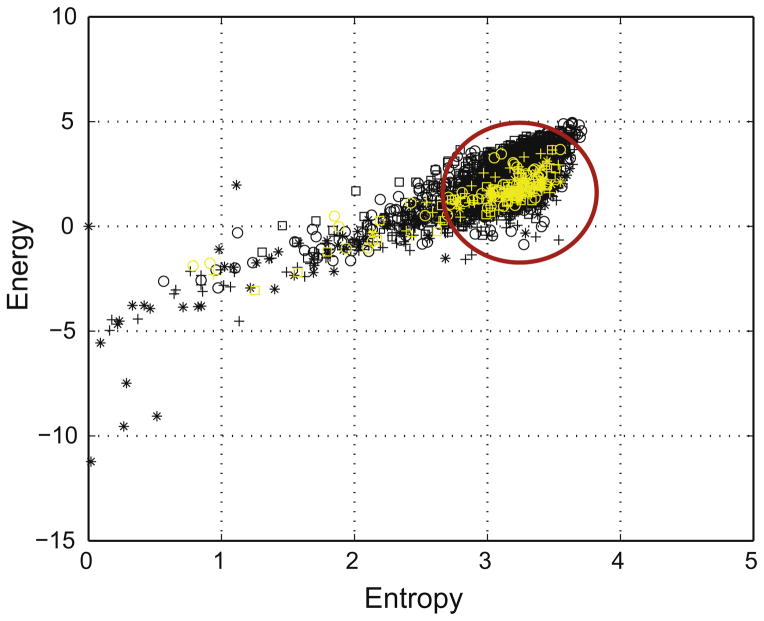
Fig. 1.

Example of energy and entropy space representation in 5 preictal epochs from one channel in one patient. The five 22 min preictal epochs (black symbols) and the five 90 s immediate preictal epochs (yellow symbols) are shown. The reference state is represented by the disk limited by the red circle.

For each patient, EEG epochs are divided into training and testing data sets (respectively TR and TS). The training data set contains 5 interictal epochs and Np = 2–5 preictal epochs, depending on the number of seizures available. The remaining data are left for testing and contain 2 or 3 preictal epochs and 5 interictal epochs. Section 2.6 depicts how data are split in the methods. In the training step, the center and the radius of the disk D are computed from a subset of the training data set (TR-A). Based on the defined features, a discriminant analysis based binary classifier is optimized to separate preictal and interictal epochs in the space of features. The remaining training subset (TR-B) is used to assess the performance of different binary classifiers such that the best performing classifier and the best performing channels are selected (see Section 2.6). The sensitivity and specificity of the resulting classifier are then assessed using the testing data set TS (see Section 2.7).

Original partition of preictal and interictal epochs is resampled into 10 different trials of training and testing data sets (named respectively TR1, TR2, …, TR10 and TS1, TS2, …, TS10) and the above procedure is repeated across trials. The validity of the method is thereafter ultimately assessed using the average classification performance across the trials (see Section 2.8).

2.3. Wavelet entropy and energy

To quantify the dynamics of the EEG locally in time and frequency, two entities are calculated from continuous wavelet analysis: energy and entropy. Continuous wavelet transform using Morse wavelet (Lilly and Olhede, 2010) is performed in a consecutive disjoint sliding 2 s window (Fig. 2a). Energy and entropy are calculated in each window in a frequency sub-band from the wavelet transform modulus along the maxima lines (see Appendix A). These maxima characterize the most important information carried in the signal by detecting oscillating singularities (Mallat and Hwang, 1992).

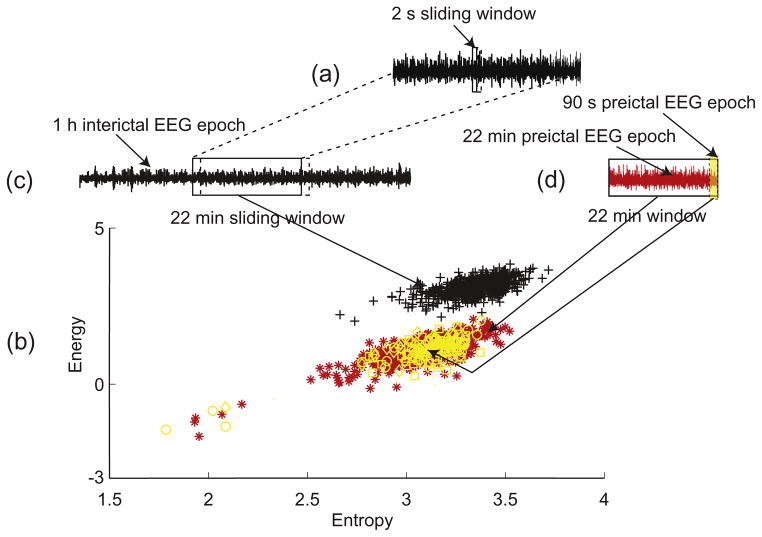
Fig. 2.

Illustration of the energy and entropy space and processing of the EEG epochs using a sliding 2 s window. (a) A 2 s window moves over the 22 min window. A point (represented by a symbol) in the energy and entropy space represented in (b) is calculated in a 2 s window. (b) Energy and entropy profile of the 22 min interictal epoch (black symbols), the 22 min preictal epoch (red symbols) and three 90 s immediate preictal epochs (yellow symbols). (c) A 22 min window moves over a 1 h interictal epoch from one channel. (d) 90 s immediate preictal epoch (yellow shaded area) and 22 min preictal epoch (red signal).

The spatiotemporal dynamics of the brain state underling an EEG epoch are represented by the energy and entropy profile (Fig. 2b). The organization of points of the energy and entropy profile in the plane S is assumed to be a characteristic of the brain state. Such a characteristic is used to identify differences between preictal and interictal states.

2.4. Feature definitions

The reference state is defined from the preictal training EEG data to discriminate the preictal and interictal states in an independent testing EEG data. It is constructed in the plane S by a disk D centered on the immediate preictal period of training data subset and which extension is obtained using preictal periods of the same training subset.

The parameters of the disk D are learned from a subset TR-A of the training preictal data set (described in Section 2.6). The center of the disk D is the mean of the 90 s immediate preictal (energy, entropy) points of the training subset TR-A. Although the uncertainty related to the definition of the seizure onset may lead to capturing some seizure dynamics in the 90 s period defining the reference state, this uncertainty is usually of the order of few seconds and should not have a major impact on the immediate preictal period. The radius of the disk D is computed from the 22 min preictal epochs such that a large proportion, set arbitrarily to 85%, of the mean energy and entropy profile is confined within the disk D. The mean energy and entropy profile is obtained by averaging energy and entropy profiles from all 22 min preictal epochs of the training subset TR-A.

The behavior of the energy and entropy profile of a given EEG epoch is measured with respect to the disk D using the following three features; the distance, the inclusion and the persistence. These features quantify the spatial and temporal organization of the energy and entropy points relative to the disk D. They are calculated in a 22 min window over the energy and entropy profile of the EEG epoch. For a preictal EEG epoch, exactly one measurement of each feature is obtained. For interictal EEG epochs, which are longer, a set of feature measurements is obtained by sliding the 22 min window over the energy and entropy profile of the EEG epoch with an overlap between windows set to 1/16 of their length (i.e., 1.375 min) (Fig. 2c and d).

The distance is defined as the Euclidean distance between the center of the disk D and the mean of the energy and entropy profile of the EEG epoch.

The inclusion is defined as the percentage of energy and entropy profile confined within the disk D. This feature quantifies the density of the energy and entropy profile relative to the disk D; a higher inclusion indicates a state with higher similarity with the reference state.

The persistence involves the temporal dimension of the energy and entropy profile and quantifies how long the state underlying the EEG epoch continuously remains close to the reference state. It is defined as the amount of time corresponding to the maximum number of consecutive 2 s windows during the EEG epoch in which the energy and entropy profile remains confined inside the disk D. High persistence indicates a tendency of the state underlying the EEG epoch to remain close to reference state. Low persistence reflects a state characterized by frequent jumps of the (energy, entropy) points inside and outside the disk D across time.

Fig. 3 illustrates these features in an example of preictal and interictal EEG epochs.

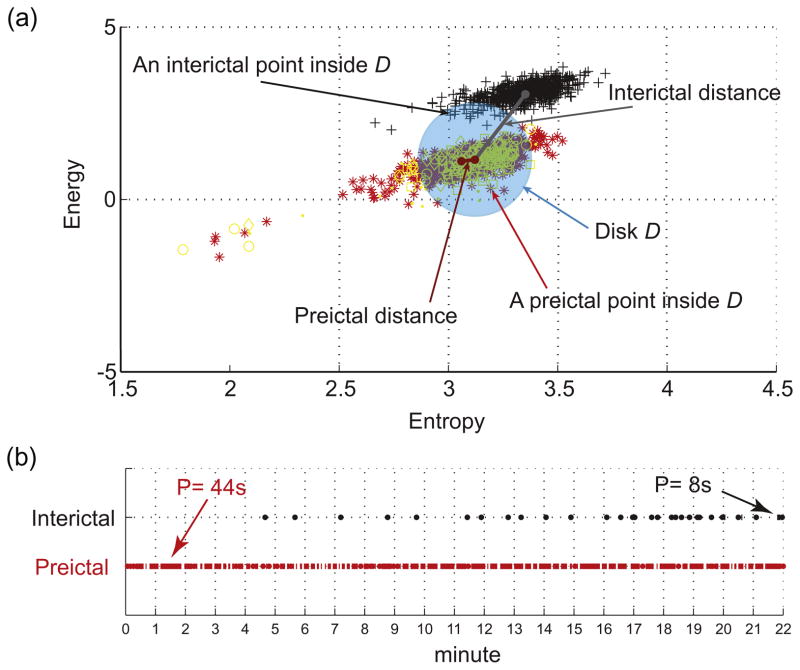
Fig. 3.

Illustration of the distance, inclusion and persistence features in the energy and entropy space. (a) Energy and entropy profiles of a 22 min window of an interictal epoch (black symbols) and a preictal epoch (red symbols) are at different distances from the center (mean point of 90 s immediate preictal energy and entropy profile shown in yellow symbols) of the disk D, calculated from a separate set of preictal epochs. Any point inside the disk D counts for the inclusion rate of the distribution. (b) Temporal distribution of the amount of time spent inside the disk D in the same preictal (red dots) and interictal (black dots) energy and entropy profiles shown in (a). The dots indicate points inside the disk (each point represents 2 s duration). The persistence is the period of time corresponding to the maximum number of temporally contiguous points in the disk D. In this example preictal persistence is 22 pts × 2 s = 44 s and interictal persistence is 4 pts × 2 s = 8 s.

2.5. Frequency band pre-selection

Using preictal and interictal epochs of the training data set TR1, we computed for each epoch the energy and entropy profile in 4 frequency bands ranging from 50 Hz to 450 Hz with a bandwidth of 100 Hz. We calculated the center of the disk D from the 90 s immediate preictal epochs and computed for each preictal epoch the distance of the 22 min window and for each interictal epoch the distances of all 22 min windows, as described above. Distributions of preictal and interictal distance values were then statistically compared for all channels using a left-tailed two-sample t-test of the null hypothesis that “preictal and interictal distance distributions have equal means” against the alternative hypothesis that the “mean of preictal distance distributions is less than the mean of interictal distance distributions”. For each patient, the frequency band in which the largest difference between distance distributions is observed is selected for subsequent analysis.

2.6. Training and discriminant analysis

We investigate five discriminant analysis techniques whereby binary classifiers are learned to separate preictal and interictal data in the features space: linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), Mahalanobis distance based analysis (MAHL) and two naïve Bayes based analyses (diagonal linear discriminant analysis (DLDA) and quadratic linear discriminant analysis (QLDA)).

The pooled covariance matrix of feature observations data must be positive defined in order for a discriminant analysis to be performed. Analyses are carried out in a supervised fashion whereby class labels (‘preictal’ and ‘interictal’) are known a priori. The resulting discriminant functions define binary classifiers which we use to identify whether a test epoch reflects a preictal or an interictal underlying state.

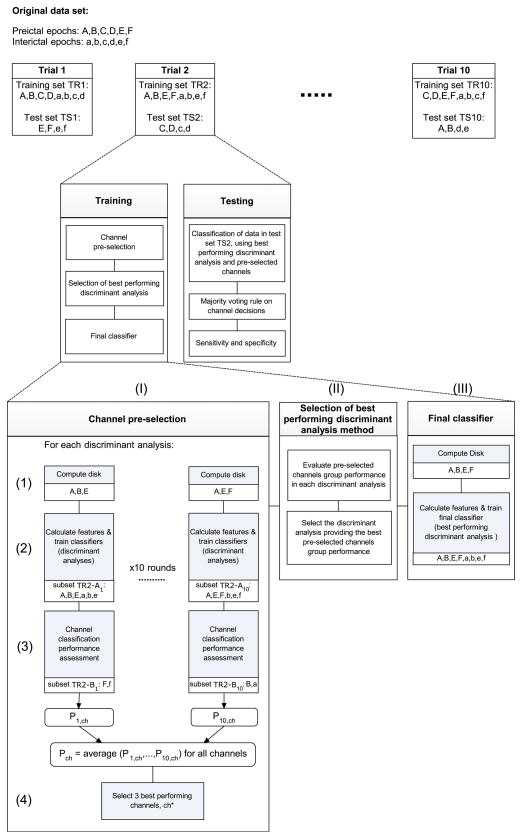
2.6.1. Channel pre-selection

Channel pre-selection is performed using subsets TR-A and TR-B (Fig. 4.I). Subset TR-A contains (Np-1) preictal epochs and 5 − 1 = 4 interictal epochs. This data set is used to learn the parameters of binary classifiers by performing discriminant analyses in the features space for each channel separately. The disk D is computed using TR-A preictal data (Fig. 4.I.1). Distance, inclusion and persistence are then calculated for TR-A preictal epochs and interictal epochs and used to learn the classifiers (Fig. 4.I.2).

Fig. 4.

Block diagram illustrating how a generic data set of 6 preictal and 6 interictal epochs is partitioned into one trial of training and testing data sets. Validation is performed using 10 trials. Three examples of data partitioning obtained by random resampling of the original data set are shown (top line). The second and third lines describe the analysis process for one trial: Processes of channel pre-selection (I), best performing discriminant analysis selection (II) and training of final classifier (III) are illustrated.

Subset TR-B, which contains one preictal and one interictal training epoch, is used to assess the performance of the classifiers on each channel (Fig. 4.I.3). We used a modified version of the score introduced by Chaovalitwongse et al. (2005) as a measure of performance:

$$P_{S,F}=1-\sqrt{{(1-S)}^2+F^2};P_{S,F}\in [0,1]$$

where S is the sensitivity of the classifier in correctly classifying the preictal epoch (S is either 0 or 1) and F is the false positives (FP) rate obtained by calculating the proportion of number of 22 min windows correctly classified as ‘interictal’ in the interictal epoch. The closer this score is to 1 the higher the channel performance.

To obtain an accurate assessment of classification performance, the above described process is repeated in 10 rounds in a leave-one- out-cross-validation fashion with different partitions of the training data in each round (TR1–TR10). Channel classification performance is then averaged over the rounds and the best 3 performing channels (the minimum number needed to apply the majority voting rule used later in classification decision) are selected for the testing phase (Fig. 4.I.4).

2.6.2. Best performing discriminant analysis method

Discriminant analyses are compared based on the group performance of the pre-selected channels obtained in each discriminant analysis (Fig. 4.II). Group performance is defined as the total sum of performance values of all pre-selected channels. The discriminant analysis method with the highest value of group performance is selected and used in defining the final classifier.

2.6.3. Final classifier

A binary classifier based on the best performing discriminant analysis method is built using all preictal and interictal epochs of the training data set TR (Fig. 4.III). The disk D is computed using all preictal training epochs. The features are calculated for all preictal and interictal training epochs as described earlier. The classifier is then trained in the features space with a priori knowledge of class labels of training preictal and interictal epochs. This classifier is thereafter used to classify preictal and interictal epochs of the unseen test data set TS. Its performance is assessed using the pre-selected channels. The majority voting decision rule is applied to channel classification results.

2.7. Performance testing

The performance of the final classifier is evaluated on the test data set TS in terms of sensitivity (percentage of correctly classified preictal epochs) and specificity, expressed as the number of false positives per hour (FP/h), with one false positive being the classification of a window in an interictal epoch as ‘preictal’. To evaluate the specificity in the context of seizure prediction, we consider the evaluated preictal epoch, i.e., 22 min, as would be done for the seizure prediction horizon (Winterhalder et al., 2003). All false positive decisions within the prediction horizon are counted as one. Such closely related false positives occur as a result of overlapping long windows.

2.8. Statistical validation

To evaluate the classification robustness and to statistically validate the test performance of the selected channels, bootstrapping approach is performed whereby 10 trials of training (TR1–TR10) and testing partitions (TS1–TS10) from each patient’s original data set are created (Fig. 4). Each trial has an equal size as the original data set and contains different partitions of training and testing sets of EEG epochs obtained by random sampling with replacement. The number of preictal and interictal epochs allocated for training and for testing is kept the same in each trial. Discriminant analyses, channel selection and testing procedures are then performed using one different data set sample in each trial. The overall classification performance is the average test performance across trials. Such measure of the classification performance is deemed statistically significant thanks to the bootstrapping approach. The resampling process provides a strong estimation of performance in prospectively classifying data sets larger than the original data set, thus providing a means of statistically validating the classification method.

3. Results

3.1. Frequency band pre-selection

The distance feature was computed for all channels of the training data. Distributions of distance measures in 2 to 4 preictal epochs and 5 interictal epochs for each patient were compared in 4 frequency bands: 50–150 Hz, 150–250 Hz, 250–350 Hz, 350– 450 Hz. Table 2 shows in each frequency band the maximum test statistic among all channels where the null hypothesis was rejected at the 5% significance level. The frequency band with highest test statistic maximum value was selected for subsequent analyses.

Table 2.

Highest test statistic (t) and p-value (p) in the t-tests performed on preictal and interictal distance distributions in 4 frequency bands for all channels. Frequency bands in which the highest t score is observed (marked with *) are selected.

Patient No.	Frequency band (Hz)
	50–150		150–250		250–350		350–450
	t	p	t	p	t	p	t	p
1	8.2967	0	11.5124	0	5.9646	0	15.5006*	0
2	27.1694*	0	22.387	0	22.1766	0	18.6769	0
3	3.5293	0.0003	17.737*	0.0039	14.4857	0	2.6902	0
4	2.1724	0.0156	3.1062*	0.0011	2.3099	0.011	2.6718	0.0041
5	1.903	0.0294	2.1412	0.0168	2.1946*	0.0148	2.0533	0.0208
6	9.5841*	0	9.198	0	9.0649	0	4.9587	0

3.2. Test performance

The results of classifying preictal and interictal epochs of the test set using the best performing discriminant analysis and the majority voting rule on the best performing channels selected in the training process are shown in Fig. 5.

Fig. 5.

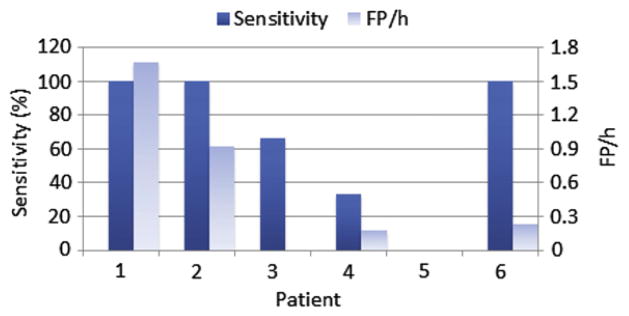
Sensitivity and FP rate of classifying preictal and interictal test data with majority voting rule applied to best performing channels selected in training. In patient 5, the sensitivity was zero.

Sensitivity varied between 0% and 100% and the FP rate between 0 and 1.67 FP/h. In 3 patients the sensitivity was 100% and in these patients the FP rate ranged from 0.23 to 1.67 FP/h.

3.3. Consistency of best performing channels across trials

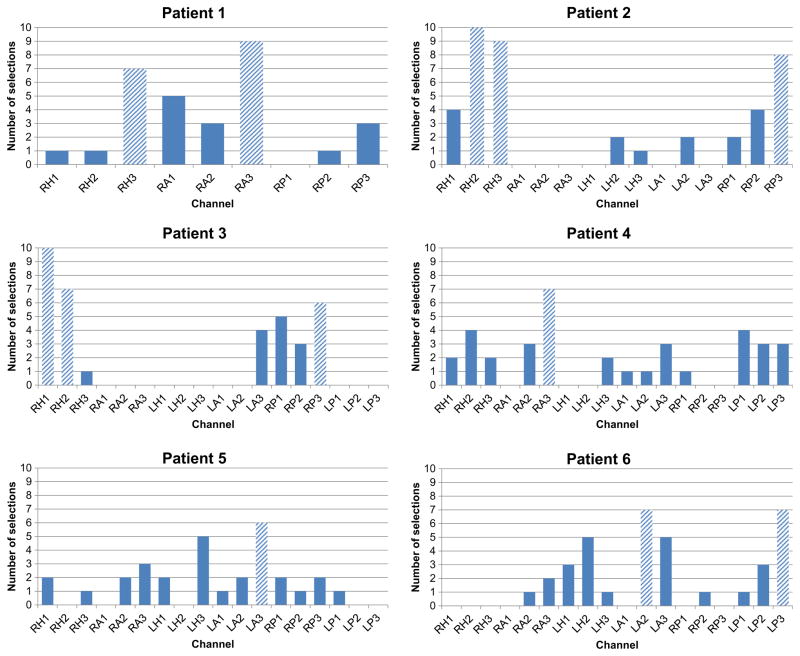
The best performing channels were selected in the training phase of each trial based on the best performing discriminant analysis and channel pre-selection criteria. Selected discriminant analyses were the same for three patients (DLDA) in each trial and varied for the other three patients where LDA was selected 7% of the time (average number of selections across all trials in all 3 patients), DQDA 37% of the time and DLDA 47% of the time. Although channels selected varied in each trial, there was a tendency for some channels (in general, from the same electrode) to be more selected than others, as shown in Fig. 6. For four patients, channels of one or two electrodes are visibly more selected than the others. In patient 1, channels RA3 (9/10 trials) and RH3 (7/10 trials) show very high selection rates. In patient 3, two clusters of channels gather around electrodes RH and RP with maximum selection rate at RH1 (10/10 trials) and RH2 (7/10 trials). One electrode, RH, appears clearly to be more selected than other electrodes in patient 2, with a maximum selection rate in RH2 (8/10 trials) and RH3 (8/10 trials). The same observation could be made for electrodes LP and LA in patient 6, with maximum in LP3 (7/10 trials) and LA2 (7/10 trials).

Fig. 6.

Number of selections of best performing channels across 10 trials. Channels selected six times or more (shaded bars) were considered to have higher selection rate than the rest of channels.

In the remaining two patients, one channel shows a selection rate relatively higher than the rest; channel RA3 (6/10 trials) in patient 4 and channel LA3 (6/10 trials) in patient 5.

The average performance scores across trials of the above-mentioned channels were generally high (Table 3), with lowest average performance of 0.71 ± 0.27 and highest average performance of 0.99.

Table 3.

Across trials average scores of the best performing channels.

Patient	Channel	Performance score
1	RA3	0.71 ± 0.27
	RH3	0.84 ± 0.11
2	RH2	0.99
	RH3	0.99 ± 0.02
3	RH1	0.93 ± 0.17
	RH2	0.89 ± 0.24
4	RA3	0.90 ± 0.14
5	LA3	0.85 ± 0.22
6	LA2	0.89 ± 0.14
	LP3	0.93 ± 0.1

3.4. Relation with seizure onset zone

Seizure onset zones (SOZ) are summarized in Table 1. The qualitative comparison between a patient SOZ and the areas with the best performing channels reveals a clear relationship: in 5 patients, these channels belong partially or completely to the SOZ and they never appear in the contra-lateral side. In patient 1 no observation could be made because of the unilateral implantation and the SOZ specified only as right mesial temporal.

3.5. Statistical validation

The test performance was measured in each trial by classifying test data using the classifier with best performing discriminant analysis and corresponding pre-selected channels with majority voting rule applied to channel decisions (scheme of Fig. 4). The mean and the variance of performance values across trials provide an estimation of the discriminative power and the robustness of the method and indicate how significant test results are. Average sensitivity and FP rate are depicted in Fig. 7. For four patients the average sensitivity exceeded 80% and the FP rate varied from 0.09 to 0.7 FP/h. Two patients showed relatively low sensitivities (59% and 56%) and FP rates of 0 and 0.52 FP/h respectively.

Fig. 7.

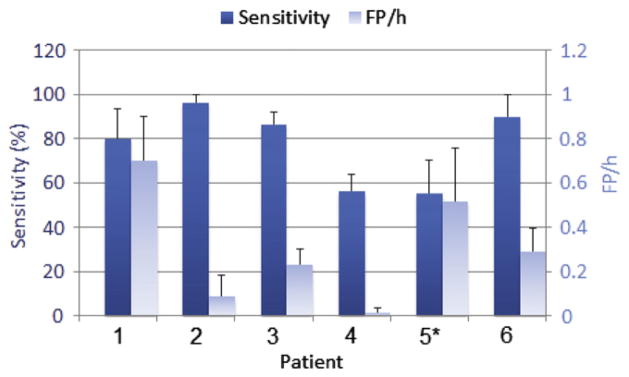
Average sensitivity and FP rate, with standard errors, in classifying the test data across 10 trials using best performing discriminant analysis and majority voting rule applied to corresponding pre-selected channels in each trial. *Based on 9 trials (one trial was not performed due to non-positive definiteness of the pooled covariance matrix of the training data when learning the classifier).

4. Discussion

We presented a new approach to discriminate preictal from interictal states using intracranial EEG recordings in patients with mesial temporal lobe epilepsy. A retrospective analysis of one subset of these recordings was made for training purpose where learning and in-sample optimization of discriminant analysis based classifiers were performed. We assessed whether this approach could lead to a seizure prediction framework by testing the performance of the classifiers in separating out of-sample preictal and interictal epochs. As the intent of this study was not to perform seizure prediction, long-term EEG data was not analyzed. To our knowledge, the idea of comparing states underlying EEG epochs based on their similarities with a hypothesized reference state defined from the preictal period has not been explored in other studies. We showed that by transforming the EEG from the temporal domain to a space defined by wavelet entropy and energy, we are able to differentiate between the state underlying the 22 min preictal epochs and the state underlying interictal epochs. By calculating features that characterize the organization of these epochs in the energy and entropy space using a disk having parameters learned from the preictal period of training data, we found that preictal and interictal epochs of independent testing data could be discriminated in many cases.

We have minimized the postictal impact on the analyzed epochs by selecting seizures that are sufficiently apart from each other and interictal epochs sufficiently away from any seizure. Postictal dynamics are by definition not present in the interictal state. Not excluding such dynamics could mislead the identification of an interictal state. The discrimination between preictal and interictal states in the postictal period however, could not be validated.

Channels were found to carry unequal discriminative power. Pre-selection of channels with best discrimination performance was performed as an in-sample optimization step. This optimization was restricted to training sets, which were excluded in testing. Channel sets that were mostly selected across trials were close or within the seizure onset zone and never in the contralateral side. This result supports our hypothesis that better discriminability should be observed on the seizure onset channels and by analyzing only these channels it may be possible to detect differences in brain dynamics between the preictal and interictal states. While this is in keeping with some early studies (Lehnertz and Elger, 1998; Martinerie and Adam, 1998; Le Van Quyen et al., 2000), it is not supported by other studies where channels with best discriminating power were remote and sometimes contralateral to the seizure onset zone (Mormann et al., 2003b, 2005; D’Alessandro et al., 2005; Le Van Quyen et al., 2005; Kuhlmann et al., 2010). It is interesting to notice that the former group of cited studies applied univariate measures while most of the latter group applied bivariate measures. Whether the concordance of our findings with one group of studies and the discordance with the other could be related to the EEG analysis approach is an arguable question.

Another training optimization procedure was the choice of best performing discriminant analysis. In general DLDA and DQDA were selected in most trials for all patients, suggesting that other discriminant analyses we investigated may be less suitable and could be excluded when considering the proposed framework in a seizure prediction technique.

Results of classifying out-of-sample data in different trials show that the proposed method yields good sensitivities (>80%) in 4 patients. The average FP rate ranged from 0.09 to 0.7 FP/h in these patients. In a context of seizure prediction, FP rates beyond 0.15 FP/h are generally questionable with respect to clinical application (Winterhalder et al., 2003). For this method to be considered in a seizure prediction context, optimization of parameters will be needed to lower the FP rate. By tuning parameters like the radius of the disk characterizing the reference state, lower values of FP rates could be realized. It is remarkable that for one patient an average performance of 99.6% sensitivity and 0.09 FP/h was achievable without such an optimization. For this patient, the method appears potentially readily convertible to a seizure prediction technique if a prediction horizon of 22 min is acceptable. Additionally, the proposed method will require a scheme for the detection of preictal state from continuous EEG data to be used for prediction. Other aspects related to performance evaluation and statistical validation of seizure prediction algorithms will also need to be taken into consideration (Schelter et al., 2006; Mormann et al., 2007).

For this method to efficiently separate preictal and interictal states, the analyzed EEG channels set must include at least one channel from a region where the dynamics of preictal and interictal state are different. In this study, this region is hypothesized and found to be the seizure onset zone. In cases where no electrode is placed in such a region, chances of detecting differences between preictal and interictal states are diminished. It is therefore expected that the method will not render high performance for all patients even if parameters were to be optimized and the discriminating power of the EEG feature was demonstrated in some patients. Accordingly, it is expected that results are poor in some patients. Nevertheless, the preimplantation information is most often sufficient to make it highly likely that at least some electrodes are near the seizure onset zone (this is the justification for implanting electrodes).

The evaluation of discriminability between preictal and interictal states in different frequency bands using the distance to reference state revealed no particular band in which a superior discriminating power is observable for all patients. Distributions of preictal and interictal distance values varied in channels and frequency bands for each patient suggesting that the preictal state is ‘closer’ to a reference state in some particular EEG frequencies than others.

The notions of ‘closeness’ and similarity between states used in this study may reflect the notion of attractor (Milnor, 1985) in the context of nonlinear dynamics theory. The reference state would share, in this context, some properties of an attractor in the space of energy and entropy for which a preictal state has a tendency to remain close and an interictal state to stay away.

The rationale behind the choice of relatively short period to define the reference state is that the latter is hypothesized to facilitate seizure occurrence within a short time. This choice however, is quite arbitrary and an evaluation of different lengths of the immediate preictal period may need to be considered in future work.

In summary, while we acknowledge the limited number of patients included in this study and the potential lack of statistical power resulting from some of the optimization procedures, we believe that the discrimination framework presented provides encouraging results and could be the core of a seizure prediction technique which is expected to be optimized in order to yield a performance that is clinically acceptable. Such a prediction technique should be tested on prospective long lasting data from a larger sample of patients than the sample presented in this study.

HIGHLIGHTS.

• Preictal and interictal epochs are distinguishable in some patients using EEG measures of similarity with a reference state defined from the immediate preictal period.

• Wavelet energy and entropy characterize the state underlying EEG epochs.

• Discriminability between preictal and interictal states varies with frequency bands.

Appendix A. Calculation of wavelet energy and entropy from lines of modulus maxima

ψ denotes a wavelet, the projection of a signal s(t) on the wavelet localized in time instant b and a scale a produces the wavelet transform of the signal s(t):

$$W_{a,b}(S)=\frac{1}{\sqrt{a}}{\int }_{-\infty }^{+\infty }S(t){\psi }^{\ast }\left(\frac{t-b}{a}\right)dt$$ (1)

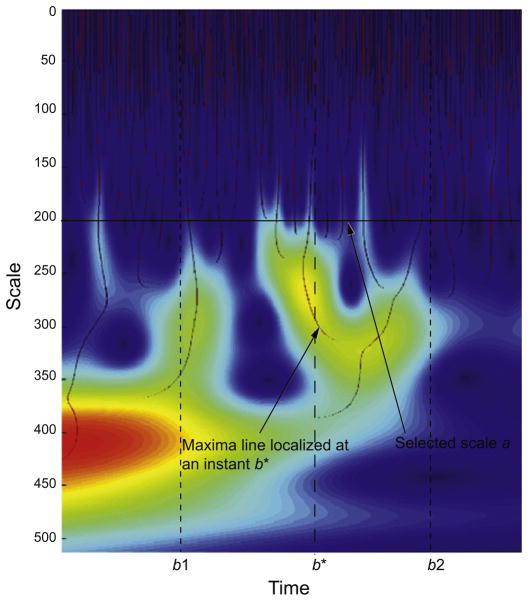
where ψ denotes the complex conjugate of ψ. By definition, a modulus maximum of the wavelet transform is any point (a₀,b₀) such that |Wa_n,b| < |Wa_n,b_n| when b is in the neighborhood of b₀. For each scale, the modulus maxima are the local maxima points across time. A maxima line is a continuous curve of modulus maxima along the scales in the time-scale plane (Mallat and Hwang, 1992). An illustration of these lines in the time-scale plane is shown in Fig. A1.

Fig. A1.

Illustration of maxima lines. Signal irregularities at a frequency corresponding to the scale a in a segment of time [b1, b2] are entirely detected from wavelet coefficients along the maxima lines localized at instants b* between b1 and b2.

Using the frequency resolution of the wavelet, to each scale a corresponds a frequency window f_a (Mallat, 1999).The energy and the entropy of the signal s(t) in the frequency band f_a and the period of time [b1, b2] could be derived in the time-scale plane solely from the wavelet coefficients along the maxima lines localized in time at the instants b* ∈ [b1, b2] and at the scale a corresponding to the frequency window f_a.

Since the modulus of wavelet coefficient W_a,b*along a maxima line is strictly positive (W_a,b* are non-vanishing coefficients) it can be expressed as exponential of some associated energy E_a,b*:

$$\mid W_{a,b^{\ast }}\mid =e^{-\frac{E_{a,b^{\ast }}}{E_0}}$$ (2)

with E₀ a normalizing energy value set arbitrarily as a calibration factor common to all analyses. It scales the wavelet amplitude in the definition of the probability distribution. The probability associated with energy values computed at the scale a and at each instant b* ∈ [b1, b2] can be expressed as a Gibbs distribution:

$$P_{a,b^{\ast }}=\frac{e^{-E_{a,b^{\ast }}}}{{\sum }_{b^{\ast }}{e}^{-E_{a,b^{\ast }}}}$$ (3)

The signal energy at the scale a (equivalently in the frequency band f_a) is the expected energy value associated to the maxima lines confined within the time period [b1, b2]:

$$E_{f_a}=\sum _{b^{\ast }\in [b1,b2]}{p}_{a,b^{\ast }}{E}_{a,b^{\ast }}$$ (4)

The entropy is defined according to the probability in Eq. (3):

$$S_{f_a}=\sum _{b^{\ast }\in [b1,b2]}{p}_{a,b^{\ast }}ln(p_{a,b^{\ast }})$$ (5)

Finally, the energy and the entropy of the signal in a frequency band B are determined by summing respectively all the energies and all entropies associated to each scale as calculated in Eqs. (4) and (5):

$$E=\sum _{f_n\in B}{E}_{f_a}$$ (6)

$$S=\sum _{f_n\in B}{S}_{f_a}$$ (7)