Modeling Between- and Within-Subject Variance in Ecological Momentary Assessment (EMA) Data Using Mixed-Effects Location Scale Models

Abstract

Ecological Momentary Assessment (EMA) and/or Experience Sampling (ESM) methods are increasingly used in health studies to study subjective experiences within changing environmental contexts. In these studies, up to thirty or forty observations are often obtained for each subject. Because there are so many measurements per subject, one can characterize a subject’s mean and variance, and specify models for both. In this article, we focus on an adolescent smoking study using EMA where interest is on characterizing changes in mood variation. We describe how covariates can influence the mood variances, and also extend the statistical model by adding a subject-level random effect to the within-subject variance specification. This permits subjects to have influence on the mean, or location, and variability, or (square of the) scale, of their mood responses. These mixed-effects location scale models have useful applications in many research areas where interest centers on the joint modeling of the mean and variance structure.

1. Introduction

Modern data collection procedures, such as ecological momentary assessments (EMA) [1, 2], experience sampling [3, 4, 5], and diary methods [6], have been developed to record the momentary events and experiences of subjects in daily life [6]. These procedures yield relatively large numbers of subjects and observations per subject, and data from these designs are sometimes referred to as intensive longitudinal data [7]. Such designs are in keeping with the “bursts of measurement” approach described by Nesselroade and McCollam [8], who called for such an approach in order to assess intra-individual variability. As noted by Nesselroade and McCollam [8], such bursts of measurement increase the research burden in several ways; however, they are necessary for studying intra-individual variation and to explain why subjects differ in variability rather than solely in mean level [6]. In this article, we describe data from a natural history study of adolescent smoking, using EMA, where interest was on determinants of the variation in the adolescents’ moods.

In mental health research, EMA methods have been used in studying pediatric affective disorders [9], eating disorders [10, 11], drug abuse [12], schizophrenia [13, 14], borderline personality disorder [15], stress and anxiety [16, 17], and sexual abuse [18]. Similarly, in smoking research, some EMA studies include those studying relapse in people who are quitting smoking [19], relapse among adolescent smokers [20], examining the urge to smoke [21], and our own EMA studies on adolescents [22, 23].

Data from EMA studies are inherently multilevel with, for example, (level-1) observations nested within (level-2) subjects. Thus, linear mixed models (LMMs, aka multilevel or hierarchical linear models) are increasingly used for EMA data analysis [7, 24]. A basic characteristic of these models is the inclusion of random subject effects into regression models in order to account for the influence of subjects on their repeated observations. The variance of these random effects indicate the degree of variation that exists in the population of subjects, or the between-subjects variance. Analogously, the error variance characterizes how much variation exists within a subject, or the within-subjects variance. These variances are usually treated as being homogeneous across subject groups or levels of covariates.

In EMA studies, it is common to have up to thirty or forty observations per subject, and this allows greater modeling opportunities than what conventional LMMs allow. In particular, one very promising extended approach is the modeling of both between-subject (BS) and within-subject (WS) variances as a function of covariates, in addition to their effect on overall mean levels. For example, if a smoker’s mood is the outcome, then one can consider the effect of covariates on their mood level (e.g., how happy/sad they are on average), as well as on their variation in mood (e.g., how labile/erratic their mood is). Or, one can examine mood changes when a person smokes in terms of the mean (does mood improve?) and variance (does mood stabilize?), and what variables might be related to those smoking-related changes of mood level and variation. Thus, by allowing WS variance to be a function of covariates, we can more directly examine the hypothesis that smoking helps to regulate mood [25]. Indeed, in a recent review, Parrott [26] stated that mood vacillation and its relationship to nicotine dependency is an important topic for future research.

Recently, Hedeker et al. [27] described a mixed model for variance modeling of EMA data. Like all LMMs, this model allows covariates and a random subject effect to influence the mean response of a subject. However, this model also includes a log-linear structure for both the WS and BS variance, allowing covariates to influence both sources of variation. Finally, a random subject effect is included in the WS variance specification. This permits the WS variance to vary at the subject level, above and beyond the influence of covariates on this variance. In this article, we more fully describe the mixed-effects location scale model of Hedeker et al. [27], and show how it can be used to model changes in mood levels and mood variation as a function of covariates. In particular, we examine the role of smoking on mood variation in adolescents. Standard software (i.e., SAS PROC NLMIXED) can be used to estimate the model parameters; a syntax example is available from the first author upon request.

2. Adolescent smoking, mood, and variability

Many prominent models of cigarette smoking maintain that smoking is reinforcing, and that smoking can relieve negative affect [28, 29]. Indeed, both adults and adolescents often claim that smoking is relaxing and reduces emotional distress [28, 30]. However, although the relationship between mood and smoking has received substantial empirical attention for adult smokers, much less is known about the acute changes in mood with smoking among adolescents. The present study, with its focus on real-time assessments of mood and smoking among adolescents, helps to shed light on this important topic.

Although there is substantial consensus among both smokers and researchers that smoking helps to regulate affect, most of the empirical work investigating the smoking-mood relationship has focused on the examination of changes in mean levels of mood with smoking. Surprisingly, although affect regulation inherently implies the modulation of variability in mood as well, the examination of variability in mood and smoking has largely been neglected. As Hertzog and Nesselroade [31] note, describing mean levels of variables is not always adequate for examining key features of developmental change. Variation also conveys important information about the phenomenon of interest. In the case of adolescent smoking and the development of dependence, variation in mood and mood changes may help to better explain the development of tolerance. Examining individual variability may enhance our ability to predict changes in smoking behavior above and beyond what can be achieved by examining mean information alone.

Important, too, in the examination of mood and smoking, is the distinction between within-person and between-person variability. Kassel and colleagues [28, 32] have argued persuasively for the need to differentiate causal, within-person mechanisms from between-person data. Whether smoking relieves negative affect is essentially a within-person question, and thus analytic models need to similarly differentiate between within-subject and between-subject effects.

Much of the research on mood and smoking has also been limited to assessments of negative affect, while ignoring positive affect. This neglect is particularly problematic given the theoretical importance of differentiating between negative reinforcement models of smoking and positive reinforcement models, especially in the development of dependence among adolescents [33]. There is also considerable evidence to support the notion that positive and negative affect are distinct constructs, and not just opposite ends of a continuum [34, 35]. Thus, in the current study, we assessed both positive and negative affect.

Finally, there may well be individual differences in the extent to which adolescents’ moods vary, and whether they vary with smoking level. We hypothesized that level of smoking would affect mood variability. Following along the lines of the development of tolerance with dependence, we hypothesized that as smoking level or experience increased, variability in overall mood would decrease.

3. Adolescent Smoking Study

Data from a natural history study of adolescent smoking motivated the application of the location scale mixed model. Students included in this study were either in 9th or 10th grade at baseline, 55.1% female, and self-reported on a screening questionnaire 6–8 weeks prior to baseline that they had smoked at least one cigarette in their lifetime. The majority (57.6%) had smoked at least one cigarette in the past month at baseline. Written parental consent and student assent were required for participation. A total of 461 students completed the baseline measurement wave. The study utilized a multi-method approach to assess adolescents in terms of self-report questionnaires, a week-long time/event sampling method via palmtop computers (EMA), and in-depth interviews.

Here, we focus on the EMA data. Adolescents carried the hand-held computers with them at all times during a seven consecutive day data collection period and were trained to both respond to random prompts from the computers and to event record (initiate a data collection interview) smoking episodes. Questions included ones about place, activity, companionship, mood, and other subjective items. The hand-held computers date and time-stamped each entry. For the analyses reported, we treated the responses obtained from the random prompts. In all, there were 14,105 random prompts obtained from the 461 students with an approximate average of 30 prompts per student (range = 7 to 71).

Two outcomes were considered: measures of the subject’s negative and positive affect (NA and PA) at each random prompt. Both of these measures consisted of the average of several individual mood items, each rated from 1 to 10, that were identified via factor analysis. Specifically, PA consisted of the following items that reflected a subject’s assessment of their positive mood before the prompt signal: I felt happy, I felt relaxed, I felt cheerful, I felt confident, and I felt accepted by others. Similarly, NA consisted of the following items assessing pre-prompt negative mood: I felt sad, I felt stressed, I felt angry, I felt frustrated, and I felt irritable. Over all prompts, and ignoring the clustering of the data, the marginal mean of PA was 6.797 (sd=1.935), while the NA marginal mean was 3.455 (sd=2.253).

Of interest is the degree of heterogeneity in these mood measures in terms of both WS and BS variation. Also, it is useful to examine whether certain covariates can explain some of the variation in these two sources of heterogeneity, over and above the influence of these covariates on the mean response. It is also reasonable to allow random subject effects for both the mean response (to allow for subjects with different average levels of mood) and for a subject’s WS variance (to allow for different levels of mood consistency). The mixed location scale model, described below, incorporates these considerations into a unified approach.

4. Mixed Location Scale Model

Consider the following mixed-effects regression model for the affect measurement y, either NA or PA, of subject i (i = 1, 2, …, N subjects) on occasion j (j = 1, 2, …, n_i occasions):

$$y_{ij}={\mathit{x}}_{ij}^{\prime }\mathit{\beta }+{\upsilon }_i+{\epsilon }_{ij},$$ (1)

where x_ij is the p × 1 vector of regressors (typically including a “1” for the intercept as the first element) and β is the corresponding p × 1 vector of regression coefficients. The regressors can either be at the subject level, vary across occasions, or be interactions of subject-level and occasion-level variables. The random subject effect υ_i indicates the influence of individual i on his/her repeated mood assessments. The population distribution of these random effects is usually assumed to be a normal distribution with zero mean and variance ${\sigma }_{\upsilon }^2$. The errors ε_ij are also assumed to be normally distributed in the population with zero mean and variance ${\sigma }_{\epsilon }^2$, and independent of the random effects. Here, ${\sigma }_{\upsilon }^2$ represents the between-subjects (BS) variance and ${\sigma }_{\epsilon }^2$ is the within-subjects (WS) variance.

To allow covariates (i.e., regressors) to influence the BS and WS variances, we can utilize a log-linear representation, as has been described in the context of heteroscedastic (fixed-effects) regression models [36, 37], namely,

$${\sigma }_{{\upsilon }_i}^2=\text{exp}({\mathit{u}}_i^{\prime }\mathit{\alpha }),$$ (2)

$${\sigma }_{{\epsilon }_{ij}}^2=\text{exp}({\mathit{w}}_{ij}^{\prime }\mathit{\tau }).$$ (3)

The variances are subscripted by i and j to indicate that their values change depending on the values of the covariates u_i and w_ij (and their coefficients). The number of parameters associated with these variances does not vary with i or j. Both u_i and w_ij would usually include a (first) column of ones for the reference BS and WS variances (α₀ and τ₀), respectively. Thus, the BS variance equals exp α₀ when the subject-level covariates u_i equal 0, and is increased or decreased as a function of these covariates and their coefficients α. Specifically, for a particular covariate u*, if α* > 0, then the BS variance increases as u* increases (and vice versa if α* < 0). Note that the exponential function ensures a positive multiplicative factor for any finite value of α, and so the resulting variance is guaranteed to be positive. The WS variance is modeled in the same way, with the exception that both time-varying and subject-varying covariates can influence the WS variance. For this reason, the covariate vector is indicated as w_ij for the WS variance. Thus, this model allows both subject-varying and time-varying covariates to influence the WS variance, but only subject-varying variables to influence the BS variance. The coefficients in α and τ indicate the degree of influence on the BS and WS variances, respectively, and the ordinary random intercept model is obtained as a special case if α = τ = 0 for all covariates in u_i and w_ij (i.e., excluding the reference variances α₀ and τ₀).

We can further allow the WS variance to vary across subjects, above and beyond the contribution of covariates, namely,

$${\sigma }_{{\epsilon }_{ij}}^2=\text{exp}({\mathit{w}}_{ij}^{\prime }\mathit{\tau }+{\omega }_i),$$ (4)

where the random subject (scale) effects ω_i are distributed in the population of subjects with mean 0 and variance ${\sigma }_{\omega }^2$. The idea for this is akin to the inclusion of the random (location) effects in equation (1), namely, covariates do not account for all of the reasons that subjects differ from each other. The υ_i parameters in (1) indicate how subjects differ in terms of their means and the ω_i parameters in (4) indicate how subjects differ in variation, beyond the effect of covariates. Notice that taking logs in (4) yields $\text{log}({\sigma }_{{\epsilon }_{ij}}^2)={\mathit{w}}_{ij}^{\prime }\mathit{\tau }+{\omega }_i$, which indicates that if the distribution of ω_i is specified as normal, then the random effects serve as log normal subject-specific perturbations of the WS variance. In other words, the WS variances follow a log normal distribution at the individual level. The skewed, nonnegative nature of the log normal distribution makes it a reasonable choice for representing variances, and it has been used in many diverse research areas for this purpose [38, 39, 40, 41, 42].

In this model, υ_i is a random effect which influences an individual’s mean, or location, and ω_i is a random effect which influences an individual’s variance, or (square of the) scale. Thus, we dub the model with both types of random effects as a mixed-effects location scale model. These two random effects are correlated with covariance parameter σ_υω. This covariance parameter indicates the degree to which the random location and scale effects are associated with each other. Details on estimation of model parameters can be found in Hedeker et al. [27]; a nice feature of the model is that standard software (i.e., SAS PROC NLMIXED) can be used for estimation.

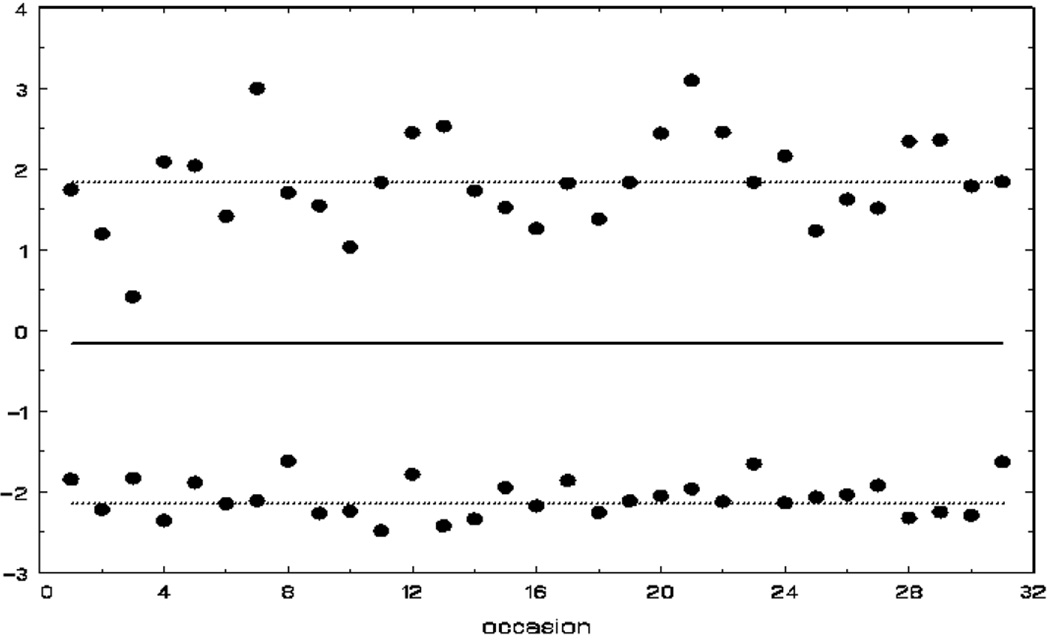
Visually, Figure 1 presents the pertinent details of the model. In this figure, the average across all subjects is depicted with the solid horizontal line, and the lines of two subjects are presented as dotted lines. Data points for these two subjects are also included in the plot. In a given dataset, there will be as many dotted lines as there are subjects, but for simplicity here we only plot two subjects. Also, for simplicity, consider all covariates as subject-varying only. The effect of covariates x on the mean response is represented by β; this effect influences the solid line by either raising or lowering it as a function of the covariates. Each dotted line is indicative of a person’s random location effect υ_i, which indicates how a subject deviates from the mean response. In the figure, one subject is above and another subject is below the mean line. The heterogeneity in these dotted lines is indicative of BS variance: if the dotted lines are close together then there is not much subject heterogeneity, conversely if the dotted lines are spread out then more heterogeneity is indicated. The effect of covariates u on this heterogeneity is represented in the model as α. The degree of variation of a person’s data points around their line is the WS variance. If the points are quite close to a subject’s line, then that subject has low WS variance (i.e., the lower subject in the Figure). Conversely, if a subject’s data points vary greatly around that person’s line then more WS variation is indicated (i.e., the upper subject in the Figure). Covariates w influence this WS variation through the coefficients τ. Finally, the model posits that covariates do not explain all of WS variance by including the random scale effect ω_i.

Figure 1.

Mean response (solid line), mean deviations of two subjects (dotted lines), and data across occasions for these two subjects (solid dots).

Results

To begin, we fit models for NA and PA without any covariates. Table 1 lists the parameter estimates of these models. Mean PA and NA scores are estimated to be approximately 6.8 and 3.5, respectively. These estimates account for the clustering of the data within subjects and allow for the fact that subjects have different numbers of occasions. In terms of the variance estimates, there is considerable heterogeneity of both location and scale between subjects. For both PA and NA, the estimates of α₀ (location variation) and ${\sigma }_{\omega }^2$ (scale variation) greatly exceed their standard error estimates. Thus, subjects differ in terms of their positive and negative affect mean level and level of variation. Interestingly, the estimates for PA are rather smaller than their NA counterparts. This suggests that there is more subject heterogeneity in both mean and variation for NA, relative to PA.

Table 1.

Positive and Negative Affect - maximum likelihood estimates and standard errors (se)^*

	Positive Affect		Negative Affect
parameter	estimate	se	estimate	se
mean β0	6.779	.058	3.482	.071
WS variance τ0	.622	.036	.741	.047
BS variance of location α0	.367	.069	.793	.069
BS variance of scale ${\sigma }_{\omega }^2$	.518	.039	.963	.069
covariance συω	−.386	.048	.765	.080

^*p < .001 for null hypothesis tests of all model parameters (i.e., H₀ : parameter = 0)

Turning to the covariance (σ_υω) estimates, these are also relatively large and of opposite sign for PA and NA. For NA, the positive covariance indicates that subjects who are high in terms of their negative affect mean also exhibit greater variation in negative affect. Thus, subjects with relatively poor moods (higher NA) fluctuate more in their mood. This could reflect the notion that better moods (less NA) may be more “trait-like” and not as reactive to different situational cues. Alternatively, this positive association might reflect a floor effect of measurement. Namely, as noted, the marginal mean of negative affect is about 3.5, or relatively low and towards the minimum of this scale. Thus, subjects who are lower than average have relatively less room to vary downward than those who are above average. Conversely, the negative covariance for PA indicates that subjects who are relatively high in terms of their mean positive affect are less varied across prompts in their positive affect responses. Again, this could suggest that more positive moods reflect trait-like positivity, or this could be a ceiling effect of measurement, since the marginal mean of PA is about 6.8, or towards the maximum value for this scale. Thus, one might argue that subjects with greater than average positive affect have relatively less room for upward movement, and so less variation.

Finally, one can re-express the parameter estimates to yield BS and WS estimates in their original scale. For BS variance, these are simply equal to exp (α₀), yielding 1.443 and 2.210 for PA and NA, respectively. For WS variance, the translation of $\text{exp}({\tau }_0+.5{\sigma }_{\omega }^2)$ (see Hedeker et al. [27]) gives 2.413 and 3.396 for PA and NA, respectively. Thus, as mentioned above, more variation, both BS and WS, is seen for NA than PA. These estimates can be further expressed as an intraclass correlation, namely the BS variance divided by the sum of the BS and WS variance. This yields values .374 and .394 for PA and NA, respectively, indicating that the data are moderately correlated within subjects for both mood variables.

To examine the effect of smoking level on mood we augmented the models for PA and NA with the subject-level covariate Smoker, an indicator of whether the subject is a current smoker (coded no=0 or yes=1). This was determined based on whether or not the subject provided at least one smoking event during the week-long data collection period. Of the 461 adolescents, 234 (51%) did provide a smoking event, while 227 (49%) did not. We also included the variable Male (coded 0=female or 1=male) to control for gender effects on mood. In this study there were 254 females (55%) and 207 males (45%). Table 2 present the results of these analyses of PA and NA.

Table 2.

Mixed location scale model of Positive and Negative Affect, N = 461 and ∑ n_i = 14105, maximum likelihood estimates, standard errors (se), and p-values

	Positive Affect			Negative Affect
parameter	estimate	se	p <	estimate	se	p <
Mean
Intercept β0	6.741	.094	.001	3.609	.118	.001
Male β1	.296	.114	.01	−.603	.136	.001
Smoker β2	−.188	.115	.10	.283	.136	.04
WS variance
Intercept τ0	.706	.060	.001	.824	.077	.001
Male τ1	−.276	.072	.001	−.453	.093	.001
Smoker τ2	.078	.071	.27	.238	.092	.01
BS variance
Intercept α0	.292	.102	.004	.908	.067	.001
Male α1	−.103	.121	.40	−.319	.113	.005
Smoker α2	.198	.120	.10	.111	.110	.31
Scale
BS variance of scale ${\sigma }_{\omega }^2$	.506	.039	.001	.908	.065	.001
covariance συω	−.361	.046	.001	.661	.073	.001

In terms of the means, males have significantly higher PA (β̂₁ = .296, p < .01) and significantly lower NA (β̂₁ = −.603, p < .001) than females. Also, smokers have significanly higher NA levels (β̂₂ = .283, p < .04) than non-smokers. For the WS variance, males elicit less varied responses on both PA and NA (τ̂₁ = −.276 and −.453, respectively, with p < .001 for both). Additionally, in terms of the BS variance of NA, males are less varied as a group than females (α̂₁ = −.319, p < .005). For smokers, there is a significant positive effect on WS variance of NA (τ̂₂ = .238, p < .01), indicating that smokers give more varied NA responses than non-smokers. The scale variance and scale-location covariance terms remain highly significant in both models, with similar interpretations as previously described.

The above model collapses all subjects with a smoking event into a single group. A closer examination of the effect of smoking considers a subject’s smoking level, and not just whether or not they are a current smoker. For this, we created a variable Psmk equaling the proportion of occasions (both random prompts and smoking events) that were smoking events for a subject. In the sample of 461, the average number and median of random prompts equaled 30, with a range of 7 to 71. Of the 234 subjects that provided a smoking event during the measurement period (approximately one week), the average was 5, the median was 3, and the range was from 1 to 42 reported events. The quartiles of the variable Psmk equaled .049 (25%), .081 (50%), and .179 (75%), relecting a moderate degree of variation in the level of smoking among these adolescents. By including both Smoker and Psmk as regressors, we are estimating a piecewise linear relationship in which the slope for Smoker reflects the difference between low-level smokers (i.e., those with the lowest value of Psmk) and non-smokers, while the slope for Psmk reflects the slope only among smokers. Table 3 lists the results using these two smoking-related variables, plus gender, in the mean model, as well as the models of WS and BS variance, of PA and NA.

Table 3.

Mixed location scale model of Positive and Negative Affect, N = 461 and ∑ n_i = 14105, maximum likelihood estimates, standard errors (se), and p-values

	Positive Affect			Negative Affect
parameter	estimate	se	p <	estimate	se	p <
Mean
Intercept β0	6.740	.094	.001	3.607	.117	.001
Male β1	.299	.114	.01	−.599	.135	.001
Smoker β2	−.192	.147	.19	.483	.175	.006
PSmk β3	.018	.742	.98	−1.530	.791	.054
WS variance
Intercept τ0	.704	.059	.001	.820	.077	.001
Male τ1	−.272	.071	.001	−.444	.092	.001
Smoker τ2	.167	.090	.07	.427	.117	.001
Psmk τ3	−.693	.430	.11	−1.446	.554	.01
BS variance
Intercept α0	.293	.102	.004	.800	.100	.001
Male α1	−.115	.123	.35	−.319	.115	.006
Smoker α2	.152	.156	.33	.192	.140	.17
Psmk α3	.370	.812	.65	−.657	.653	.31
Scale
BS variance of scale ${\sigma }_{\omega }^2$	.503	.038	.001	.893	.064	.001
covariance συω	−.356	.047	.001	.647	.071	.001

First, comparing the models with and without the Psmk variable yields likelihood ratio tests results of ${\chi }_3^2=3\text{and}8$ for PA and NA, respectively. Thus, smoking level does not significantly alter the results for PA (p = .39), but does for NA (p < .05). For NA, in terms of the mean, the low-level effect of Smoker is positive and significant (β̂₂ = .483, p < .006), whereas the effect of smoking level (Psmk) is negative and marginally significant (β̂₃ = −1.530, p < .054). This suggests that low-level smokers have the highest NA levels, relative to non-smokers and higher level smokers. Also, a similar relationship is apparent in terms of the WS variance of NA, with a significant positive effect of low-level smoking (τ̂₂ = .427, p < .006) coupled with a significant negative effect of smoking level (τ̂₃ = −1.446, p < .01). Thus, low-level smokers are more varied in their NA responses relative to non-smokers and higher level smokers. A similar, though non-significant, pattern of results is observed for the effect of smoking on the WS variance of PA. These results support the notion that the mood stabilization effect of smoking, at least in terms of NA, increases with the level of smoking.

6. Discussion

This article has presented a location-scale mixed model that augments the mean model with sub-models of the BS and WS variances. Covariates can be included in each of these sub-models. Relative to the standard mixed model, this augmented approach can be useful to identify predictors of both WS and BS variation, and to test hypotheses about these variances. Also, by including a random subject effect on the WS variance, this model can examine the degree to which subjects are heterogeneous in terms of their variation on the outcome variable, over and above the effects of covariates. The random scale effects are further allowed to be correlated with the usual random location effects. Our examples with negative and positive affect clearly show that subjects are quite heterogeneous in terms of their mood variation, and also that there is appreciable correlation between a subject’s mood level (location) and their volatility (scale). For both NA and PA, worse mood levels (higher on NA and lower on PA) were associated with greater mood volatility. Additionally, in terms of negative affect, we observed a positive curvilinear effect of smoking level on the mean and WS variance.

Modern data collection procedures, such as EMA and/or real-time data captures, are increasingly used in many research areas. These approaches often provide a fair amount of both WS and BS data, and so allow the opportunity for modeling of both WS and BS variances as a function of covariates. The question of how much WS and BS data are necessary for variance modeling purposes is difficult to address definitively. For random coefficient models, Longford [43] noted the difficulty with providing general guidelines about the degree of complexity, for the variation part of a model, that a given dataset could support. This would seem to be true here as well. Carrying out some simulations with relatively small sample sizes (e.g., 20 subjects with 5 observations each) gives the general impression that the primary issue is that the estimation algorithm does not often converge, but instead has estimation difficulties of one sort or another, in small sample situations. Clearly, more work is necessary in this area.

In this paper, we have presented the mixed location-scale model for a continuous normal outcome. We have also developed this approach for ordinal outcomes [44]. In the ordinal approach, we extend the mixed-effects logistic regression model of Hedeker and Gibbons [45] by including the log-linear modeling of BS and WS variance, as well as the random scale effect. Also, as with the model presented in this paper, SAS NLMIXED can be used to estimate the parameters of the ordinal location-scale model, and Hedeker et al. [44] includes sample syntax.

As this is a relatively new modeling technique, certain limitations and cautions should be mentioned. Our model assumes that the random location effects are normally distributed and that the random scale effects are log-normally distributed. It is unclear how robust this model is to violations of these assumptions. To some extent, this can be examined empirically using the approach of Liu and Yu [46] for models with non-normal random effects. Also, attention should be paid to outliers and influential observations, as these might have undue effects on estimation of the model parameters, especially the variance parameters.