Mechanical Resonance Enhances the Sensitivity of the Vibrissa Sensory System to Near-Threshold Stimuli

Abstract

The representation of high-frequency sensory information is a crucial problem faced by the nervous system. Rodent facial vibrissae constitute a high-resolution sensory system, capable of discriminating and detecting subtle changes in tactual input. During active sensing, the mechanical properties of vibrissae may play a key role in filtering sensory information and translating it into neural activity. Previous studies have shown that rat vibrissae resonate, conferring frequency specificity to trigeminal ganglion (NV) and primary somatosensory cortex (SI) neurons during suprathreshold sensory stimulation. In addition to frequency specificity, a further potential impact of vibrissa resonance is enhancement of sensitivity to near-threshold stimuli through signal amplification. To examine the effect of resonance on peri-threshold inputs (≤80µm at the vibrissa tip), we recorded NV and SI neurons during stimulation at multiple amplitudes and frequencies, and generated minimal amplitude tuning curves. Several novel findings emerged from this study. First, vibrissa resonance significantly lowered the threshold for evoked neural activity, in many cases by an order of magnitude compared to stimuli presented at off-resonance frequencies. When stimulated at the fundamental resonance frequency, motions as small as 8µm at the vibrissa tip, corresponding to angular deflections of less than .2 degrees, drove neural firing in the periphery and cortex. Second, a closer match between vibrissal and neural frequency tuning was found for lower amplitude motions. Third, simultaneous paired recordings demonstrated that the minimal amplitude of resonant vibrissa stimulation required to evoke responses in SI increased significantly for recordings outside the primary vibrissa barrel column, providing additional evidence for somatotopically localized frequency columns. These data demonstrate that resonant amplification can increase the sensitivity of the vibrissa sensory system to an ecologically relevant range of low amplitude, high frequency stimuli.

INTRODUCTION

The meeting that inspired this collection of articles brought together researchers from many different levels of analysis, ranging from single cell recordings in culture to whole-head human EEG studies. A central theme throughout, highlighted by the theoretical position presented by Dr. Basar, was that an understanding of oscillatory biological phenomena is crucial to understanding biological information processing. The canonical example of this kind of process is frequency-defined states in the brain, which are correlated with the optimal performance of distinct behavioral tasks and have distinct impacts on action-potential activity. A second, different kind of oscillatory context discussed was the ‘state’ of non-neural systems (Basar and Guntekin 2007). The vascular system, for example, can exist in a variety of self-generated oscillatory states, demonstrating myogenic rhythmicity in lower frequency ranges that can show global synchrony or local, independent generation (Basar and Weiss 1981). While the direct connection between these oscillatory phenomena and neural dynamics has not been determined, the local distribution of blood flow and volume regulated by functional hyperemia was discussed as a potential source of neural modulation, impacting the excitability of neurons and influencing signal transmission (Moore and Cao 2007). This hemo-neural hypothesis suggests that the two oscillatory systems may be coupled.

The present paper explores a different kind of example of a non-neural component of a sensory system that may be key to translating environmental signals into sensory information. Oscillatory phenomena in the nervous system are driven by many sources, ranging from the intrinsic resonance of single neurons (Giacomo et al., 2007) to the pattern of motor activity that supports active sensing (Carvell and Simons, 1990; Fee et al., 1997). A crucial question is how environmental signals in different frequency ranges are translated into patterns of neural activity that form sensory representations. Several examples exist of oscillatory sensory input that can drive oscillations in peripheral and central sensory representations, and these phase-locked signals may be crucial to encoding (Moore and Andermann, 2005; Cariani, 1997; Wever, 1949). An alternative, though not exclusive, form of representation derives from the transduction of sensory signals into differences in relative rates of neural activity, based on mechanical amplification at the point of entry to the system (Rinberg and Davidowtiz, 2000). A key example of this kind of transduction is the auditory system, where embodied mechanical properties of the cochlea (von Bekesy, 1960) differentially excite and drive increased firing rates in specific subsets of neurons, forming a spatial map of frequency (see Geisler, 1998 for a review).

The vibrissa sensory system is widely employed for studies of neural processing and behavior. Several lines of inference suggest that small amplitude, high-frequency ‘micromotions’ are a key sensory signal in this system (Carvell and Simons, 1990; Neimark et al., 2003; Arabzadeh et al., 2003), and recent studies have detailed these micromotions in the awake, freely-behaving animal (Ritt et al., 2008). At the point of entry to the system, the mechanical properties of the vibrissae likely impact the transduction of these sensory signals. For example, recent studies have shown that vibrissae resonate, generating a several fold increase in motion amplitude when stimulated at their fundamental resonance frequency (Neimark et al. 2002; Hartmann et al. 2003; Neimark et al. 2003; Andermann et al. 2004; Mehta and Kleinfeld 2004; Moore and Andermann 2005; Ritt et al., 2008). This pattern of frequency-specific transduction has recently been observed in animals freely sampling a variety of surfaces with their vibrissae (Ritt et al., 2008). In this context, resonance tuning was robust during contact with rough and smooth surfaces, and during more ballistic and more periodic signal transmission, indicating that these embodied mechanical properties shape representation during the transduction of a variety of types of tactual ‘natural scenes’ (Ritt et al., 2008).

Resonance-dependent amplification by the vibrissae confers band-pass neural tuning to rat trigeminal ganglion (NV) and SI neurons (Andermann et al. 2004). Further, because vibrissa resonance is dependent on vibrissa length (Hartmann et al. 2003; Neimark et al. 2003), and length varies systematically from caudal to rostral across the vibrissa pad (Brecht et al. 1997), a map of frequency-tuned neurons is overlaid on the somatotopic representation of vibrissa position. Along a dorsal-ventral arc, vibrissae have similar lengths and in turn similar frequency tuning, generating isofrequency ‘columns’ that span multiple vibrissa-related barrel columns in SI (Andermann et al. 2004).

Based on these findings, we hypothesized that resonance may contribute to the specificity of vibrissa-based frequency discrimination, by generating frequency tuning in peripheral and central neurons, and by selective engagement of regions within somatotopic maps. Further, mechanical amplification due to resonance may facilitate the detection of high-frequency information, transforming small inputs that would otherwise not surpass the sensory neural threshold into suprathreshold stimuli (Neimark et al. 2003; Moore and Andermann 2005). In the present study, we tested the impact of frequency-specific mechanical amplification on the likelihood of driving a significant neural response and, more generally, on the amplitude of sensory responses relative to input strength. To address these questions, we presented a large range of sinusoidal stimuli varying in frequency and amplitude to a vibrissa while recording neural activity, permitting the construction of minimal amplitude tuning curves (MATCs), as commonly employed in the auditory system.

We observed several-fold decreases in response thresholds for neural firing at frequencies near the vibrissa fundamental resonance frequency (FRF), and enhanced gain of suprathreshold responses. In addition, we found that threshold amplitudes for effective resonant stimuli in SI increased sharply for recordings outside the principal barrel column, underscoring the spatial localization of frequency tuning in SI (Andermann et al. 2004). Taken with previous findings, these results suggest that vibrissa resonance can substantially impact the neural representations that mediate the detection and discrimination of low-amplitude, high-frequency stimuli.

RESULTS

Minimal Amplitude Frequency Sensitivity in NV

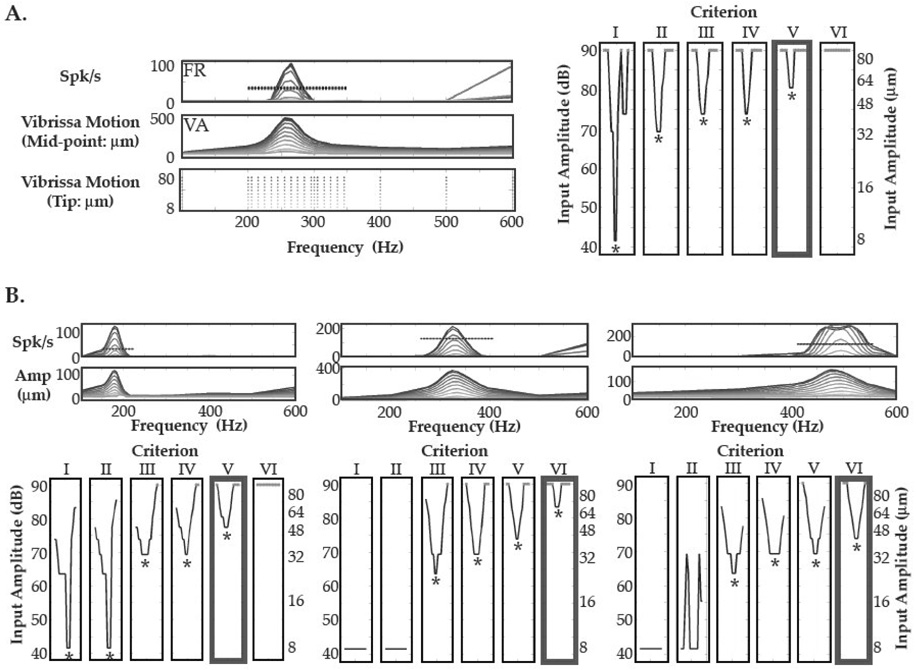
Neurons in NV demonstrated sharp frequency tuning for small-amplitude stimuli. In Figure 1A, firing rate responses of an NV unit and corresponding C2 vibrissa motion amplitudes are shown for stimuli applied in 5Hz intervals at 15 frequencies surrounding the FRF (a 265Hz range). In this example, MATCs with a well-defined ‘characteristic frequency’ (CF: the frequency at which the smallest amplitude stimulus drove a significant response) were observed for 5 of 6 criteria (Figure 1A right). As shown in Figure 1B, precise MATCs were observed for vibrissae demonstrating lower- and higher-frequency FRFs. Well-defined CFs were present in all NV receptive fields (N = 15/15) for at least one criteria employed.

Figure 1. Minimal Amplitude Tuning Curves in NV.

A. Left In all recordings (peripheral and cortical), 230 amplitude-frequency stimulus combinations were presented (3^rd panel from top), with dense sampling of 15 frequencies surrounding the vibrissa FRF (2^nd panel). Neural firing rate (FR) and vibrissa motion amplitude (VA) (1^st and 2^nd panels) are shown as a function of stimulus amplitude, with responses to larger input stimuli (e.g., 80µm) shown as darker gray scale lines. The ‘mid-point motion’ plot shows vibrissa motion measured with the opto-electrical device, while ‘tip motion’ indicates the stimulus input amplitude delivered to the distal vibrissa tip. Right Minimal amplitude tuning curves (MATC) were constructed using 6 threshold response criteria (most conservative the furthest panel on the right, most liberal on left, see Methods). Along the x-axis of each panel, the 15 sampled frequencies are plotted, from lowest frequency (Left) to highest (Right). Along the y-axis, MATCs are plotted on a motion amplitude level (MAL) decibel scale, referenced to 1µm motion. In this example, 5 of 6 criteria demonstrated frequency tuning, with well-defined characteristic frequencies (CF; marked by asterisks). The criteria level with the thickest box border (2^nd from right) shows the MATC resulting from the cut-off in activity indicated by the dashed line through the neural activation in the neural firing rate panel (FR) to the left. B. Three examples of MATCs in NV. The top row corresponds to the neural and vibrissa amplification plots as shown in 1A, with the thickest box marking the criteria indicated by the dashed line through the neural activity curves. Well-tuned responses with CFs corresponding to a tip motion of 8µm are shown in 1A and the example on the left in 1B.

Use of minimal amplitude tuning characteristics also provided a more precise correlation between vibrissa and neural frequency tuning. For the criterion that resulted in the largest occurrence of well-defined NV CFs (Criterion #3, see Methods; N = 9/15), the mean absolute distance between the CF and FRF was 2.78 ± 1.13 Hz (mean ± SE). This difference was significantly smaller than the mean absolute distance between the ‘best frequency’ (BF) and FRF calculated using 80µm amplitude frequency-mapping (16.7 ± 3.5 Hz, mean ± SE, N = 15; two-tailed t-test, P = 0.009; Andermann et al., 2004). These findings indicate that, as in the auditory system, near-threshold stimuli reveal more precise receptive field organization.

Minimal Amplitude Frequency Sensitivity in SI

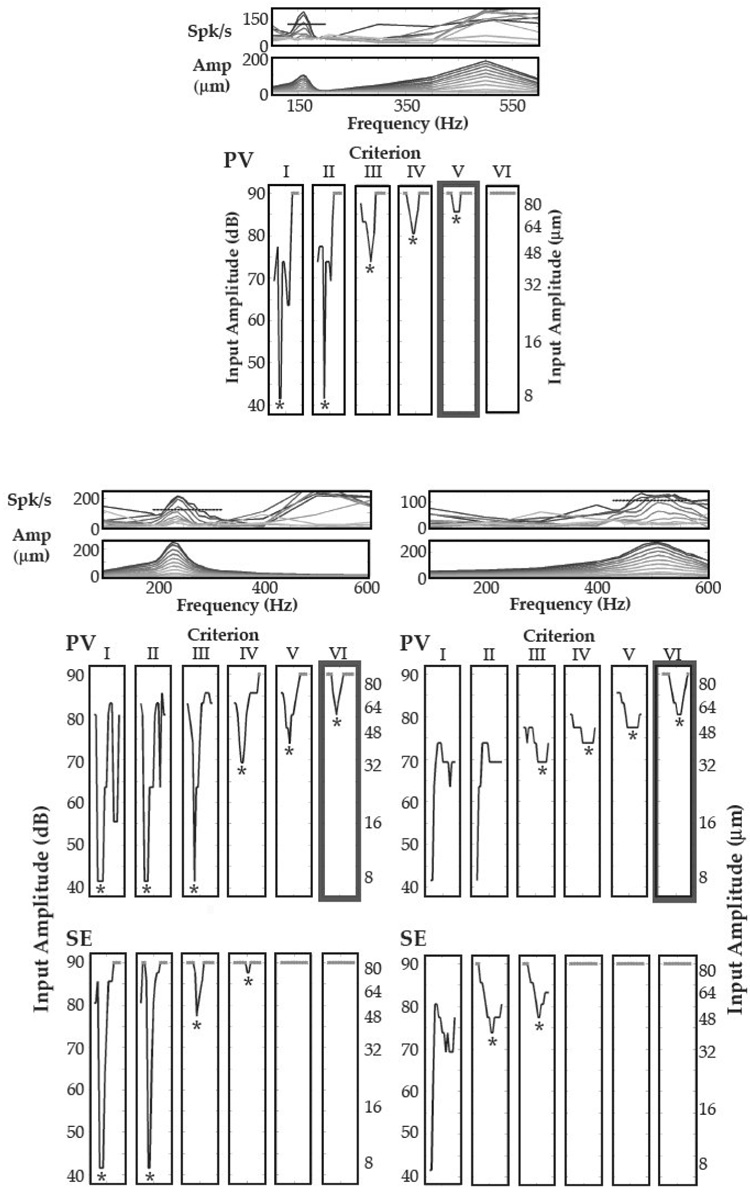
Well-defined MATCs were also present in SI. Examples of tuning curves are shown in Figure 2, demonstrating precise frequency tuning at several criteria and for a range of vibrissae. For all sites (N = 13/13), well-defined CFs were observed for at least one criterion. As with NV recordings, cortical CFs and FRFs were well matched. For the criterion that resulted in the highest probability of well-defined SI CFs for PV input (Criterion #4, see Methods, N = 10/13), the mean absolute distance between the CF and FRF was 11.3 ± 3.4 Hz (mean ± SE), which was significantly smaller than the mean absolute distance between the BF and FRF (29.4 ± 7.1 Hz, mean ± SE, N = 13; two-tailed t-test, P = 0.008).

Figure 2. Minimal Amplitude Tuning Curves in SI.

Top An example of a minimal amplitude tuning curve (MATC) in SI. Each MATC corresponds to the neural and vibrissa amplification plots above them, with the thickest box marking the criteria indicated by the dashed line (see Figure 1 for details). Below The Left and Right columns show two examples of MATCs where tuning curves were simultaneously recorded for the primary vibrissa (PV) recording and for the surround electrode (SE). Tuning of both positions was observed, with well-tuned curves and CFs observed across a broader range of statistical criteria for PV driven responses.

Vibrissa Resonance Amplification and Neural Amplification

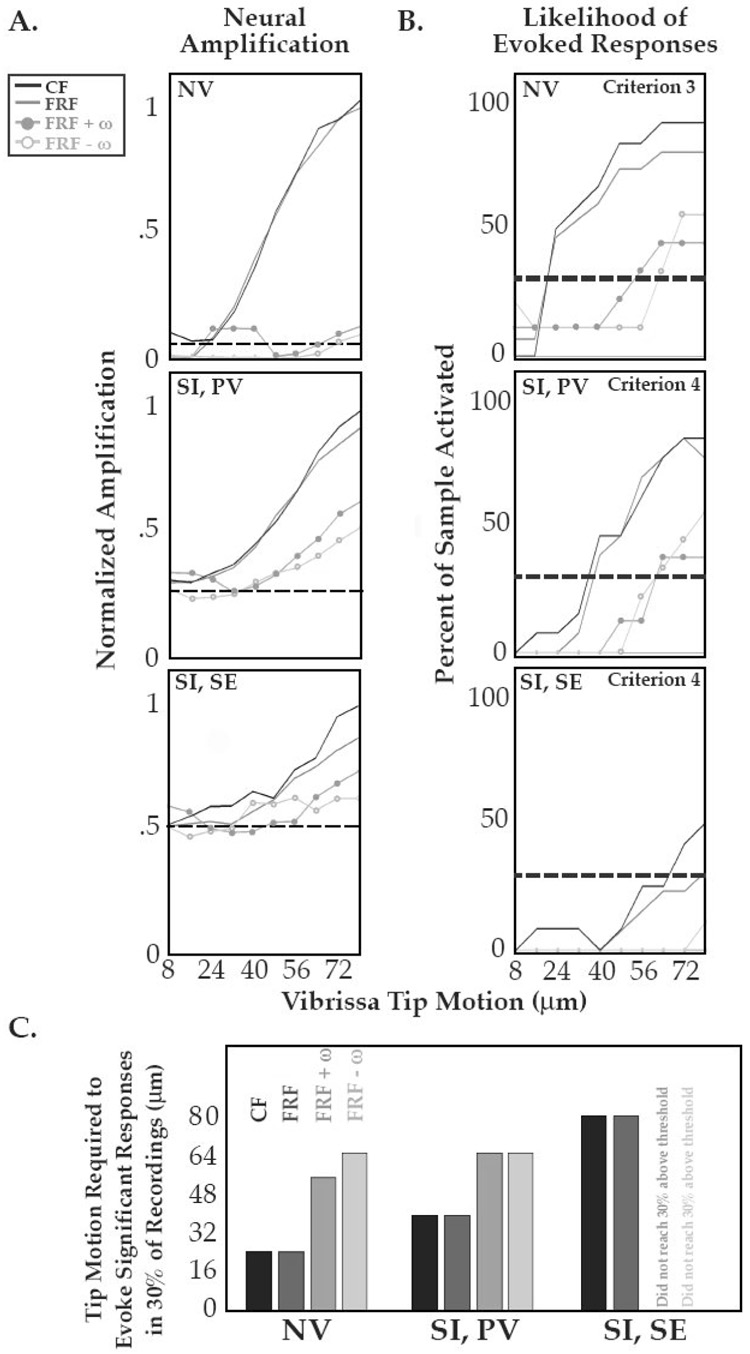
To quantify the impact of resonance on the probability of evoking a response and on the relative amplitude of neural activity, we plotted the gain in firing rate as a function of stimulus amplitude at distinct stimulus frequencies. In Figure 3A, firing rates are plotted as a function of vibrissa tip motion at the CF and FRF, and at frequencies ± ω from the FRF (ω: vibrissa resonance tuning bandwidth at ~3 dB (29%) below the amplitude at the FRF). To average across recordings, activity was normalized to the BF firing rate at 80µm.

Figure 3. Resonance-Related Amplification of Neural Activity.

A. Gain functions are shown for neural mean firing rates as a function of stimulus amplitude (8–80µm). Relative amplitude of response is shown for responses taken at the CF (black), FRF (dark gray), and at two frequencies ± 1 vibrissa motion bandwidth (±ω) from the FRF (lighter gray lines with filled and empty circle demarcations). Data were normalized to the peak evoked firing rate at the maximal stimulation amplitude (the best frequency at 80µm), and dashed lines indicate relative pre-stimulus activity levels. Top Panel NV single unit responses were taken from tuning curves defined requiring a minimum of 2 spikes/s (Criterion #3, see Methods). Middle Panel Cortical responses from recordings in the principal vibrissa barrel column (SI PV), taken from tuning curves defined requiring a minimal 128% increase above spontaneous firing rate (Criterion #4). Bottom Panel Cortical responses are shown from recordings taken simultaneously from a surround electrode (SI SE) located 350–1000µm lateral to the center (PV) representation. The same criterion was employed. B. For all peripheral and central recordings, the probability of significant neural activation at a given input amplitude is shown for the CF, FRF, and FRF + ω (gray scale scheme as in A). These curves demonstrate the relative gain in likelihood of a significant response for the stimulus input presented. Dashed gray horizontal lines indicate “stimulus detection” in 30% of recordings of neural activity using the described criteria. C. The minimal amplitude required to evoke a significant response in ≥ 30% of recordings for NV, SI PV, and SI SE sites (as in the dashed lines in B). For NV and SI PV sites, stimulation at the CF or FRF generated significant responses with motion amplitudes that were ~50% of those required when off-resonance frequencies (FRF ± ω) were presented. Further, off-resonance stimulation did not evoke consistent responses at SI SE sites, and CF or FRF stimuli required in turn about twice as much motion to drive 30% of the sample as was required at the SI PV site. The number of samples for (CF, FRF, FRF + ω, FRF − ω) were, in NV: (9, 15, 9, 9), SI PV: (10, 13, 8, 9) and SI SE: (10, 13, 8, 9). The FRF and FRF ± ω show different N due to edge effects of the sampled range.

For all recording types, off-resonance stimuli (±ω) were less effective in driving neural activity for all levels of stimulation that evoked a response, and showed a more shallow slope in response gain (Figure 3A). To quantitatively assess the resonance-driven enhancement of neural response sensitivity, we calculated the probability of significant responses at the criteria that generated the highest incidence of well-defined tuning curves and CFs (Criteria #3 for NV, N = 9/15; Criteria #4 for SI, N = 10/13). In NV, significant responses were observed for the peak of vibrissa resonance (FRF) and peak of neural sensitivity (CF) in >30% of cases with stimuli of 24µm amplitude at the vibrissa tip (Figure 3B,C). In contrast, stimuli a distance of ω in frequency from the FRF (20–60 Hz) did not reach this recruitment level until twice this amplitude was applied (≥56µm). A similar pattern was observed for SI responses to the PV: 40µm amplitude stimuli recruited >30% of the sample at the FRF or CF, while 64µm stimuli were required to drive responses at ω from the peak. For stimuli in the spatial surround in SI (SI SE), 72 and 80 µm stimuli were required to reach the 30% recruitment level for the FRF and CF, respectively, and significant activation was driven in only one case by stimuli ω from the FRF.

DISCUSSION

The principal finding of this paper is that peripheral and cortical neurons in the vibrissa sensory system were driven by small amplitude stimuli presented at the peak of vibrissa resonance, and that without this amplification, these neurons often did not demonstrate detectable activity, even when permissive statistical criteria were employed. Stimuli as small as 24 and 40 µm at the vibrissa tip consistently drove activity in NV and SI neurons, respectively. In contrast, stimuli less than 60Hz from the vibrissa fundamental resonance frequency often required a 2-fold increase in stimulus amplitude to achieve activation. In a subset of NV and SI neurons, even the smallest stimulus employed (8µm) generated well-defined receptive fields (Figure 1A and 1B left and Figure 2 top and bottom left). For the ‘macro’ vibrissae probed in this study, these motion amplitudes correspond to angular motions between 0.01° to 0.2°. To our knowledge, these are the smallest displacements ever systematically evaluated in the vibrissa sensory system, and are significantly smaller than what is typically interpreted as the ‘threshold’ for angular displacement sensitivity for cortical neurons when stimuli are applied to trimmed vibrissae (e.g., (Fox and Armstrong-James 1986; Pinto et al. 2000). In a recent study examining free behavior, vibrissa motions in this range were commonly observed, with a range of amplitudes extending several magnitudes above this level (Ritt et al., 2008).

The vibrissa resonance hypothesis, in it most general form, emphasizes that the embodied difference in the length of different vibrissae will systematically impact transduction, shaping the patterns of signals across vibrissae that will drive neural activity during perception. This prediction is supported by recent findings showing that vibrissa resonance impacts transduction in the awake, behaving animal, as the length of vibrissae predicts the frequency distribution of micro-motions generated (Ritt et al., 2008). The present study suggests that resonance amplification will influence the temporal structure and rate of neural activity in trigeminal and cortical neurons. We emphasize that even if this specific pattern of filtering is not necessarily ‘used’ by the animal to facilitate perception, these findings and previous studies (Andermann et al., 2004; Moore and Andermann, 2005) indicate that this signal will bias neural activity within the system significantly, and is therefore an important aspect of the ‘natural scene’ that a behaving animal will experience.

A more specific prediction of the vibrissa resonance hypothesis is that this embodied mechanical feature of the system could facilitate the perception of surface features. Neural signal amplification as a result of vibrissa resonance could facilitate the detection of fine textured surfaces and, more generally, of small amplitude vibrations. Rats are capable of detecting the presence of fine textures (30µm grooves spaced at 90µm intervals (Carvell and Simons 1990)). While the oscillations generated by fast transient motions across surface features are not yet well understood, 30µm vibrissa displacements at the tip, administered under the current protocol, would not have driven neural activation in most NV and SI recordings without vibrissa resonance. Even if this contact occurred at the vibrissa mid-length, the relative amplitude would be equivalent to ~60µm at the tip, a stimulus amplitude that was often unable to drive responses in the absence of resonance amplification. This aspect of the vibrissa resonance hypothesis does not emphasize the difference in frequency tuning across vibrissae, but rather the potential impact of resonant amplification across several frequency-tuned vibrissae on the detection of high-frequency information. This general principle of mechanical amplification could facilitate the detection of a rough versus a smooth surface, or of any stimulus feature (e.g., sound) that drives a resonant oscillation (Moore and Andermann 2005).

Neurons throughout the vibrissa sensory system—from the periphery to the cortical barrels—show high sensitivity to the velocity of vibrissa motion (Simons 1985; Pinto et al. 2000), and the enhanced ‘amplitude’ sensitivity observed in our MATCs likely reflects this property. The finding of velocity sensitivity has recently been extended to more naturalistic contexts, by tracking surface-dependent vibrissa motions during ‘artificial whisking’ in the anesthetized animal (Arabzadeh et al. 2005). When these recorded stimuli were played back to a passive vibrissa, NV single-unit activity and SI MUA demonstrated repeatable activity patterns that in many aspects reflected instantaneous vibrissa velocity. The present results show that the elastic properties of the vibrissae can be a crucial determinant of whether vibrissa motions surpass the neural threshold — vibrissa mechanics dictate the expression of suprathreshold velocities, and therefore shape evoked activity. Much as cochlear function is an essential component of understanding the auditory system, vibrissa transduction properties need to be considered in any comprehensive model of the vibrissa sensory system, and specifically of how information is translated into neural representation.

The present findings also have implications for understanding the spatial representation of high-frequency information. The tighter coupling between vibrissa FRF and neural CF than between FRF and BF (at 80µm) suggests a more precise transmission of the ‘map’ of frequency at near-threshold intensities. This suggestion is reinforced by the significant fall-off in sensitivity of neurons recorded on the surround cortical electrode. While only a binary description of the point spread of input from a resonating vibrissa, these data suggest that isofrequency columns in SI are precise to the approximate width of a barrel column when near threshold stimuli are employed. These findings parallel primate somatotopic maps, which demonstrate minimal distortion for near threshold stimuli (Kaas et al. 1979). With regards to active sensation, this heightened dependence of neural activity on vibrissa filter properties in the context of small amplitude motions suggests that the differences in vibrissa transduction properties across the pad will be greatest during the performance of tasks near perceptual threshold. These findings predict that during challenging surface perception, active sensing choices will reflect this dependence, potentially leading to behaviors such as a broader sampling of different vibrissae across a surface, the targeted engagement of specific vibrissae or the manipulation of vibrissal velocity or contact pressure. These findings also suggest that expression of the spatial map of frequency during free behavior is most likely to occur under conditions that generate smaller amplitude high-frequency stimuli.

There are important limitations to interpreting this study. First, these data were acquired in the anesthetized preparation, where follicle mechanics and neural responsiveness are likely altered (Simons et al.; Friedberg et al. 1999). The recent demonstration of resonance tuning during contact with rough and smooth surfaces (Ritt et al., 2008) suggests that these differences will not undermine the impact of resonance on neural activity during free behavior, but this assumption remains to be tested. Further, our receptive field-mapping paradigm, while advantageous because of its dense sampling and the quantitative control of stimulus parameters, is substantially different from vibrissa engagement during surface exploration. As such, these receptive field data obtained using classical stimulus-response paradigms must be interpreted with the caveat that they do not replicate active sensation in a natural context.

To characterize responses in SI, we employed multi-unit activity. There are drawbacks to MUA—this measure does not, for example, allow isolation of responses to specific cell types (Agmon and Connors 1992; Bruno and Simons 2002; Andermann et al. 2004). That said, our use of MUA in SI facilitated obtaining consistent and high signal-to-noise responses across a large number of conditions (231), and is often employed in auditory studies that apply dense and broad stimulus sampling (Eggermont, 1999; Schreiner and Sutter, 1992). Further, at threshold, the MUA will ostensibly reduce to the spiking activity of the single most effective neuron(s) in the region sampled by the electrode. As such, MUA provided an ideal method for assessing the lower bound on the sensitivity of suprathreshold responses in this brain region, and serves as a baseline for further single-unit studies.

EXPERIMENTAL PROCEDURES

Several methods employed parallel those of Andermann et al. (2004) and will be described briefly.

Surgery

All experiments complied with protocols approved by the Massachusetts General Hospital and Massachusetts Institute of Technology. Male Sprague-Dawley rats (N=24; 313 ± 85 g, mean ± SD:) were anaesthetized with urethane (1.2 g/kg ip initial dose) and maintained areflexive to hindpaw-pinch, with steady respiration at 80–120 breaths/min (.12 g/kg supplemental dose). Following craniotomy and durotomy, a retaining well was filled with mineral oil.

Electrophysiology

Parylene-coated tungsten microelectrodes (FHC: 2–10 MΩ impedance at 1kHz) were employed. Recordings from NV were conducted ipsilateral to vibrissa stimulation (6mm anterior to Lambda, 2mm lateral, ~10mm ventral to the cortical surface (Shoykhet et al. 2000)). Recordings from SI were conducted with single electrodes or pairs (horizontal spacing: ~350–1000µm), advanced ~500–950µm normal to the cortical surface (1–4 mm posterior to Bregma, 4–7 mm lateral), targeting lemniscal thalamocortical recipient layers as judged by response amplitude and latency. These depths were confirmed by histological reconstruction of electrolytic lesions (~18 µA for 3s) from 6 penetrations from 2 rats. Recordings were filtered (250/300-5000Hz; Neurotrack), amplified (5000×), digitized at 20kHz and stored with stimulus markers. Waveforms (1.5msec) containing voltage fluctuations exceeding ± 4 SD of pre-stimulus activity (0.5msec minimal interval between events) were saved. For analysis of multi-unit activity (MUA) in SI, all events that met these criteria were used. For analysis of single-unit activity in NV, recordings were further filtered (800–5000Hz) and separable clusters selected (custom software, MATLAB). Single-units also met the criterion that the autocorrelation was not contaminated within ± 1msec of the peak.

Vibrissa Stimulation

We employed customized high-performance piezoelectric bimorphs (Piezo Systems, Inc. Q234-H4CL-303X) with a high fundamental resonance frequency (≥800Hz, achieved by reducing piezoelectric length and attaching a light 20 mm extension), calibrated with optoelectronics and compensating voltage adjustments to <3% amplitude deviations and constant latencies for 500msec sinusoidal stimulus bursts from 0–750Hz. Voltage commands were generated in MATLAB, sent through an I/O board (NI), amplified (Thorlabs) and sent to the piezoelectric. The onset and offset of the sinusoids were tapered using a sine function (sin(2*pi*t/40), t in [0msec, 10msec]) to minimize edge effects and frequency contamination.

The principle vibrissa (PV) was determined by judgment of response intensity to manually applied stimuli. The stimulator was then rigidly attached 1–2mm from the vibrissa tip using bone wax. Deflections were made in the preferred direction of deflection for NV recordings as determined by qualitative mapping, and along the rostro-caudal axis for SI recordings. Vibrissa motion was simultaneously monitored at the midpoint using optoelectronics (Andermann et al. 2004). Only ‘macro’ vibrissae posterior to the 5^th arc were employed. To measure the amplitude of relative vibrissa motion, a sinusoid at each driving frequency was convolved with the vibrissa motion signal over set epochs (0–25, 25–50, 50–100, 100–500, 25–100 or 0–500 msec after stimulus onset), and the motion amplitude calculated as the difference between minimal and maximal values of this convolution, followed by subtraction of the same measure over an equal duration pre-stimulus.

Stimulus Protocol and Tuning Curves

Where well-defined vibrissa and neural tuning curves were evident from analysis of 80µm vibrissa stimulation from 5–600Hz or 5–750Hz (see Andermann et al., 2004), a minimal amplitude tuning curve (MATC) protocol was presented, similar to that commonly employed in auditory studies (Gelfand 1998). This paradigm consisted of 6 stimuli from 100–600Hz (100Hz intervals), and 15 stimuli sampled at 5 or 10Hz intervals surrounding the vibrissa fundamental resonance frequency (FRF). Each frequency was applied at ten amplitudes, 8 to 80µm in 8mm steps. The 231 trial types were randomized and presented at 1s intervals, with ≥4 trials/stimulus type. A matrix of the mean firing rates sampled 25–100msec post-stimulus onset in response to the 15 frequencies × 10 amplitudes surrounding the FRF was smoothed using a two-dimensional 3×3 boxcar filter (2×2 at edges).

The MATC was defined as the minimal vibrissa deflection required to exceed the threshold firing rate for each stimulation frequency. We derived MATCs using 6 criteria for denoting neural ’threshold’. For SI neurons, which demonstrated ‘spontaneous’ pre-stimulus activity, threshold criteria were 16, 32, 64, 128, 256, and 512% above the mean prestimulus rate. For NV units, which lacked consistent spontaneous activity, threshold criteria were defined as firing rates above 0.125, 0.5, 2, 8, 32, and 128 spikes/second. Similar to sound pressure level (SPL) notation for auditory MATCs (Gelfand 1998), we expressed the motion amplitude level (MAL) of the driving stimulus in decibels (dB) as (20log₁₀(A/Aref)), and chose Aref = 1µm (LaMotte and Mountcastle 1975; Andermann et al. 2004).

Peak Frequencies

For each neural recording, we calculated the ‘characteristic frequency’ (CF), the frequency with the lowest response threshold (Geisler 1998; Cheung et al. 2001; Egorova et al. 2001). The CF was defined from the 13 frequencies surrounding the FRF if the MATC had a minimum at a unique frequency or set of adjacent frequencies (in which case the median was used). Monotonic or multi-peaked MATCs were rare and were excluded from subsequent analyses. We also calculated the ‘best frequency’ (BF), the frequency at which 80µm amplitude stimuli drove a maximal response.