Kinetic Characterization of Exonuclease-Deficient Staphylococcus aureus PolC, a C-family Replicative DNA Polymerase

Abstract

PolC is the C-family replicative polymerase in low G+C content Gram-positive bacteria. To date several structures of C-family polymerases have been reported, including a high resolution crystal structure of a ternary complex of PolC with DNA and incoming deoxynucleoside triphosphate (dNTP). However, kinetic information needed to understand the enzymatic mechanism of C-family polymerases is limited. For this study we have performed a detailed steady-state and pre-steady-state kinetic characterization of correct dNTP incorporation by PolC from the Gram-positive pathogen Staphylococcus aureus, using a construct lacking both the non-conserved N-terminal domain and the 3′–5′ exonuclease domain (Sau-PolC-ΔNΔExo). We find that Sau-PolC-ΔNΔExo has a very fast catalytic rate (k_pol 330 s⁻¹) but also dissociates from DNA rapidly (k_off ∼150 s⁻¹), which explains the low processivity of PolC in the absence of sliding clamp processivity factor. Although Sau-PolC-ΔNΔExo follows the overall enzymatic pathway defined for other polymerases, some significant differences exist. The most striking feature is that the nucleotidyl transfer reaction for Sau-PolC-ΔNΔExo is reversible and is in equilibrium with dNTP binding. Simulation of the reaction pathway suggests that rate of pyrophosphate release, or a conformational change required for pyrophosphate release, is much slower than rate of bond formation. The significance of these findings is discussed in the context of previous data showing that binding of the β-clamp processivity factor stimulates the intrinsic nucleotide incorporation rate of the C-family polymerases, in addition to increasing processivity.

Introduction

DNA replication is the complex process of genome duplication involving several different proteins that form the “replisome”. A key enzyme of the replisome is the DNA polymerase, a nucleotidyl transferase that catalyzes the addition of a deoxynucleoside triphosphate (dNTP) to the nascent DNA chain. All organisms have several types of DNA polymerases of which the ones responsible for duplicating most of the genome are known as replicative polymerases. These are characterized by being highly efficient enzymes that can select the next correct nucleotide with extraordinarily high accuracy in a template-dependent manner.

The replicative polymerases of all bacteria are grouped by sequence similarity into the C-family of DNA polymerases [1], [2], but subdivide into two branches. The polC gene encodes the replicative polymerase of Gram-positive bacteria with low G+C content, while the dnaE gene encodes for the same in Gram-negative bacteria and in Gram-positive bacteria with high G+C content [3]. The replisomes of both Gram-positive and Gram-negative bacteria have been reconstituted and studied in vitro providing a wealth of knowledge about how replication occurs inside the bacterial cell [4]–[15].

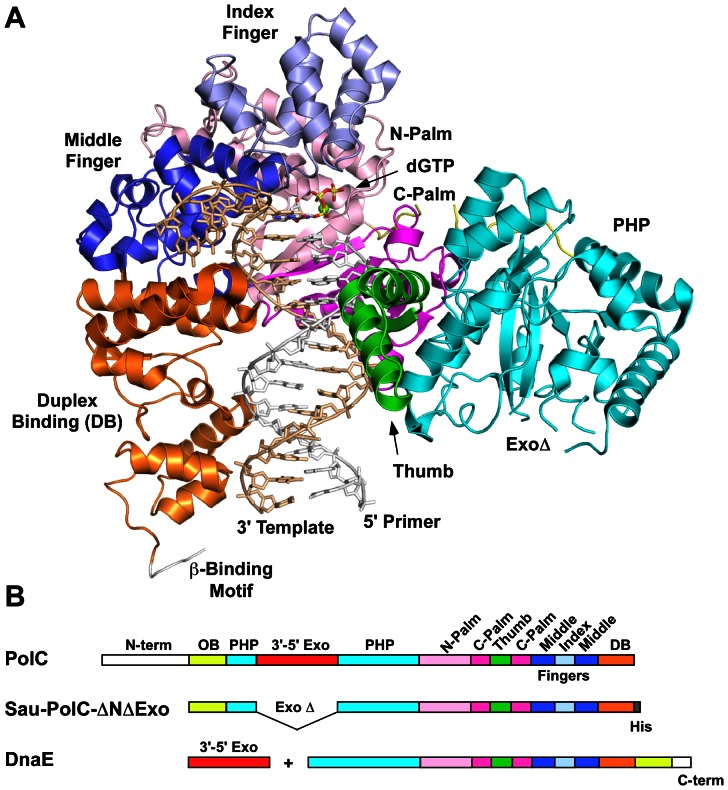
Recently, several crystal structures of C-family polymerases have been reported, including DnaE from Escherichia coli and Thermus aquaticus and PolC from Geobacillus kaustophilus [16]–[19]. Other than non-conserved N- and C-terminal extensions, the individual domains of PolC and DnaE are structurally conserved [17], as expected from sequence conservation, but differ somewhat in their linear organization in the protein (Figure 1). The OB domain of PolC is located just after the non-conserved N-terminal domain, while the OB domain of DnaE is located just before the non-conserved C-terminal domain. Additionally, PolC contains an intrinsic 3′ to 5′ exonuclease proofreading domain that is absent in DnaE. In Gram-negative bacteria, this function is performed by the epsilon (ε) subunit [20] of the replisome, which is homologous to the PolC exonuclease domain. A remarkable finding from the crystallographic studies is that the bacterial replicative polymerases are not related to the replicative polymerases from either eukaryotes or the archaea.

Figure 1. Overview of PolC structure and domain organization.

A. Structure of Gka-PolC-ΔNΔExo shown (PDB ID: 3F2B). Domains are color coded as in Figure 1B. OB domain is not shown for simplicity. The linker connecting the N-palm and PHP domains is shown (yellow). B. Sequence alignment showing domain organization of C-family polymerases.

Despite the fact that in vitro studies of the bacterial replisome have been key to delineating the main features of DNA replication in all forms of life [20], comparatively little is known about the kinetic mechanism of polymerization by C-family polymerases. This contrasts with the extensive kinetic information available for other polymerase families, including the B-family enzymes that are the replicative polymerases in eukaryotes and most archaea. Thus, the foundation for detailed structure-function studies of C-family polymerases has not yet been laid.

For all polymerases studied to date, the same overall enzymatic pathway (Figure 2) has been established for correct nucleotide incorporation [21]–[25]. The minimal pathway involves substrates binding to the polymerase in an ordered manner, with DNA binding first (step 1), followed by binding of the incoming dNTP (step 2). This is succeeded by the chemical step of bond formation (step 3). Typically, this step is preceded by a slower step along the pathway, which has been interpreted as a conformational change of the polymerase [21], [23]. Earlier structural studies suggested that this slow step might correspond to the large-scale domain movement associated with nucleotide binding [26], [27], but more recent studies have shown that motion to be too fast to be rate limiting [28], [29]. Although the conformational change accompanying nucleotide binding is faster than chemistry, it still controls specificity of nucleotide addition [30], [31]. Currently, the slower conformational change is thought to be a later, smaller-scale movement, but the precise nature of this non-covalent change is not known and may vary among different polymerases. Bond formation is followed by the release of the pyrophosphate (PPi) (step 4) generated during phosphoryl transfer. This step is generally presumed to be rapid [21] and is likely to be accompanied by the reverse of the conformational change that is induced by dNTP binding. Finally, release of the product DNA occurs (step 5), allowing the polymerase to perform subsequent rounds of catalysis. During processive synthesis, DNA would translocate along the polymerase rather than dissociate.

Figure 2. Minimal single-nucleotide incorporation reaction pathway for DNA polymerases.

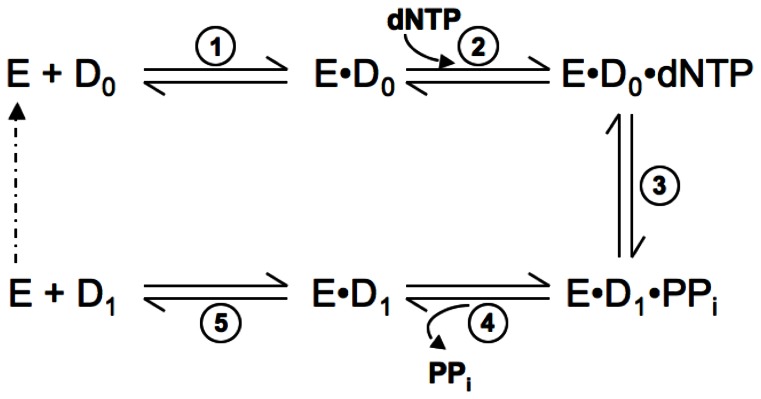
Abbreviations used were: E, DNA polymerase; D₀, unextended DNA; D₁, DNA extended by one base-pair; PPi, inorganic pyrophosphate. Dashed arrow indicates the polymerase entering another round of catalysis.

In this study we have performed both steady-state and pre-steady-state kinetic characterization of correct dNTP incorporation by an N-terminal and exonuclease domain deficient mutant of Staphylococcus aureus PolC (Sau-PolC-ΔNΔExo). This construct has the identical domain organization as the G. kaustophilus PolC used in the crystallographic study (Gka-PolC-ΔNΔExo) [17]. Furthermore, this construct has all the domains that are conserved between the PolC and DnaE polymerases (Figure 1). Hence, kinetic data obtained using this construct can be utilized directly for making structure-function correlations among the C-family polymerases and establish a foundation for future mechanistic studies of this polymerase family.

Materials and Methods

Materials

5′-6FAM labeled primer and unlabeled template oligonucleotides were purchased from Integrated DNA Technologies, Inc. Unlabeled ultrapure grade dTTP was purchased from GE Healthcare Biosciences. All the graphs and nonlinear regressions were done using GraphPad Prism, version 6.0a (GraphPad Software Inc.). Simulation of the reaction mechanism of Sau-PolC-ΔNΔExo was performed using KinTek Explorer, version 3.0 (KinTek Corp.) [32], [33].

Duplex DNA Formation

The primer and template DNA oligonucleotides were incubated together in annealing buffer (10 mM Tris-HCl (pH 8), 1 mM EDTA and 100 mM NaCl) and heated to a temperature of 95°C followed by gradual cooling to room temperature.

Expression and Purification of Sau-PolC-ΔNΔExo

S. aureus PolC lacking the N-terminal domain (amino acids 1–207) and the exonuclease domain (amino acids 415–609) and containing a C-terminal hexahistidine tag (Sau-PolC-ΔNΔExo) was expressed from a pET32A vector and was a generous gift from Thale Jarvis (Crestone Inc.). The plasmid was transformed into Rosetta(DE3)pLysS E. coli cells. Cells were grown to an OD₆₀₀ of ∼0.65 and then induced with 0.5 mM IPTG for ∼16 hrs at 17°C. All subsequent steps were carried out at 4°C. Cell pellets were resuspended in IMAC buffer (50 mM Tris-HCl (pH 7.5), 800 mM NaCl, 10 mM imidazole and 10% glycerol). In order to prevent proteolytic degradation of Sau-PolC-ΔNΔExo, EDTA-free protease inhibitor tablet (Roche) was added to IMAC buffer at a concentration of 1 tablet/10 g of cells. Cells were lysed by sonication and the clarified cell lysate was passed through Ni-NTA columns (3×5 ml). In order to reduce the NaCl concentration to 100 mM for later steps, the columns were washed with 10 column volumes of low salt IMAC buffer (50 mM Tris-HCl (pH 7.5), 100 mM NaCl, 10 mM imidazole and 10% glycerol). The protein was eluted using a linear gradient of imidazole from 10 to 400 mM in low salt IMAC buffer. During elution, two proteins with molecular weights of ∼75 kD eluted before Sau-PolC-ΔNΔExo. These are likely to be partial proteolytic products of Sau-PolC-ΔNΔExo and care was taken to remove these contaminants during elution from the Ni-NTA columns. Intact Sau-PolC-ΔNΔExo obtained from Ni-NTA chromatography was loaded onto Q-sepharose columns (HiTrap Q XL, 2×5 ml) pre-equilibrated in Buffer A (50 mM Tris-HCl (pH 7.5), 100 mM NaCl, 5 mM EDTA, 10% glycerol and 1 mM DTT). The protein was eluted from the Q column using a linear gradient of NaCl from 100 mM to 1 M in Buffer A. Eluent of the Q column was diluted ∼7 fold in Buffer A, to a NaCl concentration of ∼100 mM, and was subjected to heparin column chromatography (HiTrap Heparin HP, 2×5 ml). Buffer A was used to pre-equilibrate the heparin columns and protein was eluted using a linear gradient of NaCl ranging from 100 mM to 1 M in Buffer A. As a final step of purification, Sau-PolC-ΔNΔExo eluted from the heparin column was subjected to size exclusion chromatography using a Superdex 200 column (HiLoad 16/60 Superdex 200 pg) pre-equilibrated in storage buffer (50 mM Tris-HCl (pH 7.5), 250 mM NaCl, 5 mM EDTA, 10% glycerol and 1 mM DTT). The purified protein obtained from the size exclusion column was concentrated to ∼150–200 µM, calculated from the OD₂₈₀ of the protein sample using a theoretical extinction coefficient of 87,100 M⁻¹cm⁻¹, and was stored at −80°C.

Assays for Optimization of Enzymatic Activity of Sau-PolC-ΔNΔExo

Primer extension assays were performed in order to determine the optimum buffer conditions for the enzymatic activity of Sau-PolC-ΔNΔExo. 400 nM p/t DNA was incubated with 1 nM Sau-PolC-ΔNΔExo in PolC reaction buffer (25 mM MES-Tris (pH 8), 25 mM NaCl, 8 mM MgCl₂, 2 mM DTT and 5% glycerol). All the components of the PolC reaction buffer were kept fixed except the component whose effect was being tested. Unless mentioned otherwise, all the assays were carried out at room temperature (25°C). Assays were initiated by addition of 1 mM (final concentration) dTTP to the reaction mix. After 2 minutes, an equal volume of 250 mM EDTA was added to quench the assays. The extended and unextended primers were separated on a 17% acrylamide/7 M urea denaturing 1xTBE gel. The gel was imaged using a Typhoon 9400 scanner (GE Healthcare) and bands were quantitated using ImageQuant software (GE Healthcare). Percentage of primer extension was determined by measuring the relative intensity of the band corresponding to the extended primer with respect to the total labeled DNA (i.e. both extended and unextended primer strands). All reactions were performed in triplicate.

Steady-state Assays

Primer extension assays done for determining the steady-state parameters were performed using a KinTek RQF-3 rapid quench instrument (KinTek Corp.). Reactions were initiated by mixing a pre-equilibrated solution of 5 µM p/t DNA and 50 nM total Sau-PolC-ΔNΔExo in PolC reaction buffer (this corresponded to an active enzyme concentration of 33 nM, as described in the “Active site titration” section of the Results) to an equal volume of various concentrations of dTTP (18.76 to 600 µM) in the same buffer. Hence, the final p/t DNA and active Sau-PolC-ΔNΔExo concentrations in the reactions were 2.5 µM and 16.5 nM respectively and the final concentration range of dTTP was 9.38 to 300 µM. The assays were quenched at various time intervals by addition of 250 mM EDTA. The time intervals were adjusted such that primer extension was between 5–15%. Separation and quantitation of the extended primers was performed as described above. The concentration of primers extended for different concentrations of dTTP were plotted as a function of time and the data were fit to the steady-state rate equation:

(1)

where Y is the concentration of primer extended, [ED]_A is the concentration of active Sau-PolC-ΔNΔExo ⋅ p/t DNA binary complex that gets converted to product, k_obs is the observed rate of primer extension, t is time interval after which the reaction was quenched, and C is a constant. The observed rates were plotted as a function of dTTP concentration ([dTTP]) and the data were fit to the Michaelis-Menten equation:

(2)

where k_cat is the maximum steady-state rate and KM is the Michaelis constant for dNTP.

Measurement of DNA Dissociation Rate from Binary Complex

Kintek RQF3 rapid quench device was used to perform this experiment. 300 nM Sau-PolC-ΔNΔExo (this corresponded to an active enzyme concentration of 200 nM, as described in the “Active site titration” section of the Results) was preincubated with 160 nM p/t DNA in PolC reaction buffer in a 16 µl reaction volume. This was mixed with an equal volume of 96 µM unlabelled p/t DNA in the same buffer and incubated for various time intervals (0.005–0.05 s). Finally, ∼80 µl of 200 µM dTTP was added for primer extension (∼140 µM final concentration). At this stage the reaction was allowed to proceed for 0.028 s and quenched by collection of the sample in a microfuge tube containing 100 µl of 250 mM EDTA. Concentration of the extended primer was plotted as a function of time. Data were fit to the following exponential equation (Equation 3) and the rate of decrease of product formation was interpreted as the rate of dissociation of Sau-PolC-ΔNΔExo from the preformed Sau-PolC-ΔNΔExo ⋅ p/t DNA binary complex

(3)

where, Y is the concentration of the product formed, A is the amplitude, k is the rate of product formation, t is the first incubation time (ranging from 0.005 to 0.05 s) and C is a constant. Reactions were performed in triplicate.

Active Site Titration of Sau-PolC-ΔNΔExo

300 nM Sau-PolC-ΔNΔExo was pre-equilibrated with various concentrations of p/t DNA (20 to 1800 nM) in PolC reaction buffer. The reactions were initiated by rapid mixing of this solution with an equal volume of PolC reaction buffer containing 2 mM dTTP in a KinTek RQF-3 rapid quench instrument. Final concentrations were 10–900 nM p/t DNA, 150 nM polymerase and 1 mM dTTP. The reactions were terminated at different time intervals by addition of 250 mM EDTA. The time-courses of primer extension for different p/t DNA concentrations were fit to the full burst equation:

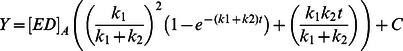(4)

where Y is the concentration of the extended primer, [ED]_A is the concentration of the preformed active enzyme ⋅ DNA binary complex that gets converted to product before turnover, k₁ is the rate of the fast phase, k₂ is the rate of the slow phase, t is the time interval after which the reaction was quenched and C is a constant. [ED]_A for different DNA concentrations thus obtained were plotted out as a function of p/t DNA concentration and fit to the following quadratic equation:

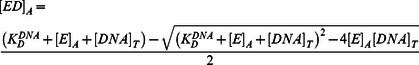(5)

where KDDNA is the dissociation constant for binding of Sau-PolC-ΔNΔExo to p/t DNA, [E]A is the concentration of active Sau-PolC-ΔNΔExo and [DNA]T is the concentration of total p/t DNA at the beginning of the assay.

K_D ^dNTP Determination

Primer extension assays were performed with a RQF-3 rapid quench instrument using final concentrations of 804 nM active Sau-PolC-ΔNΔExo, 50 nM p/t DNA and various [dTTP] (1.17 to 100 µM). Reactions were quenched by addition of 250 mM EDTA. Time courses of primer extension reactions were plotted as a function of [dTTP] and the data were fit to the full burst equation (Equation 4). The rate, k₁, and [ED]_A thus obtained were further plotted against [dTTP] and then fit to the appropriate hyperbolic equation:

(6)

(7)

where k_pol is the maximum rate of the burst of product formation, K_D ^dNTP is the dissociation constant for dNTP binding to the Sau-PolC-ΔNΔExo ⋅ p/t DNA binary complex and [ED]_A ^max is the maximum concentration of the enzyme ⋅ DNA binary complex that gets converted to product before turnover.

Unless mentioned otherwise, all reactions were done in at least three independent experiments, using two different preparations of Sau-PolC-ΔNΔExo. All data were combined and analyzed together.

Simulation

The reaction mechanism of Sau-PolC-ΔNΔExo was simulated using KinTek Explorer software. Details about the mechanism used for the simulation is discussed under “Results” section. The software was used to fit data to the simulation using an iterative procedure until a “best fit” was achieved. The simulated curves and the raw data were exported from the software and final plots overlaying the raw data with the simulated curves were prepared using GraphPad Prism. To determine the range within which each of the rate constants was constrained by the model, and to investigate the relationships between different rate contants, we computed 3-D confidence contour plots for all possible pairs of rate constants. See reference [32] for a detailed description of how to interpret these plots.

Results

PolC Purification

Recombinant Sau-PolC-ΔNΔExo was purified using Ni-NTA, anion exchange, heparin and size-exclusion chromatography. Figure 3 shows SDS-PAGE analysis of the final purified protein. Sau-PolC-ΔNΔExo migrates as expected for a protein with a theoretical molecular weight of 120 kD. As has been noted previously for full-length PolC [12], inducing protein expression at temperatures below 20°C was critical for obtaining purified protein, estimated to be ∼95% homogeneous, that did not have significant levels of proteolytic products.

Figure 3. SDS-PAGE of Sau-PolC-ΔNΔExo.

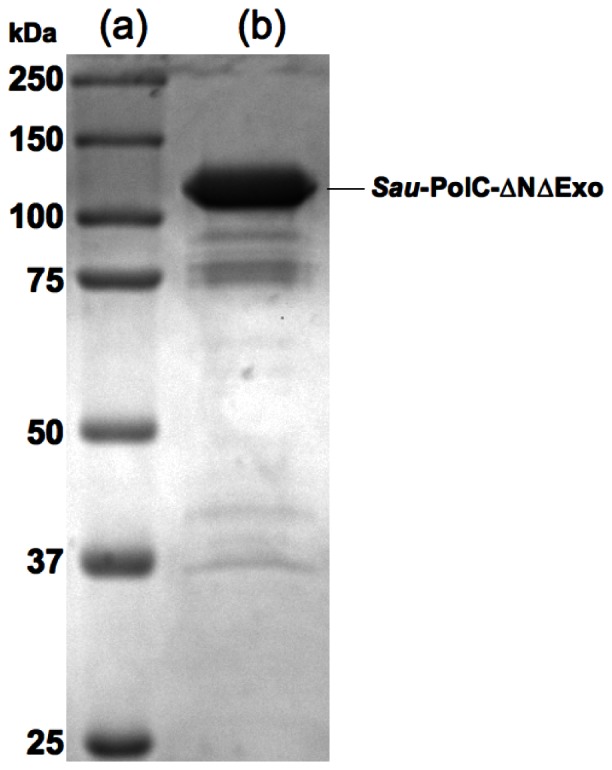
A 10% SDS-polyacrylamide gel stained with Coomassie R-250 showing purified Sau-PolC-ΔNΔExo obtained after size exclusion chromatography. (a) Kaleidoscope pre-stained marker. (b) 2.5 µM purified Sau-PolC-ΔNΔExo.

Optimal Reaction Conditions

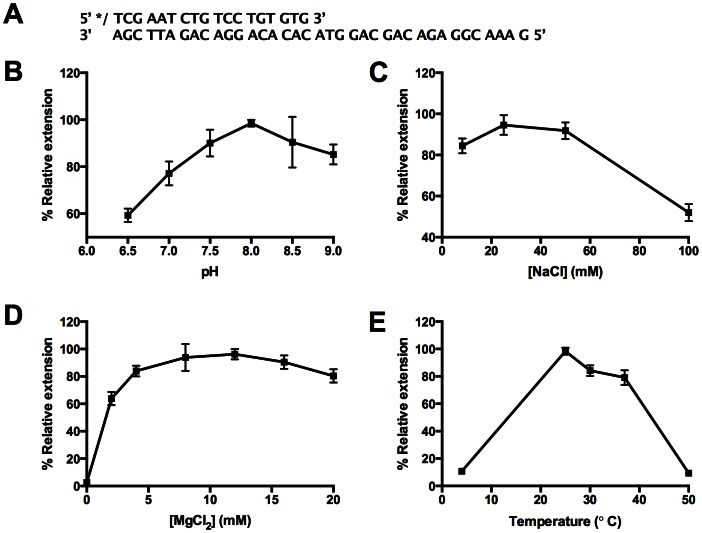
Reaction conditions for Sau-PolC-ΔNΔExo were optimized by quantitating incorporation of the next correct dNTP on a p/t DNA with an 18-bp duplex region and a 19-nt single stranded template region (Figure 4A). All reaction conditions were kept constant, except for the one whose effect was being tested. The reaction conditions varied were: pH of the buffer, concentration of NaCl, concentration of Mg²⁺ and reaction temperature (Figure 4B–E). Dependence of primer extension on the buffer pH followed a bell shaped curve typical of an acid-base reaction, with an optimum pH of 8 (Figure 4B). The rate of primer extension was found to decrease with an increase in the concentration of NaCl, with the maximum activity occurring at 25 mM NaCl (Figure 4C). A concentration of 8 to 12 mM Mg²⁺ was found to be optimal for enzymatic activity of Sau-PolC-ΔNΔExo (Figure 4D). No primer extension was observed in the absence of Mg²⁺, as expected for a polymerase using a two-metal-ion mechanism. Very little primer extension occurred at 4°C and 50°C, but, for all other temperatures tested (25°C, 30°C and 37°C), the enzyme performed well (Figure 4E). Based on these results, all subsequent reactions were performed at 25°C at pH 8 with 25 mM NaCl and 8 mM Mg²⁺.

Figure 4. Primer extension assays for optimizing enzymatic activity of Sau-PolC-ΔNΔExo.

(A) Duplex DNA sequence used for all primer extension assays performed in this study. “*/” at 5′ end of primer indicates 6-FAM label. (B) Effect of pH (C) Effect of NaCl concentration (D) Effect of Mg²⁺ concentration and (E) Effect of temperature on Sau-PolC-ΔNΔExo activity. Primer extension assays were carried out under steady-state conditions by adding 1 mM dTTP (the correct incoming dNTP) to a pre-incubated solution of 400 nM p/t DNA and 1 nM Sau-PolC-ΔNΔExo. Reactions were quenched after 2 minutes by addition of an equal volume of 250 mM EDTA. Unextended and extended primers were separated by gel electrophoresis on a 17% denaturing TBE-acrylamide gel. Fraction of primer DNA extended was determined by measuring the relative intensity of the extended primer band with respect to the total labeled DNA (extended and unextended primer).

Michaelis-Menten Kinetics

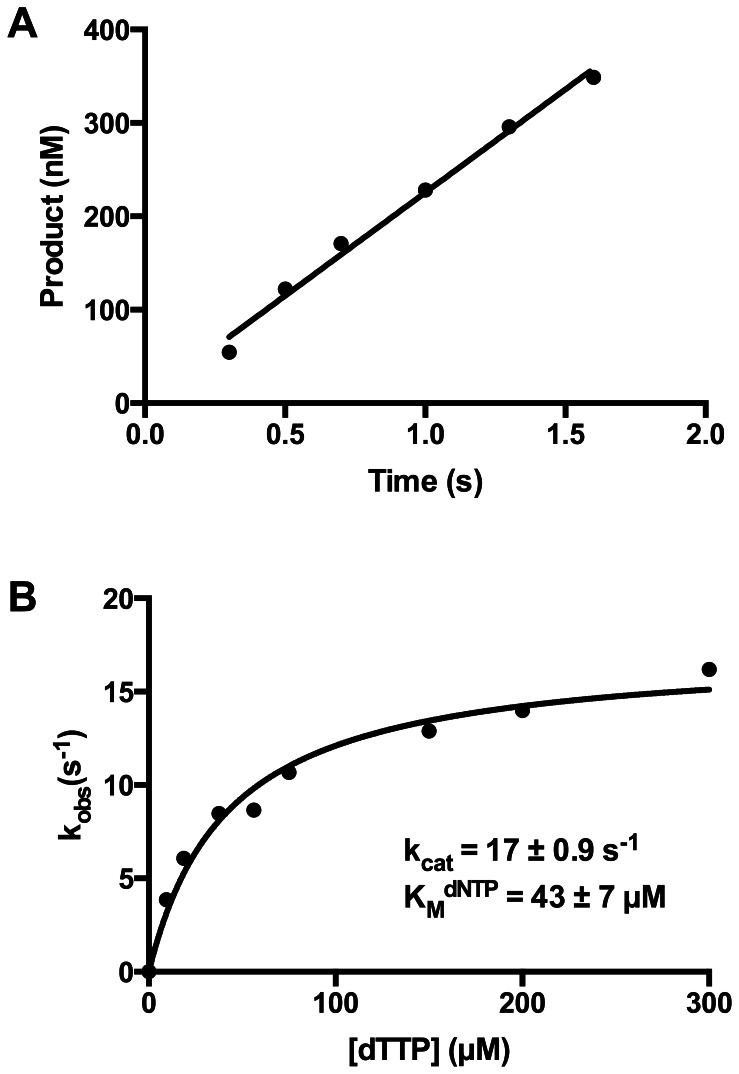
Primer extension assays were performed under steady-state conditions, with substrates present in excess of enzyme, using a final concentration of 2.5 µM p/t DNA, 16.5 nM active Sau-PolC-ΔNΔExo (see result of “Active site titration” for calculation of active enzyme concentration) and various concentrations of dTTP ranging from 9.38 to 300 µM. Observed rates of nucleotide incorporation were calculated from the concentration of product formed vs. time, using the linear portion of progress curves (Figure 5A), and were plotted as a function of [dTTP] (Figure 5B). The data were fit to the Michaelis-Menten equation (Equation 2) and gave a k_cat of 17±1 s⁻¹ and K_M ^dNTP of 43±7 µM.

Figure 5. Steady-state kinetic analysis of Sau-PolC-ΔNΔExo.

Primer extension assays were performed by adding dTTP (final concentration range 9.38 to 300 µM) to a final concentrations of 2.5 µM p/t DNA and 16.5 nM active Sau-PolC-ΔNΔExo. The reactions were quenched at different time intervals with 250 mM EDTA. (A) A typical time course of primer extension followed during the steady-state kinetic assays (final [dTTP] was 300 µM). The concentration of primer extended was plotted against time and fit to the steady-state equation (Equation 1). (B) Michaelis-Menten plot for Sau-PolC-ΔNΔExo. The observed rates of primer extension were plotted as a function of the dTTP concentration. The resulting plot was fit to the Michaelis-Menten equation (Equation 2). From the fit, steady-state rate constant (k_cat) was calculated to be 17±1 s⁻¹ and Michaelis constant for dNTP (K_M ^dNTP) was determined to be 43±7 µM.

Rate of Dissociation of p/t DNA from the Binary Complex

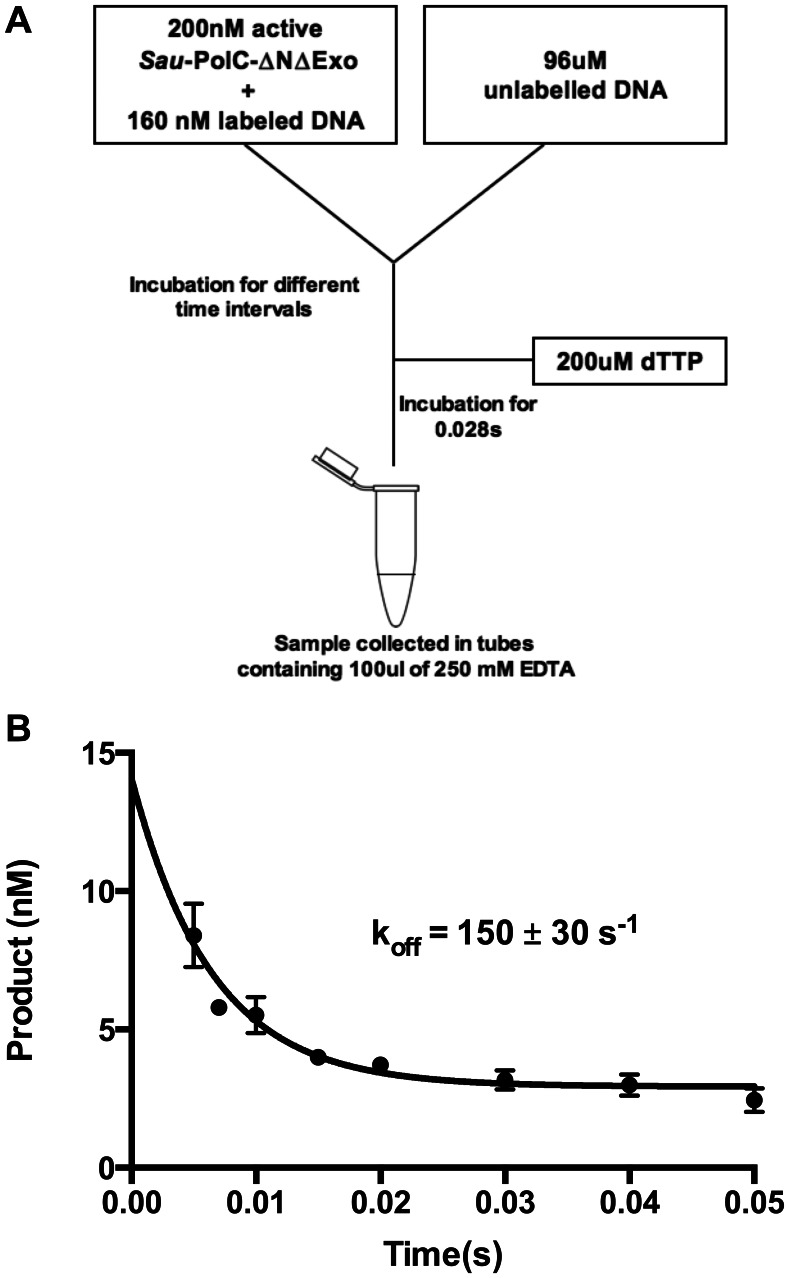
Typically, in single-nucleotide incorporation assays such as the one used here, dissociation of the DNA from the polymerase ⋅ DNA binary complex is the rate limiting step of the catalytic cycle, and the rate of this step (k_off) governs the steady-state rate (k_cat). To determine if this was the case for Sau-PolC-ΔNΔExo, we directly measured k_off using the experimental design shown in Figure 6A. For this experiment Sau-PolC-ΔNΔExo was preincubated with p/t DNA and the preformed Sau-PolC-ΔNΔExo ⋅ p/t DNA binary complex was rapidly mixed with an equal volume of unlabelled p/t DNA. The resulting reaction (containing final concentrations of 150 nM Sau-PolC-ΔNΔExo, 80 nM p/t DNA, and 48 µM unlabelled p/t DNA) was incubated for various time intervals ranging from 0.005 to 0.05 s. The unlabelled p/t DNA trapped any Sau-PolC-ΔNΔExo that dissociated from the preformed binary complex during this time. Next, dTTP was added to initiate the reaction and a further incubation of 0.028 s was performed, to allow extension of p/t DNA bound to PolC. Finally, the reaction was quenched with EDTA. A plot of labeled product formed versus the variable incubation time (0.005 to 0.05 s) showed a clear reduction in product concentration with increasing time (Figure 6B). This was attributed to the decrease in the concentration of the preformed Sau-PolC-ΔNΔExo ⋅ p/t DNA due to the dissociation of the labeled p/t DNA from the complex and rebinding of the enzyme to the excess unlabeled p/t DNA. The data fitted well to an exponential equation (Equation 3) and the rate of decrease in product formation (k_off) was found to be 150±30 s⁻¹. This indicated that for Sau-PolC-ΔNΔExo, DNA dissociation is approximately 9-fold faster than k_cat and, surprisingly, is not the rate-limiting step of the of the single-nucleotide incorporation cycle.

Figure 6. Determination of the DNA dissociation rate from polymerase ⋅ DNA binary complex (k_off).

(A) Schematic representation of the experimental procedure. (B) Plot of product formed vs time. The data were fit to a single exponential equation (Equation 3). The rate of decrease in product formation (which is equivalent to the rate of dissociation of p/t DNA from Sau-PolC-ΔNΔExo ⋅ p/t DNA binary complex (k_off)) was 150±30 s⁻¹.

Pre-steady-state Burst Kinetics

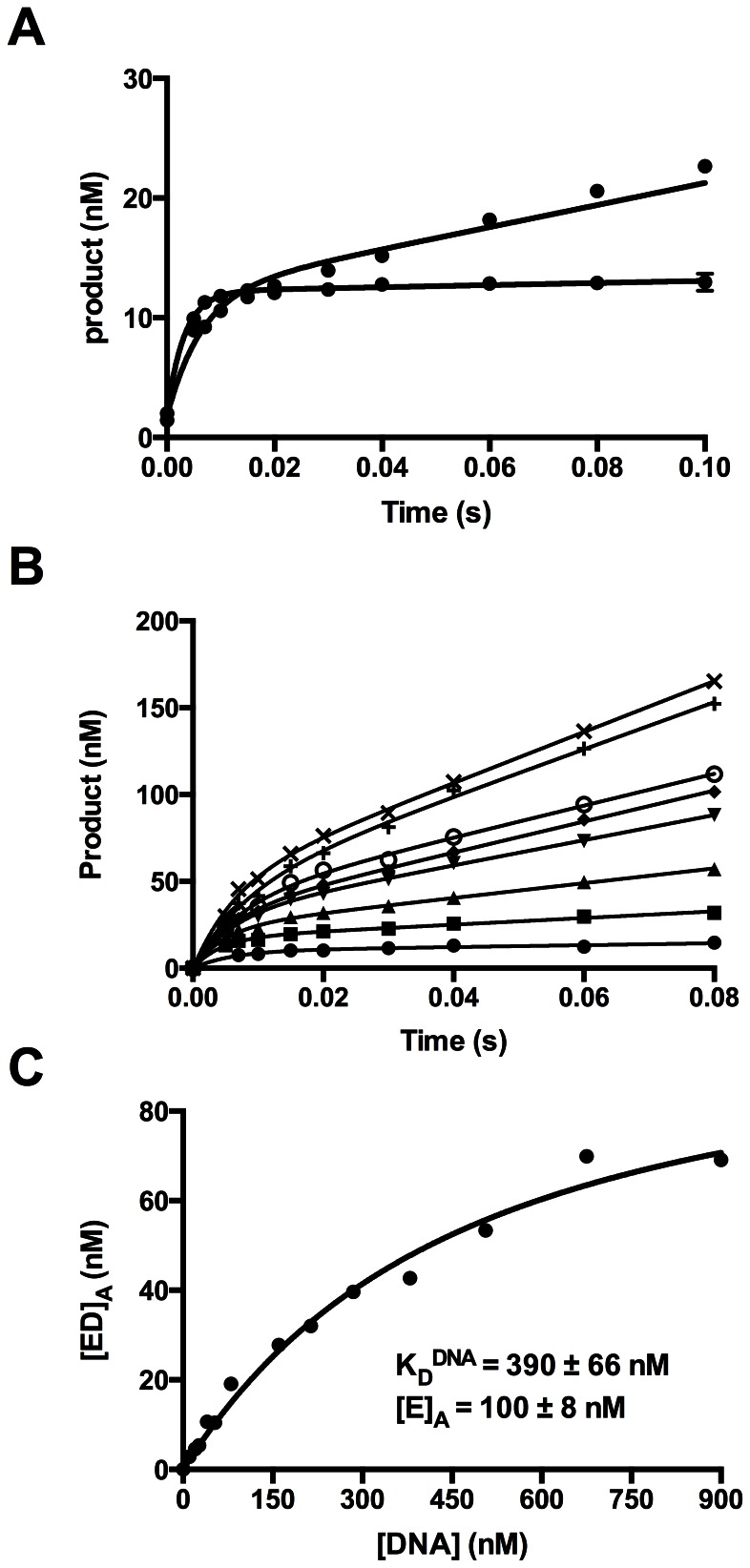
To determine if Sau-PolC-ΔNΔExo displayed a rate-limiting step after chemistry, primer extension assays were performed under pre-steady-state conditions with a total enzyme concentration of 150 nM and 80 nM p/t DNA (final concentrations). After pre-incubation to form the binary complex, reactions were started by the addition of dTTP to a final concentration of 35 µM and product formation was followed up to 0.2 s. Plot of the concentration of product formed with respect to time was biphasic in nature (Figure 7A). The fast phase represents the initial burst of dTTP incorporation by the pre-formed Sau-PolC-ΔNΔExo ⋅ p/t DNA binary complex, while the slow phase represents dTTP incorporation in subsequent rounds of primer extension, after the enzyme dissociates from the first p/t DNA substrate and rebinds another. The data were fit using the full burst equation (Equation 4) [34]. The rates of the fast and slow phases obtained were 150±30 s⁻¹ and 8.5±1 s⁻¹, respectively. Product formed during the fast burst phase was 12±1 nM, indicating that out of 150 nM of Sau-PolC-ΔNΔExo, only 12 nM formed active enzyme ⋅ DNA binary complex that got converted to product.

Figure 7. Pre-steady-state kinetics and active site titration of Sau-PolC- ΔNΔExo.

(A) A time course of primer extension under pre-steady-state condition in the presence (⋅) and absence () of unlabelled p/t DNA acting as an enzyme trap. 35 µM dTTP (with or without 48 µM of unlabelled p/t DNA) was added to 150 nM Sau-PolC-ΔNΔExo (corresponding to an active Sau-PolC-ΔNΔExo concentration of 100 nM) and 80 nM p/t DNA (all concentrations are final). In the absence of the trap, the time course was biphasic in nature and the data were fit to the full burst equation (Equation 4). The rate of the fast phase was 150±30 s⁻¹ and that of the slower phase was 8.5±1 s⁻¹, [ED]_A was found to be 12±1 nM. In the presence of the trap, the time course was monophasic and the data were fit to a single exponential equation, with a rate of 300±14 s⁻¹ and an amplitude of 11.5±0.5 nM. The data can also be fit equally well to the full burst equation, but the data were not sufficient to justify using the more complex model. (B) A representative set of primer extension assays performed during active site titration. Time resolved primer extension assays were performed using 150 nM Sau-PolC-ΔNΔExo, 1 mM dTTP and varying concentrations of p/t DNA (⋅ 40 nM, ▪ 80 nM, 160.1 nM,♦ 284.76 nM,<$>\raster="rg1"<$> 379.69 nM, ○ 506.25 nM, +675 nM and ×900 nM). The concentration of extended primer was plotted versus time and data were fit to the full burst equation (Equation 4). For ease of understanding, the background primer extension has been deducted from each time course. (C) A plot of the concentrations of pre-formed active enzyme-DNA complex getting converted to product before turnover ([ED]_A) versus DNA concentration was fit to a quadratic equation (Equation 5). K_D ^DNA was determined to be 390±70 nM and the concentration of active Sau-PolC-ΔNΔExo was found to be 100±8 nM.

Since the rate of dissociation of the DNA substrate from the binary complex (Figure 2, step 5) was very fast, it was possible that the DNA did not form a stable ternary complex even in the presence of the correct incoming dNTP (Figure 2, step 3). In order to test whether such was the case, we repeated the above burst experiment in the presence of 48 µM of unlabelled p/t DNA that was added at the same time as the dTTP. Any Sau-PolC-ΔNΔExo that dissociated from the labeled p/t DNA would be trapped by the excess unlabelled DNA, which would eliminate the slower phase. Additionally, any unstable ternary complex having a dissociation rate comparable to the rate of chemistry or faster would result in lower amplitude of product formation in the presence of the trap. Our result shows that, in the presence of the DNA trap, the slow phase was eliminated, as expected, and the amplitude of product formation was 11.5±0.5 nM (Figure 7A), identical to the amplitude in the absence of the trap.

These results indicate that although DNA dissociation from the binary complex is rapid, disassembly of the ternary complex is not rapid and, during a single nucleotide-incorporation cycle, DNA does not dissociate from the enzyme after nucleotide binds. The difference in the rates of product formation for the first and subsequent rounds of enzyme turnover, as observed in the burst experiment, indicates the presence of a slow and at least partially rate-limiting step after dNTP incorporation. The low burst amplitude suggested that binding of Sau-PolC-ΔNΔExo to p/t DNA was weak and/or only a fraction of the enzyme was active. A third possibility is the presence of an internal equilibrium in the pathway leading to a reduction in product formation. The following experiments indicate that all three of these possibilities contribute to the low burst amplitude.

Active Site Titration

The formation of a stable ternary complex and the presence of a slow, rate-limiting step after chemistry allowed us to perform burst kinetic assays to determine the apparent K_D ^DNA and the concentration of active Sau-PolC-ΔNΔExo. For these assays, the final concentration of total Sau-PolC-ΔNΔExo was 150 nM and the final DNA concentration was varied between 10 and 900 nM. Product formation for a representative set of DNA concentrations is shown in Figure 7B. The time courses were fit to the full burst equation, and the concentrations of the initial active enzyme ⋅ DNA complex that was converted into product during the first round of catalysis ([ED]_A), obtained from the amplitudes of the fast phase, were plotted as a function of DNA concentration (Figure 7C). The data were fit to a quadratic equation (Equation 5). From the fit, the apparent K_D ^DNA was determined to be 390±70 nM, indicating a relatively weak binding to DNA (Table 1), and the concentration of active Sau-PolC-ΔNΔExo was 100±8 nM, implying that ∼70% of the Sau-PolC-ΔNΔExo was active. The active enzyme concentration was lower than expected given the purity of the preparation, but the result was consistent for different preparations. From the apparent DNA binding affinity and the rate of DNA dissociation, we estimate that Sau-PolC-ΔNΔExo associates with DNA with a rate constant (k_on) of ∼4×10⁸ M⁻¹s⁻¹, which suggests that the rate of DNA binding is limited by diffusion.

Table 1. Comparison of kinetic parameters of different polymerases.

Polymerase	Family	KD DNA (nM)	KD dNTP (µM)	kpol (s−1)	koff † (s−1)	References
Sau-PolC-ΔNΔExo (observed)	C	390	4	180	150	–
Sau-PolC-ΔNΔExo (simulated)	C	–	7.5	330	–	–
Pol I (Klenow)	A	5	5.5	50	0.06	[24]
T7DNA Polymerase	A	(18)	(18)	(287)	(0.2)	[25]
E. coli Pol II	B	21	4.4	13	0.05	[48]
Mammalian Polδ	B	300	–	7	0.005	[49]
		(64)	(0.93)	(21)	(0.006)
Yeast Polδ	B	30	24	1	0.045	[50]
Human mitochondrial Polγ	B	39	14	3.5	0.03	[51], [52]
		(9.9)	(0.78)	(45)	(0.02)
Polβ	X	49	110	10	0.3	[53]
E. coli Pol IV	Y	50	441	12	0.18	[54]
		–	(51)	(22)	(0.03)

Data obtained from this study are highlighted in bold. Replicative polymerases are shown in italics. Values shown in parentheses were measured in the presence of the corresponding processivity factor.

^†For all DNA polymerases shown here except for Sau-PolC-ΔNΔExo k_off is equivalent to k_cat.

Nucleotide Binding Affinity

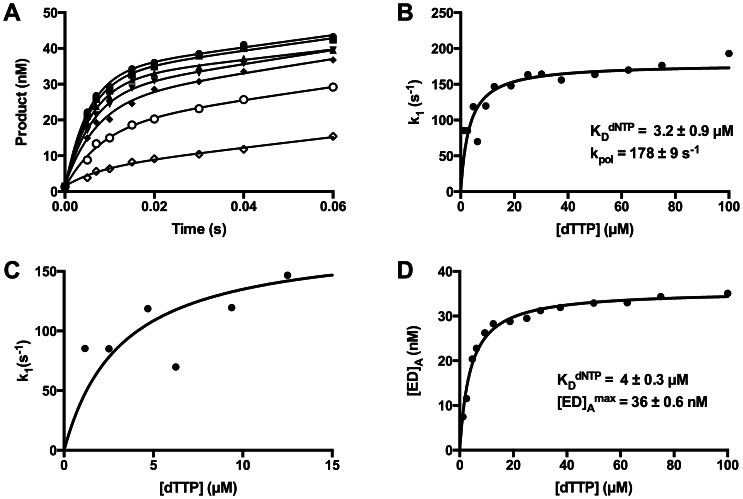
Primer extension assays were again performed under burst conditions to determine the apparent K_D ^dNTP and k_pol. For these assays the final concentrations of active Sau-PolC-ΔNΔExo and p/t DNA were 804 nM and 50 nM respectively. The concentration of dTTP was varied from 1.17 to 100 µM and a representative range of data is shown in Figure 8A. Rates of the fast phase (k₁), obtained by fitting the time course to the full burst equation, were plotted against [dTTP] and the data were fit to a hyperbolic equation (Equation 6). From the fit, the apparent K_D ^dNTP was determined to be 3.2±0.9 µM and k_pol was 180±9 s⁻¹ (Figure 8B). Although these parameters were reasonable compared to other replicative polymerases, the overall fit to the data was not good (R² of 0.75), primarily because the observed rates for lower nucleotide concentrations did not match well with the rates predicted by the hyperbolic equation (Figure 8C). The deviation of the observed nucleotide incorporation rates appeared to be due to the lower amplitudes of the fast phase at low nucleotide concentrations.

Figure 8. Determination of K_D ^dNTP of Sau-PolC- ΔNΔExo.

(A) A representative set of primer extension assays performed during K_D ^dNTP determination for Sau-PolC-ΔNΔExo. The reactions were performed with 804 nM active Sau-PolC-ΔNΔExo, 50 nM p/t DNA and various concentrations of dTTP (◊ 1.17 µM, ○ 4.69 µM, ♦ 9.4 µM, ▾ 18.75 µM, ▴ 30.14 µM, ▪ 50 µM and • 75 µM). The concentrations of extended primers were plotted against time and the plots were fit to the full burst equation (Equation 4). (B) A plot of the observed rates of the fast phase (k₁) versus [dTTP]. The data were fit to a hyperbolic equation (Equation 6). From the fit, K_D ^dNTP was determined to be 3.2±0.9 µM and maximum rate of the burst (k_pol) was found to be 178±9 s⁻¹. R² value for this fit was 0.75. (C) An enlarged view of panel (B) of up to 15 µM of [dTTP]. (D) A plot of [ED]_A versus [dTTP] was fit to a hyperbolic equation (Equation 7). From the fit, K_D ^dNTP was found to be 4.0±0.3 µM and the maximum [ED]_A was 36±0.6 nM. R² value for this fit was 0.98.

Dependence of Active Enzyme⋅DNA Binary Complex on [dNTP]

Typically, bond formation (Figure 2, step 3) is irreversible, because pyrophosphate release (Figure 2, step 4) is fast, and the binding of the incoming dNTP is a rapid equilibrium process [21]. Hence there is no equilibrium between dNTP binding (Figure 2, step 2) and bond formation. Therefore, an increase in the concentration of the incoming dNTP does not influence the concentration of the preformed active enzyme ⋅ DNA binary complex that gets converted to product before turnover ([ED]_A). This is observed as the lack of correlation in a plot of [ED]_A versus [dNTP]. Upon closer inspection of our data, however, we observed that [ED]_A obtained from the burst amplitude of the fast phase was dependent on the dTTP concentration, saturating at higher concentrations (Figure 8D) and fit well (R² of 0.98) to a hyperbolic equation (Equation 7). From the fit, the apparent K_D ^dNTP was found to be 4.0±0.3 µM and the maximum concentration of [ED]_A ([ED]_A ^max) was 36±0.5 nM. This dNTP concentration dependence of [ED]_A suggests that bond formation is reversible (Figure 2, step 3) and is in equilibrium with ground state dNTP binding (Figure 2, step 2). As a result, [ED]_A increases when increasing concentrations of dTTP drive the equilibrium towards product formation. This observation suggests that there is a slow step after catalysis but prior to PPi release that allows chemistry to be reversible.

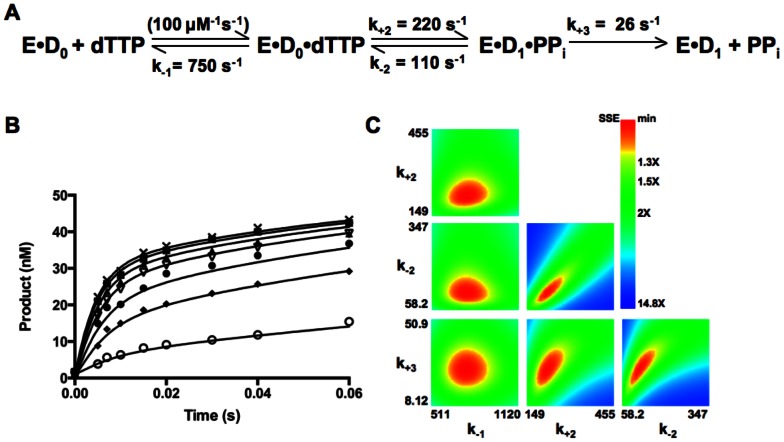
We therefore turned to using KinTek Explorer to calculate the kinetic parameters for the forward and reverse steps of chemistry accurately by numerical integration, and also to define a rate constant for the slow step immediately after chemistry. The enzymatic pathway of Sau-PolC-ΔNΔExo was simulated through a three-step mechanism: (1) dNTP binding to the polymerase ⋅ DNA binary complex, (2) dNTP incorporation, and (3) PPi release (Figure 9A). We have used this model for simplicity because, for chemistry to be reversible, PPi must be positioned at the active site to cause pyrophosphorolysis. Although PPi release is modeled as a simple binding interaction, it is likely that this step in the pathway also involves a conformational change of the polymerase-DNA complex. Thus, it is important to keep in mind that the kinetic parameters defined for PPi release may actually describe more than one elementary step that occurs immediately after chemistry. Since the ternary complex is stable, as shown in Figure 7A, we assumed that DNA would not dissociate from the enzyme when either dNTP or PPi were bound. For the simulation, the rate of dNTP association was considered to be limited by diffusion and accordingly the second order association rate constant was fixed at 100 µM⁻¹s⁻¹. Also, PPi release was assumed to be irreversible, since the concentration of PPi in solution during the reaction period would be negligible. The experimentally determined K_D ^DNA and DNA release rate (k_off) from the binary complex were used to determine the concentration of the preformed Sau-PolC-ΔNΔExo ⋅ p/t DNA complex and the second order association rate constant for the formation of the binary complex. The simulated curves were generated through iterative steps that used kinetic parameters obtained from nonlinear regression as initial values.

Figure 9. Simulation of kinetic pathway of Sau-PolC- ΔNΔExo.

(A) The three-step reaction mechanism used for the simulation. Values obtained for the different rate constants are shown alongside the appropriate step. Rate of dNTP association to the E⋅D₀ binary complex was assumed to be diffusion limited and accordingly the second order rate constant for this step was fixed at 100 µM⁻¹s⁻¹. (B) Simulated curves generated for the representative dataset shown in Figure 8A superimposed on the raw data (concentrations of dTTP shown are ○ 1.17 µM, ♦ 4.69 µM, • 9.4 µM, ▽ 18.75 µM, ▴ 30.14 µM, ▪ 50 µM and ×75 µM). (C) 3-D confidence contours for the various rate constants determined from the simulation. For each case the search was carried out up to a sum of squares error (SSE) that is 2-fold higher than the minimum SSE. The upper and lower limits of each parameter were determined using an SSE threshold of 1.2.

Simulated curves were superimposed on the representative time course data shown in Figure 8A (Figure 9B). Through numerical integration, the rate of chemistry was determined to be ∼220 s⁻¹ for the forward reaction and ∼110 s⁻¹ for the reverse reaction, yielding a net maximum rate (k_pol) of ∼330 s⁻¹. Also, the rate of pyrophosphate release following chemistry was determined to be 26 s⁻¹ and the K_D ^dNTP was 7.5 µM. From 3-D confidence contour analysis, all the calculated parameters appeared to be well constrained by the data (Figure 9C). From the simulation, the calculated rate of PPi release is much lower than the calculated rate of catalysis and is very close to the k_cat of Sau-PolC-ΔNΔExo, suggesting that PPi release (or a conformational change required for PPi release) may govern the steady-state rate.

Discussion

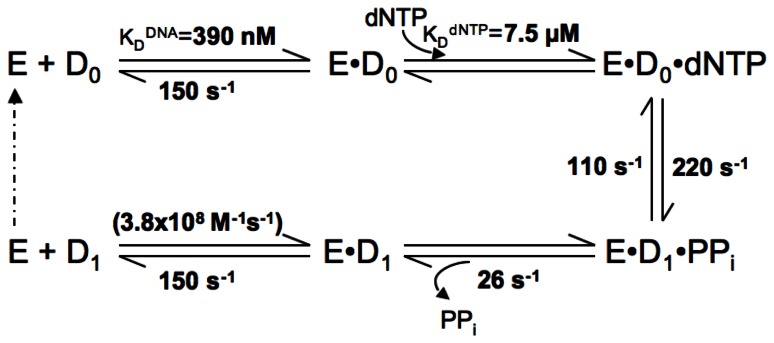
We have determined the minimal kinetic pathway (Figure 10) for Sau-PolC-ΔNΔExo and defined parameters for individual steps within the pathway using both steady-state and pre-steady-state kinetic approaches. The kinetic steps fit the same pathway used by other polymerases, but PolC exhibits several distinguishing features (Table 1). To our knowledge, this is the first comprehensive kinetic study of the catalytic subunit of the bacterial replisome. As described below, our findings provide deeper insight into several activities of the bacterial C-family polymerases that have been previously observed.

Figure 10. Minimal enzymatic pathway for Sau-PolC- ΔNΔExo.

The kinetic parameters determined are shown alongside the corresponding steps of the pathway. K_D ^dNTP, forward and reverse rates of chemistry and rate of PPi release were derived from simulation of the reaction pathway. The rate of enzyme-DNA association (k_on) was calculated from the K_D ^DNA and k_off using the relation that K_D ^DNA = k_off/k_on. It should be noted that although nucleotide binding and PPi release are each shown as single steps, they may in fact be comprised of more than one elementary step, such as a conformational change in the polymerase accompanying substrate binding and product release.

Our data show that Sau-PolC-ΔNΔExo is a fast enzyme, with a maximum nucleotide incorporation rate k_pol of 330 s⁻¹, but also binds DNA weakly, with a K_D ^DNA of 390 nM, and dissociates rapidly from DNA, with a k_off of 150 s⁻¹ when dNTP is not bound. These parameters indicate that Sau-PolC-ΔNΔExo would have a very low processivity, which is consistent with previous reports about C-family replicative polymerases being non-processive in the absence of accessory protein factors like the β-clamp [12], [35]. Furthermore, weak DNA binding is important for rapid, high fidelity DNA synthesis by bacterial replicative polymerases, as evidenced by an E. coli DnaE mutant, dnaE173, which has a single amino acid substitution of E612K [36]. The mutant enzyme binds DNA more tightly and simultaneously becomes more processive (even in the absence of clamp), but also shows a reduced rate of DNA elongation and is more error-prone [36]. The data we have obtained for Sau-PolC-ΔNΔExo are also consistent with the little kinetic data previously available for full-length C-family polymerases [37]–[39].

The most surprising result from these studies is that nucleotide binding is in equilibrium with the chemical step of the phosphoryl transfer reaction. For this to be the case, the step immediately after chemistry must be slow enough so that there is a build up of the enzyme-DNA-PPi complex resulting from chemistry, thus driving the reverse of nucleotide addition (pyrophosphorolysis). We hypothesize that PPi release after catalysis, or a conformational change that precedes PPi release, might act as a rate-limiting step in the catalytic cycle, allowing the polymerase to retain a conformation favorable to reversal of bond formation. From simulating the reaction mechanism, the rate of this slow step was calculated to be 26 s⁻¹ and is likely to be the main determinant of k_cat (17 s⁻¹).

Equilibrium between chemistry and ground state dNTP binding has not, to our knowledge, been observed previously for standard dNTPs, but has been reported for mitochondrial DNA polymerase gamma incorporating the damaged nucleotide 8-oxo-dGTP and the nucleotide analog AZT-TP [40]–[42]. Since this was not observed with standard nucleotides, it was proposed to be a mechanism for removing non-natural nucleotides. If the slow step after chemistry plays the same role for PolC, it could provide a rudimentary proofreading function.

Previous studies show that the sliding β-clamp processivity factor increases not only the processivity of the C-family polymerases but also the intrinsic rate of nucleotide incorporation. E. coli pol III core, for example, synthesizes DNA at a rate of 20 nt/sec, but the rate increases to at least 500 nt/sec in the presence of clamp [43], [44]. Similarly, the intrinsic nucleotide incorporation rate of S. aureus PolC on primed circular single-stranded DNA was estimated to be ∼80 nt/sec, and this increased to ∼480 nt/sec in the presence of the sliding clamp [12]. Association with processivity factor, however, does not always stimulate the rate of nucleotide incorporation in this way. The processivity of E. coli pol II increases from 5 to ∼1600 nucleotides in the presence of β-clamp, but nucleotides are incorporated at a rate of ∼30 nt/sec in both cases [45]. These observations led to the proposal that β-clamp not only increases the processivity of the C-family replicative polymerases, but that it also increases the rate of a limiting step in the catalytic cycle [12].

Our kinetic data suggest a mechanism by which β-clamp may increase the rate of nucleotide incorporation: by increasing the rate of the slow step immediately after chemistry. β-clamp increases processivity by encircling the DNA duplex and eliminating DNA dissociation as a step in the reaction pathway. However, since Sau-PolC-ΔNΔExo has a slow kinetic step (26 s⁻¹) between catalysis and DNA dissociation, nucleotide incorporation would not be stimulated if this was the only step in the reaction pathway that was changed. We hypothesize that β-clamp binding to PolC would speed up the rate of the slow step after chemistry, perhaps by stimulating PPi release. If the step immediately after chemistry was no longer rate limiting, we would expect the rate of processive DNA synthesis to increase to the rate of chemistry (330 s⁻¹).

Overall, the results presented here establish the kinetic foundation for future structure-function studies of the C-family polymerases by allowing a quantitative comparison of enzyme activities. Structural studies indicate that DnaE and PolC are members of the β-nucleotidyl transferase superfamily, making the bacterial replicative polymerases more closely related to eukaryotic repair polymerases (such as pol β from the X-family) than to eukaryotic or archaeal replicative polymerases [16]–[19]. Some questions that can now be addressed include: How do the C-family polymerases incorporate nucleotides more than 100-fold faster than the X-family polymerases? What contributes to the substantial differences in substrate binding between the two polymerase families? How do the replicative C-family polymerases achieve such a high fidelity of DNA synthesis? PolC has been identified as a novel drug target for antibiotics against Gram-positive bacteria [46], [47]. Beyond increasing our fundamental understanding of bacterial DNA replication, addressing these questions may help in identifying novel features of PolC that could help in developing new antibiotics against Gram-positive pathogens.

Funding Statement

This work was supported by NIH grant R01-GM080573 to J.D.P. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.