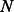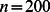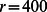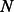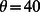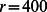Abstract
Selective sweeps are at the core of adaptive evolution. We study how the shape of coalescent trees is affected by recent selective sweeps. To do so we define a coarse-grained measure of tree topology. This measure has appealing analytical properties, its distribution is derived from a uniform, and it is easy to estimate from experimental data. We show how it can be cast into a test for recent selective sweeps using microsatellite markers and present an application to an experimental data set from Plasmodium falciparum.
Author Summary
It is one of the major interests in population genetics to contrast the properties and consequences of neutral and non-neutral modes of evolution. As is well-known, positive Darwinian selection and genetic hitchhiking drastically change the profile of genetic diversity compared to neutral expectations. The present-day observable genetic diversity in a sample of DNA sequences depends on events in their evolutionary history, and in particular on the shape of the underlying genealogical tree. In this paper we study how the shape of coalescent trees is affected by the presence of positively selected mutations. We define a measure of tree topology and study its properties under scenarios of neutrality and positive selection. We show that this measure can reliably be estimated from experimental data, and define an easy-to-compute statistical test of the neutral evolution hypothesis. We apply this test to data from a population of the malaria parasite Plasmodium falciparum and confirm the signature of recent positive selection in the vicinity of a drug resistance locus.
Introduction
The coalescent process is an established tool to describe the evolutionary history of a sample of genes drawn from a natural population [1]–[3]. For a neutrally evolving population of constant size 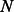 the coalescent has well understood analytical properties concerning tree shape and mutation frequency spectrum which provide a firm basis for a variety of statistical tests of the neutral evolution hypothesis [4]–[8]. Adding recombination as an evolutionary mechanism, the coalescent is usually studied in the framework of the ancestral recombination graph (ARG) [9]. The combined action of selection and recombination has been analyzed first in detail by Hudson and Kaplan [10] and, in terms of genetic hitchhiking, by Kaplan et al.
[11]. More recently, it was shown that the (non-Markovian) ARG can well be approximated by a simpler, more tractable model, the so-called Sequential Markov Coalescent [12]–[14], which is of particular interest for the efficient simulation of genealogies across large genomic regions. How single recombination events reflect on tree shape under neutrality has recently been analyzed by Ferretti et al. [15]. Here, we concentrate on tree shape in the vicinity of a selected locus.
the coalescent has well understood analytical properties concerning tree shape and mutation frequency spectrum which provide a firm basis for a variety of statistical tests of the neutral evolution hypothesis [4]–[8]. Adding recombination as an evolutionary mechanism, the coalescent is usually studied in the framework of the ancestral recombination graph (ARG) [9]. The combined action of selection and recombination has been analyzed first in detail by Hudson and Kaplan [10] and, in terms of genetic hitchhiking, by Kaplan et al.
[11]. More recently, it was shown that the (non-Markovian) ARG can well be approximated by a simpler, more tractable model, the so-called Sequential Markov Coalescent [12]–[14], which is of particular interest for the efficient simulation of genealogies across large genomic regions. How single recombination events reflect on tree shape under neutrality has recently been analyzed by Ferretti et al. [15]. Here, we concentrate on tree shape in the vicinity of a selected locus.
Selection changes the rate by which coalescent events occur and hence can lead to distortions of tree shape. It is well known [6], [16] that selective sweeps can produce highly unbalanced trees when selection acts in concert with limited recombination, i.e. at some chromosomal distance from the site under selection. Conversely, observing unbalanced trees should provide information about recent selection in a particular genomic region. In fact, this property is also the basis of Li's MDFM test [16]. A practical concern is how such distorted gene genealogies may reliably be estimated or re-constructed using polymorphism data. When working with SNPs a large genomic fragment with many polymorphic sites has to be analyzed to obtain a clear phylogenetic signal. Since for many organisms recombination and mutation rates are on the same order of magnitude [17, Table 4.1], one harvests about as many recombination as polymorphic sites when sampling genomic sequences, thus complicating tree shape estimation. To alleviate this problem one may turn to multi-allelic markers, such as microsatellites, complementing or replacing bi-allelic SNPs.
In this paper we introduce the statistic  of tree balance and, first, derive theoretical properties of this and derived statistics. Second, we show how a selective sweep affects these statistics. Third, we investigate the possibility and reliability of estimating
of tree balance and, first, derive theoretical properties of this and derived statistics. Second, we show how a selective sweep affects these statistics. Third, we investigate the possibility and reliability of estimating  from experimental data. Fourth, we define an easily applicable microsatellite based test statistic for selective sweeps. It requires clustering of microsatellite alleles into two disjoint sets and examining whether these sets are sufficiently different in size and/or whether they have a sufficiently large distance from each other. Finally, we demonstrate a practical application.
from experimental data. Fourth, we define an easily applicable microsatellite based test statistic for selective sweeps. It requires clustering of microsatellite alleles into two disjoint sets and examining whether these sets are sufficiently different in size and/or whether they have a sufficiently large distance from each other. Finally, we demonstrate a practical application.
Terminology
Consider the coalescent tree for a sample of size  . It is a binary tree without left-right orientation, with ordered internal nodes and branch lengths representing a measure of time. All leaves are aligned on the bottom line, representing the present. We use the term tree topology when talking about the branching pattern and tree shape when talking about topology and branch lengths. We remark that topology and shape can be conceptually distinguished, but in practice estimating topology relies on polymorphism patterns. Since these depend on branch lengths, i.e. on shape, topology can usually not be estimated independently. We call the size of a tree the number of leaves and the length of a tree the combined length of all branches. The height is the time interval between present and root, indicated by
. It is a binary tree without left-right orientation, with ordered internal nodes and branch lengths representing a measure of time. All leaves are aligned on the bottom line, representing the present. We use the term tree topology when talking about the branching pattern and tree shape when talking about topology and branch lengths. We remark that topology and shape can be conceptually distinguished, but in practice estimating topology relies on polymorphism patterns. Since these depend on branch lengths, i.e. on shape, topology can usually not be estimated independently. We call the size of a tree the number of leaves and the length of a tree the combined length of all branches. The height is the time interval between present and root, indicated by  in Figure 1. Let the label of the root be
in Figure 1. Let the label of the root be 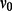 . The
. The  leaves can be grouped into two disjoint sets,
leaves can be grouped into two disjoint sets, 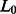 and
and 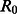 , the ‘left-‘ and ‘right-descendants’ of the root. Let
, the ‘left-‘ and ‘right-descendants’ of the root. Let 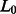 be the smaller of the two sets and
be the smaller of the two sets and 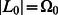 . Hence,
. Hence, 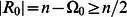 . Let
. Let 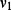 be the ‘right’ child of
be the ‘right’ child of 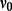 , i.e. the root of the subtree with leaf set
, i.e. the root of the subtree with leaf set 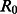 . The descendants of
. The descendants of 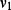 can again be grouped into two disjoint subsets,
can again be grouped into two disjoint subsets, 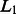 and
and 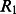 , the left- and right-descendants of
, the left- and right-descendants of 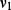 . Again, without loss of generality, let
. Again, without loss of generality, let 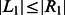 and denote
and denote 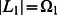 . Hence,
. Hence, 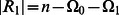 . Proceed in this way to define subsets
. Proceed in this way to define subsets 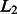 ,
, 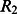 , and so on. For any tree there are
, and so on. For any tree there are 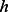 such pairs
such pairs 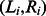 where
where 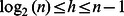 , with
, with 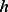 depending on the topology of the tree. The set
depending on the topology of the tree. The set 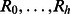 constitutes a – not necessarily unique – top-down sequence of maximal subtrees.
constitutes a – not necessarily unique – top-down sequence of maximal subtrees.
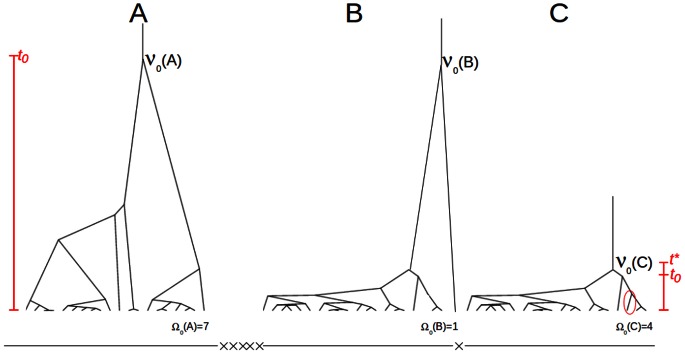
Figure 1. Coalescent trees under recombination and selection.
A: Sketch of a neutral coalescent tree with tree size 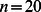 . B and C: A selective sweep in locus C leads to a tree of low height (
. B and C: A selective sweep in locus C leads to a tree of low height (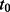 small). The selective sweep was initiated by a beneficial mutation at time
small). The selective sweep was initiated by a beneficial mutation at time 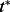 . At some distance from C, a single lineage (circled branch in C) has “recombined away” leading to the unbalanced tree shown at locus B. Note that tree height between trees B and C changes drastically and that
. At some distance from C, a single lineage (circled branch in C) has “recombined away” leading to the unbalanced tree shown at locus B. Note that tree height between trees B and C changes drastically and that 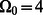 at locus C and
at locus C and 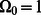 at locus B. Multiple recombination events (indicated by the crosses at the bottom line) between loci A and B lead to essentially uncorrelated trees at A and B.
at locus B. Multiple recombination events (indicated by the crosses at the bottom line) between loci A and B lead to essentially uncorrelated trees at A and B.
Results
Tree topology of the neutral coalescent
Consider a coalescent tree of size  under the neutral model with constant population size, where
under the neutral model with constant population size, where  is assumed to be large. Root imbalance is measured by the random variable
is assumed to be large. Root imbalance is measured by the random variable 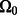 . The distribution of
. The distribution of 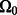 is ‘almost’-uniform [18], [19] on
is ‘almost’-uniform [18], [19] on 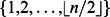 . More precisely,
. More precisely,
| (1) |
where  .,. denotes here the Kronecker symbol. The expectation is
.,. denotes here the Kronecker symbol. The expectation is
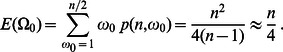 |
The variance is
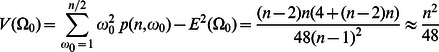 |
and the standard deviation
provided  is sufficiently large.
is sufficiently large.
The compound random variables 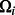 ,
, 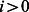 , have support which depends on
, have support which depends on  ,
, 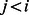 . More precisely, the distribution of
. More precisely, the distribution of 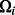 , given
, given 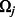 ,
, 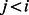 , is almost-uniform on
, is almost-uniform on 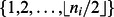 with
with
| (2) |
where 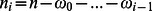 (
(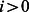 ) is a random variable which is bounded below by
) is a random variable which is bounded below by 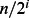 and above by
and above by  . The moments are somewhat more complicated. For instance,
. The moments are somewhat more complicated. For instance,
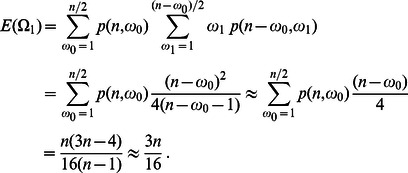 |
Continuing this way, evaluating sums iteratively and using the above approximation, one derives
| (3) |
Similary, one can obtain the second moments and combine these to
| (4) |
Define now the normalized random variables 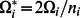 . Since
. Since  is a constant, we have for
is a constant, we have for 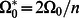
and
To calculate the moments of 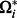 ,
, 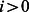 , we replace
, we replace 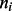 by
by 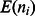 . Simulations suggest that this is acceptable, as long as
. Simulations suggest that this is acceptable, as long as 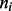 is not too small. Figure 2 shows this fact for
is not too small. Figure 2 shows this fact for 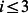 . Here we focus on
. Here we focus on 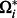 for
for 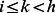 , where
, where 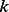 is small and
is small and  is large (
is large (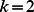 ,
, 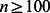 , say). Since,
, say). Since,
we obtain
| (5) |
Similarly,
| (6) |
and
It is very convenient to work with the normalized random variables 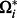 instead of
instead of 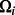 . Their support is bounded by
. Their support is bounded by  and
and 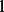 for all
for all  and they are well approximated by independent continuous uniforms on the unit interval. This considerably facilitates the handling of sums and products of
and they are well approximated by independent continuous uniforms on the unit interval. This considerably facilitates the handling of sums and products of 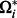 . For instance, the joint distribution
. For instance, the joint distribution 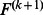 of
of 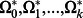 is then approximated by the continuous uniform product with distribution function
is then approximated by the continuous uniform product with distribution function
| (7) |
expectation
and variance
The coefficient of variation, 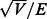 , is
, is
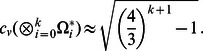 |
As is well known, the normalized sum of continuous uniforms converges in distribution to a normal random variable rather quickly. In fact, we have for the standardized sum
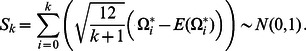 |
(8) |
In practice, already 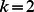 yields a distribution which is reasonably close to a normal (see Suppl. Figure S1).
yields a distribution which is reasonably close to a normal (see Suppl. Figure S1).
Figure 2. Mean and standard deviation of  and
and  for coalescent trees of size
for coalescent trees of size  .
.
Shown are the values for  independent realizations.
independent realizations.  -axis: values of
-axis: values of  (black circles) and
(black circles) and 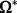 (red squares) are determined for the subtrees originating at node
(red squares) are determined for the subtrees originating at node 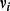 ,
, 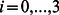 . The solid gray line shows the theoretical expectation according to eq (3).
. The solid gray line shows the theoretical expectation according to eq (3).
Linked trees
Consider now a sample of recombining chromosomes. Coalescent trees along a recombining chromosome are not independent. In particular, tree height and tree topology of closely linked trees are highly correlated. However, under conditions of the standard neutral model, correlation breaks down on short distances (Figure 3) [15]. Roughly 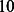 recombination events in the sample history reduce correlation by about 50%. Under neutrality and when
recombination events in the sample history reduce correlation by about 50%. Under neutrality and when 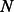 is constant, a sample of size
is constant, a sample of size  has experienced on average
has experienced on average 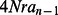 recombination events [20] (Suppl. Figure S2), where
recombination events [20] (Suppl. Figure S2), where 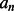 is the
is the  -th harmonic number and represents the length of the tree. Assuming a recombination rate of
-th harmonic number and represents the length of the tree. Assuming a recombination rate of 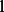 cM/Mb, population size
cM/Mb, population size 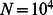 and sample size
and sample size 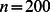 , this amounts to roughly
, this amounts to roughly 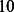 recombination events per
recombination events per  kb. If
kb. If 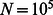 , in an interval of only about
, in an interval of only about 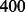 bp correlation is reduced to 50% (Figure 3). Thus, if correlation half-life is determined by roughly
bp correlation is reduced to 50% (Figure 3). Thus, if correlation half-life is determined by roughly 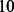 events in the sample, we estimate the correlation length
events in the sample, we estimate the correlation length 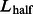 as
as
| (9) |
where  is the recombination rate per
is the recombination rate per 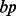 per unit time. Hence, trees may be regarded as essentially uncorrelated when considering physical distances of some
per unit time. Hence, trees may be regarded as essentially uncorrelated when considering physical distances of some 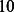 kb and sufficiently large populations and samples.
kb and sufficiently large populations and samples.
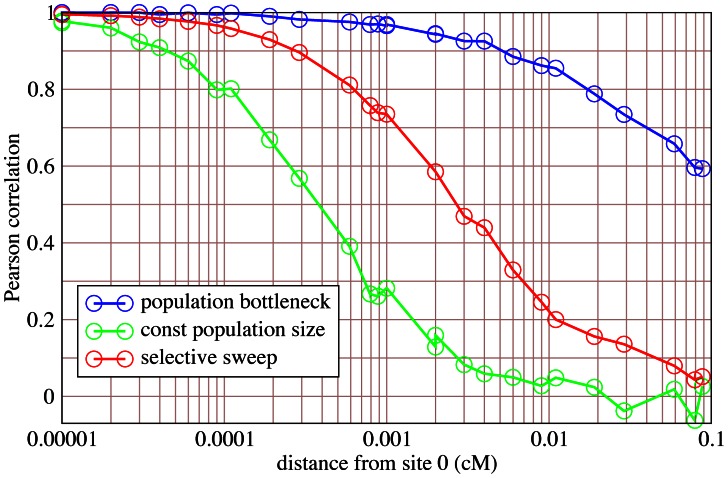
Figure 3. Correlation across distance.
Correlation based on simulations (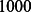 replicates) of the statistic
replicates) of the statistic  of the true tree. Pearson's correlation coefficient is measured between
of the true tree. Pearson's correlation coefficient is measured between 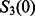 and
and 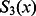 for pairs of trees at position
for pairs of trees at position  and position
and position  . Three scenarios are compared: standard neutral model with constant population size (green), population bottleneck (blue) and selective sweep (red). Sample size
. Three scenarios are compared: standard neutral model with constant population size (green), population bottleneck (blue) and selective sweep (red). Sample size 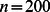 ,
, 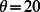 ,
, 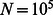 and a recombinaton rate of
and a recombinaton rate of 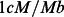 is assumed. The bottleneck parameters are:
is assumed. The bottleneck parameters are: 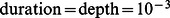 ,
, 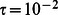 . The selective sweep has a strength of
. The selective sweep has a strength of 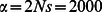 . The selected site is at position
. The selected site is at position 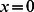 . Under standard neutrality,
. Under standard neutrality, 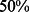 correlation is reached at position
correlation is reached at position 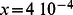 cM, corresponding to about
cM, corresponding to about 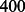 bp.
bp.
Eq (9) may be violated if population size 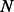 is not constant. As a biologically relevant example we consider a population bottleneck, during which the population is reduced to size
is not constant. As a biologically relevant example we consider a population bottleneck, during which the population is reduced to size 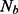 . A bottleneck is characterized by three parameters, time of onset, duration (both in units of
. A bottleneck is characterized by three parameters, time of onset, duration (both in units of 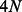 ) and depth (
) and depth (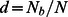 ). A bottleneck induces time dependent changes of the coalescent rate [21] and a reduction of effective population size. Particularly drastic effects on the genealogy are observed when the duration is similar to or larger than the depth [22]. Given biologically reasonable parameters, this inflation may even be larger under a bottleneck than under a selective sweep (Figure 3).
). A bottleneck induces time dependent changes of the coalescent rate [21] and a reduction of effective population size. Particularly drastic effects on the genealogy are observed when the duration is similar to or larger than the depth [22]. Given biologically reasonable parameters, this inflation may even be larger under a bottleneck than under a selective sweep (Figure 3).
Tree topology in the vicinity of a selective sweep
A positively selected allele sweeping through a population leads to a drastic reduction of tree height due to its short fixation time 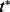 (see Figure 1C). The fixation time depends on the selection coefficient
(see Figure 1C). The fixation time depends on the selection coefficient  and population size
and population size 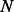 . In units of
. In units of 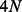 ,
, 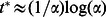 , where
, where 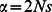 [23]. This is much smaller than the neutral average fixation time
[23]. This is much smaller than the neutral average fixation time 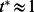 . The reduced fixation time leads to a severe reduction of genetic variability. Furthermore, external branches of the tree are elongated relative to internal branches, yielding a star-like phylogeny of an approximate length of
. The reduced fixation time leads to a severe reduction of genetic variability. Furthermore, external branches of the tree are elongated relative to internal branches, yielding a star-like phylogeny of an approximate length of 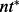 . Replacing the neutral tree length
. Replacing the neutral tree length 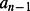 in eq (9) by this figure, we obtain the following estimate for the correlation half-life
in eq (9) by this figure, we obtain the following estimate for the correlation half-life
| (10) |
For the parameters used in Figure 3, we have 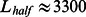 bp, which agrees well with the simulation result.
bp, which agrees well with the simulation result.
In contrast to tree height and length, tree topology at the selected site does not necessarily differ from a neutral tree; only when moving away from the sweep site, and with recombination, topology may drastically change. In fact, given a shallow tree, recombination leads with high probability to an increase of tree height and to unbalanced trees [15]. Thus, recombination events next to the selected site tend to increase tree height (see sketch in Figure 1B and C) and to create a bias in favour of unbalanced trees, i.e. trees with small 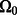 (Figure 4A). The expected proximal distance
(Figure 4A). The expected proximal distance 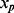 from the selected site of such a recombination event can be estimated as
from the selected site of such a recombination event can be estimated as
| (11) |
where 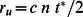 ,
,  is the per site recombination rate, and
is the per site recombination rate, and 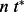 is the length of a star-like phylogeny; the factor
is the length of a star-like phylogeny; the factor 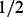 accounts for the fact that it is more likely to recombine with an ancestral chromosome (thereby increasing tree height) as long as these are more abundant than the derived chromosomes carrying the selected allele. Roughly, this is the case during the first half of the fixation time
accounts for the fact that it is more likely to recombine with an ancestral chromosome (thereby increasing tree height) as long as these are more abundant than the derived chromosomes carrying the selected allele. Roughly, this is the case during the first half of the fixation time 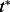 . Assuming instead of the star phylogeny a random tree topology of average length
. Assuming instead of the star phylogeny a random tree topology of average length 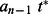 at the selected site, one obtains the larger (call it distal) estimate
at the selected site, one obtains the larger (call it distal) estimate
| (12) |
where 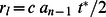 .
.
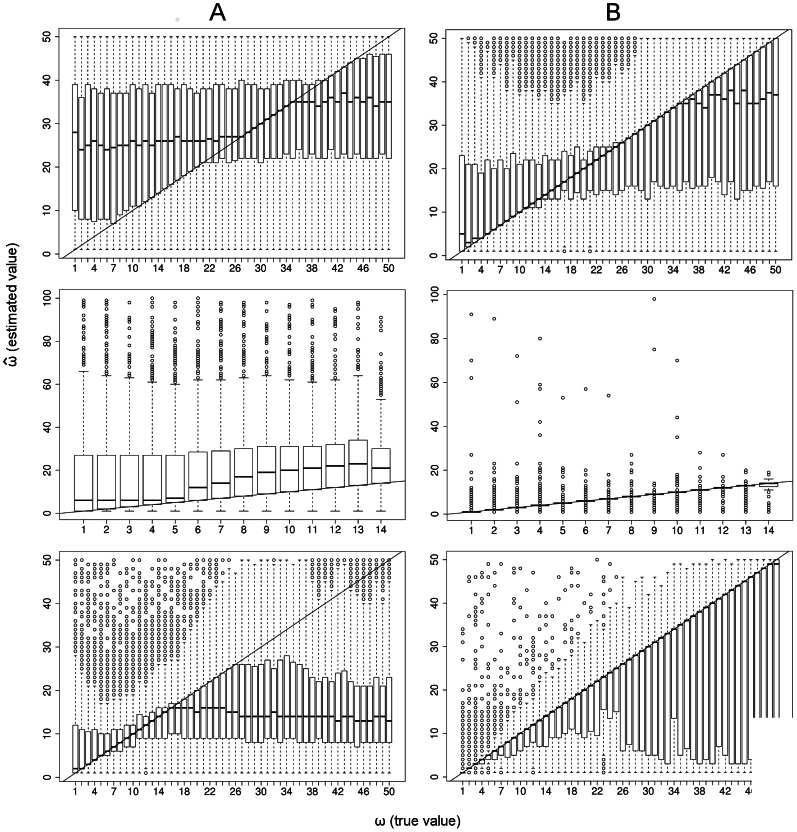
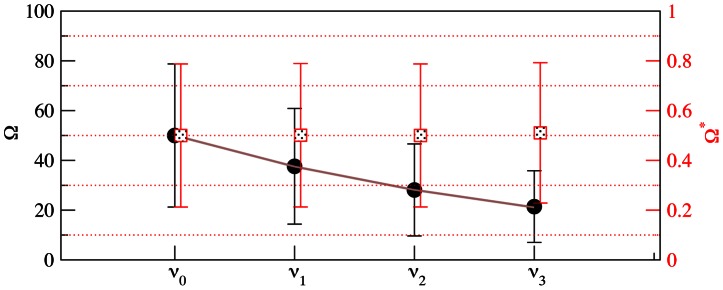
Figure 4. Estimation of  .
.
A: estimation of 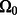 by
by 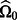 . B: estimation of
. B: estimation of 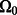 by
by 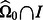 . First row: standard neutral model. Second row: Selective sweep; estimation of
. First row: standard neutral model. Second row: Selective sweep; estimation of 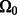 at distance
at distance 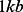 from selected site. Third row: Selective sweep; distance
from selected site. Third row: Selective sweep; distance 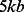 from selected site. Parameters:
from selected site. Parameters: 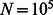 ;
; 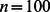 (top and bottom row);
(top and bottom row); 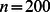 (middle row);
(middle row); 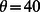 ;
; 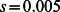 ;
; 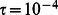 .
.
Unbalanced trees tend to have strongly elongated root branches and harbor an over-abundance of high frequency derived SNP alleles [6], [16]. With microsatellites it is usually not possible to determine the ancestral and derived states of an allele, because they mutate at a high rate and possibly undergo back-mutation. However, under the symmetric single step mutation model, the expected distance between a pair of alleles (in terms of motif copy numbers) behaves as the distance in a one-dimensional symmetric random walk and therefore increases at a rate proportional to the square root of the scaled mutation rate  (see Methods). Thus, alleles which are separated by long root branches tend to form two distinct allele clusters.
(see Methods). Thus, alleles which are separated by long root branches tend to form two distinct allele clusters.
Estimating 
Tree topology is ususally not directly observable and has to be estimated from data. We focus on estimating 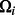 ,
, 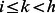 , from microsatellite data. Given a sample of
, from microsatellite data. Given a sample of  microsatellite alleles with tandem repeat counts
microsatellite alleles with tandem repeat counts 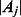 ,
, 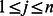 , we use UPGMA [24] to construct a hierarchical cluster diagram. If subtree topology within a particular cluster node should not be uniquely re-solvable, for instance if alleles are identical, we randomly assign the alleles of the subtree under consideration to two clusters with equal probability. This gives preference to clusters of balanced size in case of insufficient resolution. We then use the inferred tree topology
, we use UPGMA [24] to construct a hierarchical cluster diagram. If subtree topology within a particular cluster node should not be uniquely re-solvable, for instance if alleles are identical, we randomly assign the alleles of the subtree under consideration to two clusters with equal probability. This gives preference to clusters of balanced size in case of insufficient resolution. We then use the inferred tree topology 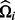 to estimate
to estimate 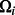 of the true tree. This procedure is conservative for the test statistics described below, since it gives preference to large values
of the true tree. This procedure is conservative for the test statistics described below, since it gives preference to large values 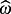 when the true value
when the true value 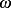 is small (Figure 4, column A). For a cluster pair
is small (Figure 4, column A). For a cluster pair 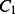 ,
, 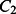 , define the distance as
, define the distance as
| (13) |
We find that UPGMA clustering gives good estimates of 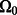 when clusters are clearly separated from each other, i.e. when
when clusters are clearly separated from each other, i.e. when 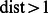 . Let
. Let 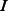 be the indicator variable for this event. Then, we have for the median
be the indicator variable for this event. Then, we have for the median
(Figure 4, column B). Without requiring 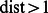 the estimate
the estimate 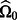 is more biased. In part, this is due to the conservative UPGMA strategy mentioned above. However, estimation of
is more biased. In part, this is due to the conservative UPGMA strategy mentioned above. However, estimation of 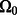 is very accurate when root branches are strongly elongated, i.e. under conditions of selective sweeps or certain bottlenecks (Figure 4, bottom).
is very accurate when root branches are strongly elongated, i.e. under conditions of selective sweeps or certain bottlenecks (Figure 4, bottom).
Application: Testing the neutral evolution hypothesis
We now turn to an application of the above results and explain how a new class of microsatellite based tests of the neutral evolution hypothesis can be defined.
Consider a sample of  alleles at a microsatellite marker and record their motif repeat numbers. Applying UPGMA clustering to the alleles, we obtain estimates
alleles at a microsatellite marker and record their motif repeat numbers. Applying UPGMA clustering to the alleles, we obtain estimates 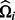 ,
, 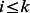 as described above. These are transformed to
as described above. These are transformed to 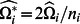 . Then, we determine the following test statistics
. Then, we determine the following test statistics
| (14) |
| (15) |
| (16) |
Thus, the test variable 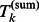 in eq (14) is the estimate of
in eq (14) is the estimate of 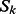 given in eq (8). Similarly,
given in eq (8). Similarly, 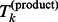 and
and 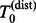 are the estimates of the product
are the estimates of the product 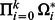 and of
and of 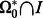 .
.
We now test the null hypothesis 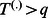 for a critical value
for a critical value 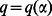 . For a given level
. For a given level  we obtain the critical value
we obtain the critical value 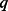 for
for 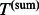 from the standard normal distribution and for
from the standard normal distribution and for 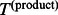 from the uniform product distribution in eq (7) (Table 1). For
from the uniform product distribution in eq (7) (Table 1). For 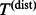 we use the critical value of the normalized version of eq (1). Generally, these critical values are conservative, since
we use the critical value of the normalized version of eq (1). Generally, these critical values are conservative, since 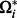 tends to over-estimate
tends to over-estimate 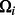 , when small (Figure 4). In particular, statistic
, when small (Figure 4). In particular, statistic 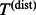 is very conservative due to the additional condition on the distance. The true critical values for level
is very conservative due to the additional condition on the distance. The true critical values for level  would be larger than those shown in Table 1.
would be larger than those shown in Table 1.
Table 1. Critical values for the tests considered in eqs (14)–(16).

|
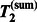
|

|
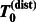
|
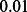
|
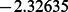
|
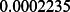
|
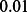
|
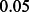
|
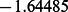
|
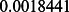
|
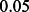
|
False positive rates and power
First, we analyzed the false positive rates under the standard neutral scenario (i.e., constant 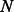 ) for different mutation rates
) for different mutation rates  and varying sample sizes
and varying sample sizes  . As reference parameter settings for simulations with msmicro (see Methods) we use sample size
. As reference parameter settings for simulations with msmicro (see Methods) we use sample size 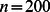 , microsatellite mutation rate
, microsatellite mutation rate 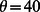 and recombination rate
and recombination rate 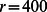 . The latter corresponds to a recombination rate of
. The latter corresponds to a recombination rate of 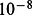 per bp per chromosome, when one assumes a population size of
per bp per chromosome, when one assumes a population size of 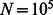 and a size of the investigated genomic region of
and a size of the investigated genomic region of 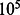 bp (
bp (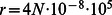 ). We placed 15 microsatellite markers at positions
). We placed 15 microsatellite markers at positions 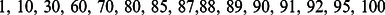 kb. As expected, we find that the false positive rates remain below their theoretical expectation for all parameter choices
kb. As expected, we find that the false positive rates remain below their theoretical expectation for all parameter choices  and
and  (Figure 5 top; Tables 2 and 3). For the simulations with selection we assumed that a site at position
(Figure 5 top; Tables 2 and 3). For the simulations with selection we assumed that a site at position 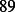 kb was undergoing a selective sweep with selection coefficient
kb was undergoing a selective sweep with selection coefficient 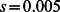 or
or 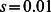 . The time since completion of the sweep was an adjustable parameter
. The time since completion of the sweep was an adjustable parameter  , with the reference setting
, with the reference setting 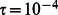 . We simulated hard selective sweeps, i.e. the selected allele is introduced as a single copy and fixed with probability about
. We simulated hard selective sweeps, i.e. the selected allele is introduced as a single copy and fixed with probability about 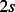 . The test statistic
. The test statistic 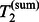 is shown in Figure 5 and power profiles for all three tests in Figure 6. We find that maximum power of the tests is attained within the interval given by eqs (11) and (12) (Figure 6 and Tables 4 and S1). Depending on the strength of selection, maximum power is close to the upper interval bound at
is shown in Figure 5 and power profiles for all three tests in Figure 6. We find that maximum power of the tests is attained within the interval given by eqs (11) and (12) (Figure 6 and Tables 4 and S1). Depending on the strength of selection, maximum power is close to the upper interval bound at 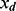 (
(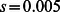 , Table S1), or removed from
, Table S1), or removed from 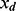 towards the interior of the interval (
towards the interior of the interval (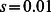 , Table 4). This is in agreement with the expectation that only very strong selective sweeps generate a star-like phylogeny, which lead to the proximal estimate
, Table 4). This is in agreement with the expectation that only very strong selective sweeps generate a star-like phylogeny, which lead to the proximal estimate 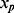 in eq (11). Thus, the location of the power maximum depends on the strength of selection and the details of the tree topology at the selected site. Maximum power for the compound tests
in eq (11). Thus, the location of the power maximum depends on the strength of selection and the details of the tree topology at the selected site. Maximum power for the compound tests 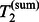 and
and 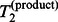 is more removed from the selected site than for the simple test
is more removed from the selected site than for the simple test 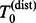 . The latter measures imbalance only at the root node
. The latter measures imbalance only at the root node 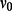 and is most sensitive to single recombination events between marker and selected site, while multiple events blur the effect. The power of all tests is sensitive to the mutation rate and to sample size (Tables S2 and S3). For the parameters tested, the power of the simple
and is most sensitive to single recombination events between marker and selected site, while multiple events blur the effect. The power of all tests is sensitive to the mutation rate and to sample size (Tables S2 and S3). For the parameters tested, the power of the simple 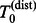 increases when
increases when  or
or  increase. For
increase. For 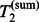 , maximum power is reached for
, maximum power is reached for 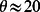 . Very small, as well as very high, mutation rates produce little power. Realistic mutation rates in insects and vertebrates are between
. Very small, as well as very high, mutation rates produce little power. Realistic mutation rates in insects and vertebrates are between 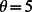 and
and 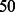 [25]–[27], thus within the powerful domain. Importantly, power can be increased by increasing sample size: all of the above tests become more powerful for large samples (Tables S3, S4 and S5). Since the tests consistently underscore the theoretical false positive rate, relaxed singnificance levels (for instance
[25]–[27], thus within the powerful domain. Importantly, power can be increased by increasing sample size: all of the above tests become more powerful for large samples (Tables S3, S4 and S5). Since the tests consistently underscore the theoretical false positive rate, relaxed singnificance levels (for instance 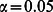 ) can be applied. At level
) can be applied. At level 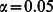 test
test 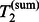 has power of more than
has power of more than 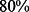 to detect recent selective sweeps (Figure 6 and Table 4). For intermediate mutation rates power of test
to detect recent selective sweeps (Figure 6 and Table 4). For intermediate mutation rates power of test 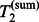 is somewhat higher than of
is somewhat higher than of 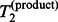 (Table S2). Generally, power profiles of
(Table S2). Generally, power profiles of 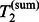 and
and 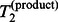 follow qualitatively the same pattern. In contrast, power of test
follow qualitatively the same pattern. In contrast, power of test 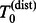 may be quite different. Interestingly,
may be quite different. Interestingly, 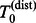 performs better than
performs better than 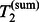 or
or 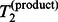 when selection is only moderately strong. Unsurprisingly, power of all tests depends heavily on the strength of selection. Also, the time since completion of the selective sweep influences power. Reasonable power can be reached if
when selection is only moderately strong. Unsurprisingly, power of all tests depends heavily on the strength of selection. Also, the time since completion of the selective sweep influences power. Reasonable power can be reached if 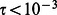 in coalescent units.
in coalescent units.
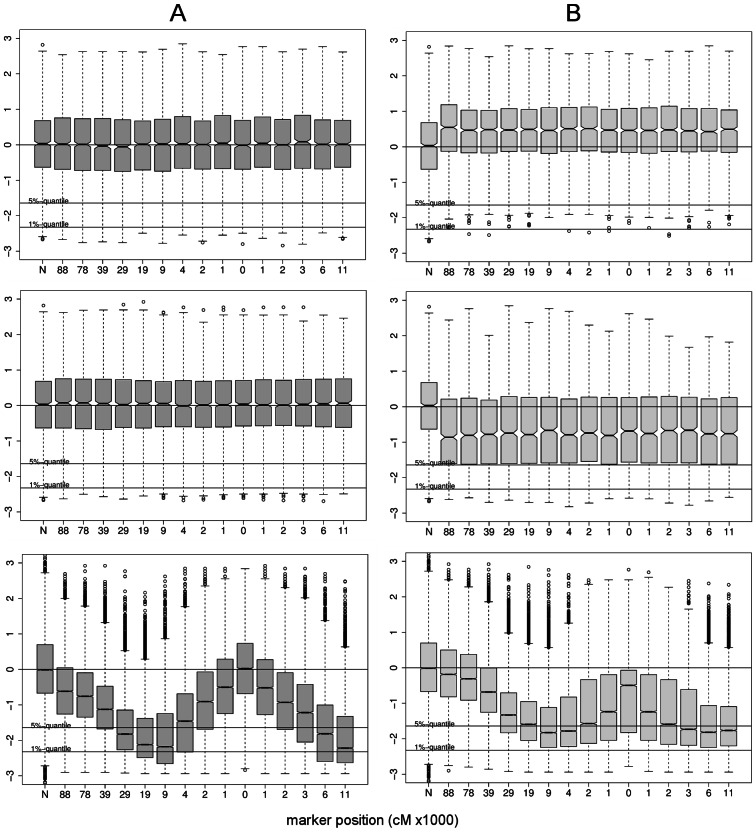
Figure 5. Profile of 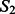 and
and 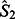 along a recombining chromosome.
along a recombining chromosome.
Plots in column A show the distribution of 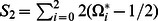 , i.e. when the tree topology is known. Plots in column B show the distribution of the estimate
, i.e. when the tree topology is known. Plots in column B show the distribution of the estimate 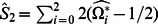 when the tree topology is unknown, but estimated from microsatellite polymorphism data. Each boxplot corresponds to one of
when the tree topology is unknown, but estimated from microsatellite polymorphism data. Each boxplot corresponds to one of 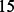 marker loci located at the positions indicated on the
marker loci located at the positions indicated on the 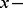 axis. The regions spans
axis. The regions spans 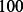 kb in total. Symmetric step-wise mutation model with
kb in total. Symmetric step-wise mutation model with 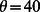 . Other parameters:
. Other parameters: 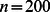 ,
, 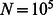 and recombination rate per bp
and recombination rate per bp
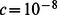 (corresponding to 1 cM/Mb). First row: standard neutral model with constant
(corresponding to 1 cM/Mb). First row: standard neutral model with constant 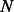 . Second row: bottleneck model with severity
. Second row: bottleneck model with severity 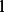 and onset
and onset 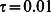 . Third row: Selective sweep at locus
. Third row: Selective sweep at locus 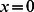 with
with 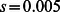 which was completed
which was completed 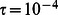 time units ago. For comparison with the theoretical expectation, the leftmost boxplot in each panel shows the standard normal distribution (labeled ‘N’).
time units ago. For comparison with the theoretical expectation, the leftmost boxplot in each panel shows the standard normal distribution (labeled ‘N’).
Table 2. Empirical false positive rate for varying  .
.
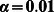
|
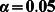
|
|||||
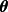
|
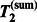
|

|
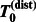
|
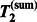
|

|
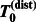
|
| 0.1 | 0.00006 | 0.00327 | 0.0001 | 0.00035 | 0.01323 | 0.00047 |
| 0.5 | 0.00523 | 0.01703 | 0.00109 | 0.01724 | 0.07931 | 0.00431 |
| 1.0 | 0.01142 | 0.01749 | 0.002 | 0.0463 | 0.08957 | 0.00887 |
| 1.5 | 0.01251 | 0.01414 | 0.00281 | 0.06365 | 0.08425 | 0.01145 |
| 2.0 | 0.01145 | 0.01127 | 0.00355 | 0.06736 | 0.07399 | 0.01354 |
| 2.5 | 0.00933 | 0.00843 | 0.00421 | 0.06579 | 0.06571 | 0.01549 |
| 3.0 | 0.00756 | 0.00663 | 0.00458 | 0.06042 | 0.05718 | 0.01781 |
| 4.0 | 0.00559 | 0.00478 | 0.00534 | 0.04936 | 0.04348 | 0.01884 |
| 5.0 | 0.00415 | 0.00315 | 0.0057 | 0.04073 | 0.03455 | 0.0208 |
| 10.0 | 0.00145 | 0.00131 | 0.00616 | 0.0244 | 0.01889 | 0.02433 |
| 20.0 | 0.00069 | 0.00049 | 0.00632 | 0.01411 | 0.01032 | 0.02685 |
| 30.0 | 0.00064 | 0.00038 | 0.00656 | 0.01018 | 0.00805 | 0.02744 |
| 40.0 | 0.00043 | 0.00035 | 0.00647 | 0.00839 | 0.00651 | 0.02702 |
| 50.0 | 0.00027 | 0.00031 | 0.006 | 0.00828 | 0.00631 | 0.02754 |
| 100.0 | 0.00028 | 0.00033 | 0.00615 | 0.00693 | 0.00591 | 0.02846 |
| 120.0 | 0.00024 | 0.00027 | 0.00614 | 0.00666 | 0.00571 | 0.02806 |
| 150.0 | 0.00024 | 0.00028 | 0.00593 | 0.00699 | 0.00548 | 0.02876 |
| 200.0 | 0.00034 | 0.00026 | 0.00624 | 0.00641 | 0.005 | 0.02844 |
Table 3. Empirical false positive rate for varying sample size  .
.
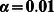
|
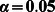
|
|||||

|
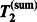
|

|
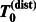
|
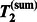
|

|
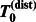
|
| 10 | N/A | N/A | 0.21417 | 0.0099 | N/A | 0.21417 |
| 20 | 0.00035 | 0 | 0.09527 | 0.01215 | 0.00035 | 0.09527 |
| 50 | 0.00055 | 0.00003 | 0.03318 | 0.0094 | 0.00286 | 0.03318 |
| 100 | 0.00052 | 0.00022 | 0.0151 | 0.00925 | 0.00527 | 0.02778 |
| 150 | 0.00044 | 0.00033 | 0.00902 | 0.00934 | 0.00609 | 0.02411 |
| 200 | 0.00039 | 0.00033 | 0.00592 | 0.00943 | 0.00684 | 0.02666 |
| 300 | 0.00038 | 0.00042 | 0.00388 | 0.00976 | 0.00828 | 0.02282 |
| 500 | 0.00042 | 0.00055 | 0.00394 | 0.01009 | 0.0093 | 0.02169 |
| 1000 | 0.00044 | 0.00104 | 0.00474 | 0.01107 | 0.01148 | 0.02057 |
Figure 6. Power to detect loci under recent selection by the three tests defined in eqs (14) to (16) .
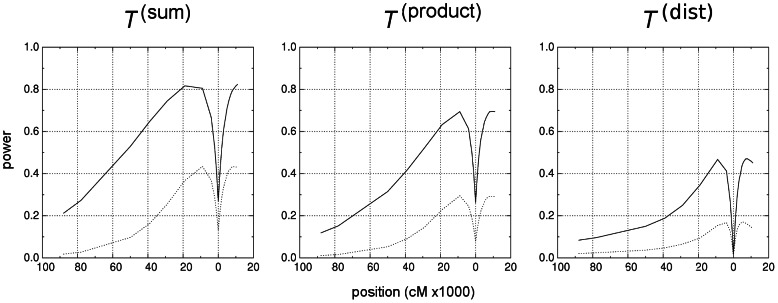
Parameters: level  (solid) and .
(solid) and . (dotted); selection coefficient
(dotted); selection coefficient  ; time since fixation
; time since fixation 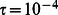 ; sample size
; sample size 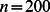 ; mutation rate
; mutation rate 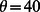 ; recombination rate
; recombination rate 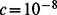 . The
. The 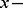 axis shows positions to the left (negative values) and right (positive values) of the locus under selection at position
axis shows positions to the left (negative values) and right (positive values) of the locus under selection at position 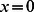 . Scale is in cM x
. Scale is in cM x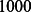 , corresponding here to kb.
, corresponding here to kb.
Table 4. Power of 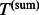 ,
, 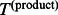 and
and 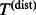 in dependence of distance to selected site.
in dependence of distance to selected site.
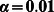
|
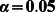
|
||||||
| distance (kb) |
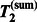
|

|
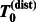
|
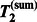
|

|
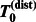
|
SKD* |
| −88.0 | 0.01794 | 0.01085 | 0.02051 | 0.21164 | 0.11855 | 0.08392 | 0.8468 |
| −78.0 | 0.02708 | 0.01613 | 0.02416 | 0.27325 | 0.15216 | 0.09606 | 0.8873 |
| −50.0 | 0.09714 | 0.0528 | 0.03672 | 0.52898 | 0.31465 | 0.1497 | 0.9353 |
| −39.0 | 0.16291 | 0.09047 | 0.04749 | 0.64722 | 0.41612 | 0.1887 | 0.9440 |
| −29.0 | 0.25581 | 0.14603 | 0.06525 | 0.74461 | 0.52288 | 0.24893 | 0.9435 |
| −19.0 | 0.3671 | 0.22901 | 0.09412 | 0.81644 | 0.63249 | 0.34637 | 0.9161 |
| −9.0 | 0.4339 | 0.29439 | 0.15377 | 0.80504 | 0.69404 | 0.46718 | 0.7931 |
| −4.0 | 0.3679 | 0.24615 | 0.16738 | 0.66659 | 0.6127 | 0.41263 | 0.5969 |
| −2.0 | 0.28585 | 0.18531 | 0.13051 | 0.52249 | 0.49368 | 0.28243 | 0.4535 |
| −1.0 | 0.21826 | 0.1383 | 0.08574 | 0.41239 | 0.39426 | 0.16926 | 0.3657 |
| 0.0 | 0.13085 | 0.07765 | 0.00971 | 0.26692 | 0.26055 | 0.01182 | 0.2670 |
| 1.0 | 0.21972 | 0.13898 | 0.08428 | 0.41424 | 0.39615 | 0.17043 | 0.3601 |
| 2.0 | 0.28701 | 0.18614 | 0.12943 | 0.52215 | 0.49205 | 0.28118 | 0.4600 |
| 3.0 | 0.33496 | 0.22226 | 0.1548 | 0.6066 | 0.56351 | 0.35927 | 0.5366 |
| 5.0 | 0.39321 | 0.26452 | 0.1706 | 0.71037 | 0.64409 | 0.44278 | 0.6549 |
| 6.0 | 0.41455 | 0.28116 | 0.16901 | 0.74565 | 0.66566 | 0.45932 | 0.6928 |
| 7.0 | 0.42253 | 0.28768 | 0.1645 | 0.77335 | 0.68215 | 0.47001 | 0.7407 |
| 8.0 | 0.4334 | 0.29241 | 0.15955 | 0.79386 | 0.69415 | 0.47023 | 0.7652 |
| 10.0 | 0.43149 | 0.29145 | 0.14693 | 0.81588 | 0.69532 | 0.45901 | 0.8091 |
| 11.0 | 0.43158 | 0.2914 | 0.13982 | 0.82358 | 0.69425 | 0.45046 | 0.8336 |
Selective sweep with 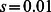 ,
, 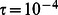 ,
, 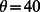 , sample size
, sample size 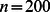 .
.
SKD-test by Schlötterer et al. [37].
We also examined how much the tests are confounded by deviations from the standard neutral model. First, we determined the false positive rates under a population bottleneck. From other studies it is known that bottlenecks with a severity (duration divided by depth) around 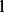 are particularly problematic [16], [28]. We find that tests
are particularly problematic [16], [28]. We find that tests 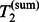 and
and 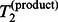 can produce substantially more false positives than expected, in particular if bottlenecks are recent (Table S6). Interestingly, test
can produce substantially more false positives than expected, in particular if bottlenecks are recent (Table S6). Interestingly, test 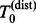 is very robust against these disturbances and the false positive rate remains clearly under the theoretical value for all onset parameters tested (Table S6).
is very robust against these disturbances and the false positive rate remains clearly under the theoretical value for all onset parameters tested (Table S6).
We note that the false positive rates of 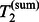 and
and 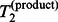 depend strongly on the bottleneck duration even when the severity is kept fixed (Table S7). Very short (duration
depend strongly on the bottleneck duration even when the severity is kept fixed (Table S7). Very short (duration 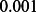 ), but heavy reductions of
), but heavy reductions of 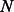 are more disturbing for
are more disturbing for 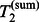 and
and 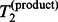 than long, but shallow bottlenecks (duration
than long, but shallow bottlenecks (duration 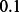 ). In contrast,
). In contrast, 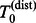 is fairly insensitive to changes of bottleneck duration (Table S7).
is fairly insensitive to changes of bottleneck duration (Table S7).
Under a model of fast population expansion (expansion rate 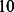 ), all tests remain below, or close to, their theoretical false positive rate. Again, test
), all tests remain below, or close to, their theoretical false positive rate. Again, test 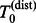 is unsensitive to population expansion and varying onset times (Table S8).
is unsensitive to population expansion and varying onset times (Table S8).
We expected that our topology based tests would yield many false positives under a model of population subdivision. As a potentially critical case we examined sampling from a population divided into two sub-populations which split 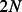 generations ago and which exchange migrants at rate
generations ago and which exchange migrants at rate  . We analyzed both varying migration rates and varying sampling schemes (Tables S9 to S12). The false positive rate for tests
. We analyzed both varying migration rates and varying sampling schemes (Tables S9 to S12). The false positive rate for tests 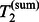 and
and 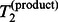 remains clearly under its theoretical expectation, even if sampling is heavily biased (sample size of sub-population
remains clearly under its theoretical expectation, even if sampling is heavily biased (sample size of sub-population 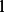 was
was 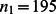 and of sub-population
and of sub-population  was
was 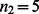 ; Table S9). In contrast, test
; Table S9). In contrast, test 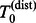 , which only measures tree imbalance at the root node, is more vulnerable to biased sampling from a sub-divided population. The false-positive rate grows up to
, which only measures tree imbalance at the root node, is more vulnerable to biased sampling from a sub-divided population. The false-positive rate grows up to 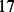 % if
% if 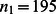 and
and 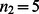 . In general, we find test
. In general, we find test 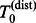 to be less vulnerable to population bottlenecks, but tests
to be less vulnerable to population bottlenecks, but tests 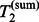 and
and 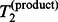 to be more robust under population substructure.
to be more robust under population substructure.
Finally, we examined how deviation from the single step mutation model would influence our tests. We modified the mutation model and allowed occasional jumps (probability 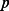 ) of larger steps. We tested jumps of step size
) of larger steps. We tested jumps of step size  (Table S13) and
(Table S13) and 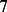 (Table S14). All tests, eminently the compound tests
(Table S14). All tests, eminently the compound tests 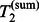 and
and 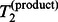 , remain clearly below their theoretical false positive rate.
, remain clearly below their theoretical false positive rate.
Case study
Emergence of drug resistance in malaria parasites is among the best documented examples for recent selective sweeps. We re-analyzed 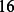 microsatellite markers surrounding a well studied drug resistance locus of malaria parasites [29] (Figure 7). The signature of recent positive selection is consistently detected by all tests on two markers somewhat downstream of the drug resistance locus pfmdr1 (marker l–
microsatellite markers surrounding a well studied drug resistance locus of malaria parasites [29] (Figure 7). The signature of recent positive selection is consistently detected by all tests on two markers somewhat downstream of the drug resistance locus pfmdr1 (marker l– and l–
and l– in the notation of [29]; Table 5). Highest significance is reported by test
in the notation of [29]; Table 5). Highest significance is reported by test 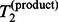 (
(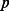 -value close to
-value close to 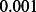 ).
). 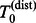 reports a
reports a 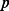 -value of
-value of 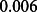 and
and 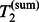 reports
reports 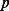 -values slightly above
-values slightly above 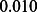 . In addition,
. In addition, 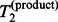 reports locus l–
reports locus l–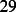 (located upstream of pfmdr1) to be significant at
(located upstream of pfmdr1) to be significant at 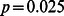 . This locus is also detected by
. This locus is also detected by  (
(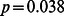 ). Other four loci are reported only by
). Other four loci are reported only by 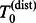 (l–
(l–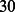 (
(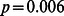 ), l–
), l–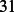 (
(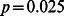 ), l–
), l–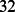 (
(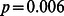 ), l–
), l–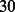 (
(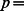 ) and l–
) and l–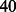 (
(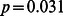 )). Discrepancies in the test results are due to their different sensitivities to various parameters. The simple and compound tests have different power profiles with power peaks at different positions from the selected site (Figure 6). Plasmodium in South-East Asia is most likely expanding and sub-structured; however, there is only limited knowledge about the details.
)). Discrepancies in the test results are due to their different sensitivities to various parameters. The simple and compound tests have different power profiles with power peaks at different positions from the selected site (Figure 6). Plasmodium in South-East Asia is most likely expanding and sub-structured; however, there is only limited knowledge about the details.
Figure 7. Traces of selection around a drug resistance locus in Plasmodium.
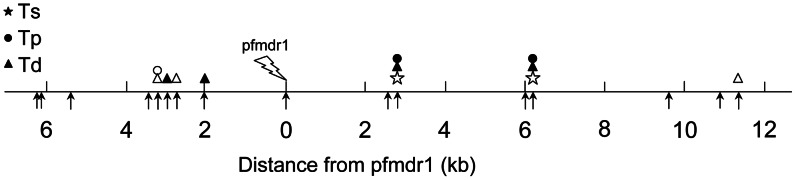
Results of tests 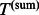 (stars),
(stars), 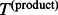 (circles) and
(circles) and 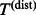 (triangles) applied to a
(triangles) applied to a 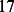 kb region sorrounding the pfmdr1 locus in P.falciparum. Shown are significant results on the 5% (open symbols) and 1% (filled symbols) levels. Positions of the examined microsatellite markers are indicated by arrows. Data from [29].
kb region sorrounding the pfmdr1 locus in P.falciparum. Shown are significant results on the 5% (open symbols) and 1% (filled symbols) levels. Positions of the examined microsatellite markers are indicated by arrows. Data from [29].
Table 5. Test statistics and 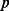 -values for the empirical data set of P.falciparum.
-values for the empirical data set of P.falciparum.
| pos |
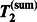
|
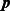 -value -value |

|
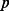 -value -value |
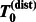
|
|||
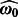
|

|
dist1 | ||||||
| l–25 | 953,644 | −0.1906 | 0.4244 | 0.0569 | 0.4537 | 146 | 324 | 1 |
| l–26 | 953,768 | 0.5591 | 0.7120 | 0.1235 | 0.6520 | 148 | 322 | 2 |
| l–27 | 954,506 | −0.7872 | 0.2156 | 0.0282 | 0.3085 | 95 | 320 | 2 |
| l–28 | 956,456 | −1.2289 | 0.1096 | 0.0069 | 0.1268 | 11 | 324 | 3 |
| l–29 | 956,686 | −0.8912 | 0.1864 | 0.0007 | 0.0254
|
6
|
314 | 4 |
| l–30 | 956,917 | −0.6710 | 0.2511 | 0.0019 | 0.0521 | 1
|
325 | 3 |
| l–31 | 957,169 | −1.3464 | 0.0891 | 0.0030 | 0.0706 | 4
|
322 | 4 |
| l–32 | 957,861 | −0.3083 | 0.3789 | 0.0024 | 0.0598 | 1
|
325 | 31 |
| l–33 | 959,894 | 0.8260 | 0.7956 | 0.0101 | 0.1629 | 147 | 326 | 2 |
| l–34 | 962,445 | −0.0498 | 0.4801 | 0.0611 | 0.4706 | 140 | 326 | 2 |
| l–35 | 962,699 | −2.1600 | 0.0154
|
1.9e-5 | 0.0014
|
1
|
326 | 23 |
| l–36 | 965,905 | −0.7369 | 0.2306 | 0.0337 | 0.3415 | 36 | 326 | 2 |
| l–37 | 966,096 | −2.2470 | 0.0123
|
1.4e-5 | 0.0010
|
1
|
326 | 9 |
| l–38 | 969,495 | 0.3941 | 0.6533 | 0.1713 | 0.7402 | 117 | 323 | 2 |
| l–39 | 970,775 | 0.1901 | 0.5754 | 0.0528 | 0.4366 | 17 | 322 | 3 |
| l–40 | 971,251 | −0.8336 | 0.2023 | 0.0025 | 0.0616 | 5* | 323 | 2 |
Given are the theoretical 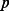 -values based on the standard normal (for
-values based on the standard normal (for 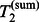 ) and on the product uniform (for
) and on the product uniform (for 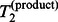 ) distributions. Values for
) distributions. Values for 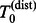 are given as raw data (
are given as raw data (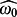 ,
,  ,
,  ). The
). The 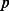 -value is
-value is 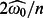 . 5% (single star) and 1% (double star) significance are indicated. Marker positions are taken from [29]. The region analyzed (about 17 kb) corresponds to about 1 cM (site under selection in bold).
. 5% (single star) and 1% (double star) significance are indicated. Marker positions are taken from [29]. The region analyzed (about 17 kb) corresponds to about 1 cM (site under selection in bold).
defined in eq (13).
As shown above, 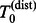 is quite sensitive to biased sampling from different sub-populations. Some of the significant results of
is quite sensitive to biased sampling from different sub-populations. Some of the significant results of 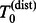 may be inflated due to sub-structure. There is also some disagreement between tests
may be inflated due to sub-structure. There is also some disagreement between tests 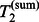 and
and 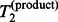 regarding significance, although both test imbalance at tree nodes
regarding significance, although both test imbalance at tree nodes 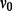 ,
, 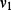 and
and 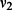 . In fact, the cases reported by the two tests may still differ in their details. Comparing the three components
. In fact, the cases reported by the two tests may still differ in their details. Comparing the three components 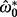 ,
, 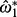 and
and 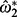 with respect to their maximum and minimum, we find that the cases reported as significant by
with respect to their maximum and minimum, we find that the cases reported as significant by 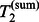 have a
have a 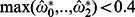 and a
and a 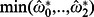 up to
up to 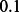 . In contrast, for
. In contrast, for 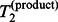 , the maximum is close to
, the maximum is close to 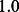 while the minimum tends to be less than
while the minimum tends to be less than 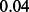 (Figure S4). Thus, test
(Figure S4). Thus, test 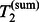 is more restrictive in the sense that all components
is more restrictive in the sense that all components 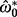 ,
, 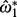 and
and 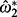 have to be small to yield a significant result.
have to be small to yield a significant result. 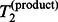 is more permissive and accepts that one of the three components may be large.
is more permissive and accepts that one of the three components may be large.
All tests agree on significance of two markers close to a site which was previously shown to have experienced a selective sweep. They also agree all on strongly increased 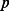 -values in the immediate vicinity of the selected site (l–
-values in the immediate vicinity of the selected site (l–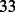 , l–
, l–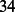 ). Together, these results confirm the accuracy and practical utility of our tests.
). Together, these results confirm the accuracy and practical utility of our tests.
Discussion
The binary coalescent has a number of well-studied combinatoric and analytic properties [1], [30], [31]. Here we only concentrate on tree topology and use a classic result of Tajima [19] to define a simple measure, 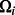 , of tree balance. It is the minimum of the left and right subtree sizes under internal node
, of tree balance. It is the minimum of the left and right subtree sizes under internal node 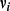 . Its normalized version is approximately uniform on the unit interval and the summation over internal nodes
. Its normalized version is approximately uniform on the unit interval and the summation over internal nodes 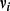 ,
, 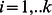 , is close to normal. Another summary statistic of tree balance is Colless' index
, is close to normal. Another summary statistic of tree balance is Colless' index  [32]. It also depends on the sizes of left- and right subtrees of the internal nodes, but its distribution is more complicated.
[32]. It also depends on the sizes of left- and right subtrees of the internal nodes, but its distribution is more complicated.  has received attention in the biological literature before [33] and, more recently, in theoretical studies, for instance by Blum&Janson [34]. A problem with Colless' index is that it is difficult to estimate if the true tree structure is unknown. But, limiting attention to the tree structure close to the root, we show that the balance measure
has received attention in the biological literature before [33] and, more recently, in theoretical studies, for instance by Blum&Janson [34]. A problem with Colless' index is that it is difficult to estimate if the true tree structure is unknown. But, limiting attention to the tree structure close to the root, we show that the balance measure  can be estimated, for instance, from microsatellite allele data by a clustering method. We found that a version of UPGMA clustering gives most reliable results.
can be estimated, for instance, from microsatellite allele data by a clustering method. We found that a version of UPGMA clustering gives most reliable results.
Coalescent trees for linked loci are not independent. However, correlation dissipates with recombinational distance. In fact, under neutral conditions only about ten recombination events are sufficient to reduce correlation in tree topology by 50%. Thus, estimating tree imbalance at multiple microsatellites can be performed independently for each marker, if they are sufficienty distant from each other. Conversely, with a very small number of recombination events,  is not drastically altered on average [15]. Thus, when working with SNPs, one may afford to consider haplotype blocks containing a few more recombination events than segragting sites and still be able to reconstruct a reliable gene genealogy. This possibility will be explored in more detail elsewhere.
is not drastically altered on average [15]. Thus, when working with SNPs, one may afford to consider haplotype blocks containing a few more recombination events than segragting sites and still be able to reconstruct a reliable gene genealogy. This possibility will be explored in more detail elsewhere.
Microsatellites have been used before as markers for selective sweeps. Schlötterer et al. [35] have proposed the lnRH statistic to detect traces of selection and Wiehe et al. [28] have shown that a multi-locus vesion of lnRH for linked markers can yield high power while keeping false positive rates low. However, a severe practical problem with the lnRH statistic is that it requires data from two populations, and for each of them two additional and independent sets of neutral markers for standardization. There are a few methods to detect deviations from the standard neutral model based on single microsatellite locus data from one population. For instance, the test by Cornuet and Luikart [36], which compares observed and expected heterozygosity, is designed to detect population bottlenecks. A test by Schlötterer et al. [37] uses the number of alleles at a microsatellite locus and determines whether an excess of the number of alleles is due to positive selection (SKD test). However, as the authors pointed out, the test depends critically on a reliable locus-specific estimate of the scaled mutation rate. We have compared SKD and the test proposed here with respect to power and false positive rates. While the SKD-test is generally more powerful, especially at larger distances from the selected site (Table 4 and Suppl. Tables S1, S5), it has higher false positive rates than the tests proposed here, in particular when compared to  (Suppl. Table S6), and for non-standard mutation models (Suppl. Tables S13, S14). Note also that under population sub-structure SKD yields up to
(Suppl. Table S6), and for non-standard mutation models (Suppl. Tables S13, S14). Note also that under population sub-structure SKD yields up to  times more false positives than our tests (Suppl. Tables S9 to S12).
times more false positives than our tests (Suppl. Tables S9 to S12).
It should be emphasized that it is the topology of the underlying genealogical tree, not the genetic variation, which constitutes the basis for the test statistics proposed here. The two steps, estimating topology, and performing the test are two distinct tasks. The quality of the tests hinges on the quality of the re-constructed genealogy. With a perfectly re-constructed genealogy the false positive rates are completely independent from any evolutionary mechanisms which do not affect the average topology, such as historic changes of population size. However, simulations show that power would still remain under 100% in this case. The robustness of topology based tests with respect to demographic changes has been shown before by Li [16] for a similar test which uses SNP data to reconstruct 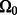 . But Li's test can only be performed if an additional non-topological criterion is satisfied and thus can only test a subset of trees with
. But Li's test can only be performed if an additional non-topological criterion is satisfied and thus can only test a subset of trees with 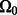 . The tests
. The tests 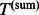 and
and 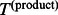 defined here rely only on topological properties of the genelaogy and we argue that multi-allelic markers, such as microsatellites, help estimating the true genealogy and improving test results. Although our analyses and simulations are based on the binary Kingman [1] coalescent, we expect that the new test statistics should be robust also under more general coalescent models, for instance when multiple mergers during the selective sweep phase are allowed [38].
defined here rely only on topological properties of the genelaogy and we argue that multi-allelic markers, such as microsatellites, help estimating the true genealogy and improving test results. Although our analyses and simulations are based on the binary Kingman [1] coalescent, we expect that the new test statistics should be robust also under more general coalescent models, for instance when multiple mergers during the selective sweep phase are allowed [38].
Despite a shift to high throughput sequencing technologies in the last decade, microsatellite typing continues to be a cost-efficient and fast alternative to survey population variability in many experimental studies. This is in particular true for projects directed towards parasite typing, e.g. of Plasmodium, and projects with non-standard model organisms, e.g. social insects [39], [40], but also for many biomedical studies.
Methods
Coalescent simulations
We simulated population samples under neutral and hitchhiking models with modified versions of the procedures described by Kim and Stephan [41] and Li and Stephan [42] and of ms [43], termed msmicro. In the modified versions we incorporated evolution of microsatellite loci under the symmetric, single step and multi-step mutation models. Microsatellite mutations are modeled as changes to the number of motif repeats, where only numbers but not particular sequence motifs are recorded. Output data comprise coalescent trees in Newick format and the state of microsatellite alleles for each of  sequences. With msmicro also multiple linked microsatellites can be modeled. Coalescent simulations were run under different evolutionary conditions: neutral with constant population size (
sequences. With msmicro also multiple linked microsatellites can be modeled. Coalescent simulations were run under different evolutionary conditions: neutral with constant population size (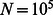 ), neutral with bottleneck (bottleneck severity
), neutral with bottleneck (bottleneck severity 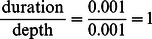 , time since bottleneck
, time since bottleneck 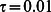 ), population size expansion (growth rate
), population size expansion (growth rate 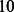 ), neutral two-island model with migration, and hard selective sweeps (selection
), neutral two-island model with migration, and hard selective sweeps (selection 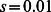 and
and 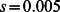 , time since fixation of sweep allele
, time since fixation of sweep allele 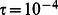 ).
).
Tree topology
Realizations 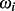 of the ‘true’ random variables
of the ‘true’ random variables 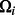 ,
, 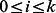 were extracted from the simulation results. Estimation of
were extracted from the simulation results. Estimation of 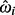 was performed by UPGMA hierarchical clustering. If a cluster node could not be uniquely resolved then we gave preference to a bi-partite partition in which the left and right subtrees were of equal or similar size. This was accomplished by randomly assigning alleles to two clusters with equal probability. To estimate
was performed by UPGMA hierarchical clustering. If a cluster node could not be uniquely resolved then we gave preference to a bi-partite partition in which the left and right subtrees were of equal or similar size. This was accomplished by randomly assigning alleles to two clusters with equal probability. To estimate 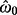 we also explored a simple clustering method which works in the following way: we first sorted alleles by size; then we divided the sorted list into two halfs. The separator was placed between those two alleles which had maximal distance (in terms of microsatellite repeat units) from each other. If this was not unique, the separator was placed between those two alleles that resulted in two sets of most similar size. While this clustering method is very effective in estimating
we also explored a simple clustering method which works in the following way: we first sorted alleles by size; then we divided the sorted list into two halfs. The separator was placed between those two alleles which had maximal distance (in terms of microsatellite repeat units) from each other. If this was not unique, the separator was placed between those two alleles that resulted in two sets of most similar size. While this clustering method is very effective in estimating 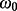 , it is less accurate than UPGMA clustering for
, it is less accurate than UPGMA clustering for 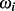 ,
, 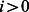 .
.
Distance between microsatellite alleles
The single step symmetric mutation model behaves as a one-dimensional symmetric random walk of step size one. The theory of random walks (e.g. [44]) tells that the average distance between the origin of the walk and the current position scales with the square root of the number 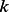 of steps. More precisely,
of steps. More precisely,
The variance is linear in 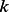 . Here, steps are represented by mutational events occuring at rate
. Here, steps are represented by mutational events occuring at rate  . Thus,
. Thus, 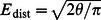 and
and 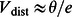 , where
, where  is Euler's constant. The empirical distance between two clusters
is Euler's constant. The empirical distance between two clusters 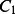 and
and 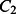 can be calculated as
can be calculated as
Supporting Information
Agreement of
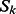 with the standard normal. Shown are the distribution functions for the standard normal distribution (green line), and for (see eq (8))
with the standard normal. Shown are the distribution functions for the standard normal distribution (green line), and for (see eq (8)) 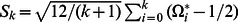 ,
, 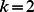 (red line) and
(red line) and 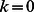 (blue line). The latter is uniform on
(blue line). The latter is uniform on 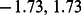 . Obviously, already for
. Obviously, already for 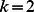 the agreement between the standard normal and
the agreement between the standard normal and 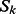 is quite good.
is quite good.
(EPS)
Average number of recombination events in neutral coalescent trees. (A) in dependence of sample size  (
(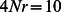 ) and (B) of the scaled recombination rate
) and (B) of the scaled recombination rate 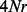 (
(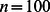 ). Red: simulation results obtained from
). Red: simulation results obtained from 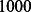 replicates of ms [43]. Shown are average (bullets) and standard deviation (whiskers). Black: theoretical value
replicates of ms [43]. Shown are average (bullets) and standard deviation (whiskers). Black: theoretical value 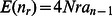 .
.
(EPS)
Distance from sweep site to first recombination site. Given that the rate of the first recombination event adjacent to a selective sweep site is 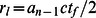 (in case of a neutral topology) or
(in case of a neutral topology) or 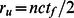 (in case of a star phylogeny) the distance between the selected site and the ‘first’ recombination event is described by a Poisson process with rate
(in case of a star phylogeny) the distance between the selected site and the ‘first’ recombination event is described by a Poisson process with rate 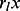 or
or 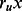 . Shown is the probability that the Poissson variable is
. Shown is the probability that the Poissson variable is  (i.e., for a “recombination free zone”) for
(i.e., for a “recombination free zone”) for 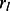 (upper curve) and
(upper curve) and 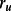 (lower curve).
(lower curve).
(EPS)
Differences between tests (A)
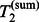 and (B)
and (B)
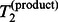 . Given a test is significant at level
. Given a test is significant at level 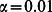 , the plots show the maximum (
, the plots show the maximum ( -axis) and the minimum (
-axis) and the minimum ( -axis) of the three terms
-axis) of the three terms 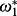 ,
, 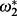 and
and 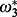 , which enter into the sum and product in
, which enter into the sum and product in 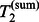 and
and 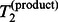 , respectively. The sum- and product-tests may yield different results, because the summands are differently constrained (here (A), the maximum
, respectively. The sum- and product-tests may yield different results, because the summands are differently constrained (here (A), the maximum 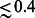 ) than the factors (here (B), the maximum may reach almost
) than the factors (here (B), the maximum may reach almost 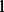 , but the minimum is smaller than in the sum-test).
, but the minimum is smaller than in the sum-test).
(PDF)
Power of
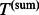 ,
,
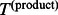 and
and
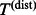 in dependence of distance to selected site. Moderate selection strength.
in dependence of distance to selected site. Moderate selection strength.
(PDF)
Power of
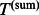 ,
,
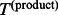 and
and
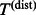 in dependence of mutation rate
in dependence of mutation rate
 .
.
(PDF)
Power of
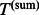 ,
,
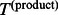 and
and
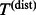 in dependence of sample size
in dependence of sample size
 .
.
(PDF)
Power of
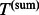 ,
,
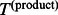 and
and
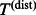 in dependence of distance to selected site. Small sample size.
in dependence of distance to selected site. Small sample size.
(PDF)
Power of
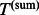 ,
,
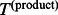 and
and
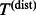 in dependence of distance to selected site. Large sample size.
in dependence of distance to selected site. Large sample size.
(PDF)
Empirical false positive rate. Bottleneck model with varying onset  of the bottleneck. Strength is fixed at
of the bottleneck. Strength is fixed at 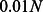 . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Bottleneck model with varying duration of the bottleneck. Severity (duration divided by strength) is fixed at 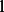 . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population expansion with varying onset  of the expansion. Expansion rate is fixed at
of the expansion. Expansion rate is fixed at 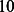 .
.
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 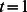 in the past and sampling scheme
in the past and sampling scheme 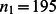 ,
, 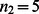 . Varying migration rate
. Varying migration rate  per generation per
per generation per 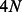 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 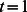 in the past and sampling scheme
in the past and sampling scheme 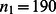 ,
, 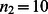 . Varying migration rate
. Varying migration rate  per generation per
per generation per 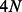 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 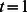 in the past and sampling scheme
in the past and sampling scheme 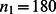 ,
, 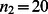 . Varying migration rate
. Varying migration rate  per generation per
per generation per 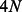 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 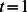 in the past and sampling scheme
in the past and sampling scheme 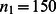 ,
, 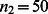 . Varying migration rate
. Varying migration rate  per generation per
per generation per 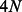 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Mutation model with jumps of size
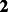 . Varying probability
. Varying probability 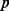 for a step of size
for a step of size  . With probability
. With probability 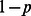 the step size is
the step size is 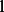 . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Mutation model with jumps of size
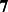 . Varying probability
. Varying probability 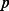 for a step of size
for a step of size 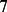 . With probability
. With probability 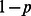 the step size is
the step size is  . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Acknowledgments
We wish to thank R. Fürst for contributing the UPGMA clustering software for microsatellite alleles, A. Schlizio for help in preparing figures and T. Anderson for sharing the raw data of a set of microsatellites from a population of P. falciparum from Thailand. Further, we would like to thank M. Hasselmann for discussion and comments.
Funding Statement
HL was supported by the National Key Basic Research Program of China (2012CB316505), the NSFC grants (31172073 and 91131010) and the Bairen Program, and through a grant to TW by the German Research Foundation (DFG-SFB680, www.dfg.de). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Kingman JFC (1982) The coalescent. Stochastic Processes and their Applications 13: 235–248. [Google Scholar]
- 2.Hudson RR (1990) Gene genealogies and the coalescent process. In: Oxford Surveys in Evolutionary Biology, volume 7. Oxford University Press. pp. 1–44.
- 3.Wakeley J (2009) Coalescent theory – an introduction. Greenwood Village, Colorado: Roberts&Company.
- 4. Ewens W (1972) The sampling theory of selectively neutral alleles. Theor Popul Biol 3: 87–112. [DOI] [PubMed] [Google Scholar]
- 5. Tajima F (1989) The effect of change in population size on DNA polymorphism. Genetics 123: 597–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Fay J, Wu C (2000) Hitchhiking under positive Darwinian selection. Genetics 155: 1405–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Fu Y (1997) Statistical tests of neutrality of mutations against population growth, hitchhiking and background selection. Genetics 147: 915–925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ferretti L, Perez-Enciso M, Ramos-Onsins S (2010) Optimal neutrality tests based on the frequency spectrum. Genetics 186: 353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Griffiths RC, Marjoram P (1996) Ancestral inference from samples of DNA sequences with recombination. J Comput Biol 3: 479–502. [DOI] [PubMed] [Google Scholar]
- 10. Hudson R, Kaplan N (1988) The coalescent process in models with selection and recombination. Genetics 120: 831–840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Kaplan NL, Hudson RR, Langley CH (1989) The “hitchhiking effect” revisited. Genetics 123: 887–899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. McVean G, Cardin N (2005) Approximating the coalescent with recombination. Philos Trans R Soc Lond B Biol Sci 360: 1387–1393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Wiuf C, Hein J (1999) Recombination as a point process along sequences. Theor Popul Biol 55: 248–259. [DOI] [PubMed] [Google Scholar]
- 14. Eriksson A, Mahjani B, Mehlig B (2009) Sequential markov coalescent algorithms for population models with demographic structure. Theor Popul Biol 76: 84–91. [DOI] [PubMed] [Google Scholar]
- 15. Ferretti L, Disanto F, Wiehe T (2013) The effect of single recombination events on coalescent tree height and shape. PLoS ONE 8 4: e60123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Li H (2011) A new test for detecting recent positive selection that is free from the confounding impacts of demography. Mol Biol Evol 28: 365–375. [DOI] [PubMed] [Google Scholar]
- 17.Walsh J, Lynch M (2013) Evolution and Selection of Quantitative Traits. Sinauer Associates. Available: http://nitro.biosci.arizona.edu/zbook/NewVolume-2/pdf.
- 18. Wedderburn JHM (1922) The functional equation g(x2) = 2 x + [g(x)]2. The Annals of Mathematics 24: 121–140. [Google Scholar]
- 19. Tajima F (1983) Evolutionary relationship of DNA sequences in finite populations. Genetics 105: 437–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Hudson R, Kaplan N (1985) Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111: 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Zivkovic D, Wiehe T (2008) Second-order moments of segregating sites under variable population size. Genetics 180: 341–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Reich D, Cargill M, Bolk S, Ireland J, Sabeti P, et al. (2001) Linkage disequilibrium in the human genome. Nature 411: 199–204. [DOI] [PubMed] [Google Scholar]
- 23. Barton N (2000) Genetic hitchhiking. Philos Trans R Soc Lond B Biol Sci 355: 1553–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sokal RR, Sneath PHA (1963) Principles of Numerical Taxonomy. New York: W. H. Freeman and Co.
- 25. Schug MD, Mackay TFC, Aquadro CF (1997) Low mutation rates of microsatellite loci in Drosophila melanogaster . Nature Genetics 15: 99–102. [DOI] [PubMed] [Google Scholar]
- 26. Fernando Vazquez J, Perez T, Albornoz J, Dominguez A (2000) Estimation of microsatellite mutation rates in Drosophila melanogaster . Genet Res 76: 323–326. [DOI] [PubMed] [Google Scholar]
- 27. Ellegren H (2004) Microsatellites: simple sequences with complex evolution. Nat Rev Genet 5: 435–445. [DOI] [PubMed] [Google Scholar]
- 28. Wiehe T, Nolte V, Zivkovic D, Schlötterer C (2007) Identification of selective sweeps using a dynamically adjusted number of linked microsatellites. Genetics 175: 207–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Nair S, Nash D, Sudimack D, Jaidee A, Barends M, et al. (2007) Recurrent gene amplification and soft selective sweeps during evolution of multidrug resistance in malaria parasites. Mol Biol Evol 24: 562–573. [DOI] [PubMed] [Google Scholar]
- 30. Griffiths RC (1984) Asymptotic line-of-descent distributions. J Math Biol 21: 67–75. [Google Scholar]
- 31.Berestycki N (2009) Recent progress in coalescent theory. Ensaios matemáticos. Sociedade Brasileira De Matemática.
- 32. Colless DH (1982) Review: [untitled]. Systematic Zoology 31: 100–104. [Google Scholar]
- 33. Kirkpatrick M, Slatkin M (1993) Searching for evolutionary patterns in the shape of a phylogenetic tree. Evolution 47: 1171–1181. [DOI] [PubMed] [Google Scholar]
- 34. Blum MGB, Franois O, Janson S (2006) The mean, variance and limiting distribution of two statistics sensitive to phylogenetic tree balance. The Annals of Applied Probability 16: 2195–2214. [Google Scholar]
- 35. Schlötterer C (2002) A microsatellite based multi-locus screen for the identification of local selective sweeps. Genetics 160: 753–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Cornuet J, Luikart G (1996) Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics 144: 2001–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Schlötterer C, Kauer M, Dieringer D (2004) Allele excess at neutrally evolving microsatellites and the implications for tests of neutrality. Proc R Soc Lond B 271: 869–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Neher R, Hallatschek O (2013) Genealogies of rapidly adapting populations. Proc Natl Acad Sci U S A 110: 437–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Stolle E, Wilfert L, Schmid-Hempel R, Schmid-Hempel P, Kube M, et al. (2011) A second generation genetic map of the bumblebee bombus terrestris (linnaeus, 1758) reveals slow genome and chromosome evolution in the apidae. BMC Genomics 12: 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Behrens D, Huang Q, Gessner C, Rosenkranz P, Frey E, et al. (2011) Three QTL in the honey bee apis mellifera l. suppress reproduction of the parasitic mite varroa destructor. Ecol Evol 1: 451–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Kim Y, Stephan W (2002) Detecting a local signature of genetic hitchhiking along a recombining chromosome. Genetics 160: 765–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Li H, Stephan W (2006) Inferring the demographic history and rate of adaptive substitution in drosophila. PLoS Genet 2: e166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Hudson RR (2002) Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18: 337–338. [DOI] [PubMed] [Google Scholar]
- 44.Feller W (1968) An Introduction to Probability Theory and Its Applications, volume 1. Wiley.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Agreement of
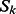 with the standard normal. Shown are the distribution functions for the standard normal distribution (green line), and for (see eq (8))
with the standard normal. Shown are the distribution functions for the standard normal distribution (green line), and for (see eq (8)) 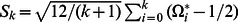 ,
,  (red line) and
(red line) and 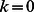 (blue line). The latter is uniform on
(blue line). The latter is uniform on 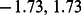 . Obviously, already for
. Obviously, already for 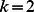 the agreement between the standard normal and
the agreement between the standard normal and 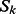 is quite good.
is quite good.
(EPS)
Average number of recombination events in neutral coalescent trees. (A) in dependence of sample size  (
(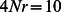 ) and (B) of the scaled recombination rate
) and (B) of the scaled recombination rate 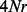 (
(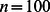 ). Red: simulation results obtained from
). Red: simulation results obtained from 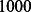 replicates of ms [43]. Shown are average (bullets) and standard deviation (whiskers). Black: theoretical value
replicates of ms [43]. Shown are average (bullets) and standard deviation (whiskers). Black: theoretical value 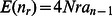 .
.
(EPS)
Distance from sweep site to first recombination site. Given that the rate of the first recombination event adjacent to a selective sweep site is 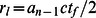 (in case of a neutral topology) or
(in case of a neutral topology) or 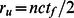 (in case of a star phylogeny) the distance between the selected site and the ‘first’ recombination event is described by a Poisson process with rate
(in case of a star phylogeny) the distance between the selected site and the ‘first’ recombination event is described by a Poisson process with rate 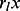 or
or 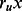 . Shown is the probability that the Poissson variable is
. Shown is the probability that the Poissson variable is  (i.e., for a “recombination free zone”) for
(i.e., for a “recombination free zone”) for 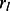 (upper curve) and
(upper curve) and 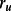 (lower curve).
(lower curve).
(EPS)
Differences between tests (A)
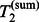 and (B)
and (B)
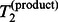 . Given a test is significant at level
. Given a test is significant at level 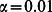 , the plots show the maximum (
, the plots show the maximum ( -axis) and the minimum (
-axis) and the minimum ( -axis) of the three terms
-axis) of the three terms 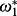 ,
, 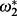 and
and 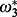 , which enter into the sum and product in
, which enter into the sum and product in 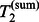 and
and 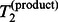 , respectively. The sum- and product-tests may yield different results, because the summands are differently constrained (here (A), the maximum
, respectively. The sum- and product-tests may yield different results, because the summands are differently constrained (here (A), the maximum 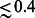 ) than the factors (here (B), the maximum may reach almost
) than the factors (here (B), the maximum may reach almost  , but the minimum is smaller than in the sum-test).
, but the minimum is smaller than in the sum-test).
(PDF)
Power of
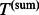 ,
,
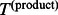 and
and
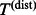 in dependence of distance to selected site. Moderate selection strength.
in dependence of distance to selected site. Moderate selection strength.
(PDF)
Power of
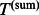 ,
,
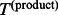 and
and
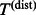 in dependence of mutation rate
in dependence of mutation rate
 .
.
(PDF)
Power of
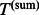 ,
,
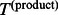 and
and
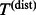 in dependence of sample size
in dependence of sample size
 .
.
(PDF)
Power of
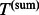 ,
,
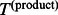 and
and
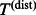 in dependence of distance to selected site. Small sample size.
in dependence of distance to selected site. Small sample size.
(PDF)
Power of
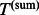 ,
,
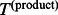 and
and
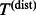 in dependence of distance to selected site. Large sample size.
in dependence of distance to selected site. Large sample size.
(PDF)
Empirical false positive rate. Bottleneck model with varying onset  of the bottleneck. Strength is fixed at
of the bottleneck. Strength is fixed at 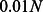 . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Bottleneck model with varying duration of the bottleneck. Severity (duration divided by strength) is fixed at  . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population expansion with varying onset  of the expansion. Expansion rate is fixed at
of the expansion. Expansion rate is fixed at 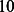 .
.
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 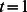 in the past and sampling scheme
in the past and sampling scheme 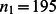 ,
, 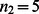 . Varying migration rate
. Varying migration rate  per generation per
per generation per 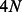 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 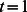 in the past and sampling scheme
in the past and sampling scheme 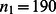 ,
, 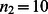 . Varying migration rate
. Varying migration rate  per generation per
per generation per 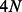 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 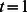 in the past and sampling scheme
in the past and sampling scheme 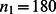 ,
, 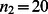 . Varying migration rate
. Varying migration rate  per generation per
per generation per 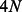 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Population sub-structure with two sub-populations, split time 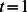 in the past and sampling scheme
in the past and sampling scheme 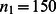 ,
, 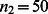 . Varying migration rate
. Varying migration rate  per generation per
per generation per 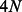 individuals. Significance levels
individuals. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Mutation model with jumps of size
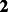 . Varying probability
. Varying probability 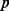 for a step of size
for a step of size  . With probability
. With probability 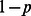 the step size is
the step size is  . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)
Empirical false positive rate. Mutation model with jumps of size
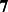 . Varying probability
. Varying probability 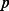 for a step of size
for a step of size 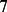 . With probability
. With probability 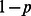 the step size is
the step size is  . Significance levels
. Significance levels  are based on theoretical formulae according to eqs (7) and (8).
are based on theoretical formulae according to eqs (7) and (8).
(PDF)