Two-layer model of coronary artery vasoactivity

Abstract

Since vascular tone is regulated by smooth muscle cells in the media layer, a multilayer mechanical model is required for blood vessels. Here, we performed biaxial mechanical tests in the intima-media layer of right coronary artery to determine the passive and active properties in conjunction with the passive properties of adventitia for a full vessel wall model. A two-layer (intima-media and adventitia) model was developed to determine the transmural stress and stretch across the vessel wall. The mean ± SE values of the outer diameters of intima-media layers at transmural pressure of 60 mmHg in active state were 3.17 ± 0.16 and 3.07 ± 0.18 mm at axial stretch ratio of 1.2 and 1.3, respectively, which were significantly smaller than those in passive state (i.e., 3.62 ± 0.19 and 3.49 ± 0.22 mm, respectively, P < 0.05). The inner and outer diameters in no-load state of intima-media layers were 1.17 ± 0.09 and 2.08 ± 0.09 mm, respectively. The opening angles in zero-stress state had values of 159 ± 21° for intima-media layers and 98 ± 15° for adventitia layers, which suggests a residual strain between the two layers. There were slightly decreased active circumferential stresses (<10%), but significantly decreased active axial stresses (>25%) in the intima-media layer compared with those in the intact vessel. This suggests that the adventitia layer affects vascular contraction. The two-layer analysis showed that the intima-media layer bears the majority of circumferential tensions, in contrast to the adventitia layer, while contraction results in decreased stress and stretch in both layers.

the epicardial coronary artery wall is composed of intima, media, and adventitia layers, while smooth muscle cells (SMC) mainly reside in the media layer. Since dysfunction in vasoactivity is present in coronary artery disease (15, 30), the assessment of active and passive properties of coronary arteries provides essential diagnostics in subjects at risk (1, 4, 9, 22, 24). In passive state, our laboratory has previously treated the vessel wall as a two-layered structure, consisting of intima-media layer (endothelial cells and SMC, as well as elastin and collagen) and adventitia layer (collagen, fibroblasts, and elastin) and carried out extensive experiments for determination of passive mechanical properties of the two layers (17, 20, 27). More recently, our laboratory determined the biaxial (circumferential and axial) active properties of intact right coronary arteries (RCA) under K⁺-induced SMC contraction (10). The mechanical properties of the isolated intima-media layer are not available to determine the active and passive contributions of the various layers of the vessel wall.

The objective of the study is to determine the biaxial (circumferential and axial) active properties in the intima-media layer and to compute the transmural distribution of stress and stretch in the intact coronary artery wall using a two-layer model (intima-media and adventitia layers). The loading (intraluminal pressure and axial tethering force) and deformation (diameter change and prescribed axial stretch) of the intima-media layer were simultaneously measured under relaxed and K⁺-induced contraction states for determination of the passive and active stress-stretch relationships, respectively. The computational results show significant change of stress and stretch distribution in the two layers as a result of SMC contraction.

MATERIALS AND METHODS

Animal preparation and vessel harvest.

Six farm pigs weighing 30 ± 5 kg were used in the study. The animal preparation was similar to that described previously (10). All animal experiments were performed in accordance with national and local ethical guidelines, including the Institute of Laboratory Animal Research Guide, Public Health Service policy, Animal Welfare Act, and IUPUI (Indiana University-Purdue University, Indianapolis) polices regarding the use of animals in research. This study was reviewed and approved by the IACUC.

Briefly, surgical anesthesia was induced with TKX (telaxol 500 mg, ketamine 250 mg, xylazine 250 mg) and maintained with 2% isoflurane. The animal was intubated and ventilated with room air and oxygen by a respiratory pump. After a midline sternotomy was performed, the animal was euthanized by an injection of pentobarbital sodium (300 mg/kg). The heart was harvested and placed in an ice-cold saline bath. A fresh RCA of ∼2.5 cm was dissected free of fat and connective tissue, and the branches were ligated with suture under dissection microscope in 4°C HEPES PSS (physiological saline solution) (10). The adventitia of RCA was carefully dissected with the aid of a stereomicroscope, with care taken to ensure that the intima-media layer remained intact (20, 27).

Active test.

Similar to the active test in intact RCA vessels (10), the intima-media layer of RCA was cannulated on both ends with connectors in an organ bath containing HEPES PSS in room temperature and aerated with 95% O₂-5% CO₂. The PSS was perfused through the vessel for several seconds to ensure the lumen was completely filled. The temperature in bath was gradually increased to 37°C in 10 min. The vessel was stretched to the in vivo length (axial stretch ratio, λ_z, of 1.3) and the intravascular pressure was set at 15 mmHg to allow the vessel to equilibrate for 45 min. The intravascular pressure was then increased to 45 mmHg, the 37°C PSS in bath was replaced by the 60 mM K⁺ PSS at the same temperature, and the vessel was equilibrated for 15 min to attain steady-state contraction. The vessel was preconditioned several times to obtain reproducible mechanical data. The transmural pressures were varied from 20 to 110 mmHg by increments of 10 mmHg. The image of the vessel was displayed on screen with a charge-coupled device (CCD) camera mounted on a stereo microscope, and the diameter changes were measured with dimensional analysis software (DIAMTRAK 3+). The axial force changes were measured by a force transducer (Fort100, World Precision Instruments) fixed with a connector on one end of the vessel. The pressure transducer, diameter tracings, and force transducer were interfaced into a computer by a Biopac system (MP100, Biopac Systems), which monitored the transient changes of pressure, diameter, and axial force. The loading and deformation measurements were then repeated for λ_z = 1.2.

Passive test.

After the active test, the organ bath was filled with Ca²⁺-free Krebs solution to relax the intima-media layer of RCA vessels, and the passive pressure-diameter-axial force relationship of the vessel was determined. The pressures were varied from 20 to 110 mmHg by a step increase of 10 mmHg for each λ_z = 1.3 and λ_z = 1.2 in turn, similar to the contraction protocol.

No-load and zero-stress state.

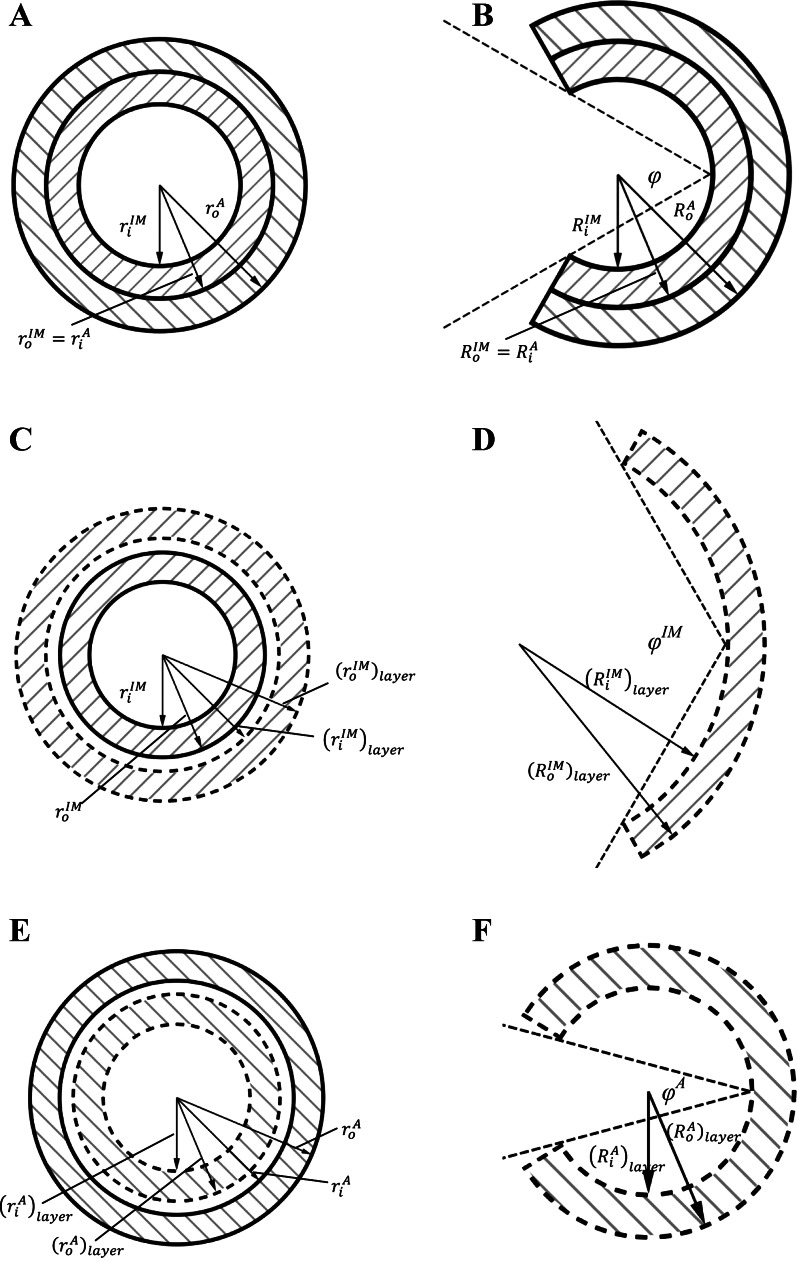
After the passive test, the intima-media layer of RCA vessels was disconnected from the organ bath, and three rings (0.5 cm length) were cut. The cross section was photographed in the no-load state (see Fig. A1C) and each ring was then cut radially at the anterior position (see Fig. A1D). The ring opened into a sector and gradually approached a constant opening angle defined as the angle subtended by two radii connecting the midpoint of the inner wall. The cross section of each sector was photographed 30 min after the radial cut, as shown in Fig. A1D. The morphological measurements of inner and outer circumferences, wall thickness, and cross-sectional area in the no-load and zero-stress state were made from the images with a morphometric analysis system (ImageJ, National Institutes of Health).

Fig. A1.

Schematic representation is shown of an intact vessel wall at no-load or loaded states (A) and zero-stress state (B). Schematic representation is shown of a single intima-media layer at no-load or loaded states (C) and zero-stress state (D). Schematic representation is shown of a single adventitia layer at no-load or loaded states (E) and zero-stress state (F). The solid lines refer to the measurements in an intact vessel wall, while the dash lines refer to those in a single layer, intima-media layer (forward slashes), or adventitia layer (backward slashes). See text for definition of terms.

Passive and active strain energy functions.

The mathematical derivation has been described previously (see Appendix of Ref. 10). In Fung's two-dimensional model without shear deformation, the passive strain energy function (W_passive) is given by:

$${\text{W}}_{\text{passive}}=\frac{C_1}{2}\left[\exp \left(Q\right)-1\right]\hspace{0.17em}\text{with}\hspace{0.17em}Q=a_1{E}_{\theta \theta }^2+a_2{\text{E}}_{zz}^2+2a_4{\text{E}}_{\theta \theta }{\text{E}}_{zz}$$ (1)

where C₁, a₁, a₂, and a₄ are material constants, and E_θθ and E_zz are circumferential and axial Green strains, respectively. An active strain energy function induced by SMC contraction was proposed as (10):

$${\text{W}}_{\text{active}}=C_2\left[\text{Erf}\left(Q\prime \right)-1\right]\hspace{0.17em}\text{with}\hspace{0.17em}Q\prime =\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_z}{b_2}-b\prime$$ (2)

where C₂, b₁, b₂, and b′ are material constants, Erf(X) is the Gauss error function, λ_θ = l/l₀ = $\sqrt{2E_{\theta \theta }+1}$ and λ_z = L/L₀ = $\sqrt{2E_{zz}+1}$ are the circumferential and axial stretch ratios. l and l₀ are the circumferential lengths in loaded and zero-stress states, respectively, and L and L₀ are axial lengths in loaded and no-load states, respectively, of the intima-media layer of RCA.

The total strain energy of K⁺-induced active vessel can be written as the sum of passive and active contributions (W_total = W_passive + W_active). The passive and active second Piola-Kirchhoff stress tensors can be determined as the derivatives of the respective strain energy functions with respect to Green strain tensor (see below). The total stress was determined from measurements of K⁺-induced contraction, while the passive stress was obtained from Ca²⁺-free measurements (active stress = total stress − passive stress).

Once the passive and active strain energy functions were determined, a two-layer analytic solution of vessel wall mechanics was carried out to compute the transmural distribution of stress and stretch in coronary artery wall, as outlined in the appendix.

Determination of material constants.

The material constants were determined by minimizing the square of difference between theoretical and experimental values of passive circumferential and axial first Piola-Kirchhoff stresses as:

$$\text{Error}={\displaystyle {\sum }_{n=1}^N\left[{\left(T_{\theta \theta \text{passive}}^{\text{theory}}-T_{\theta \theta \text{passive}}^{\text{experiment}}\right)}^2+{\left(T_{zz\text{passive}}^{\text{theory}}-T_{zz\text{passive}}^{\text{experiment}}\right)}^2\right]}$$ (3)

where T_θθpassive^theory = C₁λ_θ(a₁E_θθ + a₄E_zz)exp(Q); T_zzpassive^theory = C₁λ_z(a₂E_zz + a₄E_θθ)exp(Q); T_θθpassive^experiment = $\frac{{\mathrm{Pr}}_i}{h{\lambda }_{\theta }}$ (where P is the pressure; $r_i=\sqrt{r_0^2-\frac{A_0}{\pi {\lambda }_z}}$ is the inner radius in loaded state; r_o is the outer radius in loaded state, A₀ is the wall area in no-load state; h = r_o − r_i is the wall thickness in loaded state); T_zzpassive^experiment = $\frac{1}{{\lambda }_z}\left[\frac{F}{\pi \left(r_{\text{o}}^2-r_{\text{i}}^2\right)}+\frac{{\mathrm{Pr}}_i^2}{h\left(r_{\text{o}}+r_{\text{i}}\right)}\right]$ (where F is the axial force); and N is the total number of experimental points.

Similar to Eq. 3, the square of difference between the theoretical and experimental values of active circumferential and axial first Piola-Kirchhoff stresses is given as:

$$\text{Error}={\displaystyle {\sum }_{n=1}^N\left[{\left(T_{\theta \theta \text{active}}^{\text{theory}}-T_{\theta \theta \text{active}}^{\text{experiment}}\right)}^2+{\left(T_{zz\text{active}}^{\text{theory}}-T_{zz\text{active}}^{\text{experiment}}\right)}^2\right]}$$ (4)

where T_θθactive^theory = $\frac{2C_2}{b_1\sqrt{\pi }}\exp \left[-{\left(Q\prime \right)}^2\right]$ and T_zzactive^theory = $\frac{2C_2}{b_2\sqrt{\pi }}\exp \left[-{\left(Q\prime \right)}^2\right]$, while T_θθactive^experiment = ${\left(\frac{{\mathrm{Pr}}_i}{h{\lambda }_{\theta }}\right)}_{\text{total}}$ − T_θθpassive^experiment and T_zzactive^experiment = ${\left[\frac{F}{{\lambda }_z\pi \left(r_o^2-r_{\text{i}}^2\right)}+\frac{{\mathrm{Pr}}_i^2}{{\lambda }_{z}h\left(r_{\text{o}}+r_{\text{i}}\right)}\right]}_{\text{total}}$ − T_zzpassive^experiment were determined by total stress minus passive stress.

A limited memory quasi-Newton method for large scale optimization [L-BFGS (limited-memory Broyden-Fletcher-Goldfarb-Shanno) method] (16) was performed to minimize the error function as expressed by Eqs. 3 and 4. A FORTRAN program was developed to implement the L-BFGS method to identify material parameters C₁, a₁, a₂, and a₄ in Eq. 1 (hyperelasticity requires C₁ > 0, a₁ > 0, a₂ > 0, and a₁a₂ > a₄², see Ref. 19) and C₂, b₁, b₂, and b′ in Eq. 2. The initial guess values for C₁, a₁, a₂, and a₄ were increased iteratively from 1 kPa, 1, 1, 1 to 200 kPa, 10, 10, 10, respectively. Similarly, the initial values for C₂, b₁, b₂, and b′ were increased iteratively in the range of 1–200 kPa, 0.1–1, 0.1–1, 1–100, respectively. The values corresponding to the minimum residual values in the L-BFGS method were selected for determination of material parameters.

Monte Carlo simulations were used to determine the confidence intervals of estimated parameters (23). Based on parameters and standard error determined by the L-BFGS method, pseudorandom experimental uncertainties were added to the modeled curve to generate virtual experimental data. The generation of virtual experimental data and the estimation of the parameters were repeated to construct a statistical distribution, from which the confidence interval was determined for each parameter. A set of 100 iterations of Monte Carlo simulations were performed to determine the 95% confidence intervals for passive and active material parameters (the relative error of 95% confidence intervals between 100 and 200 iterations was < 1%).

Statistical analysis.

The mean ± SE for the six hearts was presented. ANOVA (SigmaStat 3.5) was used to compare passive and active experimental measurements in six hearts, where P < 0.05 represented statistically significant differences.

RESULTS

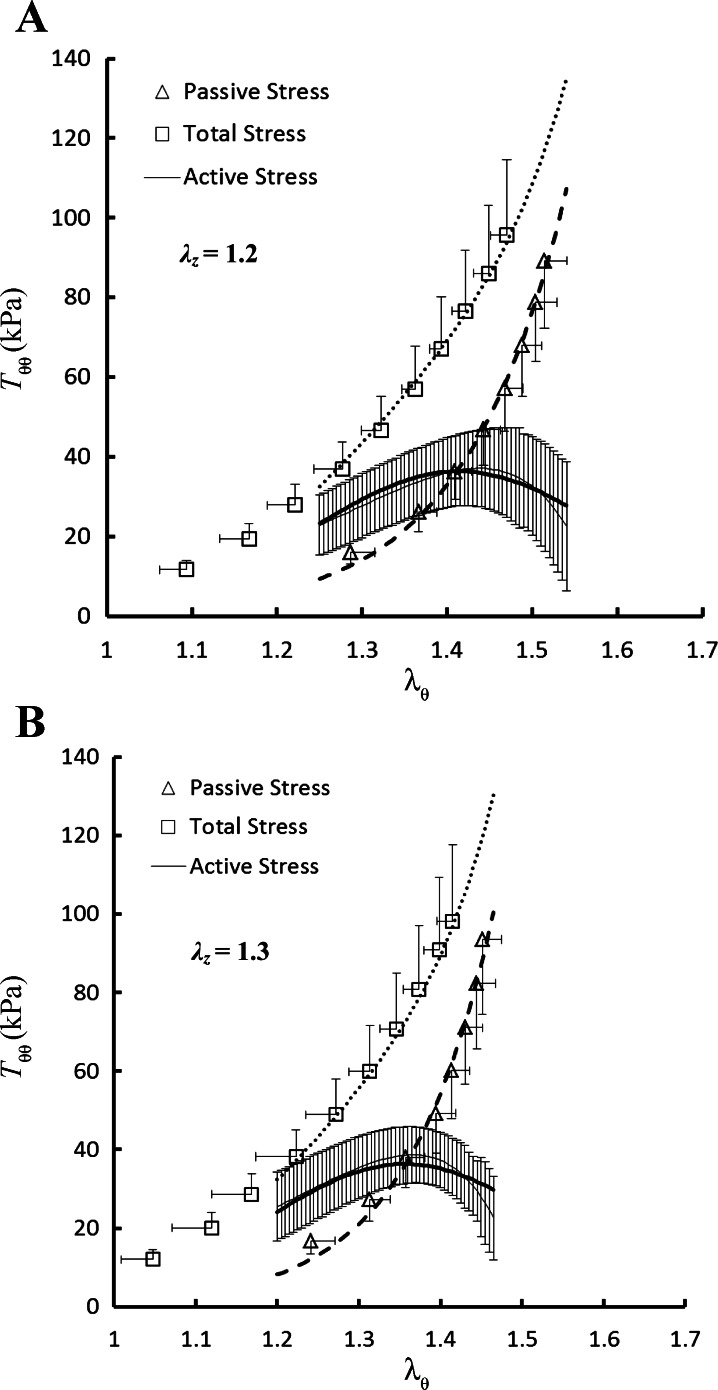
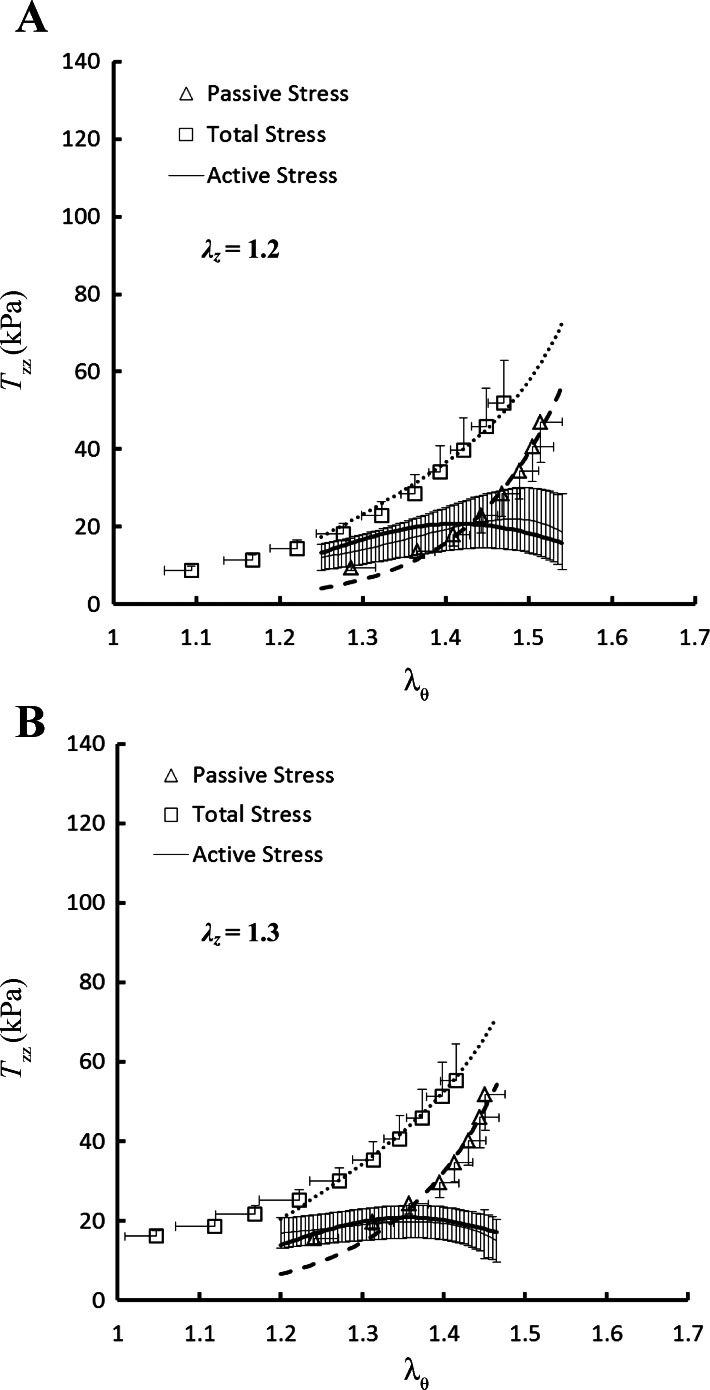
No statistically significant differences were found in the outer diameters and axial forces (P >> 0.05) among the six RCA intima-media layers in the transmural pressure range of 20 to 110 mmHg. Hence, the data were grouped together and expressed as means ± SE (averaged over six hearts). Figure 1, A and B, shows the theoretical and experimental data for the circumferential first Piola-Kirchhoff stresses (T_θθ) as a function of circumferential stretch ratios (λ_θ) at λ_z of 1.2 and 1.3, respectively. Similarly, Fig. 2, A and B, shows the axial first Piola-Kirchhoff stresses (T_zz) as a function of λ_θ at λ_z of 1.2 and 1.3, in correspondence with Fig. 1, A and B. The squares, triangles, and thin solid line with error bar of SE value in the two figures represent the measured total, passive, and active stresses, respectively, while the thick dotted, dashed, and solid lines refer to the theoretical values accordingly.

Fig. 1.

Circumferential first Piola-Kirchhoff stress (T_θθ) as a function of circumferential stretch ratio (λ_θ) at axial stretch ratio (λ_z) of 1.2 (A) and 1.3 (B) measured at K⁺-induced contraction and Ca²⁺-free-induced vasodilation. Shown are total stress (□): (Pr_i/hλ_θ)_total at contraction; passive stress (△): (Pr_i/hλ_θ)_passive at vasodilation; and active stress (thin solid line) =(Pr_i/hλ_θ)_total − (Pr_i/hλ_θ)_passive. The thick dotted, dashed, and solid lines refer to the theoretical total, passive, and active stresses, respectively.

Fig. 2.

Axial first Piola-Kirchhoff stress (T_zz) as a function of λ_θ at λ_z of 1.2 (A) and 1.3 (B) measured at K⁺-induced contraction and Ca²⁺-free-induced vasodilation. Shown are total stress (□): ${\left[\frac{F}{{\lambda }_z\pi \left(r_o^2-r_{\text{i}}^2\right)}+\frac{{\mathrm{Pr}}_i^2}{{\lambda }_{z}h\left(r_{\text{o}}+r_{\text{i}}\right)}\right]}_{\text{total}}$ at contraction; passive stress (△): ${\left[\frac{F}{{\lambda }_z\pi \left(r_o^2-r_{\text{i}}^2\right)}+\frac{{\mathrm{Pr}}_i^2}{{\lambda }_{z}h\left(r_{\text{o}}+r_{\text{i}}\right)}\right]}_{\text{passive}}$ at vasodilation; and active stress (thin solid line): ${\left[\frac{F}{{\lambda }_z\pi \left(r_o^2-r_{\text{i}}^2\right)}+\frac{{\mathrm{Pr}}_i^2}{{\lambda }_{z}h\left(r_{\text{o}}+r_{\text{i}}\right)}\right]}_{\text{total}}{\left[\frac{F}{{\lambda }_z\pi \left(r_o^2-r_{\text{i}}^2\right)}+\frac{{\mathrm{Pr}}_i^2}{{\lambda }_{z}h\left(r_{\text{o}}+r_{\text{i}}\right)}\right]}_{\text{passive}}$. The thick dotted, dashed, and solid lines refer to the theoretical total, passive, and active stresses, respectively.

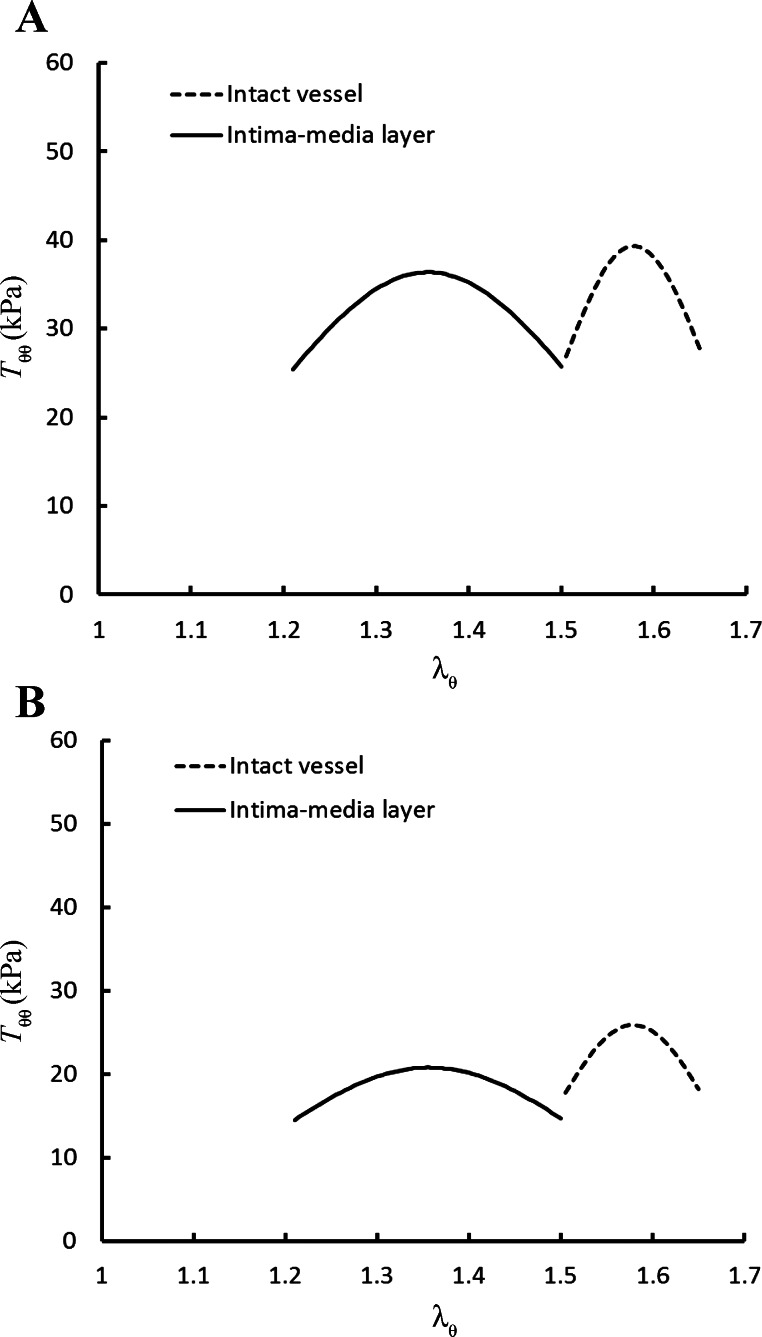
Table 1 summarizes the material constants in Eq. 1, while Table 2 lists the material constants in Eq. 2, for the six RCA intima-media layers. Table 3 shows the mean and 95% confidence interval of the estimated material constants in passive and active models, where the Monte Carlo simulations were performed for the L-BFGS fit of all experimental data of hearts 1–6. There are narrower confidence intervals for the material parameters in the active strain energy function compared with those in the passive one. We also compared the L-BFGS method with the generalized reduced gradient nonlinear optimization method (Microsoft Excel 2010) and found that the relative errors of the estimated parameters between the two methods were <2%. Based on the active strain energy function (Eq. 2) and experimentally determined material constants, we compared the theoretically predicted active stress-stretch relationship in the intima-media layer with that in the intact vessel (10), as shown in Fig. 3A (T_θθ vs. λ_θ at λ_z = 1.3) and Fig. 3B (T_zz vs. λ_θ at λ_z = 1.3).

Table 1.

Material constants of Fung's passive strain energy function (Eq. 1)

Animal Heart No.	C1, kPa	a1	a2	a4	R2 for Tθθpassive	R2 for Tzz passive
1	4.16	4.20	3.02	0.60	0.99	0.99
2	6.09	1.72	2.93	0.43	0.91	0.98
3	7.94	3.26	2.19	0.45	0.99	0.99
4	4.07	3.96	1.64	1.61	0.94	0.93
5	5.13	3.18	2.14	0.70	0.98	0.99
6	5.30	2.44	1.42	1.21	0.97	0.95
Fit of all experimental data of hearts 1–6	4.55	3.05	2.32	1.15	0.98	0.99
Mean ± SE for hearts 1–6	5.45 ± 0.59	3.13 ± 0.38	2.22 ± 0.27	0.83 ± 0.19

Material constants, C₁, a₁, a₂, and a₄, are obtained from experimental measurements of intima-media layer of right coronary artery (RCA). R², correlation coefficient; T_θθpassive, passive circumferential first Piola-Kirchhoff stresses; T_{zz passive}, passive axial first Piola-Kirchhoff stresses.

Table 2.

Material constants of K⁺-induced active strain energy function (Eq. 2) in the pressure range of 30–110 mmHg

Animal Heart No.	C2, kPa	b1	b2	b′	R2 for Tθθactive	R2 for Tzz active
1	9.36	0.22	0.44	9.08	0.81	0.75
2	5.19	0.29	0.73	6.65	0.76	0.66
3	4.58	0.20	0.39	10.0	0.82	0.52
4	14.8	0.20	0.32	11.5	0.67	0.73
5	16.8	0.29	0.46	7.29	0.78	0.58
6	4.21	0.18	0.34	11.4	0.81	0.62
Fit of all experimental data of hearts 1–6	7.88	0.24	0.43	8.60	0.93	0.73
Mean ± SE for hearts 1–6	9.17 ± 2.25	0.23 ± 0.02	0.45 ± 0.06	9.33 ± 0.83

Material constants, C₂, b₁, b₂, and b′, are obtained from experimental measurements of intima-media layer of RCA. T_θθactive, active circumferential first Piola-Kirchhoff stresses; T_{zz active}, active axial first Piola-Kirchhoff stresses.

Table 3.

Mean and 95% confidence interval of the estimated material constants for passive and active models

Model	Parameter	Mean	LCL	UCL
Passive	C1, kPa	4.55	3.53	5.56
	a1	3.05	2.76	3.34
	a2	2.32	1.85	2.80
	a4	1.15	0.94	1.40
Active	C2, kPa	7.88	7.60	8.11
	b1	0.24	0.24	0.25
	b2	0.43	0.40	0.44
	b′	8.60	8.33	8.95

LCL, lower confidence limit; UCL, upper confidence limit.

Fig. 3.

Circumferential active first Piola-Kirchhoff stress, T_θθactive^theory = $\frac{2C_2}{b_1\sqrt{\pi }}\exp \left[-{\left(\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_z}{b_2}-b{\prime }^{\prime }\right)}^2\right]$ (A), and axial active first Piola-Kirchhoff stress, T_zzactive^theory = $\frac{2C_2}{b_2\sqrt{\pi }}\exp \left[-{\left(\frac{{\lambda }_{\theta }}{b_1}+\frac{{\lambda }_z}{b_2}-b\prime \right)}^2\right]$ (B), as a function of λ_θ at λ_z of 1.3. Parameters, C₂, b₁, b₂, and b′, have values of 7.88, 0.24, 0.43, and 8.60 for intima-medial layer (Table 2) and 4.18, 0.12, 0.18, and 20.3 for intact vessel (Table 2 in Ref. 10).

The mean ± SE values of the outer diameters of RCA intima-media layers at transmural pressure of 60 mmHg in active state were 3.17 ± 0.16 and 3.07 ± 0.18 mm at λ_z of 1.2 and 1.3, respectively, which were smaller than those in passive state (i.e., 3.62 ± 0.19 and 3.49 ± 0.22 mm, respectively, P < 0.05). Moreover, the mean ± SE values of the inner and outer diameters in no-load state were 1.17 ± 0.09 and 2.08 ± 0.09 mm, respectively, while the opening angles were 159 ± 21°.

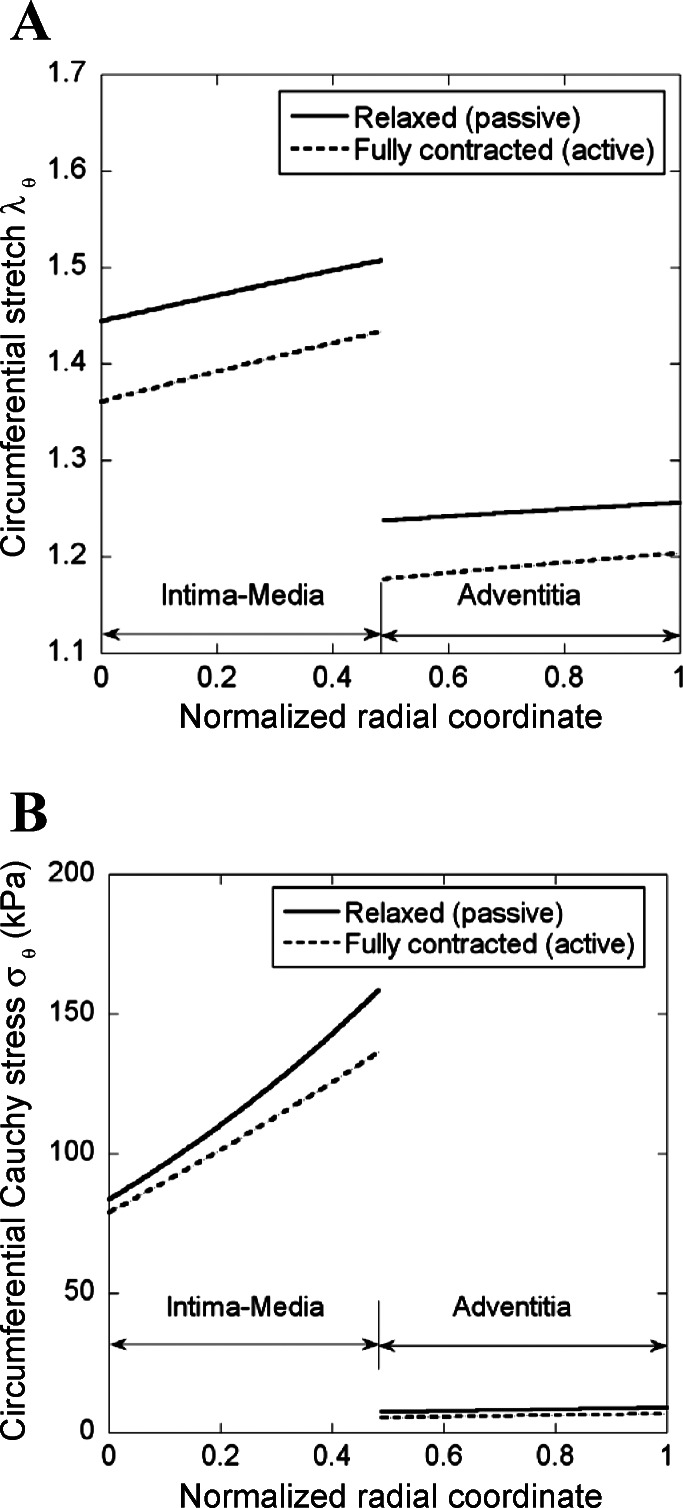
A two-layer model (see appendix) was developed to compute the transmural distribution of stress and stretch in the coronary artery wall. The material constants of passive and active strain energy functions and the stress-free geometry for intima-media and adventitia layers are listed in Tables A1 and A2, respectively, for the vessel wall mechanics analysis. Figure 4, A and B, shows the computed transmural distribution of λ_θ and Cauchy stress, respectively, in the coronary artery wall at λ_z of 1.3 and transmural pressure of 80 mmHg. The λ_θ is defined as the ratio of loaded circumferential length to the corresponding zero-stress circumferential length in each layer. There is an increase of no-load diameter as well as zero-stress circumferential length in a single intima-media layer compared with that of an intact vessel wall (Fig. A1, C and D), but a decrease in a single adventitia layer (Fig. A1, E and F). Hence, Fig. 4A shows discontinuous circumferential stretches at the interface between intima-media and adventitia layers. Similarly, Fig. 4B shows discontinuous Cauchy stresses given the difference in mechanical properties between intima-media and adventitia layers.

Fig. 4.

Computed transmural distribution of λ_θ and Cauchy stress (σ_θ) across the vessel wall at λ_z of 1.3 and transmural pressure of 80 mmHg using the two-layer model.

DISCUSSION

Based on the experimentally determined passive and active strain energy functions in the intima-media and adventitia layers, a two-layer model (see appendix) was proposed to analyze the transmural distribution of stress and stretch in the vessel wall. The experimental and computational studies show the following results: 1) the radius, circumferential length, and opening angle are increased in the intima-media layer, but decreased in adventitia layer in zero-stress state compared with those of an intact vessel wall (Fig. A1); 2) the active stress-stretch relationship, measured in the intima-media layer, shows less curvature and lower stress than that in the intact vessel (Fig. 3); 3) there is larger circumferential stress in the intima-media layer than the adventitia layer in loaded state (Fig. 4B); and 4) SMC contraction results in a significant decrease of stress and stretch in both intima-media and adventitia layers (Fig. 4, A and B).

Intima-media layer vs. intact vessel.

The intima-media and adventitia layers of blood vessel walls in passive state were found to have different mechanical properties experimentally (17, 20, 27) and theoretically (8, 21, 28). There is a lack of studies, however, on the mechanical behavior of isolated intima-media layer in the active state. Here, we fitted the biaxial mechanical measurements in the contracted intima-media layer of RCA to an active strain energy function (W_active in Eq. 2), as shown in Table 2. A comparison of results between the intima-media and intact vessel is summarized below. In the following subsection, superscript “IM” refers to the intima-media layer to distinguish it from the intact vessel.

Material constants, b₁ and b₂, in Eq. 2 represent the relative curve width of active stress as a function of circumferential and axial stretches, respectively, which are larger in the intima-media layer than the intact vessel (0.24 vs. 0.12 for b₁ and 0.43 vs. 0.18 for b₂). Since there is an increase of diameter (r_i^IM and r_o^IM) in no-load state (which corresponds to an increase of circumferential length in zero-stress state) when the adventitia is removed (see Fig. A1C), the physiological active stress occurs when 1.20 < λ_θ^IM < 1.50 (λ_θmax^IM − λ_θmin^IM = 0.30) for the intima-media layer compared with 1.50 < λ_θ < 1.65 (λ_θmax − λ_θmin = 0.15) for the intact vessel (see Fig. 3) at λ_z^IM = λ_z = 1.3. The opening angle of the intima-media layer (159 ± 21°) is larger than that of the intact vessel (126 ± 22°, Ref. 10), while a previous study showed a decreased opening angle in a single adventitia layer (98 ± 15°, Ref. 17). This suggests a residual strain between intima-media and adventitia layers in an intact vessel. The relieved residual strain in the intima-media layer as the adventitia is removed may explain why (λ_θmax^IM − λ_θmin^IM) > (λ_θmax − λ_θmin) in the physiological pressure range.

Material constants, $\frac{2C_2}{b_1\sqrt{\pi }}$ and $\frac{2C_2}{b_2\sqrt{\pi }}$, represent the peak magnitudes for circumferential and axial stresses, respectively, which have values of 37 and 20.7 in the intima-media layer and 40 and 26.2 in the intact vessel. The maximal active stress occurs when λ_z^IM = 1.36 for the intima-media layer and λ_θ = 1.58 for the intact vessel at λ_θ^IM = λ_z = 1.3. There are slightly decreased circumferential active stresses (<10%), but significantly decreased axial active stresses (>25%) in the intima-media layer compared with those in the intact vessel (see Fig. 3). These findings imply that the adventitia layer affects the contraction of media layer in epicardial coronary arteries in response to high K⁺, which is consistent with previous experimental measurements in other vessels (5, 6, 26). The differences in the magnitude of active stress between circumferential and axial directions may be related to the microstructural properties of the intima-media and adventitia layers. There is clearly a need to understand how the circumferential SMC, in conjunction with the elastin network and heterogeneous wavy collagen fibers, affects the axial force. This issue requires further investigations of vessel wall microstructure, including the quantitative measurement of elastin and collagen fiber bundles (2) and SMC distribution.

Transmural distribution of stress and stretch.

The one-layer model for an intact vessel has been widely used in computation of transmural stress and strain distribution. In passive arteries, Chuong and Fung (3) proposed a uniform stress distribution across the wall thickness due to the residual stress. Takamizawa and Hayashi (25) formulated an alternative hypothesis of uniform strain due to the residual strain. For active vessel, Matsumoto et al. (18) showed an increase of opening angle as the rat aorta changed from passive to chemically induced maximal vasoconstriction, from which they computed the transmural strain distribution and depicted the opposite spatial gradients of strain under physiological pressures. Zeller and Skalak (31), however, found a decrease of opening angle in rat saphenous artery, albeit their computed transmural strain showed similar trends as the predictions of Matsumoto et al. for vasoconstriction and vasodilation. Similar to the transmural distribution of strain, Rachev and Hayashi (22) numerically predicted the opposite spatial gradients of transmural stress between vasoconstriction and vasodilation, based on a parabolic active stress-stain relationship in the circumferential direction.

A two-layer model was used to compute the transmural stress-stretch relationship in the present study (see appendix). In contrast to the homogeneous one-layer hypothesis for an intact vessel, we found the degree of stiffness as follows: intima-media layer > intact vessel > adventitia layer (17, 20, 27). As shown in Fig. 4B, the intima-media layer bears the majority of circumferential tensions, while the adventitia serves to protect the vessel from overstretch, which is consistent with previous studies (8, 28). In the intima-media/adventitia layer, there is an increase of stress and stretch from inner to outer surfaces, which is in disagreement with reports of higher circumferential stress at the inner wall. Moreover, the K⁺-induced SMC contraction significantly reduces stress and stretch in both intima-media and adventitia layers.

Potential implications for coronary artery remodeling in hypertrophy.

Ventricular hypertrophy can result in the growth of myocardial surface (increase in base of the heart) (7, 29) and hence increase in λ_z of epicardial coronary arteries that crown the base of the heart. An increase of axial stretch may shift the peak location (i.e., the site with the maximal active stress) to lower circumferential stretch region (see a comparison of λ_z = 1.2 and λ_z = 1.3 in Figs. 1 and 2). The high blood pressure that initiates hypertrophy, however, can increase the circumferential stretch of epicardial coronary arteries. This may lead to a drop in SMC contractility, which can be a significant factor for SMC remodeling (13) and possibly coronary neovascularization (11, 12, 14). Moreover, the differences of mechanical properties and loadings of intima-media and adventitia layers may lead to different structural remodeling between the two layers in response to hypertension (13), which requires further microstructural investigations.

Critique of method.

The present study did not consider the biochemical role of adventitia layer on vascular wall mechanics. Responses to KCl or norepinephrine were found to be significantly reduced in rat carotid and iliac arteries without adventitia (6), while the adventitial adipose tissue produced vasoactive substances that influenced SMC contraction (26). We also neglected the shear stress-induced regulation of SMC contraction. Finally, additional studies are needed to investigate the stress-stretch relationship in diseased coronary vessels where the intimal layer becomes thicker (e.g., intimal hyperplasia) and stiffer (e.g., calcification) and the media layer undergoes SMC proliferation and migration.

Summary and conclusions.

We determined the strain energy functions in the intima-media layer of coronary arteries in passive and active states. There is much larger opening angle of a single intima-media layer than that of a single adventitia layer, which suggests a residual strain between the two layers in an intact vessel. The radius and circumferential length also increase in the isolated intima-media layer at zero-stress state compared with intact vessel. Consequently, a two-layer model shows an increase of stress and stretch from inner to outer surfaces in the intima-media/adventitia layer, while the intima-media layer bears the majority of circumferential tensions. SMC contraction significantly reduces stress and stretch across the vessel wall compared with the passive state.

GRANTS

This research was supported in part by National Heart, Lung, and Blood Institute Grant HL-087235 (G. S. Kassab) and American Heart Association Scientist Development Grant 0830181N (Y. Huo).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: Y.H., X.Z., X.L., and G.S.K. conception and design of research; Y.H., X.Z., and X.L. performed experiments; Y.H., X.Z., Y.C., X.L., and G.S.K. analyzed data; Y.H., X.Z., Y.C., and G.S.K. interpreted results of experiments; Y.H., X.Z., and G.S.K. prepared figures; Y.H., X.Z., and G.S.K. drafted manuscript; Y.H., X.Z., Y.C., X.L., and G.S.K. edited and revised manuscript; Y.H., X.Z., Y.C., X.L., and G.S.K. approved final version of manuscript.

Appendix

Kinematics.

A two-layer model was used to compute the transmural stress-strain relationship from stress-free to deformed vessel wall at passive and active states. The coronary artery wall was assumed to consist of two layers with distinct material properties and residual strains, i.e., the intima-media layer and the adventitia layer, and both layers were assumed to be cylindrical, orthotropic, hyperelastic, and incompressible. Superscripts “IM” and “A” refer to intima-media and adventitia layers, respectively.

Parameters, R_i^IM, R_o^IM, L₀^IM, and φ^IM are the inner radius, outer radius, axial length, and opening angle of the intima-media layer, respectively, and R_i^A, R_o^A, L₀^A, and φ^A are the corresponding parameters of the adventitia layer in zero-stress state. Given the difference between a single layer and an intact vessel, subscript “layer” refers to the measurements in a single layer, intima-media layer, or adventitia layer (Fig. A1, D and F) and the absence of the subscript represents the measurements in an intact wall (Fig. A1B). Similarly, in their respective no-load and loaded states, r_i^IM, r_o^IM, and L^IM are the inner radius, outer radius, and axial length of the intima-media layer, respectively, and r_i^A, r_o^A, and L^A are the corresponding parameters of the adventitia layer, as shown in Fig. A1, A, C, and E.

In cylindrical coordinate with R, Z, Θ for zero-stress state and r, z, θ for no-load and loaded states, we can express the following:

$$r=r\left(R\right),\theta =\frac{\pi }{\pi -\varphi }\Theta =\chi \Theta ,z={\lambda }_{z}Z$$ (A1)

where χ = π/(π − φ) is a parameter that characterizes the deformation from the zero-stress to deformed states. Here, φ is the opening angle of intact vessel wall, and φ^IM and φ^A stand for the opening angles of intima-media and adventitia layers, respectively.

As shear deformation is neglected, the deformation gradient from stress-free to deformed states is given as:

$$\text{F}=\left[\begin{array}{ccc}{\lambda }_r& 0& 0\\ 0& {\lambda }_{\theta }& 0\\ 0& 0& {\lambda }_z\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial r}{\partial R}& 0& 0\\ 0& \frac{\chi r}{R}& 0\\ 0& 0& {\lambda }_z\end{array}\right]$$ (A2)

where λ_r, λ_θ, and λ_z are the radial, circumferential, and axial stretch ratios, respectively. The Green strain tensor is defined as:

$$\text{E}=\frac{1}{2}\left[{\text{F}}^{\text{T}}\text{F}-\text{I}\right]=\left[\begin{array}{ccc}{\text{E}}_r& 0& 0\\ 0& {\text{E}}_{\theta }& 0\\ 0& 0& {\text{E}}_z\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{2}\left({\lambda }_r^2-1\right)& 0& 0\\ 0& \frac{1}{2}\left({\lambda }_{\theta }^2-1\right)& 0\\ 0& 0& \frac{1}{2}\left({\lambda }_z^2-1\right)\end{array}\right]$$ (A3)

The material incompressibility (i.e., λ_rλ_θλ_z = 1) results in the relation as follows: $r=\sqrt{r_{\text{i}}^2+\frac{R^2-R_i^2}{\chi {\lambda }_z}}$, where r and R are the radial coordinates of an arbitrary point in deformed (no-load or loaded states) and zero-stress states, respectively.

Strain energy function.

The Fung-type pseudoelastic strain energy function was used to model the passive constitutive behavior as:

$$\begin{array}{c}{\text{W}}_{\text{passive}}=\frac{C_1}{2}\left[\exp \left(Q\right)-1\right]\\ Q=a_1{\text{E}}_{\theta }^2+a_2{\text{E}}_z^2+a_3{\text{E}}_r^2+2a_4{\text{E}}_{\theta }{\text{E}}_z+2a_5{\text{E}}_z{\text{E}}_r+2a_6{\text{E}}_r{\text{E}}_{\theta }\end{array}$$ (A4)

where C₁ is a stress-like material constant, a_i (i = 1,2, … 6) are the dimensionless material constants, and W_passive refers to W_passive^IM or W_passive^A. The material constants and stress-free geometry for the intima-media and adventitia layers of RCA are listed in Tables A1 and A2, respectively (27). The Cauchy stress tensor is

$$\sigma =\text{F}·\frac{\partial {\text{W}}_{\text{passive}}}{\partial \text{E}}·{\text{F}}^{\text{T}}-P\text{I}$$ (A5)

where P is the unknown Lagrange multiplier that needs to be determined from the boundary conditions.

Table A1.

Passive and active material constants of right coronary artery for the computational model

	Passive							Active
Layer	C1, kPa	a1	a2	a3	a4	a5	a6	C2, kPa	b1	b2	b′
Intima-media	6.53	2.50	3.61	0.83	0.44	0.05	0.10	9.17	0.23	0.45	9.33
Adventitia	5.30	1.19	3.30	1.27	0.41	0.07	0.07

Table A2.

Geometric parameters of right coronary artery for the computational model

Layer	Opening Angle φ, °	Inner Radius Ri, mm	Outer Radius Ro, mm
Intima-media	150	6.407	6.656
Adventitia	108	3.379	3.603

The K⁺-induced active strain energy function (Eq. 2) was used to model the fully contraction of the intima-media layer, i.e.,

$${\text{W}}_{\text{total}}^{\text{IM}}={\text{W}}_{\text{passive}}^{\text{IM}}+{\text{W}}_{\text{active}}^{\text{IM}}$$ (A6)

The total Cauchy stress tensor in the intima-media layer is given by

$$\sigma ={\sigma }_{\text{passive}}+{\sigma }_{\text{active}}=\text{F}·\frac{\partial \left({\text{W}}_{\text{passive}}^{\text{IM}}+{\text{W}}_{\text{active}}^{\text{IM}}\right)}{\partial \text{E}}·{\text{F}}^{\text{T}}-P\text{I}$$ (A7)

The adventitia layer does not contribute to the active contraction of the artery, and thus only the passive strain energy is considered in the adventitia layer, i.e., W_total^A = W_passive^A.

Equilibrium equation.

The equilibrium equation in the cylindrical coordinate is given as:

$$\frac{\partial {\sigma }_r}{\partial r}+\frac{{\sigma }_r-{\sigma }_{\theta }}{r}=0$$ (A8)

where σ_r and σ_θ are the radial and circumferential Cauchy stresses, respectively. The boundary conditions at the inner and outer surfaces of vessel wall are:

$${\sigma }_r\left|r=r_{\text{i}}^{\text{IM}}=-p\hspace{0.17em}\text{and}\hspace{0.17em}{\sigma }_r\right|r=r_0^{\text{A}}=0$$ (A9)

An additional boundary condition is the stress balance at the interface between intima-media layer and adventitia layer:

$${\sigma }_r\left|r=r_{\text{o}}^{\text{IM}}={\sigma }_r\right|r=r_{\text{i}}^{\text{A}}$$ (A10)

Solving Eq. A8 with the corresponding boundary conditions, the radial, circumferential, and axial stress components in the intima-media layer are given by:

$$\{\begin{array}{c}{\sigma }_r^{\text{IM}}={\displaystyle {\int }_{r_{\text{i}}^{\text{IM}}}^r\left({\lambda }_{\theta }^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_{\theta }}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_r}\right)\frac{1}{r}\text{d}r-p}\\ {\sigma }_{\theta }^{\text{IM}}={\sigma }_r^{\text{IM}}+{\lambda }_{\theta }^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_{\theta }}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_r}\\ {\sigma }_z^{\text{IM}}={\sigma }_r^{\text{IM}}+{\lambda }_z^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_z}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_r}\end{array}$$ (A11)

From Eq. A10, we can obtain:

$${\sigma }_r\left|r=r_{\text{i}}^{\text{A}}={\sigma }_r\right|r=r_{\text{o}}^{\text{IM}}={\displaystyle {\int }_{r_{\text{i}}^{\text{IM}}}^{r_{\text{o}}^{\text{IM}}}\left({\lambda }_{\theta }^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_{\theta }}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_r}\right)\frac{1}{r}\text{d}r-p}$$ (A12)

Solving Eq. A8 with the corresponding boundary conditions, the radial, circumferential, and axial stress components in the adventitia layer are given by:

$$\{\begin{array}{c}{\sigma }_r^{\text{A}}={\displaystyle {\int }_{r_{\text{i}}^{\text{A}}}^r\left({\lambda }_{\theta }^2\frac{\partial {\text{W}}^{\text{A}}}{\partial {\text{E}}_{\theta }}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{A}}}{\partial {\text{E}}_r}\right)\frac{1}{r}\text{d}r}+{\displaystyle {\int }_{r_{\text{i}}^{\text{IM}}}^{r_{\text{o}}^{\text{IM}}}\left({\lambda }_{\theta }^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_{\theta }}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{IM}}}{\partial {\text{E}}_r}\right)\frac{1}{r}\text{d}r-p}\\ {\sigma }_{\theta }^{\text{A}}={\sigma }_r^{\text{A}}+{\lambda }_{\theta }^2\frac{\partial {\text{W}}^{\text{A}}}{\partial {\text{E}}_{\theta }}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{A}}}{\partial {\text{E}}_r}\\ {\sigma }_z^{\text{A}}={\sigma }_r^{\text{A}}+{\lambda }_z^2\frac{\partial {\text{W}}^{\text{A}}}{\partial {\text{E}}_z}-{\lambda }_r^2\frac{\partial {\text{W}}^{\text{A}}}{\partial {\text{E}}_r}\end{array}$$ (A13)

Given the appropriate strain energy functions, Eqs. A8–A13 were used to solve the transmural stress-strain relationship from stress-free to deformed vessel wall at both passive and active states.