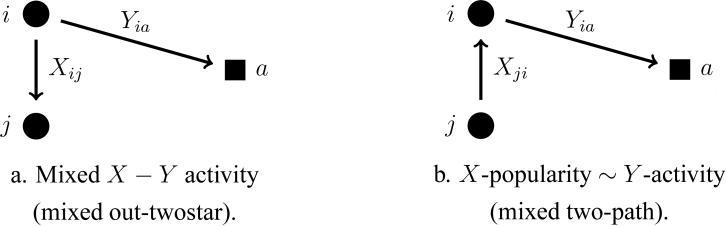A model for the multiplex dynamics of two-mode and one-mode networks, with an application to employment preference, friendship, and advice

Abstract

We propose a new stochastic actor-oriented model for the co-evolution of two-mode and one-mode networks. The model posits that activities of a set of actors, represented in the two-mode network, co-evolve with exchanges and interactions between the actors, as represented in the one-mode network. The model assumes that the actors, not the activities, have agency.

The empirical value of the model is demonstrated by examining how employment preferences co-evolve with friendship and advice relations in a group of seventy-five MBA students. The analysis shows that activity in the two-mode network, as expressed by number of employment preferences, is related to activity in the friendship network, as expressed by outdegrees. Further, advice ties between students lead to agreement with respect to employment preferences. In addition, considering the multiplexity of advice and friendship ties yields a better understanding of the dynamics of the advice relation: tendencies to reciprocation and homophily in advice relations are mediated to an important extent by friendship relations.

The discussion pays attention to the implications of this study in the broader context of current efforts to model the co-evolutionary dynamics of social networks and individual behavior.

1 Motivation

Two-mode networks are often used to represent the association between social actors and activities, groups, or events with which the actors may be affiliated. For this reason two-mode network are also called affiliation networks (Wasserman and Faust, 1994, Chapter 2). Following Borgatti and Everett (1997) we understand the concept of affiliation in a broad sense to include membership in organizations and groups, participation in activities, and association between individuals and values, beliefs, or attitudes. The latter type of attributes do not always lead to a structure that one might regard as a two-mode network. One may pose the requirement that sharing such values, beliefs, or attitudes should lead to contacts between the actors, thereby representing a social focus (Feld, 1981) for the actors constituting the first mode. As a generic term for the second mode of the network we will use the term activity rather than the more usual event (cf. Faust, 1997), to underscore our focus on enduring affiliations as well as the duality between actors and activities (Breiger, 1974).

Joint participation of actors in activities will go together with other interactions and/or exchanges between these actors. We go with friends to meeting places, we may make new friends there whom subsequently we also meet elsewhere, and we may interrupt friendships relations with people whom we never meet at any meeting place. We talk with friends about our convictions, the number of shared convictions may influence the probability to remain friends, and our friends may convince us of their views. Thus, a two-mode network often goes together with interactions that can be described by one-mode networks. An example is provided by the socio-semantic networks of Roth and Cointet (2010), where researchers who interact may be led to using the same concepts, and the use by scientists of the same concepts may promote, or cement, their interaction. The present article presents a methodology for studying the co-evolution, or interdependent dynamics, of one-mode networks representing interactions among a set of actors and two-mode networks representing the affiliation of these actors with a socially relevant set of activities or settings. The model combines (two-mode) ‘membership network analysis’ and (one-mode) ‘social-relations network analysis’ (Breiger, 1974, p. 183). It builds upon earlier models for dynamics of single networks, proposed for one-mode networks by Snijders (2001) and for two-mode networks by Koskinen and Edling (2010). We add to available models the possibility of representing the interdependence between the different networks.

The mutual association between one-mode and two-mode networks was studied recently by Roth and Cointet (2010). The methods discussed and proposed in this paper and ours are complementary. Roth and Cointet (2010) present descriptive methods for the level of the entire network and communities within the network, uncovering a variety of interesting patterns in the data and comparing these with what would be expected under a uniformly random null model. We focus on the micro-level of actors in the network and their immediate surroundings, and propose a model that allows the combination of several different generative principles (‘effects’), thus permitting statistical inference by testing a theory or hypothesis while controlling for alternative theories or principles. A further difference between the two approaches is that Roth and Cointet (2010) consider a growing network, where nodes can enter the network, and ties cannot be terminated. Our model assumes fixed node sets and allows creation as well as termination of ties. Entry of actors or activities into the system, and exit from the system, may be allowed by using the methods of Huisman and Snijders (2003) and Ripley, Snijders and Preciado (2012).

We illustrate the model in a study of a cohort of MBA students, who are strongly oriented toward preparing themselves for the job market and finding a desired employer. Shared employment preferences lead to association and common orientations between individuals, thereby defining a meaningful two-mode network, that may be expected to be interdependent with the friendship and advice-related interactions between individuals (cf. Kilduff, 1990). Job search in this group of students may be regarded as providing a social context, i.e., a configuration of “foci and individuals, where each individual is related to some foci but not to others” (Feld, 1981, p. 1016). The foci in our illustration are potential employers and the individuals are the MBA students. For the exchanges between the students both friendship and advice are relevant, and therefore we consider not only the co-evolution of a two-mode and a one-mode network, but also the co-evolution of these two one-mode networks. The example thus illustrates not only the multiplexity arising from a combination of affiliation networks and interaction networks, but also the multiplexity of two one-mode interaction networks. Available statistical models for multiplexity are of a cross-sectional nature (see Lazega and Pattison, 1999; Pattison and Wasserman, 1999). The longitudinal nature of our approach leads to clarifying the time ordering of different relational events. For example, we show (cf. Section 7) that the tendency toward certain structures in the advice network can be understood as emerging from the friendship network and the dependency of advice on friendship.

We continue the article by discussing the primary kinds of dependence between two-mode and one-mode networks in Section 2 and then outline the proposed model in Section 3. The example of the networks of MBA students is introduced in Section 4. The empirical model specification is presented in Section 5 and the results in Section 6. Section 7 discusses how these results illustrate that emergent properties in networks may be understood better by considering the co-evolution of multiple networks, and Section 8 gives further conclusions.

2 Dependencies between one-mode and two-mode networks

Perhaps the most interesting aspect of network evolution is the feedback of network structure onto itself: how does current, or past, network structure lead to changes in ties and thereby to change of network structure, or – as the case may be – dynamic regeneration or confirmation of network structure? A co-evolutionary model of a one-mode and a two-mode network must represent, in addition to the internal dynamic dependencies of each of these networks, the dependencies across networks. Within-network dependencies are represented here as in the models proposed by Koskinen and Edling (2010) for two-mode and Snijders (2001) for one-mode networks. This paper focuses on the cross-network dependencies: how does the one-mode network influence the two-mode network, and vice versa how does the two-mode network influence the one-mode network.

For a brief overview of notation, suppose that one two-mode network and one one-mode network are being considered. The two-mode network is denoted Y, the node sets (modes) being a set 𝒩 of social actors i and a set 𝒜 of social activities a. This network is composed of tie variables Y_ia for i ∈ 𝒩 $a\in \mathcal{A}$, with Y_ia = 1 if actor i participates in activity a, and Y_ia = 0 otherwise. The one-mode network X has node set 𝒩 and directed tie variables X_ij for i, $j\in \mathcal{N}(i\ne j)$, indicating the existence of an interaction tie from actor i to actor j. We assume that there is no meaningful directionality in the two-mode network that would imply a distinction between ties directed from 𝒩 to 𝒜, and ties directed from 𝒜 to 𝒩. Notionally we represent the two-mode ties as being directed from 𝒩 to 𝒜, but this has no special interpretation. Everywhere in this paper replacing an index by a + sign denotes summation over this index.

The first mode 𝒩 represents the set of actors, who choose elements of a set 𝒜 of activities or affiliations that constitutes the second mode. Thus, only the first mode has agency, and we do not explicitly model situations where individuals would like to join activities but may be refused by the activities, or where the memberships are the results of two-sided match-making as in Logan (1998).

The one-mode and two-mode networks have no dyads in common, so that dyadic dependencies do not arise. Two basic types of dependencies between the one-mode and the two-mode networks are by actors and by triads. We consider them in turn.

2.1 Actor-level dependencies

At the actor level, a fundamental issue is how positional characteristics of an actor in one network affect her position in the other network. As positional characteristics of actors i ∈ 𝒩, we consider in the one-mode network the outdegrees X_i+ and indegrees X_+i, and in the two-mode network the outdegrees Y_i+1. Outdegrees in either network will be regarded as expressions of activity, while indegrees in the one-mode network will be regarded as expressions of popularity. Depending on the meaning of the networks, these interpretations may be replaced by other appropriate representations. Combining the various types of degree in the roles where one network is the antecedent (‘explanatory variable’) while the other network is the consequence (‘dependent variable’) yields the following four mixed degree-related effects.

1. One-mode activity ⇒ two-mode activity (nominating many friends leads to many activities; X_ij ⇒ Y_ia in Fig. 1a);

2. two-mode activity ⇒ one-mode activity (having many activities leads to nominating many friends; Y_ia ⇒ X_ij in Fig. 1a);

3. one-mode popularity ⇒ two-mode activity (being nominated by many friends leads to many activities; X_ji ⇒ Y_ia in Fig. 1b);

4. two-mode activity ⇒ one-mode popularity (having many activities leads to being nominated by many friends; Y_ia ⇒ X_ji in Fig. 1b).

The first two of these effects influence the number of mixed two-stars in the network, and the last two the number of mixed two-paths, as illustrated in Figure 1.

Figure 1.

Circles, left, are actors in 𝒩. The square, right, is an activity in 𝒜.

2.2 Triadic dependencies

Closed triads are impossible in two-mode networks (cf. Robins and Alexander, 2004). However, mixed triads are possible, and represent mixed transitive closure: e.g., a friend's club is my club, or a clubmate is a friend, see Figure 2. More abstractly, specifying the two causal or temporal directions, the twopath consisting of a one-mode tie $i\stackrel{X}{\to }j$ followed by a two-mode tie $j\stackrel{Y}{\to }a$ can be closed by a two-mode tie $i\stackrel{Y}{\to }a$; and agreement between i and j in the form of the two-mode two-instar $\left(i\stackrel{Y}{\to }a\stackrel{Y}{\leftarrow }j\right)$ can be closed by the one-mode tie $i\stackrel{X}{\to }j$. This leads to the following possibilities.

1. One-mode out-tie ⇒ two-mode agreement (‘I become/stay a member of a club having as a member somebody whom i consider a friend’: {X_ij and Y_ja} ⇒ Y_ia in Fig. 2);

2. One-mode in-tie ⇒ two-mode agreement (‘I become/stay a member of a club having as a member somebody who calls me a friend’: {X_ij and Y_ia} ⇒ Y_ja);

3. Two-mode agreement ⇒ one-mode out-tie (‘I become/stay friends with members of my club’: {Y_ia and Y_ja} ⇒ X_ij).

Figure 2.

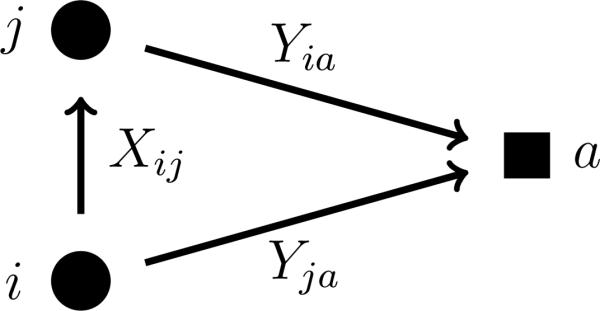
One-mode tie ~ two-mode agreement (mixed triplet). Circles, left, are actors in 𝒩. Squares, right, are activities in 𝒜.

These effects influence the number of the mixed triplets, see Figure 2, each by adding a different tie in this triplet. The fact that these three effects all have the consequence of promoting the same type of mixed triads implies that they may be difficult to distinguish empirically. This may be the more so for the former two, as both have the two-mode network as the dependent variable.

3 Basic model

The model is described here as a model for the co-evolution of one one-mode and one two-mode network. It can be extended in a straightforward way to the co-evolution of arbitrary numbers of networks of either kind. The model extends stochastic actor-oriented models for the dynamics of one-mode networks (Snijders, 2001) and for the dynamics of networks and behavior (Steglich, Snijders and Pearson, 2010), to which a tutorial introduction is given in Snijders, van de Bunt and Steglich (2010). For further background and explanations we refer to these papers. We assume that the data available derive from a panel study of the two networks: for time points t₁, t₂, . . . , t_M (where M ≥ 2), the one-mode network and the two-mode network are observed, and represented by their adjacency matrices X(t₁), Y(t₁) to X(t_M), Y(t_M). Two fundamental model assumptions are that the networks change, unobserved, between the observation moments at arbitrary time points, while at each moment of change only a single tie variable X_ij (t) or Y_ia(t) may change. This framework was proposed by Holland and Leinhardt (1977). Mathematically the first assumption is formulated by saying that (X(t), Y(t)) is a continuous-time stochastic process, where time parameter t traverses the interval from t₁ to t_M. The two assumptions together decompose the change process that brought one observation (X(t_m), Y(t_m)) to the next (X(t_m+1), Y(t_m+1)) into its smallest components, changes of single tie variables. The advantage is that instead of having to specify how one network is transformed into a later observed, quite different network, we only need to specify the probability distribution for the creation and termination of any single tie. This probability distribution is specified as a Markov process, i.e., the probability of a change of a tie variable at time t is assumed to depend on the current configuration at this moment, (X(t), Y(t)) – and on available covariates –, and not on earlier states of the two networks. The model consists of one component for changes in the one-mode network X, depending on the current state of X as well as Y; and another component for changes in the two-mode network Y, depending on the current state of Y as well as X. The model expresses the feedback between the one-mode and two-mode networks: as soon as a tie changes in either network, this affects the network neighborhood in both networks of all nodes involved directly or indirectly, and thereby this affects the probabilities of later tie changes.

The model is actor-oriented, reflecting the agency of the nodes in the first node set, 𝒩. At random time moments, the actors i ∈ 𝒩 may change their outgoing ties in the two-mode network, Y_ia for a ∈ 𝒜, or in the one-mode network X_y for j ∈ 𝒩. These changes are stochastic, and – like the models earlier proposed – the models for these changes are split in (1) a model for the timing and frequency of changes and (2) a model for the choice of the changes. The model (1) for timing and frequency of changes often can be kept quite simple, with a constant rate of change for the one-mode network and another constant rate of change for the two-mode network. The word ‘constant’ refers here to constancy across actors and between two consecutive observations t_m–1 and t_M. Sometimes it can be relevant to let rates of change depend on actor attributes or positional characteristics, cf. Snijders (2001), but this possibility is not considered here. Model specification focuses on model (2) for the choice of tie changes. This is represented by so-called evaluation functions. These are functions of the personal network of the actors, defined separately for the one-mode network and the two-mode network. (We use the term ‘personal network’ for the two-mode as well as for the one-mode network.) Probabilities of tie changes by the actors are higher accordingly as they lead to higher values of the evaluation functions. Thus, the evaluation functions express the characteristics of their personal networks toward which the actors seem to be attracted.

A mathematical description of the model is given in the Appendix. Here we focus on the mathematical formulae representing the dependencies between the two-mode and the one-mode networks described in Section 2. The evaluation function for the two-mode network is defined as a linear combination

$$f_i^Y(x,y)=\sum _k{\beta }_k^Y{s}_{ki}^Y(x,y),$$ (1)

where the functions $s_{ki}^Y(x,y)$, called effects, are descriptives of the personal network, or extended personal network, of actor i. The effects to be included must be chosen by the researcher based on research questions, theory, and knowledge of the social setting of the network; the symbols ${\beta }_k^Y$ represent statistical parameters indicating how strongly each effect affects the evolution of the two-mode network. At any moment in time, given that actor i is allowed to make a change in the two-mode network while the current two-mode network is y and the current one-mode network is x, the probability of making a tie change that would lead to a new two-mode network y′ is higher accordingly as the resulting value of $f_i^Y(x,y^{\prime })$ is higher. Similarly, the evaluation function governing changes in the one-mode network is modeled by

$$f_i^X(x,y)=\sum _k{\beta }_k^X{s}_{ki}^X(x,y).$$ (2)

To express the dependencies discussed in Section 2, the effects will have to depend also on the other network: $s_{ki}^Y(x,y)$ must also depend on x and $s_{ki}^X(x,y)$ must depend also on y.

First we consider the four nodal, or degree-related effects. The effect denoted as “one-mode activity ⇒ two-mode activity” states that the drive for actors i toward high values of the two-mode outdegree y_i+1 is stronger when their one-mode outdegree x_i+ is higher. This can be expressed by the function $s_{ki}^Y(x,y)=x_{i+}{y}_{i+}$: a positive parameter ${\beta }_k^Y$ for this effect will imply that the probability of a change from outdegree y_i+1 to outdegree (y_i+1 + 1) will be larger when the current one-mode outdegree x_i+ is larger. With the appropriate changes for the other nodal effects, this leads to the following specifications.

1. One-mode activity ⇒ two-mode activity: dependent variable Y, effect formula $s_{ki}^Y(x,y)=x_{i+}{y}_{i+}$;

2. two-mode activity ⇒ one-mode activity: dependent variable X, effect formula $s_{ki}^X(x,y)=y_{i+}{x}_{i+}$;

3. one-mode popularity ⇒ two-mode activity: dependent variable Y, effect formula $s_{ki}^Y(x,y)=x_{+i}{y}_{i+}$;

4. two-mode activity ⇒ one-mode popularity: dependent variable X, effect formula $s_{ki}^X(x,y)=y_{i+}{x}_{+i}$.

The formulas for (1.) and (2.) have the same right-hand side, but refer to different dependent variables. The same holds for formulas (3.) and (4.).

Next to these specifications based on the product of the two degrees, other mathematical functions could be used. For example, it may sometimes be reasonable to suppose that there are ‘decreasing marginal returns’ of higher and higher degrees. For the “one-mode activity ⇒ two-mode activity” effect, for instance, this can be reflected by specifying the effect as $s_{ki}^Y(x,y)=\varphi \left(x_{i+}\right)y_{i+}$ where ϕ(x) is a concave function such as, for example, ϕ(x) = √x (Snijders et al., 2010).

Second, we consider the three mixed triadic closure effects, see Figure 2. Following a similar reasoning, these can be mathematically specified as follows.

1. One-mode out-tie ⇒ two-mode agreement ({X_ij and Y_ja} ⇒ Y_ia): $s_{ki}^Y(x,y)={\sum }_{j,a}{x}_{ij}{y}_{ja}{y}_{ia}$.

2. One-mode in-tie ⇒ two-mode agreement ({X_ji and Y_ja ⇒ Y_ia): $s_{ki}^Y(x,y)={\sum }_{j,a}{x}_{ji}{y}_{ja}{y}_{ia}$.

3. Two-mode agreement ⇒ one-mode out-tie ({Y_ia and Y_ja} ⇒ X_ij): $s_{ki}^X(x,y)={\sum }_{j,a}{y}_{ia}{y}_{ja}{x}_{ij}$.

4 Friendship, advice, and employment preference in an MBA class

We now adopt the modeling framework sketched above to obtain a more detailed understanding of the co-structuration of social interaction between job searchers, and their orientation toward specific potential employers. The latter is represented by a two-mode network, in which the first mode is constituted by the students, and the second by the potential employers. The specific setting is a cohort of students in an MBA program, the social interactions are friendship and advice. Thus, we study how the two-mode network of employment preference co-evolves with two one-mode networks of friendship and advice.

4.1 Background

It is well recognized that social networks among labor market participants affect important aspects of the matching between individuals and organizations (Granovetter, 1974). For this reason, the dual association between individuals looking for jobs and (actual or potential) employers is at the heart of sociological models of hiring (Petersen et al., 2000), economic models of job search and matching (Pissarides, 1990), and organizational models of group affiliation (McPherson, 1983), employment choice (Kilduff, 1990), and recruitment-based competition (Sorensen, 2004).

A number of empirical studies have tried to model the two-mode association between individuals and organizations as the outcome of a combination of attributes of the individuals, characteristics of the organizations, and dimensions of the one-mode association between individuals (‘social networks’). According to Montgomery (1992, p. 586), for example, in the analysis of job search, “[n]etwork structure may be the crucial independent variable”. Perhaps less generally appreciated is the fact that the process of job search itself represents a focused activity that increases mutual awareness, and facilitates the development of personal relationships (Feld, 1981, 1982). According to this view, the presence of network ties is not only an antecedent, but also in part an outcome of the dual association between individuals and organizations.

The process of job search as a focused activity capable of generating network ties is clearly illustrated by Kilduff (1990) in a study of MBA students that has provided direct inspiration to our own empirical work. Kilduff examines how friendship networks between MBA students affect their employment choice. He argues that students use other students as sources of information about prospective employers. This suggests that the job search process generates information that students share through friendship networks and then use to form preferences and expectations about potential employers – which later on is likely to affect their organizational affiliation decisions. Building on his findings, we suggest that processes of job search are affected by, and at the same time affect social networks of interactions between labor market participants. Job search is a domain where one-mode social networks and two-mode affiliation networks affect one another. To the best of our knowledge, however, an analytical statistical framework that affords simultaneous examination of how social networks between individuals and affiliation networks (networks between individuals and groups) co-evolve and shape one another was not available until now.

4.2 Research setting and design

As Kilduff (1990) observed in his study of employment choice and social networks among MBA students, the social life of participants in professional management is organized around one basic question: “What kind of job shall I have when I finish my MBA?” We followed a cohort of 75 MBA students enrolled in one of the leading Italian Business Schools throughout their program and in the process of choosing their employers. Our own observation during the 17-month period confirmed that students constantly discuss and exchange information about their employment preferences and job search strategies. In the corridors, where upcoming recruitment schedules were posted, students exchanged opinions, shared job interview experiences, and discussed the pros and cons of the various companies. We observed that students not only discussed their employment preferences openly, but frequently also devised collective strategies to approach target companies.

The data set analyzed is the result of a three-wave network panel design. The overall observation period is the entire duration of the MBA program and the observation points (‘waves’) are roughly equally spaced (March, July, and early November). We relied on the conventional roster method to collect information on social networks. The questionnaire was administered individually and personally to each student (100% response rate). Building on extensive prior research on interpersonal networks in organizations (Lazega, 2001; Kilduff and Krackhardt, 2008) we focused on networks of friendship and advice relations. Each respondent was presented with a complete list of names and asked to report the presence of the specified relation with the other classmates. For friendship we asked respondents to indicate the names of classmates with whom they felt they had developed meaningful social ties outside the specific context of the program. The questionnaire specified examples of social activities typically considered as signals of friendship such as going to the movies, attending sport events, having dinner, playing football, or going shopping. For advice relations we asked respondents to indicate the names of students to whom they recurrently referred for information and advice on course-related matters. The questions were framed in a non-judgmental manner. Respondents were assured that there were no right or wrong answers, privacy would be protected, and they were completely free to select as many or few names as they wished. The same questions were asked at each of the three data collection occasions.

For the information about students’ employment preferences, note that it is common for business schools to actively develop interfaces with relevant segments of the market for professional managers. Business schools maintain lists of companies that regularly send recruiters on campus to interview and select students during job fairs, recruitment campaigns, and other such events. Each student was requested to express his or her preference for potential employers by mentioning a maximum of ten organizations. A total of one hundred different companies were mentioned. The remarks made earlier in this section about the social importance of employment preferences and job search activities imply that shared preferences for employers may indeed be interpreted in this social context as a social focus, i.e., a “social, psychological, legal or physical entity around which joint activities are organized” (Feld, 1981, p. 1016). For this reason we consider it useful to represent the dual relation by students and their expressed employment preferences as an affiliation network.

In addition, we collected information on a variety of individual attributes such as gender, age, academic background, and nationality to control for sources of individual heterogeneity. Additional information on the research design and the sample may be found in Lomi et al. (2011).

4.3 Some descriptives

First we provide descriptive statistics of attributes of Students (Table 1). This is followed by descriptives for each of the three networks considered on its own (Tables 2-3). Finally we describe the association between the networks (Table 4).

Table 1.

Percentages and averages for students (standard deviations in parentheses).

Business administration background	50%
Foreign (non Italian)	13%
Males	62%
Work experience more than 2 years	52%
Average Age	29.1 (3.2)
Performance (range 22–29)	26.0 (1.6)

Table 2.

Descriptives for two-mode employment preference network

	t 1	t 2	t 3
Average outdegree students	4.7	4.1	3.1
Average indegree employers	3.6	3.1	2.3
s.d. indegree employers	4.3	4.1	3.5
s.d. outdegree students	2.8	2.4	2.3

Table 3.

Descriptives for friendship (‘Fr.’) and advice (‘Adv.’) networks: Average degree; standard deviations of in- and outdegrees; reciprocity measured as fraction of ties being reciprocated; clustering measured as fraction of triplets i → j → k for which also the tie i → k exists.

	Fr. t1	Fr. t2	Fr.t3	Adv. t1	Adv. t2	Adv. t3
Av. degree	9.9	9.2	8.3	4.1	4.9	4.5
s.d. in/out	6.2/9.5	5.5/9.3	5.3/6.8	5.6/2.5	5.5/3.1	5.7/3.2
Reciprocity	0.58	0.54	0.57	0.29	0.33	0.33
Clustering	0.44	0.40	0.38	0.24	0.24	0.26

Table 4.

Correlations between outdegrees of the three networks, for the three time points separately.

	t 1		t 2		t 3
	Fr.	Adv.	Fr.	Adv.	Fr.	Adv.
Advice	.10		.33		.35
Empl. pref.	.28	.34	.22	.27	.29	.21

As Table 1 shows, the prevalent academic background of students is economics and business (approximately 50%). Other academic backgrounds include engineering (14%), humanities (13%), political sciences (11%), law (8%) and natural sciences (4%). The proportion of foreign (non-Italian) students is approximately 13%. Female students account for 38%. Students in MBA programs are slightly older than students in other master programs (average age 29), and have typically been exposed to relevant professional experiences (here 52%). Information on average grades obtained during the program is included to control for observable individual differences in performance.

Stability between consecutive observations for the employment preference network can be measured by Jaccard coefficients (Batagelj and Bren, 1995; Snijders et al., 2010) (values are between 0, obtained if all ties change, and indicating all ties stay the same). The values are .27 for the t₁ ⇒ t₂ transition and .33 for t₂ ⇒ t₃. These values may be considered to be of intermediate size. The stability of the one-mode networks is rather high: Jaccard coefficients for network stability vary between 0.47 and 0.55 for friendship and between 0.38 and 0.44 for advice.

From Table 2 it can be seen that the average degree in the two-mode network decreases over time, revealing the job search process to become progressively more focused.

Table 3 shows that average degrees in the friendship and advice networks do not change much over time. The friendship network shows a strong tendency toward reciprocity. The advice network also shows a tendency toward reciprocity, but weaker. Friendship shows a stronger tendency toward transitivity than advice. For friendship, outdegrees are more variable than indegrees, which might reflect differential response tendencies. For advice the indegrees are more variable than the outdegrees; a cause may be the existence of a few attributes that clearly qualify students as potential advisors, such as discipline, performance, and willingness to help, whereas friendship is based on mutual attraction and homophily on relevant characteristics, processes which do not lead to differential indegrees.

For cross-network associations, a description at the tie level is meaningful only for the association between the two one-mode networks; at the actor level, we give correlations between outdegrees as descriptions of the association between activity in the three networks. The tie-level association between the friendship and advice networks can be expressed again by the Jaccard coefficient, which over the three observations assumes the values .18, .25, and .24. Under assumptions of independence between friendship and advice the expected Jaccard coefficients would be .04 (all three observations); the observed values, while not very high, are considerably higher. The correlations between the outdegrees for the three networks, for each observation moment, are given in Table 4. The outdegrees may be regarded as indications of the activity level with respect to the three networks. The correlations are positive but not high. Summarizing, there are positive associations, with moderate values, between the three networks, at the tie level (for friendship and advice) as well as the actor level (outdegrees).

5 Model specification

In this section we first establish the basic goal of our empirical examination, and then discuss the model specification in the form of lists of effects of the kind $s_{ki}^Y(x,y)$ and $s_{ki}^X(x,y)$ included in the evaluation functions (1) and (2). As a general remark, note that one-mode networks are richer in local structure than two-mode networks – the latter being defined by a restriction, viz., the impossibility of ties between the two modes – and therefore more effects are possible for one-mode than for two-mode networks.

5.1 Aims of the analysis

The general aim of the empirical study is to investigate mutual dependencies between how the dynamics of friendship and advice depend on the employment preference network, and how the dynamics of the latter (two-mode) network depend on the two one-mode networks. The main hypothesis concerns the existence of a mutually constitutive relation between these three networks sustained by the triadic effects discussed in Section 2: having employment preferences in common promotes friendship and advice ties; and vice versa, friendship and advice ties promote the sharing of employment preferences. Second, we are interested in cross-network dependencies at the actor level between all three networks, as well as on the dyadic level between friendship and advice.

We control for a variety of within-network dependencies and dependencies on exogenous factors. More specifically, we are also interested in how results for the dynamics of networks when considered on their own (the ‘uniplex’ network analyses) are modified by including the cross-network dependencies; in other words, how the self-organization of a given network may be partly mediated by other networks.

5.2 Uniplex two-mode specification

The data collection for the two-mode network limited the out-degrees to 10. This upper bound was respected in the simulations using the actor-oriented model.

A number of effects for the dynamics of two-mode networks were proposed by Koskinen and Edling (2010), which leads to the following list. These effects are related to the effects for exponential random graph models for cross-sectionally observed two-mode networks, cf. Agneessens and Roose (2008) and Wang, Sharpe, Robins and Pattison (2009). In the first place, there are various effects related to the degrees of the students and of the employers in the two-mode network, reflecting the average degrees and the dispersion of both types of degree. Recall that two-mode ties are represented as being directed from the student to the employer.

1. Outdegree: this expresses the balance between creating and deleting ties.

2. Outdegree activity : the extent to which students who currently nominate many employment preferences continue doing so; when this effect has a positive parameter ${\beta }_k^Y$, it reinforces or exacerbates existing outdegree differentials.

3. Indegree popularity : the extent to which current indegrees contribute to the probability that employers become or remain receivers of ties; a positive indegree popularity effect can be interpreted as a Matthew effect (“the rich get richer”, de Solla Price, 1976), where employers who at the current moment receive many choices are, ‘because’ of this, popular among the students also for new choices. If associated with a positive parameter, this effect reinforces or exacerbates existing indegree differentials. Two other important effects for two-mode networks are the three-path and four-cycle effects, cf. Figure 3.

4. The three-path effect for actor i is measured by the number of three-paths where this actor is in the position with two ties, as pictured in Fig. 3.a. This can be expressed as

   $$\sum _{j,a,b;j\ne i,b\ne a}{y}_{ia}{y}_{ib}{y}_{ja}.$$ (3)

   Instead of this, we use the closely related definition

   $$s_{ki}^Y(x,y)=\sum _{j,a,b}{y}_{ia}{y}_{ib}{y}_{ja}=\sum _a{y}_{ia}{y}_{i+}{y}_{+a},$$ (4)

   because this has the nice interpretation of degree assortativity: it expresses the extent to which students with high out-degrees tend to mention employers with high in-degrees. The difference between these two definitions is a function of the number of two-paths and the total number of ties, and therefore with adequate control for these lower-order configurations, the use of (4) will be equivalent to the use of (3).
5. The four-cycle effect expresses the extent to which students who share one employment preference, will also tend to get, or keep, more employment preferences in common. This effect is discussed in Robins and Alexander (2004) and Koskinen and Edling (2010) and may be regarded as a two-mode version of closure. In line with Agneessens and Roose (2008) this can be interpreted in two different ways: as a consequence of latent attributes of students, determining their being attracted to the same employers; or as a consequence of social influence between students. It is measured by the number of four-cycles in which the focal actor i is involved,

   $$s_{ki}^Y(x,y)=\sum _{j,a,b}{y}_{ia}{y}_{ib}{y}_{ja}{y}_{jb},$$ (5)

   where the term ‘cycle’ is used disregarding the nominal orientation of the ties.

Figure 3.

Three-paths and four-cycles. Circles, left, are actors in 𝒩. Squares, right, are activities in 𝒜.

5.3 Uniplex one-mode specification

For the dynamics of the two one-mode networks, friendship and advice, as far as this follows from endogenous (within-network) dependence and dependence on exogenous covariates, we follow the general experience in the analysis of longitudinal network data summarized in the rules suggested in Snijders et al. (2010), where further motivation and mathematical formulae may be found. For friendship and advice the same model specification will be used to obtain comparability. The following structural effects are included in the objective function.

• Outdegree: see its description above for the two-mode case;

• reciprocity: the extent to which i → j leads to j → i;

• transitive triplets: the tendency for friends of friends to become or remain friends, and similar for advisers, i.e., for i → j → k to lead to i → k;

• three-cycles: the tendency for i → j → k to lead to triadic closure in a cyclical direction, k → i;

• indegree popularity: see its description above for the two-mode case;

• outdegree popularity: the extent to which current outdegrees contribute to the probability that individuals become or remain receivers of ties (which has no analogy for the two-mode network);

• outdegree activity: see its description above for the two-mode case.

For individual covariates, we can specify the ‘ego’ or ‘sender’ effect, expressing that higher values of this variable lead the students to send more ties; the ‘alter’ or ‘receiver’ effect, expressing that higher values of this variable lead the students to receive more ties; the ‘similarity’ effect, expressing that pairs of students with more similar values have a higher tendency to be tied; and, relevant for categorical variables, the ‘same’ effect, expressing that pairs of students with the same value have a higher tendency to be tied. The nature of the academic environment and of the expertise that is the presumed basis of the advice relation leads to academic performance as a main explanatory variable for the advice relation. Ego, alter, as well as similarity effects are relevant here. As we wish to use the same model specification for both one-mode relations, this also is used for the friendship dynamics. As control variables, we use sex (ego, alter, and ‘same’ effects) and having the same nationality.

5.4 Cross-dependencies between one-mode networks

Cross-network dependencies between the two-mode and one-mode networks were discussed in Sections 2 and 3 and are not repeated here. For the co-evolution of the two one-mode networks, friendship and advice, some additional dyadic cross-network dependencies can be specified. The first is the direct tie-level effect, where a tie according to relation W (here denoting the other one-mode network) leads to a tie according to the dependent one-mode network X.

$$•\text{Direct association}:s_{ki}^X(x,w)=\sum _j{w}_{ij}{x}_{ij}.$$ (6)

The second is mixed reciprocity, or generalized exchange: the reciprocation of a W-tie by an X-tie.

$$•\text{Mixed reciprocity}:s_{ki}^X(x,w)=\sum _j{w}_{ji}{x}_{ij}.$$ (7)

Mixed triads are also possible in the co-evolution of two one-mode networks. They were fitted in preliminary models for the co-evolution of friendship and advice but were not significant. They are further not discussed here.

5.5 Parameter estimation

Parameters were estimated by the method of moments, using the procedures and algorithms analogous to those in Snijders, Steglich and Schweinberger (2007), employing the RSiena package (Ripley et al., 2012) of the statistical system R (R Development Core Team, 2011). As mentioned in the first two of these references, parameters can be tested by referring the t-ratio (estimate divided by standard error) to a standard normal distribution. In all cases, good convergence was obtained with all t-ratios for convergence less than 0.1, as advised in the manual.

Some clearly non-significant effects were dropped from the model. Several non-significant effects were retained in the results presented below because they were of primary interest (cross-network effects) or because it was preferred to report the same models for friendship and advice. Dropping further non-significant effects did not lead to important changes in the remaining results.

6 Results

As a background we first briefly present results for the dynamics of each network when studied by itself, i.e., the uniplex dynamics. Then we discuss results for the multiplex dynamics.

6.1 Uniplex results

The results for each network separately express models in which mutual dependencies between the networks are ignored. This serves as a description of the dynamics of the networks when considered on their own, and as a point of reference for the multiplex dynamics. Table 5 reports the parameter estimates for the dynamics of friendship, advice, and employment preference with their associated standard errors.

Table 5.

Results: Separate models for evolution of friendship, advice, and employment preference.

	Friendship		Advice		Empl. pref.
Effect	par.	(s.e.)	par.	(s.e.)	par.	(s.e.)
Out-degree	–1.840**	(0.233)	–2.267**	(0.321)1	–2.595**	(0.118)
Reciprocity	1.604**	(0.097)	1.329**	(0.131)	—
Transitive triplets	0.188**	(0.017)	0.320**	(0.038)	—
Three-cycles	–0.095**	(0.030)	–0.065	(0.061)	—
Four-cycles	—		—		0.090**	(0.019)
Indegree popularity	0.218** (✓)	(0.062)	0.245** (✓)	(0.057)	0.086**	(0.014)
Outdegree popularity	–0.383** (✓)	(0.065)	–0.346* (✓)	(0.143)	—
Outdegree activity	–0.079† (✓)	(0.041)	–0.088 (✓)	(0.062)	0.085**	(0.019)
Outd.-ind. assortativity	—		—		–0.012**	(0.003)
Same nationality	0.240**	(0.080)	0.450**	(0.124)	—
Sex (M) alter	–0.016	(0.070)	–0.043	(0.092)	—
Sex (M) ego	–0.158*	(0.070)	–0.269**	(0.096)	—
Same Sex	0.277**	(0.065)	0.168†	(0.086)	—
Performance alter	–0.015	(0.023)	0.129**	(0.036)	—
Performance ego	–0.076**	(0.024)	–0.107**	(0.034)	—
Performance similarity	0.764**	(0.188)	0.735**	(0.245)	—

The (✓) symbol means that the transformation ϕ(x) = √x is used for transforming the degrees in the role of independent variables, cf. Section 3.

Significance symbols:

^†p < 0.10

^*p < 0.05

^**p < 0.01 (two-sided).

To assist interpretation, note that the parameters are the coefficients β^Y and β^X in (1) and (2). For their interpretation, note that these are multiplied by the effects $s_{ki}^Y(x,y)$ and $s_{ki}^X(x,y)$ to give the probabilities of change in the evaluation functions; cf. equations (1)–(2) and also (10)–(11) in the Appendix. Hence these are non-standardized parameters on a logistic scale. The parameter estimates in Table 5 for the indegree popularity and outdegree activity effects are larger for the one-mode networks than for the two-mode networks because (to obtain a better fit) for the one-mode network dynamics, the degrees in the roles of independent variables are transformed by a square root, leading to decreased variability especially at high values which is compensated by larger parameter values. For comparing effects of covariates it should be kept in mind that nationality and sex are dichotomous while performance has a range from 22 to 29 and standard deviation 1.6; performance similarity is a dyadic transformation of performance defined in such a way (see Snijders et al., 2010) that it is scaled between 0 and 1, the value 1 (maximum similarity) meaning that the two students have the same performance, and 0 meaning that one student has the minimum (22) and the other the maximum (29) value of performance. This is the reason for the smaller numerical values of the parameter estimates (and standard errors) of the alter and ego effects of performance.

The results for friendship and advice are rather similar. The tendencies toward reciprocity and transitivity, as well as the tendency to have few three-cycles for the friendship network, are in line with other results for dynamics of networks with a component of sociability. Indegree popularity is positive, indicating a Matthew effect and a tendency to differentiated indegrees. Outdegree popularity is negative, indicating that those who mention a lot of friends or advisors are less popular when considered by others as potential friends or advisors, respectively. For friendship as well as advice there is a tendency towards homophily especially with respect to performance, and also (but less strongly) for nationality and sex. Males tend to ask less for advice and (less strongly) to mention fewer friends. High performers tend to ask for advice less, and to be asked more; there is no similar tendency for friendship. The main differences between the dynamics of the advice and the friendship networks are that advice is more strongly transitive, and more strongly dependent on performance of senders and receivers; and that homophily with respect to nationality is stronger, and for sex weaker, for advice as compared to friendship.

For the employment preference network, there were no significant effects of actor variables: the students’ sex, nationality, performance, or experience did not have significant effects on the dynamics of the number of preferred employers mentioned. There was a significant effect toward four-cycles: if a pair of students has one employment preference in common, then it is likely that they will get more in common, or keep several common interests if these exist already. There also are significant effects of indegree popularity and outdegree activity: students mentioning many employers will continue doing so, or further augment this tendency; employers attracting much attention from students likewise will continue this or get even more attention. Finally, there is a negative indegree-outdegree assortativity, meaning that students who mention many employers differ especially from those who mention few, by mentioning more of the less popular employers.

6.2 Multiplex results

The results for the co-evolution of friendship, advice, and employment preference are given in Table 6. The table presents asterisk signs representing two-sided p-values. In the interpretations below, one-sided p-values are used in cases where theoretically a positive effect is expected. We first discuss the interpretation of the cross-network effects, working upward from the bottom of Table 6.

Table 6.

Results: Co-evolution of friendship, advice, and employment preference.

	Friendship		Advice		Empl. pref.
Effect	par.	(s.e.)	par.	(s.e.)	par.	(s.e.)
within-network
Out-degree	–2.980**	(0.284)	–4.135**	(0.424)	–2.525**	(0.141)
Reciprocity	1.280**	(0.119)	0.517**	(0.158)	—
Transitive triplets	0.153**	(0.018)	0.243**	(0.038)	—
Three-cycles	–0.06 l†	(0.032)	–0.087	(0.062)	—
Four-cycles	—		—		0.085*	(0.031)
Indegree popularity	0.386** (✓)	(0.064)	0.330** (✓)	(0.053)	0.071**	(0.018)
Outdegree popularity	–0.354** (✓)	(0.073)	0.062 (✓)	(0.152)	—
Outdegree activity	0.023 (✓)	(0.045)	0.013 (✓)	(0.075)	0.074**	(0.021)
Outd.-ind. assortativity	—		—		–0.010**	(0.003)
Same nationality	0.203*	(0.084)	0.327**	(0.125)	—
Sex (M) alter	—0.033	(0.070)	0.038	(0.098)	—
Sex (M) ego	–0.147*	(0.074)	–0.182†	(0.099)	—
Same Sex	0.237**	(0.072)	0.052	(0.094)	—
Performance alter	–0.022	(0.028)	0.151**	(0.040)	—
Performance ego	–0.098**	(0.026)	–0.059	(0.038)	—
Performance similarity	0.789**	(0.189)	0.465†	(0.261)	—
between-network: dyadic
Friendship	_—		1.792**	(0.220)	_—
Reciprocal friendship	—		0.356*	(0.180)	—
Advice	1.672**	(0.227)	—		—
Reciprocal advice	0.730**	(0.193)	—		—
between-network: actor-level
Friendship ind. popularity	—		–0.273** (✓)	(0.064)	—
Friendship outd. activity	—		–0.300** (✓)	(0.055)	0.0101*	(0.0055)
Advice ind. popularity	–0.151** (✓)	(0.048)	—		—
Advice outd. activity	–0.214** (✓)	(0.076)	—		–0.014	(0.021)
Empl. choice outd. activity	0.235* (✓)	(0.101)	0.202 (✓)	(0.124)	—
between-network: mixed triads
Employment pref. agreement	–0.085	(0.066)	0.151†	(0.078)	—
Friendship leading to agreement	—		—		–0.065	(0.074)
Advice leading to agreement	—		—		0.274†	(0.153)

The (✓) symbol means that the transformation ϕ(x) = √x is used for transforming the degrees in the role of independent variables, cf. Section 3.

Significance symbols:

^†p < 0.10

^*p < 0.05

^**p < 0.01 (two-sided)

Of the four hypothesized mixed triadic effects (cf. Section 5.1 and Figure 2), two are significant. Agreement with respect to employment preference leads to advice ties (t = 0.151/0.078 = 1.93, one-sided p = 0.03) and advice ties lead to agreement with respect to employment preference (t = 0.274/0.153 = 1.79, one-sided p = 0.04).

There are some actor-level dependencies between employment preference and friendship. Interest in many employers leads to nominating many friends (t = 0.235/0.101 = 2.32, two-sided p = 0.03) and there is some evidence also for the reverse (t = 0.0101/0.0055 = 1.84, two-sided p = 0.07).

There are rather strong negative actor-level effects between friendship and advice. Being mentioned by many as an advisor leads to being mentioned by few as a friend (t = –0.151/0.048 = –3.15, two-sided p < 0.01) and vice versa (t = –0.273/0.064 = –4.27, two-sided p < 0.001). Mentioning many advisors leads to mentioning few friends (t = –0.214/0.076 = –2.82, two-sided p < 0.01) and vice versa (t = –0.300/0.055 = –5.45, two-sided p < 0.001). This could be interpreted as a kind of specialization: students mention either many friends or many advisors, but not many of both; and students are mentioned either by many as a friend or by many as an advisor, but not both.

The dyad-level effects between the friendship and the advice networks are strong. Direct effects are very strong, with estimated parameter values of 1.672 and 1.792. Reciprocal effects, where j mentioning i as an advisor leads to i mentioning j as a friend, and vice versa, are also strong, but less so than the direct effects. Asking for advice seems to be reciprocated by friendship more strongly (parameter value 0.730) than the other way around (0.356). Summarizing the cross-network effects between friendship and advice, it can be concluded that these networks are positively related at the dyadic level but negatively at the actor level.

The comparison between the uniplex and multiplex (or multivariate) analysis is discussed in the next section.

7 Emergence and Mediation

By considering jointly the evolution of a one-mode and a two-mode network, as represented in Tables 5 and 6, one obtains a richer and potentially deeper insight in the processes driving the changes in both of these networks than by considering the evolution of both networks separately.

The representation of the internal dynamics of the two-mode network of employment preferences, given in the right-hand columns of Tables 5 and 6, is not changed a lot by taking into account the effects of the friendship and advice networks. The effects of friendship and advice on the employment preference network, where high friendship outdegrees lead to high employment preference outdegrees, and where advice ties lead to shared preferences for employers, do not replace or alter the within-network dependencies.

The situation is different for the interdependence of friendship and advice. The parameters for reciprocity in Table 6 are lower than the corresponding parameters in Table 5, especially for advice where the reciprocity parameter drops from 1.3 to 0.5. This suggests that the socially stabilizing effect for advice of reciprocation appears to be not a matter of the advice relation itself, but is for a large part mediated by friendship. Also the homophily effects found for advice turn out to be partially mediated by friendship: one could say that students turn to similar others for friendship who then become advisors, but what in the uniplex analysis seems to be homophily in advice ties is largely a byproduct of the multiplexity of advice with friendship.

This insight obtained from multiplex dynamics has interesting substantive interpretations for the study of advice relations, enriching conclusions from studies of uniplex dynamics of advice such as Lazega, Mounier, Snijders and Tubaro (2010). Asking for advice potentially leads to loss of status (Blau, 1955); to facilitate advice relations, therefore, compensatory strategies often are used. Direct reciprocity (exchanging advice for advice) is one such strategy, generalized reciprocity (exchanging advice for something else, but not for status) is another (Lazega and Pattison, 1999), and also homophily can contribute to mitigating the risk of status differentials associated with an advice tie. Here we see that what in the uniplex analysis of Table 5 seems to be direct reciprocity (parameter value 1.329), turns out to be better explained (in the multiplex analysis of Table 6) as embeddedness of the advice tie in a multiplex tie including friendship (direct effect: parameter value 1.792), preferably reciprocal (parameter value 0.356), with a residual component of ‘pure’ direct reciprocity (value 0.517). This result is in line with, but it also goes beyond, the cross-sectional results produced by Lazega and Pattison (1999). Similarly, what in the uniplex analysis seems to be a homophily strategy for diminishing risks of status loss due to advice can be interpreted in part as a consequence of multiplexity of advice with friendship.

8 Conclusions

Social settings both generate, and are influenced by social networks (Feld, 1981; Pattison and Robins, 2002). Yet, no model has been available so far to assist in representing and analyzing how such duality unfolds over time. In this paper we filled this gap. We have presented a statistical model for the co-evolution of a two-mode and a one-mode network, in line with actor-oriented models for the evolution of uniplex two-mode (Koskinen and Edling, 2010) and one-mode (Snijders, 2001) networks and with models for the co-evolution of networks and behavior (Steglich et al., 2010). These models can be used to study the co-evolution of interactions between actors and their social settings. Studying the interdependent dynamics for several networks, one-mode and/or two-mode, can yield deeper insights than studying dynamics of single networks. The model elaborated here assumes that all agency resides in the actors who are the first mode of the two-mode network (constituting also the node set of the one-mode network). The activities or events constituting the second mode are assumed to be merely recipients of choices. In some situations this is a reasonable assumption, or a reasonable approximation, but in others (cf. Logan, 1998) it makes more sense to assume that both modes have agency, and some coordination, matching, or negotiation process takes place for ties to be created. New models will be needed for such an approach.

The model was applied to studying the interdependent dynamics of (two-mode) labor market preferences and (one-mode) friendship and advice relations in a cohort of MBA students. Preferences with respect to potential employers were regarded as social settings in which job seekers “meet”, and establish or change their social connections. We found evidence for mixed triadic effects between the two-mode network and the advice network: being an advisor leads to agreement on labor market preferences, and those agreeing about labor market preferences tend to become advisors. In addition, we found actor-level effects linking the two-mode network and the friendship network: a high number of employment preferences leads to higher numbers of friendship nominations and vice versa. This confirms our initial idea that the employment preferences may be regarded as social foci, and are meaningfully linked to the friendship and advice networks. However, the types of links are different: for advice the link is with agreement about employment preferences, i.e., content; for friendship the link is with the amount of activity, i.e., expression.

In addition, we found strong interdependence between the friendship and advice networks, the dependence being positive at the dyadic level, interpretable as multiplexity; and negative at the actor level, interpretable as specialization.

In two-mode and one-mode networks alike, various network structures may come about through similarity on unobserved variables; this is discussed in the two-mode context in Agneessens and Roose (2008). In our analysis, the variables available did not contribute to explaining the two-mode network dynamics. It will be interesting in future studies to collect variables on both of the modes that are predictive of the matching process that is fundamental for the creation of two-mode links.

Since the two-mode network can be regarded as an array of changing binary attributes of the actors, there is a similarity between the co-evolution of a one-mode and a two-mode network as studied here, and the co-evolution of (one-mode) networks and behavior as studied in Steglich et al. (2010). The two-mode network represents multiple binary attributes; the behavior as studied in the mentioned paper corresponds to one, or a few, binary or ordinal discrete attributes. The main mathematical difference is that, when the attributes are regarded jointly as a two-mode network, the nodes in the second mode 𝒜 are regarded as being exchangeable – or conditionally exchangeable given their attributes, if these are available for the second mode. This goes along with a difference in the usual number of attributes (many for the two-mode network approach, few for the behavior approach) which leads to a difference in focus of attention (a collective of various kinds of activities or attributes, versus one or a few specific behaviors). However, the basic mathematical models are quite similar.

Research questions about the interdependent selection of network partners and social influence exerted by network partners on each other's behavior can be combined in a natural way with research about the co-evolution of one-mode and two-mode networks. As an example, consider a co-evolving one-mode network of friendship, two-mode network of activities, and behavior variable representing lifestyle, with a research question concerning peer influence on lifestyle. Then an important question is: what is the relevant peer group that may influence the lifestyle of any given actor? It could be the personal network of the actor; but it could also be the group of those participating in the same activities as the focal actor, or a larger group such as the neighborhood where the actor lives. If the activities are self-selected, just like the friendship network, then the first two are associated and a large amount of data will be necessary to differentiate between them. Given relevant data, a combination of the models proposed in this paper and those in Steglich et al. (2010) could be used in principle to answer this type of research question.

Highlights.

• A stochastic actor-oriented model is presented for the co-evolution of one-mode and two-mode networks.

• The dynamics is studied of friendship, advice, and employment preferences in an MBA cohort.

• There is a positive triadic dependency between advice ties and agreement in employment preferences.

• Advice and friendship are positively associated at the dyad level and negatively at the actor level.

• Reciprocation and homophily in advice are largely mediated by friendship relations.

Appendix

The model for representing the multiplex dynamics of one- and two-mode networks may be summarized as follows. The model is a continuous-time Markov chain, and the state (Y, X) consists of the two-mode network Y and the one-mode network X. At any given moment, the time elapsing until the next opportunity for change in either network – which is called a ministep – has an exponential distribution. This is a property of Markov processes (Norris, 1997). The timing component of the model determines its duration as well as who will be the actor i who will make this step and whether this step will be for the one-mode or the two-mode network. Given that actor i can make a ministep in a given network, the choice as to which outgoing tie variable of this actor will be changed, or whether nothing will be changed at all, is determined by the choice component of the model. This is further specified in detail below.

1. Timing component

The rate functions ${\lambda }_i^Y(x,y)$ and ${\lambda }_i^X(x,y)$, respectively, represent, given current states x and y of the two networks, the expected number of occasions per unit of time for actor i to have the opportunity for making a change in one of the outgoing ties Y_ia(t) or, respectively, one of the ties X_ij(t). Using properties of Markov processes and the exponential distribution (Norris, 1997), this can be summarized as follows.

Consider any time moment t with current state (x, y). The waiting time until the next opportunity for change by any actor in either of the two networks is exponentially distributed with expected value

$$\frac{1}{{\lambda }_{+}^Y(x,y)+{\lambda }_{+}^X(x,y)},$$ (8)

where

$${\lambda }_{+}^Y(x,y)=\sum _{i\in \mathcal{N}}{\lambda }_i^Y(x,y),{\lambda }_{+}^X(x,y)=\sum _{i\in \mathcal{N}}{\lambda }_i^X(x,y).$$

Given an opportunity for change, the probabilities that this is an opportunity for actor i to make a change either in the two-mode network or in the one-mode network, respectively, are given by

$$\frac{{\lambda }_i^Y(x,y)}{{\lambda }_{+}^X(x,y)+{\lambda }_{+}^Y(x,y)}\text{and}\frac{{\lambda }_i^X(x,y)}{{\lambda }_{+}^X(x,y)+{\lambda }_{+}^Y(x,y)}.$$ (9)

2. Tie choice component

The evaluation function $f_i^Y(x,y)$ represents the relative propensity for actor i to make a change toward state y of the two-mode network given that the one-mode network has state x; similarly, $f_i^X(x,y)$ represents the relative propensity for actor i to make a change toward state x of the one-mode network, given that the two-mode network has state y. These propensities are measured on the scale of log-probabilities, and their values may be compared only between changes that are permitted from a given current state. As we mentioned above, permitted changes are all the changes of one particular single tie variable in the given network by the given actor.

Some additional notation is needed to express the probability distributions. Since tie variables Y_ia and X_ij are dichotomous, a change of a tie variable – creation or termination of a tie – can be regarded as a toggle of the tie variable: a change of Y_ia or X_ij into 1 – Y_ia or 1 – X_ij, respectively. For a given network y, we denote by y^(±ia) the network in which tie variable Y_ia is toggled into 1 – Y_ia, while all other tie variables remain the same:

$$\begin{array}{cc}\hfill y_{jb}^{(\pm ia)}& =y_{jb}^{(\pm ia)}\text{for all}(j,b)\ne (i,a);\hfill \\ \hfill y_{ia}^{(\pm ia)}& =1-y_{ia}^{(\pm ia)},\hfill \end{array}$$

and similarly for x^(±ij).

When actor i has the opportunity to change a two-mode tie, and the current state of the system is (x, y), the two-mode networks that can be obtained are y^(±ia) for any $a\in \mathcal{A}$, together with the current y. For the potentially resulting networks, the evaluation function assumes the values $f_i^Y(x,y^{(\pm ia)})$. The conditional probability of changing the affiliation tie to a is

$$\mathrm{P}\left\{Y\left(t\right)\text{changes to}{y}^{\left(ia\right)}\mid X\left(t\right)=x,Y\left(t\right)=y\right\}=\frac{\text{exp}\left(f_i^Y\left(x,y^{(\pm ia)}\right)\right)}{f_i^Y(x,y)+\sum _{b\in \mathcal{A}}\text{exp}\left(f_i^Y\left(x,y^{(\pm ib)}\right)\right)}.$$ (10)

It is assumed that one of the options for actor i is not to change anything (where an interpretation is that i is satisfied with the network as it is), which is represented by the term $f_i^Y(x,y)$, the evaluation function for the current network, in the denominator of (10).

Similarly, when actor i has the opportunity to change a one-mode tie, the one-mode networks that can be obtained as a result of this change are all x^(±ij) for j ≠ i as well as the current x. The evaluation function has for the resulting changed networks the values $f_i^X(x^{(\pm ij)},y)$. By 𝒩 (i) we denote the set of all actors except i, i.e., $\mathcal{N}\left(i\right)=\{j\in \mathcal{N}\mid j\ne i\}$. The probability of making a particular change at such an opportunity of change is defined as

$$\mathrm{P}\left\{X\left(t\right)\text{changes to}{x}^{\left(ij\right)}\mid X\left(t\right)=x,Y\left(t\right)=y\right\}=\frac{\text{exp}\left(f_i^X\left(x^{(\pm ij)},y\right)\right)}{\text{exp}\left(f_i^X\left(x,y\right)\right)+\sum _{h\in \mathcal{N}\left(i\right)}\text{exp}\left(f_i^X\left(x^{(\pm ih)},y\right)\right)}.$$ (11)

The model is specified further by defining the rate functions and evaluation functions. With respect to rate functions, attention here is restricted to rate functions that are constant between measurement moments. Extensions to rate functions depending on attributes or positional characteristics of the actors are possible as in Snijders (2001). We discussed the specification of evaluation functions in Sections 3 and 5.