How muscle fiber lengths and velocities affect muscle force generation as humans walk and run at different speeds

SUMMARY

The lengths and velocities of muscle fibers have a dramatic effect on muscle force generation. It is unknown, however, whether the lengths and velocities of lower limb muscle fibers substantially affect the ability of muscles to generate force during walking and running. We examined this issue by developing simulations of muscle–tendon dynamics to calculate the lengths and velocities of muscle fibers from electromyographic recordings of 11 lower limb muscles and kinematic measurements of the hip, knee and ankle made as five subjects walked at speeds of 1.0–1.75 m s⁻¹ and ran at speeds of 2.0–5.0 m s⁻¹. We analyzed the simulated fiber lengths, fiber velocities and forces to evaluate the influence of force–length and force–velocity properties on force generation at different walking and running speeds. The simulations revealed that force generation ability (i.e. the force generated per unit of activation) of eight of the 11 muscles was significantly affected by walking or running speed. Soleus force generation ability decreased with increasing walking speed, but the transition from walking to running increased the force generation ability by reducing fiber velocities. Our results demonstrate the influence of soleus muscle architecture on the walk-to-run transition and the effects of muscle–tendon compliance on the plantarflexors' ability to generate ankle moment and power. The study presents data that permit lower limb muscles to be studied in unprecedented detail by relating muscle fiber dynamics and force generation to the mechanical demands of walking and running.

INTRODUCTION

The dependence of muscle force on the length and velocity of muscle fibers has long been established (Bahler et al., 1968; Gordon et al., 1966; Hill, 1953). Many studies have shown that the length and velocity of muscle fibers can have a large effect on muscle force generation in various experimental assays, yet it is not fully understood how much the force–length and force–velocity properties of lower limb muscles affect force generation during human locomotion. Understanding how the muscle forces generated during locomotion are affected by the force–length and force–velocity properties requires estimation of the length of muscle fibers relative to their optimal length (i.e. normalized fiber length) and the velocity of muscle fibers relative to their maximum shortening velocity (i.e. normalized fiber velocity) during gait.

The normalized lengths and velocities of muscle fibers are difficult to measure during walking and running. Absolute lengths and velocities of the muscle fascicles have been studied using ultrasound during walking and running (Farris and Sawicki, 2012; Fukunaga et al., 2001; Lichtwark et al., 2007) and while joints are moved through a range of motion (Chleboun et al., 2001; Ichinose et al., 2000; Kawakami et al., 1998; Maganaris, 2001). These studies provide valuable measurements of the absolute lengths and velocities of a few muscles, including gastrocnemius, soleus, biceps femoris and vastus lateralis. However, ultrasound imaging alone does not determine normalized muscle fiber lengths or velocities. Normalized fiber lengths can be determined from measurements of sarcomere lengths. Sarcomere lengths have been measured in the upper extremity by using laser diffraction during surgery (Lieber and Fridén, 1998). Measurement of sarcomere lengths with microendoscopy is less invasive than laser diffraction (Llewellyn et al., 2008), but this technique has not yet been adapted for use during human locomotion. Thus, there is a not a comprehensive view of the normalized fiber lengths and velocities for lower limb muscles during walking and running at multiple speeds.

Increasing walking speed has been linked to increasing fiber shortening velocity in musculoskeletal simulations of soleus and gastrocnemius (Neptune and Sasaki, 2005), and ultrasound measurements of gastrocnemius medialis (Farris and Sawicki, 2012). In Neptune and Sasaki's simulations, muscle activation and force increased with walking speed in all muscles except soleus and gastrocnemius; in these muscles, activation increased but force decreased once subjects walked faster than 80% of their preferred walk–run transition speed. The authors attributed this decrease in force to decreasing fiber lengths and increasing fiber shortening velocity at higher walking speeds (Neptune and Sasaki, 2005). In Farris and Sawicki's experiments, estimated peak gastrocnemius medialis force decreased as subjects walked faster, coinciding with an increase in fiber shortening velocity. When the subjects switched to a running gait, peak gastrocnemius medialis force increased and shortening velocity decreased (Farris and Sawicki, 2012). It is unknown whether the plantarflexors are the only muscles in which fiber lengths and velocities play such an important role in modulating force generation ability with gait speed or if the same phenomenon occurs in other major muscles of the lower limb. Estimates of normalized fiber lengths, velocities, activations and forces over a range of walking and running speeds in multiple lower limb muscles are necessary to understand how muscle fiber lengths and velocities affect muscle force generation.

The goal of this work was to answer two questions. (1) Does walking or running speed affect the ability of lower limb muscles to generate force (i.e. the force generated per unit activation)? (2) Does the transition from fast walking to slow running affect force generation by changing fiber lengths or fiber velocities?

MATERIALS AND METHODS

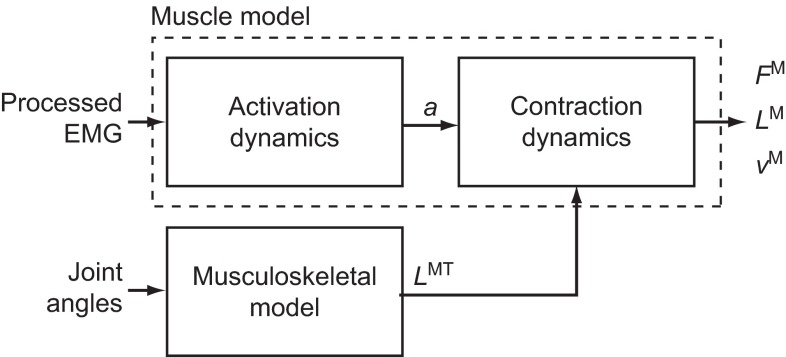
We developed simulations of muscle–tendon dynamics that calculate the normalized muscle fiber lengths, normalized muscle fiber velocities and forces generated by 11 lower limb muscles from electromyography (EMG) and joint kinematics (Fig. 1). We used a computer model of the musculoskeletal system that represents the geometry of the bones, the kinematics of joints, and the lines of action and force-generating properties of lower limb muscles. We measured surface EMG in 11 muscles and joint angles at the hip, knee and ankle as subjects walked and ran at different speeds on a treadmill. We used these data to create simulations of muscle–tendon dynamics. We analyzed these simulations to determine how muscle force generation ability changed with walking speed, running speed and the transition between fast walking and slow running. Details of the musculoskeletal model, the experimental setup and the simulation methodology are provided below.

Fig. 1.

Simulation of muscle fiber length and velocity from inputs of processed electromyography (EMG) and joint angles. Processed EMG was used as muscle excitation and a first-order model of activation dynamics determined activation (a) for each muscle. Joint angles from motion capture and a musculoskeletal model determined muscle–tendon length (L^MT). Activation and muscle–tendon length were used with an equilibrium model of muscle–tendon contraction dynamics to produce a forward simulation of muscle force (F^M), fiber length (L^M) and fiber velocity (v^M).

Musculoskeletal model

The musculoskeletal model of the lower limb (Fig. 2A) created previously (Arnold et al., 2010) was adapted for this study. The model includes the geometry of the bones of the lower limb and pelvis that were created by digitizing the bones of a 170 cm tall male subject (Arnold et al., 2000; Delp et al., 1990). The model includes six degrees of freedom for the pelvis to move through space and five degrees of freedom for the ankle, knee and hip joints to define motions of each body segment. The ankle is a revolute joint between the tibia and talus, defined by one degree of freedom (dorsiflexion/plantarflexion) (Inman, 1976). The knee has a single degree of freedom (flexion/extension) and uses the equations reported previously (Walker et al., 1988; Delp, 1990) to define the translations and rotations between the femur, tibia and patella as functions of knee flexion angle. The hip is a ball and socket joint with three degrees of freedom (flexion/extension, adduction/abduction and internal/external rotation).

Fig. 2.

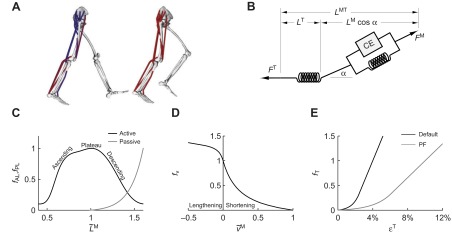
(A) A musculoskeletal model describing the geometry and force generation properties of 11 lower limb muscles used. (B) A Hill-type equilibrium model of muscle–tendon contraction dynamics. Muscle was represented as a passive elastic element in parallel with an active contractile element (CE). Tendon was represented as a non-linear elastic element in series with the muscle. The muscle–tendon length (L^MT) derived from the path geometry and joint angles was used to compute muscle fiber length (L^M), fiber shortening velocity (v^M), tendon length (L^T), pennation angle (α), muscle force (F^M) and tendon force (F^T). (C) The force–length curves modeled the effects, active/passive force–length multipliers f_AL and f_PL, of normalized fiber length, 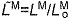, on the active and passive force generated by muscle fibers. The active force–length curve included ascending, plateau and descending regions. (D) The force–velocity curve modeled the effect, force–velocity multiplier f_v, of normalized fiber velocity, 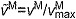, on the active force generated by muscle fibers. The force–velocity curve included shortening () and lengthening (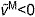) regions. (E) The tendon force–strain curve modeled the proportion of maximum isometric force, tendon force–strain multiplier f_T, in the tendon as a function of the strain in the tendon [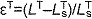]. The force in the tendon would equal maximum isometric force (i.e. f_T=1) at a tendon strain of 10% in the plantarflexors (PF) or 4% in all other muscles.

The model includes 35 muscles of the lower limb, of which 11 were analyzed in this study: gastrocnemius lateralis, gastrocnemius medialis, soleus, tibialis anterior, gluteus maximus, gluteus medius, vastus lateralis, vastus medialis, biceps femoris long head, semitendinosus and rectus femoris. We included only the muscles for which we measured surface EMG. Line segments approximate the muscle–tendon path from origin to insertion. In the case of muscles with broad attachments (e.g. gluteus medius), multiple muscle paths are used. Muscle–tendon paths that wrap over bones, deeper muscles or retinacula include these anatomical constraints as wrapping surfaces or via points. This model of musculoskeletal geometry enables calculations of muscle–tendon lengths (i.e. origin to insertion path length) and moment arm of each muscle. We altered our previous model (Arnold et al., 2010) to accommodate the joint angles reached during running by increasing the knee range of motion from 0–100 deg to 0–130 deg. We verified that muscle moment arms crossing the knee maintained agreement with those reported elsewhere (Buford et al., 1997) in the extended range. Two muscles, biceps femoris long head and gastrocnemius lateralis, required alterations to wrapping geometry to produce accurate moment arms in the increased range of motion.

Each muscle was modeled as a single fiber with a Hill-type contractile element in series with a compliant tendon (Fig. 2B). The length of the muscle fiber and its tendon and the pennation angle between them describe the muscle's architecture. The parameters used to model the architecture and the maximum isometric force of each muscle were taken from measurements of muscle architecture in 21 cadavers (Ward et al., 2009). Optimal fiber length (L^M_o) and pennation angle at optimal fiber length (α_o) are taken directly from the reported values with the assumption that fibers connected serially within the fascicle create a functional unit so that fiber and fascicle length are equivalent (Trotter et al., 1995). Tendon slack length (L^T_s) was set knowing that Ward and colleagues measured fiber lengths and sarcomere lengths at a specific joint configuration. The tendon slack length of each muscle–tendon unit was then set by placing the model in this same joint configuration and ensuring that the fiber length and sarcomere length equaled the experimental measurements (Arnold et al., 2010). We set maximum fiber contraction velocity (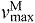) to 15 optimal fiber lengths per second (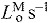) in all muscles, a value consistent with a previous simulation study of running (Thelen et al., 2005). Maximum isometric force of each muscle in the model (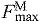) was calculated from physiological cross-sectional area and a specific tension of 61 N cm⁻². We increased maximum isometric force by a factor of two for all muscles, so that the model could generate joint moments of the same magnitude our subjects produced during running. In this model, increasing maximum isometric force of a muscle does not affect fiber lengths and velocities because tendon stiffness is normalized to maximum isometric force. The magnitudes of the force, moment and power that each muscle produces increase, but the relative lengths of the muscle fiber and tendon are unaffected.

The muscle architecture parameters define a muscle–tendon model for each muscle by scaling four normalized curves that relate muscle kinematics to force (Fig. 2C–E) (Zajac, 1989). These normalized force curves specify force-scaling multipliers to calculate muscle fiber force (F^M) and tendon force (F^T) as functions of normalized fiber length (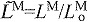), normalized fiber shortening velocity ( 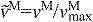where ), and tendon strain [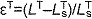]. The active force–length curve, passive force–length curve (Fig. 2C), and force–velocity curve (Fig. 2D) specify the active force–length (f_AL), passive force–length (f_PL) and force–velocity (f_ν) multipliers, which, along with activation, determine the muscle force:

(1)

where a is activation on a scale from 0.05 to 1. A non-zero lower bound for activation is used to prevent a singularity in computation. Activation dynamics are described by a first-order differential equation relating a muscle excitation to muscle activation rate (Thelen et al., 2003). Tendon force is normalized relative to maximum isometric muscle force. The force–strain curve (Fig. 2E) specifies the force–strain multiplier (f_T) that determines the tendon force:

(2)

Two of the force generation curves – active force–length f_AL and force–velocity f_ν – were described using natural cubic splines (Zajac, 1989). The two remaining force generation curves – passive force–length f_PL and tendon strain f_T – were described using exponential functions (Thelen, 2003).

Experimental data

We collected motion data for five subjects walking and running on a force-plate instrumented treadmill (Bertec Corporation, Columbus, OH, USA). The subjects were all experienced long distance runners who reported running at least 30 miles per week (mean ± s.d.: age 29.2±6.3 years; height 1.80±0.03 m; and mass 72.4±5.7 kg). The subjects walked at 1.00, 1.25, 1.50 and 1.75 m s⁻¹ and ran at 2.0, 3.0, 4.0 and 5.0 m s⁻¹. The positions of 30 lower limb markers were measured using an eight-camera motion capture system (Vicon, Oxford Metrics Group, Oxford, UK). Marker positions and ground reaction forces were low-pass filtered at 15 Hz with fourth order, zero-phase, Butterworth and critically damped filters, respectively (Robertson and Dowling, 2003). Heel strike and toe off were identified from the vertical ground reaction force of the right foot using Matlab (MathWorks, Natick, MA, USA). Subjects were informed on all aspects of the study and provided prior consent according to the policies of our Institutional Review Board.

Surface EMG data (Delsys Inc., Boston, MA, USA) were collected for the 11 muscles listed above. Muscles were identified by palpation and electrodes were applied to the muscle belly. The application of the electrodes was verified by having the subject perform a series of tests emphasizing activation of each muscle group and observing the EMG signal. The EMG data were processed in Matlab to approximate muscle excitation on a scale of 0.05 to 1 (Fig. 3). The raw signal was high-pass filtered at 30 Hz using a zero-phase, fourth order Butterworth filter and rectified (Buchanan et al., 2004). The rectified signal was then low-pass filtered at 10 Hz (Kamen and Gabriel, 2009). For each subject, we used the highest value in the smoothed data for each muscle across the full time range of all the trials (typically in the fastest speed, but not necessarily in a gait cycle that was part of the final analysis) to normalize the data to range from 0.05 to 1.00. A lower bound of excitation greater than zero was required to use the equilibrium model presented in Eqns 1 and 2 because this model has a singularity when activation goes to zero. Although it is possible to have a lower bound on activation (0.01 instead of 0.05), this change increases required simulation time and does not benefit this study because we focused on the portion of the gait cycle when muscle activation and forces were highest. We applied a 40 ms delay to the processed EMG to account for electromechanical delay between surface EMG and force production. This matched the value employed by other EMG-driven simulation studies (Buchanan et al., 2005; Lloyd and Besier, 2003), fell within the range reported in the literature (10–100 ms) (Corcos et al., 1992; Guimaraes et al., 1995), and yielded temporal synchronization between the simulated ankle moments and ankle moments calculated from inverse dynamics for the same subject.

Fig. 3.

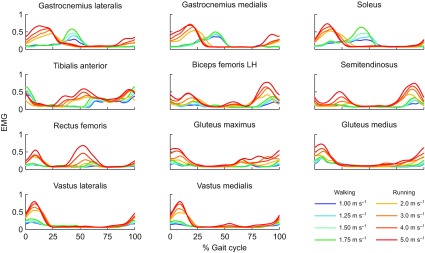
Average experimentally measured and processed EMG for 11 muscles for subjects walking at four speeds and running at four speeds (N=5). We collected surface EMG for 11 lower limb muscles: gastrocnemius lateralis, gastrocnemius medialis, soleus, tibialis anterior, biceps femoris long head (LH), semitendinosus, rectus femoris, gluteus maximus, gluteus medius, vastus lateralis and vastus medialis. The raw signal was high-pass filtered at 30 Hz, rectified, and low-pass filtered at 10 Hz. Each subject's filtered EMG measurements were normalized to the maximum value detected for each muscle across all speeds.

Simulation of muscle–tendon dynamics during walking and running

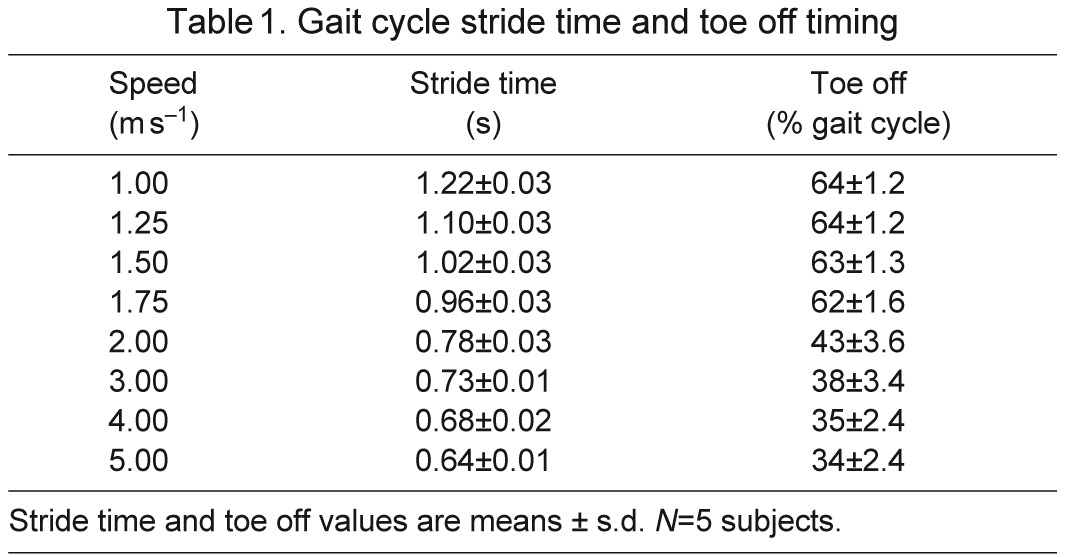
We used a musculoskeletal model scaled to each subject's anthropometry to calculate joint angles during walking and running. The muscle architecture parameters were scaled so that the ratio of optimal fiber length and tendon slack length to total muscle–tendon length was the same as in the generic model. An inverse kinematics algorithm determined the generalized coordinates of the model that best tracked the subject's measured marker data (Fig. 4). Stride-to-stride variation of joint angles at the hip, knee and ankle for each subject was low (see supplementary material Figs S1–S3). Ground reaction forces, joint kinematics, stride time and toe-off time (Table 1) agreed with previous studies (Schache et al., 2011; Schwartz et al., 2008).

Fig. 4.

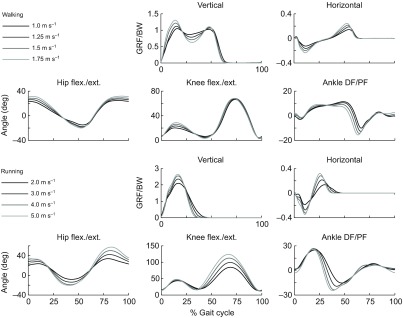
Average experimentally measured ground reaction forces and joint kinematics for subjects walking at four speeds (top) and running at four speeds (bottom) (N=5). Vertical and horizontal ground reaction forces per body weight (GRF/BW) were used to identify three consecutive joint cycles from heel strike to heel strike. Joint angles (in degrees) for the hip (flexion/extension), knee (flexion/extension) and ankle (dorsiflexion/plantarflexion), were calculated from marker data using an inverse kinematics algorithm and a musculoskeletal model scaled to each subject. These joint kinematics were prescribed during the forward simulations.

Table 1.

Gait cycle stride time and toe off timing

The subjects' joint angles and muscle excitations from EMG drove the forward dynamic simulation of activation and muscle–tendon contraction dynamics using a two-state (activation and fiber length) equilibrium muscle model in OpenSim 2.4 (Seth et al., 2011). The time derivatives of fiber length and activation were integrated forward in time using a Runge-Kutta-Merson integrator with a maximum step size of 0.01 s and a numerical accuracy of 10⁻⁸ (Sherman et al., 2011). This process was implemented and automated using OpenSim's programming interface. The library of these simulations will be made publicly available at simtk.org.

Testing the simulations

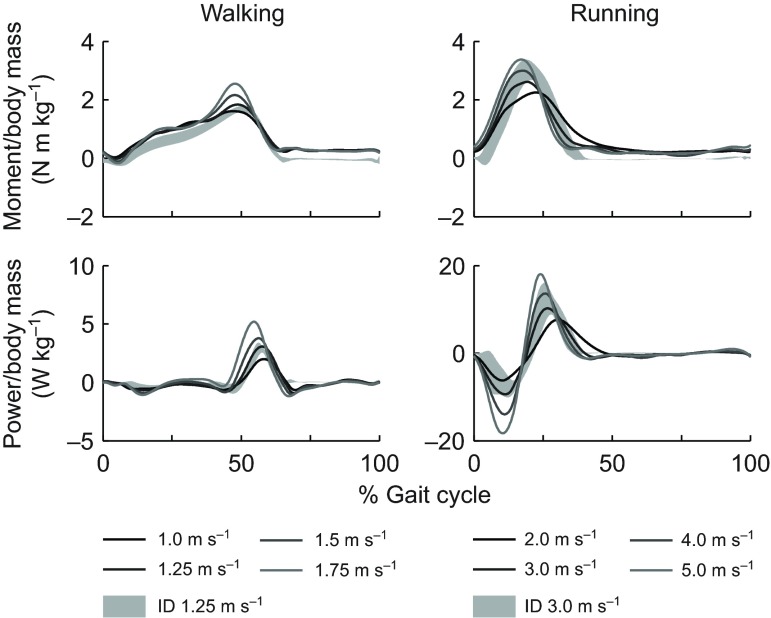
We compared the sum of ankle moments and powers produced by muscles crossing the ankle with net ankle moment and power calculated with inverse dynamics. Our simulations included only a subset of lower limb muscles, and thus should not be expected to generate joint moments and powers that match experimental moments and powers from inverse dynamics at the hip and knee. At the ankle, however, the sum of soleus, gastrocnemius medialis and lateralis, and tibialis anterior produce 90% of the plantarflexion moment and over 50% of the dorsiflexion moment in the fully actuated model (Arnold et al., 2010) and should generate realistic joint moments and powers. In both walking and running, the peak plantarflexion moments observed in the simulation and inverse dynamics were within 5% of the gait cycle of each other (Fig. 5, upper row; supplementary material Fig. S4). Joint powers from the simulation were within 1 s.d. of the inverse dynamics results (Fig. 5, lower row; supplementary material Fig. S5).

Fig. 5.

Average simulated ankle joint moments and powers generated by muscles crossing the ankle in walking and running trials (N=5). Ankle joint moments generated by gastrocnemius lateralis, gastrocnemius medialis, soleus and tibialis anterior during each simulation were summed. The summed moment was multiplied by the ankle angular velocity to calculate ankle joint power. Simulated ankle moment and power were compared with values calculated using inverse dynamics (ID). Shaded regions indicate ±1 s.d. of ID results for the five subjects at 1.25 and 3.0 m s⁻¹. See supplementary material Figs S4 and S5 for all speed comparisons.

A comparison of ankle moment and power between the simulation and inverse dynamics results indicated the need for higher Achilles' tendon compliance than used in previous simulation studies (Hamner et al., 2010; Liu et al., 2006; Thelen et al., 2003). We tested values of tendon strain at maximum isometric force from 3.3 to 12% and found that ankle moment and power were in best agreement with inverse dynamics results when this parameter was 10% for soleus, gastrocnemius lateralis and gastrocnemius medialis. This yielded tendon strains during the simulations of up to 8% in soleus and gastrocnemius lateralis and 7% in gastrocnemius medialis. Experimental results from ultrasound studies have reported tendon strains of 5–9% for gastrocnemius medialis (Kawakami et al., 2002; Kubo et al., 2000; Lichtwark and Wilson, 2007; Muramatsu et al., 2001; Muraoka et al., 2002), suggesting that an increase in tendon compliance is warranted for these muscles.

Assessing muscle force generation ability

We calculated normalized fiber length (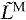), normalized fiber velocity (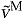), active force along the tendon (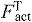), and activation (a) from simulations of each subject at each speed averaged over three consecutive gait cycles. We assessed the force generation ability of a muscle as the active force produced along the tendon divided by the concurrent activation and the maximum isometric force that muscle could produce:

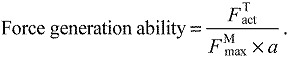(3)

The equilibrium equation that defined the muscle–tendon model was:

(4)

The active contribution from the contractile element was:

(5)

Thus, force generation ability combined the effects of fiber length, velocity and pennation angle on a muscle's ability to generate active force in the direction of the tendon:

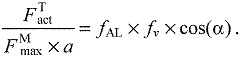(6)

We calculated this value at the instant of peak active force along the tendon for each muscle, speed and subject. If this value differed between two gait speeds, then the speed with the lower value would demand more activation to generate the same amount of force.

To determine whether gait speed had an effect on force generation ability, we performed a one-way (four speeds) repeated measures (five subjects) ANOVA for each muscle in walking and running. We broke down the effects of fiber length and velocity on force generation by examining the active force–length and force–velocity multipliers, f_AL and f_ν, at the instant of peak active force along the tendon. We determined whether there was a difference across the walk-to-run transition by comparing these values for walking at 1.75 m s⁻¹ with those for running at 2.0 m s⁻¹. We applied the Jarque–Bera test to screen for normality. If the sample of a multiplier was not normal in both speeds, we used the Wilcoxon signed-rank test to compare multipliers for that muscle; otherwise, we used a paired Student's t-test. A significant difference was detected at P<0.05 for all tests.

All but five muscles had normally distributed samples of f_ν (the effect of fiber velocity on muscle force) and f_AL (the effect of fiber length on muscle force) in both slow running and fast walking. These samples were compared using the paired Student's t-test. Two muscles had one non-normal sample of f_ν (gastrocnemius lateralis and rectus femoris) and three had one non-normal sample of f_AL (biceps femoris long head, gastrocnemius medialis and semitendinosus). P-values for these samples reflect the Wilcoxon signed-rank test.

RESULTS

Force generation ability changes with gait speed in multiple muscles

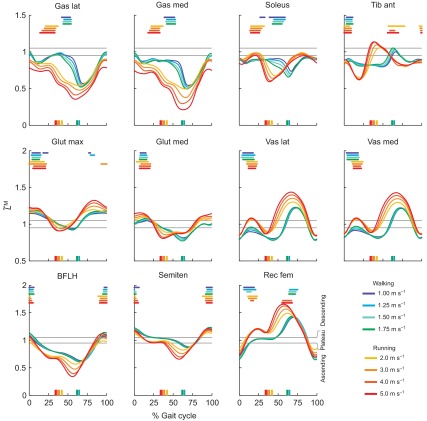
Gait speed had a significant effect on force generation ability in five muscles during walking and three muscles during running (Fig. 6). During walking, force generation ability decreased with increasing gait speed in gastrocnemius lateralis, gastrocnemius medialis and soleus, revealing that as speed increases, more activation was needed to generate the same force. In the vasti, the opposite was true, indicating that with increasing walking speed less activation was needed to generate the same force. During running, the force generation ability of gluteus maximus, gluteus medius and semitendinosus decreased with increasing speed.

Fig. 6.

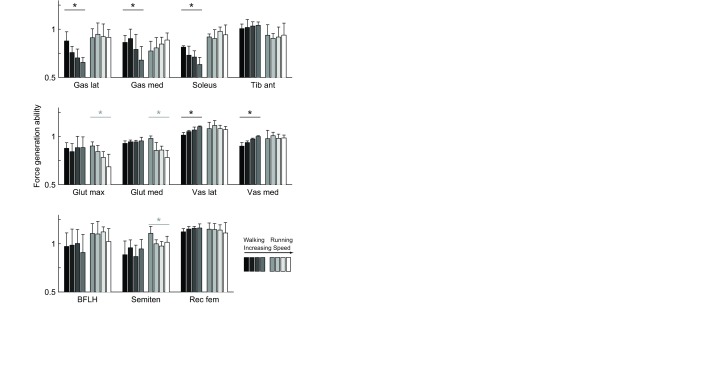
Force generation ability in 11 muscles at eight speeds (mean and 1 s.d., N=5). Force generation ability of gastrocnemius lateralis (Gas lat), gastrocnemius medialis (Gas med), soleus, tibialis anterior (Tib ant), gluteus maximus (Glut max), gluteus medius (Glut med), vastus lateralis (Vas lat), vastus medialis (Vas med), biceps femoris long head (BFLH), semitendinosus (Semiten) and rectus femoris (Rec fem) in walking (darker bars, 1.0–1.75 m s⁻¹) and running (lighter bars, 2.0–5.0 m s⁻¹); a repeated measures ANOVA indicated that speed had a significant effect (*P<0.05) in five muscles during walking and three muscles during running.

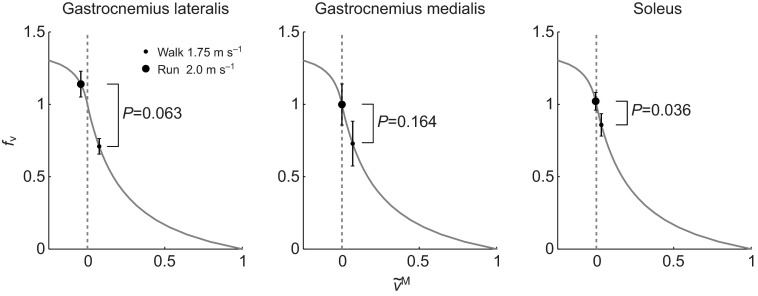
Soleus operates at fiber velocities more favorable for force generation during slow running compared with fast walking

We detected a significant difference in f_ν between slow running and fast walking in soleus (P=0.036) (Fig. 7). This muscle had higher values of f_ν in running at 2 m s⁻¹ (mean ± s.d., 1.00±0.06) than in walking at 1.75 m s⁻¹ (0.87±0.08). Even though gait speed and the shortening velocity of the muscle–tendon unit were higher in running, the change from walking to running reduced fiber shortening velocity and moved soleus fibers from concentric to isometric contraction. A similar phenomenon is suggested in gastrocnemius lateralis and medialis but the differences were not statistically significant. The mean and standard deviation of f_ν during running and walking was 1.12±0.09 and 0.71±005 for gastrocnemius lateralis (P=0.063) and 0.98±0.14 and 0.76±0.15 for gastrocnemius medialis (P=0.164). The transition to running further magnified the force generation ability of soleus via a significant increase in f_AL between fast walking (0.92±0.03) and slow running (0.97±0.02) (P=0.004). This was caused by an increase in length that moved the fibers closer to optimal length.

Fig. 7.

Mean and 1 s.d. (N=5) of the force–velocity multiplier (f_v) at the instant of largest active force in walking at 1.75 m s⁻¹ (small dot) and running at 2.0 m s⁻¹ (big dot) plotted on the force–velocity curve. A paired Student's t-test (gastrocnemius medialis and soleus) or a Wilcoxon signed-rank test (gastrocnemius lateralis) was used identify differences in f_v in between walking and running. The change from walking to running decreased fiber shortening velocity (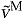) and increased f_v in soleus. We did not detect a significant difference between walking and running in gastrocnemius medialis and gastrocnemius lateralis.

We detected a significant difference in f_ν between slow running and fast walking in vastus lateralis (P=0.043) and vastus medialis (P=0.049). Both muscles had lower values of f_ν in running at 2 m s⁻¹ (vastus lateralis 1.08±0.09, vastus medialis 1.05±0.11) than in walking at 1.75 m s⁻¹ (vastus lateralis 1.19±0.02, vastus medialis 1.18±0.02). This occurred despite the fact that fibers attained faster lengthening velocities in running than in walking, because the peak active force occurred later in the gait cycle for running, when the fibers had passed their peak lengthening velocity.

Fiber lengths and velocities of lower limb muscles during walking and running

The normalized fiber lengths and velocities over the gait cycle (Figs 8, 9) of muscles crossing the ankle (top rows) were qualitatively different between walking and running. In running, the stance portion of the gait cycle is shorter (Table 1) and ankle plantarflexion angle peaks earlier in the gait cycle (Fig. 4), yielding a phase shift in the fiber lengths and velocities between walking and running. Soleus is a good example; peak fiber length and the transition from isometric to shortening fibers occur earlier in the gait cycle in running versus walking. When it is active, soleus behaves more eccentrically in running than in walking. This stood in contrast to the muscles crossing the knee and hip (Figs 8, 9, middle and bottom rows) in which the normalized fiber lengths and velocities of running could be described roughly as faster walking. These seven muscles were more strongly affected by increases in the knee and hip joint range of motion and velocity, which increased the magnitude of the fiber lengths and velocities but preserved their shape and timing. For example, in semitendinosus the fiber lengths and the timing of their maxima were tightly clustered when the muscle was active at the beginning of stance and end of swing, and fiber velocities increased as gait speed increased from 1 to 5 m s⁻¹.

Fig. 8.

Average normalized fiber length (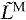) and period of highest activation of 11 muscles during gait at four walking speeds and four running speeds (N=5). Colors indicate gait speed in walking (1.00–1.75 m s⁻¹) and running (2.00–5.00 m s⁻¹). Thick horizontal lines indicate portions of the gait cycle when a muscle's activation exceeded 80% of the maximum value for that speed. Vertical lines on the abscissa indicate the instant of toe off for each of the eight speeds. Thin grey lines bound the plateau of the force–length curve, where normalized fiber length is between 0.95 and 1.05.

Fig. 9.

Average normalized fiber velocity (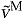) and period of highest activation of 11 muscles during gait at four walking speeds and four running speeds (N=5). Colors indicate gait speed in walking (1.00–1.75 m s⁻¹) and running (2.00–5.00 m s⁻¹). Thick horizontal lines indicate portions of the gait cycle when a muscle's activation exceeded 80% of the maximum value for that speed. Vertical lines on the abscissa indicate the instant of toe off for each of the eight speeds. When fibers are shortening, 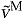is positive; when fibers are lengthening, 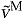is negative.

DISCUSSION

Our first goal was to determine whether the force generation ability of lower limb muscles changed with walking or running speed; it did in eight of the 11 muscles studied. In some cases, force generation ability increased with speed and in other cases it decreased, even though muscles must generate larger forces and moments at higher speeds. As humans walk faster, knee extension and ankle plantarflexion moments increase (Kirtley et al., 1985; Schwartz et al., 2008). As our subjects walked faster, the force generation ability of the vasti increased but the force generation ability of the plantarflexors decreased. This suggests that the architecture of the vasti favors the demand for higher forces at higher walking speeds, but the architecture of the plantarflexors is less able to meet the demand for higher forces at higher walking speeds. As humans run faster, hip flexion and extension moments increase (Schache et al., 2011). We found that the force generating ability of gluteus maximus, gluteus medius and semitendinosus decreased with running speed. As the architecture of muscles crossing the hip diminishes their force generating ability at higher running speeds, these muscles would require higher levels of activation to meet the demand for higher forces.

Our second goal was to determine whether the transition from fast walking to slow running affects force generation by changing fiber lengths or fiber velocities. We found that it did in soleus, reducing fiber velocities so that they were more favorable for force generation. This finding and the effect of walking speed on the plantarflexors' force generation ability, described above, support the hypothesis that the walk-to-run transition in human gait is influenced by the force generation ability of the plantarflexors. Though our conclusion agrees with previous reports (Neptune and Sasaki, 2005; Farris and Sawicki, 2012), our results did not show a decrease in muscle force as subjects walked faster. The peak active force generated by the gastrocnemius lateralis and soleus rose as speed increased (supplementary material Fig. S6), but this came at the cost of an even larger increase in activation to overcome the decrease in force generation ability. When the subjects switched to running at 2 m s⁻¹, soleus was able to generate more force with less activation. The peak force generated by gastrocnemius medialis varied little with walking speed (supplementary material Fig. S6); an increase in activation offset the decreasing force generation ability.

Three factors may account for the fact that we did not observe a decrease in plantarflexor force as subjects walked faster. First, our highest walking speed (1.75 m s⁻¹) was less than the highest walking speed studied previously (Neptune and Sasaki, 2005; Farris and Sawicki, 2012). By testing slower speeds, we may have overlooked a decrease in force that occurs at higher speeds. Second, the plantarflexors in our model had longer fibers and more complaint tendons than those in the model used by Neptune and Sasaki (Neptune and Sasaki, 2005). Third, Farris and Sawicki calculated gastrocnemius medialis force from net ankle moment with the assumption that the relative activation of all three plantarflexors was the same (Farris and Sawicki, 2012). As we measured EMG in the three major plantarflexors, we did not have to make this assumption. Despite these differences, all of these studies reached the same conclusion, that transitioning from fast walking to a running gait enables the plantarflexors to generate more force.

Force and power generation in the plantarflexors depends on muscle–tendon compliance. Muscle–tendon compliance is a consequence of the ratio of tendon slack length to optimal fiber length (Zajac, 1989). In muscles with long tendons and short fibers, like the plantarflexors, the stretch of the tendon at high force has a large effect on the normalized fiber length. When muscle–tendon compliance is low (e.g. in hip muscles), tendon stretch is small relative to the muscle fibers, and thus muscle fiber lengths and velocities are determined predominantly by the joint angles, joint angular velocities and muscle moment arms. When muscle–tendon compliance is high, muscle fiber length and velocity are more dependent on the activation level and tendon stretch (Arnold and Delp, 2011). Ultrasound measurements of the plantarflexors have revealed that motion of the fibers diverges from the motion of the muscle–tendon unit (Fukunaga et al., 2001; Lichtwark et al., 2007; Lichtwark and Wilson, 2006), which we observed in our simulations. When the muscle–tendon unit lengthens in early stance of walking, the fibers are nearly isometric or possibly shortening; when the whole muscle–tendon unit shortens in late stance, the tendon shortens rapidly and the fibers shorten more slowly.

Muscle–tendon compliance makes the fiber lengths, velocities and forces of the plantarflexors sensitive to tendon mechanical properties. To study this, we altered the plantarflexors' tendon mechanical properties by changing tendon strain at maximum isometric force from 3.3% to 12%. With a stiff tendon, simulated tendon stretch of the plantarflexors over the gait cycle was lower than tendon stretch measured by ultrasound at the same speeds (Farris and Sawicki, 2012). Consequently, plantarflexor fibers lengthened too fast during early stance, leading to high forces and excessive negative ankle joint power. Then, they shortened too fast in late stance, generating low forces and producing insufficient positive ankle joint power. With a tendon compliance of 10% strain at maximum isometric force, the plantarflexors' peak tendon stretch during the gait cycle was within the range reported in the aforementioned ultrasound study (10–15 mm) and the simulated muscles produced ankle moments and powers that matched the subjects' moments and powers estimated from inverse dynamics (Fig. 5; supplementary material Figs S4, S5). These findings echo the work by Krishnaswamy and colleagues (Krishnaswamy et al., 2011), who suggested that high tendon compliance and high muscle–tendon compliance enable the neural control system (modeled by EMG input) to take advantage of muscle architecture to efficiently generate ankle moments during gait.

Our estimates of where lower limb muscles operate on the force–length curve during gait can be compared with experimental measurements made with ultrasound. Tibialis anterior was active on the ascending limb in our simulations, falling within the ascending and plateau behavior previously observed (Maganaris, 2001). Vastus lateralis was active on the ascending limb during walking and the plateau to early descending limb during running, consistent with previous findings (Ichinose et al., 2000). We observed that soleus was predominantly active on the ascending limb of the force–length curve during running and walking, reaching as far as the plateau during running. This behavior agrees with results reported by Rubenson and colleagues (Rubenson et al., 2012), who paired ultrasound measurements during walking and running with isometric measurements that characterized subject-specific force–length behavior. That our simulated normalized fiber lengths fell within the same regions of the force–length curve that others have observed adds confidence that these simulations represent fiber dynamics accurately.

Although EMG normalization influences the distribution of simulated muscle force, we are confident that our normalization method did not compromise the results of this study. We normalized subjects' filtered EMG to the maximum value observed for each muscle over all gait speeds. This normalization method will cause the estimated excitation to be over-estimated if the muscle was not maximally excited during any of the trials. The impact of such an error on the muscle fiber length and velocity depends on muscle–tendon compliance. In muscles where the ratio of tendon slack length to optimal fiber length is less than two (vastus lateralis, vastus medialis, semitendinosus, gluteus maximus and gluteus medius), fiber lengths and velocities are not sensitive to excitation level [see figs 4 and 6 of Arnold and Delp (Arnold and Delp, 2011)]. Gastrocnemius medialis, gastrocnemius lateralis and soleus have the highest muscle–tendon compliance in our study; however, it is reasonable to expect that soleus and the gastrocnemeii reach a true maximum excitation in the gait speeds we studied (Prilutsky and Gregor, 2001). This adds confidence that our simulations generated appropriate forces. There are three muscles in our study that would be moderately sensitive to excitation level (tibialis anterior, rectus femoris and biceps femoris). Interestingly, these are the muscles for which we did not detect a significant effect of gait speed on force generation ability. They are also the muscles in which Prilutsky and Gregor (Prilutsky and Gregor, 2001) concluded the walk-to-run transition is triggered by high activation during swing phase. Perhaps different muscles have different triggers for the walk-to-run transition; this would be an interesting comparison to investigate further in future studies.

Fiber length, fiber velocity and activation are not the only determinants of muscle force, and in focusing our study on these properties we omitted other factors. For example, our model does not account for variable gearing in pennate muscles (Azizi et al., 2008), residual force enhancement (Herzog et al., 2006), changes to the force–velocity curve due to submaximal activation, sarcomere and fiber heterogeneity, or the effects of short time history (for review, see Huijing, 1998). Some of these modeling simplifications make it difficult to produce a model that can simultaneously match slow and fast movement, perhaps leading to an overestimation of peak ankle moment and power in walking and an underestimation of peak ankle moment and power in running (supplementary material Fig. S4). The three changes that we made to the generic lower limb model (Arnold et al., 2010) may have partially compensated for these simplifications: (1) we strengthened all the muscles to reflect younger athletic subjects; (2) we increased the maximum shortening velocity; and (3) we increased Achilles' tendon compliance in accordance with the latest ultrasound studies made on the human Achilles' tendon. These modest changes were able to produce kinematics of the fiber and tendon in agreement with previous studies and muscle forces that yielded moments and powers that were in agreement with inverse dynamics moments and powers evaluated directly from motion-capture data.

We simplified muscle structure by assuming that all fibers in a muscle are the same length and travel the entire length of the fascicle. Three-dimensional fiber geometry produces a distribution of fiber lengths and models of muscle fibers based on MRI data have indicated that lumped parameter models may overestimate fascicle excursions (Blemker et al., 2007; Blemker and Delp, 2006). Microdissection of muscle fibers in humans and animals has shown that, in some muscles, fibers do not traverse the entire length of a fascicle, but are connected serially (for review, see Trotter, 1993). This feature has the most influence on muscle function in long strap-like muscles when forces are low (Trotter et al., 1995). To mitigate this issue, our study excludes some muscles where this is most problematic (e.g. sartorius and gracilis), our questions focus on high force conditions, and our model uses muscle architecture data for which sarcomere lengths have been associated with fascicle length in known postures.

The small number of subjects included in this study limits our findings. Although we did not find a trend with speed in many muscles, we could not conclude that there were no speed effects because of insufficient statistical power. Thus, we may have underestimated the effects of speed in some muscles, such as biceps femoris long head and rectus femoris, which had no significant trends. We may also have underestimated the differences for gastrocnemius lateralis and medialis across the walk-to-run transition, as each muscle lost force generating ability as walking speed increased, but did not have a statistically significant change when subjects transitioned to running.

While the plantarflexors were endowed with more tendon compliance than other muscles (Fig. 2E), our conclusions are not dependent on this aspect of the model. When plantarflexor tendons were modeled with the same force–strain curve as the other muscles, they showed the same trends with gait speed and across the walk-to-run transition. The decrease in force generation ability as subjects walked faster and the increase that occurred when they switched to a running gait are caused by changes in gait kinematics, muscle activation and the high ratio of tendon slack length to optimal fiber length in these muscles. Other muscles have lower ratios of tendon slack length to optimal fiber length, so a change to the force–strain curve of the tendons associated with these muscles has a relatively small effect on their fiber lengths, fiber velocities and forces.

Our study provides two important contributions to understanding lower limb muscle function during human locomotion. First, the results reveal how muscle fiber lengths and velocities affect muscle force generation over a range of walking and running speeds. Our findings support the hypothesis that the walk-to-run transition in human gait is influenced by the decline in force generation ability of the plantarflexors at higher walking speeds. Second, we have estimated normalized muscle fiber lengths and velocities in walking and running at multiple speeds in 11 muscles. Our results do not replace in vivo measurements of fascicle length; recent subject-specific measurements of the force–length relationship and fascicle length during walking and running have provided more information about the operating lengths of soleus and the influence of tendon stretch during gait (Rubenson et al., 2012). Our approach, however, ties fiber lengths and velocities to regions of the force–length and force–velocity curves, provides insights into muscles that have not been imaged during locomotion, and permits comparisons among muscles with diverse architecture. The simulations and data associated with this paper (see https://simtk.org/home/muscfib_walkrun) permit the nature of muscle force development in walking and running to be studied in unprecedented detail.

LIST OF SYMBOLS

a

activation

f_AL

active force–length multiplier; the modeled effect of fiber length on contractile muscle force

F^M

total force in the muscle fibers

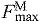
maximum isometric muscle force

f_PL

passive force–length multiplier; the modeled effect of fiber length on passive muscle force

f_T

tendon force–strain multiplier; the modeled effect of tendon strain on the tendon force

F^T

total force in the tendon

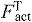
active force in the direction of the tendon

f_ν

force–velocity multiplier; the modeled effect of fiber velocity on contractile muscle force

L^M

muscle fiber length

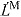
time derivative of muscle fiber length

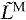
normalized fiber length: L^M/

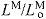
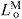
optimal muscle fiber length

L^MT

muscle tendon unit length

L^T

tendon length

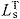
tendon slack length

ν^M

muscle fiber shortening velocity: –

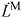
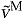
normalized fiber velocity:

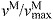
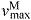
maximum muscle fiber shortening velocity

α

pennation angle

α_o

pennation angle at optimal fiber length

ε^T

tendon strain from slack length

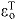
tendon strain at maximum isometric force; parameter used to set tendon compliance