Quantifying discrimination of Framingham risk functions with different survival C statistics

Abstract

Cardiovascular risk prediction functions offer an important diagnostic tool for clinicians and patients themselves. They are usually constructed with the use of parametric or semi-parametric survival regression models. It is essential to be able to evaluate the performance of these models, preferably with summaries that offer natural and intuitive interpretations. The concept of discrimination, popular in the logistic regression context, has been extended to survival analysis. However, the extension is not unique. In this paper, we define discrimination in survival analysis as the model’s ability to separate those with longer event-free survival from those with shorter event-free survival within some time horizon of interest. This definition remains consistent with that used in logistic regression, in the sense that it assesses how well the model-based predictions match the observed data. Practical and conceptual examples and numerical simulations are employed to examine four C statistics proposed in the literature to evaluate the performance of survival models. We observe that they differ in the numerical values and aspects of discrimination that they capture. We conclude that the index proposed by Harrell is the most appropriate to capture discrimination described by the above definition. We suggest researchers report which C statistic they are using, provide a rationale for their selection, and be aware that comparing different indices across studies may not be meaningful.

1. Introduction

The Framingham Heart Study is a population-based cohort study with subjects attending routine examinations every two years since 1948 [1–3]. At each visit all attendees undergo a physical exam and laboratory assessment of cardiovascular risk factors [3]. In addition, a detailed history of cardiovascular endpoints is maintained with events constantly verified by a committee of three experts. Framingham investigators have defined cardiovascular disease (CVD) as the occurrence of any of the following: coronary heart disease (CHD; myocardial infarction, coronary death, angina pectoris or coronary insufficiency), cerebrovascular disease (stroke or transient ischemic attack), congestive heart failure, and peripheral vascular disease [4]. Over the years researchers have evaluated the relationship between CVD risk factors and incident CVD events [5–9]. Various statistical models have been proposed and utilized to quantify these relationships. Gordon and Kannel used logistic regression to assess the influence of multiple risk factors on the development of CHD [5]. Anderson et al. employed a nonproportional hazards accelerated failure Weibull model to relate age, systolic and diastolic blood pressure, cigarette smoking status, total and HDL cholesterol, presence of diabetes, and ECG left ventricular hypertrophy to the incidence of CVD, and to develop prediction functions [6]. Wilson et al. [7] used the Cox proportional hazards model [10] to relate risk factor categories to 10-year incidence of CHD. Recently, D’Agostino et al. have presented new risk functions (also based on the Cox model [10]) that can be used for CVD and its component diseases [9]. These functions can be used to calculate the probability of developing an event of interest (for example, CVD or CHD) in a given time horizon (usually 10 years), based on a baseline risk factor profile.

It is natural at this point to ask how well these calculated risks match the reality. The answer may be given on several different levels, leading to different measures of model performance [11–17]. One of them is to investigate the model’s ability to distinguish those who develop the event of interest (hence-forth ‘events’) from those who do not (‘nonevents’) based on the predicted probabilities of survival. This is referred to as discrimination. Discrimination of statistical models involving dichotomous outcomes has been studied and discussed quite extensively in the literature (see, e.g., [17] for a review). One of the most popular measures in this context is the area under the ROC curve (AUC), often called the ‘C statistic’, a name derived from its nonparametric estimator, which takes a form of a concordance (hence the ‘C’) index. Its construction was suggested by Bamber [18] and is described in [19–21]. It compares all subjects who experienced an event of interest with those who did not and calculates the proportion of pairs for which the predicted probability of event is higher for the subject who experienced an event. This approach works well for logistic regression but has two important limitations in the context of time-to-event analysis. First, it does not take into account the extra information offered by knowing individual survival times in addition to the event status. Second, it cannot handle subjects censored before the time point for which risk is to be calculated.

The extension of AUC to survival outcomes is not unique and several approaches have been proposed to achieve this goal. The following section presents them in detail. The most commonly used extension is due to Harrell et al. [22, 23] and it has been extensively studied by Pencina and D’Agostino [24]. It extends the logic of the AUC to the case of possibly right-censored survival time outcomes and assesses the amount of agreement or concordance between predictions and outcomes comparing not only events and nonevents but also events that happened at different points in time. It can also be viewed as a weighted area under the ‘incident/dynamic’ ROC curve proposed by Heagerty and Zheng [25]. The nonparametric estimator of the survival AUC proposed by Harrell et al. [23] and formalized by Pencina and D’Agostino [24] has recently been updated by Uno et al. [26].

Chambless and Diao [27] defined a time-dependent AUC in a different manner, focusing only on event versus nonevent comparisons. Unlike the definition of Harrell et al., survival times enter the definition only implicitly, through their impact on event indicator at a given time point. Gönen and Heller [28] proposed a different way of assessing concordance applicable to proportional hazards models. By reversing the definition proposed by Harrell et al. [22,23] and utilizing the properties of the Cox model [10], they arrived at an index based only on estimated regression coefficients and observed risk factor profile.

The purpose of this paper is to investigate the extensions of the AUC to survival data and determine to what degree the choice of the measure impacts the results. Our primary focus is on studies with prospective follow-up and prespecified maximum duration. Furthermore, we are interested in predicting the risk of events in a given time horizon, which is common for all subjects. The list of metrics is by no means exhaustive, but it includes those most commonly seen by authors in clinical applications. The investigation of differences between the measures is carried out using theoretical examples, simulations, and practical applications to the Framingham risk functions derived on a subset of data from Ref. [9] with available 30-year follow-up.

The paper is organized as follows. First, in Section 2, we discuss the concept of discrimination of survival models. In Section 3 we define the four measures we intend to compare. Theoretical examples are presented in Section 4. Section 5 contains an application of the four metrics to the Framingham Heart Study models predicting incident CVD over 30 years of follow-up and to simulated data. Conclusions are presented in Section 6.

2. Concept of discrimination in survival analysis

Consider a cohort of N subjects, free of the event of interest, whose baseline risk factor characteristic is measured at time T = 0 (the beginning of the study). Furthermore, assume that these subjects are followed for a maximum time of T_END, at which follow-up terminates, and that we are interested in predicting the risk of an event happening before time τ satisfying 0 <τ ≤ T_END. Models can be fitted based on full follow-up data extending until T_END or data censored at τ. Evaluation of model performance will use data censored at τ. For each subject ‘i’ coming from this cohort we observe a triplet (T_i, P_i, D_i), where T_i denotes the observed time on study equal to the minimum of survival time T_i^S and censoring time T_i^C (i.e., T_i = min(T_i^S,T_i^C)), P_i represent the corresponding model-based predicted probability of experiencing an event before τ and D_i is the event indicator at time τ (i.e.,D_i = 1 if ‘i’ experienced the event of interest before τ and D_i = 0 otherwise). If T_i > τ we set T_i = τ, and D_i = 0.

To illustrate the above assumptions, we consider five subjects in a study with a maximum follow-up time of T_END = 14 years and time horizon for risk prediction set at τ = 10 years, as presented in Figure 1.

Figure 1.

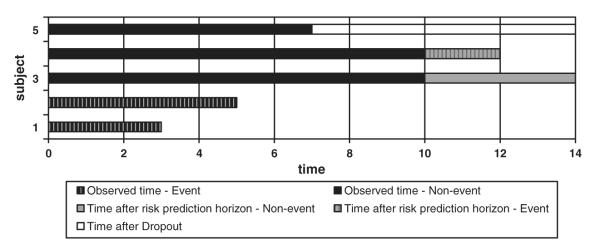
Observed versus actual times.

Subject 1 experiences the event of interest after 3 years and thus T₁ = T₁^S = 3 and D₁ = 1. Similarly, subject 2 experiences an event after 5 years and T₂ = T₂^S = 5, D₂ = 1. Subject 3 survives until study end, T₃^S = 14. Because we are only interested in what happens in the first 10 years, the observed time T₃ = 10 and D₃ = 0. Subject 4 experiences the event at time T₄^S = 12, but this is after τ = 10, so again, T₄ = 10 and D₄ = 0. Finally, subject 5 discontinues his/her participation in the study without the event after T₅^C = 7, yielding T₅ = 7 and D₅ = 0.

Recall that for binary outcomes discrimination is defined as the model’s ability to separate those who develop events from those who do not. This definition can be extended to survival data as the model’s ability to separate those with longer event-free survival from those with shorter event-free survival within time horizon τ. Note that this definition implies separation of those who develop events from those who do not and would reduce to the standard binary case definition if all subjects developed events at the same time and there were no premature discontinuations. In keeping with the logic used in the binary outcome case, the survival definition conditions on the observed to assess the predicted. Furthermore, note that the survival definition does not include any comparisons between subjects who do not experience events before τ (either censored at τ or dropping out before τ) as the full extent of their event-free survival cannot be determined. The definition does, however, imply that the model needs to distinguish between subjects with events occurring at different times (so called ‘event vs event’ comparisons). Finally, the word ‘separate’ may, but need not be, equated with ranking — distances can be built into measures that capture the correctness of ordering in a manner exemplified by discrimination slope used in the binary outcome case [29].

Figure 1 helps us illustrate the comparisons that need to be made to assess discrimination and highlights differences between binary and survival applications. In the binary context, subjects 1 and 2 would be compared with 3 and 4 but 1 and 2 would not be compared with each other. In contrast, in survival data, subjects 1 and 2 would be compared because we can determine that subject 2 survived longer. Furthermore, in the binary case, subject 5 could not be compared with anyone unless an assumption on their event status was made. This is not the case for survival data, where subject 5 can be compared with subjects 1 and 2 because we know that she/he survived longer.

3. Discrimination C statistics

In this section we define the four survival C statistics that we intend to compare. First, however, we recall the definition of the AUC in the binary outcome case

$${\mathit{AUC}}_{\text{binary}}=P(P_i>P_j\mid D_i=1,D_j=0).$$ (1)

Assuming the 10-year horizon in the example from Figure 1, only subjects 1 and 2 are compared with 3 and 4, unless we make an assumption about the survival status of subject 5 at τ = 10 years. This leads to only four pairs (out of 10 possible) contributing to the calculations.

3.1. Chambless and Diao’s C

The simplest extension of the binary AUC to survival was proposed by Chambless and Diao [27]. It incorporates the time component to event status

$$\mathit{AUC}\left(\tau \right)=P(P_i>P_j\mid D_i(\tau )=1,D_j(\tau )=0).$$ (2)

The sample estimator is derived using the Bayes rule applied to formula (2)

$$C_{\mathit{CD}}=\frac{E\left(\right(1-S(\tau \mid P_j))\cdot S(\tau \mid P_i)\cdot I(P_i<P_j\left)\right)}{E(1-S(\tau \mid P_i\left)\right)\cdot E\left(S\right(\tau \mid P_i\left)\right)},$$ (3)

where S and I are the survival and indicator functions, respectively and E denotes expectation, which in this case reduces to the sample mean. Of note, S(τ|P_i) = P_i if the model was developed on the same data on which its performance is being assessed.

In the example from Figure 1, all 10 pairs contribute to the calculations but these contributions are in the form of values from the (0, 1) interval rather than 1’s for concordance and 0’s for discordance.

In simple terms, C_CD can be viewed as a standardized average product of event probabilities multiplied by survival probabilities, where the event probabilities always come from a subject with higher predicted risk and the product of the average event and survival probabilities serves as the standardizing factor.

3.2. Harrell, Pencina and D’Agostino’s C

The first index that incorporates ‘event versus event’ comparisons (i.e., subjects 1 vs 2 in Figure 1) in the calculation of discrimination of a survival model was proposed by Harrell et al. [23] and described by Pencina and D’Agostino [24]. It can be defined [26] as

$$\mathit{AUC}\left(\tau \right)=P(P_i>P_j\mid T_i^S<T_j^S,T_i^S<\tau ).$$ (4)

Note that the above definition is based on actual survival times, which may not be observed for censored individuals. Hence, the sample estimator must use the observed time on study. The first estimator has been suggested by Harrell et al. [23] and formalized by Pencina and D’Agostino [24]

$$C_{\mathrm{HPD}}=\frac{\sum _{i\ne j}\left\{I\right(P_i>P_j)\cdot I(T_i<T_j,T_i<\tau )\cdot I(D_i=1\left)\right\}}{\sum _{i\ne j}\left\{I\right(T_i<T_j,T_i<\tau )\cdot I(D_i=1\left)\right\}},$$ (5)

where I denotes the indicator function. If P_i’s allow ties, I = 0.5 can be used in cases where P_i = P_j but not for T_i = T_j. In Figure 1, seven pairs contribute to the estimation: the four from the binary case plus three comparisons between subjects 1, 2, and 5. Concordance or discordance is assessed in terms of 1’s and 0’s.

The condition from the numerator is referred to as concordance and the one in the denominator as comparability. The statistic can be simply described as the probability of concordance given comparability. The necessary and sufficient condition for comparability requires that the subject with shorter observed time experienced an event. The subject with longer observed time could either have been censored (at the end of follow-up or prematurely) or experienced an event. The presence of ‘event versus event’ comparisons distinguishes Harrell’s AUC from the one proposed by Chambless and Diao. On the other hand, exclusion of pairs where the person with shorter follow-up time discontinued the study prematurely from the pool of comparable subjects implies that C_HPD depends on the censoring mechanism. This is not desirable because censoring is usually regarded as a nuisance that should not influence the results.

3.3. Uno’s estimator of Harrell’s AUC

To overcome the last shortcoming, Uno et al. [26] proposed a different estimator for the AUC defined by formula (4). They used the ‘inverse probability weighting’ technique of Cheng et al. [30] to arrive at

$$C_{\mathrm{Uno}}=\frac{\sum _{i,j}\left\{I\right(P_i>P_j)\cdot I(T_i<T_j,T_i<\tau )\cdot I(D_i=1)\cdot G{\left(T_i\right)}^{-2}\}}{\sum _{i\ne j}\left\{I\right(T_i<T_j,T_i<\tau )\cdot I(D_i=1)\cdot G{\left(T_i\right)}^{-2}\}}.$$ (6)

Symbol I again denotes the indicator function and G(T_i) is the Kaplan–Meier estimator of the censoring time distribution. Uno et al. [26] showed that formula (6) provides a consistent estimator for the AUC defined by (4), whereas estimator (5) converges to a quantity that still depends on censoring. The same seven pairs of subjects from Figure 1 as those used by formula (5) contribute to the estimation, but here the additional quantity G(T_i) needs to be estimated.

3.4. Gönen and Heller’s k

A different concordance index has been proposed by Gönen and Heller [28]. Maintaining the notation used throughout this paper, its theoretical definition can be given as

$$k=P(T_j>T_i\mid P_i\ge P_j).$$ (7)

We observe that the above calculates the probability that of any two subjects, the one with a more adverse model-based risk profile will have a shorter survival time. This is a reversal of the definition used by Harrell et al., Pencina and D’Agostino, Uno et al., and Chambless and Diao and the AUC from the binary case, all of which condition on the observed survival experience to compare model-based risks. Moreover, if the concept of discrimination is to be associated with distinguishing between events and nonevents as it is in the binary case, the concordance index proposed by Gönen and Heller does not fit this framework. This difference between the definitions parallels the one between sensitivity and specificity (binary, Chambless and Diao’s and Harrell’s AUCs) versus positive and negative predicted values (Gönen and Heller’s k). The first three AUCs compare predictions based on observed survival experience; Gönen and Heller’s k tries to predict who survives longer based on the relationship of linear predictors or event probabilities from the model.

Gönen and Heller apply their definition to Cox regression models and use the proportional hazards representation to arrive at an estimator for k. Assuming again that subjects are ordered according to increasing linear predictors β^trX_i (or equivalently, decreasing predicted probabilities of survival) it can be formulated as

$$C_{\mathrm{GH}}=\frac{2}{N(N-1)}\sum _{i<j}\left\{\frac{I({\beta }^{\mathit{tr}}{X}_i>{\beta }^{\mathit{tr}}{X}_j)}{1+\exp ({\beta }^{\mathit{tr}}{X}_j-{\beta }^{\mathit{tr}}{X}_i)}+\frac{I({\beta }^{\mathit{tr}}{X}_i<{\beta }^{\mathit{tr}}{X}_j)}{1+\exp ({\beta }^{\mathit{tr}}{X}_i-{\beta }^{\mathit{tr}}{X}_j)}\right\}.$$ (8)

A striking feature of this estimator is its dependence only on the linear predictor values evaluated for different combinations of risk factors. This implies that C_GH can be calculated knowing only the Cox regression coefficients and risk factor levels. The actual survival experience is used only implicitly: it comes in through the Cox regression coefficients, which were obtained using the full survival data. This way C_GH implicitly accounts for information offered by individuals discontinuing the study prematurely. We further note that for any two subjects, the expression under summation in (8) takes values that range from 0.5 to 1. When linear predictors are very close to each other it approaches 0.5 and when they are far apart it gets close to 1. This gives C_GH an interpretation of a measure, which assigns a distance to each pair of subjects and then averages these distances over all pairs. Of note, unlike in the case of C statistics defined by (5) and (6), all pairs are used in the calculation of C_GH. Thus, C_GH measures the separation of all subjects, even those who did not experience events. All 10 pairs from Figure 1 contribute to the calculations but indirectly, through the Cox model.

4. Four theoretical examples

Here we present four theoretical examples intended to better illustrate the differences between the definitions of survival AUCs presented in the previous section. They represent extreme cases and are meant to improve the intuition rather than serve as likely scenarios.

Example 1

Predictors are not related to outcomes

In this case formula (2) reduces to

$$\mathit{AUC}\left(\tau \right)=P(P_i>P_j\mid D_i(\tau )=1,D_j(\tau )=0)=P(P_i>P_j)=0.5$$

The same is true for formulas (4) and (7) and hence each AUC is equal to 0.5. Of note, for models based on regression techniques, which are developed and assessed on the same data, 0.5 is the minimum value for the AUC. Our example shows that it is theoretically attainable.

Example 2

Predicted probabilities P_i take only two values, one for events and one for nonevents, and the value for events is higher

This example can be viewed as using the event indicator as the sole predictor. The condition P_i > P_j for any i representing an event and j representing a nonevent guarantees that the Chambless and Diao’s AUC will be equal to 1. For Harrell’s AUC, however, we get concordance for all the event versus nonevent comparisons, but not for the event versus event comparisons, and hence 0:5 < AUC < 1, with the value increasing towards 1.0 with the decreasing number of events (it would actually reach 1 if we had only one event). For Gönen and Heller’s AUC we also have 0:5 < AUC < 1, because of the fact that the concordant event versus nonevent comparisons are only a subset of all comparisons made.

Example 3

Predicted probabilities P_i for events are ordered according to decreasing survival times and for nonevents they are all tied at a value smaller than the minimum probability among events

A model with these properties can be viewed as having perfect discrimination according to the definition proposed in Section 2. Thus, given the fact that Harrell’s AUC compares only events to events or events to nonevents, it has to equal 1. Similarly, Chambless and Diao’s AUC also equals 1, given perfect separation of events from nonevents. However, Gönen and Heller’s AUC will still be less than 1, because there will be nonevents for whom P_i ≥ P_j but survival times are tied and hence they are not concordant.

Example 4

Follow-up is sufficiently long for every subject to develop an event and predicted probabilities P_i are ordered according to decreasing survival times

This modification of Example 3 guarantees that Gönen and Heller’s k is equal to 1. Harrell’s AUC is also equal to 1 because of the fact that only concordant pairs are comparable in this scenario. Chambless and Diao’s AUC is not defined as absence of nonevents does not allow for its calculation.

In summary, we conclude that the statistics considered here range from 0.5 (Example 1) to 1 (Examples 2, 3 and 4) but the upper bound is not reached for the same scenarios. Chambless and Diao’s AUC requires the least discriminatory ability of the predictor to reach 1 — it is accomplished in the case of perfect separation of events and nonevents with ties within events and nonevents. Gönen and Heller’s k seems the most stringent with its value usually being the lowest. Example 3 is of particular interest here, showing that perfect ordering of events and perfect differentiation between events and nonevents are not sufficient for Gönen and Heller’s k to reach 1, contrary to the other statistics considered. This means that the degree of separation required by k to reach perfection goes beyond what would be required from a model according to the definition of discrimination proposed in Section 2. This is not surprising, because k measures the separation between all subjects, regardless of their event status. Example 4 shows that it is possible for k to reach 1. Harrell’s AUC appears to be more stringent than Chambless and Diao’s AUC but less so than k: we see that it reaches 1 in Example 3 (where k does not) but not in Example 2 (Chambless and Diao’s AUC does). Theoretically, it is possible to construct examples in which the above ordering does not hold but these instances are of no practical interest. Overall, as pointed out in example 3, Harrell’s AUC is the metric most consistent with the definition of discrimination in survival proposed in Section 2.

The four examples presented in this section focused on extreme cases intended to illustrate the behavior of the different definitions where they were likely to diverge. To acquire a better sense of the extent of the potential differences in practical situations, we apply our different AUCs in the next section to evaluate the discrimination of two Framingham Heart Study risk prediction models and to several other models based on simulated data.

5. Application to Framingham risk prediction models and simulated data

We illustrate the application of the developments presented in the previous sections with an example from the Framingham Heart Study, which served as their motivation. A subset of a sample analyzed by D’Agostino et al. [9], consisting of 2762 women and 2388 men, 30 to 74 years of age, who attended Framingham Cohort examination 11 or Offspring examination 1 free of cardiovascular disease was followed for a maximum of 38 years (median 28 years) for the development of CVD. Two separate Cox proportional hazards models were fitted: the one for men included only age as predictor to illustrate a case of poor to average discrimination and high event rate (10-year Kaplan–Meier event rate 17.4%, 30-year rate 49.3%) and the one for women included all standard CVD risk factors (age, systolic blood pressure and antihypertensive treatment, total and HDL cholesterol, diabetes, and smoking status) to illustrate a case of good discrimination and moderate event rate (10-year Kaplan–Meier event rate 10.3%, 30-year rate 35.8%). The assumption of proportional hazards could not be rejected using the ‘exposure times the logarithm of time’ test [31] at the 0.05 level. Competing cause of non-CVD mortality was ignored for simplicity of model development and presentation. We estimated C_CD, C_HPD, C_Uno, and C_GH for years 1 through 30, each time refitting the model and treating the maximum year (1 through 30) as censoring point.

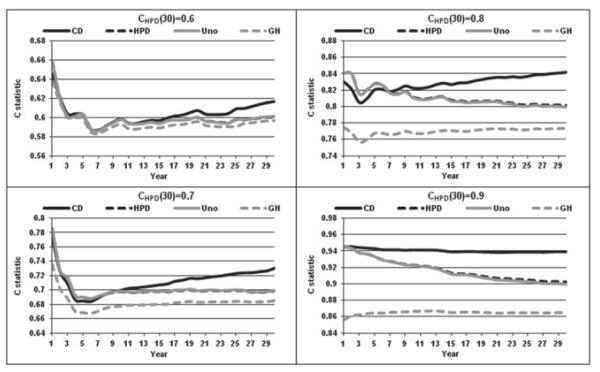
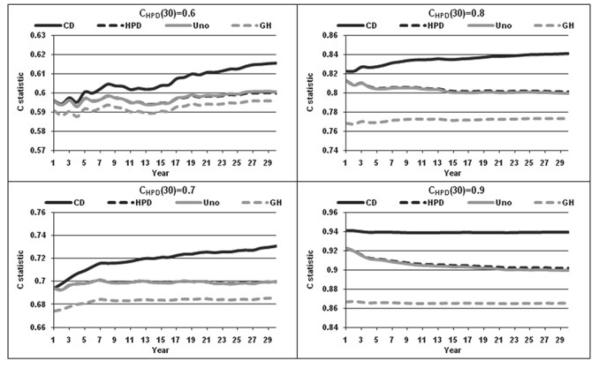
Numerical simulations encompassing a range of common-practice scenarios were also undertaken. We generated models based on the Weibull distribution with increasing, constant, and decreasing hazards, corresponding to shape parameters of 1.5, 1.0, and 0.5. The 30-year event rates were set to 15%, 30%, and 45%. Models with C_HPD at 30 years equal to 0.6, 0.7, 0.8, and 0.9 were considered. Finally, random exponential drop-out was modeled with 30-year rates of 0%, 20%, and 40% and the sample size was set to 10,000.

Figures 2 and 3 present the four different C statistics calculated over 30 years of follow-up on the Framingham data, for men and women, respectively. First, we note that all four indices start at their highest values for very short follow-up durations, then go down somewhat rapidly and either plateau or go back up. This initial spike may be explained by the fact that early events occur among the sickest individuals that probably have the most adverse risk profiles and are easy to identify. Furthermore, in both figures, C_CD dominates or almost dominates the other C statistics. This is not surprising given the simplified task of distinguishing only events from nonevents. Of interest, however, C_CD remains very close or even below C_HPD and C_Uno for shorter follow-up durations and then it separates sharply. C_HPD and C_Uno are almost indistinguishable, which is not surprising given that the percentage of drop-outs is low. C_GH is consistently the lowest at all times and remains relatively parallel to C_HPD and C_Uno. Overall, we believe the following relationship is approximately true: C_GH ≤ C_Uno ≈ C_HPD ≤ C_CD.

Figure 2.

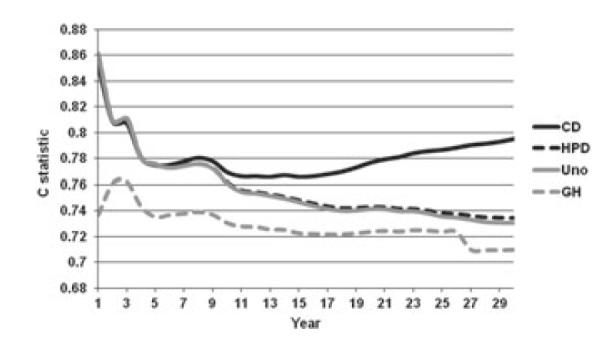
C statistic on 30-year follow-up in Framingham Men.

Figure 3.

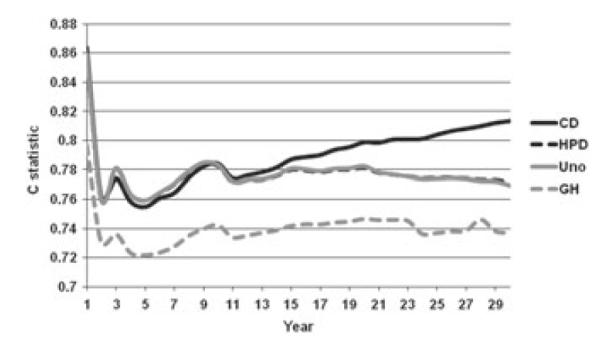
C statistic on 30-year follow-up in Framingham Women.

The simulated scenarios generally agreed with the findings observed in the Framingham data. Figures 4 and 5 display results for the Weibull models with increasing and decreasing hazards, respectively and event rates equal to 30% and 20% drop outs rates. The relationship: C_GH ≤ C_Uno ≈ C_HPD ≤ C_CD held for all cases. The difference between C_GH and the three other statistics increased with increasing number of events. For larger values of the C statistics, the separation of C_CD from C_Uno or C_HPD was more rapid and pronounced. In general, larger values of C led to larger separation between the indices. Similar to the practical example, the two estimators of Harrell’s AUC, C_Uno and C_HPD remained very close for all cases considered. These results remained consistent for different drop-out rates and different event rates (data not shown). The initial spike in the C statistics observed in the Framingham data (with increasing hazard of 1.56) remained only in the Weibull models with increasing hazard and for smaller long-term C statistics. It is conceivable that the early performance spike can be expected when the number of events is not too large and performance not very good. In general (ignoring the initial spike, if present), C_CD tends to show an increasing pattern, C_GH tends to remain constant and C_HPD and C_Uno remain constant or decrease with time. The latter can be attributed to the increasing proportion of event vs. event comparisons in the calculation of C_HPD and C_Uno. Moreover, one might expect the predictive ability of baseline measurements to go down with time if no risk factor updating takes place. If the proportionality of hazards is perfectly satisfied, the performance should remain constant, an effect seen for C_GH, which explicitly makes this assumption.

Figure 4.

C statistic for increasing hazard Weibull.

Figure 5.

C statistic for decreasing hazard Weibull.

6. Conclusions

In this paper we focused on discrimination in survival analysis defined as the model’s ability to separate those with longer event-free survival from those with shorter event-free survival within time horizon τ. This definition remains consistent with the one used in the binary case, conditioning on the observed to evaluate the model-based risk. Against the backdrop of this definition, we examined three popular extensions of binary AUC to survival analysis and concluded that only the version proposed by Harrell et al. [22, 23] and studied by Pencina and D’Agostino [24] and Uno et al. [26] remains consistent with the postulated definition. In contrast, the concordance index proposed by Chambless and Diao [27] is the closest to the original definition of the AUC used in the binary case, but does not take full advantage of the time-to-event information. Gönen and Heller’s k, which quantifies how well the reality matches what was predicted by the model, deviates from discrimination viewed in the ‘classical’ sense, which assesses how well what was predicted by the model matches reality.

Of the quantities considered, only the AUC proposed by Harrell et al. [22,23] is based solely on ranks and thus invariant to monotone transformations of the linear predictor or predicted probability of event. The fully nonparametric nature of this metric makes validation straight-forward. This is not true for the other two indices: Chambless and Diao [27] suggest refitting of the model on the validation set using the linear predictor from the development set as the sole exposure. This is necessary to factor out the potential impact of calibration on the assessment of discrimination. The problem might be even more complicated for Gönen and Heller’s k; if no adjustment was made, model performance on the validation set would depend only on the distribution of risk factors in the validation set without any regard to the observed survival experience — a rather counter-intuitive property.

On the basis of the theoretical, practical, and numerical examples, we conclude that the C statistics considered here are not identical and can yield values that are as far as 0.10 apart. Because all of them apply to different definitions of discrimination in survival analysis, they should not be expected to produce the same values and should not be compared with each other across different studies. In particular, one needs to be careful when attaching labels of ‘good’ or ‘poor’ discrimination not to base them on values applicable to a different C statistic than the one being reported. For example, using Chambless and Diao’s C one might conclude that the model presented in Figure 2 offers ‘good’ discrimination (C_CD ≈ 0:74), but the application of Uno’s C would suggest that the discrimination is rather ‘weak’ (C_Uno ≈ 0:69).

Different concordance indices may be preferred in different situations. In studies focusing on long-term risk prediction, for which not only avoiding an event but also extending survival is important, and in which not all subjects experience the event of interest, the definition of discrimination given in Section 2 seems optimal and is best captured by Harrell et al.’s index. Prospective follow-up studies of long duration in the fields of cardiovascular disease, cancer, or HIV are all members of this category. Gönen and Heller’s k might provide complementary information (i.e., how well will the reality match the model rather than how well the model matches the reality) but its range might be restricted.

A different situation is encountered in clinical trials or studies of short duration where the focus is solely on event versus nonevent status. Even though the interest lies in binary outcome, survival analysis techniques are applied to account for subjects with incomplete follow-up. In this context, Chambless and Diao’s index might be the preferred measure of choice because it keeps the binary focus and is able to handle censoring.

We have considered two different estimators proposed for Harrell’s AUC as defined by formula (4). The one proposed by Uno et al. [26] has been shown to be consistent and invariant to censoring distributions in cases where censoring is independent from model covariates. The latter property might be particularly important in studies with long follow-up and high drop-out rates [26]. Our results suggest that in applications with data similar to that of the Framingham Heart Study, little difference can be expected between C_Uno and C_HPD. For studies with large sample sizes, large numbers of events, and limited drop-out rates, researchers might prefer C_HPD because of its lower computational intensity.

Several extensions of our work seem natural. First, we considered only concordance indices to measure discrimination. It would be of interest to see how other measures of discrimination in survival analysis fare in light of the definition presented in Section 2. Second, we focused on a limited number of theoretical and simulated cases. In particular, an investigation into the less practically encountered cases of nonmonotone and nonproportional hazards would be of interest. The impact of a nonrandom drop-out mechanism should also be studied. Finally, discrimination measures for competing-risk models also need to be investigated.

In conclusion, we recommend Harrell et al.’s AUC [22,23] as the preferred concordance index in studies where not only the event status but also survival times matter. At the very least, we urge researchers to report which formulation of the survival AUC they are using and provide a rationale for their selection.