Abstract
The area under the receiver operating characteristic curve (AUC) is the most commonly reported measure of discrimination for prediction models with binary outcomes. However, recently it has been criticized for its inability to increase when important risk factors are added to a baseline model with good discrimination. This has led to the claim that the reliance on the AUC as a measure of discrimination may miss important improvements in clinical performance of risk prediction rules derived from a baseline model. In this paper we investigate this claim by relating the AUC to measures of clinical performance based on sensitivity and specificity under the assumption of multivariate normality. The behavior of the AUC is contrasted with that of discrimination slope. We show that unless rules with very good specificity are desired, the change in the AUC does an adequate job as a predictor of the change in measures of clinical performance. However, stronger or more numerous predictors are needed to achieve the same increment in the AUC for baseline models with good versus poor discrimination. When excellent specificity is desired, our results suggest that the discrimination slope might be a better measure of model improvement than AUC. The theoretical results are illustrated using a Framingham Heart Study example of a model for predicting the 10-year incidence of atrial fibrillation.
Keywords: risk prediction, discrimination, AUC, IDI, Youden index, relative utility
1. Introduction
Risk prediction algorithms are standard tools in diagnostic and preventive medicine. Developed for a wide range of adverse conditions they are meant to aid, not replace, clinicians in decisions about treatment. The onset or presence of the disease is usually treated as a binary or survival outcome and its association with predictors is established based on statistical models or model-free data-driven techniques. Historically, linear discriminant analysis (LDA) was first used for this purpose (Fisher 1936). Later it was replaced by logistic regression (Walker and Duncan 1967) and more recently by the Cox proportional hazards model (Cox 1972). But other approaches have also been explored (Vapnik 1998). The area under the receiver operating characteristic curve (AUC, Hanley and McNeil 1982) has become the reporting standard in the assessment of performance of these algorithms. It is a measure of discrimination, or the model’s ability to separate those with events from those without events. Random assignment of risks yields an AUC of 0.5, whereas perfect separation of events from nonevents leads to an AUC of 1. Once a satisfactory model has been developed, it can then be translated into a prediction rule (Steyerberg et al. 2010) intended to help clinicians place patients in the appropriate risk categories which might suggest further testing or pharmacologic or lifestyle intervention. The performance of these rules has usually been assessed in terms of the familiar metrics of sensitivity, specificity, positive and negative predictive values, or their summaries which include the Youden’s index (Youden 1952), net benefit (NB) and relative utility (RU) (Vickers and Elkin 2006, Baker et al. 2009). A nice review of various criteria that can be used to evaluate risk prediction models and rules has been given by Gail and Pfeiffer (2005). These authors observe that “high discriminatory power can be more important in a screening application than in deciding whether or not to take a preventive intervention that has both beneficial and adverse effects”.
Considerable effort has been dedicated to identifying new variables which are meant to improve the performance of a given risk model and then the corresponding rule. Change in the AUC has been the most common way of capturing improvement in discrimination over the given risk model. However, it has been criticized for its inability to increase once a certain level of discrimination has been achieved (Cook 2007). It has been shown that extremely strong predictors are needed to achieve what would be viewed as satisfactory increase in discrimination (Pepe 2004, Ware 2006). In response, the difference in discrimination slopes (Yates 1982) called the integrated discrimination improvement (IDI) has been proposed as an alternative way to capture improvement in model performance (Pencina & D’Agostino et al. 2008). However,, some researchers have argued strongly for application of performance metrics that describe the performance of prediction rules rather than the models from which the rules were generated. Vickers and Elkin (2006) have re-introduced the concept of net benefit and Baker et al. (2009) suggested its scaled version called the relative utility. The net reclassification improvement (NRI) proposed by Pencina and D’Agostino (Pencina & D’Agostino et al. 2008) can also be classified into this category.
However, in many settings the exact form of the prediction rule is not known or varies depending on the definition of outcome, duration of follow-up and the population under study. Moreover, some rules might use dynamic classification thresholds which depend on certain patient characteristics (for example, age). Finally, the use of risk prediction model serves only as one aid in the clinical decision (D’Agostino & Pencina 2012) and thus it may not be possible to define it precisely. In these settings, reliance on the global measures of model performance (AUC, discrimination slope) might be the best one can do.
Thus, researchers studying the contribution of new biomarkers are left with the choice of either reporting metrics that are more global and objective, yet less clinically relevant (ΔAUC, IDI), or measures that have immediate clinical interpretation but may lack universal applicability due to their dependence on often arbitrarily-selected thresholds (ΔNB, ΔRU and NRI). The difficulty of moving the AUC beyond a certain level and the multitude of the alternative measures have led many applied researchers to believe that important improvements in model performance would be missed if one relied only on the increase in the AUC. But the fact that markers with very large effect sizes are needed to increase the AUC does not automatically imply that small increases are sufficient and likely to translate into meaningful gains in clinical performance.
In this paper we attempt to address this question by studying the relationship between the global (AUC, discrimination slope) and clinical measures (sensitivity, specificity, Youden’s index, NB, RU) which would enable us to translate the increments in the AUC and IDI into corresponding increases in clinical metrics. If the same increase in the AUC (or discrimination slope) translates into the same gain in performance of a clinical rule, irrespective of the strength of discrimination of the baseline model, the argument against the use of the AUC due to its inability to increase for better baseline models will have to be re-evaluated. If, on the other hand, the relationship of increase in AUC with gain in performance depends on baseline AUC, the argument against the change in AUC as a measure of model improvement will be supported.
The paper is organized as follows. In section 2 we introduce the notation, define our measures of interest and derive basic relationships under multivariate normality. In section 3 we study the impact of the increments in the AUC and discrimination slope on measures of clinical performance. An example based on the Framingham Heart Study model for incident atrial fibrillation (AF) is presented in section 4 and discussion and summary of main findings are given in section 5.
2. Measures of performance
Our goal is to gain insight into the numerical values of popular performance metrics applied to models with binary outcomes. The problem can be greatly simplified if we assume multivariate normality of risk factor distribution within event and non-event subjects. Once normality is adopted, we can further assume that the prediction model was built using linear discriminant analysis which is optimal in terms of maximizing various performance metrics, including the AUC (Su & Liu 1993). Because we are concerned with concepts, rather than exact relationships and inference, the developments presented below do not account for the uncertainties due to estimation.
2.1 Relationships under assumption of linear discriminant analysis
We adopt notation similar to Pencina, D’Agostino and Demler (2012). Let D be an event indicator (1 for the events, 0 for the non-events) and X represent a vector of m risk factors. Assume: X | D=1 ~ N(μ1,∑1) and X | D=0 ~ N(μ0,∑0), where μ1,μ0 are the vectors of means and ∑1,∑0 are the variance-covariance matrices and N denotes the normal distribution. Furthermore, let us assume homoscedasticity with ∑ = ∑1 = ∑0. Furthermore, let δ = μ1 − μ0 denote the vector of the mean difference between the events and non-events. The LDA classification function is given by:
| (1) |
where b =∑−1·δ. Furthermore, is known as the (squared) Mahalanobis (1936) distance between event and non-event subjects. With the above definitions and relying on the assumption of normality we have:
| (2) |
| (3) |
Reliance on formula (1) for the classification function (assigning a person to an event if and to a non-event otherwise) implies equal prior probabilities of being classified as event versus non-event. This may not be realistic, especially in situations where the true event rate, p = P(D=1), is not equal to 0.5. However, empirical priors can be easily built into function (1) leading to an updated classification function:
| (4) |
Assuming equal costs of misclassification, one would assign a person to the event category if and to non-event otherwise. This rule can be easily updated with misclassification costs (Morrison 1990). Denote by c10 the cost of classifying a true event as a non-event and by c01 the cost of classifying a true non-event as an event. Then the classification rule would classify a person as an event if:
| (5) |
Rule (5) can be expressed in terms of predicted probability of event based on the LDA model. This probability is calculated as . Rephrasing rule (5) in terms of probabilities, we classify a person as an event if
| (6) |
If t denotes the probability threshold for classification as event, rule (6) implies a relationship between this threshold and misclassification costs known from decision theory: .
2.2. Classification into 2 categories
With the above notation and assumptions we are ready to express the familiar classification performance metrics in easy to calculate form. Let Φ denote the standard normal cumulative distribution function. We have:
Sensitivity at threshold t:
| (7) |
Specificity at threshold t:
| (8) |
We observe that both sensitivity and specificity depend only on the squared Mahalanobis distance, true disease prevalence (or incidence) and classification threshold. The latter two quantities can be considered constant. Thus, assuming a fixed classification threshold, the following summary metrics also depend only on the squared Mahalanobis distance.
Youden’s index at threshold t (Youden 1950):
| (9) |
Net benefit at threshold t (Vickers & Elkin 2006):
| (10) |
Relative utility at threshold t (assuming no treatment in the absence of risk prediction as in (Baker et al. 2009)):
| (11) |
We note that larger values for each of the above three metrics imply better performance; however, unlike the Youden’s index, net benefit and relative utility can take negative values.
2.3 Measures of improvement in model performance based on classification into two categories
Measures defined by formulas (7)-(11) characterize performance of a single model based on p predictors. Now we can define measures of improvement in model performance. Assume we constructed another model adding n additional (Y, multivariate normal) predictors to the m predictors (X) in the original model and used the LDA to obtain the classification functions. Denote by pm+n (X,Y) predicted probabilities based on the “new” model and by Mm+n2 the corresponding squared Mahalanobis distance. Because p and t are not affected, the metrics presented by (7)-(11) for the case of m predictors remain the same in the case of m+n predictors, with subscript m replaced by m+n. We define the following measures of improvement in model performance:
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
The last two equations defined the original and weighted net reclassification improvement introduced as a measure of correct re-assignment into clinically meaningful risk categories (Pencina & D’Agostino 2008, Pencina et al. 2011). The above definitions hold without the LDA or normality assumptions. However, with these additional assumptions, we observe that for a given threshold t, they are all uniquely determined by the squared Mahalanobis distances for models based on m and m+n predictors.
2.4 Global measures of performance
Su and Liu (1993) have shown that under our LDA assumptions the AUC can be expressed as a simple function of the squared Mahalanobis distance:
| (18) |
Furthermore, Pencina, D’Agostino and Demler (2012) have shown that discrimination slope is also a function of squared Mahalanobis distance and the disease prevalence (incidence) rate p:
| (19) |
Another measure of overall performance can be constructed by calculating the continuous NRI(>0) (Pencina et al. 2011) for the risk model of interest compared to the “intercept-only” or “null” model. The continuous NRI(>0) was defined as a measure of incremental value and not global performance, yet if we use a model which assigns the probability equal to the event rate for every individual as the baseline model (i.e. “intercept-only” or “null” model), we obtain a measure of global performance which quantifies the gain over the “null” model. This logic is analogous to the likelihood ratio approach, where the global test of the model at hand is conducted against the null model. We have:
| (20) |
Thus continuous NRI of a model with m predictors against the null model which assign a constant to everyone is equal to twice the Youden index evaluated at the prevalence (incidence) rate p. This result does not require the LDA or normality assumptions to hold. Hence, we do not need to consider NRI(>0) separately. To measure improvement in model performance, we can calculate the increases in the AUC and discrimination slope, known as the ΔAUC and IDI (Pencina & D’Agostino et al. 2008).
3. Implications under normality
In this section we use the set of formulas and relationships developed earlier to gain some insight into the numerical values of the metrics of model performance. We address the question whether increments in the AUC and discrimination slope achieved over different starting values should be interpreted differently.
Several researchers have argued that the AUC is not sensitive enough to detect smaller but possibly clinically meaningful improvements in model performance. Part of this perception can be attributed to the incorrect application of the test of DeLong et al. (DeLong et al. 1988) to compare two nested AUCs. Demler et al. (2012) have shown that in such applications the test is overly conservative. Still, it remains true that very large odds ratios (Pepe et al. 2004) or effect sizes (Ware 2006) of the new predictors are necessary to appreciably increase the AUC beyond the baseline model, especially in situations where the baseline model performs well (i.e. has high AUC). A more important question might be as follows: Suppose we have two different baseline models with AUCs that are not necessarily equal; when a set of risk factors is added to each model and the resulting increase in the AUC is the same for each model, do these two increases have the same interpretation across the two baseline models? If the AUC is used as the performance standard, the answer is obviously yes. However, if we use sensitivity, specificity or one of the threshold-based metrics defined in section 2as a measure of model improvement instead of the AUC, does this statement still hold true?
To address the above problem we have to decide on what basis the classification threshold would be determined. One approach, quite commonly used for diagnostic devices, requires that certain specificity is achieved. This specificity is then translated into the classification threshold. An alternative approach uses costs of misclassification to determine the threshold, using identities similar to the one given by formula (6). We explore the implications of both approaches here.
3.1 Sensitivity at fixed specificity as function of AUC and discrimination slope
Some authors have convincingly argued that for set specificity, one would use the partial area under the curve rather than the overall AUC (Dodd and Pepe 2003). However, the overall AUC remains the reporting standard for a vast majority of applications (Tzoulaki et al. 2009) and is the focus of this paper.
Solving equation (8) for and equation (18) for Mm2 and substituting into equation (7) we obtain:
| (21) |
where Φ−1 is the inverse of the standard normal cumulative distribution function and Sp is the desired level of specificity. A more general form of equation (21) can be obtained using the results of Su and Liu (1993). Assume unequal but proportional variances within event groups, i.e. ∑1 = c·∑ and ∑0 = ∑, where c is the proportionality constant. Then it can be shown (see equation (3) in Su and Liu (1993)) that
| (22) |
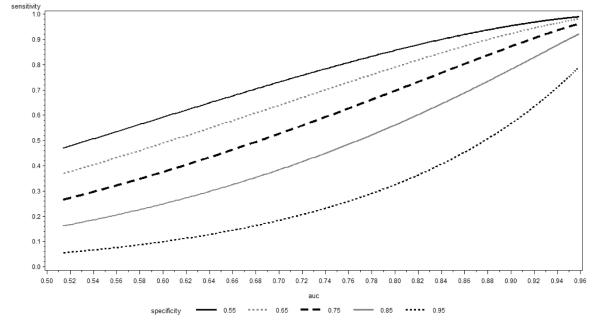
In Figure 1 we plot sensitivity calculated using (21) as a function of the AUC for selected levels of specificity equal to 0.95, 0.85, 0.75, 0.65 and 0.55. We observe that for larger values of specificity, the derivative of the presented curve increases for most of the range whereas for smaller specificity it decreases. Using the definition of the normal cumulative distribution function and some calculus it can be shown that the inflection point happens at observation has important practical consequences. If large specificity is desired, reliance on the increase in the AUC as a measure of model performance may lead to under-estimation of the impact of new predictors on sensitivity. On the other hand, for small specificities, larger increases in sensitivity are observed for smaller baseline AUCs: in this case reliance on a fixed increment in the AUC might over-estimate the impact on sensitivity; however, we note that specificity values much below 0.75 are unlikely to be acceptable in the majority of practical applications. The results remain similar when we relax the assumption of homoscedasticity and employ equation (22) with various choices of c.
Figure 1.
Sensitivity at constant Specificity as function of AUC
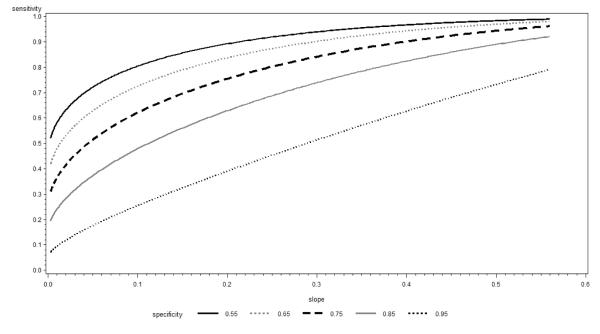
In Figure 2 we present the corresponding plots of sensitivity but this time against the discrimination slope as the independent variable. Discrimination slope depends on the prevalence (incidence) of events and thus we examined these plots for rates varying between 0.05 and 0.50. Since the conclusions were similar, Figure 2 uses event rate of 0.1 as an example. We observed that the derivative of the sensitivity line remains relatively constant as a function of the discrimination slope only in the case of specificity equal to 0.95 and decreases with the increasing discrimination slope for smaller values of specificity with this effect amplified as specificity becomes smaller. Thus, using the gain in sensitivity at a pre-specified specificity as a metric, a fixed increment in discrimination slope adequately describes the impact of new predictors for very large values of specificity and over-estimates this impact for smaller values. This observation holds across different event rates; however, the pool of specificity values for which the fixed increment in discrimination slope does an adequate job widens with increasing event rate (i.e. the value of specificity do not have to be as high if the event rate is higher).
Figure 2.
Sensitivity at constant Specificity as function of Discrimination Slope
In conclusion, if maximizing sensitivity at a fixed specificity level will be used in clinical applications, the increments in the AUC translate into proportional increments in the sensitivity as long as the pre-specified values of specificity are not too high or too low. For the low values the fixed increment in the AUC over-estimates and for the high values it under-estimates achievable gains in sensitivity. For very large values of specificity, the discrimination slope provides a better metric. However, for low and intermediate values of specificity, the fixed increment in the discrimination slope over-estimates the achievable gain in sensitivity.
One of the criticisms of reliance on a fixed level of specificity might be that it requires a change in the classification threshold when the model is updated with new risk factors. This in turn implies that the fraction of people classified as high risk is different for the two models and hence the comparison of sensitivities is not entirely fair (we would expect a model which assigns more people as high risk to have a better sensitivity). To address the extent of this issue we examined the fractions of people classified as high risk as a function of model strength expressed by the AUC. Overall, these differences were small. For example, when the AUC increased from 0.65 to 0.70, the fraction of individuals classified as high risk increased from 5.9% to 6.3% at specificity=0.95 and from 27% to 27.8% at specificity=0.75. The corresponding increases were also small when the AUC increased from 0.85 to 0.90: 8.8% to 10.2% at specificity=0.95 and 30.4% to 31.2% at specificity=0.75.
3.2 Relative utility and Youden’s index as functions of AUC and discrimination slope – theoretical results for equal variances
In many instances classification is made based on a pre-established threshold rather than the desired level of specificity. Any metric has to depend on the selection of this threshold. Moreover, fixing the threshold implies that both sensitivity and specificity can change when the underlying model improves. As outlined in the previous section there are numerous ways to combine these two into a single metric. The simplest combination is achieved by the Youden (1950) index, which weights sensitivity and specificity equally. This weighting achieves certain optimality properties as outlined by Hilden and Glasziou (1996). However, it has been criticized by the advocates of the decision analysis who point out that it implies weighting of misclassification costs proportional to the odds of non-events, which may not be realistic in many applications (Steyerberg et al. 2012). Instead, they propose threshold-based weightings as presented in the definitions of net benefit (10) and relative utility (11). Of note, the problem of optimal threshold selection is not present in decision analysis – the threshold is based on costs which need to be known or estimated a priori.
One measure merits particular attention as it combines several metrics discussed thus far: the Youden index evaluated at the threshold equal to the event rate (Y(p)). We note that it is equal to NRI(> 0) evaluated against the null model and to the relative utility and is proportional to the net benefit. Its increment is also equal to the 2-category NRI with the event rate as a single threshold. Furthermore, equations (7) and (8) imply that in this case the sensitivity and specificity are equal. All of this makes Y(p) an obvious metric against which to compare the AUC and discrimination slope. However, event rate used as a threshold with equal sensitivity and specificity implies rather low to intermediate levels of specificity that may not be acceptable in many settings. That is why we will also consider classification based on cut-offs equal to twice or thrice the event rate. In the latter case the Youden index and relative utility (which still remains proportional to net benefit) use different weights and thus we present both in our plots.
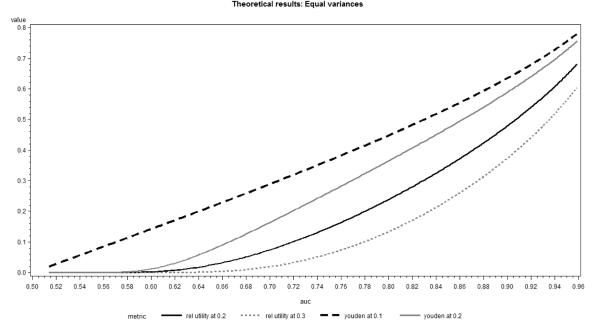
In Figure 3, we present these metrics as a function of the AUC when the incidence rate equals 0.1. We observe that the relationship between AUC and Youden’s index (or relative utility) calculated at the event incidence is approximately linear for most of the range. As the classification threshold increases, the relationship quickly moves away from linearity, such that the same increase in the AUC for weaker baseline models translates into much smaller increase in Youden’s index or relative utility. The nature of the relationships remains similar for different incidence rates.
Figure 3.
Youden Index and Relative Utility as function of AUC
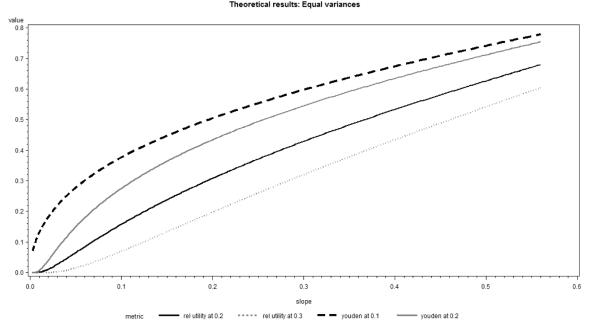
The situation changes substantially when we use the discrimination slope rather than the AUC as the independent variable (Figure 4). Then the relative utility at the threshold equal to 0.3 (three times the incidence rate) displays roughly linear relationship with the discrimination slope, whereas relative utilities and Youden indices for lower thresholds, including the incidence rate itself, suggest a larger impact of the change slope for weaker models. Similar relationships hold for different event rates.
Figure 4.
Youden Index and Relative Utility as function of Discrimination Slope
Thus we conclude that for smaller risk thresholds (i.e. closer to the incidence rate) a fixed increment in the AUC translates into approximately similar increases in the Youden index or relative utility. On the contrary, for larger risk thresholds, the same increment in the AUC leads to much larger gains in the Youden index and relative utility for models with higher baseline AUC values. A different pattern occurs for the discrimination slope, where for large risk thresholds (multiples of the event rate) fixed changes in the AUC lead to constant or even increasing changes in the Youden index or relative utility as a function of the baseline model AUC. For smaller risk thresholds (close to the event rate) the reverse is true: the same fixed increments in the AUC have a decreasing impact on the change in the Youden index or relative utility as a function of the baseline model AUC. Similar general relationship remains approximately true for different event rates.
3.3 Relative utility and Youden’s index as functions of AUC and discrimination slope – simulated results for unequal variances
While in our experience the homoscedastic linear discriminant model provides a reasonable approximation in many real-life cases, such assumption may be overly restrictive. Moreover, logistic regression has practically replaced linear discriminant analysis as a method of obtaining predicted probabilities in models with binary outcomes. Thus, it is of interest to see how well our results hold when variances are not equal within the event groups and predicted probabilities come from logistic regression. We simulated univariate normal predictors, separately for the event and non-event groups. The mean of the predictor was equal to zero among non-events and allowed to change among events from 0.1 to 5.0 to cover the full range of AUCs and discrimination slopes. We considered situations with predictor variance ratios (variance for event versus variance for non-events) between 0.5 and 2.0. Larger ratios were not practical, as they led to either sensitivity or specificity being always equal to zero (regardless of the effect size) for classification thresholds different than the event rate.
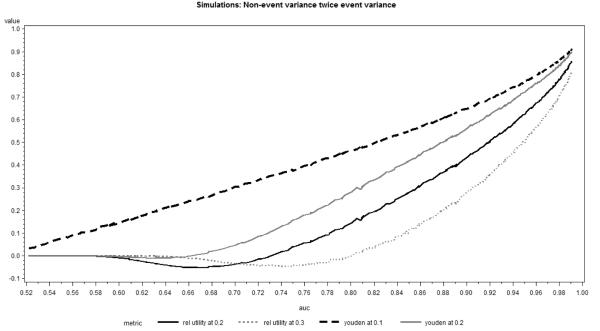
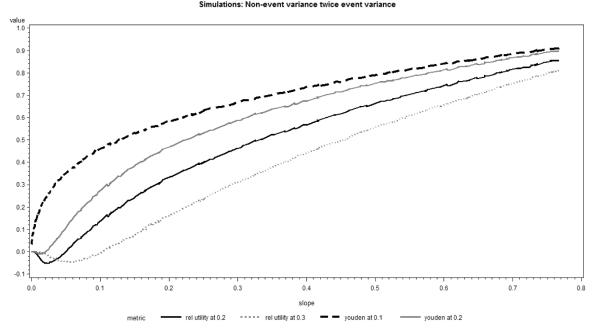
In general, the results of simulations confirmed our theoretical findings and the respective plots in Figures 5 and 6 were similar to those presented in Figures 3 and 4. For all scenarios considered, the relationship of AUC and Youden’s index or relative utility at incidence rate remained fairly linear. Even though the general form of the relationship remained similar to other situations, in the case of non-event variance substantially larger than the event variance and large classification thresholds (at least twice the incidence) relative utility and Youden’s index briefly decreased with increasing AUC or discrimination slope (Figures 5 and 6). This finding is mainly of theoretical interest, because it can be explained by the extremely low sensitivity in this setting, which is not likely to occur in practical applications.
Figure 5.
Youden Index and Relative Utility as function of AUC
Figure 6.
Youden Index and Relative Utility as function of Discrimination Slope
4. Practical example
To illustrate the relationships described in the previous section we analyzed Framingham Heart Study data used to construct a prediction model for 10-year incidence of atrial fibrillation (AF). This data has been described in detail by Schnabel et al. (2010). A sample of 3120 Framingham participants aged 29 to 86 free of AF at baseline examination between 1995 and 1998 were available for analysis. A total of 203 cases of AF occurred within 10 years of follow-up, giving an event rate of 0.065 (for simplicity we ignore the time-to-event aspect of the data; however, we note that all metrics presented here generalize to this setting). Four logistic regression models were fit: the baseline model and then three additional models with variables subsequently added to the previous model. The variables used in the baseline model and the order of the subsequent variables added to the model were selected artificially to better illustrate our theoretical findings. Model 1 included sex, body mass index (BMI), height and previous diagnosis of congestive heart failure (yes/no). In Model 2, we added systolic blood pressure to Model 1; in Model 3, we added age to Model 2. Finally, in Model 4 we added prevalence of hypertension treatment (yes/no) and b-natriuretic peptide to Model 3. The variables included were not necessarily normally distributed and some of them were binary. This was done on purpose to see if the theoretical findings developed under normality are generally followed in a real life application. We considered risk cut-offs at the event rate (0.065) as well as twice and thrice the event rate (0.130 and 0.195). The AUCs, discrimination slopes, Youden indices, relative utilities and levels of sensitivity at specificity fixed at 0.75, 0.85 and 0.95 were estimated directly from the data.
The results are presented in Table 1 where we focused mainly on comparing Model 1 versus Model 2 and Model 3 versus Model 4, as the difference in the AUCs between these model pairs were similar (0.038 and 0.037). In general, the results agree with our theoretical findings. We note that that even though the increments in the AUC are similar, the corresponding increments in discrimination slope are different – IDI comparing models 1 and 2 equals only 0.012 and comparing models 3 and 4 is 0.033. Based on our theoretical finding we would expect the changes on relative utility/Youden index at the cut-off of 0.065 to be similar for models 1 versus 2 and 3 versus 4, since the increments in the AUC we were similar. This is in fact the case. Furthermore, the same is true for sensitivity at specificity levels fixed at 0.75 and 0.85. On the other hand, we would expect the increases in relative utility and Youden index at 0.195 (three times event rate) to be larger going from model 3 to 4 than from model 1 to 2, given the difference in discrimination slopes. Our data confirms these expectations.
Table 1.
Change in performance measures for different models for prediction of incident atrial fibrillation.
| Model* | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| AUC | 0.625 | 0.663 | 0.767 | 0.804 |
| Discrimination Slope | 0.014 | 0.026 | 0.073 | 0.106 |
| Yo(0.065)=RU(0.065) | 0.174 | 0.225 | 0.397 | 0.459 |
| Yo(0.130) | 0.024 | 0.101 | 0.269 | 0.388 |
| Yo(0.195) | 0.021 | 0.029 | 0.186 | 0.273 |
| RU(0.130) | 0.011 | 0.041 | 0.131 | 0.262 |
| RU(0.195) | 0.011 | 0.004 | 0.071 | 0.131 |
| Sens at Spec=0.95 | 0.079 | 0.148 | 0.232 | 0.325 |
| Sens at Spec=0.85 | 0.261 | 0.320 | 0.483 | 0.547 |
| Sens at Spec=0.75 | 0.404 | 0.468 | 0.626 | 0.695 |
Model 1 contains sex, BMI, height and previous diagnosis of congestive heart failure; Model 2 contains Model 1 variables plus systolic blood pressure; Model 3 contains Model 2 variables plus age; Model 4 contains all Model 3 variables plus hypertension treatment and B-natriuretic peptide.
5. Discussion
In this paper we investigated the relationship between global and clinical (category-based) measures of model performance. Our developments under multivariate normality, suggest that if the models at hand are to be translated into clinical rules which do not require very large specificity (risk threshold is closer to the event rate), the AUC is an adequate global measure of improvement in model performance. Its increments translate into similar increments in the measures of clinical performance and the claim that the AUC masks important improvements that could be achieved in the clinical setting are unfounded. If on the other hand, highly specific rules are desired (risk threshold is much larger than the event rate), the reliance on the AUC may hide potentially meaningful improvements in the metrics of clinical performance.
We have also assessed the behavior of the discrimination slope which has been proposed as an alternative to the AUC in the assessment of discrimination and whose increment, known as the IDI, has been suggested as a more sensitive measure of incremental value of novel markers that the change in the AUC. Our results suggest that if large specificity is desired, the discrimination slope does in fact lead to a more accurate assessment of incremental value – its relationship with measures of clinical performance (sensitivity at high specificity levels, relative utility or Youden index at high risk thresholds) is approximately linear, which indicates that the same increment in the discrimination slope translates into similar increments in the clinical measures. However, in cases of lower specificity, the discrimination slope may over-estimate the clinical impact of new predictors added to a model with good discrimination: the slope will tend to increase faster than the clinical metrics.
Our suggestion of adequacy of the AUC should not be confused with the fact that the AUC is harder to increase if the baseline model performs well. Under normality, this is a simple consequence of equation (18) and the shape of the normal cumulative distribution function. Thus, while increasing the AUC from 0.65 to 0.66 may mean the same thing as increasing it from 0.85 to 0.86, yet the latter increase is much harder to accomplish.
The important limitations of our study include the assumption of multivariate normality, linear discriminant analysis and limited number of clinical metrics and risk thresholds considered. Extensions of the theoretical findings to non-normal settings and survival models are necessary to support more general conclusions, even if they were to be based on simulations. We submit that we employed the most popular metrics of clinical performance, but acknowledge that not everyone may agree with us. Finally, the effects seem monotone with respect to the risk threshold and we selected thresholds that seem more realistic from the practical standpoint, so we do not expect that major new insights could be derived from considering more thresholds. As an interesting side, we point out that the choice of event rate as the default risk threshold may not be unreasonable in settings were no established cut-offs exist and costs of misclassification are too difficult to ascertain. If this selection is made, several distinct metrics attain the same value. Making such selection, however, one must be mindful of the misclassification costs it implies as well as of the fact that it implies poor specificity is most settings.
In summary, we suggest that it is reasonable to report the AUC increment because changes in the AUC tend to be proportional to changes in clinical measures of prediction performance. However, this proportionality does not always hold. If the application of a risk model is anticipated and clinically relevant measures can be identified then these should be reported as well.
Acknowledgements
This research has been supported by National Heart, Lung, and Blood Institute’s Framingham Heart Study; contract/grant number: N01-HC-25195. Dr. Pencina has been additionally supported by NIH/ARRA Risk Prediction of Atrial Fibrillation; grant number: RC1HL101056.
Contributor Information
Michael J. Pencina, Boston University, Dept. of Biostatistics Harvard Clinical Research Institute CrossTown, 801 Massachusetts Ave. Boston, MA 02118 Tel. 617-358-3386 mpencina@bu.edu.
Ralph B. D’Agostino, Boston University, Dept. of Mathematics and Statistics Harvard Clinical Research Institute 111 Cummington St. Boston, MA 02215.
Joseph. M Massaro, Boston University, Dept. of Biostatistics Harvard Clinical Research Institute CrossTown, 801 Massachusetts Ave. Boston, MA 02118.
References
- Baker SG, Cook NR, Vickers A, et al. Using relative utility curves to evaluate risk prediction. J R Stat Soc Ser A Stat Soc. 2009;172(4):729–748. doi: 10.1111/j.1467-985X.2009.00592.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook NR. Use and misuse of the receiver operating characteristics curve in risk prediction. Circulation. 2007;115(7):928–935. doi: 10.1161/CIRCULATIONAHA.106.672402. [DOI] [PubMed] [Google Scholar]
- Cox DR. Regression Models and Life Tables. J. R. Statist. Soc. Series B. 1972;34:187–220. [Google Scholar]
- DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing areas under two or more correlated reciever operating characteristics curves: a nonparamentric approach. Biometrics. 1988;44(3):837–845. [PubMed] [Google Scholar]
- Demler OV, Pencina MJ, D’Agostino RB., Sr. Misuse of DeLong test to compare AUCs for nested models. Statist Med. 2012;31:2577–2587. doi: 10.1002/sim.5328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodd, Pepe MS. Partial AUC estimation and regression. Biometrics. 2003;54:614–623. doi: 10.1111/1541-0420.00071. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The use of multiple measurements in taxonomic problems. Annals of Eugenics. 1936;7:179–88. [Google Scholar]
- Gail MH, Pfeiffer RM. On criteria for evaluating models of absolute risk. Biostatistics. 2005;6(2):227–239. doi: 10.1093/biostatistics/kxi005. [DOI] [PubMed] [Google Scholar]
- Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- Hilden J, Glashiou P. Regret Graphs, Diagnostic Uncertainty and the Youden’s Index. Statist Med. 1996;15:969–986. doi: 10.1002/(SICI)1097-0258(19960530)15:10<969::AID-SIM211>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- Mahalanobis PC. On the generalized distance in statistics. Proceedings of the National Institute of Sciences of India. 1936;2:49–55. [Google Scholar]
- Morrison DF. Multivariate Statistical Methods. 3rd ed McGraw-Hill; New York: 1990. [Google Scholar]
- Pencina MJ, D’Agostino RB, Sr., D’Agostino RB, Jr., et al. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Statist Med. 2008;27(2):157–172. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
- Pencina MJ, D’Agostino RB, Sr., Steyerberg E. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Statist Med. 2011;30(1):11–21. doi: 10.1002/sim.4085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pencina MJ, D’Agostino RB, Demler OV. Novel metrics for evaluating improvement in discrimination: net reclassification and integrated discrimination improvement for normal variables and nested models. Statist Med. 2012;31:101–113. doi: 10.1002/sim.4348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe MS, Janes H, Longton G, et al. Limitations of the Odds Ratio in Gauging the Performance of a Diagnostic, Prognostic, or Screening Marker. Am. J. Epidemiol. 2004;159(9):882–890. doi: 10.1093/aje/kwh101. [DOI] [PubMed] [Google Scholar]
- Schnabel RB, Larson MG, Yamamoto JF, et al. Relations of Biomarkers of Distinct Pathophysiological Pathways and Atrial Fibrillation Incidence in the Community. Circulation. 2010;121(2):200–207. doi: 10.1161/CIRCULATIONAHA.109.882241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010 Jan;21(1):128–38. doi: 10.1097/EDE.0b013e3181c30fb2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steyerberg EW, Pencina MJ, Lingsma HF, et al. Assessing the incremental value of diagnostic and prognostic markers: a review and illustration. Eur. J. Clin. Invest. 2012 Feb;42(2):216–228. doi: 10.1111/j.1365-2362.2011.02562.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su JQ, Liu JS. Linear Combinations of Multiple Diagnostic Markers. J. Am. Stat. Assoc. 1993;88:1350–55. [Google Scholar]
- Tzoulaki I, Liberopoulos G, Ioannidis JPA. Assessment of claims of improved prediction beyond the Framingham risk score. JAMA. 2009;302(21):2345–52. doi: 10.1001/jama.2009.1757. [DOI] [PubMed] [Google Scholar]
- Vapnik V. Statistical Learning Theory. Wiley; New York: 1998. [Google Scholar]
- Vickers AJ, Elkin EB. Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making. 2006;26(6):565–574. doi: 10.1177/0272989X06295361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker SH, Duncan DB. Estimation of the probability of an event as a function of several independent variables. Biometrika. 1967;54:167–79. [PubMed] [Google Scholar]
- Ware JH. The limitations of risk factors as prognostic tools. N. Engl. J. Med. 2006;355:25. doi: 10.1056/NEJMp068249. [DOI] [PubMed] [Google Scholar]
- Yates JF. External correspondence: decomposition of the mean probability score. Organ Behav. and Hum. Per. 1982;30:132–156. [Google Scholar]
- Youden WJ. Index for rating diagnostic tests. Cancer. 1950;3(1):32–35. doi: 10.1002/1097-0142(1950)3:1<32::aid-cncr2820030106>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]