Transition state stabilization by general acid catalysis, water expulsion, and enzyme reorganization in Medicago savita chalcone isomerase

Abstract

In aqueous solution, Medicago savita chalcone isomerase (CHI) enhances the reaction rate for the unimolecular rearrangement of chalcone (CHN) into flavanone by seven orders of magnitude. Conformations of CHN and their relative free energies in water and CHI were investigated by the thermodynamic perturbation method. In water, CHN adopts two conformations (I and II) with conformation I being higher in energy than conformation II by 3 kcal/mol. Only I can give rise to a near attack conformer (NAC) where the nucleophile O2′ and the electrophile C9 are placed in proximity. In CHI, I binds less tightly than II by ≈2 kcal/mol, resulting in the free energy for NAC formation being ≈2 kcal/mol higher in the enzyme than in water. This unfavorable feature in the ground state of the CHI reaction requires the predominant catalytic advantage to be taken in the step of NAC → transition state (TS). From the molecular dynamics simulations of apo-CHI, CHI complexed with CHN (CHI·CHN) and CHI·TS, we found: (i) Lys-97-general-acid catalysis of the O2′^- nucleophilic addition; (ii) expulsion of three water molecules in the process of TS formation; (iii) release of enzyme structural distortion on TS formation. In the conclusion, CHI's remarkable efficiency of stabilizing the TS and its relatively poor ability in organizing the ground state is compared with chorismate mutase whose catalytic prowess, when compared with water, originates predominantly from the enhanced NAC population at the active site.

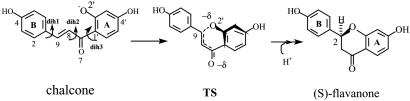
The intramolecular ring-closure reaction of chalcone → flavanone (see Scheme 1) has been studied extensively structurally and mechanistically (1–3). The rate constant k_cat is 38 s^-1 for the enzymatic reaction, and k_non is 10^-6 s^-1 for the water reaction (1). The pH dependences of the noncatalyzed and catalyzed reactions are much the same, suggesting that ionization of the substrate phenolic O2′ occurs in water for both enzymatic and nonenzymatic reactions (1). The crystal structures of chalcone isomerase (CHI) complexed with flavanones reveal an absence of an enzyme-based nucleophilic species near the substrate, showing that CHI is not directly involved in the enzymatic reaction through covalent interaction (3). Drawing on all experimental data, Noel and colleagues (2, 3) explain the catalytic mechanism of CHI as a combination of two effects. One is active site molding of the substrate into the reactive conformation and the other is stabilization of the enolate-like transition state (TS) by forming a hydrogen-bonding network with Thr-48 and Tyr-106 at the ketone O7. However, quantitative comparison of these two contributions has not been reached because of the experimental difficulty of perturbing each component selectively. Here we report our computational studies to assess the relative importance of ground state and TS effects in the CHI catalysis.

Scheme 1.

We have used two methods to achieve this goal. First, we measure the free energies (ΔG_N° values) for forming reactive ground-state conformers [near attack conformers (NACs), ref. 4] in water and at the enzyme active site. Formation of NAC is a prerequisite for reactants to enter the reaction regardless of the environment. ΔG_N° is part of the experimentally determined activation energy (ΔG^‡) as shown in Eqs. 1 and 2. Thus, the difference in ΔG_N° in water and the enzyme (i.e.,

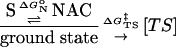[1]

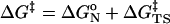[2]

ΔΔG_N° = ΔG_N°|_wat - ΔG_N°|_enz) is an estimation of the ground-state contribution to the kinetic advantage (ΔΔG^‡ = ΔG^‡|_wat - ΔG^‡|_enz) of the enzymatic reaction over the water reaction. Subsequently, the difference in the free energies in water and the enzyme on going from NAC to the TS (ΔΔG_TS^‡) can be obtained by subtracting ΔΔG_N° from the experimentally determined ΔΔG^‡. The value of ΔΔG_TS^‡ can be used as a maximum limit for the enzyme's ability, as compared with water, in stabilizing the TS relative to NAC. The contributing components for the catalysis of NAC to the TS (ΔΔG_TS^‡) can be extracted by comparing structures of enzyme·substrate (E·S) complexes and E·TS. We have observed with chorismate mutase (5) that, when ΔΔG_N° predominates ΔΔG^‡, the enzyme–ligand interaction does not change much on going from E·S to E·TS. Whereas for prolyl isomerase (6) and orotidine decarboxylase (7), ΔΔG_N° accounts for a negligible portion of ΔΔG^‡, and the enzymes bind their respective TSs more tightly than NACs. This finding justifies our use of ΔΔG_TS^‡ for estimating the TS stabilization effect.

Materials and Methods

Parameterization. The rates of the chalcone (CHN) → flavanone rearrangements have been reported for both enzymatic and nonenzymatic reactions when hydroxy substituents are at 4,4′ and 6′ positions of CHN (1). In our study, 4,2′,4′-trihydroxychalcone (CHN) and the corresponding TS were used because K_m·k_cat/k_non is the largest among those examined. The force fields for dihedral rotations of CHN (dih1, dih2, and dih3, defined in Scheme 1) were obtained from the OPLS parameter sets (8). Force-field parameters for dih2 were further calibrated by comparing the energy profile of the molecule 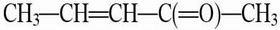calculated at the HF/6-31G(d) level. Atomic charges for the B-phenyl rings of CHN and the TS were adopted from the standard charmm 27 topology file (9). Atomic charges for the other portions of CHN and the TS were calculated by Restrained ElectroStatic Potential (10) fitting to the electrostatic potential generated at the B3LYP/6-31+G^** level by the Merz–Kollman scheme (11). The electrostatic potentials were calculated on the energy-optimized geometries (at the B3LYP/6-31+G^** level) of the model system where the B ring of CHN was replaced by a methyl group. For the ground state, CHN O2′ was protonated to represent O2′ hydrated in water or by the enzyme residue Lys-109 (see Fig. 3). This procedure avoids obtaining a distorted geometry when using an anionic CHN in the gas-phase calculation. For the TS, CHN O2′ was deprotonated and a water molecule was added near O7 to stabilize the enolate form. Such stabilization occurs in both water and the enzyme. The TS structure was confirmed by a single imaginary frequency at the C9—O2′ bond stretching mode at the HF/6-31+G^* level of theory. The final atomic charges of these portions of CHN and the TS are provided in Table 2, which is published as supporting information on the PNAS web site. All these ab initio and density functional calculations were done by using the program gaussian98 (12).

Fig. 3.

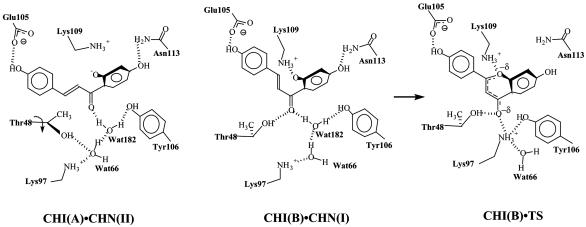
The active-site geometries with CHN and TS bound to it. CHI(A)·CHN(II) and CHI(B)·CHN(I) are the two active-site geometries observed in our MD simulation of CHI·CHN. CHI(B)·TS is the geometry of active site B in our MD simulation of CHI·TS. Active site A is not reactive in catalysis and is not shown as complexed with the TS.

Molecular Dynamics (MD) Simulation. MD simulations of CHN in water, CHN complexed to CHI, and TS complexed to CHI and apo-CHI have been performed by using the program charmm ²⁵ (9). For the water simulation, a molecule of CHN was placed in a periodic water box (30 × 30 × 30 ų). The TIP3P model (13) was used for solvent water and CHN was modeled as anionic by deprotonating O2′. The crystal structure (PDB ID code 1EYQ; ref. 3) of the enzyme from Medicago savita complexed with flavanone was used as the initial coordinates of the enzymes for the CHI·CHN and CHI·TS simulations. The crystal structure of apo-enzyme (1EYP; ref. 3) was used for the apo-enzyme simulation. The flavanones at both active sites of the CHI·flavanone crystal structure were replaced by 2′-oxyanionic CHNs. In the CHI·TS simulation, the O2′—C9 bond length was adjusted to 1.85 Å by using the harmonic force constant of 1,000 kcal·mol^-1·Å^-2 to represent the TS structure obtained from the ab initio calculation. Each of the apo-enzyme and the enzyme complexes was then solvated in a periodic box of TIP3P water with dimensions of 100 × 74 × 60 A³. Each system was energy-minimized during 200 steps of steepest descent and adopted bases Newton–Rapheson methods (9). The energy-minimized system was subsequently heated to 300 K for 30 ps before a production dynamics simulation. During the production dynamics simulation, the temperature was maintained at 300 K by coupling to a heat bath with a coupling constant of 5 s^-1. The pressure was constantly maintained by Berendsen algorithm (14) with an isothermal compressibility of 4.63 × 10^-5 atm^-1 and a pressure coupling constant of 5.0 ps. Coordinates were saved every 100 time steps. The production dynamics simulations were carried out for 5 ns for CHN in water and 1 ns for each of CHI·CHN, CHI·TS, and apo-CHI.

Thermodynamic Perturbation (TP). Free energies required for NAC formation in water and the enzyme were estimated by using TP methods (15, 16) implemented in the thermodynamic simulation method module of the program charmm 27. For the TP calculations MD snapshot structures taken from the respective simulations in equilibrium were used. The size of the water box was reduced to 24 × 24 × 24 ų for the water simulation for computational efficiency. For enzyme simulation, a 25-Å spherical system from each active site centered at CHN O7 was selected, and a stochastic boundary condition was used to simulate a continuous environment. Each system was energy-minimized at every 5° of the dih2, ranging from 0° to 180°. At each window, the system was equilibrated for 200 ps, followed by production dynamics for another 200 ps. During the production dynamics simulation, dih2 was perturbed by ±10°. Perturbation data were recorded every 20 fs.

Results and Discussion

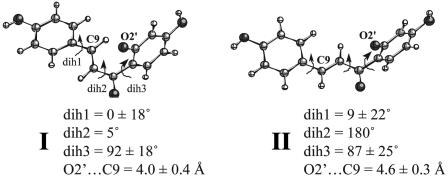
Ground-state conformers of CHN are defined by three dihedral angles: dih1, dih2, and dih3 (Scheme 1). Cis and trans forms of dih1 are identical due to the symmetry of the B ring. A set of MD simulations of CHN in water shows that dih3 is in the range of 50–130° regardless of dih1 and dih2. The distribution of dih3 is bell-shaped and centered at 90°. Geometries of dih3 = 0° or 180° are not local minima despite the maximized conjugation between the phenol and the ketone when coplanar. This finding is probably because the steric conflict between the α,β-conjugated double bond and the bulky 2′-hydroxy substituent of the B ring hinders the planar geometries. Thus, two conformations exist for CHN in water (Fig. 1, CHN I and II). Conformer I (dih2 = ≈0°) has the nucleophilic O2′ and the electrophilic C9 in proximity, whereas conformer II (dih2 = ≈180°) has C9 turned away from O2′. The contact between O2′ and C9 (i.e., the O2′ · · · C9 distance, ≤3.85 Å, based on the charmm 27 parameter set) is a prerequisite for the CHN → flavanone reaction. Because of the molecular structure of CHN, the C9 · · · O2′ distance is a sufficient criterion for determining whether a given conformation is conducive for the reaction. Such reactive conformers are categorized as NACs (4). TP calculations were performed for a total of 8 ns (200 ps for each window × 40 windows) each in water and the two enzyme active sites to determine free energies required for the conversion of II to I (ΔG°_{II → I}) and for the further formation of NAC (ΔG°_{I → NAC}).

Fig. 1.

Two conformers of CHN in water. The structures are taken from the minimum points of the free energy profile (shown in Fig. 2 A).

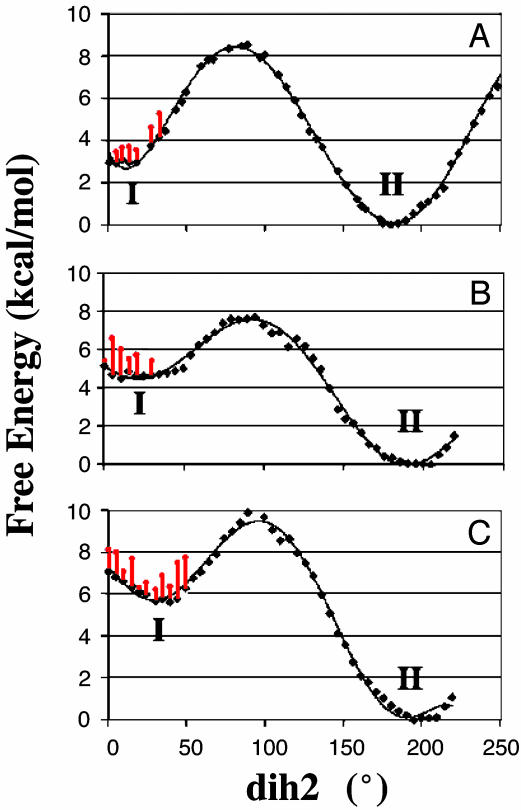
In water conformer II is more stable than I by 3.0 kcal/mol (Fig. 2A). To determine the free energy required for I → NAC conversion, free energy for NAC formation at each dih2 geometry was calculated from the frequency of NAC formation during the dynamics simulation at each window (Fig. 2, red bars). The TP method uses holonomic constraints, making this calculation possible (16). One might expect that the contact between O2′ and C9 could require partial desolvation of O2′ oxyanion, making NAC formation unfavorable. However, we found that NAC of the lowest energy is formed from I at the additional free energy cost of 0.5 kcal/mol at dih2 = 5°. Water molecules hydrating O2′ remain stable even when C9 and O2′ are in contact. Among water molecules in the first hydration shell of O2′, those near C9 exchange with bulk solvent 10–100 times more slowly (≈0.03–0.1 ps^-1) than do others (≈1–10 ps^-1). When O2′ approaches C9, a water molecule near C9 reorients itself such that the plane of H—O—H faces parallel to the plane of the α,β-conjugated double bond. This orientation leaves the space between C9 and O2′ unoccupied and, in turn, makes the C9 · · · O2′ contact feasible without losing water hydrogen bonds at O2′.

Fig. 2.

Free energy profiles of CHN in water (A), enzyme active site A (B), and enzyme active site B (C). Black lines represent changes in free energy when rotating dih2 of CHN. Red bars represent additional free energy costs required to form NAC from each point of the dih2 geometry.

In the M. savita CHI active site CHN binds to the binding pocket that mainly consists of hydrophobic residues. A few electrostatic interactions occur at the hydroxy substituents and the enone group, but most of them are very weak, except for the interactions with Lys-109 and Thr-48/Tyr-106 (Fig. 3 and Table 1). From our MD simulation of a dimeric CHI fully solvated in water, we found that CHN binds to the CHI active site in a position quite different from that of the flavanone in the crystal structure. For instance, the B ring is progressed ≈3 Å toward Glu-105 in CHI·CHN as compared with CHI·flavanone. Despite the difference, however, the major hydrogen bond network in CHI·CHN is similar to the one in the crystal structure of CHI·flavanone. In our MD simulations two rotamers of Thr-48 were seen in the dimeric enzyme, one at each active site (Fig. 3). One Thr-48 rotamer found in the B active site interacts with CHN O7, whereas the other rotamer in the active site A does not form a hydrogen bond with O7. These conformations are stable during the 1-ns simulation period. From the six crystal structures of dimeric CHI·flavanone and apo-CHI, four active sites have Thr-48 conformation similar to that in the active site A of our simulation, and the remaining eight crystal structures have a Thr-48 conformation similar to the active site B of our simulation. From this, we infer that the two Thr-48 rotamers are similar in energy. This inference is in accord with the experimental result that the mutation of Thr-48 into Ala alters K_m by 0.5- to 2-fold, depending on the variation of CHN. Our free energy simulations for dih2 rotation were performed independently for each active site. The free energy content of I is 4.5 kcal/mol above II in the active site A and 5.5 kcal/mol above II in the active site B (Fig. 2 B and C). This finding shows in both active sites that II binds more tightly than I by the energy difference of 1.5–2.5 kcal/mol. This difference is because the enzyme distorts conformer I, as evidenced from the elevated energy level near the region of dih2 = 0°. In the enzyme, the distorted geometry (dih2 = 30–40°) is a local minimum structure of I. We did not find any advantage that CHI might take from this distortion. For example, free energy for NAC formation from the distorted I in the enzyme is similar to that from the planar I in water: 1.5 and 0.2 kcal/mol in the enzyme active sites A and B, respectively, and 0.5 kcal/mol in water. Because the free energies for the II → I conversion are 4.5, 5.5, and 3.0 kcal/mol in the active sites A and B and in water, respectively, the total free energies for NAC formation (ΔG_N°) are 6.0, 5.7, and 3.5 kcal/mol in the active sites A and B and in water, respectively. (In ref. 17, we excluded consideration of the binding of nonproductive conformation II.) Distortion is disadvantageous for the reaction because it breaks the conjugation between the double bond and carbonyl, leading to a reduced electrophilicity of C9. Thus, these features show that the enzymatic reaction does not gain any kinetic advantage over the nonenzymatic reaction from NAC formation, and the catalysis is solely driven by TS stabilization.

Table 1.

The average^* electrostatic interaction distances (Å)

Ligand (atom)...enzyme (atom) or water	CHI·CHN (II)	CHI·CHN (I)	CHI·TS
07...Thr48 (OG1)	5.9 ± 0.6	2.8 ± 0.1	2.9 ± 0.2
07...Lys97 (NZ)	6.8 ± 0.6	6.1 ± 0.4	2.7 ± 0.1
07...Tyr106 (OH)	5.1 ± 0.5	5.0 ± 0.4	4.2 ± 0.3
07...Water (O)†	3.2 ± 0.9	2.7 ± 0.2	3.0 ± 0.3
02′...Lys109 (NZ)	7.3 ± 1.2	3.1 ± 0.7	2.8 ± 0.1
04...Glu105 (OE)	5.1 ± 1.3	4.5 ± 4.4	3.7 ± 0.9
04′...Asn113 (ND2)	3.9 ± 1.8	3.5 ± 0.5	7.1 ± 1.0

^*The values are averaged over the period of 400 to 1,000 ps, during which the ligands are in their equilibrium positions

^†The distance is between O7 of CHN (or TS) and the oxygen of the nearest water molecule in each system; i.e., Wat182 in CHI·CHN(I) and CHI·CHN(II), and Wat66 in CHI·TS (see Fig. 3)

Three Mechanisms for TS Stabilization. By comparing the structures of CHI·CHN(I) and CHI·TS taken from the respective MD simulations, we found three catalytic features in the conversion of CHN(I) to the TS: general-acid catalysis by Lys-97, entropic catalysis by water expulsion, and release of the enzyme backbone strain on formation of the TS. Because CHI·CHN(I) and CHI·NAC are structurally and energetically very similar, these features account for the catalysis on the conversion of NAC to the TS. The starting structures for both CHI·CHN(I) and CHI·TS simulations were derived from the same crystal structure of the CHI·flavanone complex (3). Thus, any change that is observed in the comparison of CHI·CHN(I) and CHI·TS structures is a reflection of differences in the geometry and charge distribution of CHI·CHN(I) and CHI·TS.

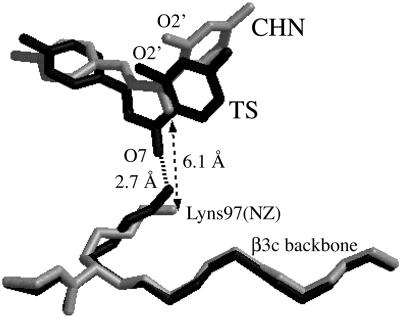
General-Acid Catalysis by Lys-97. Superposition of the MD structures of CHI·CHN(I) and CHI·TS by matching the backbones reveals a significant positional shift of the ligand by 3.4 Å toward Lys-97 in the B active site of CHI·TS (Fig. 4). This movement of the TS occurs within 200 ps from the starting position. The TS remains stable at this shifted position throughout the simulation. Because Lys-97 is deep inside the active site, the movement of CHN toward Lys-97 in the active site B requires the ligand to enter the hydrophobic cleft. The cleft is too narrow for the bulky ground state because of the van der Waals repulsion between C9 and O2′, but partial formation of the C9—O2′ bond in the TS allows the TS to fit in the cleft. This interaction in reality will accompany proton transfer from the protonated amino group of Lys-97 to the TS O7, stabilizing the developing negative charge at the enolate O7 (Scheme 1). The importance of Lys-97 as the general acid, however, is not recognized in the sequence alignment (3). A psi-blast search (18) of sequence databases reveals that Lys-97 is conserved only in the same legume family. Enzymes of other families have methionine or threonine at this position. Only CHIs from the legume family can use both 6′-hydroxy and 6′-deoxychalcone as substrates, whereas the enzymes from other family members isomerize only 6′-deoxychalcone (19). It is possible that they have evolved differently after a certain branch point to cope with specialized biological requirements. Studies of a Met or Thr mutant of Lys-97 of the legume family enzymes would be valuable.

Fig. 4.

Superposition of enzyme-bound CHN(I) (gray) and the TS (black) when matching the backbone of the β3c strand. Only heavy atoms are shown.

The movement of the TS observed in the active site B does not occur in the active site A, leaving O7 of the TS ≈4.0 Å from the amino terminus of Lys-97. As in the ground state, the Thr-48 hydroxyl interacts with O7 in the active site B but not in the active site A. This finding suggests that the interaction between Thr-48 and O7 increases the probability of the correct movement of the TS toward Lys-97, which may explain the 1,000-fold slower reaction rate of the Thr48Ala mutant as compared with the wild-type enzyme (2).

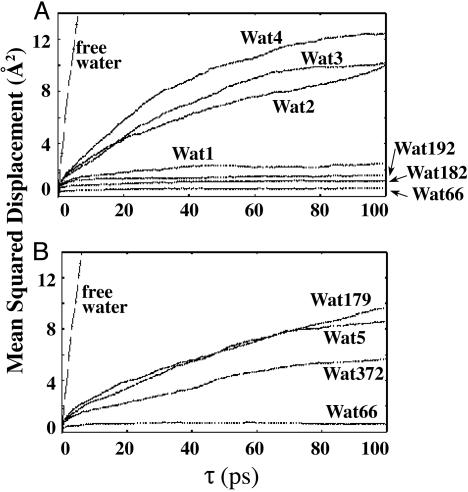
Water Expulsion. In the crystal structures of CHI complexed with flavanones only one to two water molecules are seen in the backside of the ligand-binding pocket. In our MD simulations of CHI·CHN(I) seven water molecules are trapped in the binding site. They remain in the cavity throughout the 1-ns MD trajectory of CHI·CHN(I). Analysis of the mean squared displacement (MSD; Fig. 5) of these water molecules reveals that four of them (Wat1, Wat192, Wat182, and Wat66 in Fig. 5A) are tightly bound in the active site, having <2 Ų MSD for τ ≤ 100 ps. Three others (Wat2 to Wat4) are weakly bound, circulating inside the binding site that is capped by the A ring of CHN. In the CHI·TS, only one water molecule (Wat66) is tightly bound (MSD ≤ 2 Ų/100 ps) and three other water molecules (Wat5, Wat372, and Wat179) are weakly bound (Fig. 5B). Thus, on going from CHI·CHN(I) to CHI·TS, three tightly bound water molecules are released. This release is an entropic advantage of the CHI reaction relative to the water reaction.

Fig. 5.

MSDs of enzyme-bound water molecules as functions of time τ in CHI·CHN(I) (A) and CHI·TS (B). Square of displacement during τ picoseconds was calculated for a certain water molecule every 100 ps of the production dynamics. MSD is a mean value of the square displacement averaged over the trajectory (i.e., MSD(τ) = 〈|p(t) - p(t + τ)|²〉, where p(t) is position vector of a water molecule at time t and the average is taken over the simulation length). A free water molecule is represented by a straight line, whereas a tightly bound water exhibits little change in MSD as τ increases. Wat1 through Wat5 are water molecules that have been incorporated in the simulation by the solvation process. The remainder of the water molecules are present in the parent crystal structure (1EYQ), and the labeling number is preserved as in the crystal structure. In the crystal structure, only Wat66 and Wat182 are seen as bound at the active site.

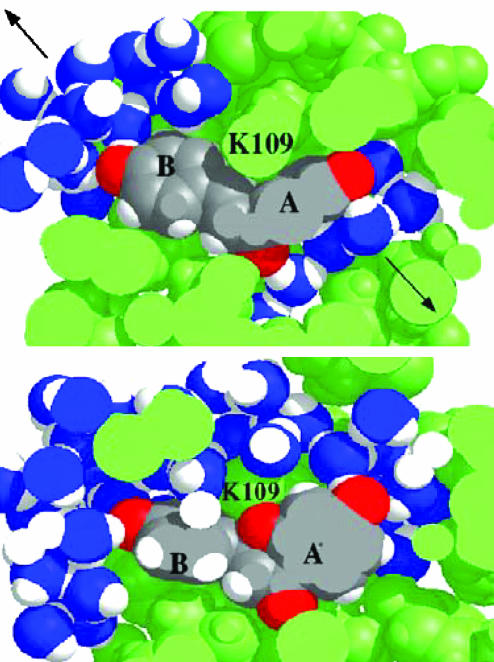
The molecular basis for the release of water molecules appears to lie in the structural and positional change of CHN during the reaction. In CHI·CHN, the A ring of CHN lies parallel to the protein surface because of the C9—O2′ van der Waals repulsion (Fig. 6A). This caps the binding site and prevents CHN from going further inside the narrow binding cleft. The capped binding site has room sufficient to hold seven water molecules. In CHI·TS, however, partial formation of the bond C9—O2′ makes the A ring perpendicular to the surface. This bond formation brings the TS down to the bottom of the active site and at the same time induces expulsion of water molecules (Fig. 6B). Experimental (20) and theoretical (21) estimations of translational entropy that is released when a frozen water molecule becomes completely free are ≈5 kcal/mol. Although the narrow shape of the TS exposes some hydrophobic residues buried in the ground state and this would partially compensate for the entropic gain by water release, the enzymatic reaction would overall have an entropic advantage over the water reaction.

Fig. 6.

The dissected view of CHI·CHN(I)(A) and CHI·TS (B), cutting from the solvent toward the interior of the binding pocket. The water oxygens are blue, the active site residues are green. CHN/TS is identified by its atomic definition.

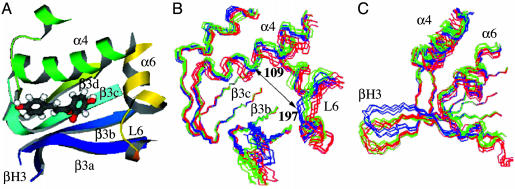
Enzyme Reorganization. Comparing the enzyme backbones from the MD structures of CHI·CHN(I) and CHI·TS shows that the active site becomes open in the TS (Fig. 7). The connecting hairpin βH3 between β3a and β3b is bent toward the active site in the ground state but is distant from the active site in the CHI·TS complex (Fig. 7B). The bending angle measured by Thr-48(O)—Arg-36(HN)—Gly-37(CA) is closer to 180° in CHI·TS by 30° than the CHI·CHN(I) structure. The extended conformation of βH3 in CHS·TS appears to be intrinsically more stable because the bidentate hydrogen bonds formed at the hinge point of the bending, i.e., β3a[residue 36(O)]-β3b[residue 47(HN)] and β3a[36(O)]-β3b[48(HN)] are stable in CHI·TS but not in CHI·CHN(I). This finding is also supported by the observation that βH3 adopts the extended conformation in our simulations of apo-enzyme solvated in water (Fig. 7B). Similarly, loop L6 comes closer to the active site in both CHI·TS and apo-CHI, but is far away in CHI·CHN(I) (Fig. 7C). When choosing Cα of Lys-109 in the α4 helix (Fig. 6B) as a reference point, Cα of Val-197 in L6 is 11.2 ± 0.5 Å from the reference point in CHI·CHN(I), whereas it is 12.1 ± 0.6 Å and 14.3 ± 0.6 Å from the reference point in CHI·TS and apo-CHI, respectively. The cost of moving L6 and βH3 toward the active site in the ground state appears to be paid by van der Waals contacts between CHI and ligand that are present in CHI·CHN(I) but not in CHI·TS and apo-enzyme. Thus, when the bulky CHN(I) becomes the smaller TS, the favorable contact between the ligand and the enzyme disappear and it brings L6 and βH3 back to the geometry favorable in the apo-status. This result suggests that release of the enzyme strain on the formation of the TS contributes to reducing the activation energy.

Fig. 7.

(A) Ribbon representation of the active site backbone when observed from the solvent view. (B) Superposition of apo-CHI (red), CHI·CHN(I) (blue), and CHI·TS (green) structures by matching the backbone of β3c-β3d. The double-headed arrow is between K109 and V197. (C) A lateral view of the structures in B.

Conclusion

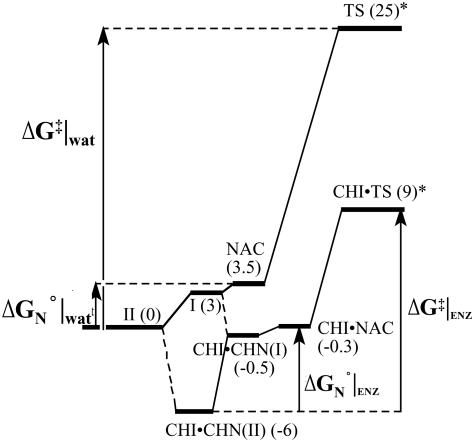
In this article, we report our computational studies on the catalytic mechanism of CHI from M. savita. The enzyme enhances the rate of the unimolecular rearrangement of CHN → flavanone by 10⁷-fold relative to the noncatalyzed reaction in water. In general, rate enhancement of enzymatic reaction over reaction in water can be attributed to two factors, promotion of NAC formation and TS stabilization. To compare quantitatively these two factors in the CHI catalysis, we have calculated free energies for NAC formation in both water and the enzyme (Fig. 8). The extent of TS stabilization can be subsequently calculated by subtracting NAC formation energy from the total activation energy, obtained from the experimental rate constants (Eqs. 1 and 2). Two conformers, I and II, exist in water. NAC is formed only from I. Surprisingly, we found that enzyme binds II more tightly than I by 2.5 kcal/mol, leading to easier NAC formation in water by 2 kcal/mol relative to the enzyme. It follows that the rate enhancement of the enzymatic over the water reaction is attributed to the step going from the NAC to the TS. A series of MD simulations of CHI complexed with the substrate CHN and the TS, and the apo-enzyme, reveal three mechanisms by which CHI achieves the TS stabilization. First, electrostatic stabilization comes about when CHN O7 approaches the Lys-97 protonated amino group by a movement of 3.4 Å as it becomes the TS. Second, this movement and the change in the shape of the ligand induces expulsion of three water molecules from the active site on going from CHI·CHN(I) to CHI·TS. Third, the enzyme backbone structure changes so that the βH3 hairpin and the L6 loop, which move closer to the ligand-binding pocket as CHI(I) binds, recede away from the ligand-binding pocket on formation of the TS and returns to the apo-status. The catalytic roles of these three events on the CHI·CHN(I) → CHI·TS transition are explained in order as general acid catalysis by Lys-97, entropic gain by water expulsion, and conformational energy retention in the TS enzyme, respectively. These provide means for preferential stabilization of the TS in the CHN reaction.

Fig. 8.

Energy diagram for the enzymatic and nonenzymatic isomerization of CHN to flavanone. The energy diagram in the enzymatic reaction considers only active site B conformation. Active site A conformation is not reactive, represents about half of the enzyme concentration, and thus can be ignored in the overall reaction coordinate. Numbers in parentheses are free energy contents (kilocalories per mole) relative to II in water. Numbers with ^* are from experimental data (refs. 1 and 2).

The catalytic strategy of CHI, which relies most on TS stabilization rather than ground-state NAC formation, is in marked contrast to the catalytic strategy of chorismate mutase for the Claisen rearrangement of chorismate (5, 17). The divergence of these two enzymatic intramolecular reaction mechanisms is not apparent in the experimental kinetic parameters because they share similar k_cat, K_m, and k_non values. This comparison shows that K_m·k_non/k_cat cannot be used as a measure for the TS stabilization energy. The important lesson from this comparison is that the catalysis occurs where it is most needed, as noted by Jencks (22). Chorismate mutase assists NAC formation because NAC formation is very unfavorable in water (≈8 kcal/mol) (5). Once NAC is formed at the active site, the enzyme does not require much further assistance to achieve the physiologically relevant reaction rate. So the enzyme simply watches the rearrangement occur after it molds chorismate into NAC. For CHN isomerization, however, NAC is readily formed in water (3.5 kcal/mol). This ease of NAC formation takes away a possible advantage that CHI could achieve by assisting NAC formation at the active site. Instead, CHI achieves a great rate enhancement by preferentially stabilizing the TS as compared with substrate by general-acid catalysis, restoration of solvent entropy, and release of strain in the Michaelis complex on TS formation.