Medical Mitigation Model: Quantifying the Benefits of the Public Health Response to a Chemical Terrorism Attack

Abstract

The Chemical Terrorism Risk Assessment (CTRA) and Chemical Infrastructure Risk Assessment (CIRA) are programs that estimate the risk of chemical terrorism attacks to help inform and improve the US defense posture against such events. One aspect of these programs is the development and advancement of a Medical Mitigation Model—a mathematical model that simulates the medical response to a chemical terrorism attack and estimates the resulting number of saved or benefited victims. At the foundation of the CTRA/CIRA Medical Mitigation Model is the concept of stock-and-flow modeling; “stocks” are states that individuals progress through during the event, while “flows” permit and govern movement from one stock to another. Using this approach, the model is able to simulate and track individual victims as they progress from exposure to an end state. Some of the considerations in the model include chemical used, type of attack, route and severity of exposure, response-related delays, detailed treatment regimens with efficacy defined as a function of time, medical system capacity, the influx of worried well individuals, and medical countermeasure availability. As will be demonstrated, the output of the CTRA/CIRA Medical Mitigation Model makes it possible to assess the effectiveness of the existing public health response system and develop and examine potential improvement strategies. Such a modeling and analysis capability can be used to inform first-responder actions/training, guide policy decisions, justify resource allocation, and direct knowledge-gap studies.

Introduction

With significant investments being made in the defense against and preparation for terrorist attacks, the US Government requires a process for prioritizing strategies to mitigate risk from these threats. Homeland Security Presidential Directives 18 and 22 call for a quantitative risk assessment of chemical threats, establish a national policy, and direct actions to strengthen the ability of the US to prevent, protect, respond to, and recover from terrorist attacks employing toxic chemicals and other chemical incidents [1, 2]. In response, the Chemical Security Analysis Center, under the Directorate of Science and Technology within the Department of Homeland Security, performs the biennial Chemical Terrorism Risk Assessment (CTRA) and the Chemical Infrastructure Risk Assessment (CIRA). One aspect of the CTRA/CIRA programs is to mathematically model the medical response employed following a chemical attack on the general public. Referred to as the CTRA/CIRA Medical Mitigation Model, the objective is to estimate the number of injured victims that would be saved by or benefit from the actions of first responders, medical personnel, and local, state, and national authorities. Such a capability permits assessment of the current public health response system and allows for the examination of mitigation strategies, thus helping to inform strategic planning efforts and policy decisions.

Methods

The general approach used to construct the CTRA/CIRA Medical Mitigation Model was to “parameterize” the event: divide it into a series of discrete events or actions (e.g., the time delay for a victim to become symptomatic after exposure) and turn each event/action into a corresponding, quantifiable model parameter. Each of these model parameters was permitted to have any number of dependencies, including chemical used, severity of exposure, and route of exposure. Detailed logic was then developed to ensure the various parameters are used appropriately and reflect the progression of a real scenario. When assigning values to each parameter, data-based values were preferred, but subject matter expert (SME) estimation and/or extrapolation from literature were often necessary. To this end, medical toxicology and emergency medicine SMEs were contracted to support a parameter quantification approach rooted in the Delphi Method [3].

The parameter quantification approach had three steps. First, SMEs were educated on the model methodology and the data collection approach. Next, model parameter values were assigned during a series of teleconferences using Microsoft^® Live Meeting. To facilitate the quantification process, all chemicals were categorized into groups called toxidromes. A given toxidrome contained chemicals that result in similar human health effects (e.g., pulmonary), and chemicals in the same toxidrome shared the same parameter values where appropriate. Two core SMEs were assigned to each toxidrome and participated in the series of teleconferences needed to complete the quantification for that toxidrome. In the third and final step, all model parameter values were reviewed and revised during a daylong workshop. One workshop was held for each toxidrome, and invitees included the two core SMEs as well as external SMEs from government, the medical community, and industry. Based on the workshop discussions and the experience and knowledge of those in attendance, the parameter values were accepted or modified by the group.

Model Methodology—Key Characteristics

Several key characteristics of the model are introduced below. A thorough mechanistic overview is provided following this discussion.

Key Characteristic 1: Use of a Stock-and-Flow Framework

The foundation of the CTRA/CIRA Medical Mitigation Model is the concept of stock-and-flow modeling. Originating from system dynamics, a “technique for framing, understanding, and discussing complex issues and problems” [4], the stock-and-flow approach is common when modeling intricate systems that change over time. In fact, the UK's National Health Service Confederation has stated: “System dynamics is a way of thinking about the future which focuses on ‘stocks’ and ‘flows’ within processes and the relationships between them. It is a risk-free way of refining plans before implementation using computer simulation and can facilitate ideas for both specific solutions and generic ‘new world’ rules. It is particularly useful in promoting understanding and systemic change over long patient pathways which cross multiple health and social care agencies [5].”

As the name suggests, a stock-and-flow model consists of “stocks” and “flows.” For the CTRA/CIRA Medical Mitigation Model, stocks are states or stages that individuals progress through during an event/response. Several hypothetical stocks are shown in Fig. 1 as blue boxes (e.g., “Exposed”). Flows, shown in Fig. 1 as solid-lined arrows, represent rates of change, allowing individuals to move from one stock (state) to another. Flows are typically manipulated or governed by events, shown in the figure as red boxes. For example, victims in the Exposed stock do not progress to the Symptomatic stock until the chemical to which they were exposed causes them to experience effects (i.e., the time delay for symptom onset). The stock-and-flow modeling approach allows victims to be created at different times, progress at different rates, and impede each others’ movement when appropriate.

Fig. 1.

Simplified medical mitigation stock-and-flow model diagram

Key Characteristic 2: Consideration of Different Event Types

The CTRA/CIRA Medical Mitigation Model includes four basic event types: overt event, chemical supply chain (CSC) event, covert event, and detected event. Consideration of different event types is necessary because each has unique characteristics that influence how the attack is discovered and the ensuing response, ultimately impacting the effectiveness of the medical response.

An overt event is an immediately evident event. Examples include an explosion in a public place or the wetting of a crowd with an agricultural sprayer. Although referred to as overt, it is not known that a chemical attack has taken place; rather, it is only known that something wrong or out of the ordinary has occurred, and subsequently, first responders are deployed to the scene. A CSC event is a specific type of overt event in which a chemical infrastructure is targeted. An example is the release of a chemical from a tanker truck punctured by an improvised explosive device. First responders are deployed to the scene of a CSC event and have the opportunity for a more efficient response (e.g., identification of the specific threat through placard identification, knowledge of the targeted infrastructure, etc.). A covert event is not readily apparent. Examples include the discreet release of a chemical into a building’s heating, ventilation, and air conditioning system or the intentional contamination of a food product prior to distribution. There is no immediate response to a covert event; discovery of the attack only results after the presentation and subsequent examination/diagnosis of a sufficient number of symptomatic victims. Finally, a detected event is a specific type of covert event in which the attack occurs in a location with chemical detection equipment.

Key Characteristic 3: Consideration of Different Victim Types

The CTRA/CIRA Medical Mitigation Model divides injured victims into three types. For a given scenario, the total number of each victim type is determined via dose–response (probit) calculations in external consequence models that are also part of the CTRA/CIRA programs. Inclusion of different victim types is an important step towards considering the dose dependencies of toxicology and pharmacology. It permits victim type-dependent quantification of parameters and allows the model to capture not only the number of lives saved but also the number of nonlethally injured victims who benefit from the response. The three types of injured victims are defined below. These definitions were used to define appropriate medical end points for each toxidrome; the end points were then used to define the probit values for each victim type.

Mild/Moderate

A mild/moderate injury is a nonlethal injury; these victims have injuries of sufficient severity such that 50 to 100 % of them would seek care under normal (i.e., non-mass casualty) conditions (note: all are assumed to eventually seek care under the CTRA/CIRA scenarios).

Severe

A severe injury is a nonlethal injury; these victims have injuries that cause performance degradation or otherwise affect the abilities of the individual. These victims would seek care and be admitted under normal (i.e., non-mass casualty) conditions.

Life-Threatening

A life-threatening injury is considered a direct threat to the individual’s life; these injuries cause death if not sufficiently treated.

In addition to the three injured victim types, the model also considers worried well individuals that receive limited or no exposure to the chemical and have no symptoms directly caused by the exposure, yet seek medical attention. Inclusion of the worried well is important because they can consume resources and create delays for injured victims. The number of worried well individuals in a scenario is based on the number of injured victims in that scenario and a data-based multiplier.

Key Characteristic 4: Inclusion of Detailed Treatment Definitions and Time-Resolved Efficacy

In the CTRA/CIRA Medical Mitigation Model, each victim type is permitted to have a unique treatment regimen for every chemical–exposure route combination. The model employs the concept of tiered treatment for each unique treatment regimen. Under this approach, victims are first candidates for and can be saved/benefited by tier 1, the first logical treatment. A treatment (or medical countermeasure) in the model is an item or procedure needed/desired by the victims; it is allowed to be any type of medical attention, ranging from oxygen to pharmaceuticals to specialty equipment such as full-feature mechanical ventilators. Depending on the efficacy (success rate) of a treatment, it has the potential to save or otherwise benefit its recipients.

Upon receipt of tier 1, the victims may be given tier 2 (a different treatment) and thus have a second chance of being saved/benefited. The model allows for up to three tiers of treatment. Furthermore, to capture all options available to medical personnel during a mass casualty situation, the model accommodates alternative treatments. Alternative treatments are treatments that can be used if the primary (ideal) treatment is completely consumed or unavailable. For example, if the tier 2 treatment is diazepam, it may be permissible to administer lorazepam as an alternative. Each tier has one primary treatment and up to two alternatives.

Efficacy was defined by medical toxicology and emergency medicine SMEs for every applicable combination of medical countermeasure, chemical, exposure route, and victim type. Furthermore, it was defined as a band as a function of time, as shown in the hypothetical example in Fig. 2. Use of an efficacy band allows the model to account for variability and uncertainty surrounding this parameter. In the example shown in Fig. 2, the bounds on the hypothetical vertical slice suggest that the receipt of that treatment at time “x” yields a success rate of 25 to 70 % (for the relevant chemical, exposure route, and victim type). The model treated this range as a uniform distribution when assigning a specific efficacy value to a treatment.

Fig. 2.

Hypothetical example of a treatment’s efficacy definition

Key Characteristic 5: Consideration of Different Medical Countermeasure Stockpiles

The model allows for three separate stockpiles from which medical countermeasures can originate: (1) local (supplies from hospitals or community disaster caches in the city of the attack), (2) regional (supplies from regionally-based programs or surrounding areas), and (3) national (supplies from the Federal Government or areas outside the regional area). For each medical countermeasure and stockpile, appropriate quantities and delays for physical delivery were defined. The exact description of each stockpile varies from countermeasure to countermeasure based on stockpiling practices and the existence of deployment programs. For example, supplies from the “national” stockpile may refer to supplies from hospitals in surrounding states, supplies from the Strategic National Stockpile, or both, depending on the specific countermeasure.

Mechanistic Overview

Figure 3 provides a conceptual illustration of the CTRA/CIRA Medical Mitigation Model. In this figure, stocks are represented as blue boxes. The stocks include the victims’ end states on the far right of the figure. Flows permitting victim movement between the stocks and to the end states are represented as arrows. These arrows often pass through red boxes denoting the event/action controlling that flow. The finely dotted lines represent the transfer of information. Finally, logic, restrictions, or other key inputs appear as yellow boxes. The black boxes containing letters are used in the text to guide the reader.

Fig. 3.

Conceptual diagram of the CTRA/CIRA medical mitigation model

External consequence models are responsible for providing the time, number, and severity of exposures from an attack scenario. This information is used by the CTRA/CIRA Medical Mitigation Model to pull the appropriate number of injured victims into the Exposed stock, denoted by box “A” in Fig. 3, at the appropriate times. As indicated by the subdivisions within this and the other stocks, the different victim types are tracked separately throughout the model. Injured victims typically remain in the Exposed stock until the effects of the chemical become apparent (i.e., for the duration of the time for symptom onset parameter; note that italics are used to denote model parameters); once this delay passes, the victims move to the Symptomatic stock, denoted by box “B.” Like many model parameters, the time for symptom onset can be defined as a function of victim type. Each injured victim type, therefore, has its own symptom onset time and can become ill (i.e., move to the Symptomatic stock) at unique rates. Furthermore, if the time for symptom onset is defined as a distribution for a given victim type, different victims of the same victim type are assigned different onset times and thus move at different rates.

Symptomatic victims begin seeking care, or care is sought for them, as soon as they become ill. A collocation time parameter captures the delays/activities associated with becoming physically collocated with medical personnel. The flow path seen in Fig. 3 around the Symptomatic stock, labeled “Exposed Seeking Care,” permits victims in the Exposed stock to begin seeking care prior to the onset of symptoms under special circumstances, such as the recognition of a sufficient number of ill victims at a single location.

As injured victims become symptomatic, the model populates the Worried Well stock based on the previously introduced multiplier (worried well multiplier; box “C” in Fig. 3). The worried well experience a delay for becoming worried/deciding to seek care and a delay for becoming physically collocated with medical personnel.

Upon completion of the collocation delay, victims (injured and worried well) move to the Access to Medical Care stock. Entrance into this stock signifies that the victim has traveled to a point of care (e.g., hospital, field response area, etc.) or medical personnel have come to the victim (e.g., ambulance). The next step, denoted by box “D” in Fig. 3, depends on the phase of the response. For the purposes of this effort, phase I requires the victims to experience a delay for medical personnel to determine the appropriate treatment. Phase II assumes that the appropriate treatment has been identified and universally communicated. Thus, a delay to determine the treatment is no longer needed in phase II, but a delay for decontamination of victims is enforced.

After treatment identification/decontamination, victims move to the Candidates for Treatment stock. Upon entering this stock, victims are subjected to restriction factors, denoted by box “E” in Fig. 3. When appropriate, these model parameters are used to prevent victims from becoming a candidate for a treatment. Such a capability is needed as some patients may be denied a treatment due to sufficient benefit from a previous treatment or concerns over the side effects or limited supply of the treatment.

Victims that “pass” the restriction factors and move to the Candidates for Treatment stock are not guaranteed to receive treatment. For example, it is possible for life-threatening victims to die while waiting to receive treatment—or even before becoming candidates. This possibility is illustrated in Fig. 3 by the overarching flow path (box “F”) and the Death event. Similarly, it is also possible for severe, mild/moderate, and worried well victims to tire/recover and exit medical care.

The ability to treat victims in the Candidates for Treatment stock is partially dependent on the availability of medical countermeasures. Box “G” in Fig. 3 identifies the Available Countermeasures stock; the various medical countermeasures accumulate here as they arrive and are removed as they are consumed. Through the Candidates for Treatment stock and the Available Countermeasures stock, the model tracks medical countermeasure supply and demand. When both demand and supply exist, the model simulates the administration of treatment. The rate of treatment depends on administration-related considerations, including the time to administer a treatment, the capacity to administer a treatment, and victim prioritization rules.

When a treatment is administered to a victim, its efficacy (chance of success) is calculated by the model using predefined efficacy versus time relationships. Regardless of the efficacy value, treatment is ultimately either successful or unsuccessful. The success or failure of a treatment determines the victim’s end state. Efficacious treatment appears in Fig. 3 as a solid line and failed treatment appears as an irregular dashed line.

Box “H” in Fig. 3 identifies the Dead end state; these individuals received treatment but did not survive. All life-threatening victims receiving treatment that was not efficacious are tallied in this end state. In contrast, box “I” identifies the Alive, Saved end state. By definition, only the life-threatening victims were at risk of dying, and thus, they are the only victim type that can be “saved.” If their treatment was successful, they are tallied here. Life-threatening victims that died before receiving treatment are tallied in the Untreated, Dead end state.

Boxes “J” and “K” in Fig. 3 denote end states for the severe, mild/moderate, and worried well victims that received treatment. While these victims were not at risk of dying, they were able to “benefit” from efficacious treatment (e.g., improved quality of life, reduced suffering, etc.). If treatment was efficacious, they are placed in the Alive, Benefited end state. If treatment was not efficacious, they are instead tallied in the Alive, Not Benefited end state. Lastly, any severe, mild/moderate, and worried well victims that did not receive treatment are tallied in the Untreated, Alive end state.

The sum of victims in all end states equals the total number of victims involved in the event. By comparing the magnitude of the different end states, it is possible to assess the effectiveness of the medical response. Model results can be used to assess the effectiveness of the current (i.e., “baseline”) public health response system. Model results can also be used to assess the impact of alternative public health response system strategies, such as increased stockpiling of resources, forward placement of countermeasures, more effective countermeasures, and expanded detection capabilities.

Results

The CTRA/CIRA Medical Mitigation Model estimates the number of lives saved or benefited by the public health response system. While all actual model results are sensitive, notional results are presented here for illustrative purposes.

A hypothetical scenario was created in which a city of approximately one million people was targeted with a gas belonging to the pulmonary toxidrome. The population densities in the regional and national areas surrounding the targeted city (required for the determination of regional and national medical countermeasure quantities) were assumed to reflect the average population density across the US. Recognizing that such an attack could have varying levels of success or failure depending on the exact attack scenario and conditions, a varying number of injuries (evenly distributed among the three injury types) were examined here. In all cases, the exposures were assumed to be uniformly distributed over a period of 30 min.

Notional results for this hypothetical scenario are plotted in Fig. 4. To generate this plot, 1,000 simulations of the model were completed at discrete, logarithmically spaced event sizes. The plot presents the fraction of life-threatening victims that are saved (i.e., the number of life-threatening victims that are saved divided by the total number of life-threatening victims) as a function of the size of the event (i.e., the total number of life-threatening victims). The different lines indicate the distribution of the fraction saved for a given event size. For example, attacks resulting in 1,000 life-threatening victims resulted in a mean percent saved of 64 %, with the 5th and 95th percentiles being 57 and 76 % saved, respectively. Also shown for each event size are the 25th percentile, 75th percentile, and median fraction saved. Although not shown here, a similar figure could be generated based on the number of victims that benefit from the response.

Fig. 4.

Notional fraction saved results

Results such as those presented in Fig. 4 allow for a straightforward analysis of the ability of the medical response system to respond to chemical events. Based on the notional results in the figure, it is clear that the ability to respond is highly dependent on event size. For smaller events (e.g., 100 life-threatening victims), almost all life-threatening victims (95 %) are saved on average. The average percent saved, however, decreases to 64 % with an order of magnitude increase in event size, and to 21 % with an increase of two orders of magnitude. Such insight, when combined with intelligence or perception of realistic event sizes, can be instrumental in guiding policy and funding to improve defense posture in an efficient manner.

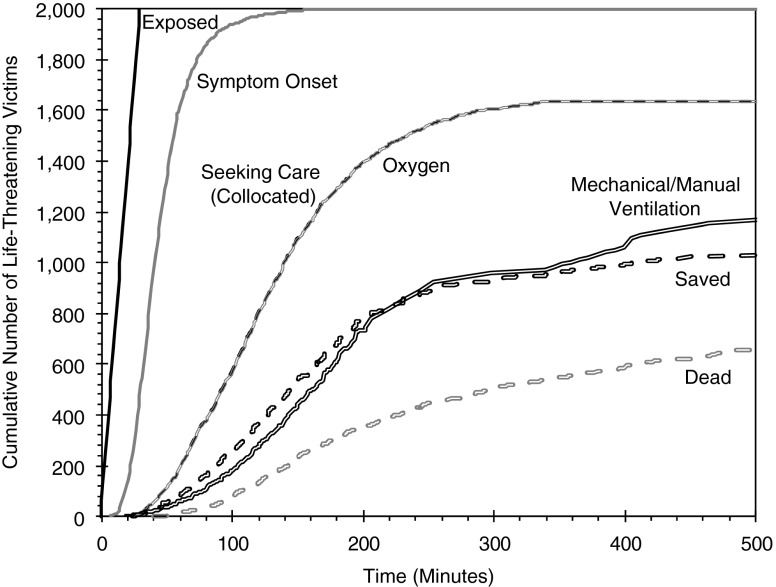
Figure 5 provides a detailed, time-resolved snapshot of a single model simulation with an event size of 2,000 life-threatening victims. Specifically, this figure illustrates the cumulative progression of life-threatening victims for the first 500 min of the simulation. The Exposed line reflects the exposure of 2,000 life-threatening victims equally distributed across the first 30 min of the event. The Symptom Onset line indicates that nearly all victims are symptomatic within 150 min of the release. The Collocated line specifies when the victims arrive at medical care. The lines labeled with different treatments indicate the number of administered treatments. Lastly, the Saved and Dead lines represent the general end states of the life-threatening victims.

Fig. 5.

Notional time-resolved results for a single simulation

The time-sensitive plot in Fig. 5 allows for a detailed understanding/analysis of the event and the ability of the medical response system to respond. In this example, the overlap of the Collocation line with the Oxygen line indicates that oxygen is administered almost immediately upon entrance to medical care throughout the entire event. This result indicates that oxygen possesses a combination of large quantities, sufficient capacity (personnel) to treat, short administration time, and rapid delivery.

Looking at other treatments, the Saved line in Fig. 5 is seen to closely follow the Mechanical/Manual Ventilation line. Thus, it can be reasoned that, for this set of notional data, the ability to save victims is highly dependent on the receipt of ventilation. The two lines begin to deviate from this relationship at around 200 min, when supplies of these countermeasures become a limiting factor (~700–800 treatments consumed). At this point, the number of ventilation treatments does not meet demand (as evidenced by the decrease in the slope of the line). The relationship between the ventilation treatment and the number saved appears to weaken further at around 350 min, as sharp increases in administered treatments do not yield similar increases in the number saved. This trend indicates that the effectiveness of ventilation is becoming increasingly limited.

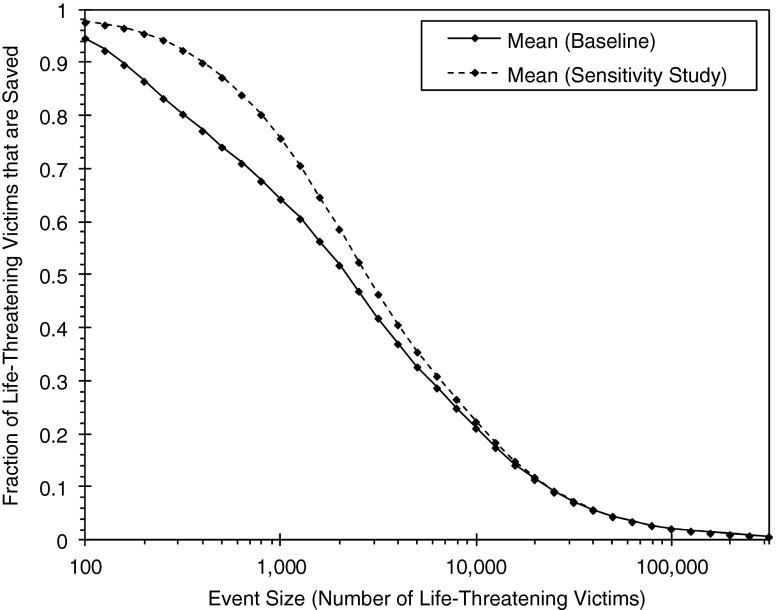
The Medical Mitigation Model also allows for the analysis of alternative mitigation strategies or sensitivity studies. For example, a change in the baseline results due to an increased number of medical countermeasures, improved countermeasure deployment speed, greater countermeasure efficacy, improved detection capability, or faster decontamination throughput times could be evaluated. Figure 6 illustrates changes in the notional results presented in Fig. 4 after an increased ventilation treatment capacity (i.e., increased personnel to provide ventilation treatments). For simplicity, only the means of the baseline and sensitivity study results are shown in the figure.

Fig. 6.

Notional fraction saved results for an alternative mitigation strategy implemented into the CTRA/CIRA medical mitigation model

As seen in Fig. 6, the increased capacity leads to a notable increase in saved victims for many event sizes, with the greatest increases at event sizes of <1,000 victims. Clearly, for these event sizes in this notional scenario, treatment capacity is a key contributor to the ability to save victims. At larger event sizes (1,000+ victims), however, the impact of the increase in capacity is reduced and eventually becomes negligible. Thus, other factors, such as countermeasure quantities and arrival times, are more important for larger event sizes. As illustrated by this exercise, a wide variety of mitigation strategies can be investigated quickly without the need to devote significant resources.

Conclusions

A mathematical model, referred to as the CTRA/CIRA Medical Mitigation Model, was developed to simulate the medical response that would be employed following a chemical attack on the general public. By estimating the number of lives saved or benefited by the response, the model allows for examination of the existing medical response system as well as potential mitigation strategies. As evidenced by illustrative results using notional data, such a capability permits policy makers to make informed decisions on the allocation of resources and helps response personnel better understand their ability to respond and identify areas where improvement is possible.