Features versus Context: An approach for precise and detailed detection and delineation of faces and facial features

Abstract

The appearance-based approach to face detection has seen great advances in the last several years. In this approach, we learn the image statistics describing the texture pattern (appearance) of the object class we want to detect, e.g., the face. However, this approach has had a limited success in providing an accurate and detailed description of the internal facial features, i.e., eyes, brows, nose and mouth. In general, this is due to the limited information carried by the learned statistical model. While the face template is relatively rich in texture, facial features (e.g., eyes, nose and mouth) do not carry enough discriminative information to tell them apart from all possible background images. We resolve this problem by adding the context information of each facial feature in the design of the statistical model. In the proposed approach, the context information defines the image statistics most correlated with the surroundings of each facial component. This means that when we search for a face or facial feature we look for those locations which most resemble the feature yet are most dissimilar to its context. This dissimilarity with the context features forces the detector to gravitate toward an accurate estimate of the position of the facial feature. Learning to discriminate between feature and context templates is difficult however, because the context and the texture of the facial features vary widely under changing expression, pose and illumination, and may even resemble one another. We address this problem with the use of subclass divisions. We derive two algorithms to automatically divide the training samples of each facial feature into a set of subclasses, each representing a distinct construction of the same facial component (e.g., closed versus open eyes) or its context (e.g., different hairstyles). The first algorithm is based on a discriminant analysis formulation. The second algorithm is an extension of the AdaBoost approach. We provide extensive experimental results using still images and video sequences for a total of 3, 930 images. We show that the results are almost as good as those obtained with manual detection.

I. Introduction

Face detection is a fundamental task in computer vision, with broad applications in face recognition, human-computer interaction, behavioral analysis, and computer graphics, to name but a few. Because of its many uses, face detection has received considerable attention, especially in the past several years [50], [16], [51]. By face detection, we generally mean that a bounding box (or an ellipsoid) enclosing the face (or faces) in an image at approximately the correct scale needs to be specified. At present, several algorithms exist which can provide reliable detections of faces in images. Furthermore, recent results demonstrate how face detectors can be made to work faster and more accurately under varying conditions [44], [19], [49], [18], [48].

However, most of the applications named above require that we extract additional information from the face image. For example, problems in human-computer interaction may require information of the gaze direction for the design of smart interfaces [53] and lip movement for viseme interpretation [12]. To this end, eyes and mouth detectors have been developed in recent years. In other applications, as in the recognition of identity using the appearance-based approach in face recognition, we will require to warp the detected face to a norm (or mean) shape before comparing the texture maps [28]. In this case, additional information, such as the location of the nose and chin will be necessary. And, in yet other applications, such as shape-based recognition of expression requires an accurate extraction of the shape of each of the facial components.

Fueled by these needs and by the recent success of face detectors, research on this area is now moving toward a more precise and detailed detection of the internal facial components of the face [9], [8], [20]. By internal facial components, we mean the brows, eyes, nose and mouth. In addition, it is useful to provide a detection of the chin line, which provides the lower limits of the face.

To date, the facial feature that has received most attention is the eye, because these play a central role in human-computer interaction applications as well as in psychophysical experiments. In a recent paper, Moriyama et al. [35] demonstrate that precise and detailed detection and feature extraction from the eye region is already possible. Although the algorithm is still complex in comparison to current face detectors, it nicely illustrates that the problem is in reach. Unfortunately, this approach is tailored to do eye detection and cannot be easily extended to the detection of other facial components.

Using other approaches, several authors have focused their attention on the detection of other facial features, e.g. [45], [46], [15], [6]. Rather than providing a precise and detailed detection of all major features, these alternative algorithms demonstrate that an estimate of the position of the internal facial components (or their corners) is possible. For example, in a recent paper, Heisele et al. [15] developed a system capable of detecting the corners and centers of the brows, eyes, mouth and nose. To make these results more useful, facial feature trackers able to track the detected facial components under varying expressions, illumination and partial occlusions have been developed over the years [8], [37], [39], [53].

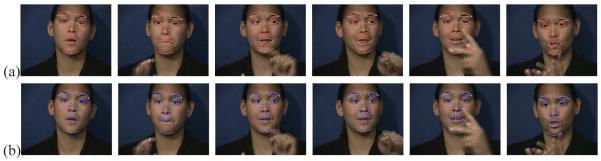
Based on the results summarized above, the next natural step in face detection is to define algorithms that can provide a detailed and accurate detection of all the internal facial features and the chin line. By detailed, we mean that a complete description of the outline of each facial component is to be provided. Fig. 1(a) shows an example. By precise, we mean that the results automatically provided by the algorithm should be comparable to those given by human manual markings.

Fig. 1.

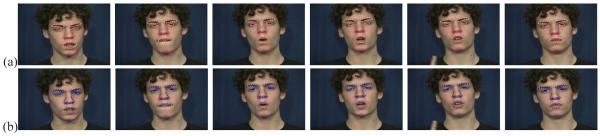
Shown here are examples of accurate and detailed face detections. In (a), we show the automatic detection obtained with the algorithm defined in this paper. For comparison, (b) shows a manual detection of the same facial components on the same images.

In the present paper, we introduce an approach that can achieve such detailed and precise detection of the major facial components enumerated in the preceding paragraphs. An example of our automatic detection was shown in Fig. 1(a). In Fig. 1(b), we show the results obtained by manually delineating the same facial features in the same images. We will demonstrate that the results obtained with the algorithm derived in this paper are generally comparable to those obtained by such a tedious manual marking.

To achieve such accurate detection and feature extraction, we employ the idea of context features. To properly define this term, let us look at an example. Imagine we want to design an algorithm that detects the center of the eyes in an image. The classical approach in pattern recognition would be to collect a set of training images of eyes and non-eyes. The non-eye set is usually a collection of natural scenes. This allows us to determine which statistics best discriminate between eye patches and patches of other objects. In general, this approach works reasonably well, but it fails to provide an accurate estimate of the center of the eyes, because an image of a non-centered eye patch is more similar to the eye class than to the non-eye class. What we really want to design is a system that can discriminate between eye-looking patches and (actual) well-centered eye windows. This can be resolved by using patches containing non-centered eyes as the non-eye class and correctly centered eye patches as the eye class. We refer to these non-eye patches as the context of the feature to be detected, because they define the context information of the eye itself. The same applies to other features, e.g., brows, nose, mouth and, also, the face. Examples of faces versus their context (non-faces) are shown in Fig. 2(a-b). Examples of eyes versus their context are shown in Fig. 2(c-d). Note that the definition of context used in this paper is not the one employed in other publications. In object recognition, context usually refers to background features surrounding the object. For example, a black blob placed next to a computer would be interpreted as a mouse, while the same blob in a street scene is generally perceived as a person [42]. In the present paper, we are not interested in determining the object’s class based on such contextual cues. Instead, we want to use the context of a facial feature, which is quite constant across identities, to provide a precise estimate of the feature’s location. Our approach is related to the probabilistic semi-local context features approach of [3] and the context-based detection of [47]. The main difference is that our goal is to provide as precise and detailed a detection (of a known class) as possible. Two other related works to ours are those of [41] and [23]. The first uses negative samples from the face area. The second paper employs misaligned samples as the negative class.

Fig. 2.

Sample images of (a) faces, (b) non-faces (i.e., face context), (c) eyes, and (d) non-eyes (i.e., eye context).

Using these context features, we can now learn to discriminate between facial features and their context. However, the discrimination of similar classes (such as these features and their contexts) is a challenging problem, because faces and facial features have a large within-class variance. Faces, for example, come at different sizes, shapes and colors. Age, illumination and expression also changes the image of a face. Eyes can be larger or smaller, closed or open, and the iris comes with a variety of stroma and can be oriented at all possible directions. Mouths are also very different across individuals, and expression affects them most. All these changes combined make the within-class variations of facial components large, and very similar to the between-class differences (which are now given by the context features).

To resolve the problem of modeling large inter-class variation, we will use the idea of subclass divisions in Subclass Discriminant Analysis (SDA) [56]. In SDA, the goal is to divide each class (e.g., faces) into a set of subclasses, each having a small within-subclass variability. In the case of faces, one subclass may correspond to longer or thinner faces, while another subclass may represent faces seen under different illuminations or expressions. Similarly, eyes will be divided in many subclasses, one of which may represent close eyes and another wide open eyes. The same is true for the feature context class (e.g., non-eyes). One subclass will correspond to one type of context, while a different subclass will represent a very different type of context; e.g., different eyebrows. Fig. 3 shows an example, where each subclass is represented by a Gaussian distribution. Following this approach, the subspace spanned by each subclass can be accurately computed. The union of these feature spaces defines the features versus context approach.

Fig. 3.

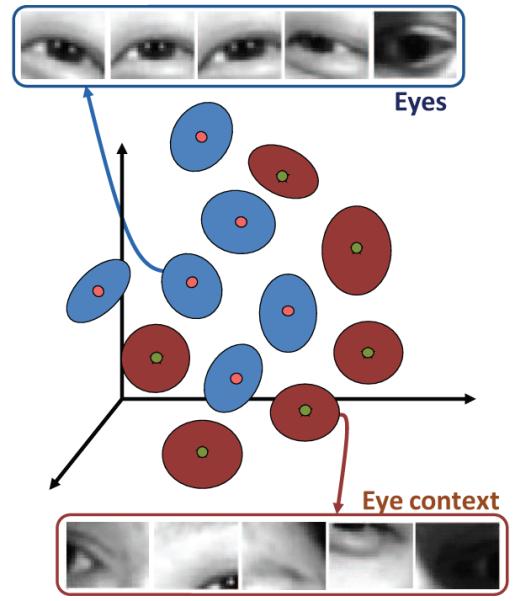
In the proposed approach, the features (e.g., eyes) and their context (e.g., eye context) are divided into subclasses. Each of the subclasses defines a different configuration of the feature or context (e.g., open versus close eyes). In the appearance-based approach, the dimensions of the feature space correspond to the brightness of each of the pixels of the image. Here, only three dimensions representing the ones with largest variance are shown for illustration. Additional illustrations are shown in the Supplementary Documentation.

Once the center and corner positions of each facial component are known, we can use the same approach described above to estimate the feature’s shape. In this last step, we will use the gradient and color information of each feature to learn to discriminate these from non-feature parts. This, in combination with the system described above, provides the precise and detailed detections previously shown in Fig. 1(a).

Although the detailed detection is quite obvious from simply looking at the image results in Fig. 1, one may wonder how accurate these results really are. This is not an easy question to answer, because the ground-truth is not (and cannot be) known. One approach would be to compare the results obtained with the manual markings given by a person. The problem with such an approach, is that we do not know how accurate humans are at delineating each of the facial components. We resolved this issue as follows. First, we designed a system which allows users to zoom in at any specified locations to facilitate delineation of each of the facial features. Then, we asked three people (herein referred to as judges) to manually delineate each of the facial components of all the face images used in the experimental results section of this paper – a total of 3, 930 face images. A small selection of these manual markings is shown in Fig. 1(b). Next, we compared how the markings of each of the three judges diverge from the other two. The within-judge variability was (on average) 3.8 pixels, corresponding to a percentage of error of 1.2% in terms of the size of the face. This gives us an estimate of the accuracy of the manual detections. As we will see later in the paper, the average error of the proposed algorithm was 7.3 pixels (or 2.3%), almost as accurate as manual detection.

The results provided by the algorithm defined in this paper will thus be instrumental in the applications outlined at the beginning of this section – computer vision, human-computer interaction, behavioral analysis, and computer graphics. An important application is in the construction of active shape models [4] and in shape analysis [25] techniques, which require large amounts of labeled data for training. Accurate and detailed facial feature detection is also necessary in the analysis of facial expressions with FACS (Facial Action Coding System) [10], [53], behavioral analysis [7] and in the analysis of non-manuals in American Sign Language (ASL) [31]. ASL non-manuals are facial expressions that convey grammatical information in a signed sentence. ASL non-manuals are crucial for the understanding of ASL but difficult to obtain due to large variations in expression and occlusions. We will demonstrate how the proposed approach can be successfully applied to this challenging problem.

The rest of the paper is organized as follows. In Section II, we describe the key ideas underlying the approach defined in this paper and provide derivations for the modeling of the subspaces. Section III provides detailed derivations of the face detector. Section IV does the same for the eyes and eyebrows. Section V describes the detection of the remaining facial components, i.e., nose, mouth and chin. An alternative formulation based on the idea of subclass division with AdaBoost is derived in Section VI. Extensive experimental validation and applications are in Section VII. We conclude in Section VIII.

II. Features versus Context

The main goal of this section is to derive a classifier that can discriminate between patches containing a certain feature (e.g., an eye center) and context features (e.g., eye corners). As outlined in the introduction of this paper, this approach will allow us to discriminate between the context of the feature and the feature itself, yielding the accurate detections we need.

Accurate detection of faces and facial features is still a challenging task, mainly because these have a large variability. Adding the generative processes of pose, expression and illumination to this problem makes the detection task extremely challenging. Cast shadows, glasses, and partial occlusions also make our goal elusive.

The common approach to building a classifier that learns this high variability of features (e.g., eyes) has met with difficulties, even when powerful non-linear algorithms and thousands of training examples have been used [51]. This is due to the complexity of the subspace or manifold defining each feature. As a consequence, the resulting classifier may be able to give an estimate over the position of the feature’s location, but fail to provide an accurate detection of its center and bounding box (i.e., correct estimate of the feature’s size). To resolve these issues without resorting to complex algorithms, we will use the idea of SDA [56].

In the two-class classification problem, the goal of SDA is to learn to discriminate between the samples in the two classes by dividing these into a set of subclasses. The algorithm starts with a single subclass per class. If this division is not sufficient to successfully separate the training samples in the two specified classes, the algorithm divides each class into two subclasses. This division process is repeated until the training samples are correctly classified. A key concept in SDA is how to know when the training and (potential) testing data will be correctly classified. Some subclass divisions will provide an adequate classification of the classes, while others will not. To determine this, we employ a recent result [30] on discriminant analysis (DA) methods. First, recall that DA algorithms typically use a generalized eigenvalue decomposition equation of the sort A⁻¹BV = VΛ, where A and B are the metrics (given by symmetric, positive semi-definite matrices) to be minimized and maximized, and V and Λ are the eigenvectors and eigenvalues defining the subspace where the classes are hopefully best separated. In SDA, the metric to be minimized is the covariance matrix ${\Sigma }_X=n^{-1}{\sum }_{i=1}^n({\mathrm{x}}_i-\mu ){({\mathrm{x}}_i-\mu )}^T$, where μ is the mean feature vector of the n training samples X = {x₁, … , x_n}, and the metric to be maximized is the between-subclass scatter matrix

$${\Sigma }_B=\sum _{j=1}^{K_1}\sum _{l=1}^{K_2}{p}_{1j}{p}_{2l}({\mu }_{1j}-{\mu }_{2l}){({\mu }_{1j}-{\mu }_{2l})}^T,$$

where μ_il is the sample mean of the n_il feature vectors in the l^th subclass of class i, $p_{\mathit{il}}=\frac{n_{\mathit{il}}}{n}$ defines the prior of that subclass, and K_i is the number of subclasses in each of the two classes, i = {1, 2}.

The between-subclass scatter matrix forces samples from different classes to be projected as far apart as possible in the subspace defined by the first p eigenvectors of V. At the same time, the covariance matrix ensures that samples belonging to the same class fall close to one another. The problem with this DA approach is that these two metrics may favor completely different solutions for V. In [30], it is shown that a DA technique may not yield good classifications whenever the sum of the inner products between the q^th eigenvector given by the metric to be maximized and the first q eigenvectors given by the metric to be minimized is larger than zero. The value given by these inner products is called the conflict between metrics, since this specifies when the two metrics favor different solutions for V. Note that when these inner products equal to one, it means that the metrics favor completely orthogonal (opposite) solutions. When the inner products are zero, they vote for the same solution and, hence, there is no conflict. On average, DA algorithms have been shown to work best when this conflict value is low [30], [56], [54]. In this paper, we extend on this result to learn to discriminate between the subclasses defining the facial features and their context. This approach is key to identify an appropriate number of subdivisions of the training samples. The ability to automatically determine the adequate number of subdivisions for each of the two classes is what makes our approach different from other subclass-based algorithms such as [55], [11]. For example, the algorithm in [55] uses a similar set of metrics to those of SDA, but requires that the number of subclasses in each class be known or specified by the user.

In our approach, each class will be divided into a number of subclasses using the well-known K-means clustering algorithm, because this permits to model the many non-linearities of the training data efficiently. The value of K, that is, the number of subclasses (K = K₁ + K₂), is given by the value which minimizes the conflict between the metrics of SDA, Fig. 3.¹ Here, we use the K-means algorithm to divide each class into a set of subclasses, rather than the nearest-neighbor approach presented in [56], because the latter does not allow for the modelling of the complex non-linearities observed in the face and facial feature data that we need to model.

The approach described thus far in this section addresses the problem of modelling different types of features (e.g., different shapes, illuminations and orientations of the same feature). Therefore, we are now in a position to model the challenging sets of face features and their context (i.e., surroundings). This process is key for the accurate detection of each class and is defined next.

To better understand the role of context features in the accurate detection of a facial component recall that when a classifier does not precisely detect the facial feature it has been trained on, it usually provides a close estimate. This is because cast shadows, eyeglasses and others will make a neighboring area look like the actual feature to the classifier. To resolve this, we train the classifier to discriminate between the feature and its neighboring areas – the cause of these imprecise detections. This creates a pulling effect toward the desirable location, Fig. 3. The pulling effect can be formally defined as a decrease of the probability of the context features (given by its mixture of Gaussians) and an increase of the probability of the feature (given by the other mixture).

The subspace where the feature and its context are best separated, is simply given by the first p eigenvectors of

$${\Sigma }_B\mathrm{V}={\Sigma }_X\mathrm{V}\Lambda ,$$

where V is a matrix whose columns are the eigenvectors of ${\Sigma }_X^{-1}{\Sigma }_B,\Lambda =\mathit{diag}({\lambda }_1,\dots ,{\lambda }_q)$ is a diagonal matrix of corresponding eigenvalues, with λ₁ ≥ … ≥ λ_q ≥ 0, q is the dimensionality of the data (i.e., size of the patch), ${\mathrm{x}}_i\in {\mathbb{R}}^q$, and $p\le \mathit{rank}\left({\Sigma }_X^{-1}{\Sigma }_B\right)\le q$.

In the following sections we describe how this general approach can be applied to the accurate detection of faces, eyes, noses and mouths.

III. Face Detection

We first derive the general approach for the detection of faces in stills. This is followed by a description of how to improve these results when detection is to be carried out over a video sequence.

A. Detection in stills

We first collect a set of training images containing different types of faces and facial configurations under different illuminations, with different expressions, and at different poses. We limit the faces to be nearly frontal views with rotation angle less than 30° in each direction. We will use these images to do detection within ±25°. The positions and sizes of the faces are obtained from manual markings. These images are normalized to have a bounding box of 30 × 30 pixels. The training set corresponds to 51, 664 images of cropped faces.

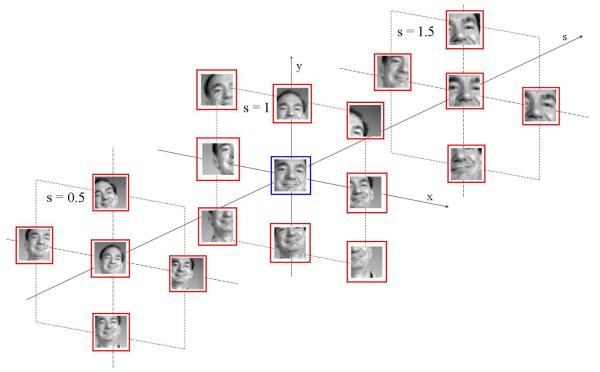
For clarity, let us label each image with the vector (x, y, s)^T representing the parameters of a cropped image, with (x, y) the position of the face in the image patch and s its scale; i.e., $s=\frac{30}{l}$, where l is the length of the bounding box of the face. Following this notation, we see that, in this first set representing the correctly localized faces, all images are labelled with the center position of the image patch (denoted (x₀, y₀)) and unit scale (s = 1), because all images have been normalized to be centered faces of 30 × 30 pixels. In contrast, the non-face training set contains image patches with different labels. In particular, we include two types of context information. The first set corresponds to cropped images located in the neighboring areas of the faces but at the correct scale (s = 1); that is, imprecisely localized faces. More formally, (x₀+δx,y₀+δy, 1), where δx = δy = {−15, … , −6, −5, 5, 6, … , 15}. The second set of training images representing the non-face class corresponds to faces cropped at an incorrect scale and at correct and incorrect locations, (x₀ + δx,y₀ + δy, 1 + δs), where δx = δy = {−15, … , −2, −1, 0, 2, 1, … , 15}, and δs = {−.6, −.5, −.4, −.3, .3, .4, .5, .6}. The total number of non-face samples generated using this approach was 114, 992. These training sets are illustrated (for one of the training images) in Fig. 4. In this figure the image in the middle of the figure (marked with a blue bounding box) corresponds to one of the training samples in the face set. The rest are training samples of the non-face (i.e., face context) set. Note the non-face set defines where not to detect the face – precisely at those places and scales where face detection algorithms are known to have most of their errors.

Fig. 4.

Training sample of the face class (shown within the blue box) and the non-face set (shown within the red squares).

To increase robustness to rotation, we extend the training set by including the images obtained by applying in-plane rotations within the range of −15° to 15°. The cropped images are mean- and norm-normalized to make them invariant to the intensity of the light source.

K-means clustering is applied to these training sets. Each K-means clustering is repeated five times to be less sensitive to initializations. The number of clusters (subclasses), K, is obtained as defined in Section II, yielding K₁ = 34 for the face class and K₂ = 12 for the non-face group (recall, K = K₁ + K₂ = 46). Note that even though the non-face class had a larger number of samples, the number of subclasses is larger for the face group. This reinforces the theoretical observation made earlier on the high variability of the within-class measure of faces. We also note that the number of subclasses does not tend to be large number, even though the number of samples is quite large. This suggests that the proposed approach is able to model the similarities of the features and their context correctly.

The means and covariances of the resulting subclasses, μ_i and Σ_i, for the face and non-face subclasses are then calculated, Fig. 5(a-b). To detect the face in a new image, we do an exhaustive search on all possible windows at multiple scales over the region of pixels with skin color. The skin color model is defined using a Gaussian distribution representing the HSV color space, N(μ_c, Σ_c), with μ_c = (μ_H, μ_S, μ_V)^T and Σ_c = diag(σ_H, σ_S, σ_V). Over 3 million skin-color sample points were used to train the model. Morphological operations are used to fill in holes in the face region and delete small isolated (non-face) areas [28].

Fig. 5.

A selection of the mean feature vectors representing (a) faces, (b) face context, (c) eyes, and (d) eye context.

To test the different scales s, each test image patch t_sj, centered at the j^th image pixel, is resized to the appropriate scale of 30 × 30 pixels and compared to the learned subclasses. Formally,

$$\underset{i}{\arg \min }{({\mathrm{V}}^T{\mathrm{t}}_{\mathit{sj}}-{\mathrm{V}}^T{\mu }_i)}^T{\mathrm{V}}^T{\Sigma }_i^{-1}\mathrm{V}({\mathrm{V}}^T{\mathrm{t}}_{\mathit{sj}}-{\mathrm{V}}^T{\mu }_i),$$ (1)

with subclasses i = 1 through K₁ representing the first class (face) and subclasses i = K₁ + 1 to K₁ + K₂ the second class (non-face). The minimum of these distances gives the class label of the j^th position at scale s. Two examples of this process are shown in Fig. 6.

Fig. 6.

(a,c) Detection results as given by (1) at each of the possible scales. (b,d) Final face detection as given by the mean window after outliers deletion.

Note that at each scale, Fig. 6(a), one obtains a distinct detection of the face. At large and small scales there is generally no detection (as expected). But, at the correct scale, we will normally have several detections, since a small (1-3 pixels) displacement of the image window was considered a correct detection during training. We now need to define a mechanism to combine these detections into a single one. To do this, let us denote the face detections at scale s as (u_sj, v_sj, s)^T, where (u_sj, v_sj) is the position of the window image t_sj within the scaled image. A two-step voting method is then applied. First, the scale with the most detections is selected as the reference scale. Face patches detected at two scales above or below this reference scale are eliminated. In the second step, the remaining detections are normalized by their scale value (u_sj/s, v_sj/s, 30/s)^T before being combined together as

$$V(u_j,v_j)=\sum _s{(u_{\mathit{sj}}∕s,v_{\mathit{sj}}∕s,30∕s)}^T.$$

This provides a voting over each image location. Detected face regions having a small overlap with the top voted region are reclassified as non-faces. The final estimation of the face position (center and scale), (u, v, s)^T, is given by the mean over the remaining overlaps, Fig. 6(b,d).

B. Face detection in video

In many applications, as it is the case in the analysis of non-manuals in ASL, we are interested in detecting faces in all frames of a video sequence. In ASL, for instance, the variability in facial expressions may contain grammatical cues on top of the classical ones of intonation and emotional content [31]. In such cases, we can apply our face detector derived in the preceding section at each frame of the video sequence. Still, the results of our face detector, as those of any other algorithm, may be imprecise in a few of the frames. This is particularly true when there are occlusions or large rotation angles. Since we are now detecting faces in a video sequence, we can make use of the continuity of the motion of the subjects to correct the detection errors.

Let f_t = (u, v, s)^T, where (u, v) is the center of the detected face, s the estimate of the scale, and t the frame number. We fit a Gaussian model over the position and scale values given by all frames, N(μ_f, Σ_f), with μ_f = (μ_u, μ_v, μ_s)^T the mean and ${\Sigma }_{\mathrm{f}}=\mathit{diag}({\sigma }_u^2,{\sigma }_v^2,{\sigma }_s^2)$ the variances. We can now use the Mahalanobis distance,

$$d_{\mathit{Mh}}^2={({\mathrm{f}}_t-{\mu }_{\mathrm{f}})}^T{\Sigma }_{\mathrm{f}}^{-1}({\mathrm{f}}_t-{\mu }_{\mathrm{f}}),$$

to detect outliers. In our algorithm, we consider distances larger than 2.5 to correspond to false detections. This value is chosen to set the (probability of) confidence interval to ~ 90%.

Once the outliers have been excluded, those frames that had a missed detected face will not have any estimate of the location of the face. In these cases, the location and scale of the face is estimated using a linear interpolation of the neighboring frames (i.e., those previous and subsequent frames with correct detection). This will provide a smooth transition between frames. Examples of this process are shown in Fig. 7.

Fig. 7.

(a) Detection results on the individual frames, with occlusions larger than those learned by the algorithm. Large occlusions can cause misdetections. (b) Misdetections corrected using the Gaussian model.

IV. Eyes Detection

After (holistic) face detection, eyes are the facial feature to have received the largest attention, mostly because these play a major role in face recognition and human-computer interaction problems. Unfortunately, accurate detection of the eye centers has often require highly sophisticated methods [35]. In this section, we use the general approach defined above to derive a simple algorithm to detect the eye center and its corners. These results are then used to extract the shape of the iris and the eye lids.

A. Detecting the center and corners of the eyes

A major reason behind the difficulty of precise eye detection is the high variability of these. Although most eyes may seem quite the same at first, closer analysis of a set of cropped eyes (i.e., in isolation) reveals a different picture, Fig. 2(c). Eyes may have very distinct shapes (mostly across ethnicity and race, but not exclusively), pupil size, and colors. Furthermore, cast shadows, glasses, and lighting have a strong influence on how eyes appear in an image. In addition, eyes can be open, closed or any way in between, and the iris may be pointing at any direction. For now, we are interested in finding the eye center, regardless of the position of the iris, and its bounding box.

To detect the center of each eye, we use the main approach defined in Section II. Here, the first class is well-centered eyes, represented by images of cropped eyes at the correct positions, while the second class corresponds to cropped images of the same size (24 × 30 pixels) located in the neighboring areas of the eye. Fig. 8 shows how the eye window is centered (class 1) while the eight accompanying background windows (class 2) are located off center. To increase robustness to scale and rotation, we expanded the training set by including the images obtained when rescaling the original training images from .9 to 1.1 at intervals of .1, and by adding in-plane rotated versions of them within the range of −15° to 15°. This yields a total of 25, 780 samples for class 1 (the eye class) and 41, 248 samples for class 2 (non-eyes). Examples are shown in Fig. 2(c-d). Images are mean- and norm-normalized to make them invariant to the intensity of the light source. We only train a left eye detector. Detections of the right eye are done by generating a mirror image of the right eye region. As above, we used the stability criterion of [30] to determine the most appropriate number of subclasses clustered with K-means. This yields K₁ = 23 and K₂ = 11, Fig. 5.

Fig. 8.

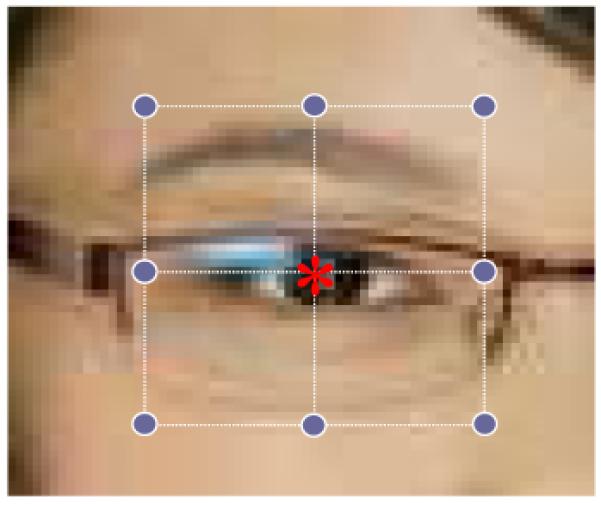
The red star in the figure corresponds to the center of the eye window used to generate the training data for eyes. The blue dots represent the window centers of the background samples. The distance from the eye center and the background window is set to 24 pixels.

To detect the eyes in a new image, we do an exhaustive search in a pre-specified region within the face detection box. These potential eye regions were obtained from a statistical analysis of the eye location over the manually detected eyes previously used to train our classifiers. The goal is to establish where the eyes are with respect to the bounding box found by the holistic face detector. These regions are shown in Fig. 9(a). The figure shows two eye regions per eye. To detect the eye centers in a previously unseen face, we first search for them within the smaller green region (since this includes ~ 90% of the eye centers in our training set). If no eye is detected in this region, we move our search to the wider blue region (which includes 100% of the training instances). These regions are in effect the priors of our classifier, and although one could also estimate the distribution within them, a simple uniform probability provides the results we need. Note that these search regions are not only tuned to the classifiers previously defined, they also make the search much faster and robust (preventing the search to move over shadowed regions that may resemble an eye).

Fig. 9.

(a) Priors: region where the eye centers are in the training images. (b) Voting: results of the detection of the center of the eyes at different scales. (c) Final detection of the eye region.

As in training, the test image is also re-scaled to s = {.9, 1, 1.1}. At each scale, each of the cropped images t_sj, of 24 × 30 pixels and centered at the j^th pixel within the eye-search region, is compared to the learned subclasses using Eq. (1).

The minimum of the distances given by (1) provides the class label of the j^th position at scale s within the eye region, Fig. 9(b). Let us denote this class label (u_sj, v_sj, s)^T, where (u_sj, v_sj)^T is the center position of the window image t_sj, and s is the scale. The results obtained at different scales are normalized and added, ∑_s D(u_sj/s, v_sj/s, s/s). This provides a voting over each location, Fig. 9(b). Detected eye regions having a small overlap with the top voted region are reclassified as background. The final estimation of the eye position (center and bounding box) is given by the mean of all remaining detections, Fig. 9(c). This voting approach may remind the reader of a generalized Hough transform, where the shape of an object is detected using a similar approach.

If a video sequence is available, as it is the case in the ASL application presented earlier, we can further refine the detection as we did in Section III for faces. Here, we use a similar Gaussian model to that employed earlier. The only difference is that this modeling includes the positions of the two eyes as well as the angle θ defined between the horizontal axis and the line connecting the two eye centers. Detected outliers (i.e., false detections) are eliminated and substituted by a linear interpolation between the previous and subsequent frames with correct detection.

B. Eye and eyebrows shape

With the face and eyes detected, we can move to the next phase of extracting the detailed information we need. The very first thing we need to do is to determine the left and right margins for each eye. This we can do by detecting the eye corners. To achieve this, we repeat the process defined above for detecting the center of the eyes but apply it to the detection of their corners. The same process is needed here because eye corners also conform to a large variety of shapes, textures and colors (makeup and eyeglasses being a major problem that needs to be learned). We build two detectors: one to detect inner corners and another for the outer. We train on the left eye and apply it to detect both – right and left. To detect the corners of the right eye we simply flip the image (i.e., mirror image). Two results of eye corner detection are shown in Fig. 10.

Fig. 10.

Eye corners are represented with an asterisk. The iris is shown as a circle, of which, the red segment is the visible part. The upper and lower contours of the shape of the eye are shown in blue.

The iris can generally be readily detected as the minimum of all the average circle areas. This can be defined as a convolution,

$$\begin{array}{c}\hfill \mathbf{P}=\mathrm{conv}(\mathbf{I},\mathbf{H})\hfill \\ \hfill (u_p,v_p)=\underset{u,v}{\arg \min }\mathbf{P}(u,v),\hfill \end{array}$$

where I is the grayscale images and H is a circle mask of radius r_I. This method could have false detection if the image included heavy shadows or dark makeup around the eye area. To prevent these false detections, we first obtain all local minima and then select the one that has the largest gradient between each detected local minimum and the eye. The highest gradient will be given when moving from the darkness of the iris to the whiteness of the conjunctiva, making it a robust detector. Fig. 10 shows the detected iris as a circle. In the above equation, the image I corresponds to a crop of the detected face. In this case, the face has also been normalized to have the line connecting the eye centers parallel to the x-axis.

While the iris region is dark, the eye lids are of skin color. This is especially true for the lower lid, since this has a very limited mobility and is not highly affected by deformations, shadows and others. However, the lids need closer analysis becuase makeup and small occlusions (such as eyeglasses) may present some difficulties. To address this, we apply a correlation with various line orientations θ. The one that gives the highest average gradient in its normal direction is chosen as the best match. Then, the lid contours can be defined by means of a cubic spline passing through the detected points. The final result is illustrated in Fig. 10.

Once the shape of the eyes has been determined, we move to the extraction of the brow’s shape. With the position and shape of the eyes known, the detection of the brows is made much easier. For instance, the x position of the eyebrows is very restrictive, since this has to be very similar to that of the eyes. Similarly, the y position of the eyebrows is always above the eyes and its position range is very limited. Since the eyebrows are either darker or lighter than the skin, it is easy to detect these by searching for non-skin color in the region above the eyes. We define the eyebrow search window as follows. First, the distance d_eyes between the two eye centers is calculated. Then, two search windows are defined, each of width d_eyes and height 2d_eyes/3, which ensures the inclusion of 100% of the training samples. The bottom limits of these two windows are set to be equal to that of the line connecting the eye’s centers. To avoid confusion with the eyes region, the eye regions are eliminated from the windows. This deletion can be readily accomplished, because we already know the eyes’ shape.

To detect the eyebrows in the search window defined above using color information, we use the same HSV color space defined earlier, N(μ_c, Σ_c). Using this model, the pixels above the eye regions that fit to the color model are eliminated. The remaining set of pixels defines the potential region for the brows. To obtain a detailed and accurate description of their shape, we use the gradient information. A Laplacian operator is applied to the non-skin color region. The pixels with highest gradient in each column are kept as potential descriptors of the eyebrow’s shape. Binary image morphology is applied to the result to generate a uniform region. Only the largest, continuous region is kept. Two example results obtained with this approach are shown in Fig. 11.

Fig. 11.

Two examples of eyebrow detection. (a) Binary description of the brow. (b) Final contour detection.

V. Detection of Other Facial Features

The approach defined above can also be used to detect the other facial features. Moreover, with a good detection of the face and the eyes, the location of the rest of features is already approximately known. We start by detecting the nose, then move to the mouth and conclude with the detection of the chin line.

A. Nose

The position of the nose is arguably the easiest to estimate because, as opposed to other features such as the eyes, brows and mouth, the nose cannot undergo large deformations. However, extracting the contour of the nose is still challenging, since this is highly influenced by cast shadows or smooth texture. Cast shadows are especially strong for caucasians, who have larger noses. Smoothness is more prominent in Asian faces. What we do know is that the nose should be within the two eye centers about the x axis and below these about the y axis. The nose search region is thus defined as that below the lower eye lid and between the two eye centers.

We train a nose classifier following the procedure detailed in Section II. Here, we used 2, 765 samples to represent the nose class and 4, 424 image patches corresponding to the nose context, yielding K₁ = 14 (for the nose class) and K₂ = 10 (the nose context class). We see that, as expected and consistent with our theory and previous results, the number of subclasses in the nose class is larger, since noses have a larger variability than their context. Even more interesting is to note that the number of subclasses in the nose class is smaller than that of the face or eye classes. This is also consistent with the claim made at the beginning of this section where we noted that noses are less variable than faces and eyes.

We test detection at scales .9, 1 and 1.1 and combine the results using the voting approach defined earlier, Fig. 12(a). To extract the nose contour, we calculate the gradient of the image and generate its projection onto the x and y axes, Fig. 12(b). This gives us two histograms of the gradient, G_x and G_y. To eliminate outliers, such as shadows and makeup, we find the bounding box containing max(G_x)/2 and max(G_y)/2. This provides a tighter, more precise estimate of the location of the nose. The nostrils are detected as the two darkest (i.e., two minima in graylevel) points within this tighter bounding box, Fig. 12(b). The outer gradient curve is taken to be the nose edge. The final result is shown in Fig. 12(b).

Fig. 12.

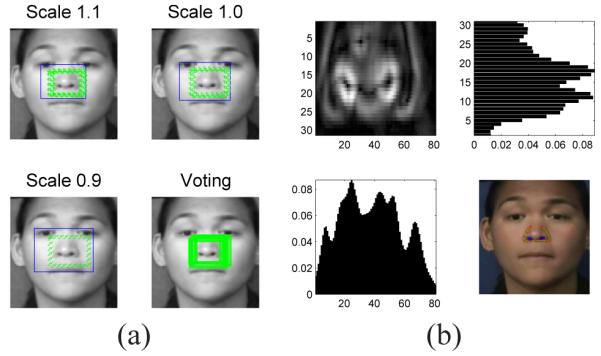
(a) Shown here is an example of nose detection using the subclass approach defined in this paper. Refinement is done with a voting approach over various scales. (b) From left to right and top to bottom: gradient of the nose region found in (a), y projection of the gradient, x projection, and final detection of the nose shape and nostrils.

B. Mouth

The mouth is highly deformable, making an accurate and precise detection of it challenging. Sophisticated algorithms have been recently defined to address this problem [7]. Here, we use our methodology to derive a fast, accurate and detailed detection. A mouth corner detector is defined using the subclass-based classifier presented in Section II. We use 4, 600 mouth corner samples and 7, 360 images to represent the context. This yielded K₁ = 17 and K₂ = 7. We only train a left corner classifier. To detect the right corners, we create mirror images of the testing windows. An example detection is given in Fig. 13(a). Once again, we test at scales .9, 1 and 1.1 and combine the results with the proposed voting method. The bounding box of the mouth is then obtained following the same procedure described for the nose, Fig. 13(b).

Fig. 13.

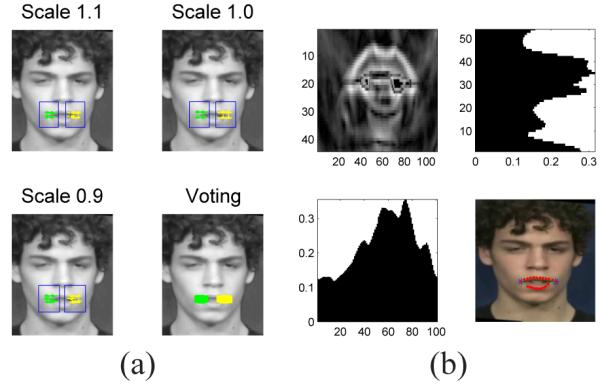
(a) Mouth corner detection. (b) Gradient of the mouth window, its x and y projection, and the final result.

Mouths are rich in color, which makes the final process of delineating them feasible. Here, we use a similar process to that employed earlier – skin color and Laplacian edge detection. In particular, we extract three features, given by saturation, hue, and Laplacian edges. These three masks are thresholded at values T_s, T_h and T_g before being combined into a single response. The three values are determined as follows. Since the lips color makes the saturation of the lips higher than that of skin, T_s is set as the average saturation value. To be able to deal with different kinds of lips, an adaptive T_h is computed using a valley seeking algorithm as was done in [29]. In this approach, the valleys (i.e., minima) in the histogram are searched using an iterative procedure. At the initial step, the histogram is partitioned using a large number of regions. Each region boundary (i.e., threshold) is moved toward the closest minimum using the gradient of the histogram. As more than one threshold collide into the same minimum, these are combined into a single one, reducing the number of clusters. When the algorithm converges to a final solution (i.e., all the thresholds are at one of the minima), the lip hue is defined by the largest of the resulting cluster, which yields T_h. Finally, to determine T_g, we note that the boundary of the mouth, especially around the corners, has strong edge response when compared with the face regions of the cheek. Therefore, T_g is set to be the mean of the gradient of all the pixels within the face region. The final extraction of the contour of the upper and lower lips are given by the outer contour of the mouth mask, Fig. 13(b).

C. Detecting the chin line

The chin is given by a slightly curved edge below the mouth. However, this can be easily occluded by cast shadows or by the hand and clothing. In some cases, the chin line is unclear, because the texture of the neck or lower lip is too smooth to provide a clear delineation. To address these issues, we first extract the edges from a bounding box located immediately below the mouth and then find the best match between the edge points and a quadratic (ellipsoidal) curve. The shortest distances from the edge points to the current fit, d, are calculated and assigned positive or negative labels depending on whether these are above or beneath this current fit. A Gaussian model is fitted to this result, N(μ_d, σ_d). The edge points with distance ∣d∣ larger than T_d pixels are eliminated, with T_d being the larger of 10 and 2σ_d. This fitting process is repeated over the remaining of the points, until no points are excluded. The resulting set of points corresponds to the detection of the chin. Examples of the final fit were given in Fig. 1. Three examples with occlusions are now shown in Fig. 14.

Fig. 14.

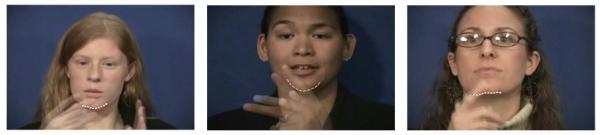
A few examples of chin detection with partial occlusions.

VI. Subclass AdaBoost

In the formulation defined in the preceding sections, we have employed the idea of subclass divisions in discriminant analysis to derive our algorithm. Other techniques could have been used. Among them boosting, and especially Adaptive Boosting (AdaBoost) [13], has shown its potential in several computer vision problems [24], [44], [36], [43]. AdaBoost-based face detection [44] is generally regarded as one of the most appealing approaches, since it provides robust, real-time detections. However, this approach has not been successfully applied to the accurate detection of the internal facial components, because the same AdaBoost approach does not work well when used to detect the internal facial components. To resolve this problem, we will now derive a subclass-based AdaBoost algorithm and use it within our general approach of features versus context.

To begin with, let us reformulate the AdaBoost feature selection approach of [44] within the idea of subclasses. In this approach, which we will refer to as Subclass AdaBoost (SubAdaBoost), the goal is to divide the training samples in each class into the number of subclasses which maximizes classification. Here, the i^th training sample is usually referred to as (x_i, y_i), where x_i is the sample image and y_i equals zero if the sample belongs to the first class and one if it corresponds to the second class.

In feature selection with AdaBoost, we iteratively select the j^th feature associated to the lowest classification error. By combining the different feature selections, we obtain a more accurate (stronger) classifier. At each iteration, this is achieved by training a classifier h_j(x_i), ∀i, for each of the possible features j. The classification error for each of these classifiers is simply given by ∊_j = ∑_i w_i∣h_j(x_i) – y_i∣, where w_i is the weight associated to the i^th sample. In AdaBoost, each sample is weighted according to its relevance for building the classifier. In the first iteration, all samples in the same class are weighted equally, that is w_1,i = 1/2a if y_i = 0 and w_1,i = 1/2b when y_i = 1, where a and b are the number of samples in the first and second class, respectively. These weights are to describe a probability distribution and, hence, at each iteration t, they are normalized, w_t,i = w_t,i/∑k w_t,k. Then, after selecting the feature which minimizes ∊_j at iteration t, we update the weights as

$$w_{t+1,i}=w_{t+1,i}{\beta }_t^{1-e_i},$$

where e_i = 0 when the i^th sample x_i is correctly classified and e_i = 1 otherwise, and ${\beta }_t={∊}_t^{\ast }∕1-{∊}_t^{\ast }$, with ${∊}_t^{\ast }={\min }_j{∊}_j$. This reweighting ensures that at the next run of the algorithm, the samples that are still misclassified will be given more importance than those that have already been successfully classified.

The procedure defined above provides the set of features and, hence, weak-classifiers needed to correctly classify (most of) the training data. These weak classifiers can now be combined to generate the strong classifier h(x), which is set to 1 if ${\sum }_t{\alpha }_t{h}_t\ge \frac{1}{2}{\sum }_t{\alpha }_t$, and 0 otherwise; where ${\alpha }_t=\log {\beta }_t^{-1}$.

When each class is divided into subclasses, the resulting classifiers can be combined with a union operator. First, we apply the above algorithm to obtain the strong classifier for each of the subclasses. The strong classifier of subclass k is given by

$$h_{c,k}=\{\begin{array}{cc}1,\hfill & \sum _t{\alpha }_t{h}_t\ge \frac{1}{2}\sum _t{\alpha }_t\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Here, h_c,k is the strong classifier that discriminates between the k^th subclass in class c and the samples inthe other class (i.e., ∀ x_i with y_i ≠ c) c = 0,1. The final classifier is given by $H_c={\bigcup }_{k=1}^{K_c}{h}_{c,k}$, where K_c is the total number of subclasses in class c.

Note that, since in our case we have two-class classification problems (e.g., non-faces versus faces), we only need to train for the strong classifiers h_1,k, which discriminates between the k^th subclass in class 1 and all the samples in the other class (i.e., ∀ x_i with y_i = 0). The final classifier is $H_1={\bigcup }_{k=1}^{K_1}{h}_{1,k}$. There is no need to determine K₀ or train for h_0,k, since $H_0={\bigcap }_{k=1}^{K_1}\overline{h_{1,k}}$. Note also that unlike classical AdaBoost, SubAdaBoost can readily discriminate classes containing disjoint subsets.

It is known that AdaBoost algorithms reduce the classification error in a number of steps proportional to the sample size n [2]. This means that the selection of an adequate partition of classes into subclasses is proportional to s²n, where s is the number of partitions to be tested. We use cross-validation to do the selection of the subclass number K_i. The training data-set is first randomly divided into N disjoint subsets. N – 1 of these subsets are used for training the SubAdaBoost classifier defined above. At this stage, s classifiers are obtained, each with K₁ subclasses, i.e., {1, … , s}. The remaining subset is then used for validation, resulting in the classification accuracies R_i, i = {1, … , s}. The number of subclasses K₁ is taken to be that yielding the minimum classification error, i.e., K₁ = arg min_i R_i. Using this approach on the same training set described earlier, we obtained K₁ = 9 for faces, K₁ = 10 for eyes, K₁ = 15 for noses, and K₁ = 12 for mouth corners. The only difference to the previous derived SDA formulation, is that we now use the Haar-like features of [44], which have been shown to provide good results in detection tasks such as these.

VII. Experimental Results

We tested the proposed approach with images (stills) and video sequences. Before we do this, we define how to estimate the accuracy of the proposed method.

A. Accuracy of the manual versus automatic detections

To properly compare our results with those obtained with manual detection, we need to have a representation that is common to both. To this end, we first used the approach derived in this paper to find the shape of each of the internal facial features and the chin. We then resample these curves with a total of 98 equally distanced feature points. The corner points specify the beginning and end of a curve. The rest of the points are uniformly located on each of the curves to facilitate comparison with the manual markings.

The basic error measurement used in our experiments is the mean Euclidean distance. It is defined as follows. Each detection result is represented as a 2 × l matrix F_i, corresponding to the 2D coordinates of the l feature points. Let i = {1, 2} define two detections, which can be obtained either manually or automatically. Also, let F_i(k) represent the 2D coordinates of the k^th feature point. Then, a comparison of the two detections is given by

$$d({\mathbf{F}}_1,{\mathbf{F}}_2)=\frac{1}{l}\sum _{k=1}^k{\Vert {\mathbf{F}}_1\left(k\right)-{\mathbf{F}}_2\left(k\right)\Vert }_2,$$

with ∥ · ∥₂ is the 2-norm of a vector. Also, note that in our case l = 98.

To perform a fair comparison with the manual detection results, we provided three “judges” with specific instructions on how to mark 139 feature points around the same facial features detected by our algorithm. The judges had the option to magnify any portion of the image. After manually marking each of the images, the facial feature contours were obtained with a least-squares fit over the fiducials defining each of the facial features. All resulting curves were then resampled to a total of 98 feature points to yield the same detection as that given by the proposed algorithm.

To determine how accurate these manual detections were, we proceed as follows. The mean detection error for the manual detections, denoted e_M, was estimated by comparing the results given by the three judges. Let ${\mathbf{M}}_{\mathit{ij}}\in {\mathbb{R}}^{2\times 98}$ denote the manual marking of the i^th image as given by the j^th judge. Then,

$$e_M=\frac{1}{3m}\sum _{i=1}^{m}d({\mathbf{M}}_{i1},{\mathbf{M}}_{i2})+d({\mathbf{M}}_{i1},{\mathbf{M}}_{i3})+d({\mathbf{M}}_{i2},{\mathbf{M}}_{i3}),$$

where m is the total number of manually delineated faces. Also, denote the standard deviation of this value as st_M.

Another common way to represent the above result, is as a percentage of the error in terms of the size of the face, which can be calculated as

$$E_M=\frac{1}{6m}\sum _{i=1}^m\frac{d({\mathbf{M}}_{i1},{\mathbf{M}}_{i2})+d({\mathbf{M}}_{i1},{\mathbf{M}}_{i3})+d({\mathbf{M}}_{i2},{\mathbf{M}}_{i3})}{r_i},$$

where r_i is the face radius (in pixels) of the i^th face image, which is estimated manually. A typical alternative for the percentage of error is to use (half of) the intra eye distance d_eyesi/2 in lieu of the radius in our last equation [6], [33], with i specifying the image. We denote this alternative error measure $E_M^e$.

After obtaining the mean detection error of the manual detections, we can calculate the mean detection error of the proposed algorithm, denoted e_A. In order to do that, we compare the automatic detections ${\mathbf{A}}_i\in {\mathbb{R}}^{2\times 98}$ to each of the results given by the three judges M_ij, where, as above, i specifies the image and j the judge. This is the same as We have

$$e_A=\frac{1}{3m}\sum _{i=1}^{m}d({\mathbf{A}}_i,{\mathbf{M}}_{i1})+d({\mathbf{A}}_i,{\mathbf{M}}_{i2})+d({\mathbf{A}}_i,{\mathbf{M}}_{i3}).$$

The standard deviation of of this value is denoted st_A and the percentage of the error in terms of the size of the face is $E_A=1∕6m{\sum }_{i=1}^m\left(d\right({\mathbf{A}}_i,{\mathbf{M}}_{i1})+d({\mathbf{A}}_i,{\mathbf{M}}_{i2})+d({\mathbf{A}}_i,{\mathbf{M}}_{i3}\left)\right)∕r_i$. Again, E^e_A is obtained by substituting r_i with d_eyei in the above equation.

Ideally, we want e_A ≈ e_M, st_A ≈ st_M, E_A ≈ E_M and E^e_A ≈ E^e_M. This would indicate that the proposed algorithm is as accurate as the human judges.

B. Detection in stills

The test images used in this first experiment were obtained from the AR and XM2VT face databases. The AR face database [26] includes four different expressions (neutral, happy, anger and scream). Each expression appears twice. We use these eight images for a total 50 subjects, yielding a first set of 400 test images. To increase the variability in face shape, we also used the eight images for a total of 100 subjects from the XM2VT database [32], which provides a second set of 800 images and a combined total of 1, 200.

The face and facial feature detections given by the proposed algorithm are compared to the manual markings given by the three judges. The judges’ mean detection error is e_M = 3.1 pixels with standard deviation st_M = .8 pixels, which corresponds to a mean percentage error E_M = 1.1% (E^e_M = 3%).

We repeated the same analysis using the manual detections given by the three judges on the 1, 200 images and those obtained by the proposed algorithm. Several examples are given in Fig. 15. The results were e_A = 8.4 pixels and st_A = 1.2 pixels, or E_A = 2.7% (E^e_A = 6.9%).

Fig. 15.

Shown here are the automatic face and facial feature detections obtained in the images of the AR and XM2VT face databases.

C. Detection in video

Our next experiment considers the video sequences of ASL nonmanuals. These video sequences were selected because the variability in expression and pose is large. We collected 35 sequences of approximately 77 frames each, providing a total of 2, 730 frames. These sequences were signed by 7 different subjects. Each face is approximately 300 × 250 pixels.

In some applications, such as in the modeling of ASL nonmanuals, occlusions can be very large. To gain robustness to these, a Kalman filter [17] is employed to smooth each of the detected fiducials. An example of our detection results was shown in Fig. 1(a). We now show ten additional examples in Fig. 16. The error was e_M = 4.1 pixels with standard deviation st_M = 1, which means a percentage of error of E_M = 1.3% in terms of the size of the face. An example of manual detection was shown in Fig. 1(b). In comparison, the proposed algorithm yielded e_A = 6.9 pixels and st_A = 1.5 pixels. This corresponds to E_A = 2.2%. Similarly, E^e_M = 3.1% and E^e_A = 5.1%. Again, the accuracy provided by the proposed approach is only slightly below that of an automatic detection.

Fig. 16.

Shown here are ten examples of the automatic detection of faces and facial features as given by the proposed approach.

D. Facial feature detection using SubAdaBoost

SubAdaBoost is utilized to detect the the internal facial features. Then, we employed the same algorithms described in Section IV-V to get the outline of each of them. For testing, we used the same 1, 200 still images from the AR and XM2VT face databases described above. The mean detection error for SubAdaBoost is e_A = 9.0 pixels with standard deviation st_A = 1.3 pixels. This yields a percentage of error for the automatic detection of E_A = 2.8%. We also used the 2, 730 frames from the ASL video sequences described earlier. Here, the mean detection error was e_A = 7.8 pixels (E_A = 2.4%) with standard deviation st_A = 1.9. We see that the face detection algorithm based on SubAdaBoost provides only slightly lower classification results than that of the SDA-based algorithm. This further demonstrates the generality of the features-vs-context framework described in this paper. Nevertheless, the SDA implementation does not only result in slightly superior results, but carries a lower training time.

A final outstanding question is to demonstrate the utility of the subclass divisions advanced in this paper, Fig. 3. If such subdivisions were indeed necessary, then the results obtained with the sub-class-based methods defined above should provide lower error rates than those generated when SDA and SubAdaBoost are substituted by their unimodal counterparts, i.e., Linear Discriminant Analysis (LDA) and AdaBoost. In the following, we provide such a comparison. We also present the error rates obtained when we substitute the subclass-based approach with a simple Principal Component Analysis (PCA). We use all the 3, 930 images described above.

In Fig. 17 we show the results. The figure includes two plots. The first one summarizes the percentage of error rate (E_A) given by each of the algorithms. We see that SDA provides the smallest error, followed by SubAdaBoost as predicted by our theory. In the second plot of this figure, we show the detection rate achieved by each of the implementations of the algorithm.The detection rate is defined as the percentages of times each feature point is successfully detected by the algorithm.² Again, SDA and SubAdaBoost provide the best detection, as expected. The error rates for each of the facial components are also similar. In the SDA-based implementation we have: (6.36, 2.12) for the face, (4.51, 1.53) for the eyes, (4.36, 1.50) for the nose, and (10.31, 3.41) for the mouth; with (e_A, E_A). The corresponding errors in SubAdaBoost are: (10.06, 3.44), (8.45, 2.94), (8.58, 2.92), and (9.67, 3.18).

Fig. 17.

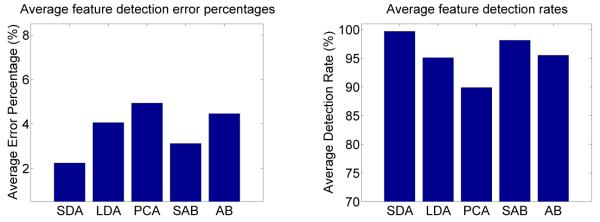
Comparative results of the proposed algorithm implemented with SDA, SubAdaBoost (denoted SAB in the figure), LDA, AdaBoost (denoted AB) and PCA. The left plot summarizes the percentage of error, E_A. The right plot summarizes the detection rate of each of the algorithms. These results are the average over all the images in the AR, XM2VT and ASL databases.

E. Training active appearance models

As summarized in the introduction of this paper, the precise and detailed detection of facial features has a large number of applications. In the experiments above, we have shown an application to do detection of facial expressions of emotion and grammar. We now turn to another application – modeling and tracking of facial shape and texture. A typical way to achieve this is by means of the Active Appearance Model (AAM) approach [5]. Other related approaches are the early work on deformable models of [52], the component-based model of [21], the two-level shape model of [22], the extended active shape model of [33], the edge-based shape model of [34], and the generative shape regularization model of [14], among others.

All these approaches have proven their potential in several applications and in particular in face modeling. However, their major general drawback is that to train subject-independent models, we usually require of a large number of manually annotated samples – typically thousands. The labeled data must include the location of each of the fiducials we want to add to the face model.

In this section, we show that the detections obtained with the proposed algorithm are better or similar to those obtained with AAMs. Even then, however, AAMs have the advantage of providing a model of the face, which can be used to further analyze or synthesize images. For this reason, we show that we can employ the detections provided by the proposed algorithm to train a AAM. This eliminates the need for manual intervention.

In Fig. 18, we plot the cumulative error distribution of the error (in pixels) and percentage of error of the detailed face detection results of the proposed algorithm over all the 3, 930 images. The cumulative error distribution g_Z(z) is formally defined as the probability that the error Z is smaller than z, i.e., P(Z < z). Close analysis of the results in this figure show they are better than or comparable to some of the most advanced AAM-based algorithms such as that of [6], [33].

Fig. 18.

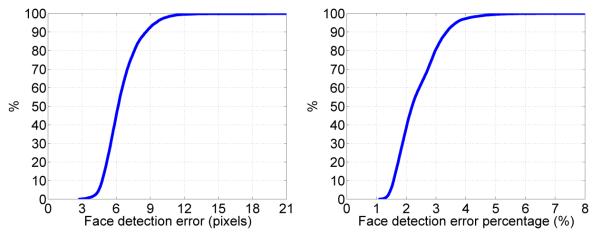
Shown here are the cumulative error distributions of the face detection error and the percentage of error of the proposed algorithm. The results are calculated over the 3,930 images described in the text.

Since the databases used in the literature and those used here are not always the same, we also conducted a second experiment using the proposed algorithm and AAMs. Here, we selected 50 subjects from the AR face database. the images of 80% of the subjects were used for training an AAM. Testing was conducted over the remaining images. This division was done randomly for a total of five times to test the viability of subject-independence. The average error was e_A = 11.8, E_A = 4.3%, with an AAM fitting converge rate of 91%. We see that the error rates are above those given by our algorithm (which were ≈ 2.7%).

As anticipated above, we could also employ the detection results of our algorithm to train an AAM, since these models can then be used to resolve additional problems. We used two of the sequences from the ASL database described in the preceding sections for each of the subjects to train subject-specific AAMs. We then used each of the trained AAMs to detect and track the same fiducials on the other three sequences of our ASL database. Examples of the AAM fitting results are shown in Fig. 19. In (a) we show the results obtained when the AAM is trained using the automatic labeling given by the algorithm defined in this paper. In (b) we show the results obtained after training with the manually labeled set. The average error over all the testing images (for all subjects) when using the manually labeled data is e_A = 5.5 pixels, with st_A = 1.8 pixels, E_A = 1.8%. The same average error and standard deviation obtained when training the AAM with the automatic annotations given by our algorithm are e_A = 7.8 pixels, st_A = 1.7 pixels, and E_A = 2.5%, respectively. We see that the results obtained with the automatically labeled data are almost as small as those given by the manually labeled data.

Fig. 19.

(a) Fitting results given by the AAM trained with the automatically labeled data. The training data was generated fully automatically as described in this paper. (b) Comparison results obtained with the AAM trained with the manual data given by the average of the three judges.

VIII. Conclusions

The development of face detection algorithms using the appearance-based approach has resulted in the design of quite accurate methods. By face detection, we understand that a bounding box of approximately the correct size is located around each face in the image.

To move the field forward, research is now emphasizing three different and equally important fronts. The first is to provide a detection of the internal facial components, i.e., brows, eyes, nose, mouth, and chin. The second effort is directed toward deriving algorithms that generate detections as accurate as manual markings. And, the third goal is to move from the estimate of the bounding box to a detailed extraction of the shape of each of the facial features detected by the algorithm. The present paper has defined an approach to address these three problems.

These problems have been resolved using a common approach, where we learn to discriminate between the actual facial features and their context. This is in contrast to most algorithms designed to date, where it is learned to discriminate between samples of the features and samples of natural scenes. However, when using this latter approach, faces and their facial features tend to be detected imprecisely, because a crop image of a non-centered face is more similar to the face class than to the non-face (natural scenes) class.

Learning to discriminate between similar classes is however a challenging task, especially when the within-class variability is large. To resolve this problem we have taken advantage of the idea of subclass divisions. Here, the goal is to divide each class into a group of subclasses until each subclass can be readily distinguished from the subclasses of the other class. We have derived two algorithms to select the most adequate number of subclasses. The first of these algorithms is based on a discriminant analysis framework, while the second extends on the AdaBoost formulation. We have shown that the former yields slightly better results and at a lower computational cost.

Our experimental results (on a total of 3, 930 images) demonstrates that the detections obtained with this approach are almost as small as those obtained with manual annotations.