Time series analysis of personal exposure to ambient air pollution and mortality using an exposure simulator

Abstract

This paper describes a modeling framework for estimating the acute effects of personal exposure to ambient air pollution in a time series design. First, a spatial hierarchical model is used to relate Census tract-level daily ambient concentrations and simulated exposures for a subset of the study period. The complete exposure time series is then imputed for risk estimation. Modeling exposure via a statistical model reduces the computational burden associated with simulating personal exposures considerably. This allows us to consider personal exposures at a finer spatial resolution to improve exposure assessment and for a longer study period. The proposed approach is applied to an analysis of fine particulate matter of <2.5 μm in aerodynamic diameter (PM_2.5) and daily mortality in the New York City metropolitan area during the period 2001–2005. Personal PM_2.5 exposures were simulated from the Stochastic Human Exposure and Dose Simulation. Accounting for exposure uncertainty, the authors estimated a 2.32% (95% posterior interval: 0.68, 3.94) increase in mortality per a 10 μg/m³ increase in personal exposure to PM_2.5 from outdoor sources on the previous day. The corresponding estimates per a 10 μg/m³ increase in PM_2.5 ambient concentration was 1.13% (95% confidence interval: 0.27, 2.00). The risks of mortality associated with PM_2.5 were also higher during the summer months.

INTRODUCTION

There exists substantial epidemiological and toxicological evidence on the adverse health effects of ambient air pollution.^1–3 Population-based studies have had an important role in establishing regulatory standards, such as the National Ambient Air Quality Standards (NAAQS), to protect public health.⁴ For exposure assessment, these studies routinely use concentrations measured at outdoor monitors where ambient levels serve as a surrogate for pollution from outdoor sources. However, individuals spend the majority of their time indoor and air pollution exposures include both ambient and non-ambient sources. Consequently, there has been a continual effort to understand the relationship between ambient concentrations and personal exposures,^5,6 as well as the bias in risk estimates when ambient concentrations are used to derive exposure metrics.⁷ Studies have also suggested that factors affecting ambient contribution to personal exposure may modify air pollution health risks.^8,9

Exposures from both ambient and non-ambient sources depend on the locations (microenvironments) and the amount of time spent at the locations. Exposure levels can vary in different microenvironments, such as vehicle, restaurant or home, depending on how much ambient pollutant penetrates indoor and the presence of indoor sources (e.g., environmental tobacco smoke, cooking, cleaning). Empirical findings from panel studies have provided considerable knowledge on how different sources contribute to personal exposures.^10–13 These results, along with data on human daily activity patterns,¹⁴ have led to the development of several personal exposure simulators. Examples include the probabilistic NAAQS Exposure Model,¹⁵ the Air Pollutants Exposure Model¹⁶ and the Stochastic Human Exposure and Dose Simulation (SHEDS).¹⁷

An exposure simulator predicts daily exposure for a hypothetical individual by first randomly assigning a time sequence of activity pattern that describes the amount of time the individual spends in different microenvironments. The activity pattern is selected to match the characteristic of the individual such as age, sex and occupation. Simplified versions of the exposure simulators based on statistical models have also been proposed.^18–20 Exposure simulators were originally developed to assess the impacts of regulatory policies. The ability to obtain exposure distribution for the at-risk population has encouraged their application in health studies. For example, Shaddick et al.²¹ and Reich et al.²² used simulated exposures to characterize daily group-level exposures to particulate matter (PM) and examined their effects on daily mortality. Also, Berrocal et al.²³ utilized SHEDS in an analysis of birth weight and fine PM exposure during pregnancy.

This paper describes a modeling framework for estimating the short-term health effects of personal exposures to ambient air pollution in a time series design. The proposed approach is applied to an analysis of fine PM of <2.5 μm in aerodynamic diameter (PM_2.5) and daily mortality in the five-county New York City metropolitan area during the period 2001–2005. We choose to focus on the associations between mortality and personal exposures to PM_2.5 of ambient origin, whereas previous studies have used total personal exposures as the exposure metrics. Studies have shown that exposures to ambient and non-ambient fine PM have low correlations. Also, ambient and non-ambient PM often differ in size range and composition.²⁴ Moreover, the NAAQS regulates ambient concentrations and estimating specifically the health effects attributable to outdoor sources enables risk assessment that is policy relevant.

We follow previous approaches to link simulated personal daily exposure to PM_2.5 from SHEDS and the health outcome; but we also consider several extensions aimed at reducing computational burden, and improving exposure assessment for the at-risk population. First, in a time series analysis, the outcomes are daily counts of adverse events aggregated over a geographical region that typically involves a large at-risk population and a long study period. Simulating personal exposures for each day is computationally intensive, which limits their use in health studies. We address this challenge by considering a statistical emulator approach. Specifically, personal exposures are only simulated for a subset of the study days. We then build a model between ambient concentrations and simulated average personal exposures in order to impute exposures for the entire study period. The modeling approach is carried out in a Bayesian framework such that uncertainty in exposure estimation can be easily propagated into risk estimation. Using longer study period also allows us to examine seasonal differences in the health effects.

We also consider simulating exposures at a finer spatial resolution compared with previous studies. For example, Holloman et al.¹⁸ generated individuals across a county, while Shaddick et al.²¹ and Reich et al.²² generated individuals in small areas around air quality monitors. Similar to most time series analyses, these studies assumed that the pollutant concentration is relatively smooth across the study area. However, exposure to air pollution can still vary spatially because of: (1) spatial variation in demographic characteristics that can contribute to different activity and commuting patterns; and (2) spatial variation in housing type that can contribute to different ambient contributions to indoor concentration. Moreover, ambient concentration of air pollution can exhibit fine-scale spatial variation, especially in an urban setting. We therefore choose to simulate exposures across all census tracts in the five-county study region. Tract-level exposures are then combined to derive an overall population-weighted exposure for risk estimation.^25,26

In this paper, our goal is not to determine which metric (ambient concentration versus personal exposure) is optimal. Instead, we wish to compare the risk estimates obtained from the two exposure metrics. Empirical results from panel studies have demonstrated that ambient concentration differs from personal exposure on the individual level. Our work addresses an important scientific question because true personal exposures cannot be obtained directly in a large population-based study such as a time series analysis.

METHODS

Mortality and Air Pollution Data

Detailed mortality data were obtained through the National Center for Health Statistics. For the period 2001–2005, daily mortality counts for those aged 65 or above were assembled in the New York City metropolitan area. Our study region consisted of the following five counties: Bronx, Kings (Brooklyn), New York (Manhattan), Queens and Richmond (Staten Island). Based on the International Statistical Classification of Diseases 10th revision, we considered deaths because of cardiovascular (I00–I79) and respiratory diseases (J10–J18, J21–J47 and J69–J70). Total population count by sex, and housing type (single-unit detached, single-unit attached, multiple-unit attached and other) were obtained from Census 2000 for 2105 tracts.

Mean daily temperature and dew-point temperature were obtained from the National Oceanic Atmospheric Administration's National Climatic Data Center. Daily ambient PM_2.5 data were obtained from the Statistically Fused Air Quality database (http://www.epa.gov/esd/land-sci/lcb/lcbsfads.html). The database contains predicted daily PM_2.5 concentration averaged over contiguous 12 km by 12 km grid cells. Predictions are based on a Bayesian space-time hierarchical model²⁷ that combines (1) PM_2.5 data from the Air Quality System network and (2) outputs from the Models-3/Community Multiscale Air Quality model.²⁸

Personal exposures to PM_2.5 because of outdoor sources were obtained from the SHEDS version 3.7.¹⁷ First, we generated 23 hypothetical individuals for each census tract (a total of 48,415 across the study region). The simulation was conducted such that the 23 individuals reflect the demographic proportions of sex, age and residential housing type in each census tract. By simulating individuals within each tract, this approach captured the variation in exposure associated with different at-risk population compositions across census tracts. A smoking status was also randomly assigned using sex-specific smoking prevalence statistics obtained from the New York City Department of Health and Mental Hygiene.^29,30 Then for each day in April, July, October and December of the year 2002, the activity pattern of each individual was randomly matched to a diary from EPA's Consolidated Human Activity Database. The diary describes the amount of time an individual spends in various microenvironments for a particular season, day of the week and individual characteristics. In-vehicle exposures are estimated based on a revised approach recommended by Liu and Frey.³¹

Let X_i (t,s) denote the simulated personal exposure to ambient PM_2.5 from SHEDS for individual i on day t in census tract s. Daily exposures were calculated by averaging time-weighted exposure to ambient PM_2.5 in nine microenvironments across a 24-h period. Specifically, let C_ik(t,s) and T_ikh(t,s) denote the concentration of ambient PM_2.5 and time spent in microenvironment k during hour h. SHEDS considers nine microenvironments including outdoor, home, office, school, store, restaurant, bar, in-vehicle and all other indoor. Then,

$$X_i(t,s)=\sum _{k=1}^9\sum _{h=1}^{24}\frac{1}{24}{C}_{ik}(t,s)T_{ikh}(t,s)$$

For non-residential microenvironments, C_ik(t,s) was determined by a linear function based on empirical analysis of concurrent indoor and outdoor PM_2.5 measurements for these microenvironments:

$$C_{ik}(t,s)=b_{k}W(t,s)$$

where W(t,s) is the predicted ambient level obtained from the FSD database linked to the tract centroid. The slope parameters were assumed known where b_outdoor = 1.0, b_office = 0.18, b_school = 0.60, b_store = 0.75, b_restaurant = 1.0, b_bar = 1.0, b_vehicle = 1.0 and b_other = 0.85.¹⁷ The coefficient for home was determined by the mass balance equation

$$b_{\text{home}}=\frac{P\times \mathrm{ach}}{\mathrm{ach}+k}$$

where P represents the penetration factor; k represents the deposition rate; and ach represents the air exchange rate. Uncertainty in the contribution of ambient PM_2.5 at home was accomplished via a two-stage Monte Carlo approach by assigning probabilistic distribution to the parameters. For each individual, SHEDS randomly selects values based on the following distributions. We assumed P to be triangular (0.70, 0.78, 1.0) and k to be normal with mean 0.40 and SD 0.01. We assumed ach to be log-normal with season-specific geometric mean (spring: 0.40, summer: 0.64, fall: 0.22, winter: 0.45) and geometric SD (spring: 1.82, summer: 2.09, fall: 1.72, winter: 2.03).^32–34

Exposure Estimation

Denote X̃(t,s) the sample mean calculated across the 23 simulated personal exposures for each tract. We considered the following random-effect model to relate the tract-level population-average exposures to ambient PM_2.5 concentrations. We refer to this model as the emulator for SHEDS. We allowed all parameters in the model to be season specific because in the SHEDS simulation, contribution of ambient PM_2.5 at home and the associated uncertainty are season specific. To simplify notation, in the following discussion we drop the index for seasons on the model parameters.

$$\begin{array}{c}\hfill \log \stackrel{‒}{X}(t,s)={\alpha }_0\left(s\right)+{\alpha }_1\left(s\right)\log W(t,s)+\epsilon (t,s)\hfill \\ \hfill {[{\alpha }_0\left(s\right),{\alpha }_1\left(s\right)]}^{\prime }={\tilde{Z}}^{\prime }\left(s\right)[{\beta }_0,{\beta }_1]+\theta \left(s\right)+v\left(s\right)\hfill \\ \hfill \epsilon (t,s)\sim N(0,{\tau }^2)\theta \left(s\right)\sim \mathrm{MCAR}(0,\Sigma )v\left(s\right)\sim N(0,V)\hfill \end{array}$$

We assumed a linear relationship between the log average personal exposure and the log ambient concentration with tract-specific intercept α₀(s) and slope α₁(s). Daily variation in exposure because of different activity patterns is captured by the residual term ε(t, s), which is Gaussian with mean zero and variance τ². Exploratory analysis showed that the residual error increases with ambient concentrations and the logarithmic scale was chosen to stabilize heteroskedasticity. Tract-specific intercepts and slopes were modeled with tract-level covariates Z̃(s) for population characteristics that can influence personal exposure to ambient PM_2.5. Based on the SHEDS algorithm, we included two variables: percent male in the 23 simulated individuals and percent single-unit detached housing unit from Census 2000. We also considered average age as an additional covariate but found that it did not improve prediction. This may be due to the study population being restricted to those aged 65 or above.

We allowed α₀(s) and α₁(s) to vary smoothly in space by including spatial random effects θ(s) and an unstructured random effects ν(s) with heterogeneity covariance V. The spatial random effects aim to capture residual effects such as higher-order interactions between the covariates that may exhibit spatial similarity. Specifically, we modeled θ(s) as a multivariate conditionally autoregressive model (MCAR). The model is specified through spatial adjacencies and a conditional covariance Σ. Let s ~ s₀ denote that census tract s and s₀ are spatial neighbors, and m_s be the number of spatial neighbors of tract s. The MCAR model entails that the distribution of θ(s₀) given all other locations is Gaussian with conditional mean $1∕m_s\underset{s\sim s_0}{\Sigma }\theta \left(s\right)$ and conditional variance 1/m_sΣ.

Parameter estimation for the emulator was carried out under a Bayesian framework using Markov Chain Monte Carlo (MCMC). Parameters β₀ and β₁ were assigned Gaussian prior with mean zero and variance 100². The residual variance τ² followed an inverse-Gamma (0.001, 0.001); Σ and V followed inverse-Wishart distributions with scale matrices of diagonal element 0.1² and 4 degrees of freedom. We used Gibbs sampling to analyze the posterior distributions of all unknown parameters. Analyses were carried out in R 2.8.0 with sub-routines written in C. After 10,000 burn-in samples, we ran an additional 25,000 iterations. To reduce autocorrelation between samples, we saved every fifth sample, resulting in a total of 5000 posterior samples. MCMC convergence was assessed by examining the trace plots of several representative parameters.

We imputed daily tract-level exposures for the complete study period using the emulator as follows. Specifically, let superscript j = 1, ..., 5000 indicate the jth posterior sample. Then the tract-specific logarithmic average exposure X^(j)(t, s) can be sampled from a Gaussian distribution with mean ${\alpha }_0^{\left(j\right)}\left(s\right)+{\alpha }_1^{\left(j\right)}\left(s\right)\log W(t,s)$ and variance τ^2,(j). Similarly, at each iteration, the spatially varying bias terms ${\alpha }_0^{\left(j\right)}\left(s\right)$ and ${\alpha }_1^{\left(j\right)}\left(s\right)$ are sampled from a bivariate Gaussian distribution with covariance V^(j), and means $Z^{\prime }\left(s\right){\beta }_0^{\left(j\right)}+{\theta }_0^{\left(j\right)}\left(s\right)$ and $Z^{\prime }\left(s\right){\beta }_1^{\left(j\right)}+{\theta }_1^{\left(j\right)}\left(s\right)$, respectively. The Bayesian estimation approach allows straightforward transformation between the logarithmic and original scale. For imputing tract-specific intercept and slopes, we used the percent male from Census 2000 instead of those calculated from the 23 simulated individuals by SHEDS. We did not use the simulated SHEDS results directly as exposure on days when SHEDS was run. Instead, we used the corresponding predictive samples to incorporate uncertainty in the simulated exposures.

As our daily mortality counts were aggregated across five counties, we computed a weighted-average of the tract-level exposures for the time series analysis. Although we can use tract-level exposures directly to conduct time series analysis within each tract, the number of events on each day is likely to be too small for Poisson regression. In a time series analysis where the health outcome is aggregated over a large geographic unit, the desired exposure should represent the average levels of personal exposure to ambient PM_2.5 across the at-risk population. Therefore, for each day t, average exposure across the entire study area was obtained by weighting the tract-specific average exposures by the population at-risk:

$$X^{\left(j\right)}\left(t\right)={\left(\sum _{s=1}^{2105}P\left(s\right)\right)}^{-1}\left(\sum _{s=1}^{2105}P\left(s\right)X^{\left(j\right)}(t,s)\right)$$

where P(s) denote the population size above age 65 in tract s based on Census 2000. We also calculated exposure using ambient concentrations by replace X^(j)(t, s) with W(t, s).

To evaluate the predictive performance of our emulator, we conducted an additional analysis by first leaving out five randomly selected days from each census tract. We then calculated the prediction root mean-squared error between the true values and their posterior predicted mean by averaging all imputed X^(j)(t) across each missing day. We also examined the empirical 95% coverage probability by calculating the proportions of true values that fell between the 2.5th and 97.5th quantiles of the imputed X^(j)(t).

Mortality Model and Risk Estimation

Relative change in the rate of mortality associated with variation in daily PM_2.5 exposure was estimated via Poisson regression. We examined the effects of same-day (lag 0), 1-day prior (lag 1), 2-day prior (lag 2) and 3-day prior (lag 3) exposure. We also considered an unconstrained distributed lag model, where exposures at lag 1–3 were included in the mortality model simultaneously.³⁵ A cumulative effect of lag 1–3 was then obtained by summing the 3 coefficients. We also considered season-specific relative risks by including interactions between the exposure and indicators of seasons (winter: December–February, spring: March–May, summer: June–August, fall: September–November). Following Samet et al.,³⁶ we controlled for seasonal trends and weather effects via natural cubic splines with degrees of freedom d, including (1) calendar time (d = 8 per year), (2) current-day temperature (d = 6) and average temperature for the previous three days (d = 6); (3) current-day dew-point temperature (d = 3) and average dew-point temperature for the previous three days (d = 3); and (5) indicators for day of the week.

Given the 5000 imputed time series of X^(j)(t), we considered two approaches to estimate relative risks. In the “exposure simulation” approach, we fitted the health model repeatedly with each exposure time series and combined the resultant risk estimates and their standard error in a multiple imputation framework. We also considered a two-stage “Bayesian” approach where we carried out a second MCMC by treating the imputed time series as a prior distribution for the exposures. This second approach differs from exposure simulation in that the health data are used to help learn about the exposures and computation details can be found in Peng and Bell.³⁷ Moreover, we did not conduct a full Bayesian analysis where the emulator and the mortality model are fitted simultaneously. Therefore, here we assume that the mortality data do not provide information to estimate the relationship between ambient concentrations and personal exposures. However, the mortality data may provide information about the exposures through the mortality model, especially if the exposure model is specified incorrectly.

RESULTS

Based on Census 2000, the study population includes approximately 0.94 million persons aged 65 or above with an average 79 cardio-respiratory deaths per day. Table 1 summarizes daily population-weighted exposure metrics calculated using ambient PM_2.5 concentrations or predicted personal exposure to ambient PM_2.5. Both concentrations and exposures were higher during the summer months. Personal exposures also exhibited smaller temporal variation compared with ambient concentrations. The SDs describe the between-day variation in average personal exposures, not the between-individual variation in personal exposure. The decrease in temporal variation is likely a result of personal exposures representing only a fraction of ambient concentrations.

Table 1.

Mean and SD of daily PM_2.5 ambient concentrations (μg/m³) and personal exposures (μg/m³) by season.

	PM2.5 concentration		PM2.5 exposure		Ratioa
	Mean	SD	Mean	SD	Mean
Spring	14.30	7.75	7.54	3.99	0.53
Summer	17.50	9.25	10.39	5.44	0.60
Fall	13.27	7.96	5.80	3.32	0.44
Winter	15.37	7.77	8.37	4.16	0.55

^aRatio of PM_2.5 exposure divided by PM_2.5 concentrations and averaged across days.

The daily exposure to concentration ratios also varied across seasons and were higher during the summer months. Although intuitively people spent more time indoor during the winter, this period does not correspond to the lowest concentration–exposure ratio. In our SHEDS simulation, we assumed the air exchange rate parameter (ach) in winter to be relatively high. This follows empirical studies, which have demonstrated that greater indoor–outdoor temperature differences were associated with higher ach because convection may be the dominant mechanism for air exchange.

To summarize the random tract-specific intercepts and slopes in the emulator, Table 2 gives the season-specific posterior means and 95% posterior intervals (PI) of the average α₀(s) and α₁(s) calculated across all tracts. We present the exponentiated intercepts because it roughly describes the ratio between ambient concentrations and simulated exposure on its original scale when α₁(s) is close to 1. Coefficient α₁(s) describes the multiplicative bias in ambient concentration on the logarithmic scale. Estimates of the random-effect SDs are also given in Table 2 to describe the between-tract variation (heterogeneity) on the relationship between concentration and exposure. On average, we found the intercepts to be higher during the summer and lower during the fall. The PIs of the intercept means also do not overlap, indicating that on average across census tracts, seasonal effects on the relationship between ambient concentration and personal exposure are significantly different.

Table 2.

Mean and SD of the tract-specific intercepts α₀(s) and slopes α₁(s) relating ambient concentrations and personal exposures.

	Exponentiated intercepts α0(s)		Slopes α1(s)
	Mean across tracts	SD across tracts	Mean across tracts	SD across tracts
Spring	0.560 (0.557, 0.564)	0.014 (0.011, 0.017)	0.977 (0.975, 0.980)	0.010 (0.008, 0.013)
Summer	0.613 (0.610, 0.615)	0.016 (0.014, 0.019)	0.989 (0.988, 0.990)	0.006 (0.004, 0.008)
Fall	0.492 (0.491, 0.493)	0.031 (0.029, 0.032)	0.956 (0.955, 0.958)	0.018 (0.016, 0.020)
Winter	0.569 (0.566, 0.573)	0.021 (0.019, 0.024)	0.984 (0.982, 0.987)	0.008 (0.006, 0.011)

The summary statistics were calculated across 2105 census tracts. Posterior means and 95% posterior intervals are presented.

Table 3 gives the predictive performance of the emulator that relates tract-level ambient concentrations and personal exposures. Predictive statistics were calculated using the back-transformed (original) PM_2.5 levels. Higher prediction errors are associated for the summer and winter months. Overall the root mean-squared errors were small compared with the daily PM_2.5 exposure levels. We also found the emulator to be well calibrated where the 95% prediction intervals are close to the desired coverage probabilities for all seasons.

Table 3.

Predictive performance of the emulator for relating census tract-level ambient concentrations and personal exposures.

	RMSEa (μg/m3)	PI lengthb (μg/m3)	PI Probc (%)
Spring	0.37	1.38	94.6
Summer	0.74	2.43	94.8
Fall	0.35	1.30	94.6
Winter	0.45	1.61	94.5

^aRoot mean-squared error.

^bAverage 95% posterior predictive interval length.

^cEmpirical coverage probability of the 95% posterior predictive interval length.

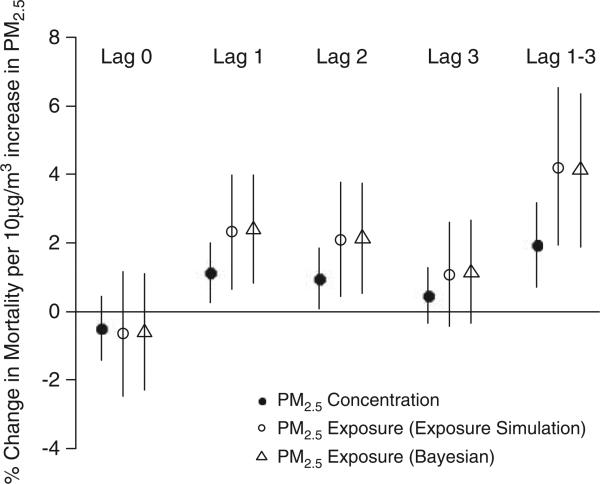
Figure 1 shows the percent increase in mortality associated with ambient PM_2.5 exposure. The standard approach where ambient concentrations were used as a surrogate measure is also presented. The two different approaches for utilizing imputed time series of PM_2.5 exposure to estimate relative risks were indicated by different symbols. The risks associated with personal exposures were higher than those where ambient concentrations were used directly. The Bayesian approach produced very similar results compared with the exposure simulation approach, the latter of which is more computationally efficient.

Figure 1.

Percent increase in mortality associated with ambient PM_2.5 exposure and concentration. Lag 1–3 represents the cumulative effect obtained from an unconstrained distributed lag model. For PM_2.5 exposure, two estimation methods (exposure simulation and Bayesian) are considered.

With the exposure simulation approach, we estimated that a 10 μg/m³ increase in PM_2.5 exposure was associated with a 2.32% (95% PI: 0.68, 3.94), 2.08% (95% PI: 0.42, 3.73) and 1.09% (95% PI: –0.41, 2.63) increase in daily mortality rate for lag 1, 2 and 3, respectively. The corresponding risk estimates per 10 μg/m³ increase in PM_2.5 concentration were 1.13% (95% CI: 0.27, 2.00), 0.95% (95% CI: 0.07, 1.84) and 0.46% (95% CI: –0.35, 1.27). The cumulative effects of lag 1–3 were 4.13% (95% PI: 1.81, 6.45) and 1.94% (95% CI: 0.70, 3.18) per 10 μg/m³ increase in PM_2.5 exposure and concentrations, respectively. Table 4 shows the cumulative effects of lag 1–3 stratified by season. We found that the greatest risk occurred during the summer months with a percent increase in mortality of 6.85% (95% PI: 3.10, 10.60) and 3.99% (95% CI: 1.87, 6.12) per 10 μg/m³ increase in PM_2.5 exposure and concentrations, respectively.

Table 4.

Percent increase (95% posterior intervals) in mortality associated with ambient PM_2.5 exposure and concentration due to lag 1–3 by season.

	PM2.5 exposure	PM2.5 concentration
Spring	1.21 (–3.50, 5.90)	0.65 (–1.78, 3.09)
Summer	6.84 (3.10, 10.60)	3.99 (1.87, 6.12)
Fall	3.45 (–1.91, 8.83)	1.42 (–0.87, 3.72)
Winter	1.90 (–2.52, 6.39)	1.13 (–1.29, 3.55)

DISCUSSION

The proposed statistical emulator for population-level average exposure represents a hybrid approach that combines ideas from both a fully statistical and a fully stochastic model. Specifically, stochastic exposure simulators can effectively incorporate state-of-the-art knowledge in various aspects of personal exposure assessment. Statistical emulators then provide a computationally efficient way to estimate exposure for large population-based study and propagate exposure uncertainty as dictated by the stochastic simulation algorithm. To our knowledge, this is the first study that uses personal exposure estimates in a time series design where the analytic approach is comparable to those studies using ambient concentrations. Owing to its computational burden, previous studies that examined the health effects of personal exposures to air pollution could only consider simplified health models or with sample size much smaller than the epidemiologic studies today.

In this study, the computation time is approximately 5–6 h to simulate exposures for 50,000 individuals in a 30-day time period on a quad-core Window-based PC. The emulator can be fitted within 3 h and imputation is completed within minutes. Our modeling strategy is based on a random-effect specification with second-level covariates and can be fitted in standard software such as SAS or WinBUGS. This will significantly decrease the computation time further and facilitate the use of exposure simulators in future studies of air pollution and health.

We chose to conduct exposure and risk estimation in two stages. This reduces computation and is particularly important because in practice, the health model is often run many times with the same exposures to examine: (1) different health outcomes (e.g., causes of death or hospital admission); (2) different risk-windows in terms lag-effects; (3) and different degrees of confounder control as sensitivity analysis. Stratified or subset analysis are also frequently conducted to examine effect modifications.

Similar to previous studies, we found the risk estimates associated with exposures to be greater than that associated with concentrations, indicating a negative bias in the concentration-response function when ambient levels are used as a proxy for exposure. Another potential explanation to this observation may be related to exposure misclassification, which attenuates the true effects. The magnitude of the bias also approximates the ratio between daily concentration and exposure level. It is possible that additive bias is effectively controlled by the temporal smoothers in the time series model. We believe our approach and results underscore the importance of exposure metric definition and may help shed light on how this choice can impact the risk estimates.

When stratified by season, we found that ambient PM_2.5 concentration and exposure were positively associated with mortality in all seasons, but only statistically significant in the summer months. This result agrees with a previous seasonal analysis of PM₁₀ and mortality in northeastern United States.³⁸ As the composition of PM varies both geographically and seasonally, this finding should be explored in other regions and may have important policy implication such as the need for seasonal PM_2.5 control strategies. Our results do not exclude the possibility of an adverse PM_2.5 effect during non-summer months. For example, during winter months in Northeastern United States, the PM_2.5 mass includes a higher proportion of elemental carbon, which has been linked to several health outcomes.^39,40 However, elemental carbon often exhibits high spatial heterogeneity in their concentrations. As our time series analysis is conducted over five counties and we used total PM mass as exposure, the winter effect estimate may be attenuated because of larger exposure measurement error. Another possible explanation is statistical power. The summer months had the greatest temporal variation in both concentration and exposure levels. Moreover, during the winter months, it may be difficult to identify the effect of particulate matter from the strong effect of infectious diseases, which is aggressively controlled for using the temporal smoother.

The emulator approach presented here has several limitations that offer potential model extensions. First, we only considered modeling the mean population exposure and not its variation. Time series analysis is ecological in nature where specification bias exists due the aggregation.⁴¹ However, the acute health effects of ambient air pollution is typically very small and specification bias is likely to be minor compared with that arises from the using ambient concentrations as personal exposure. In this study, we chose to simulate small number of individual exposures at a finer spatial resolution and did not have sufficient sample to incorporate estimated exposure variances. Approaches to model population exposure variance efficiently, especially when spatial dependence is considered, warrant further investigation. Another limitation is the use of Census 2000 data both in fitting the exposure model and for predicting daily exposures. We assumed that the tract-specific relationships between ambient concentrations and exposures are season specific and do not vary between years. With the availability of Census 2010 data, one potential extension is to incorporate temporal changes in the demographic variables that influences α₀(s) and α₁(s). Another source of demographic data is the American Community Survey where yearly, 3-year and 5-year statistics are available at different spatial resolutions.

There are additional challenges in estimating personal exposure to ambient air pollution that our approach does not consider and warrant further investigation. First, SHEDS, like other stochastic and statistical simulators, requires ambient concentration as an input. We chose US EPA's fusion product because it provides daily concentrations with complete spatial coverage. However, the 12 km by 12 km grid cell cannot capture heterogeneity at finer spatial scale and better characterization of ambient concentration, especially in urban community, may improve exposure estimation. We also did not consider uncertainty in the concentration measurements. The EPA fused database provides SD for the predicted concentration and motivates additional methodological work to incorporate this uncertainty in the risk estimates. Our results also rely on the validity and applicability of the dairies in CHADS, as well as the assumptions in the concentration–exposure relationships dictated by SHEDS. For example, we simulated exposures using SHEDS only for 4 months to describe the season-specific concentration–exposure relationships. Therefore, imputation carried out in months where simulations were not run relied on the distributional assumptions of the season-specific SHEDS parameters. To our knowledge, previous studies have not considered how these parameters may influence population-based exposure and risk estimation in a time series design. We believe the computational advantage of our emulator approach can be applied to examine the robustness of the risk estimates through sensitivity analysis.