Efficient Bloch-Siegert B₁⁺ mapping using spiral and echo-planar readouts

Abstract

The Bloch-Siegert (B-S) B₁⁺ mapping technique is a fast, phase-based method that is highly SAR limited especially at 7T, necessitating the use of long TRs. Spiral and echo-planar readouts were incorporated in a gradient-echo based B-S sequence to reduce SAR and improve its scan efficiency. A novel, numerically optimized 4ms B-S off-resonant pulse at + 1960 Hz was used to increase sensitivity and further reduce SAR compared to the conventional 6 ms Fermi B-S pulse. Using echo-planar and spiral readouts, scan time reductions of 8-16 were achieved. By reducing the B-S pulse width by a factor of 1.5, SAR was reduced by a factor of 1.5 and overall sensitivity was increased by a factor of 1.33 due to the nearly halved resonance offset of the new B-S pulse. This was validated on phantoms and volunteers at 7T.

INTRODUCTION

B₁⁺ mapping is important in a number of MR applications like parallel transmit RF pulse design, correction of T₁ maps for accurate MR relaxometry and pharmacokinetic modeling, removing transmit sensitivity weighting in images, and in B₁ shimming. A number of techniques have been proposed for B₁⁺ mapping and they fall into two broad categories: amplitude-based and phase-based methods. A popular amplitude-based method is the Double Angle Method (DAM) [1], where two gradient or spin echo images are acquired at excitation angles of α and 2α and the ratio of the two images used to derive the B₁⁺ maps. DAM suffers from long scan times due to the long repetition times (TRs) needed to ensure complete T₁ recovery and is also inaccurate at low flip angles, restricting its usage. The saturated DAM method [2] addresses the long TR issue of conventional DAM by preceding the sequence with a saturation pulse, but still suffers from lower SNR due to incomplete T₁ recovery. In addition to poor performance at low flip angles, DAM-based methods are also subject to errors arising from differing slice/slab profiles due to different flip angles of the two DAM acquisitions and transmitter non-linearity effects. Recently, an improved double-angle-based method known as Double Angle Look Locker (DALL) [3,4] has been introduced, which uses the Look-Locker concept of measurement during driven-recovery and nonlinear fitting of the driven-recovery signal equation to estimate T1* and consequently B₁⁺ values at the two flip angles. The Actual Flipangle Imaging (AFI) method [5] overcomes most of the limitations of amplitude-based methods by using the same flip angle at two different TRs to estimate B₁⁺. However, AFI is very sensitive to the degree of RF spoiling achieved [6,7], necessitating large spoiler gradients, thereby prolonging scan times. It is also accurate only over a narrow range of B₁⁺ and in a regime where the TRs are less than T₁. The use of relatively short TRs makes adequate spoiling even harder to achieve.

Morrell et al. [8] have proposed a phase-based method that addresses some of the issues of amplitude-based methods. This method uses the phase introduced by an RF pulse 2 about the x-axis followed by an RF pulse α about the y-axis for B₁⁺ mapping. The use of on-resonant pulses makes the method sensitive to B₀ heterogeneity and chemical shift effects. The recently proposed Bloch-Siegert (B-S) B₁⁺ mapping [9] is a rapid, phase-based method, eliminating some of the common issues (saturation effects, inadequate spoiling, TR dependence) faced by magnitude-based methods discussed above, while using short TRs to keep the scan times short. The excitation RF pulse is independent of the off-resonant B-S RF pulse, adding flexibility to the choice of pulse sequence parameters. While B-S B₁⁺ mapping is relatively fast, its accuracy depends on the energy of the B-S pulse (which directly determines the amount of B-S phase shift, but also the SAR for a given TR). This makes the B-S B₁⁺ mapping method SAR intensive, and is especially noticeable at 7T.

Accelerated B₁⁺ mapping using conventional amplitude-based methods with spiral [2] or echo-planar (EPI) readouts [10,11] have been proposed. The use of efficient readout schemes can significantly reduce scan time and could be useful for multi-channel B1 mapping at 7T [12,13]. In this work, we investigated two methods to accelerate the B-S method using spiral and echo-planar imaging (EPI) readouts, especially for use at 7T where the high SAR of the B-S pulse has limited its application. We also developed a shorter, more efficient B-S pulse to further improve sensitivity and reduce SAR.

METHODS

All experiments were performed on a GE 7T scanner (GE Healthcare, Waukesha WI) using a quadrature transmit and 16-channel receive birdcage head coil (Nova Medical Inc., Wilmington, MA). A conventional 2D gradient echo (GRE) pulse sequence was modified to incorporate either spiral or echo-planar readouts in addition to the off-resonance Bloch-Siegert pulse. The slice rephasing gradient lobe was moved to the right of the B-S pulse, effectively acting as a crusher gradient for the B-S pulse. This minimized any excitation effects from the B-S pulse, which could cause ghosting artifacts and compromise the accuracy of the B₁⁺ estimation. For the spiral sequence, four interleaves with a modified variable density trajectory were used. This trajectory uses a critically sampled Archimedean spiral sampling for the central region and a variable density undersampled spiral for the outer region as described in [14]. The number of interleaves was chosen as a compromise between blurring artifacts (single interleaf) and long scan times (higher number of interleaves). For the interleaved EPI sequence, echo-train-lengths (ETL) of 4 and 8 were used, corresponding to 16 and 8 interleaves respectively.

Pulse sequence parameters were as follows- 2D GRE: 24 cm FOV, 128×64 matrix, 5 mm slice thickness, 1-3 slices, 50° nominal excitation flip angle, TR 300ms, TE 7.2/9.2ms, scan time: 20s;

Interleaved EPI: 24 cm FOV, 128×64 matrix, 1-3 slices, 5 mm thick, 50° flip, ETL 4-8 (16 or 8 interleaves), TR 300ms, TE 7.96 ms, scan time: 2.5-5s;

Spiral: 24 cm FOV, 4 interleaves, 2048 readout points, 16 ms readout length, effective in-plane spatial resolution of 5 mm, 5 mm thick, 1-3 slices, 50° flip, TR 300 ms, TE 9.3 ms, scan time: 1.25s. Spiral k-space data were reconstructed using custom offline reconstruction software, which performed density compensation, regridding and 2D FFT [14].

A doped CuSO₄ phantom and human volunteers (after informed consent) were scanned using all the sequences described above. In addition, a 4-shot spiral B-S sequence with 24 slices covering the whole brain was acquired to illustrate the capabilities of whole brain B₁⁺ mapping using our accelerated technique. The sequence parameters were as follows- Spiral: 24 cm FOV, 4 interleaves, 2048 readout points, 16 ms readout length, effective in-plane spatial resolution of 5 mm, 24 slices 5 mm thick, 50° flip, TR 1670 ms, TE 7.1 ms, scan time: 12s.

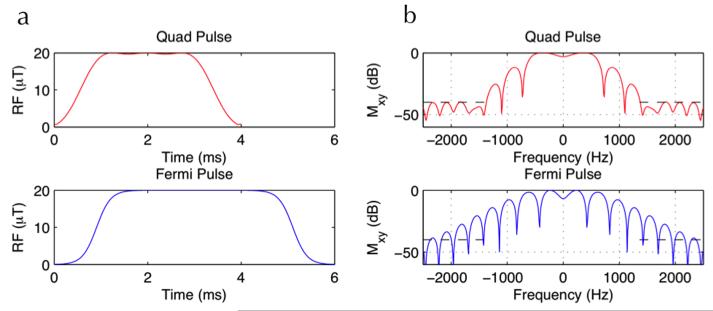
A numerically optimized 4 ms Bloch-Siegert pulse, using a fixed frequency offset of 1960 Hz, was used [11]. This real valued pulse (hereafter referred to as Quad pulse) was designed using the quadratic programming function in MATLAB (Mathworks, Natick, MA), maximizing the Bloch-Siegert phase accumulation given the constraints of maximum amplitude of the B-S pulse and maximum permissible on-resonance excitation. We compared this optimized pulse to the more conventional 6ms Fermi-shaped Bloch-Siegert pulse, originally used by Sacolick et al. [9], which used a frequency offset of 4000 Hz, with an amplitude envelope determined by a Fermi function. The 4ms Quad B-S RF pulse and the conventional 6ms Fermi B-S pulse are shown in Figure 1a and their corresponding frequency response profiles in Figure 1b. By reducing the Quad B-S pulse width by a factor of 1.5 compared to the 6ms Fermi B-S pulse, SAR was reduced by a factor of 1.5 whilst achieving increased sensitivity, the latter due to the nearly halved resonance offset of the Quad B-S RF pulse. For comparison purposes, a 2D GRE sequence with a single-echo readout was used to acquire B-S maps using the 6 ms Fermi B-S pulse [4] and the optimized 4 ms pulse. The SAR was 2.1 W/kg using the Fermi 6 ms pulse and 1.3 W/kg using the Quad 4 ms pulse. B₁⁺ maps were computed from the phase difference image between the two B-S acquisitions as described in [9] and [11] using a MATLAB script (Mathworks, Natick, MA). Five repetitions of each B₁⁺ map were performed for noise statistics. Angle-to-noise ratio (ANR) maps were created by dividing the mean B₁⁺ map by the standard deviation of the B₁⁺ map for each case.

Figure 1.

RF pulse profiles (left column) and the corresponding frequency response plots (right column) for the 4ms quad B-S pulse (top row) and the conventional 6ms Fermi B-S pulse (bottom row). Note the high degree of stop-band suppression achieved at 1960 Hz using the 4ms pulse.

Since the SAR and by extension the minimum TR of the pulse sequence is determined mostly by the B-S pulse, the fewer the B-S pulses played out, the more efficient the sequence. The use of echo-planar or spiral readouts significantly increases the proportion of k-space that can be acquired per B-S pulse, thereby increasing the SAR-efficiency of the resulting B-S B₁⁺ mapping sequence significantly. Alternatively, the decreased scan time can be traded off for SAR reduction by increasing the TR. In our experiments, we fixed the TR based on the SAR constraints imposed for the conventional GRE sequence (2.1 W/kg for the Fermi 6 ms pulse and 1.3 W/kg for the Quad 4 ms pulse) and then used spiral/EPI readouts to reduce the total scan time while maintaining the same SAR.

RESULTS

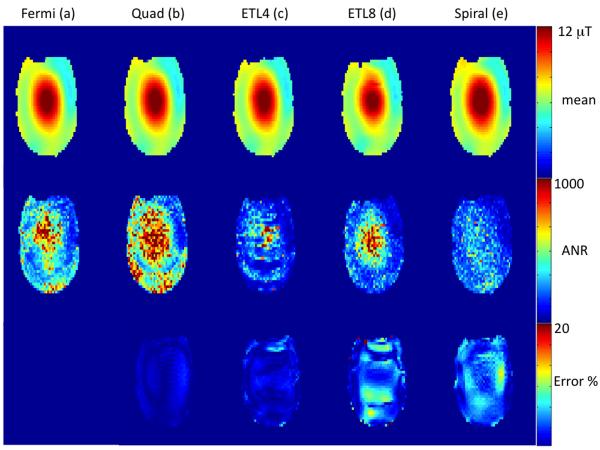
The top panel of Figure 2 shows mean B₁⁺ maps from a representative phantom slice obtained using the conventional 2D GRE B-S sequence with a 6 ms Fermi B-S pulse (a), 4 ms Quad B-S pulse (b), echo-planar imaging with ETL 4 (16 interleaves) (c) and ETL 8 (8 interleaves) (d) and spiral GRE with 4 interleaves (e). The spiral and EPI sequences were both acquired with the 4ms Quad B-S pulse and the conventional GRE acquired with both the 4 and 6 ms B-S pulses. The angle-to-noise ratio (ANR) maps for the 5 methods are shown in the middle panel of Figure 2 and the difference maps with the GRE 6 ms Fermi B-S pulse as a reference are shown in the bottom panel of Figure 2 expressed as % error. Both the EPI and spiral sequences show <10% maximum error despite their significantly reduced scan time (factors of 4, 8 and 16). The Quad 4ms pulse shows an increased ANR (factor of 1.3) as expected due to the reduced off-resonance frequency offset of the pulse. An increase of a factor of 2 due to the roughly halved resonance offset is compensated by a reduction in pulse width of a factor of 33%, resulting in a theoretical increase by a factor of 1.33. There is also minimal compromise in sensitivity using the accelerated imaging methods despite reductions in scan time by factors of 4, 8 (EPI) or 16 (spiral). The spiral B₁⁺ maps show a small reduction in ANR in the center of the phantom compared to interleaved EPI and conventional GRE sequences. Some residual ghosting is apparent in the interleaved EPI sequence especially with ETL=8 (8 interleaves).

Figure 2.

Comparison of mean B1+ maps (top panel), ANR (middle panel) and % error (bottom panel) from a head-neck phantom at 7T. The first two columns show conventional 2D gradient echo sequence using the 6 ms Fermi pulse (a) and the 4 ms quad pulse (b). The last three columns are echo-planar readouts with echo train lengths of 4 and 8 (c-d) and a spiral readout (e). The 4ms pulse was used for echo-planar and spiral readout cases.

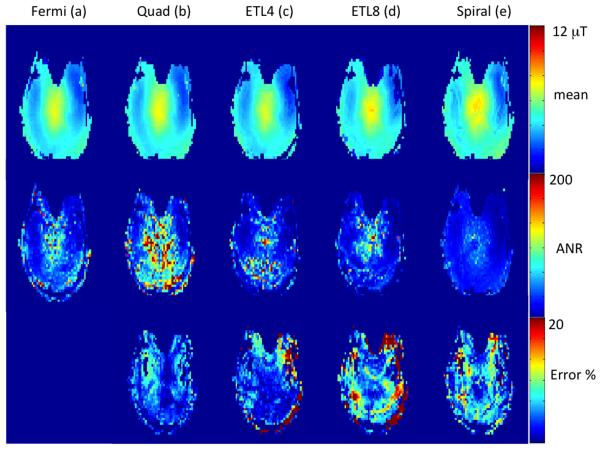
B₁⁺ mapping results from the brain of a healthy human volunteer are shown in Figure 3. B₁⁺ maps from an axial brain slice obtained using the conventional GRE B-S sequence with a 6 ms Fermi B-S pulse (a), 4 ms Quad B-S pulse (b), echo-planar imaging with ETL 4 (16 interleaves) (c) and ETL 8 (8 interleaves) (d) and spiral GRE with 4 interleaves (e). The spiral and EPI sequences were both acquired with the 4ms Quad B-S pulse. The angle-to-noise ratio (ANR) maps for the 5 methods are shown in the middle panel of Figure 3 and the difference maps with the GRE 6 ms Fermi B-S pulse as a reference are shown in the bottom panel of Figure 3 expressed as percentage error. Both the EPI and spiral sequences show <10% maximum error despite their significantly reduced scan time (factors of 4, 8 and 16). Note the increased ghosting artifacts in EPI with ETL 8 (d), presumably due to suboptimal echo-alignment in the bipolar EPI readout. They are similar to the phantom maps showing minimal reduction in sensitivity with acceleration and increased ghosting artifacts from EPI at ETL=8. The Quad 4ms pulse displays the same increase in ANR compared to the Fermi pulse as seen in the phantom experiments.

Figure 3.

Comparison of mean B1+ maps (top panel), ANR (middle panel) and % error (bottom panel) from a human brain at 7T. The first two columns show conventional 2D gradient echo sequence using the 6 ms Fermi pulse (a) and the 4 ms quad pulse (b). The last three columns are echo-planar readouts with echo train lengths of 4 and 8 (c-d) and a spiral readout (e). The 4ms pulse was used for echo-planar and spiral readout cases.

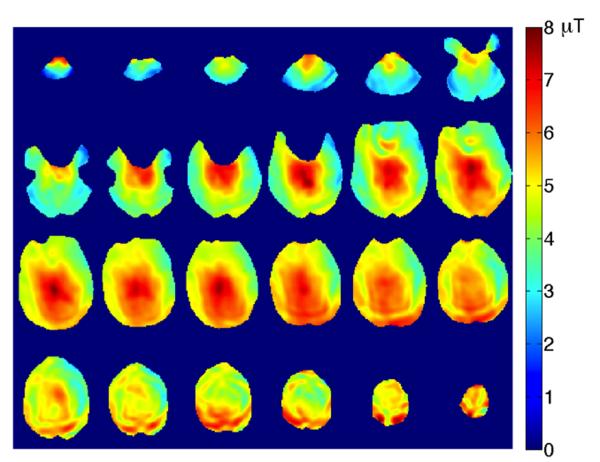
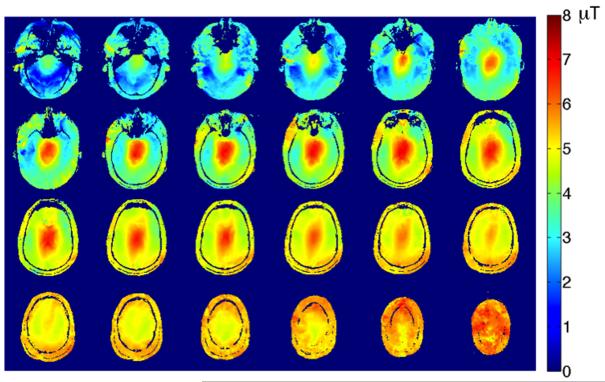
Figure 4 shows B₁⁺ maps from 24 slices covering the whole brain obtained from a healthy volunteer using the spiral B-S B₁⁺ mapping sequence. The total scan time was 12s demonstrating the scan efficiency and sensitivity of the proposed B₁⁺ mapping sequence.

Figure 4.

Whole brain coverage B1+ maps obtained using the spiral readout B-S sequence with 4 interleaves and the 4 ms B-S pulse in 12 seconds.

DISCUSSION AND CONCLUSIONS

We have demonstrated the use of echo-planar and spiral readouts to significantly reduce the scan time of the Bloch-Siegert B₁⁺ mapping method, enabling its use at higher field strengths with scan time reductions of 8-16. The scan time reduction could also be traded off with SAR to increase the sensitivity of the method, for example. We also used an optimally designed Quad RF pulse that further improved sensitivity and reduced SAR by reducing the resonance offset and pulse width.

Artifacts due to off-resonance effects, gradient imperfections etc. typically manifest as ghosting and image distortion in EPI and as blurring in spiral imaging. Because B₁⁺ mapping is an inherently low spatial resolution application, artifacts from spiral imaging might be more easily tolerated than artifacts from EPI. The spiral readouts used in B-S B₁⁺ mapping had 4 interleaves (equivalent of 4 shots) whereas EPI with ETL = 8 corresponded to 8 shots and EPI with ETL = 4 to 16 shots. We observed a significantly increased level of ghosting in EPI for ETL > 16, presumably due to suboptimal echo-alignment and, consequently, phase correction. We therefore restricted our EPI ETL to < 8. Because of the relatively low spatial resolution and lower ETLs used, we did not observe any significant image distortion in our EPI scans as can been seen in comparisons with the GRE images (Fig 2-3). The use of smaller ETLs in EPI made the spiral sequence roughly twice as efficient as EPI for the same TR and resolution. Our EPI phase correction was based on aligning the 0^th and 1^st order phase using a calibration prescan. A more sophisticated phase correction correcting for higher order terms may enable the use of higher ETLs with EPI, improving its efficiency. The ANR of the B₁+ maps using spiral was slightly lower than that of EPI presumably due to off-resonance effects.

While we have focused on brain imaging in this work where off-resonance effects from lipid resonances are minimal, these might play a more significant role in body applications like abdominal and breast imaging. Lipid off-resonance effects can further exacerbate artifacts in EPI or spiral imaging due to the lengthy readout times. In such situations, either a water-only excitation pulse or more conventional fat suppression methods may be able to mitigate the effects of lipid resonances. However, the elimination of lipid signal may limit the ability of this method to perform B₁ mapping in lipid-filled regions such as breast and abdomen. EPI sequences are more robust to off-resonance effects and suboptimal shimming than spiral sequences and might perform better in the body than spiral.

The original B-S method proposed by Sacolick et al. [9] is SAR limited at high field strengths due to the 6 ms Fermi pulse, necessitating the use of long TRs and prolonging scan times. The use of spiral/echo-planar readouts helped reduce scan times by factors of 8-16. The Quad 4ms pulse used in this paper can be used to further trade off sensitivity and SAR in a more flexible manner. Maintaining the same amplitude, SAR is reduced by a factor of 1.5 and sensitivity increased by a factor of 1.33. By keeping sensitivity or ANR fixed, SAR can be reduced by a factor of 2 or by keeping SAR fixed, sensitivity/ANR can be increased by a factor of 2. The pulse width of the B-S pulse can be further reduced down to 2 ms or even 1 ms to further decrease SAR and improve sensitivity. Preliminary theoretical analyses seem to corroborate this. The reduced B-S RF pulse widths imply shorter TEs which could be useful for increasing signal in brain areas near the sinuses, where there is severe signal loss due to T₂^* dephasing. With high performance, high fidelity gradient systems and a better phase correction technique, it should be possible to acquire single shot spiral and EPI images, which would further improve the efficiency of the B-S B₁⁺ mapping technique. Figure 5 shows B₁⁺ maps from 24 slices covering the whole brain obtained from a healthy volunteer using a single-shot spiral B-S B₁⁺ mapping sequence in 6s, highlighting the potential of single-shot B₁⁺ mapping.

Figure 5.

Whole brain coverage B1+ maps obtained using the single-shot spiral readout B-S sequence with the 4 ms B-S pulse in 6 seconds, highlighting the scan time efficiency improvement.

In conclusion, by using spiral/echo-planar readouts and optimally designed B-S RF pulses, we were able to achieve scan time reductions of 8-16 compared to the conventional GRE based B-S B₁⁺ method, significantly reducing overall scan times and increasing SAR efficiency.