Abstract
A feedback receptor regulation model was incorporated into a pharmacodynamic model to describe the stimulation of hemoglobin (Hb) production by endogenous erythropoietin (EPO). The model considers the dynamic changes that take place in the EPO receptor (EPOR) pool under phlebotomy-induced anemia. Using a 125I-rhEPO tracer the EPO clearance changes are evaluated longitudinally prior to and following phlebotomy-induced anemia to indirectly evaluate changes in the EPOR pool size, which has been shown to be linearly related to the clearance. The proposed model simultaneously captures the general behavior of temporal changes in Hb relative to EPO plasma clearance in five lambs (r=0.95), while accounting for the confounding variables of phlebotomy and changes in the blood volume in the growing animals. The results indicate that under anemia the EPOR pool size is up-regulated by a factor of nearly two over baseline and that the lowest and highest EPOR pool sizes differ by a factor of approximately four. The kinetic model developed and the data-driven mechanism proposed serves as a starting point for developing an optimal EPO dosing algorithm for the treatment of neonatal anemia.
Keywords: Erythropoietin receptor, Dosing optimization, Pharmacodynamics, Pharmacokinetics, sheep
Introduction
Erythropoietin (EPO) is a 30.4 kD glycoprotein hormone [1] , the primary function of which is to regulate erythrocyte production. It does so by binding to specific cell-surface receptor (EPOR) on erythroid progenitor cells located primarily in the bone marrow [2-3]. This results in the differentiation and proliferation of erythroid progenitors.
Although the mechanisms involved in EPO elimination and site of degradation is still not completely understood, several studies suggest that receptor-mediated elimination of EPO plays an important role in its elimination [4-6]. Our previous studies in sheep provided evidence that bone marrow plays a major role in EPO elimination and that EPOR are up-regulated as a result of phlebotomy-induced anemia [7-9].
The objective of the present study in sheep is twofold: Primarily, the study is aimed at analyzing the pharmacodynamics of EPO while considering the complex, feedback-controlled dynamic changes taking place in the EPOR pool during phlebotomy-induced anemia. These events influence hemoglobin (Hb) production and are important determinants for optimizing EPO dosing. Secondarily, the study is aimed at quantifying the relative changes in the size of the EPOR pool. This is done to assess the degree of change in the erythropoietic efficacy of EPO encountered during anemia as a result of regulatory changes in the EPO receptor pool.
Although this study does not directly measure the number of EPOR in bone marrow, changes in EPO clearance provide an indirect measure of the relative changes in the EPOR pool size [10]. In this study we report that the changes in EPOR pool size are linked to the pharmacodynamics of Hb production. To do so, a receptor-mediated disposition model for EPO was linked to the changes in the EPOR pool size.
Materials and Methods
Subjects
Surgical and experimental procedures were approved by the local institutional animal care review committee prior to the study. Five healthy 2-month-old sheep weighing 21.3±3.63 kg (mean ± SD) were studied. The animals were housed in an indoor, light- and temperature-controlled environment. Surgery was performed under pentobarbital for insertion of jugular venous catheters. Ampicillin (1 g twice a day) was administered daily for the first three postoperative days.
Study protocol
EPO clearance was determined following the intravenous administration of tracer doses of biologically active 125I-rhEPO (14×104 ± 2.5 ×104 cpm/kg) over less than 30 seconds. This is equivalent to 0.1 U/kg EPO or less than 0.01 percent of maximum endogenous EPO concentration. Ten to 15 plasma samples were drawn over the 7–8 hour period following 125I-rhEPO dosing. To minimize erythrocyte loss, plasma was removed by centrifugation and the red blood cells (RBC) reinfused. 125I-rhEPO concentrations were analyzed by an immunoprecipitation assay method as previously described [11]. To establish baseline EPO clearance, two or three 125I-rhEPO PK studies were done prior to phlebotomy. A hemoglobin level of 3-4 g/dL established by removing ~60% of the sheep's RBCs. This was accomplished by an isovolemic exchange phlebotomy where an equal volume of saline was transfused for each volume of blood removed. Each animal underwent two separate phlebotomies 4–6 weeks apart. To determine the pattern of change in EPO clearance following phlebotomy, 7–14 125I-rhEPO PK studies were performed following each phlebotomy. Endogenous EPO concentration was measured in triplicate using a double antibody radioimmunoassay (RIA) procedure as previously described [12]. Linear assay values for EPO concentrations were obtained between 10 and 450mU/ml in the sheep RIA.
125I-rhEPO disposition model
A mathematical model was used to describe changes in plasma 125I-rhEPO level. The model applied is based on a tracer interaction method ,TIM, [13] combined with disposition decomposition analysis, [14] (Eq.1). Ca(t) is the concentration of the of 125I-rhEPO tracer in the blood plasma being sampled, and Cb(t) is the concentration of endogenous native EPO
| (1) |
K is the first order constant of the linear elimination pathway, Vm and Km are the Michaelis-Menten parameters of the nonlinear elimination pathway, and G and γ are distribution function parameters, while * denotes convolution.
Since Ca≪ Cb due to the use of tracer doses, Eq.1 can be simplified into:
| (2) |
Thus, the model proposes that the rate of irreversible elimination of EPO from the sampling compartment occurs via two parallel routes, namely a nonlinear elimination route demonstrating Michaelis-Menten kinetic behavior (represented by parameters Vm and Km), and a linear elimination route demonstrating first order elimination kinetic behavior (rate parameter K). This elimination kinetics model is consistent with our previous finding [13, 15] that EPO is eliminated nonlinearly via a receptor mediated erythropoietic mechanism by the bone marrow and linearly via a non-erythropoietic mechanism.
The EPO plasma concentration profile from a single intravenous 125I-rhEPO tracer bolus dose was well described by a biexponential disposition function. The 125I-rhEPO clearance (Cl(t)) was calculated using Eq.3.
| (3) |
where D is the 125I-rhEPO dose and the AUC is the area under the curve for the concentration of 125I-rhEPO time calculated from the biexponential disposition function.
Despite the fact that the clearance function, Cl(t), presented throughout this work is determined from the biexponential disposition function, a mechanistic interpretation of the Cl(t) value can still be made based on the model presented in Eq.2. Assuming that the concentration of unlabeled EPO (Cb(t)) was constant over the relatively short duration of the 125I-rhEPO PK study (7-8 hrs), it follows from Eq.2 that the clearance of EPO at the time of 125I-rhEPO PK study can be represented parametrically as shown in Eq.4.
| (4) |
The Cl(t) represents the summation of elimination via two routes namely, non-receptor mediated ,ClNR and receptor mediated ,ClR clearances as shown in Eq. 5-7. EPO's volume of distribution is denoted by VEPO. The time in Eqs. 1 and 2 is relative to the administration of 125I-rhEPO in the tracer PK study, while the time for the remaining equations is measured relative to the beginning of the study.
| (5) |
| (6) |
| (7) |
Since previous studies demonstrated that phlebotomy did not have a significant effect on non-receptor mediated clearance [16], ClNR that was assumed to be constant (scaled to the bodyweight) during all PK studies. Receptor mediated clearance on the other hand was assumed to change over study period as a result of changes in number of EPO receptors reflected in the changing value of Vm(t). Based on an assumed proportional relationship between the EPOR pool size and Vm(t), the relative value of EPOR can be described as shown in Eq.8.
| (8) |
ClNR was fixed to 6.58 mL/kg/hr as previously determined [16]. Likewise, the value of Km was fixed to 523 mU/mL based on our previous analysis [13].
Pharmacodynamic Hb mass balance model
Hb production is stimulated by EPO through a stimulation function fstim(t):
| (9) |
where kstim is the Hb production stimulation rate constant at the start of the study, Wt(t) is the body weight, Emax is the maximum Hb production rate scaled to the bodyweight, EC50is the EPO concentration that results in Hb production rate that is 50% of the scaled Emax.
To account for body weight change, Hb production was assumed to be proportional to the body weight to the power ¾ [17]. Hb production before the beginning of the study (t<0) was assumed to be constant scaled to body weight to the ¾ power. Hb production rate after the beginning of the study (t>0) was related to plasma EPO concentrations by a Michaelis-Menten Emax model [18]. To account for change in number of EPO receptors, Hb production rate was scaled to the relative change in number of receptors by multiplying with the ratio as shown in Eq. 9
The Hb production model assumed that RBCs have a time invariant lifespan (τRBC) with no variability (i.e. point distribution) [19-21]. Change in amount of Hb produced endogenously is given by:
| (10) |
with initial conditions:
where a is the time between erythroid progenitor cells stimulation by EPO and the appearance of newly produced RBCs in the circulation, and b is the time between erythroid progenitor cells stimulation by EPO and the removal of the resulting RBCs from circulation by senescence. The RBCs lifespan (τRBC) is the difference b – a.
In the above model, RBCs were assumed to be removed only by aging when they reach the lifespan. Phlebotomy on the other hand, represents a removal of cells of all ages up to τRBC[22]. The time interval over which the phlebotomy affects Hb mass balance depends on the lifespan of RBCs. Assuming “m” phlebotomies that occurred over a time period equal to the lifespan of RBCs, the fraction of Hb that remains in circulation after the ith phlebotomy, denoted FP(i), that occurred at time tP(i) is given by Eq.11. Thus, FP(i) is the fraction of Hb remaining immediately after the ith phlebotomy relative to the amount present immediately before the ith phlebotomy. The phlebotomy correction term at time “PC(t)” is the multiplication of fractions remaining for all phlebotomies that occurred between t – τRBC and t.
| (11) |
where AP(tp(i)) is the amount phlebotomized at tp(i)
| (12) |
where tp(1)≥ t − τRBC and tp(m)<t
| (13) |
with initial conditions:
The estimated amounts of Hb in the circulation were converted into observed concentrations by dividing by the total blood volume . In order to account for blood volume expansion as a result of growth, total blood volume was adjusted according to the body weight:
| (14) |
Sheep body weight
Sheep body weight during the study was estimated using a 4th order polynomial. To estimate the body weight before the beginning of the study and after birth (−60 < t ≤ 0 days), which is needed to calculate fstim(t), the growth rate (denoted by kgrowth) over the first two months of life (t<60 days) was estimated separately from five lambs. In these lambs, body weight values were collected over the first 50-60 days of life. The average value of kgrowth estimated in these lambs was used to estimate body weight for the current sheep subjects before the beginning of the study and after birth (−60 < t ≤ 0 days). To account for pre-birth body weight which is needed to calculate fstim(t) for t<-60 days, an exponential function that describes the dynamics of in utero growth was used [23]. The explicit equation for body weight is displayed in Eq.15.
| (15) |
where α0,α1,α2,α3, and α4 are 4th order polynomial parameters and G_AGE is the gestational age of the term lamb which was fixed to be 150 days [24-25].
Data analysis
All modeling was conducted using WINFUNFIT, a Windows (Microsoft) version evolved from the general nonlinear regression program FUNFIT [26], using ordinary least squares fit to each individual subject's Hb concentration-time profile. The amount of Hb removed and administered by each phlebotomy, at the time of removal was accounted for by WINFUNFIT using a generalized events processing module. The events processing module integrates the differential equation exactly up to the time of the event and adding or removing the appropriate amount and then continuing integrating the differential equation with new initial conditions set at the appropriate event times. The EPO plasma concentrations were nonparametrically represented using a linear spline function.
To summarize the uncertainty in the individual subject parameter estimates, the relative standard error (RSE%) of the estimate was calculated for each parameter as:
| (16) |
where SE and P are the standard error of the parameter and the estimate of the parameter, respectively.
Results
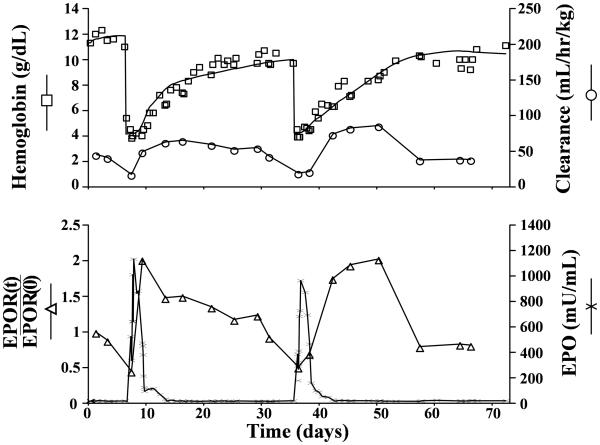
The Hb mass balance model fit along with plasma EPO concentration for a representative sheep are shown in Figure 1. The model accurately captures the general behavior of the Hb concentration data (r =0.95±0.035). The pharmacodynamic model parameters are summarized in Table 1.
Figure 1.
Representative individual subject fits of model equations to observed plasma hemoglobin (□), total clearance (○), erythropoietin (χ), and EPOR fraction (△). Hb values were obtained from the Hb mass balance fit (Eq.9-14). EPO values were obtained experimentally using RIA. Total clearance and EPOR fraction are obtained from 125I-rhEPO disposition model (Eq.1-8).
Table 1.
A summary of parameter estimates from the hemoglobin mass balance model
| Sheep No. |
α (day) |
τRBC (day) |
Emax (g/day.kg0.75) |
EC50 (mU/mL) |
kstim (g/day.kg0.75) |
rb | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | RSE%a | Value | RSE%a | Value | RSE%a | Value | RSE%a | Value | RSE%a | ||
| 1 | 0.95 | 16.5 | 104 | 5.9 | 1.37 | 2.23 | 97.8 | 3.12 | 0.41 | 1.65 | 0.89 |
| 2 | 2.26 | 13.3 | 84.5 | 9.31 | 1.61 | 7.39 | 70.4 | 14.1 | 0.63 | 2.32 | 0.97 |
| 3 | 3.55 | 8.84 | 68.8 | 1.56 | 1.36 | 0.99 | 57.1 | 1.91 | 0.33 | 1.67 | 0.97 |
| 4 | 1.71 | 17.9 | 124 | 11.6 | 1.28 | 7.32 | 24.6 | 19.8 | 0.49 | 1.87 | 0.97 |
| 5 | 2.22 | 13.3 | 82.7 | 2.71 | 1.05 | 1.88 | 52.4 | 3.51 | 0.56 | 1.21 | 0.94 |
|
| |||||||||||
| Mean | 2.14 | 14.0 | 92.7 | 6.21 | 1.34 | 3.96 | 60.5 | 8.48 | 0.48 | 1.74 | 0.95 |
| CV (%) | 44.4 | 25.1 | 23.1 | 68.6 | 15.1 | 79.0 | 44.2 | 94.3 | 24.5 | 44.4 | 3.73 |
RSE%, relative standard error
r, correlation coefficient.
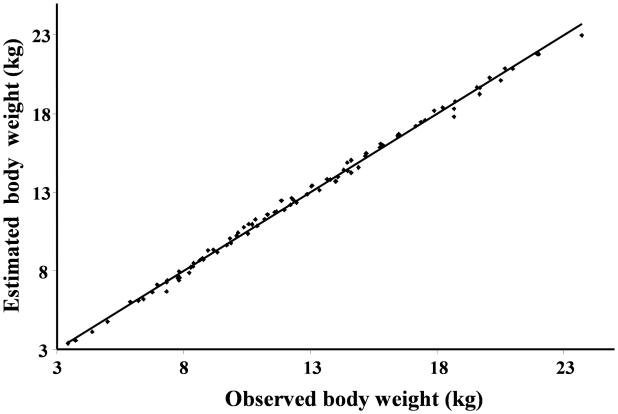
The average value of kgrowth that describes growth over the first two months of life (t<60 days) was estimated to be 0.285±0.027 kg/day. As displayed in Figure 2, the body weight function described accurately the body weight data over the first two months of life (average R2=0.996, range 0.989-0.998). The body weight data presented in Figure 2 represent data over the first two months of life for lambs from different study protocol. This data was included in the analysis to describe the growth over the first two months of life. This information was used to describe Hb production before the beginning of the study (Eq.9 and Eq.15).
Figure 2.
Bodyweight values over the first two months of life estimated using linear function (wt=α0+kgrowth·t) vs. actual bodyweight values for all lambs.
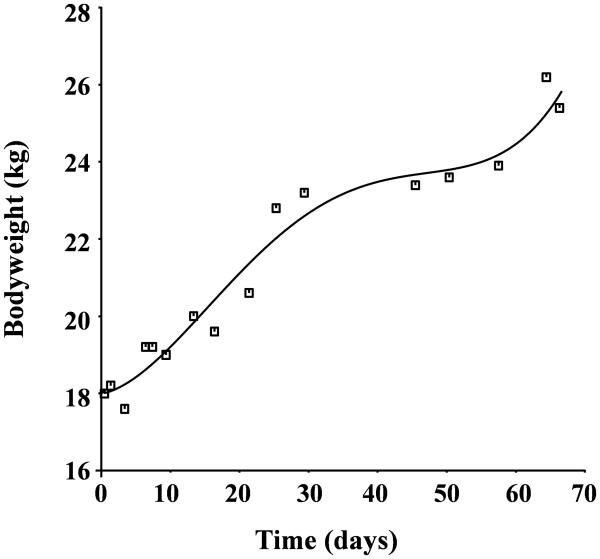
Individual sheep's Hb concentration-time profiles contained on average 76 Hb values (range 71 to 83), 92 plasma EPO concentrations (range 82 to 107) and 23 bodyweight data time points (range 19 to 32). The body weight measurements are well represented by a 4th order polynomial (Figure 3). At the beginning of the study, the baseline Hb was 10.4±2.05 g/dL, the EPO concentration average was 22.7±11.8 mU/ml, the clearance average value was 48.2±10.9 ml/kg/hr, and the average weight was 21.3±3.63 kg. At the end of the study, the Hb average was 9.8±1.55 g/dl, EPO concentration was 18.4±4.72 mU/ml, the clearance average value was 39.2±6.03 ml/kg/hr, and body weight was 32.2±4.58 kg. Paired t-test results indicate that there is no significant difference in the value of Hb, EPO concentration, and clearance between the values reported at the beginning of the study and at the end of the study (p>0.05). The body weight of the sheep was significantly higher at the end of the study compared to the beginning of the study (p<0.05). Thus, there is a need to account to animal growth in the model.
Figure 3.
Bodyweight over the study period. The curve fitted to the lamb bodyweight is a 4th order polynomial
The newly produced Hb appears in the circulation 2.14±0.95 days after stimulation by erythropoietin. The lifespan of RBCs (τRBC = b − a, Eq.12) was estimated to be 92.7±21.3 days and the bodyweight scaled Hb production constant, kstim, was determined to be 0.48±0.12 g/day.kg¾. The Michaelis-Menten Emax model parameters were successfully evaluated for all sheep. The predicted maximum achievable Hb production rate, Emax, was found to be 1.34±0.20 g/day.kg¾, and EC50 was found to be 60.5±26.7 mU/mL.
Discussion
This study provides a quantitative estimation of the rate of Hb synthesis in sheep and considers its functional and mechanistic relationship to the EPO plasma concentration, while also accounting for other important confounding variables, including change in number of EPOR, phlebotomy, and growth. Because of its importance for EPO efficacy and dosing, special attention is focused on the regulatory kinetic mechanism of the EPOR pool size. In contrast to other previous models that describe erythropoiesis [22, 27] the current model explicitly accounts for changes in the number of EPOR as a result of up-regulation while simultaneously accounting for continuous growth and the expression of blood volume and the volume of distribution expansion as a function of the increase in body weight.
Previously, we proposed a model that describes the change in the density of EPOR in the form of change in EPO clearance values [8]. We also demonstrated that clearance is linearly related to the density of EPOR m-RNA in the bone marrow [10]. In this manuscript we utilized information obtained from previous work about EPOR and clearance changes to describe erythropoiesis under stress conditions. Although other models implicitly accounted for EPOR changes in the form of negative feedback inhibition of progenitor cells production, they did not have any measure of the actual change in EPOR density [28].
EPO clearance as a measure of EPOR pool size
The clearance parameters obtained by the analysis provides an indirect quantification of the EPOR populations under the well supported assumption that EPO's elimination is largely via EPORs. The recent study by Nalbant et al. (2010) has shown that the change in EPOR pool size can be estimated as a linear function of the EPO clearance [10]. From this finding it follows that the quantity of EPOR is proportional to VM (Eq. 8). The pattern of change in EPOR shown in Figure 1 was consistently observed for all five study animals after both phlebotomies. The decrease in EPOR that coincides with the increase in the EPO concentration can be explained by a temporary consumption with regulatory feedback correction and the findings from molecular biology investigations that some EPOR are not recycled after interaction with EPO [29-30]. Since Vm(t) is proportional to the quantity of EPOR the subsequent increase in ClR(t) and Vm(t) indicates an up-regulation of EPOR.
Several studies have demonstrated EPOR up-regulation as a result of exposure to high EPO levels and/or under hypoxic conditions. It was reported that the incubation of murine cell lines with EPO for 6 days increases the number of EPOR per cell without changing EPOR binding affinity [31]. Bernaudin et al. also reported EPOR up-regulation in rat brain endothelial cell line and cortical astrocyte cell cultures as a result of hypoxic conditions [32]
RBC Pharmacodynamic Parameters
The estimated mean value for the lag time,α , between erythroid progenitor cells stimulation by EPO and the appearance of newly produced RBCs in the circulation was 2.14 days. This is a higher estimate than the previously reported value in sheep of 0.797 days [33]. This may be explained by the facts that the previous analysis included a peripheral effect site compartment, while the current analysis does not. Also, the lag time was calculated under steady-state conditions while recognizing that the lag time increases under stress conditions, but we did not correct for that [33-34]. The average of individual RBC lifespans (τRBC= b − a) was found to be 92.7 days compared to the reported value of 120 days in adult sheep [35].
EPOR regulatory changes, EPO efficacy and EPO dosing strategy for treatment of anemia
It is evident from examining the relative change in the size of the EPOR pool , EPOR(t)/ EPOR(0) (Fig. 1) that an up-regulation due to anemia by a factor close to 2 is possible relative to the basal EPOR level and that the lowest and highest EPOR pool sizes can differ by a factor close to 4 (=2/0.5). Since according to mass balance principles the rate of progenitor activation is expected to be proportional to the quantity of EPOR, these changes in the EPOR pool size will significantly influence the efficacy of EPO. Such changes need to be considered when formulating an EPO dosing optimization algorithm. Due to the great similarity of the erythropoietic physiology between mammalian species it is anticipated that a similar EPOR regulatory mechanism model exists in humans. Thus, the kinetic model and mechanism proposed in this pre-clinical study may serve as a starting point for the development of an optimal EPO dosing algorithm to that of neonatal anemia. Because of the mathematical complexity of the present regulatory model, a complete dosing optimization will require extensive computational analysis. However, the simple core principles of the model provide several simple guiding principles: Accordingly, an optimal dosing strategy should in general maximize the interaction between EPO and EPOR. Specifically, EPO should be administered when the number of EPOR are close to maximally up-regulated. Similarly, in recognizing a temporary loss of EPOR following an initial dosing, the subsequent dosing should, to achieve the highest efficacy, be postpones until the EPOR again have increased by the regulatory feed-back control. Several studies have demonstrated that subcutaneous administration of EPO is more efficacious than intravenous dosing [36-38], which according to our model can be explained by the fact that the duration of high plasma EPO concentration is longer in subcutaneous than intravenous administration, thus allowing the exogenous EPO to still be present after the EPORs are up-regulated.
Conclusion
The present study and previous findings in the literature demonstrates that under conditions of severe tissue hypoxemia hematopoietic EPOR are up-regulated as a part of a feedback regulation. The EPOR pool size, in turn, determines the magnitude of response to EPO in stimulating erythrocyte production. Frequent estimation of EPO clearance as a measure of EPOR pool size and the use of mass balance principles allowed for the mathematical determination of the in vivo erythropoiesis rate and its relationship to endogenous plasma EPO concentrations under sever hypoxemic conditions. The mechanistically oriented EPO's PK/PD model we propose could be used as a valuable tool for a better elucidation of EPO's complex erythropoietic effect and for designing an optimal dosing for EPO to maximize its erythropoietic effect.
Acknowledgements
This study was supported by National Institutes of Health Grant No. P01 NIH HL46925, NIH R21 GM57367, and by Children's Miracle Network Telethon of Iowa. The recombinant human EPO used in the EPO RIA was a gift from Dr. H. Kinoshita of Chugai Pharmaceutical Company, Ltd. (Tokyo, Japan). The rabbit EPO antiserum used in the EPO RIA was a gift from Gisela K. Clemens, Ph.D. We thank Robert L. Schmidt for collection and organization of the data.
Grant sponsor: National Institutes of Health Grant No. P01 NIH HL46925, NIH R21 GM57367 and by Children's Miracle Network Telethon of Iowa. The recombinant human erythropoietin used in the study was a gift from Dr. H. Kinoshita of Chugai Pharmaceutical Company, Ltd. (Tokyo, Japan).
References
- 1.Davis JM, et al. Characterization of recombinant human erythropoietin produced in Chinese hamster ovary cells. Biochemistry. 1987;26(9):2633–8. doi: 10.1021/bi00383a034. [DOI] [PubMed] [Google Scholar]
- 2.Sawada K, et al. Purification of human blood burst-forming units-erythroid and demonstration of the evolution of erythropoietin receptors. J Cell Physiol. 1990;142(2):219–30. doi: 10.1002/jcp.1041420202. [DOI] [PubMed] [Google Scholar]
- 3.Sawyer ST, Krantz SB, Goldwasser E. Binding and receptor-mediated endocytosis of erythropoietin in Friend virus-infected erythroid cells. J Biol Chem. 1987;262(12):5554–62. [PubMed] [Google Scholar]
- 4.Krzyzanski W, Wyska E. Pharmacokinetics and pharmacodynamics of erythropoietin receptor in healthy volunteers. Naunyn Schmiedebergs Arch Pharmacol. 2008;377(4-6):637–45. doi: 10.1007/s00210-007-0225-z. [DOI] [PubMed] [Google Scholar]
- 5.Mufson RA, Gesner TG. Binding and internalization of recombinant human erythropoietin in murine erythroid precursor cells. Blood. 1987;69(5):1485–90. [PubMed] [Google Scholar]
- 6.Freise KJ, et al. Increased erythropoietin elimination in fetal sheep following chronic phlebotomy. Pharm Res. 2007;24(9):1653–9. doi: 10.1007/s11095-007-9295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Widness JA, et al. Change in erythropoietin pharmacokinetics following hematopoietic transplantation. Clin Pharmacol Ther. 2007;81(6):873–9. doi: 10.1038/sj.clpt.6100165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chapel SH, et al. Receptor-based model accounts for phlebotomy-induced changes in erythropoietin pharmacokinetics. Exp Hematol. 2001;29(4):425–31. doi: 10.1016/s0301-472x(01)00614-2. [DOI] [PubMed] [Google Scholar]
- 9.Chapel S, et al. Changes in erythropoietin pharmacokinetics following busulfan-induced bone marrow ablation in sheep: evidence for bone marrow as a major erythropoietin elimination pathway. J Pharmacol Exp Ther. 2001;298(2):820–4. [PubMed] [Google Scholar]
- 10.Nalbant D, et al. Evidence of receptor-mediated elimination of erythropoietin by analysis of Epo receptor mRNA expression in bone marrow and erythropoietin clearance during anemia. J Pharmacol Exp Ther. 2010 doi: 10.1124/jpet.109.163568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Widness JA, et al. A sensitive and specific erythropoietin immunoprecipitation assay: application to pharmacokinetic studies. J Lab Clin Med. 1992;119(3):285–94. [PubMed] [Google Scholar]
- 12.Widness JA, et al. Temporal response of immunoreactive erythropoietin to acute hypoxemia in fetal sheep. Pediatr Res. 1986;20(1):15–9. doi: 10.1203/00006450-198601000-00004. [DOI] [PubMed] [Google Scholar]
- 13.Veng-Pedersen P, et al. A differential pharmacokinetic analysis of the erythropoietin receptor population in newborn and adult sheep. J Pharmacol Exp Ther. 2003;306(2):532–7. doi: 10.1124/jpet.103.052431. [DOI] [PubMed] [Google Scholar]
- 14.Veng-Pedersen P, et al. Kinetic evaluation of nonlinear drug elimination by a disposition decomposition analysis. Application to the analysis of the nonlinear elimination kinetics of erythropoietin in adult humans. J Pharm Sci. 1995;84(6):760–7. doi: 10.1002/jps.2600840619. [DOI] [PubMed] [Google Scholar]
- 15.Al-Huniti NH, et al. Pharmacokinetic/pharmacodynamic analysis of paradoxal regulation of erythropoietin production in acute anemia. J Pharmacol Exp Ther. 2004;310(1):202–8. doi: 10.1124/jpet.104.066027. [DOI] [PubMed] [Google Scholar]
- 16.Veng-Pedersen P, et al. Pharmacokinetic tracer kinetics analysis of changes in erythropoietin receptor population in phlebotomy-induced anemia and bone marrow ablation. Biopharm Drug Dispos. 2004;25(4):149–56. doi: 10.1002/bdd.395. [DOI] [PubMed] [Google Scholar]
- 17.Holford N. Dosing in children. Clin Pharmacol Ther. 2010;87(3):367–70. doi: 10.1038/clpt.2009.262. [DOI] [PubMed] [Google Scholar]
- 18.Al-Huniti NH, et al. Pharmacodynamic analysis of changes in reticulocyte subtype distribution in phlebotomy-induced stress erythropoiesis. J Pharmacokinet Pharmacodyn. 2005;32(3-4):359–76. doi: 10.1007/s10928-005-0009-3. [DOI] [PubMed] [Google Scholar]
- 19.Landaw SA. Factors that accelerate or retard red blood cell senescence. Blood Cells. 1988;14(1):47–67. [PubMed] [Google Scholar]
- 20.Freise KJ, et al. Modeling time variant distributions of cellular lifespans: increases in circulating reticulocyte lifespans following double phlebotomies in sheep. J Pharmacokinet Pharmacodyn. 2008 doi: 10.1007/s10928-008-9089-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Krzyzanski W, Woo S, Jusko WJ. Pharmacodynamic models for agents that alter production of natural cells with various distributions of lifespans. J Pharmacokinet Pharmacodyn. 2006;33(2):125–66. doi: 10.1007/s10928-006-9007-3. [DOI] [PubMed] [Google Scholar]
- 22.Freise KJ, Widness JA, Veng-Pedersen P. Erythropoietic response to endogenous erythropoietin in premature very low birth weight infants. J Pharmacol Exp Ther. 2010;332(1):229–37. doi: 10.1124/jpet.109.159905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Koong LJ, Garrett WN, Rattray PV. A description of the dynamics of fetal growth in sheep. J Anim Sci. 1975;41(4):1065–8. doi: 10.2527/jas1975.4141065x. [DOI] [PubMed] [Google Scholar]
- 24.Kisker CT, Robillard JE, Clarke WR. Development of blood coagulation--a fetal lamb model. Pediatr Res. 1981;15(7):1045–50. doi: 10.1203/00006450-198107000-00014. [DOI] [PubMed] [Google Scholar]
- 25.Jobe A, et al. Lung protein leaks in ventilated lambs: effects of gestational age. J Appl Physiol. 1985;58(4):1246–51. doi: 10.1152/jappl.1985.58.4.1246. [DOI] [PubMed] [Google Scholar]
- 26.Veng-Pedersen P. Curve fitting and modelling in pharmacokinetics and some practical experiences with NONLIN and a new program FUNFIT. Journal of Pharmacokinetics & Biopharmaceutics. 1977;5(5):513–531. doi: 10.1007/BF01061732. [DOI] [PubMed] [Google Scholar]
- 27.Neelakantan S, et al. Erythropoietin pharmacokinetic/pharmacodynamic analysis suggests higher doses in treating neonatal anemia. Pediatr Int. 2009;51(1):25–32. doi: 10.1111/j.1442-200X.2008.02648.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Woo S, et al. Population pharmacokinetics and pharmacodynamics of peptidic erythropoiesis receptor agonist (ERA) in healthy volunteers. J Clin Pharmacol. 2008;48(1):43–52. doi: 10.1177/0091270007309702. [DOI] [PubMed] [Google Scholar]
- 29.Gross AW, Lodish HF. Cellular trafficking and degradation of erythropoietin and novel erythropoiesis stimulating protein (NESP) J Biol Chem. 2006;281(4):2024–32. doi: 10.1074/jbc.M510493200. [DOI] [PubMed] [Google Scholar]
- 30.Becker V, et al. Covering a broad dynamic range: information processing at the erythropoietin receptor. Science. 2010;328(5984):1404–8. doi: 10.1126/science.1184913. [DOI] [PubMed] [Google Scholar]
- 31.Broudy VC, et al. Dynamics of erythropoietin receptor expression on erythropoietin-responsive murine cell lines. Blood. 1990;75(8):1622–6. [PubMed] [Google Scholar]
- 32.Bernaudin M, et al. A potential role for erythropoietin in focal permanent cerebral ischemia in mice. J Cereb Blood Flow Metab. 1999;19(6):643–51. doi: 10.1097/00004647-199906000-00007. [DOI] [PubMed] [Google Scholar]
- 33.Freise KJ, et al. Pharmacodynamic analysis of time-variant cellular disposition: reticulocyte disposition changes in phlebotomized sheep. J Pharmacokinet Pharmacodyn. 2007;34(4):519–47. doi: 10.1007/s10928-007-9056-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Brugnara C. Use of reticulocyte cellular indices in the diagnosis and treatment of hematological disorders. Int J Clin Lab Res. 1998;28(1):1–11. doi: 10.1007/s005990050011. [DOI] [PubMed] [Google Scholar]
- 35.Tucker E. Red cell life span in young and adult sheep. Res Vet Sci. 1963;4:11–23. [Google Scholar]
- 36.Kaufman JS, et al. Subcutaneous compared with intravenous epoetin in patients receiving hemodialysis. Department of Veterans Affairs Cooperative Study Group on Erythropoietin in Hemodialysis Patients. N Engl J Med. 1998;339(9):578–83. doi: 10.1056/NEJM199808273390902. [DOI] [PubMed] [Google Scholar]
- 37.Ashai NI, Paganini EP, Wilson JM. Intravenous versus subcutaneous dosing of epoetin: a review of the literature. Am J Kidney Dis. 1993;22(2 Suppl 1):23–31. doi: 10.1016/0272-6386(93)70178-2. [DOI] [PubMed] [Google Scholar]
- 38.Brown MS, et al. Single-dose pharmacokinetics of recombinant human erythropoietin in preterm infants after intravenous and subcutaneous administration. J Pediatr. 1993;122(4):655–7. doi: 10.1016/s0022-3476(05)83559-0. [DOI] [PubMed] [Google Scholar]