Pharmacodynamic analysis of stress erythropoiesis: change in erythropoietin receptor pool size following double phlebotomies in sheep

Abstract

A feedback receptor regulation model was incorporated into a pharmacodynamic model to describe the stimulation of hemoglobin (Hb) production by endogenous erythropoietin (EPO). The model considers the dynamic changes that take place in the EPO receptor (EPOR) pool under phlebotomy-induced anemia. Using a ¹²⁵I-rhEPO tracer the EPO clearance changes are evaluated longitudinally prior to and following phlebotomy-induced anemia to indirectly evaluate changes in the EPOR pool size, which has been shown to be linearly related to the clearance. The proposed model simultaneously captures the general behavior of temporal changes in Hb relative to EPO plasma clearance in five lambs (r=0.95), while accounting for the confounding variables of phlebotomy and changes in the blood volume in the growing animals. The results indicate that under anemia the EPOR pool size is up-regulated by a factor of nearly two over baseline and that the lowest and highest EPOR pool sizes differ by a factor of approximately four. The kinetic model developed and the data-driven mechanism proposed serves as a starting point for developing an optimal EPO dosing algorithm for the treatment of neonatal anemia.

Introduction

Erythropoietin (EPO) is a 30.4 kD glycoprotein hormone [1] , the primary function of which is to regulate erythrocyte production. It does so by binding to specific cell-surface receptor (EPOR) on erythroid progenitor cells located primarily in the bone marrow [2-3]. This results in the differentiation and proliferation of erythroid progenitors.

Although the mechanisms involved in EPO elimination and site of degradation is still not completely understood, several studies suggest that receptor-mediated elimination of EPO plays an important role in its elimination [4-6]. Our previous studies in sheep provided evidence that bone marrow plays a major role in EPO elimination and that EPOR are up-regulated as a result of phlebotomy-induced anemia [7-9].

The objective of the present study in sheep is twofold: Primarily, the study is aimed at analyzing the pharmacodynamics of EPO while considering the complex, feedback-controlled dynamic changes taking place in the EPOR pool during phlebotomy-induced anemia. These events influence hemoglobin (Hb) production and are important determinants for optimizing EPO dosing. Secondarily, the study is aimed at quantifying the relative changes in the size of the EPOR pool. This is done to assess the degree of change in the erythropoietic efficacy of EPO encountered during anemia as a result of regulatory changes in the EPO receptor pool.

Although this study does not directly measure the number of EPOR in bone marrow, changes in EPO clearance provide an indirect measure of the relative changes in the EPOR pool size [10]. In this study we report that the changes in EPOR pool size are linked to the pharmacodynamics of Hb production. To do so, a receptor-mediated disposition model for EPO was linked to the changes in the EPOR pool size.

Materials and Methods

Subjects

Surgical and experimental procedures were approved by the local institutional animal care review committee prior to the study. Five healthy 2-month-old sheep weighing 21.3±3.63 kg (mean ± SD) were studied. The animals were housed in an indoor, light- and temperature-controlled environment. Surgery was performed under pentobarbital for insertion of jugular venous catheters. Ampicillin (1 g twice a day) was administered daily for the first three postoperative days.

Study protocol

EPO clearance was determined following the intravenous administration of tracer doses of biologically active ¹²⁵I-rhEPO (14×10⁴ ± 2.5 ×10⁴ cpm/kg) over less than 30 seconds. This is equivalent to 0.1 U/kg EPO or less than 0.01 percent of maximum endogenous EPO concentration. Ten to 15 plasma samples were drawn over the 7–8 hour period following ¹²⁵I-rhEPO dosing. To minimize erythrocyte loss, plasma was removed by centrifugation and the red blood cells (RBC) reinfused. ¹²⁵I-rhEPO concentrations were analyzed by an immunoprecipitation assay method as previously described [11]. To establish baseline EPO clearance, two or three ¹²⁵I-rhEPO PK studies were done prior to phlebotomy. A hemoglobin level of 3-4 g/dL established by removing ~60% of the sheep's RBCs. This was accomplished by an isovolemic exchange phlebotomy where an equal volume of saline was transfused for each volume of blood removed. Each animal underwent two separate phlebotomies 4–6 weeks apart. To determine the pattern of change in EPO clearance following phlebotomy, 7–14 ¹²⁵I-rhEPO PK studies were performed following each phlebotomy. Endogenous EPO concentration was measured in triplicate using a double antibody radioimmunoassay (RIA) procedure as previously described [12]. Linear assay values for EPO concentrations were obtained between 10 and 450mU/ml in the sheep RIA.

¹²⁵I-rhEPO disposition model

A mathematical model was used to describe changes in plasma ¹²⁵I-rhEPO level. The model applied is based on a tracer interaction method ,TIM, [13] combined with disposition decomposition analysis, [14] (Eq.1). C_a(t) is the concentration of the of ¹²⁵I-rhEPO tracer in the blood plasma being sampled, and C_b(t) is the concentration of endogenous native EPO

$$\frac{{\mathit{dC}}_a\left(t\right)}{\mathit{dt}}=-(K+\frac{V_m\left(t\right)}{K_m+C_b\left(t\right)+C_a\left(t\right)}+\frac{G}{\gamma })\cdot C_a\left(t\right)+G\cdot e^{-\gamma \cdot t}\ast C_a\left(t\right)$$ (1)

K is the first order constant of the linear elimination pathway, V_m and K_m are the Michaelis-Menten parameters of the nonlinear elimination pathway, and G and γ are distribution function parameters, while * denotes convolution.

Since C_a≪ C_b due to the use of tracer doses, Eq.1 can be simplified into:

$$\frac{{\mathit{dC}}_a\left(t\right)}{\mathit{dt}}=-(K+\frac{V_m\left(t\right)}{K_m+C_b\left(t\right)}+\frac{G}{\gamma })\cdot C_a\left(t\right)+G\cdot e^{-\gamma \cdot t}\ast C_a\left(t\right)$$ (2)

Thus, the model proposes that the rate of irreversible elimination of EPO from the sampling compartment occurs via two parallel routes, namely a nonlinear elimination route demonstrating Michaelis-Menten kinetic behavior (represented by parameters V_m and K_m), and a linear elimination route demonstrating first order elimination kinetic behavior (rate parameter K). This elimination kinetics model is consistent with our previous finding [13, 15] that EPO is eliminated nonlinearly via a receptor mediated erythropoietic mechanism by the bone marrow and linearly via a non-erythropoietic mechanism.

The EPO plasma concentration profile from a single intravenous ¹²⁵I-rhEPO tracer bolus dose was well described by a biexponential disposition function. The ¹²⁵I-rhEPO clearance (Cl(t)) was calculated using Eq.3.

$$\mathit{Cl}\left(t\right)=\frac{D}{\mathit{AUC}}$$ (3)

where D is the ¹²⁵I-rhEPO dose and the AUC is the area under the curve for the concentration of ¹²⁵I-rhEPO time calculated from the biexponential disposition function.

Despite the fact that the clearance function, Cl(t), presented throughout this work is determined from the biexponential disposition function, a mechanistic interpretation of the Cl(t) value can still be made based on the model presented in Eq.2. Assuming that the concentration of unlabeled EPO (C_b(t)) was constant over the relatively short duration of the ¹²⁵I-rhEPO PK study (7-8 hrs), it follows from Eq.2 that the clearance of EPO at the time of ¹²⁵I-rhEPO PK study can be represented parametrically as shown in Eq.4.

$$\mathit{Cl}\left(t\right)=K\cdot V_{\mathit{EPO}}+\frac{V_m\left(t\right)}{K_m+C_b\left(t\right)}\cdot V_{\mathit{EPO}}$$ (4)

The Cl(t) represents the summation of elimination via two routes namely, non-receptor mediated ,Cl_NR and receptor mediated ,Cl_R clearances as shown in Eq. 5-7. EPO's volume of distribution is denoted by V_EPO. The time in Eqs. 1 and 2 is relative to the administration of ¹²⁵I-rhEPO in the tracer PK study, while the time for the remaining equations is measured relative to the beginning of the study.

$$\mathit{Cl}\left(t\right)={\mathit{Cl}}_{\mathit{NR}}+{\mathit{Cl}}_R\left(t\right)$$ (5)

$${\mathit{Cl}}_{\mathit{NR}}=K\cdot V_{\mathit{EPO}}$$ (6)

$${\mathit{Cl}}_R\left(t\right)=\frac{V_m\left(t\right)}{K_m+C_b\left(t\right)}\cdot V_{\mathit{EPO}}$$ (7)

Since previous studies demonstrated that phlebotomy did not have a significant effect on non-receptor mediated clearance [16], Cl_NR that was assumed to be constant (scaled to the bodyweight) during all PK studies. Receptor mediated clearance on the other hand was assumed to change over study period as a result of changes in number of EPO receptors reflected in the changing value of V_m(t). Based on an assumed proportional relationship between the EPOR pool size and V_m(t), the relative value of EPOR can be described as shown in Eq.8.

$$\frac{\mathit{EPOR}\left(t\right)}{\mathit{EPOR}\left(0\right)}=\frac{V_m\left(t\right)}{V_m\left(0\right)}=\frac{{\mathit{Cl}}_R\left(t\right)\cdot (K_m+C_b\left(t\right))}{{\mathit{Cl}}_R\left(0\right)\cdot (K_m+C_b\left(0\right))}$$ (8)

Cl_NR was fixed to 6.58 mL/kg/hr as previously determined [16]. Likewise, the value of K_m was fixed to 523 mU/mL based on our previous analysis [13].

Pharmacodynamic Hb mass balance model

Hb production is stimulated by EPO through a stimulation function f_stim(t):

$$f_{\mathit{stim}}\left(t\right)\{\begin{array}{cc}{k}_{\mathit{stim}}\cdot {\left(\mathit{Wt}\left(t\right)\right)}^{3∕4}\hfill & \mathit{if}t\le 0\hfill \\ \frac{\mathit{EPOR}\left(t\right)}{\mathit{EPOR}\left(0\right)}\cdot \frac{E_{\max }\cdot C_b\left(t\right)}{{\mathit{EC}}_{50}+C_b\left(t\right)}\cdot {\left(\mathit{wt}\left(t\right)\right)}^{3∕4}\hfill & \mathit{if}t>0\hfill \end{array}\phantom{\}}$$ (9)

where k_stim is the Hb production stimulation rate constant at the start of the study, Wt(t) is the body weight, E_max is the maximum Hb production rate scaled to the bodyweight, EC₅₀is the EPO concentration that results in Hb production rate that is 50% of the scaled E_max.

To account for body weight change, Hb production was assumed to be proportional to the body weight to the power ¾ [17]. Hb production before the beginning of the study (t<0) was assumed to be constant scaled to body weight to the ¾ power. Hb production rate after the beginning of the study (t>0) was related to plasma EPO concentrations by a Michaelis-Menten E_max model [18]. To account for change in number of EPO receptors, Hb production rate was scaled to the relative change in number of receptors by multiplying with the ratio $\frac{\mathit{EPOR}\left(t\right)}{\mathit{EPOR}\left(0\right)}$ as shown in Eq. 9

The Hb production model assumed that RBCs have a time invariant lifespan (τ_RBC) with no variability (i.e. point distribution) [19-21]. Change in amount of Hb produced endogenously is given by:

$$\frac{\mathit{dHb}\left(t\right)}{\mathit{dt}}=f_{\mathit{stim}}(t-a)-f_{\mathit{stim}}(t-b)$$ (10)

with initial conditions:

$$\mathit{Hb}\left(0\right)={\int }_{t-b}^{t-a}{f}_{\mathit{stim}}\left(u\right)\mathit{du}{\mid }_{t=0}={\int }_{0-b}^{0-a}{f}_{\mathit{stim}}\left(u\right)\mathit{du}$$

where a is the time between erythroid progenitor cells stimulation by EPO and the appearance of newly produced RBCs in the circulation, and b is the time between erythroid progenitor cells stimulation by EPO and the removal of the resulting RBCs from circulation by senescence. The RBCs lifespan (τ_RBC) is the difference b – a.

In the above model, RBCs were assumed to be removed only by aging when they reach the lifespan. Phlebotomy on the other hand, represents a removal of cells of all ages up to τ_RBC[22]. The time interval over which the phlebotomy affects Hb mass balance depends on the lifespan of RBCs. Assuming “m” phlebotomies that occurred over a time period equal to the lifespan of RBCs, the fraction of Hb that remains in circulation after the i^th phlebotomy, denoted F_P(i), that occurred at time t_P(i) is given by Eq.11. Thus, F_P(i) is the fraction of Hb remaining immediately after the i^th phlebotomy relative to the amount present immediately before the i^th phlebotomy. The phlebotomy correction term at time “PC(t)” is the multiplication of fractions remaining for all phlebotomies that occurred between t – τ_RBC and t.

$$F_P\left(i\right)=1-\frac{A_P\left(t_p\left(i\right)\right)}{\mathit{Hb}\left(t_p\left(i\right)\right)}$$ (11)

where A_P(t_p(i)) is the amount phlebotomized at t_p(i)

$$\mathit{PC}\left(t\right)=\prod _1^m{F}_p\left(i\right)$$ (12)

where t_p(1)≥ t − τ_RBC and t_p(m)<t

$$\frac{\mathit{dHb}\left(t\right)}{\mathit{dt}}=f_{\mathit{stim}}(t-a)-\mathit{PC}\left(t\right)\cdot f_{\mathit{stim}}(t-b)$$ (13)

with initial conditions:

$$\mathit{Hb}\left(0\right)={\int }_{t-b}^{t-a}{f}_{\mathit{stim}}\left(u\right)\mathit{du}{\mid }_{t=0}={\int }_{0-b}^{0-a}{f}_{\mathit{stim}}\left(u\right)\mathit{du}$$

The estimated amounts of Hb in the circulation were converted into observed concentrations by dividing by the total blood volume $\left(V_{\mathit{Hb}}^{\mathit{total}}\right)$. In order to account for blood volume expansion as a result of growth, total blood volume was adjusted according to the body weight:

$$V_{\mathit{Hb}}^{\mathit{total}}\left(t\right)=\mathit{Wt}\left(t\right)\cdot V_{\mathit{Hb}}$$ (14)

Sheep body weight

Sheep body weight during the study was estimated using a 4^th order polynomial. To estimate the body weight before the beginning of the study and after birth (−60 < t ≤ 0 days), which is needed to calculate f_stim(t), the growth rate (denoted by k_growth) over the first two months of life (t<60 days) was estimated separately from five lambs. In these lambs, body weight values were collected over the first 50-60 days of life. The average value of k_growth estimated in these lambs was used to estimate body weight for the current sheep subjects before the beginning of the study and after birth (−60 < t ≤ 0 days). To account for pre-birth body weight which is needed to calculate f_stim(t) for t<-60 days, an exponential function that describes the dynamics of in utero growth was used [23]. The explicit equation for body weight is displayed in Eq.15.

$$\mathit{Wt}\left(t\right)=\{\begin{array}{cc}{\alpha }_0+{\alpha }_1\cdot t+{\alpha }_2\cdot t^2+{\alpha }_3\cdot t^3+{\alpha }_4\cdot t^4\hfill & \mathit{for}t>0\hfill \\ {\alpha }_0+k_{\mathit{growth}}\cdot t\hfill & \mathit{for}-60<t\le 0\hfill \\ \mathit{wt}(t=-60)\cdot \frac{e^{(0.1281-0.00038\cdot (G\_\mathit{AGE}+t+60))\cdot (G\_\mathit{AGE}+t+60)}}{e^{(0.1281-0.00038\cdot (G\_\mathit{AGE}+60))\cdot (G\_\mathit{AGE}+60)}}\hfill & \mathit{for}t\le -60\hfill \end{array}\phantom{\}}$$ (15)

where α₀,α₁,α₂,α₃, and α₄ are 4^th order polynomial parameters and G_AGE is the gestational age of the term lamb which was fixed to be 150 days [24-25].

Data analysis

All modeling was conducted using WINFUNFIT, a Windows (Microsoft) version evolved from the general nonlinear regression program FUNFIT [26], using ordinary least squares fit to each individual subject's Hb concentration-time profile. The amount of Hb removed and administered by each phlebotomy, at the time of removal was accounted for by WINFUNFIT using a generalized events processing module. The events processing module integrates the differential equation exactly up to the time of the event and adding or removing the appropriate amount and then continuing integrating the differential equation with new initial conditions set at the appropriate event times. The EPO plasma concentrations were nonparametrically represented using a linear spline function.

To summarize the uncertainty in the individual subject parameter estimates, the relative standard error (RSE%) of the estimate was calculated for each parameter as:

$$\mathrm{RSE}\%=\frac{\mathrm{SE}}{\left|\mathrm{P}\right|}\cdot 100$$ (16)

where SE and P are the standard error of the parameter and the estimate of the parameter, respectively.

Results

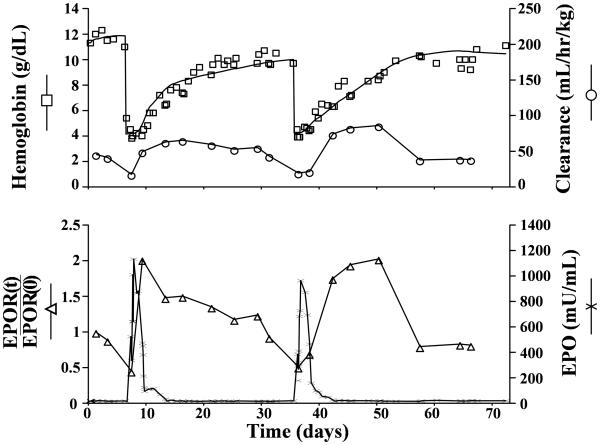
The Hb mass balance model fit along with plasma EPO concentration for a representative sheep are shown in Figure 1. The model accurately captures the general behavior of the Hb concentration data (r =0.95±0.035). The pharmacodynamic model parameters are summarized in Table 1.

Figure 1.

Representative individual subject fits of model equations to observed plasma hemoglobin (□), total clearance (○), erythropoietin (χ), and EPOR fraction (△). Hb values were obtained from the Hb mass balance fit (Eq.9-14). EPO values were obtained experimentally using RIA. Total clearance and EPOR fraction are obtained from 125I-rhEPO disposition model (Eq.1-8).

Table 1.

A summary of parameter estimates from the hemoglobin mass balance model

Sheep No.	α (day)		τRBC (day)		Emax (g/day.kg0.75)		EC50 (mU/mL)		kstim (g/day.kg0.75)		rb
	Value	RSE%a	Value	RSE%a	Value	RSE%a	Value	RSE%a	Value	RSE%a
1	0.95	16.5	104	5.9	1.37	2.23	97.8	3.12	0.41	1.65	0.89
2	2.26	13.3	84.5	9.31	1.61	7.39	70.4	14.1	0.63	2.32	0.97
3	3.55	8.84	68.8	1.56	1.36	0.99	57.1	1.91	0.33	1.67	0.97
4	1.71	17.9	124	11.6	1.28	7.32	24.6	19.8	0.49	1.87	0.97
5	2.22	13.3	82.7	2.71	1.05	1.88	52.4	3.51	0.56	1.21	0.94
Mean	2.14	14.0	92.7	6.21	1.34	3.96	60.5	8.48	0.48	1.74	0.95
CV (%)	44.4	25.1	23.1	68.6	15.1	79.0	44.2	94.3	24.5	44.4	3.73

^aRSE%, relative standard error

^br, correlation coefficient.

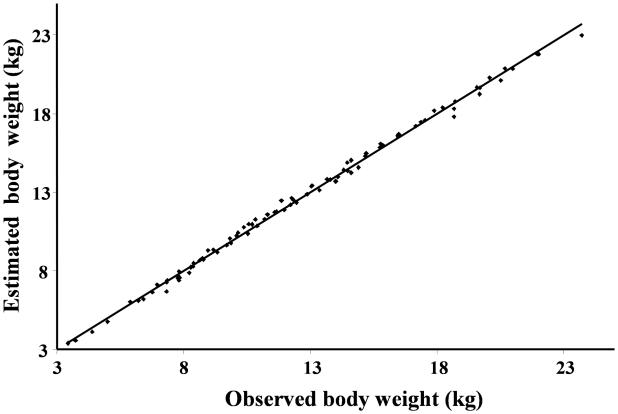
The average value of k_growth that describes growth over the first two months of life (t<60 days) was estimated to be 0.285±0.027 kg/day. As displayed in Figure 2, the body weight function described accurately the body weight data over the first two months of life (average R²=0.996, range 0.989-0.998). The body weight data presented in Figure 2 represent data over the first two months of life for lambs from different study protocol. This data was included in the analysis to describe the growth over the first two months of life. This information was used to describe Hb production before the beginning of the study (Eq.9 and Eq.15).

Figure 2.

Bodyweight values over the first two months of life estimated using linear function (wt=α₀+k_growth·t) vs. actual bodyweight values for all lambs.

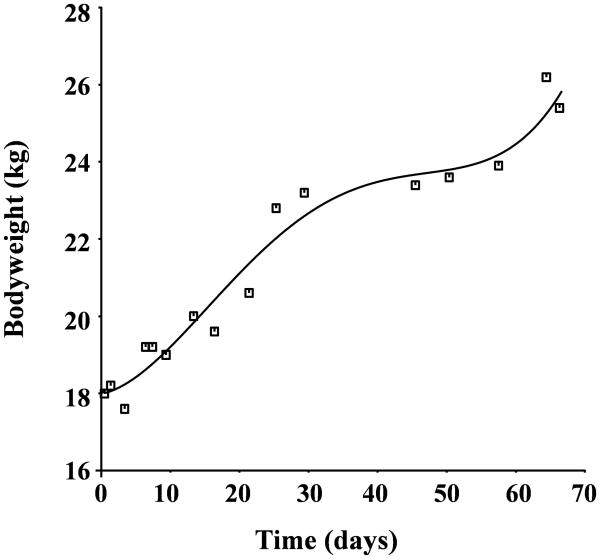
Individual sheep's Hb concentration-time profiles contained on average 76 Hb values (range 71 to 83), 92 plasma EPO concentrations (range 82 to 107) and 23 bodyweight data time points (range 19 to 32). The body weight measurements are well represented by a 4^th order polynomial (Figure 3). At the beginning of the study, the baseline Hb was 10.4±2.05 g/dL, the EPO concentration average was 22.7±11.8 mU/ml, the clearance average value was 48.2±10.9 ml/kg/hr, and the average weight was 21.3±3.63 kg. At the end of the study, the Hb average was 9.8±1.55 g/dl, EPO concentration was 18.4±4.72 mU/ml, the clearance average value was 39.2±6.03 ml/kg/hr, and body weight was 32.2±4.58 kg. Paired t-test results indicate that there is no significant difference in the value of Hb, EPO concentration, and clearance between the values reported at the beginning of the study and at the end of the study (p>0.05). The body weight of the sheep was significantly higher at the end of the study compared to the beginning of the study (p<0.05). Thus, there is a need to account to animal growth in the model.

Figure 3.

Bodyweight over the study period. The curve fitted to the lamb bodyweight is a 4^th order polynomial

The newly produced Hb appears in the circulation 2.14±0.95 days after stimulation by erythropoietin. The lifespan of RBCs (τ_RBC = b − a, Eq.12) was estimated to be 92.7±21.3 days and the bodyweight scaled Hb production constant, k_stim, was determined to be 0.48±0.12 g/day.kg^¾. The Michaelis-Menten E_max model parameters were successfully evaluated for all sheep. The predicted maximum achievable Hb production rate, E_max, was found to be 1.34±0.20 g/day.kg^¾, and EC₅₀ was found to be 60.5±26.7 mU/mL.

Discussion

This study provides a quantitative estimation of the rate of Hb synthesis in sheep and considers its functional and mechanistic relationship to the EPO plasma concentration, while also accounting for other important confounding variables, including change in number of EPOR, phlebotomy, and growth. Because of its importance for EPO efficacy and dosing, special attention is focused on the regulatory kinetic mechanism of the EPOR pool size. In contrast to other previous models that describe erythropoiesis [22, 27] the current model explicitly accounts for changes in the number of EPOR as a result of up-regulation while simultaneously accounting for continuous growth and the expression of blood volume and the volume of distribution expansion as a function of the increase in body weight.

Previously, we proposed a model that describes the change in the density of EPOR in the form of change in EPO clearance values [8]. We also demonstrated that clearance is linearly related to the density of EPOR m-RNA in the bone marrow [10]. In this manuscript we utilized information obtained from previous work about EPOR and clearance changes to describe erythropoiesis under stress conditions. Although other models implicitly accounted for EPOR changes in the form of negative feedback inhibition of progenitor cells production, they did not have any measure of the actual change in EPOR density [28].

EPO clearance as a measure of EPOR pool size

The clearance parameters obtained by the analysis provides an indirect quantification of the EPOR populations under the well supported assumption that EPO's elimination is largely via EPORs. The recent study by Nalbant et al. (2010) has shown that the change in EPOR pool size can be estimated as a linear function of the EPO clearance [10]. From this finding it follows that the quantity of EPOR is proportional to V_M (Eq. 8). The pattern of change in EPOR shown in Figure 1 was consistently observed for all five study animals after both phlebotomies. The decrease in EPOR that coincides with the increase in the EPO concentration can be explained by a temporary consumption with regulatory feedback correction and the findings from molecular biology investigations that some EPOR are not recycled after interaction with EPO [29-30]. Since V_m(t) is proportional to the quantity of EPOR the subsequent increase in Cl_R(t) and V_m(t) indicates an up-regulation of EPOR.

Several studies have demonstrated EPOR up-regulation as a result of exposure to high EPO levels and/or under hypoxic conditions. It was reported that the incubation of murine cell lines with EPO for 6 days increases the number of EPOR per cell without changing EPOR binding affinity [31]. Bernaudin et al. also reported EPOR up-regulation in rat brain endothelial cell line and cortical astrocyte cell cultures as a result of hypoxic conditions [32]

RBC Pharmacodynamic Parameters

The estimated mean value for the lag time,α , between erythroid progenitor cells stimulation by EPO and the appearance of newly produced RBCs in the circulation was 2.14 days. This is a higher estimate than the previously reported value in sheep of 0.797 days [33]. This may be explained by the facts that the previous analysis included a peripheral effect site compartment, while the current analysis does not. Also, the lag time was calculated under steady-state conditions while recognizing that the lag time increases under stress conditions, but we did not correct for that [33-34]. The average of individual RBC lifespans (τ_RBC= b − a) was found to be 92.7 days compared to the reported value of 120 days in adult sheep [35].

EPOR regulatory changes, EPO efficacy and EPO dosing strategy for treatment of anemia

It is evident from examining the relative change in the size of the EPOR pool , EPOR(t)/ EPOR(0) (Fig. 1) that an up-regulation due to anemia by a factor close to 2 is possible relative to the basal EPOR level and that the lowest and highest EPOR pool sizes can differ by a factor close to 4 (=2/0.5). Since according to mass balance principles the rate of progenitor activation is expected to be proportional to the quantity of EPOR, these changes in the EPOR pool size will significantly influence the efficacy of EPO. Such changes need to be considered when formulating an EPO dosing optimization algorithm. Due to the great similarity of the erythropoietic physiology between mammalian species it is anticipated that a similar EPOR regulatory mechanism model exists in humans. Thus, the kinetic model and mechanism proposed in this pre-clinical study may serve as a starting point for the development of an optimal EPO dosing algorithm to that of neonatal anemia. Because of the mathematical complexity of the present regulatory model, a complete dosing optimization will require extensive computational analysis. However, the simple core principles of the model provide several simple guiding principles: Accordingly, an optimal dosing strategy should in general maximize the interaction between EPO and EPOR. Specifically, EPO should be administered when the number of EPOR are close to maximally up-regulated. Similarly, in recognizing a temporary loss of EPOR following an initial dosing, the subsequent dosing should, to achieve the highest efficacy, be postpones until the EPOR again have increased by the regulatory feed-back control. Several studies have demonstrated that subcutaneous administration of EPO is more efficacious than intravenous dosing [36-38], which according to our model can be explained by the fact that the duration of high plasma EPO concentration is longer in subcutaneous than intravenous administration, thus allowing the exogenous EPO to still be present after the EPORs are up-regulated.

Conclusion

The present study and previous findings in the literature demonstrates that under conditions of severe tissue hypoxemia hematopoietic EPOR are up-regulated as a part of a feedback regulation. The EPOR pool size, in turn, determines the magnitude of response to EPO in stimulating erythrocyte production. Frequent estimation of EPO clearance as a measure of EPOR pool size and the use of mass balance principles allowed for the mathematical determination of the in vivo erythropoiesis rate and its relationship to endogenous plasma EPO concentrations under sever hypoxemic conditions. The mechanistically oriented EPO's PK/PD model we propose could be used as a valuable tool for a better elucidation of EPO's complex erythropoietic effect and for designing an optimal dosing for EPO to maximize its erythropoietic effect.