Cyclic competition of mobile species on continuous space: pattern formation and coexistence

Abstract

We propose a model for cyclically competing species on continuous space and investigate the effect of the interplay between the interaction range and mobility on coexistence. A transition from coexistence to extinction is uncovered with a strikingly non-monotonic behavior in the coexistence probability. About the minimum in the probability, switches between spiral and plane-wave patterns arise. A strong mobility can either promote or hamper coexistence, depending on the radius of the interaction range. These phenomena are absent in any lattice-based model, and we demonstrate that they can be explained in terms of nonlinear partial differential equations. Our continuous-space model is more physical and we expect the findings to generate experimental interest.

I. INTRODUCTION

The coexistence of competing species in spatially extended ecosystems is key to biodiversity in nature. Understanding the dynamical mechanisms of and identifying factors promoting coexistence are a fundamental problem of continuous interest not only in evolutionary biology but also in nonlinear science [1–5]. Species coexistence has been investigated in a variety of systems, such as in microbes, [6–9], ant colonies [10, 11], parasites and hosts [12, 13], predator-prey dynamics [14] and interference competition [15] etc. Existing models are mostly macroscopic in the sense that they focus on the dynamical evolutions of species populations [1, 2]. For any given species, its population is merely a coarse-grained average quantity that is not capable of reflecting the possibly complicated interactions among its own individuals and with those from other competing species. To gain a deeper and more comprehensive understanding of the dynamics of coexistence, microscopic models that describe the competitions among species at the level of individual interactions of the stochastic nature are necessary [3, 16–24]. In this regard, a class of microscopic models is proposed based on cyclic, nonhierarchical competitions [e.g., as described by the classical “rock-paper-scissor” (RPS) game] on spatial lattices. Such competitions have been observed in several real ecosystems [8, 25–27]. The fundamental importance of RPS-like competition in sustaining biodiversity for limited resources in nature has been emphasized through experimental investigations [6, 7]. Theoretical and computational studies of the RPS model have revealed that, due to the presence of stochasticity, local interaction and dispersal can ensure the coexistence of species. More recently, individual mobility as a common feature in ecosystems has been incorporated into spatial games to better model competition dynamics of species and the organization of spatial patterns [18, 20–22].

All existing microscopic models of the competition dynamics of dispersing species assume lattices as the underlying spatial structure on which movements of individuals and their interactions with neighboring individuals occur. While there were efforts to investigate the effect of shortcuts among nonadjacent sites on the competition dynamics [28, 29], in these models the space is still discrete. Considering that, in realistic ecosystems, the physical space that supports the dynamics is continuous, it is of interest to ask what might happen to RPS dynamics and species coexistence in a continuous space. The purpose of this paper is to study this issue. In particular, we construct a continuous-space RPS model for mobile species and address one fundamental question: what is the role of species-interaction range in coexistence? This issue has not been investigated in previous discrete-space models, as the interaction range was usually limited to neighboring individuals. In our continuous-space model, the interaction range becomes a physical parameter that can be adjusted. Since, in discrete-space models, mobility is the single most important parameter whose effect on species coexistence has been the focus of most previous works, our continuous-space model allows us to explore the fundamental interplay between two parameters, i.e., mobility and interaction range, with respect to coexistence/extinction.

Our main results are the following. (1) When the interaction scale in the continuous space is increased, the probability of coexistence exhibits a non-monotonic behavior with one local minimum and one local maximum, regardless of the size of the continuous space. Close to the minimum, a switching behavior in the spatial patterns occurs between spiral and plane waves, as a result of the collision of spirals and stochastic effects. (2) Contrary to the basic result from the discrete-space models that high mobility induces extinction, we find that the role of mobility as to whether it promotes or prevents coexistence depends on the range of spatial interaction. To substantiate these findings, we have derived a theoretical model based on nonlinear partial differential equations (PDEs) to analyze some of the results obtained from direct simulations of RPS dynamics. The PDE model can successfully reproduce the dependence of the spiral wavelength on the interaction range as well as the switch from plane waves to spiral waves. However, the model cannot reproduce the non-monotonic coexistence probability due to the absence of intrinsic stochastic effect. Our continuous-space RPS model enriches greatly the possibilities to explore and predict the dynamics of cyclically interacting species in a physically more realistic way, facilitating experimental research on species competitions and biodiversity.

In Sec. II, we describe the RPS model on continuous space and investigate species coexistence with respect to interaction range, pattern formation, and individual mobility. In Sec. III, a PDE model is proposed to explain the results produced by stochastic model and an explanation for the transition between spiral- and plane-wave patterns in terms of examining the wavelength. In Sec. IV, we study an alternative model for specie coexistence by separating competition and reproduction in the RPS game. Conclusions are presented in Sec. V.

II. COMPETITION DYNAMICS ON CONTINUOUS SPACE

A. Model description

We consider three cyclically competing subpopulations (referred to as A, B and C) on a square cell of linear size L = 1 under periodic boundary conditions. The species compete with each other for limited resources according to the following general rules:

$$\begin{array}{cc}\hfill & \mathit{AB}\stackrel{u}{\to }\mathit{AA},\hfill \\ \hfill & \mathit{BC}\stackrel{u}{\to }\mathit{BB},\hfill \\ \hfill & \mathit{CA}\stackrel{u}{\to }\mathit{CC},\hfill \end{array}$$ (1)

which occur only if the distance between two individuals is less than r, the interaction radius. At each simulation step, a randomly chosen individual i from one species eliminates, within its interaction range, one individual j from the next species in the cycle at rate u. At the same time, i reproduces at the position of j. In this sense, competition and reproduction occurs simultaneously and the two processes are combined. Mobility is incorporated into the dynamics such that individuals can move to a random position within the same range of radius r, and this occurs at rate s. The probabilities of competition and movements are normalized by (u+s), i.e., their probabilities are u/(u + s) and s/(u + s), respectively. In the absence of mobility, the probability of competition is 1, regardless of the value of u. Individuals from all three species are represented by points in the plane at different locations. Initially the plane is randomly populated with individuals from all three species. To make an unbiased comparison for different population sizes, we normalize the radius r by the average distance between individuals: $R=r\sqrt{N}$, with N being the total population size.

B. Species coexistence and pattern formation

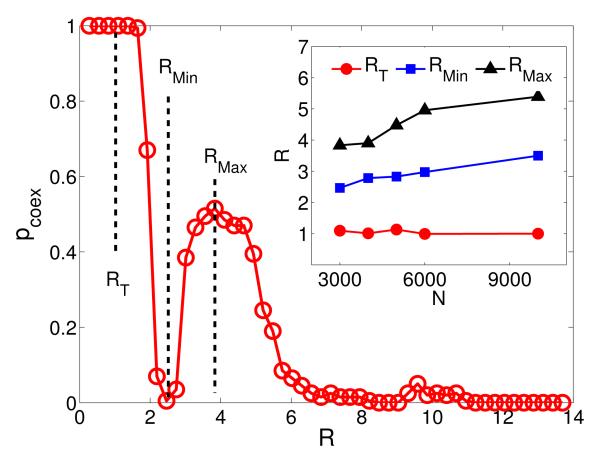
We first study the case where mobility is absent and focus on the effect of interaction range on the coexistence probability p_coex. The results are shown in Fig. 1. We find that, when the radius R is close to zero, the system reaches a trivial, static coexistence state where the average distance between individuals is greater than the interaction range, so effectively there are no interactions among most individuals and no death/birth can occur, in contrast to what can happen in a dynamic equilibrium. As R exceeds the critical value R_T ≈ 1.0, the system experiences an abrupt transition to a dynamical coexistence state in which all species survive in the form of certain spatial patterns. When R is increased from R_T, p_coex exhibits a non-monotonic behavior, reaching a local minimum at R_Min and a local maximum at R_Max > R_Min. This is counterintuitive because one may expect a monotonic decrease in p_coex based on the existent result in the literature that local interactions ensure coexistence while it is lost at larger scales [6, 7]. However, our results demonstrate a nontrivial transition in p_coex from small to large values with an optimal degree of coexistence occurring for R = R_Max. We observe further that coexistence is ruled out for large interaction range, which is consistent with the results from E.coli experiment [6, 7].

FIG. 1.

(Color online.) Coexistence probability p_coex as a function of the radius R of interaction range in the absence of individual mobility for N = 3000, L = 1, where p_coex is defined to be the ratio of the number of the survival cases to the total number (200) of independent simulation realizations. The probability is calculated after a transient time T ∝ N from random initial configurations with the same densities of three species. The inset shows the dependence of R_T, R_Min and R_Max on the population size N.

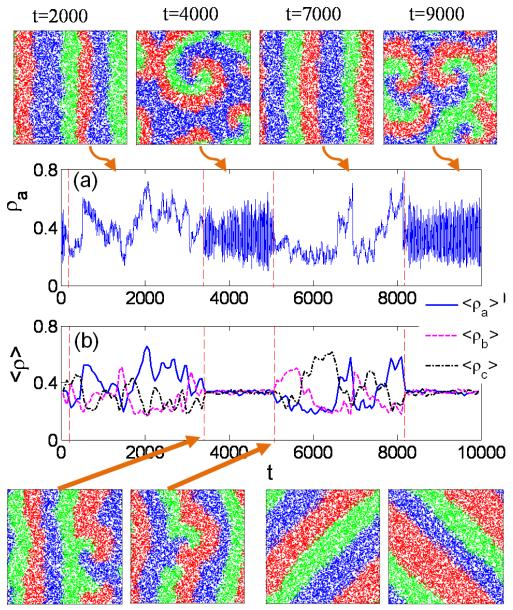
For R ≲ R_Max, the underlying spatial pattern switches between spiral and plane waves in time, as shown in Fig. 2 (top row). Both types of patterns are relatively stable to generate coexistence but, due to the stochastic effect, intermittent switches between the patterns occur. The evolutions of species densities (ρ_a, ρ_b, or ρ_c) associated with the two types of patterns are also quite different. In particular, in the spiral-wave phase each density exhibits relatively high frequency oscillations as compared to the plane-wave phase [Fig. 2(a)]. Figure 2(b) shows the average densities of the three species over a time window. Typical patterns occurring near the switching points are also shown in Fig. 2 (bottom row, left two panels). The transition from plane to spiral wave patterns occurs due to the stochasticity-induced penetration of individuals of one species into the domain of neighboring species and exclusion of individuals of the next species in the cyclic loop. At the mixing point, due to the cyclic competition, three species twist and form spiral waves, breaking the plane wave. On the other hand, the transition from spiral to plane wave can be ascribed to the collision of two large local spiral waves. After they collide and vanish, the outgoing wavefront becomes approximately straight, decreasing significantly the curvature of the wave. Thus, when the wavelength of spiral waves is proper, stochastic effects intrinsic to the underlying dynamical system can trigger the transition. In general, the probability of finding the switch between spiral and plane waves is related with the probability of species coexistence. There are two major directions along which the plane wave can travel: axial and diagonal directions, as shown in Fig. 2 (bottom row, right two panels), due to the symmetry in both orthogonal axes. It is noteworthy that spiral waves are quite common in excitable media and population dynamics [30–34], and traveling waves have been found in a number of cyclic populations [35]. However, the switch between the two types of waves is rarely studied, especially in stochastic systems. In this regard, our work provides quantitative insight into this issue.

FIG. 2.

(Color online.) For N = 10000 and R = 4.25, pattern transition between plane waves and spiral waves (top row), (a) the corresponding time series of species density ρ_a, (b) average species density 〈ρ_a〉, 〈ρ_b〉, 〈ρ_c〉, typical patterns about the transition point (two left panels, bottom row), and plane wave traveling along diagonal directions (two right panels, bottom row). The rapid oscillations in the density are due to the fact that, in the spiral-wave phase, the curved boundaries between different species generate relatively large interaction areas so that many more individuals can interact with others in a random manner. The average species density 〈ρ〉 is taken by down-sampling the original time series and the average values are taken over 100 time steps.

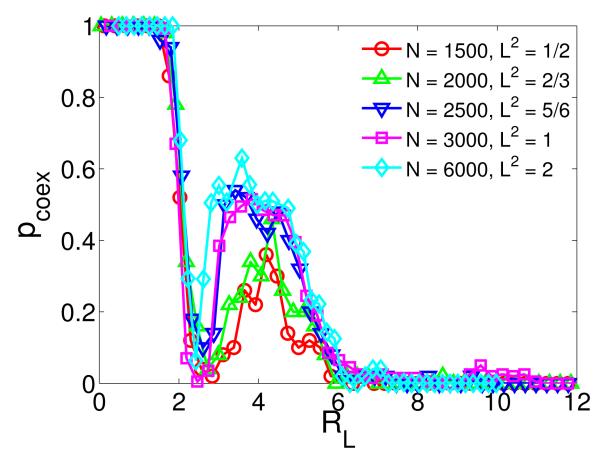
Since the nontrivial relations between the normalized selection range R and the coexistence probability P_coex and the pattern switch are for the special case of L = 1, it is of interest to justify the validity of such results in general cases. We take into account the effect of the size of the square lattice on the coexistence curve by defining a rescaled selection range R_L ≡ (r/d – 1)/L + 1, where r ∈ [0, L] is the physical or original selection range, and $d=L∕\sqrt{N}$ is the average distance between two neighboring individuals when individuals are uniformly distributed on the square cell initially. For L = 1, we have $R_L(L=1)=r\sqrt{N}=R$ so that the rescaled selection range R_L reduces to the normalized selection range R shown in Figure 1. The interpretation of R_L is understood as follows. The average distance d between neighboring individuals is the first critical distance above which the system experiences an abrupt transition from static to dynamical coexistence, thus we set d to be the unit of the selection range. The scale factor 1/L is used to normalize the size of the square cell. The rescaled selection range R_L can ensure R_L = R = 1 when r = d. Figure 3 shows the effect of the cell size associated with different population N on the coexistence probability p_coex. We can see that p_coex does not depend on the size of the square lattice except for small populations, e.g., N = 1500 and N = 2000, where the stochastic effect becomes more prominent, suppressing coexistence because of the spatial non-uniformity, leading to lower peak values of p_coex. In contrast, for N > 2000, the curves of p_coex ~ R_L collapse into a single one, regardless of the size of the square cell, indicating that the size L has little effect on coexistence.

FIG. 3.

(Color online.) The effect of the size of the square cell on the coexistence probability p_coex with respect to the rescaled selection range R_L. We compute coexistence curves for five different combinations of the cell size L and the total population N. The non-monotonic behavior of p_coex ~ R_L is independent of the cell size, as indicated by the collapse of the three curves into a single one for N = 2500, 3000, 6000. The peaks for N = 1500 and 2000 are lower, due to a relatively stronger stochastic effect for smaller values of N.

Although the cell size L with respect to the rescaled selection range R_L has little effect on the coexistence behavior and the spatial pattern, it is of interest to explore how the cell size L influences the pattern switch for fixed physical selection range r. We have thus carried out simulations by fixing the density of individuals and choosing some typical values of r. As shown in Fig. 4(a), r is chosen to be at the peak of the coexistence probability P_coex for L² = 2. The switch between spiral and plane waves is found to be quite common under this condition [Fig. 4(a)]. However, for the same value of r, when L² is reduced to 1/2, the pattern switches no longer occur and two species become extinct [Fig. 4(a)]. This phenomenon can be explained by taking the relationship between L and R_L into account. For fixed values of r and species densities, according to the definition of the rescaled selection range R_L, we have R_L ~ 1/L. If L is reduced, R_L is enhanced, resulting in a change in R_L from that associated with the local maximum of P_coex to that in the extinction region, as shown in Fig. 3. Further insights can be obtained by examining the wavelength, which is determined exclusively by r, irrespective of the value of L. When L is reduced for fixed r, the wavelength becomes relatively larger as compared to L and exceeds the cell size, leading to extinction. We have also examined the values of r about the local minimum value of P_coex. As shown in Fig. 4(c), for L² = 5/6, there are switches between the two kinds of patterns. However, when L² is increased to 2, switches can never occur [Fig. 4(d)] because R_L due to the increase of L is changed to the left side of the local minimum, which is outside of the pattern switch region. We have also studied the size effect on the spatial patterns for other values of r. The effect can be explicitly predicted in terms of the change in the rescaled selection range R_L. All these imply that the cell size has a great influence on the spatial pattern for a fixed physical selection range. The spatial patterns are thus determined by the rescaled selection range R_L with respect to different cell sizes.

FIG. 4.

(Color online.) Spatial patterns at physical selection range r = 0.0913 for (a) cell size L² = 2 and (b) L² = 1/2, and at r = 0.0365 for (c) cell size L² = 5/6 and (d) L² = 2. For all these patterns, the density N/L² of individuals is fixed to be 3000. In (a), the rescaled selection range R_L = 3.82, which corresponds to the R_Max in Fig. 3. Spiral waves and plane waves can switch between each other at this R_L. In (b), species go extinct for smaller cell size than (a), because R_L = 6.66, is in the extinction region. In (c), R_L = 2.10, close to R_Min in Fig. 3; while in (d), by increasing L, R_L decreases to 1.71, which is outside of the pattern switch region (the peak), so that pattern switch never occurs.

C. Role of individual mobility

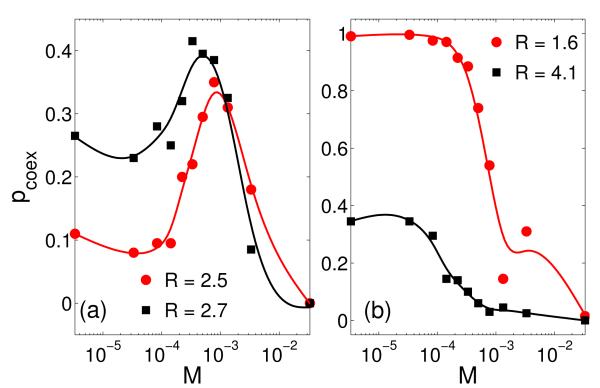
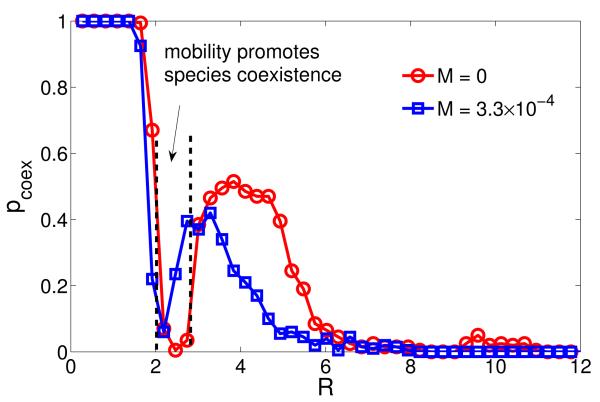
We next investigate the role of individual mobility. A macroscopic mobility can be defined by rescaling the mobile rate s of individuals using the system population N according to M ≡ s/N [20, 21]. We find that mobility can either promote or hamper coexistence, depending on the interaction radius R, in contrast to previous results [20] that large mobility typically leads to extinction. For R ≈ R_Min, the coexistence probability p_coex can be enhanced by mobility, as shown in Fig. 5(a). We see that there exists an optimal value of mobility M at which p_coex is considerably larger than that without mobility, suggesting a positive role of mobility on continuous plane in promoting coexistence. However, in other regions of R values, p_coex can be reduced by increasing M, as shown in Fig. 5(b). These results reveal a more complicated role of mobility in ecosystems than previously thought: species movements to gain essential life-sustaining resources can either facilitate or jeopardize coexistence. Species movements are somewhat equivalent to the expansion of interaction range in the sense that individuals outside the range of a certain individual can be reached when the individuals are mobile. We can thus rescale the value of R by the mobility and the resulting curve in Fig. 1 would shift to the left by a small amount so that the value of p_coex at R_Min is augmented. This phenomenon is illustrated in Fig. 6. We can see that not only at R ≈ R_Min (as evidenced in Fig. 5), but also within a relatively large region of the selection range around R ≈ R_Min can mobility promote biodiversity. In the meantime, the negative role of mobility in biodiversity can also be seen in other regions of Fig. 6 around the peak of p_coex.

FIG. 5.

(Color online.) For N = 3000, coexistence probability p_coex as a function of the individual mobility M for different values of interaction range R. (a) For R = R_Min = 2.5, a proper value of M can considerably enhance the coexistence probability p_coex. (b) In other region of R, as is M increased, coexistence is always inhibited.

FIG. 6.

(Color online.) Comparison of the coexistence curves for M = 0 and M = 3.3 × 10⁻⁴ (u = s), where the population size is N = 3000. When mobility is present, in the region between two dashed lines, mobility promotes coexistence. Other parameters are the same as in Fig. 1.

III. PDE MODEL AND EXPLANATION FOR THE COEXISTENCE-EXTINCTION TRANSITION

A. Derivation of PDE model

We now derive a set of partial differential equations based on the complex Ginsburg-Landau equation (CGLE) to explain our numerical findings. The starting point is to decompose the reaction AB → AA as AB → A⊘ + A⊘ → AA, where ⊘ denotes an empty position. The two reactions occur simultaneously within the range of radius R. Let a(r, t), b(r, t) and c(r, t) denote the densities at position r and time t for the three subpopulations, respectively. We obtain the following PDEs:

$$\begin{array}{cc}\hfill {\partial }_{t}a(\mathit{r},t)=& D\Delta \left[a\right(\mathit{r},t)+c(\mathit{r},t\left)\right]+[1-\rho (\mathit{r},t\left)\right]\frac{1}{S_R}.\hfill \\ \hfill & {\int }_{G_{\mathit{r}}}d{\mathit{r}}^{\prime }a({\mathit{r}}^{\prime },t)-a(\mathit{r},t)\frac{1}{S_R}{\int }_{G_{\mathit{r}}}d{\mathit{r}}^{\prime }c({\mathit{r}}^{\prime },t),\hfill \\ \hfill {\partial }_{t}b(\mathit{r},t)=& D\Delta \left[b\right(\mathit{r},t)+a(\mathit{r},t\left)\right]+[1-\rho (\mathit{r},t\left)\right]\frac{1}{S_R}.\hfill \\ \hfill & {\int }_{G_r}d{\mathit{r}}^{\prime }b({\mathit{r}}^{\prime },t)-b(\mathit{r},t)\frac{1}{S_R}{\int }_{G_{\mathit{r}}}d{\mathit{r}}^{\prime }a({\mathit{r}}^{\prime },t),\hfill \\ \hfill {\partial }_{t}c(\mathit{r},t)=& D\Delta \left[c\right(\mathit{r},t)+b(\mathit{r},t\left)\right]+[1-\rho (\mathit{r},t\left)\right]\frac{1}{S_R}.\hfill \\ \hfill & {\int }_{G_r}d{\mathit{r}}^{\prime }c(\mathit{r},t)-c(\mathit{r},t)\frac{1}{S_R}{\int }_{G_{\mathit{r}}}d{\mathit{r}}^{\prime }b({\mathit{r}}^{\prime },t),\hfill \end{array}$$ (2)

where D is a diffusion constant induced by the finite interaction range, G_r specifies the circular interaction domain of radius R centered at r, ρ(r, t) is the total species density and S_R is the area of the interaction domain G_r. We use the average density within the interaction range to approximate the density at the center. To explain the construction of the PDE model, we consider the density of one species, say a(r, t). Firstly, the increment in a(r, t) with time at position r, ∂_ta(r, t), is proportional to the probability of empty space density 1 – ρ(r, t) and the average density of its own species within its interaction range (1/S_R) ∫_Gr dr′a(r′, t), according to the reaction rule A⊘ → AA. Secondly, the decrement of the density of species A with respect to time, −∂_ta(r, t), is proportional to the density of itself a(r, t) and its prior species in the cycle within the interaction range (1/S_R) ∫_Gr dr′ c(r′, t), according to the reaction rule CA → C⊘. However, to incorporate the long-range interaction parameterized by selection range R, diffusions of both A and C should be taken into account, which are characterized by two diffusion terms DΔ[a(r, t) + c(r, t)]. The diffusion term on the right-hand side of the first equation in Eq. (2) thus characterizes the copying of an individual from prior specie to the neighborhood of an individual from next species; while other terms in the equation correspond to the competition and reproduction. Although mobility in the stochastic model is not explicit, a finite interaction range plays the same role in individual mobility as the diffusion term in the PDE model.

We solve Eq. (2) numerically by discretizing the unit space into a K × K square lattice so that solving three partial differential equations is equivalent to solving 3K² ordinary differential equations. In particular, let a(r₁, r₂, t), b(r₁, r₂, t), and c(r₁, r₂, t) denote the species densities at site (r₁, r₂), (r₁, r₂, = 1,…, K) and at time t for A, B, C, respectively, where r₁, r₂ are the coordinates of the two spatial dimensions. The terms containing the diffusion operator Δ can be approximated by using the finite-difference method:

$$\begin{array}{cc}\hfill \Delta a(r_1,r_2)& \approx \left[a\right(r_1-1,r_2)+a(r_1+1,r_2)+a(r_1,r_2-1)\hfill \\ \hfill & +a(r_1,r_2+1)-4a(r_1,r_2)]∕{\left(\delta r\right)}^2,\hfill \end{array}$$

subject to periodic boundary conditions. Here δr = L/K denotes the grid size. The integration term

$$\frac{1}{S_R}{\int }_{G_{\mathit{r}}}d{\mathit{r}}^{\prime }a({\mathit{r}}^{\prime },t)$$

is thus replaced by the sum

$$\frac{1}{N_R}\sum _{m,n,a(m,n,t)\in G(r_1,r_2)}a(m,n,t),$$

where G(r₁, r₂) represents the circular interaction range with radius R centered at site (r₁, r₂), and N_R is number of sites inside G(r₁, r₂). The whole system is then transformed to a set of coupled ordinary differential equations and can be solved using any standard numerical integration method. To incorporate stochasticity intrinsic to the evolutionary dynamics in the game framework, we add a small noise term in the PDEs, which results in switchings from plane to spiral waves [Fig. 7]. However, the imposed stochastic terms is incapable of producing the non-monotonic dependence of the coexistence probability on the interaction radius because the intrinsic stochasticity, which is essential to the evolution of the ecosystem, cannot be described exactly by an extra term that is independent of the system dynamics.

FIG. 7.

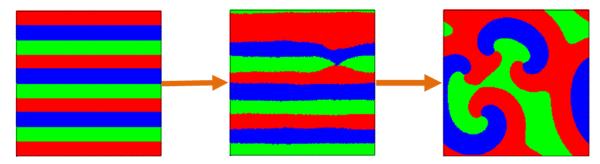
(Color online.) Pattern transition from a plane to a spiral wave as predicted by the theoretical PDE models.

B. Wavelength and spatial correlation

Assessing the wavelength of the spiral waves is key to understanding the transition from coexistence to extinction as the interaction radius R is increased. The wavelength can be determined by the method in Ref. [21]. Specifically, the spatial correlation function of one of the species, say A, between locations r and r′ can be defined as

$$C_{\mathit{AA}}(\mid \mathit{r}-{\mathit{r}}^{\prime }\mid )=\langle a(\mathit{r},t)a({\mathit{r}}^{\prime },t)\rangle -\langle a(\mathit{r},t)\rangle \langle a({\mathit{r}}^{\prime },t)\rangle ,$$ (3)

where 〈...〉 denotes the time average after the system has reached a steady state. The final spatial correlation C_AA is given by the average of all correlation values that have the same spatial length,

$$C_{\mathit{AA}}\left(l\right)=\frac{1}{N_{\mathit{r},{\mathit{r}}^{\prime }}}\sum _{\mid \mathit{r}-{\mathit{r}}^{\prime }\mid =l}{C}_{\mathit{AA}}(\mid \mathit{r}-{\mathit{r}}^{\prime }\mid ).$$ (4)

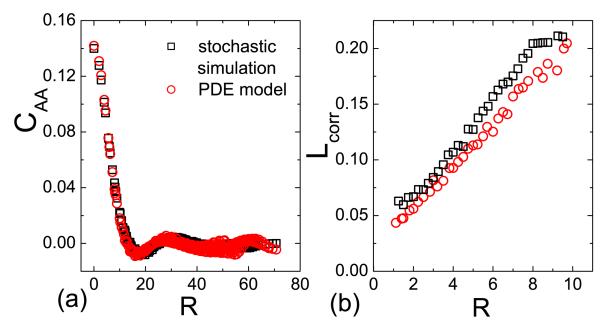
To compare results from different simulation settings, we multiply the length l by $\sqrt{N}$ to yield R. The wavelength is proportional to the critical spatial correlation: C_AA(L_corr) ≡ C_AA(0)/e [21]. The Results of wavelength calculation from the stochastic simulation and the PDE model are displayed in Fig. 8. For the spatial correlation function [Fig. 8(a)], the results from both approaches agree well with each other for large values of R, validating our PDE model. Furthermore, we observe from Fig. 8(b) that L_corr is approximately a linearly increasing function of R, suggesting the relation D ~ R².

FIG. 8.

(Color online.) For N = 10000, dependence of spatial correlation C_AA (a) and correlation length L_corr (b) on the interaction range R from both stochastic simulation (R = 2.5) and the PDE model (D = 0.00045R²), where C_AA as a function of R is obtained from Eqs. (3) and (4). Here, we select a spatial position r and calculate C_AA as a function of |r – r′| according to Eq. (3). We then count all C_AA’s with the same |r – r′| and calculate an average of them, which yield C_AA as a function of the normalized distance R.

The coexistence-extinction transition in Fig. 1 can then be understood based on the spatial patterns associated with the correlation between the wavelength and the interaction radius, as follows. For R = R_Max, we have numerically found that species coexist through two anti-spiral waves whose wave-length approaches the size of the entire square region. The anti-spiral waves are relatively stable, leading to the local maximum in p_coex. As R is increased from R_Max, due to the linear correlation, the wavelength will exceed the size of the square and extinction becomes more likely, as reflected by the sharp decrease in p_coex. For R ≲ R_Max, the wave-length is decreased together with an increase in the number of spirals. In this case, collisions of spirals begin to occur, leading to transitions between the spiral and plane waves, which suppress coexistence. This effect leads to a local minimum in p_coex at R_Min on the left hand side of R_Max. However, for smaller values of R, the spatial region is shared by a number of spiral waves of small wavelength. The collision among some of them will be accompanied by the generation of some new small spirals, which will not affect the dynamical equilibrium of the system. As a result, the coexistence probability is large. This phenomenon is consistent with previous results from discrete-lattice models in the literature that small interaction scales ensure species coexistence. In fact, when the wavelength of spirals is small compared to the size of the spatial region, plane waves are unlikely to arise [36].

IV. ALTERNATIVE MODEL: SEPARATING REPRODUCTION FROM COMPETITION

We consider a more general scenario by separating competition and reproduction in the model in Section II. We aim to examine whether the non-monotonic behavior in the coexistent probability and the switchings of spatial patterns hold for this more realistic interaction. In this new model, three sub-populations interact with each other on a square cell of linear size L as follows:

$$\begin{array}{cc}\hfill & \mathit{AB}\to A\oslash ,A\oslash \to \mathit{AA},\hfill \\ \hfill & \mathit{BC}\to B\oslash ,B\oslash \to \mathit{BB},\hfill \\ \hfill & \mathit{CA}\to C\oslash ,C\oslash \to \mathit{CC},\hfill \end{array}$$ (5)

where ⊘ stands for empty site. As before, the competition and reproduction occur only in a circular region of radius r. At each simulation step, a randomly selected individual i kills one individual j from next species. At the same time, i leaves its offspring at a random location within the interaction range. Initially, the cell is randomly occupied by three species whose densities are approximately identical. The main difference between this model and the model (1) lies in the locations of the offsprings. Specifically, in model (1), the offspring of an individual replaces another individual from the next species in the cycle; whereas in the model (6), the place of birth is random.

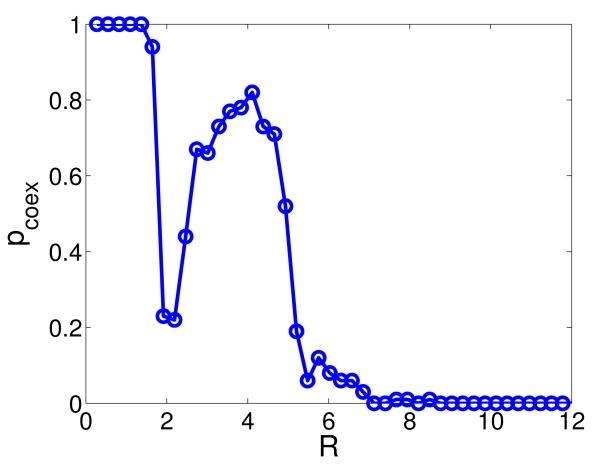
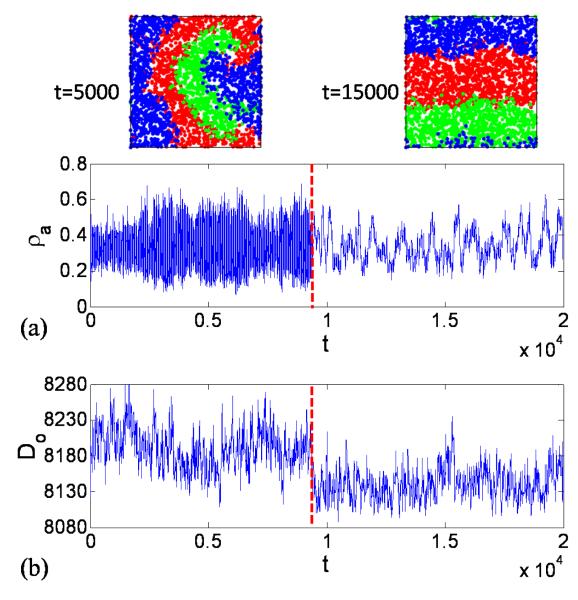
Stochastic simulations are carried out for different values of the interaction radius R, as shown in Fig. 9. The coexistence probability p_coex exhibits a non-monotonic behavior with respect to R with a peak at about R = 4, analogous to the result from model (1). This implies that the non-monotonic dependence of species coexistence on interaction range is an intrinsic feature of cyclic competition dynamics on continuous space, regardless of the place of the birth of descendants. Spatial patterns and time series of the species densities are displayed in Fig. 10(a). We observe switchings between spiral and plane waves, where the time series of the former exhibit fluctuations with higher frequency than the latter.

FIG. 9.

(Color online.) Coexistence probability p_coex as a function of normalized interaction radius R in model (6) in the absence of individual mobility. Other parameters are the same as in Fig. 1.

FIG. 10.

(Color online.) For model (6) with N = 3000 and L = 1, (a) spatial patterns and the corresponding time series of species density ρ_a and (b) time series of the overlapping distance D_o in the interaction range.

Since the birth locations of offsprings are random, we study the spatial distribution of species associated with two types of wave patterns. Since the resources within the square cell are limited and fixed, the spatial distribution of species indicates resources utilization. For example, if individuals are uniformly distributed on the space, resources are fully used and the competitions among species are relatively mild. In contrast, if species disperse inhomogeneously on the space, some areas with high species densities are faced with severe competition due to the shortage of resources. To characterize the resource utilization, we investigate the overlap in the interaction ranges among individuals, which can be simply measured by the distance among individuals. To be concrete, we define the overlapping distance between individuals i and j as

$$D_{\mathit{ij}}=\{\begin{array}{cc}2r-d_{\mathit{ij}},\hfill & \text{if}{d}_{\mathit{ij}}<2r\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (6)

where d_ij is the distance between i and j. Then the total overlapping distance is

$$D_o=\sum _{i,j=1,i\ne j}^N{D}_{\mathit{ij}}.$$ (7)

The lower the value of D_o, the more the resources are utilized. The time series of D_o corresponding to p_coex for spiral waves and plane waves are shown in Fig 10(b). We find that plane waves tend to benefit more from the utilization of resources that spiral waves. This is due to the fact that the boundaries among species associated with plane waves are shorter than those with spiral waves. Since competition and reproduction occur near the boundaries among different species, the spiral waves with longer boundaries can induce more spatial heterogeneity caused by reproduction at random locations.

V. CONCLUSION

In conclusion, we have generalized cyclic-competition dynamics to continuous space and addressed a key issue: the interplay between interaction range and species mobility and its role in coexistence. Model predictions in both the small and large limits of the interaction range are consistent with those from the E.coli experiments. In the intermediate interaction range, our study predicts a non-monotonic behavior in the coexistence probability, which is independent of the size of the square cell, the populations size and the relationship between competition and reproduction. Near the local minimum of the probability, a transition between spiral and plane wave patterns arises, where coexistence can be greatly enhanced through a proper choice of the mobility. When the reproduction process is separated from the competition, the plane waves of species organization benefits more from the utilization of resources than the spiral waves. We have derived a general PDE model with results that agree with those from direct stochastic simulations of the competition dynamics. Our work provides a more comprehensive and physical understanding of the dynamics of cyclically competing populations with respect to the fundamental issue of coexistence.