Artifacts in polarization sensitive OCT caused by polarization mode dispersion

Abstract

Polarization Mode Dispersion (PMD) severely degrades images of biological tissue measured with polarization sensitive Optical Coherence Tomography (PS-OCT). It adds a bias to the local retardation value that can be spatially confined, resulting in regions of seemingly high sample birefringence that are purely artificial. Here, we demonstrate and analyze this effect, both experimentally and with numerical simulations, and show that artifacts can be avoided by limiting the system PMD to less than the system axial resolution. Even then, spatial averaging over a dimension larger than that characteristic of speckle is required to remove a PMD-induced bias of the local retardation values.

Polarization sensitivity (PS) can significantly enhance the utility of Optical Coherence Tomography (OCT) by complementing the structural intensity signal with additional information on the birefringence properties of tissue [1,2]. Despite the development of fiber-based PS-OCT [3], the clinical utility of PS-OCT through fiber-probes has been limited.

One challenge for fiber-based PS-OCT is Polarization Mode Dispersion (PMD). It has been previously demonstrated that in most practical scenarios PMD, and not signal to noise ratio (SNR), dominates polarimetry noise, i.e., creates a randomization of the measured polarization states [4]. In the present study, we processed the detected polarization states to derive the local retardation using the Stokes formalism [5]. We found that PMD results in a spatially varying bias of retardation values that can mislead the interpretation of sample birefringence.

As light propagates along a single mode fiber, its polarization state is likely to change due to small amounts of stress-induced birefringence. PMD describes the variation of this polarization change as a function of wavelength and is manifested by the temporal splitting of the principal polarization states of a signal pulse, i.e., differential group delay (DGD) [6]. In OCT this corresponds to an axial shift of the point spread function (PSF) between two principal input polarization states. A general input state is a superposition of these two and results in a degraded PSF. DGD quantifies the magnitude of the temporal (axial) splitting, scales with the square root of the fiber length with typical values of 100fs·km^−1/2, and is very sensitive to fiber motion. A more substantial contribution originates from optical circulators, which provide a sensitivity advantage that can be critical for clinical OCT [7], but which can add more than 50fs of DGD for each port combination. Conventional models of PS-OCT, however, neglect PMD effects.

As illustrated in Fig. 1, pronounced discrepancies are commonly found when comparing birefringence maps obtained with different amounts of system PMD. The data of Fig. 1 were obtained using a fiber-based, frequency-domain system at 1300nm, similar to the one described in [4], in which PMD was altered by replacing the fiber circulator in the sample arm with a 50/50 fiber coupler. The presence of system PMD not only added unbiased noise to the reconstructed birefringence maps, but also introduced regions of seemingly high sample birefringence that were absent in the control images. The local retardation of the intimal layer in image 1(c) suggests an elevated concentration of collagen [8], whereas the control image 1(f) points to the opposite finding and reveals the artificial nature of the birefringence observed in the presence of PMD.

Fig. 1.

Intensity (a, d), local retardation (b, e) and enlarged views (c, f) of a cadaveric human coronary artery, measured with the circulator, (a)-(c), and the fiber coupler, (d)-(f). (g) Local retardation in [deg/μm] averaged in depth over the first 150μm of the intima along β indicated in (b) and (e).

To elucidate the origin of PMD artifacts, we write one of the two complex conjugate terms of the recorded signal as function of the wavenumber k:

$${\mathbf{f}}^q\left(k\right)=\alpha \left(k\right)\cdot {\mathbf{J}}_B\left(k\right)\cdot {\mathbf{J}}_S\left(k\right)\cdot {\mathbf{J}}_A\left(k\right)\cdot {\mathbf{e}}_{in}^q.$$ (1)

Bold capitals are matrices and bold lower case designates vectors. J_A and J_B are the system Jones matrices from the source to the sample, and from the sample to the receiver, respectively. Their k-dependence is specified by the PMD of these elements. J_S is the sample Jones matrix, α(k) is the source power spectrum, and e^q_in=[e_x, e_y]^T= e_xe_x+e_ye_y is the q-th input polarization state. According to the modulation scheme with processing in the Stokes domain, e¹_in=[1, 0]^T and e²_in=2^−1/2[1, i]^T, alternating between adjacent A-lines. Assuming only birefringence (without diattenuation) and polarization independent scattering, the sample matrix can be modeled as

$${\mathbf{J}}_S\left(k\right)={\int }_{z=0}^{\infty }\chi \left(z\right){\left[\left[e^{i2k{n}_{o}z},0\right],\left[0,e^{i2k{n}_{e}z}\right]\right]}^{T}dz,$$ (2)

where χ(z) is the scalar, axial scattering profile in a medium with ordinary and extraordinary refractive indices n_o and n_e, respectively. The depth variable z was set to zero on the sample surface, and the integral takes into account the double path through the medium. Any unitary transformation aligning the laboratory frame with the principal axes of the sample has been absorbed into J_A and J_B. To reconstruct the tomogram, the Fourier transform of Eq. (1) is taken, where transformed variables are designated in italic:

$${\mathit{t}}^q\left(z\right)=\int {\mathbf{f}}^q\left(k\right)e^{-i2kz}dk=\alpha \left(z\right)\ast {\mathit{J}}_B\left(z\right)\ast {\mathit{J}}_S\left(z\right)\ast {\mathit{J}}_A\left(z\right)\cdot {\mathbf{e}}_{in}^q.$$ (3)

This reveals the detrimental effect of the wavenumber dependence of J_A(k) and J_B(k). The sample signal J_S(z) is convolved—denoted by a star—with the PSF α(z), and linear combinations of the elements of J_A(z) and J_B(z). Only in the absence of PMD, J_A and J_B reduce to constant unitary transformations that are directly multiplied with J_S(z), yielding the usually assumed expression in PS-OCT. In the presence of sufficient PMD, the convolution distorts the sample signal and can explain the observed artifacts.

Next, the retrieved Jones vectors are expressed in the Stokes formalism: s_n(z)=Tr{σ_n·t·t^†}, n=[1,2,3]; the dagger denotes the conjugate transpose, and σ_n is the Pauli basis. Then, the Stokes vectors are filtered with a smoothing kernel of width w_X and height w_Z in order to reduce speckle and limit the impact of low-signal regions that are dominated by large polarimetry noise. The local retardation is finally retrieved by comparing the filtered and normalized Stokes vectors at depths offset by dz to find the local retardation matrix R(z):

$${\mathbf{s}}^q(z+dz∕2)=\mathbf{R}\left(z\right)\cdot {\mathbf{s}}^q(z-dz∕2).$$ (4)

With two measured polarization states, equation (4) is in principle underdetermined, but assuming that R(z) is a pure rotation, characterized by a rotation axis r and a rotation angle φ, it can be found with geometric reasoning [5]. Local retardation is expressed as φ/dz.

In order to further investigate PMD artifacts, a phantom (rubber cut from a fiber dust cap and strained by stretching) was measured with a bench-top scanner. The sample provided a homogenous backscattering signal with stress-induced birefringence. The retrieved local retardation, displayed in Fig. 2, exhibited a periodic variation when measured with the circulator. Moving the sample fiber could change the amplitude and position of the observed fringes. Replacing the circulator with the coupler produced a far more homogenous local retardation and removed the sensitivity to fiber movement.

Fig. 2.

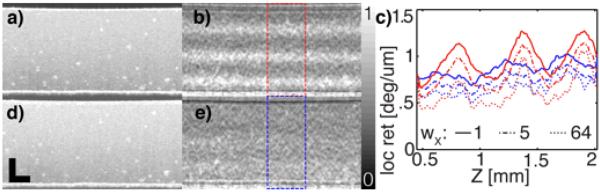
Intensity (a, d) and local retardation (b, e) of the rubber phantom, post-averaged over 20 adjacent B-scans (circulator (a, b), and fiber coupler (d, e)). Scale bars: 500μm. (c) Average profiles over 20 B-scans and the ROI in (b) and (e) for various w_X.

Fig. 2(c) displays averaged retardation profiles for different filtering parameters. For both, the coronary imaging and the rubber phantom, we set w_Z=dz=8*Δz. w_X was set to 12Δx for the coronary images and 5Δx for Figs. 2(b) and (e). A Gaussian kernel was applied before circularizing the data for the coronary imaging, whereas a square kernel was used for the rubber phantom. Δz=6.7μm was the axial sampling distance (in air), and Δx=1mrad or Δx=10μm were the angular and lateral sampling steps for the circumferential and bench-top scanning, respectively. f_Z=13μm and f_X=30μm were the axial and lateral FWHM of the intensity PSF for both configurations. For the coronary tissue, the depth axis z was corrected assuming a refractive index of n=1.33. No correction was applied for the rubber sample.

Fig. 2(c) demonstrates that increased averaging of the Stokes vectors removes a significant local retardation bias, while the peaks of the PMD-induced local retardation values prove resistant to averaging. The accumulated birefringence of the sample to a given depth contributes to the effective PMD and makes it depth dependent. The chain rule of PMD [6] states, that

$$\tau ={\tau }_B+{\mathbf{M}}_B\cdot {\tau }_S+{\mathbf{M}}_B\cdot {\mathbf{M}}_S\cdot {\tau }_A,$$ (5)

where τ is the PMD vector in the Stokes domain, and M_B and M_S are the Stokes operators and τ_B, τ_S, τ_A the PMD vectors corresponding to J_B, J_S and J_A, respectively. M_S rotates the PMD vector of the system input side around its optic axis and creates a variation of the norm of the system PMD, τ_PMD(z)=|τ|(z). The amplitude of this modulation depends on the precise orientation of the different contributions, but the periodicity is defined through the sample birefringence by 2πdz/φ. Although τ_PMD(z) is not accessible in the experiment, the results suggest that averaging helps to converge towards the true local retardation value if τ_PMD(z) is below a critical value. For higher PMD, the retrieved local retardation is resistant to averaging and results in artificial values.

In the attempt to quantify the amount of system PMD, an attenuated mirror reflection was used to obtain a measure of J_sys(k)= J_B(k)·J_A(k). Expressing the complex valued f^q(k) in the Stokes domain, the optic axis r and the angle of rotation φ of the overall optical system could be retrieved independently for each wavenumber. The PMD vector is given by τ = r ∂φ/∂ω + φ ∂r/∂ω where ω=ck and c is the speed of light. The derivatives were evaluated at the central wavenumber after vectorial unwrapping of φr. During the measurement, the sample fiber was gently moved to obtain ensemble measurements (by changing the relative orientation of τ_A and τ_B). A mean value of 85fs and 5.6fs, respectively, for the two system configurations was found. For comparison, the axial resolution expressed as a time delay was τ_C=2f_Z/c=87fs.

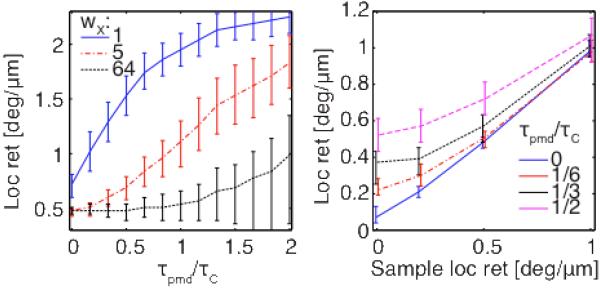
To assess the impact of system PMD in more detail and examine the effect of various reconstruction parameters, we performed numerical simulations. The sample was modeled according to equation (2) as individual point scatterers, spaced on a sub-resolution scale, and producing fully developed speckle. The birefringence was adjusted to result in local retardation ranging from 0 to 1deg/μm. The system matrices J_A and J_B were each constructed in a manner similar to [9] by multiplying 50 linear birefringent elements with random orientation and calibrated birefringence—linearly dependent on the wavenumber—to obtain a specified ensemble PMD value. For each nominal amount of PMD, 25 independent realizations were taken to compute 64 independent A-lines for each setting of the sample birefringence. Noise corresponding to an SNR of 30dB was added and the local retardation was reconstructed for a wide range of parameters: w_X, w_Z and dz. Unlike in the experiment, τ_PMD(z) can be computed for the simulation. 2D histograms of τ>_PMD(z) versus local retardation averaged over the 64 A-lines were populated by the various PMD realizations to get the expectation values for local retardation. Fig. 3(a) reports these values as function of τ_PMD(z). Importantly, the local retardation error depends on the ratio of τ_PMD to the system temporal resolution τ_C: PMD deteriorates local retardation irremediably, even for significant averaging, if the DGD it induces exceeds the axial width of the PSF. For smaller levels of system PMD, spatial averaging over a dimension several times larger than characteristic speckle is required to remove a local retardation bias. As seen in panel 3(b), this bias is most significant for low sample birefringence. The experimental setting corresponded to τ_PMD/τ_C of 1 and 0.07, with the fiber circulator and the fiber coupler, respectively.

Fig. 3.

(a) Local retardation expectation and 20% and 80% quantiles indicated by error-bars (dz=47μm, w_Z=1, φ/dz=0.5deg/μm). (b) Local retardation expectation versus sample birefringence (w_X = 5, otherwise identical to (a)).

Averaging is equally beneficial along the axial and the lateral direction. Whereas the simulated A-lines feature independent speckle realizations, the kernel width has to be normalized by the speckle in the experimental case and along the axial direction in both settings. Averaging over a dimension N-times the characteristic speckle size reduces the bias by 1/sqrt(N) in the absence of sample birefringence. Likewise, the error scales with 1/dz.

Both dz and w_Z limit the axial resolution of the local retardation in a similar manner, thus both can be maximized within an acceptable trade-off with axial resolution. As this usually only allows for very moderate averaging, lateral averaging is still needed to obtain an accurate measure of sample birefringence, even if the system only features moderate amounts of PMD.

Post-averaging the retrieved retardation reduces the standard deviation and provides a smoothed local retardation profile, but does not remove the retardation bias. Interestingly, averaging before retrieving the retardation is naturally possible for processing in the Stokes domain, but it has no equivalence in the Jones formalism. Several indirect averaging mechanisms in the Jones formalism were evaluated by Gotzinger et al. [10].

Most biological tissue feature relatively low birefringence, and sample-induced PMD is usually negligible compared to system PMD—at least for fiber-based catheter systems that use several meters of single mode fiber, possibly in combination with circulators. The interaction of the system PMD with the sample birefringence, however, results in a depth-dependent PMD that can create locally confined retardation offsets. Aligning the input fiber to avoid PMD is not possible, because the two input polarization states are orthogonal in the Stokes domain. Further, the rotation of the catheter creates a variation of the system PMD, and makes a simple calibration impossible. Using a set of three calibration signals, we have recently shown that it is possible to independently characterize J_A and J_B, correct for the system PMD, and thereby eliminate all resulting artifacts [11].

In summary, we have shown that system PMD results in localized artificial retardation values and adds a systemic bias to the measured local retardation. Averaging over several speckle realizations mitigates these artifacts, which can be achieved efficiently in the Stokes domain. Yet, even extensive averaging can retrieve the underlying local retardation only if system PMD is limited to less than the system axial resolution.