Cardiac motion compensation and resolution modeling in simultaneous PET-MR: a cardiac lesion detection study

Abstract

Cardiac motion and Partial Volume Effects (PVE) are two of the main causes of image degradation in cardiac PET. Motion generates artifacts and blurring while PVE lead to erroneous myocardial activity measurements. Newly available simultaneous PET-MR scanners offer new possibilities in cardiac imaging as MRI can assess wall contractility while collecting PET perfusion data. In this perspective, we develop a list-mode iterative reconstruction framework incorporating both tagged-MR derived non-rigid myocardial wall motion and position dependent detector Point Spread Function (PSF) directly into the PET system matrix. In this manner, our algorithm performs both motion “deblurring” and PSF deconvolution while reconstructing images with all available PET counts. The proposed methods are evaluated in a beating non-rigid cardiac phantom whose hot myocardial compartment contains small transmural and non-transmural cold defects. In order to accelerate imaging time, we investigate collecting full and half k-space tagged MR data to obtain tagged volumes that are registered using non-rigid B-spline registration to yield wall motion information. Our experimental results show that tagged-MR based motion correction yielded an improvement in defect/myocardium contrast recovery of 34-206% as compared to motion uncorrected studies. Likewise, lesion detectability improved by respectively 115-136% and 62-235% with MR-based motion compensation as compared to gating and no motion correction and made it possible to distinguish non-transmural from transmural defects, which has clinical significance given inherent limitations of current single modality imaging in identifying the amount of residual ischemia. The incorporation of PSF modeling within the framework of MR-based motion compensation significantly improved defect/myocardium contrast recovery (5.1-8.5%, p<0.01) and defect detectability (39-56%, p<0.01). No statistical difference was found in PET contrast and lesion detectability based on motion fields obtained with half and full k-space tagged data.

1. Introduction

PET myocardial perfusion imaging is considered as the gold standard for detection and evaluation of Coronary Artery Diseases (CAD). The magnitude and extent of ischemia, rather than stenosis severity, is the best predictor of which CAD patients are most likely to benefit from revascularization procedures (Hachamovitch et al 2003, Tonino et al 2009). However, detection and assessment of small peri-infarct myocardial regions is hampered by motion blurring and partial volume effects (PVE), in particular in the case of non-transmural infarcts.

Heart motion, caused by both the pumping action of the heart (cardiac motion) and breathing (respiratory motion), is the most important cause of image resolution degradation in cardiac PET imaging. Although the intrinsic spatial resolution of modern whole-body PET scanners is in the range of 4-5mm, the displacements of 13-23 mm (O’Dell et al 1995, Slomka et al 2004) and 4.9-9 mm (Boucher et al 2004, Blume et al 2010) due to cardiac and respiratory motion, respectively, result in more than 10mm (FWHM) effective spatial resolution (Daou 2008). Additionally, the mismatch between emission and attenuation data due to heart motion can cause severe artifacts in cardiac PET as the attenuation characteristics of the lungs may be projected onto the myocardial wall, yielding false-positive ischemia (Ter-Pogossian et al 1982). Cardiac (Hickey et al 2004, Yang et al 2005), respiratory (Dawood et al 2007, Vines et al 2007) or even dual (i.e. both respiratory and cardiac) gating techniques (Büther et al 2009, Teräs et al 2010) have been explored in static PET because they alleviate motion blurring while being a tool for clinicians to assess ventricular function. However, because each gate is reconstructed using typically 1/8^th - and even 1/64^th for dual gating- of the PET events, motion effects are removed in the gates at the expenses of the Signal to Noise Ratio (SNR). Also, gating is not effective in dynamic cardiac imaging of rapid dynamic functions, such as myocardial blood flow, due to the substantial noise associated with rejecting a large number of detected events in low counts dynamic frames.

In order to overcome the SNR limitations associated with cardiac gating, methods taking advantage of organ motion have been proposed. The motion fields can be used into two different ways: the most straightforward approach consists in “registering/un-warping” reconstructed PET gates back to a reference frame and sum the resulting motion-corrected volumes; the whole process is done post-reconstruction (Klein and Huesman 2002, Slomka et al 2004, Dawood et al 2008, Gigengack et al 2012); the second, more accurate and yielding higher quality images as it preserves Poisson statistics, proposes embedding the motion information into the iterative reconstruction process via the PET system matrix (Rahmim et al 2004, Qiao et al 2006, Li et al 2006, Lamare et al 2007). To capture respiratory or cardiac organ motion, investigators proposed to use 4D gated CT scans performed sequentially with the PET exam (Qiao et al 2006, Lamare et al 2007), reconstructed PET gates directly (Slomka et al 2004, Gigengack et al 2012 for cardiac and Dawood et al 2008 for respiration) or MRI (Guerin et al 2011, King et al 2011, Chun et al 2012 for respiration). However, unlike motion of the heart caused by breathing (which can be approximated as rigid motion at the PET resolution (Segars et al 2007)) motion caused by the beating heart is complex and non-rigid, involving torsional and within-wall motion components such as shearing or radial thickening. Accurate measurement of these motion components with conventional tomographic imaging (such as CT, MR or PET) is challenging as the myocardium appears uniform, so that the intramural motion distribution often has to be inferred from epi- and endocardial boundaries. In addition, cardiac PET gates are limited by poor intrinsic spatial resolution and noise yielding lower resolution motion information, while the use of sequential 4D gated CT for the sole purpose of measuring motion remains impractical, due to obvious patient radiation exposure concerns and lack of simultaneity between PET and CT modalities in PET/CT scanners.

Once motion is compensated, the spatially varying and limited detector Point Spread Function (PSF) becomes an important factor that deteriorates SNR and introduces a systematic underestimation bias in measured myocardial radiotracer uptake given the small thickness of the myocardial wall (typically 10 mm) as compared to the scanner resolution. Limited resolution is also the cause of important signal cross-contamination between the cardiac chamber, regions with perfusion defect and normal myocardial tissue that prevents from accurate quantitation of local radiotracer uptake (Iida et al 1991). Iterative reconstruction approaches can enhance image resolution and reduce PVE by establishing an accurate relationship between projection and image spaces through the modeling of scanner’s PSF in the PET system matrix. PSF modeling can be performed in projection (Panin et al 2006, Alessio et al 2006) or image domains (Reader et al 2003, Sureau et al 2008, Cloquet et al 2010), both approaches require obtaining an accurate model of the scanner’s PSF. This can be achieved with multiple point sources measurements, eventually using a sophisticated robot (Panin et al 2006), manually (Cloquet et al 2010) or with Monte-Carlo simulations (Alessio et al 2006).

There has been recently a very active effort by all major imaging manufacturers towards building simultaneous PET-MR scanners and such scanners are now available and offer promising possibilities in cardiac PET imaging. On the one hand, cardiac MR offers the most accurate approach to detecting the presence and assessing the extent of myocardial scar using the late gadolinium contrast enhancement (LGE) MRI. Moreover, MRI allows measuring organs’ displacements with high temporal and spatial resolution. On the other hand, PET allows quantifying extent and severity of ischemia but is less sensitive for detection of non-transmural scars because of its limited spatial resolution resulting from both motion and PVE as discussed above. When PET and MR data are acquired simultaneously, in contrast to sequential PET-CT, the information measured with one modality (e.g., organ motion measured with MRI) can improve information content of the other modality (e.g., correct PET for motion), and we have recently demonstrated substantial improvement in image quality and lesion detectability in the lower-abdomen (Guerin et al 2011, Chun et al 2012).

In this work, we propose and evaluate a novel dedicated simultaneous cardiac PET-MR acquisition and reconstruction framework tackling both issues of non-rigid cardiac motion and limited PSF of the scanner. We obtain accurate non-rigid wall motion by measuring complex intramural motion using MR tagging (Axel and Dougherty 1989) and incorporate the computed wall motion field directly into the system matrix of a list-mode PET OSEM reconstruction with no additional radiation dose to the patient. In contrast to the conventional static attenuation map, the incorporation of the motion field within the PET reconstruction enables the use of a “time-dependent” attenuation map that is deformed by the motion field and is consistent with the emission distribution throughout the entire acquisition. In addition to the motion field, we incorporated into the PET system matrix a position-dependent PSF model of the scanner. We use image-based rather than projection-based PSF modeling as it is the only practical option compatible with list-mode reconstruction, so that cardiac dynamic studies with low statistics may also benefit from our approach. To make the MR acquisition time compatible with the clinical setting, we explore partially sampled k-space data acquisition strategies and demonstrate similar performance to fully sampled k-space data. We validate our methods in a realistic cardiac beating PET-MR phantom with both transmural and non-transmural cold myocardial defects. We use a channelized Hotelling Observer (CHO) to evaluate the detectability of myocardial defects in the motion-corrected images as compared to usual reconstruction methods such as cardiac gating or no motion correction.

2. Materials and methods

2.1. Data acquisition

2.1.1. Simultaneous PET-MR scanner

All acquisitions were performed on a Siemens PET-MRI prototype scanner installed in the Department of Radiology (Athinoula A. Martinos Center for Biomedical Imaging) at our institution. This system is composed of an MR compatible PET scanner module (BrainPET) inserted into a Siemens 3T Magnetom Tim Trio, allowing simultaneous acquisition of PET list-mode and MR data. The PET system, which operates in a fully 3-D mode, uses 27648 2.5×2.5×20 mm³ LYSO crystals in 32 detector modules. It has a 32-cm axial and 19.25-cm transaxial field of view (FOV). Time-synchronization between acquired PET and MR data was achieved by placing trigger events in both MR and PET data streams.

2.1.2. Cardiac beating phantom

To assess the performance of our motion correction approach, we built a realistic cardiac beating phantom. As depicted in figure 1, we created a myocardial compartment by interleaving two inflatable balloons and filling the in-between space with radioactive gel. The two balloons were suspended into a hot methyl-cellulose background enclosed in a cylindrical container. The activity concentration ratio of myocardium to background was of 3:1. Three different inserts of cold gel (A. B and C) of various size and volume (V_A = 1.7 mL, V_B = 0.95 mL and V_C = 1.0 mL) were placed at different locations in the myocardial compartment to mimic myocardial defects. Defects A, B, and C occupied respectively 100% (mimics transmural defect), 50%, and 30% of the myocardium wall. The MR signal in the three defects was enhanced using gadolinium, to mimic an LGE study. The inner-most balloon chamber (equivalent to a left-ventricle, LV) was connected to a ventilator that inflated and deflated the phantom at a rate of 65 times per minute. The pressure in the LV was tracked by a sensor whose output signal was amplified and thresholded to create a trigger pulse at the beginning of each cardiac cycle to mimic an R-wave induced EKG trigger. This pulse was encoded and sent to the list-mode stream allowing retrospective binning of PET events into their corresponding cardiac phases. The same signal was sent to the MR scanner to trigger the tagged MRI acquisition detailed in the next section. PET and MR data were acquired simultaneously and processed offline.

Figure 1.

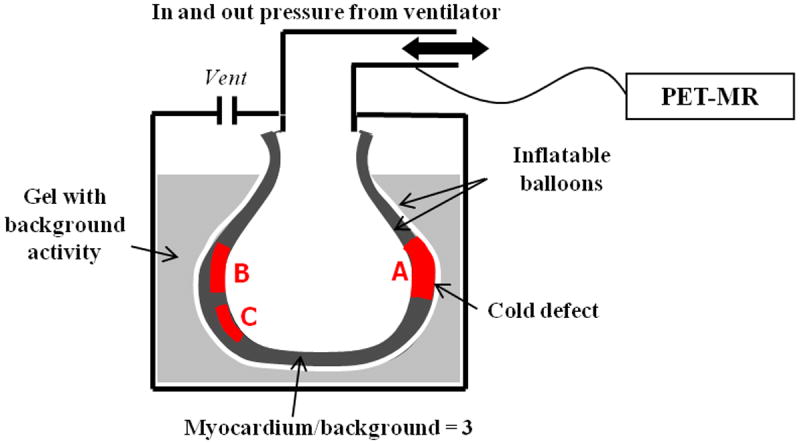
Schematics of cardiac phantom with ~1cm thick myocardial compartment filled with hot ¹⁸F gel. One transmural (A) and two non-transmural (B, C) cold Gd enhanced defects were added to the myocardium. The beating rate was of 65 beats/min.

2.2. MR tagging

In this work, we used tagged MR data acquired simultaneously with PET list-mode to measure the heart motion field. In tagged MR, a special sequence of Radiofrequency (RF) pulses and gradient is played in order to spatially encode the magnetization. This modulation causes a series of parallel stripes (or tags) that persist in the myocardial muscle within the limits of the relaxation times. During the myocardium contraction, the tag lines deform due to the motion of the underlying tissue. Therefore, tagging followed by acquisition of a temporal sequence of MR images reveal the motion that has occurred in the medium since the tagging instant. The intensity contrast created between saturated and unsaturated regions allows assessing the motion even when the tissue is homogeneous, as is the case of myocardium.

The tagging sequence used in this work is 1-1 SPAMM (SPAtial Modulation of Magnetization (Axel and Dougherty 1989)). The SPAMM tags follow a sinusoidal spatial distribution of wave vector k = γGT along the direction of tagging gradient G which allows to measure the motion in that particular direction. The motion in all three directions of space is therefore measured by acquiring the whole heart volume with 3 orthogonal tagging directions, which leads to time-consuming acquisitions. However, due to the specific spectral properties of the tagged medium, one possible approach to reduce scan times is acquiring partially sampled rather than fully sampled k-space (McVeigh and Atalar 1992, Fischer et al 1993). In figure 2(a), a k-space image of the cardiac phantom tagged perpendicularly to the read-out axis is shown in order to illustrate this point. The SPAMM peaks (result of the Fourier transform of the tags sinusoidal spatial modulation) are located in k-space near k_x = 0, distorting their shapes along the tagging direction as the tags deform through the cardiac cycle. As a result, only a small portion of the total number of k-lines actually contains the useful motion information and hence significant MR acquisition time can be saved by skipping these k-lines in the acquisition. In this work, both full and half k-space of tagged MR data was acquired yielding to a 50% decrease in acquisition time. As illustrated qualitatively by figure 2(b) and (c), images obtained using full or half k-space depict identical tag lines deformation due to motion.

Figure 2.

Tagged MR k-space data of the cardiac phantom (a) and corresponding images reconstructed using fully sampled (b) and 50% of the k-space (c). The dotted lines in (a) represent the portion of the k-space corresponding to image (c). The SPAMM peaks are located along the read-out axis so that the motion information spreads along that direction.

In our acquisitions, tagging was synchronized with the beating motion cycle by our “R-wave” trigger and applied at the beginning of each cardiac cycle. A multi-slice/multi-phase Gradient Recalled Echo (GRE) MRI acquisition of 9 volumes, one for each cardiac phase, followed tagging to reveal the motion throughout the cycle. The parameters of the GRE sequence were TE=2.41 ms, TR = 100 ms, FA = 25° (flip angle), tagging distance = 8 mm as described in (Axel and Dougherty 1989) with in-plane resolution of 1×1mm and slice-thickness 8 mm. The three motion components along x, y and z axes were all measured in-plane (i.e. with high resolution) by acquiring each tagging direction using different slices orientation.

2.3. Motion estimation

Several techniques were presented in the past to estimate motion using tagged MR volumes, such as the HARmonic Phase (HARP) (Osman and Prince 2004). However, the main drawback of phase tracking methods is that one needs to isolate the spectral peaks corresponding to the tags from the rest of the k-space data (Figure 2.a)). Innovative filtering schemes have been proposed for that purpose, but the DC component may still interfere in the process (Ledesma-Carbayo et al 2008). In this work, we estimate the motion fields using B-spline non-rigid registration of tagged magnitude MR volumes (Ledesma-Carbayo et al 2008, Chun et al 2012). Since the B-spline registration acts directly on magnitude images, this intensity-based approach avoids the aforementioned limitations of phase tracking methods, and has the advantage of remaining fully automatic and fast (Ledesma-Carbayo et al 2008, Chun et al 2010). The registration algorithm estimates a spatial mapping between points coordinates of two tagged volumes -a target f_tar and a source image volume f_src - through the estimation of a non-rigid B-spline warping operator T̂ such that:

$$\widehat{T}={\mathrm{arg\; min}}_T\left[{\mathrm{\Psi }}_{\mathit{SSD}}\left({\mathbf{f}}_{\mathit{tar}},T{\mathbf{f}}_{\mathit{src}}\right)+\eta R(T)\right]$$ (1)

where Ψ_SSD is a dissimilarity measure (sum of squared differences -SSD) η is a regularization parameter, and R(T) is a regularizer. The regularization term penalizes the differences between adjacent B-spline coefficients and renders the motion fields smooth and invertible and hence more realistic (Chun and Fessler 2009). A regular spacing of 4 pixels was used to place B-spline knots in the source image. A bi-level multi-resolution strategy was used to increase the robustness and speed of the registration algorithm (Ledesma-Carbayo et al 2008). A first estimate of the motion field is computed on a coarse, sub-sampled image volume and serves as an initial guess for solving the task at the original, finer level, so that the solution is approached by gradual refinements. To estimate the motion in all 3 directions of space, 9 MR volumes corresponding to 9 cardiac phases were obtained by combining (summing) three MR volumes tagged in orthogonal directions for each cardiac phase. Temporally adjacent volumes were successively registered using the proposed algorithm. B-spline interpolation was used for motion fields’ composition in order to estimate the motion between each frame and the reference frame at end-diastole (ED). These motion fields were calculated using both fully and partially sampled k-space data and incorporated into the PET reconstruction as detailed below.

2.4. Image reconstruction

Simultaneous PET-MR scanners allow accurate alignment of PET and MR data in both spatial and temporal domains. This enables accurate motion correction of PET data using simultaneously acquired tagged MR. In this perspective, we have developed a list-mode PET reconstruction strategy in which all detected PET coincidences are reconstructed to a single reference motion frame at end-diastole (ED). This maximizes SNR while removing cardiac motion blurring. We also incorporate PSF modeling in the PET system matrix to minimize PVE while reducing noise propagation in the reconstruction process. The PSF modeling accounts for finite resolution effects such as photon non-collinearity, parallax errors and intrinsic detector resolution (Reader et al 2003)). To the best of our knowledge, this is the first attempt to incorporate both non-rigid motion correction and PSF modeling within a single PET iterative reconstruction framework.

Given N LORs measured in M cardiac motion frames, the log-likelihood function is:

$$L=\sum _{n=1}^N\log \left[\sum _{i=1}^I{\stackrel{\sim }{p}}_{\mathit{ni}}(t_n)f_i+\overline{S}{c}_n(t_n)+{\overline{R}}_n(t_n)\right]-\sum _{i=1}^I{\stackrel{\sim }{s}}_i{f}_i$$ (2)

Where n is the LOR index, {f_i}_i=1…I are the activity voxel values in the reference frame that we want to estimate, t_n is the motion frame to which belongs event n amongst the M frames, p̃_ni (t_n) is the motion-dependent system matrix element at a given frame t_n which represents the probability of an emission occurring in voxel i at motion frame t_n being detected along LOR n, ${\left\{{\stackrel{\sim }{S}}_i\right\}}_{i=1\dots I}={\left\{\sum _{m=1}^M\mathrm{\Delta }{t}_m\sum _{k=1}^K{\stackrel{\sim }{p}}_{ki}(t_m)\right\}}_{i=1\dots I}$ is the sensitivity map with Δt_m the time duration of frame t_m, and S̅c_n (t_n) and R̅_n (t_n) are respectively the mean scatter and random counts estimated in LOR n and motion frame t_n.

The motion-dependent system matrix P̃(t_m), whose elements are {p̃_ni (t_m)}_{K × I}, is decomposed as:

$$\stackrel{\sim }{P}(t_m)=A(t_m)\mathit{SXBM}(t_m)$$ (3)

In this decomposition, M(t_m) is an I × I image-space 3D motion operator registering a given motion frame t_m to the reference frame computed using the motion fields provided by simultaneously acquired and registered tagged volumes. Note that the motion is estimated with sub-pixel accuracy (with respect to PET resolution), at the MR resolution, so that M(t_m) is in fact an interpolation operator (tri-linear interpolation in our implementation). Matrix B models the position-dependent PSF in the image domain, matrix X with dimensions K × I is the forward-projection operator implemented using Siddon’s method (Siddon 1985) and K × K diagonal matrices S and A(t_m) contain respectively LORs normalization factors and LORs motion-dependent attenuation correction factors. The deformed phantom attenuation map {μ(t_m)} was obtained by deforming the reference attenuation map {μ_ref} in ED frame into every motion frame t_m using operator M (t_m). In this work, we obtained {μ_ref} by acquiring a single gated GRE volume that was subsequently segmented into 2 tissue classes: air (μ = 0.00 cm⁻¹) and soft-tissue (μ = 0.096 cm⁻¹). The static attenuation maps of both the MR coil and patient bed were also used in the attenuation calculations. Our fully 3D list-mode PET reconstruction algorithm yields the following iterative equation:

$$f_i^{(\mathit{iter}+1)}=\frac{f_i^{(\mathit{iter})}}{{\stackrel{\sim }{s}}_i}\sum _{n=1}^N\frac{{\stackrel{\sim }{p}}_{\mathit{ni}}\left(t_n\right)}{\left[\sum _{j=1}^I{\stackrel{\sim }{p}}_{\mathit{nj}}\left(t_n\right)f_j^{(\mathit{iter})}\right]+\overline{S}{c}_n+{\overline{R}}_n}$$ (4)

Scatter fractions were computed using single scatter estimation method (Watson 2000) and scaled to the tails of the emission data outside the phantom. Random fractions were estimated using events collected in a delayed coincidence window smoothed by a Gaussian filter. In (4), we used the average scatter and random fractions rather than the motion-dependent ones as in (2), assuming that the changes of scatter and random distributions caused by the cardiac motion are negligible.

2.5. PSF modeling

PVE, caused by the limited PET spatial resolution, lead to underestimation of myocardium uptake and lower defect-myocardium contrast. PVE can be significantly reduced by modeling PSF of the scanner in either projection or image space. We chose to perform PSF modeling in the image domain because it is straightforward to implement the modeling in our list-mode reconstruction. The transaxial spatial resolution of the PET-MR scanner varies largely across the FOV mainly due to the lack of depth of interactions (DOI) measurements. Previous study shows that the radial spatial resolution changes from 2.5 mm FWHM at the center of the FOV to 4.5 mm FWHM at 10 cm off axis (Pichler et al 2010). To assess the resolution throughout the FOV and compute operator B in (3), we used 0.5mm F-18 point sources measurements in air (Sureau et al 2008, Cloquet et al 2010). For a given axial position, 4 point sources were simultaneously positioned at radial positions r=1.1, 2.9, 7.5 and 10.2 cm each with different azimuthal angles across the PET-MR scanner FOV. To do so, we placed a vertically oriented rigid cardboard base outside the PET FOV and positioned the point sources in the FOV by connecting them to the rigid base using long thin sticks of a material with negligible attenuation. We acquired ~2M of prompts coincidences list-mode for 2 different axial positions (z=0 and z=5 cm). The point-source data was reconstructed using 0.5×0.5×0.5 mm voxel, 10 iterations and 4 subsets. No resolution modeling was included into the reconstruction. The reconstructed point-source profiles were fitted with Gaussian functions to extract the width parameters (σ) along radial, tangent, and axial directions. These values were then used to obtain σ for any given point within the FOV by linear interpolation.

2.6. Assessment of image quality and myocardial defect detectability

2.6.1. Reconstruction methods

We acquired tagged MR volumes and 45 minutes PET list-mode data on the cardiac phantom using the PET-MR scanner. The PET list-mode events were binned into N_R = 15 3-minutes independent noise realizations and were reconstructed with the following five different methods:

1. N-MC (No Motion Correction): All the events in each noise realization were reconstructed regardless of cardiac motion.

2. G (Gating): Only the events detected at ED in each noise realization were reconstructed (i.e., the first and last frames of the 9 frames).

3. F-MC: Motion correction was applied to all the PET events in each noise realization using the motion fields derived from the full-k-space tagged MR volumes.

4. H-MC: Motion correction was applied to all the PET events in each noise realization using the motion fields derived from the half-k-space tagged MR volumes.

5. R (Reference): It is the same as G except all the events in the entire 45 minute acquisition were used. The reconstructed image volume was treated as the “noise-free” gold standard for our study.

All images were reconstructed on a 2-mm isotropic voxel grid using 7 iterations and 12 temporal subsets. If not otherwise specified, all reconstruction methods included PSF modeling. To preserve spatial resolution gain provided by PSF modeling, no post-filtering was applied to the reconstructed images. We performed assessment on both the defect/myocardium contrast recovery and defect detectability with the first four reconstruction methods described above (i.e., N-MC, G, F-MC, H-MC).

2.6.2. Defect/myocardium contrast recovery and noise level assessment

The defect/myocardium contrast recovery was calculated for all three defects and reconstruction method. For a given noise realization r, the defect/myocardium contrast c_r was computed as:

$$c_r=1-\frac{{\mathit{Def}}_r}{{\mathit{Myoc}}_r},$$

where Myoc_r and Def_r are the mean voxel intensities within myocardium and defect ROIs respectively. The mean defect/myocardium contrast recovery coefficient was then computed as:

$$C=\frac{1}{N_R}{\sum }_{r=1}^{N_R}{c}_r.$$ (5)

The image background statistical noise level was evaluated using the following metric (Tong et al 2010, Sureau et al 2008, Cloquet et al 2010):

$$\mathit{SN}=\frac{\sqrt{\frac{1}{N_R-1}{\sum }_{r=1}^{N_r}(m_r-\overline{m})}}{\overline{m}}$$ (6)

where $m_r=\frac{1}{I}\sum _{i\in \mathbf{b}}{b}_{i,r}$ is the mean voxel value within background ROI b for noise realization r and $\overline{m}=\frac{1}{N_R}{\sum }_{r=1}^{N_R}{m}_r$ is the average of background ROI means over the N_R available noise realizations.

2.6.3. Defect detectability study

We also evaluated the performances of the proposed reconstruction methods on a myocardial defects detection task in SKE-BKE (Signal-Known-Exactly Background-Known-Exactly). To avoid complicated human observer studies, we used a linear mathematical observer, the channelized Hotelling observer (CHO) which has been proven to be a good predictor of human observer performance in detecting lesions within images with highly correlated noise, as is the case for PET or SPECT (Gifford et al 2000). The CHO is a matched filter constructed with channels modeling the human visual system. A 5-channels radially symmetric Laguerre-Gauss was used as a template to approximate the Hotelling Observer (Park et al 2007). To assess the detection performance provided by a given reconstruction method, the CHO SNR can be used (Abbey and Barrett 2001, Kulkami et al 2007):

$${\mathit{SNR}}_{\mathit{CHO}}^2={\left(\langle {\mathbf{f}}_0\rangle -\langle {\mathbf{f}}_1\rangle \right)}^{T}U{\left(U^T\left(\frac{1}{2}\right)\left(K_{{\mathbf{f}}_0}+K_{{\mathbf{f}}_1}\right)U\right)}^{-1}{U}^T\left(\langle {\mathbf{f}}_0\rangle -\langle {\mathbf{f}}_1\rangle \right)$$ (7)

where U is the template, f_i is a vector containing N_R objects (slices) for hypothesis H_i, i ∈ {0;1} (H₀ “lesion-absent” and H₁ “lesion-present”), 〈•〉denotes the mean operator and the K_fi average image covariance matrix over all N_R noise realizations. For each of the 3 defects, planes centered either on the Gd enhanced defects or on the surrounding myocardial compartment were extracted from the reference ED non-tagged MR volume. Their geometrical characteristics (defect center coordinates, plane orientation) were used to extract, for each defect, reconstruction method and noise realization, a set of PET slices representing the cases when the defect is present (hypothesis H₀) or absent (hypothesis H₁) in the myocardium. The CHO SNR was computed using (7) on the obtained sets of slices. The statistical significance of differences obtained between the 4 reconstruction methods was assessed by calculating p-values using a permutation test.

3. Results and discussion

Figure 3 shows one of the MR slices acquired in both the ES and ED frames. Defects A (transmural) and B (non-transmural) can be clearly seen due to the signal enhancement by Gd. The in-plane displacement vectors shown on the ES image were obtained by non-rigid registration using (1). Deformation of the tag lines can be seen in the homogeneous regions, such as the background and the myocardium. A large displacement gradient was observed between “apical” and “lateral walls”. Since Gd. shortens tissue T1 recovery, the tagging grid pattern disappears faster in the defects than in other tissues, which may affect defect motion estimates in the latest frames (i.e. the furthest away from the tagging instant). However, this effect was neglected in the present study.

Figure 3.

MRI axial slices of the cardiac phantom for the reference ED untagged (a), tagged (b) and tagged ES (c) cardiac phases. In c), arrows represent the displacement from ES to ED. With MR tagging technique, motion fields can be accurately estimated across the entire phantom including the homogeneous regions, such as the background and the myocardium.

Figure 4 shows an axial slice of the phantom through the three defects. All the PET images were reconstructed for one of the noise realizations, which corresponds to 3 minutes acquisition. The motion “deblurring” achieved with our algorithm considerably reduced the spillover from the myocardium to the background and the defects. As a result, the motion corrected PET images have better defect/myocardium contrast, higher apical and lateral walls intensities and allow more accurate identification of the defects and myocardial wall boundaries than the motion uncorrected ones. Gating (G) method effectively froze the motion by using only 22% of the total counts, which caused the significantly increased image noise. In contrast, because F-MC and H-MC used all the PET data, they achieve similar noise levels as N-MC but with the motion blurring removed. The contrast of the “lateral” wall, which has the biggest motion, benefits the most from the motion correction method. By restoring the thin myocardial wall around defect B, motion-corrected images clearly highlighted this non-transmural defect that was almost invisible in lateral wall of the motion-uncorrected images.

Figure 4.

Reconstructed PET images of the cardiac phantom with gating, no motion correction (N-MC) and motion-corrected methods (F-MC and H-MC). MR-based motion correction removed motion blurring in the myocardium wall and the three defects without increasing the noise as compared to the gating method.

The advantages of motion correction can be further illustrated in figure 5 which shows the fused images of PET and untagged MR ED. These results demonstrate that our PET-MR based motion correction method makes it possible to distinguish non-transmural from transmural defects. This has high clinical significance because current single-modality imaging technique, such as PET, MR, or SPECT, has inherent limitations in identifying the amount of residual ischemia, i.e. non-transmural defects.

Figure 5.

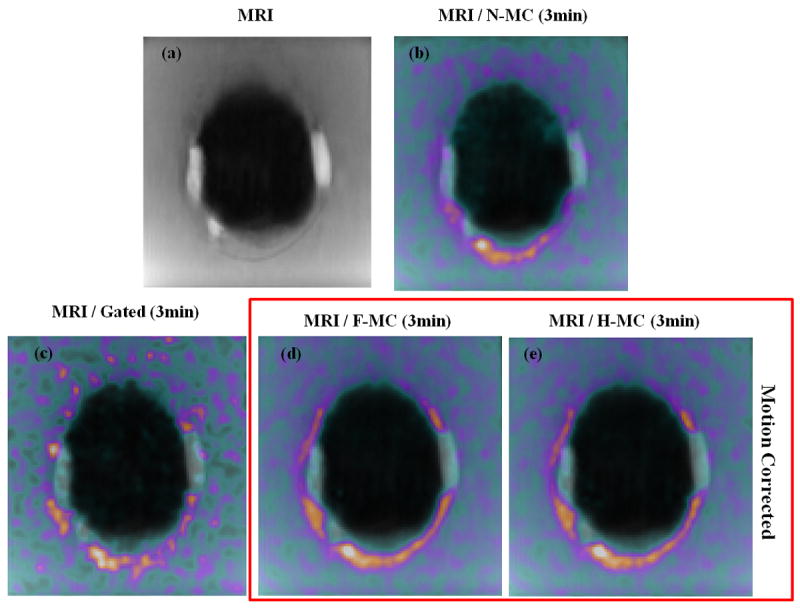
Non-tagged MR and fused MRI and PET images. In b), c), d) and e), MR image was fused with the PET image reconstructed using respectively N-MC, G, F-MC and H-MC. Motion correction visibly enhances the spatial registration between PET and MRI as compared to N-MC, allowing a better visualization of the scar tissue (LGE) and PET perfusion defects.

Figure 6 shows the defects/myocardium contrast recovery coefficients, which were computed using (5) for all three defects and the five reconstruction methods, at one iteration (it=7). The contrasts range from 0.48±0.03 to 0.86±0.02, 0.12±0.04 to 0.47±0.02 and 0.62±0.04 to 0.82±0.02 for defect A, B, and C respectively. Contrast degradations are more pronounced in non-transmural versus transmural defects because they are more prone to myocardial signal spillover caused by motion and PVE. Our motion correction method yields similar defect contrast to the gated method and comparable performance to the study gold standard (Ref), which means the motion blurring was successfully removed. As compared to the uncorrected method, the motion correction improves the defect/myocardium contrast recovery dramatically in the range of 34 to 206%, p < 0.001. Smaller variance in the defect/myocardium contrast recovery estimates were obtained with F-MC and H-MC as compared to G because more PET data were used in the reconstruction.

Figure 6.

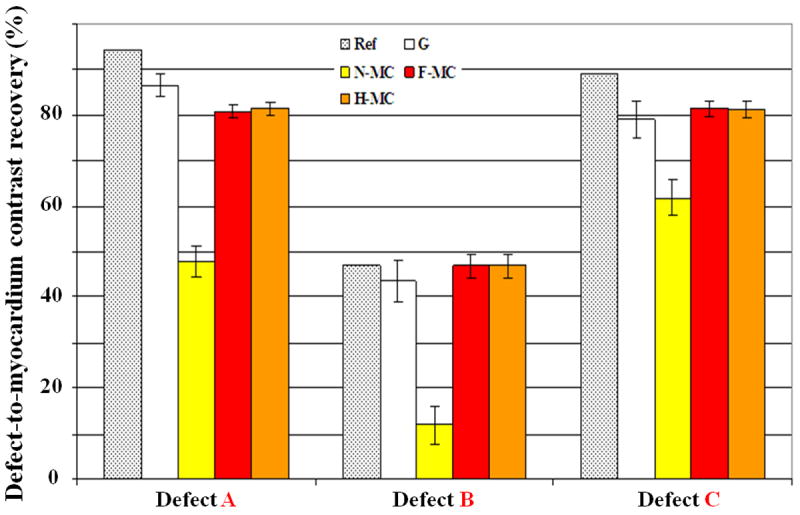
Mean contrast between defects and myocardium computed over 15 noise realizations using gating (G), no motion correction (N-MC) and motion-corrected (F-MC and H-MC) methods. MR based motion correction significantly improves PET defect/myocardium contrast values as compared to N-MC. The proposed methods achieve comparable performance to the gold standard (Ref) of the study.

To assess the performance of PSF modeling, gated and motion corrected PET image volumes were reconstructed with or without PSF modeling. Figure 7 shows that PSF modeling yields less PVE with more homogeneous apex and lateral walls as compared non-PSF modeling.

Figure 7.

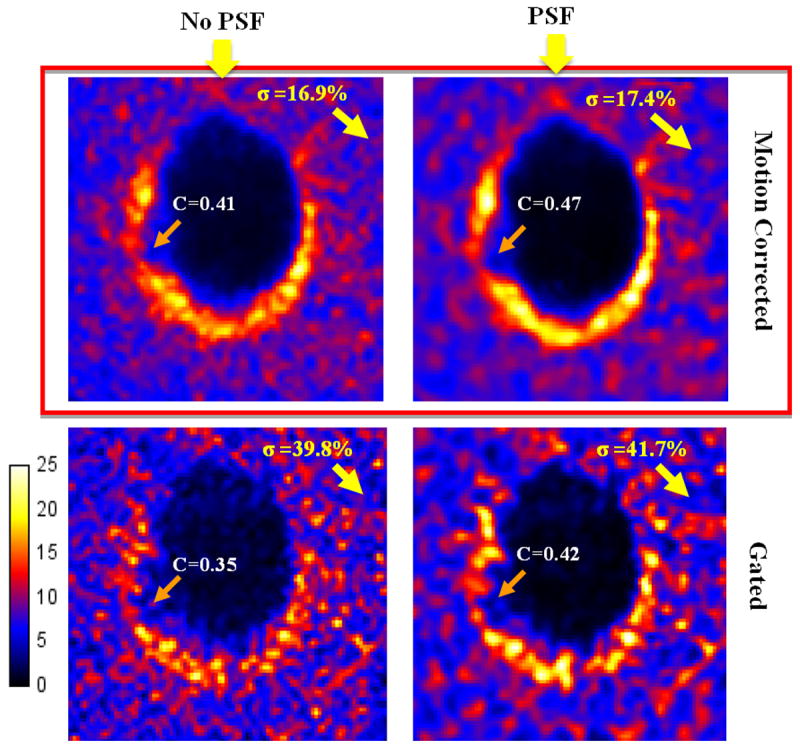
Images reconstructed with or without PSF modeling. PSF modeling reduces PVE and improves contrast.

Because image noise propagation properties are different for different reconstruction methods, image noise levels calculated using (7) are plotted against defect/myocardium contrast recovery in Figure 8 for a fair comparison. At a given noise level, PSF modeling results in better defect/myocardium contrast recovery as compared to no PSF modeling. At a given defect/myocardium contrast recovery, PSF modeling yields reduced noise level. The addition of PSF modeling to the motion-correction reconstruction algorithm improves defect/myocardium contrast recovery by about 5.1-8.5%, n=3, p < 0.01 versus no PSF modeling, with the biggest improvement being observed for the thinnest non-transmural defect located in the lateral walls of the phantom (defect B). More importantly, the reconstructions including PSF modeling allow recovering cold defects contrasts at levels that cannot be obtained without PSF modeling, as was observed in (Sureau et al 2008, Cloquet et al 2010). This shows that one not only needs to correct for non-rigid motion to obtain more quantitative images but that better performances are obtained when one can model both non-rigid motion and PSF within the same PET reconstruction process.

Figure 8.

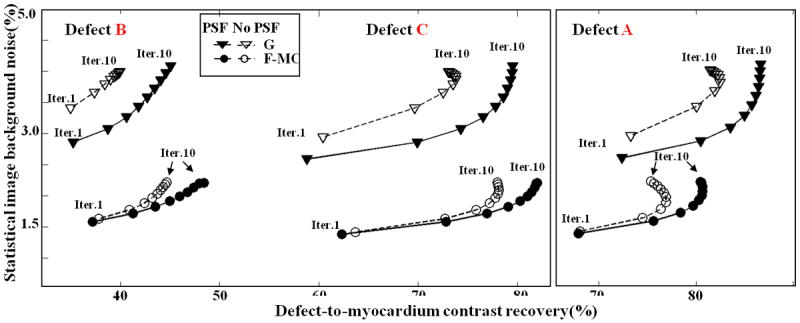
The defect-to-myocardium contrast recovery with and w/o PSF modeling for all the three defects. Contrast and image background noise level were computed over 15 noise realizations.

We show in Figure 9 the defect detectability assessed with CHO SNR at one image iteration (it=7). Note that since multiple noise realizations are needed to compute the CHO SNR, the defect detectability for the gold standard (Ref) cannot be assessed as it is obtained by reconstructing all available PET events in the same gate. F-MC enhances the defect detectability by +136%, +235% and +62% (p < 0.001) for defect A, B, and C, respectively, as compared to N-MC. The improvement is the highest (+235%) for defect B located in the lateral wall which underwent the largest motion. Conversely, improvement was the lowest for defect C, which underwent the smallest motion in the apex of the phantom. The improvements with F-MC versus G are +128%, +115% and +136% (p < 0.001) for defect A, B, and C, respectively. Such improvements resulted from the fact that all the PET data were used in F-MC while only part of the data were used in G. These results show that the proposed motion-correction algorithm largely improves task-based myocardial defects CHO detection SNR as compared to both gating and no motion correction. The little CHO detection SNR difference between F-MC and H-MC was found to be statistically not significant, (p > 0.1) therefore tagged MR imaging time (at about 6min for half k-space acquisition in our study) can be significantly reduced without compromising defect detectability.

Figure 9.

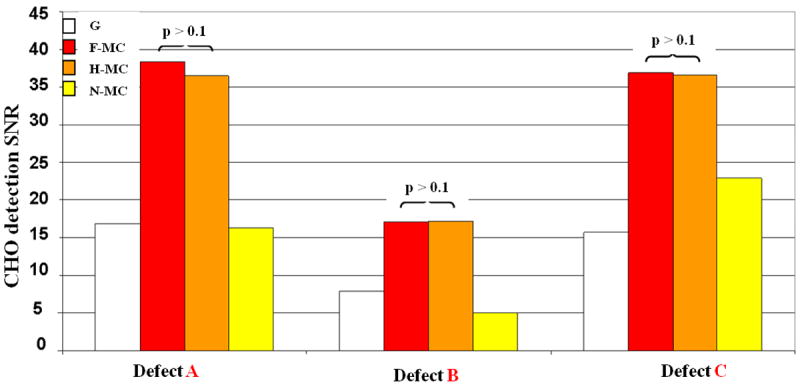
CHO detection SNR s computed over 15 noise realizations for gating (G), no motion correction (N-MC) and motion-corrected methods (F-MC and H-MC). Motion correction significantly increases defect detectability as compared to G and N-MC. The best improvement was observed for non-transmural defect B, which had the lowest volume and the largest motion.

Finally, Figure 10 shows the CHO detection SNR computed at each iteration for F-MC with and without inclusion of the PSF model in the reconstruction. At matched levels of noise, PSF modeling significantly increased lesion detectability CHO SNR (by 39-56%, n=3 p < 0.01) as compared to no PSF modeling.

Figure 10.

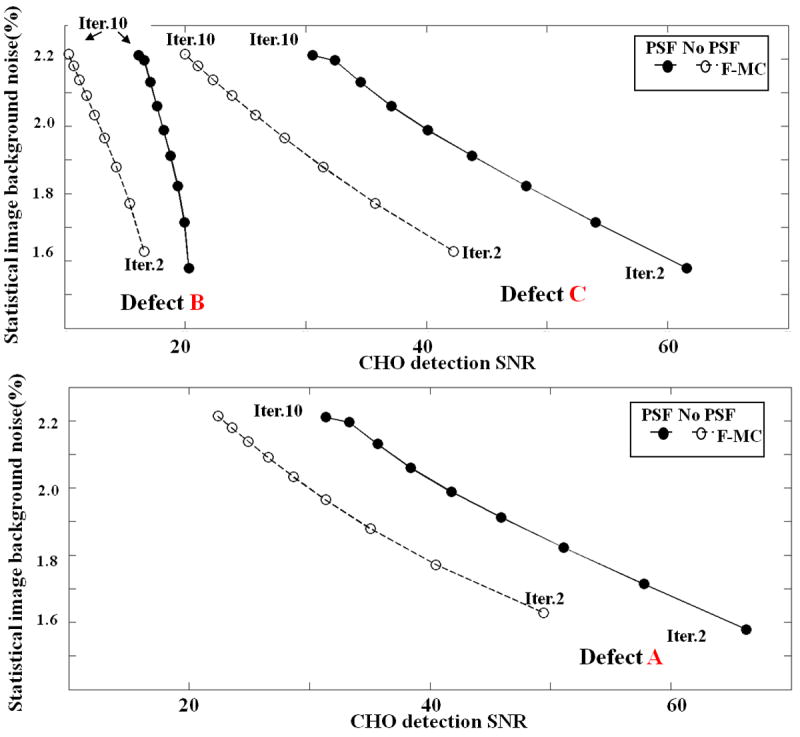
CHO detection SNR computed for all the three defects for F-MC with and without PSF modeling. At similar level of noise, PSF modeling significantly increases defects CHO detection SNR.

Note that, in this study, the “ventricular chamber” of our phantom contains air and not “hot” fluid as one would find in a real subject. Worse motion degrading effects might be expected in the latter case since defect signal would experience extra contamination from ventricular chamber activity besides myocardium and background. One may hence expect the proposed methods to produce comparable or even greater improvements on defect contrast and detectability in such case.

The authors acknowledge the fact that this phantom study solely focuses on correcting non-rigid motion due to heart contractions. In a clinical PET-MRI scenario, one would also need to take into account respiratory-induced motion of the heart, spanning over longer periods of time (4-5 seconds), with displacements amplitudes of 4.9-9mm (Boucher et al 2004, Blume et al 2010) and with highly subject-dependent hysteretic behaviors (Nekrke et al 2001). While tagging is optimal in measuring cardiac motion due to little cardiac cycle duration (~1 sec.) as compared to the tags persistence in the medium (~800ms), it might not be easy to employ tagging for measuring respiratory movement. But, given its quasi-rigid nature at whole-body PET resolution levels, respiratory motion could be measured with lower-resolution –non-tagged- MR volumes of the subject’s torso acquired in free-breathing conditions (King et al 2011). Respiratory motion fields could then be combined with cardiac motion fields measured with MR tagging at a given respiratory position (eventually with navigator respiratory rejection) and further inserted into the proposed reconstruction framework to perform a full compensation of the heart’s motion occurring during the acquisition. Given the amplitude of the displacements considered, significant impact on image quality and image-derived quantitative measurements are to be expected. Future work will be devoted to the design and implementation of such acquisition procedures in our recently installed whole-body simultaneous PET-MRI.

4. Conclusion

In this paper, we have proposed and validated a novel dedicated simultaneous cardiac PET-MR acquisition and reconstruction framework that significantly improves cardiac PET images quality. Our algorithm tackles two of the main limitations actual of cardiac PET imaging by performing both motion “deblurring” and scanner’s PSF deconvolution, while reconstructing PET images with all available data. In order to achieve this, we incorporated both tagged-MR derived wall motion information and position dependent scanner PSF modeling directly into the system matrix of a modified list-mode PET OSEM reconstruction algorithm. The proposed methods were evaluated in a cardiac beating phantom study. Our methods significantly improve heart wall reconstruction, images quantitative accuracy as well as both transmural and non-transmural myocardial defects CHO detection SNR as compared to conventional reconstruction methods such as gating or no motion correction. Reduced MR tagging acquisition times can be obtained by acquiring partially sampled k-space without affecting the proposed methods.