Neuromodulatory changes in short-term synaptic dynamics may be mediated by two distinct mechanisms of presynaptic calcium entry

Abstract

Although synaptic output is known to be modulated by changes in presynaptic calcium channels, additional pathways for calcium entry into the presynaptic terminal, such as non-selective channels, could contribute to modulation of short term synaptic dynamics. We address this issue using computational modeling. The neuropeptide proctolin modulates the inhibitory synapse from the lateral pyloric (LP) to the pyloric dilator (PD) neuron, two slow-wave bursting neurons in the pyloric network of the crab Cancer borealis. Proctolin enhances the strength of this synapse and also changes its dynamics. Whereas in control saline the synapse shows depression independent of the amplitude of the presynaptic LP signal, in proctolin, with high-amplitude presynaptic LP stimulation the synapse remains depressing while low-amplitude stimulation causes facilitation. We use simple calcium-dependent release models to explore two alternative mechanisms underlying these modulatory effects. In the first model, proctolin directly targets calcium channels by changing their activation kinetics which results in gradual accumulation of calcium with low-amplitude presynaptic stimulation, leading to facilitation. The second model uses the fact that proctolin is known to activate a non-specific cation current I_MI. In this model, we assume that the MI channels have some permeability to calcium, modeled to be a result of slow conformation change after binding calcium. This generates a gradual increase in calcium influx into the presynaptic terminals through the modulatory channel similar to that described in the first model. Each of these models can explain the modulation of the synapse by proctolin but with different consequences for network activity.

1 Introduction

Short-term synaptic dynamics such as facilitation and depression are observed in most synapses (Mamiya et al. 2003; Pan and Zucker 2009; Zucker and Regehr 2002). Although the functional significance of these forms of synaptic plasticity in oscillatory networks is still mostly unknown, several studies have proposed a variety of roles for synaptic dynamics that is important for the proper function of these networks (Abbott et al. 1997; Chance et al. 1998; Dittman et al. 2000; Galarreta and Hestrin 1998; K. M. MacLeod et al. 2007; Mamiya and Nadim 2005; Manor et al. 2003; Nadim et al. 2003; Reyes et al. 1998; Rose and Fortune 1999; M. V. Tsodyks and Markram 1997). Most synapses are also subject to neuromodulation that changes their strength and short-term dynamics (Barriere et al. 2008; Kreitzer and Regehr 2000). The neuromodulators that change synaptic release often do so by targeting presynaptic voltage-gated calcium channels (Wu and Saggau 1997; Bieda and Copenhagen 2004; Wang et al. 2006; Zucker and Regehr 2002). Neuromodulators also target other types of ion channels that may be permeable to calcium but not known to be involved in synaptic transmission. It is possible that calcium entry through such channels may act as a modulator of synaptic dynamics (Verhoog and Mansvelder 2011; Bardoni et al. 2004; Berretta and Jones 1996). Here we use a computational model to examine the mechanisms by which neuromodulators could affect synaptic strength and dynamics through direct effects on presynaptic voltage gated calcium channels and through indirect effects mediated by calcium entry through non-specific cation current channels.

The oscillatory pyloric network of the crab stomatogastric nervous system is an extensively studied system for the effects of neuromodulators (Marder and Bucher 2007). Previous studies of the pyloric network have explored the actions of neuromodulators on ionic currents (Johnson et al. 2003), synaptic strength (Ayali et al. 1998; Thirumalai et al. 2006) and, more recently, short-term synaptic dynamics(Johnson et al. 2011; Johnson et al. 2005; Zhao et al. 2011). The Zhao et al. (2011) study examined the effect of the endogenous neuropeptide proctolin on the strength and short-term dynamics of the inhibitory synapse from the LP to the PD neuron in the pyloric network. This synapse is the sole chemical feedback from the pyloric follower neurons to its pacemaker group and its dynamics are potentially important in shaping the network output. The LP to PD synapse is dominated by a strong graded component whose strength is enhanced by proctolin. The short-term dynamics of this component are also modified by proctolin in an unusual manner: the synapse shows short-term depression in control saline whereas, in the presence of proctolin, low-amplitude (< 25 mV) presynaptic stimulation causes facilitation, while high-amplitude (> 25 mV) stimulation causes depression. Although the mechanisms underlying these synaptic modifications by proctolin are not known, the switch from depression to facilitation is correlated with slowly accumulating Ca²⁺ entry in the presynaptic cell in the presence of proctolin, suggesting a presynaptic mechanism (Zhao et al. 2011).

We investigate possible mechanisms underlying the modulation of the strength and short-term dynamics of the LP to PD synapse by proctolin by considering two simple mechanistic models that explain the observed effects of proctolin. In the first model, which is based on a previous more detailed model (Zhou et al. 2007), we examine the possibility that proctolin targets the presynaptic voltage-dependent calcium currents (I_Ca), consistent with the observed increase in Ca²⁺ influx from pulse to pulse (see Fig. 1). Calcium currents are a common target through which modulators can regulate transmitter release (Fossier et al. 1999; Hige et al. 2006; Johnson et al. 2003; Wu and Saggau 1997). In this model, proctolin modifies the activation kinetics of I_Ca in the LP neuron which, in turn, results in different levels of calcium entry in this neuron depending on the amplitude and timing of the LP neuron membrane potential. The distinct levels of calcium concentration in the LP neuron, in turn, result in different levels of synaptic release.

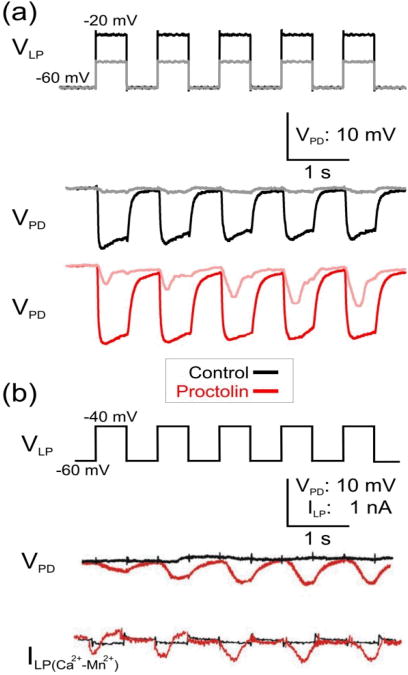
Figure 1. Proctolin modulates the short-term dynamics of the LP to PD inhibitory synapse in response to presynaptic depolarization pulses of different amplitude.

(a) LP neuron was voltage-clamped at -60 mV and stimulated with a series of five square pulses of 40 mV (V_LP: black trace) or 20 mV (V_LP: gray trace) amplitudes in control saline and in 10⁻⁶ M proctolin and the synaptic potentials were recorded in the PD neuron. In control saline the LP to PD synapse was depressing. In proctolin, in response to 20 mV presynaptic pulses, the synapse showed facilitation (pink) but it remained depressing (red) in response to the 40 mV pulses. (b) The proctolin-induced facilitation of the LP to PD synapse in response to low amplitude 20 mV presynaptic pulses is associated with the activation of Ca²⁺-like inward current ΔI_LP=I_LP(Ca²⁺)−I_LP(Mn²⁺) (Zhao et al. 2011). The amplitude of the current ΔI_LP exhibits no change in control (black) and increases in proctolin (red) with each pulse.

A second related model takes into account the fact that proctolin activates a voltage-gated modulatory inward current, I_MI (Golowasch and Marder 1992; Swensen and Marder 2000). I_MI is a nonspecific cation current, permeable to Na⁺ and K⁺, whose gating properties were shown by Golowasch and Marder (1992) to be strongly affected by extracellular Ca²⁺, suggestive of an external pore block by Ca²⁺ ions, much like the Mg²⁺ block in NMDA-receptor channels. In this model, we assume that the Ca²⁺ block of the I_MI channels is not total and the channels are partially permeable to Ca²⁺. In the presence of proctolin, the MI channels are activated, thus providing an additional source of Ca²⁺ ions in the presynaptic LP neuron which, together with the Ca²⁺ entry through voltage-gated Ca²⁺-channels, accounts for the modulation of synaptic release. The modulation of the short-term synaptic plasticity in this model depends on the slow kinetics of Ca²⁺ influx through the MI channels.

Because of the limited number of elements in our models, we can use an optimization algorithm to find the parameter sets that best fit the experimental data. The optimization algorithm produces a number of parameter sets that are consistent with the observed neuromodulatory effects of proctolin on this synapse. Analysis of these data sets can reveal the features of the model that are most critical for explaining the experimental data, and the correlations between parameter values can be used to uncover the inter-dependence among different model elements. Interestingly, each of the two proposed models of proctolin action can explain the modulation of the LP to PD synapse by proctolin, but the two models point to different targets of action by this neuromodulator.

2 Methods

Each model consists of a set of differential equations that describe the ionic currents I_Ca or I_MI and the intracellular calcium concentration [Ca²⁺]_i in the presynaptic LP neuron, as well as a passive model that captures the synaptic potential in the postsynaptic PD neuron. We make no assumptions on the compartmentalization of [Ca²⁺]_i and therefore all spatial distribution of Ca²⁺ is ignored. We have measured synaptic potentials in the PD neuron by voltage clamping the presynaptic LP neuron after blocking all neuronal activity and applying a train of voltage pulses. Therefore, the only ionic currents considered in the presynaptic LP neuron are the calcium current I_Ca (present in both models) and the modulator-activated inward current I_MI (present only in model II). We assume that the calcium current in the LP neuron I_Ca has only one component involving both activation and inactivation processes

$$I_{\mathit{\text{Ca}}}={\overline{g}}_{\mathit{\text{Ca}}}{m}^{2}h(V-V_{\mathit{\text{Ca}}})$$ (1)

where V_Ca = 100mV is the reversal potential and ḡ_Ca is the maximum conductance of I_Ca. The activation (m) and inactivation (h) variables are given by

$$\frac{\mathit{\text{dx}}}{\mathit{\text{dt}}}=\frac{x_{\infty }-x}{{\tau }_x},x=m,h$$ (2)

where

$$m_{\infty }=\frac{1}{1+\text{exp}(-\frac{V+V_m}{S_m})}$$ (3)

is the steady-state activation and

$$h_{\infty }=\frac{1}{1+\text{exp}(-\frac{V+V_h}{S_h})}$$

is the steady-state inactivation. The time constant of activation (τ_m) and inactivation (τ_h) are fixed in both cases and produce sufficient slow recovery of calcium channels from inactivation for all voltage levels. This slow recovery generates a gradual decrease in Ca²⁺ current from pulse to pulse. This is the main mechanism of synaptic depression of the LP to PD synapse in both models. Experimental observations suggest that I_Ca in the LP neuron consists of two components, a transient and a sustained one. Because of the slow time constant for inactivation, the current expression in Eq. 1 provides a simple model of a composition of these two components.

The calcium concentration in the presynaptic LP neuron is described by

$$\frac{d{[{\mathit{\text{Ca}}}^{2+}]}_i}{\mathit{\text{dt}}}=-\frac{{[{\mathit{\text{Ca}}}^{2+}]}_i}{{\tau }_{\mathit{\text{Ca}}}}-\lambda I_{\mathit{\text{Ca}}}$$ (4)

where the time constant of calcium (τ_Ca) is kept at a constant value. The last term in Eq. 4 represents the Ca²⁺ influx and $\lambda =\frac{1}{2\mathit{\text{FV}}}=0.1\mu M/(\mathit{\text{nA ms}})$, where F is Faraday's constant and V is the volume. In model II, Eq. 4 has an additional term corresponding to the influx through the modulatory channel (see Eq. 11).

The synaptic current model assumes the standard fourth-order Ca²⁺ cooperativity of neurotransmitter release (Schneggenburger and Neher 2005):

$$g_{\mathit{\text{syn}}}={\overline{g}}_{\mathit{\text{syn}}}\frac{K_{\mathit{\text{Ca}}}^4{[{\mathit{\text{Ca}}}^{2+}]}_i^4}{K_{\mathit{\text{Ca}}}^4+{[{\mathit{\text{Ca}}}^{2+}]}_i^4}$$ (5)

where ḡ_syn is the maximal synaptic conductance and K_Ca is the calcium affinity of neurotransmitter release.

The inhibitory postsynaptic potential (IPSP) in the PD neuron is given by

$$C\frac{\mathit{\text{dV}}}{\mathit{\text{dt}}}=-g_{\mathit{\text{syn}}}(V-V_{\mathit{\text{syn}}})-g_m(V-V_{\mathit{\text{rest}}})$$ (6)

where C = 1nF is the membrane capacitance, V_syn = −80mV is the synaptic reversal potential, V_rest = −60mV is the resting potential of postsynaptic membrane which is a holding potential using voltage-clamp in experiment, and g_m is the intrinsic membrane conductance. These values lie in ranges consistent with experimental data (Buchholtz et al. 1992; Golowasch and Marder 1992; Swensen and Marder 2001).

In the optimization algorithm, all model parameters (with the exception of ion reversal potentials, membrane capacitance C and the constant λ in Eq. (4)) were considered to be free variables and their values were determined by optimizing the fit between a single experimentally-observed and the model-simulated potential of the PD neuron. At each step of the optimization algorithm, corresponding to a particular set of parameter values, the time course of the PD voltage was computed both in the control condition and in the presence of proctolin, for two values of presynaptic stimulation amplitude (20mV and 40mV). The numerical solution of differential equations describing model I or model II was performed using MATLAB's built-in ode15s solver for stiff systems (MathWorks, Inc.). The optimized objective function equals the time integral of the absolute difference between the observed and the simulated PD voltage time courses, with an arbitrary scaling freedom between the two sets of time traces. Deviations corresponding to the four cases (two amplitudes of presynaptic stimulation in control and in the presence of proctolin) were all summed together, resulting in a single cost function. Only a single free scaling parameter was allowed for the set of all four time traces. An additional term describing the deviation between the simulated and the observed degree of short-term synaptic plasticity was added to the objective function, to ensure that optimization achieves facilitation for small amplitude stimulation in proctolin, and short-term depression for high-amplitude stimulation. To ensure sufficient sampling of parameter value ranges, parameter optimization was preceded by a random search through a large volume of the parameter space, and sufficiently small objective function values obtained during such random searches were then used as starting points of subsequent parameter optimization. Several hundred random parameter combinations were typically probed before starting each parameter optimization run. Only those optimized parameter sets that passed a goodness-of-fit threshold were included for later analysis.

The unconstrained nonlinear minimization of the objective function (total deviation function) described above is performed using MATLAB's built-in fminsearch routine (MathWorks, Inc.), which implements derivative-free Nelder-Mead Simplex Method (Lagarias et al. 1998).

In model I, the optimization is performed over the following 16 model parameters (see Results, and Fig. 2): K_Ca, ḡ_syn, ḡ_Ca, g_m, τ_h, τ_Ca, ${\tau }_m^c$, V_h, S_h, V_m, S_m, ${\mathit{\text{V}}}_{\mathit{\text{m}}}^{\mathit{\text{p}}},{\mathit{\text{S}}}_{\mathit{\text{m}}}^{\mathit{\text{p}}},A_{\tau }^p,V_{\tau }^p,S_{\tau }^p$

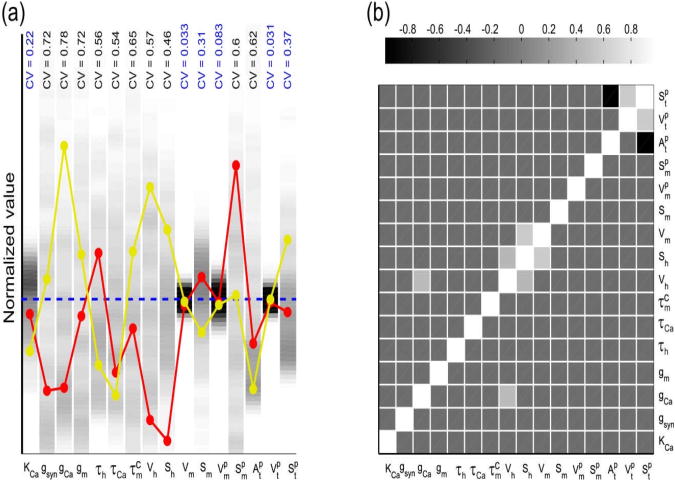
Figure 2. Optimized parameter sets showing the changes in activation kinetics of presynaptic Ca²⁺ channels in model I.

A total of 256 randomly-seeded parameter sets were optimized for model I to fit the experimental recording of the synaptic outputs in control and proctolin for two different presynaptic voltage amplitudes (see Methods). (a) The distribution of parameter values for each of the 16 parameters in model I is indicated in grayscale, with darker tones representing greater distribution density. The value of each parameter was normalized to the mean value of its distribution (dashed blue line) for comparison; these mean values are: K_Ca = 1.3μM, ḡ_syn = 14.1nS / μM⁴, ḡ_Ca = 1.8nS, g_m = 0.46μS, τ_h = 1.6s, τ_Ca = 33.6ms, ${\tau }_m^c=39.7ms$, V_h = 78.5mV, S_h = 41mV, V_m = 42mV, S_m = 8.7mV, $V_m^p=50\mathit{\text{mV}},S_m^p=2.8\mathit{\text{mV}},A_{\tau }^p=2.0s,V_{\tau }^p=50.5\mathit{\text{mV}},S_{\tau }^p=5.9\mathit{\text{mV}}$ Two parameter sets are also shown for comparison (red and yellow), demonstrating that good fits to the data did not require a consistent relationship among all parameters. Six out of 16 parameters were relatively tightly constrained by the optimization technique (coefficient of variation < 0.4 shown in blue). (b) Pair-wise correlations among the best-fit parameters indicate that few parameter pairs showed any significant (R > 0.5) co-variation. See Results for additional description.

In model II, there are 15 optimized parameters (see Results and Fig. 5): K_Ca, ḡ_syn, ḡ_Ca, g_m, g_MI, τ_h, τ_Ca, τ_m, V_h, S_h, V_m, S_m, V⁺, S⁺, k⁻

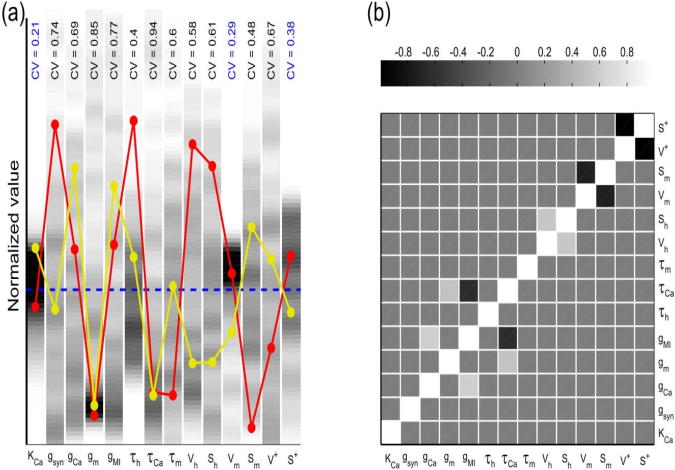
Figure 5. Optimized parameter sets showing the modulation of MI channels by proctolin in model II.

A total of 198 randomly-seeded parameter sets were optimized for model II to fit the experimental recording of the synaptic outputs in control and proctolin for two different presynaptic voltage amplitudes (see Methods). (a) The distribution of parameter values for 14 of 15 parameters in model II. (In all parameter sets K⁻ converged to a value very close to the lower limit of 0.1 s⁻¹ during optimization, and is not shown.) The value of each parameter was normalized to the mean value of its distribution (dashed blue line) for comparison; these mean values are: K_Ca = 1.9μM, ḡ_syn = 5.1nS / μM⁴, ḡ_Ca = 29.4nS, g_m = 34.8nS, g_MI = 2.06nS, τ_h = 587ms, τ_Ca = 26.5ms, τ_m = 41.8ms, V_h = 61.6mV, S_h = 27.7mV, V_m = 36.8mV, S_m = 14.1mV, V⁺ = 14.7mV, S⁺ = 3.61mV. Two parameter sets are also shown for comparison (red and yellow), demonstrating that good fits to the data did not require a consistent relationship among all parameters. Three out of the 14 parameters were relatively tightly constrained by the optimization technique (coefficient of variation < 0.4 shown in blue). (b) Pair-wise correlations among the best-fit parameters indicate that few parameter pairs showed any significant (R > 0.5) co-variation.

3 Results

3.1 Neuromodulation of the LP to PD synapse

The LP to PD synapse is known to display short-term depression in the absence of proctolin (Manor et al. 1997). To characterize short-term plasticity of the LP to PD synapse, we injected a train of high- and low-amplitude (V_LP in Fig. 1A) into the voltage clamped LP neuron and recorded the postsynaptic potential in the PD neuron (V_PD in Fig. 1A). The IPSP recorded in the PD neuron showed depression with high-amplitude presynaptic pulses and little response with low-amplitude pulses (Fig. 1A Control). (The low-amplitude response in control is often small or shows some depression (Zhao et al. 2011).) In contrast, the IPSP in proctolin showed depression with high-amplitude pulses but facilitation with low-amplitude pulses (Fig. 1A Proctolin).

As we have reported previously, this change in the short-term synaptic dynamics in the presence of proctolin is independent of the waveform shape used and is also present when the presynaptic neuron is voltage clamped with realistic bursting waveforms (Zhao et al. 2011). Here, we will focus primarily on the response to a train of depolarizing square pulses to simplify the description of the kinetics that may be involved in producing short-term depression or facilitation.

To unmask the underlying cause for facilitation, the experiments with low-amplitude pulses were performed in saline containing normal levels of Ca²⁺ or after substituting the Ca²⁺ with Mn²⁺ (and therefore blocking synaptic transmission), in both control and in 10⁻⁶ M proctolin (Fig 1B). In all conditions, we made simultaneous measurements of the presynaptic current (I_LP) and the postsynaptic potential. The difference between the presynaptic currents measured in normal saline and in Mn²⁺ was considered a putative Ca²⁺ current (ΔI_LP = I_LP(Ca²⁺) − I_LP(Mn²⁺) in Fig. 1B). In the example shown, in control saline there was little synaptic response and no apparent synaptic plasticity was observed (V_PD, black trace in Fig. 1B). In contrast, the synaptic response showed facilitation in proctolin (with normal Ca²⁺; V_PD, red curve in Fig. 1B). The putative calcium current was small in control conditions and its amplitude showed no variation with each subsequent pulse (ΔI_LP, black trace in Fig. 1B). However, in the presence of proctolin, this current increased in amplitude with each subsequent pulse, indicating accumulation of Ca²⁺ currents (ΔI_LP, red trace in Fig. 1). When the average amplitudes of the presynaptic inward current ΔI_LP and the IPSPs are compared, there is a positive correlation between the presynaptic inward current and the postsynaptic potentials (Zhao et al. 2011).

The data shown indicated that facilitation is likely caused primarily by an increase in Ca²⁺ current from pulse to pulse, rather than slow clearance of free or bound residual [Ca²⁺]_i (Zucker and Regehr 2002). Increase in Ca²⁺ influx has been shown to underlie short-term facilitation in other synapses as well (Bertram et al. 2003; Xu et al. 2007). Thus, any minimal model of proctolin effects on synaptic dynamics should involve a mechanism of calcium influx modulation by proctolin. Here we propose two possible mathematical models based on the kinetics of voltage-gated Ca²⁺ currents in the presynaptic LP neuron to explore the mechanisms underlying the effects of proctolin described above.

3.2 Model I: Ca²⁺-channel model

In model I, we assumed that proctolin targets and modifies the activation kinetics and activation time constant of presynaptic Ca²⁺ channels. Such a change of kinetics and time constant constitute a minimal assumption allowing the model to reproduce experimentally observed voltage-dependence of the shift from depression to facilitation by proctolin.

The activation time constant of I_Ca in control conditions was set to a constant value ${\tau }_m^C$. This time constant was allowed to be modulated by proctolin under the functional constraint:

$${\tau }_m^P(V)=\frac{A_{\tau }^P}{\text{cosh}\left(\frac{V+V_{\tau }^P}{S_{\tau }^P}\right)}.$$ (7)

Parameters $A_{\tau }^P,V_{\tau }^P$ and $S_{\tau }^P$ (determined by data fit optimization) yield activation which is slow at low voltages but fast at high voltages. Further, we assumed that the steady-state activation parameters V_m and S_m for m_∞ given by Eq. 3 is altered by proctolin; we denote the corresponding values ${\mathit{\text{V}}}_{\mathit{\text{m}}}^{\mathit{\text{p}}}$ and ${\mathit{\text{S}}}_{\mathit{\text{m}}}^{\mathit{\text{p}}}$ (see Fig. 2(a)).

All model parameters were determined using an optimization algorithm to fit the observed time courses of postsynaptic potentials in both control and proctolin conditions and with presynaptic amplitudes of 20mV and 40mV. A total of 256 randomly-seeded parameter sets were optimized (see Methods) and the overall range of parameter distributions obtained for the fits is shown in Fig. 2. About a thousand other randomly seeded optimized parameter sets that did not pass our goodness of fit threshold were excluded from our analysis.

Within the best fits, the majority of the 16 optimized model parameters had values with a wide distribution, as seen in the coefficient of variation of the normalized parameter values (CV≥0.4; Fig. 2(a)). The high variability of the conductance parameters in particular is at least in part explained by the scaling freedom between model and experimental data (see Methods). However, some parameters, such as the midpoint and slope (only in control) of the Ca⁺⁺ current activation curve and the parameters determining its time constant in proctolin were relatively constrained (CV<0.4). Another constrained parameter was K_Ca, the calcium affinity of neurotransmitter release.

As seen in the two examples shown in Fig. 2(a), there was no global relationship among parameter sets that provided best fit values in this model. We therefore examined whether there are two-parameter correlations among these parameters. Few parameter pairs showed strong positive or negative pair-wise correlations and those that did were mostly restricted to the parameters of the Ca⁺⁺ current activation curve and time constant (Fig 2(b)).

Figure 3 demonstrates the effects of proctolin in model I for one optimized parameter set (red parameter set in Fig. 2(a)) in response to two different voltage levels in the presynaptic LP neuron, both in control (left panels) and in proctolin (right panels). For any presynaptic pulse amplitude, the model shows an increase in Ca²⁺ influx through the Ca²⁺ channels, leading to greater IPSP amplitude in PD neuron in proctolin than in control due to the modification of steady-state activation of Ca²⁺ channels by proctolin (Figs. 3(e) and 3(f)).

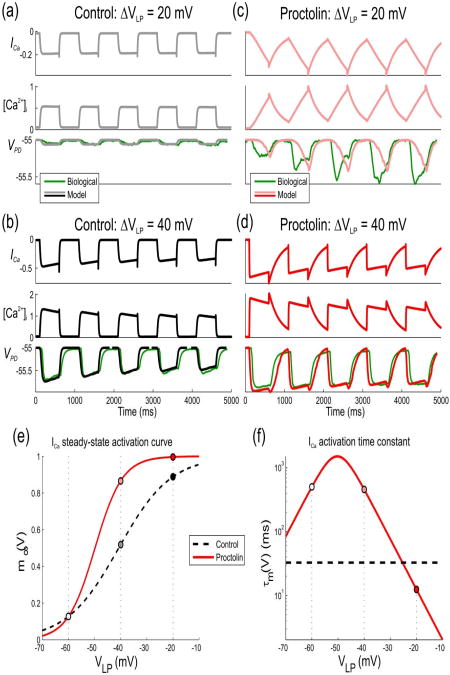
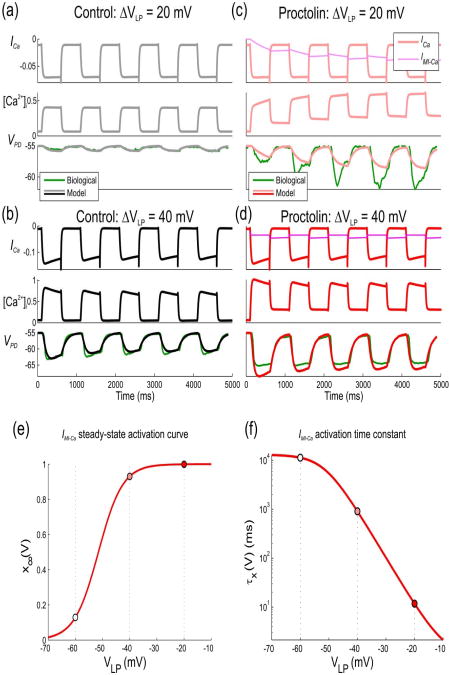
Figure 3. Effects of proctolin in model I on LP to PD synaptic transmission for a sample parameter set.

The response of the model with the parameter set shown in red in Fig. 2(a) to trains of low- and high-amplitude pulses in control and proctolin is compared to a biological recording (green traces) of the IPSPs in the PD neuron in one experiment different than the one shown in Fig. 1(a)). (a) The model response to low-amplitude (20 mV) pulses in the presynaptic LP neuron in control shows no significant IPSP in the PD neuron. (b) The model response to high-amplitude (40 mV) presynaptic pulses shows synaptic depression in control. (c) A switch to synaptic facilitation by proctolin. Proctolin changes the steady-state activation and time constant of I_Ca which leads to a gradually-increasing IPSP in the PD neuron due to the gradual increase of [Ca²⁺]_i in presynaptic terminal. (d) Although Ca²⁺ entry is enhanced with high-amplitude voltage pulses in proctolin, a change in the activation kinetics results in synaptic depression. (e) Steady-state activation of I_Ca in control and in proctolin. Proctolin shifts the activation curve to the left and changes its slope, which leads to enhanced synaptic strength of the LP to PD synapse in the biological range. (f) Activation time constant of I_Ca in control and in proctolin. Parameter values are: K_Ca = 1.17μM, ḡ_syn = 6.06nS / μM⁴, ḡ_Ca = 8.09nS, g_m = 0.416μS, τ_h = 2.08s, τ_Ca = 18.4ms, ${\tau }_m^c=32.8\mathit{\text{ms}}$, V_h = 19.1mV, S_h = 4.56mV, V_m = 40.8mV, S_m = 10mV, $V_m^p=49.8\mathit{\text{mV}},S_m^p=5.27\mathit{\text{mV}},A_{\tau }^p=1.51s,V_{\tau }^p=50.3\mathit{\text{mV}},S_{\tau }^p=5.51\mathit{\text{mV}}$

The change in the activation curve and kinetics results in a significantly greater IPSP in the PD neuron due to the gradual increase in free residual Ca²⁺ concentration in the presynaptic terminal for low presynaptic voltage pulses. This, in turn, results in a shift of the synaptic activation curve to lower voltages, consistent with the predictions from experimental data (Zhao et al. 2011).

In this model, proctolin application resulted in much slower activation of Ca²⁺ channels at low voltages as compared to control, leading to synaptic facilitation due to a slow accumulation of I_Ca. For the high-amplitude (40 mV) pulses, synaptic depression is present both in control and in proctolin, since the time constant of activation at high voltage is close to the value in the control condition.

3.3 Model II: Modulatory channel model

In this model, we explored the alternative hypothesis that Ca²⁺ influx through MI channels can sufficiently describe the effects of proctolin on synaptic strength and dynamics without any direct modulation of the Ca²⁺ current. Previous experimental studies have suggested that MI channels are blocked by Ca²⁺ at low presynaptic voltages. The removal of Ca²⁺ from the extracellular medium results in a linear I-V relationship for I_MI, much like the effect of removing Mg²⁺ on NMDA receptor channels (Golowasch and Marder 1992). Therefore, it is conceivable that modulatory channel binding with Ca²⁺ would induce a slow conformation change of this channel that leads to a greater calcium influx. This would lead to a change in Ca²⁺ permeability of this channel when Ca²⁺ block is removed by depolarization. This putative mechanism is analogous to Mg²⁺ influx through NMDA channel which occurs even though the channels are blocked by Mg²⁺ (Stout et al. 1996). We propose a conformational change in the MI channels based on the following state diagram:

$$C^0\underset{k_1^{-}}{\overset{k_1^{+}}{\rightleftarrows }}{C}^1\underset{k_2^{-}}{\overset{k_2^{+}}{\rightleftarrows }}O$$ (8)

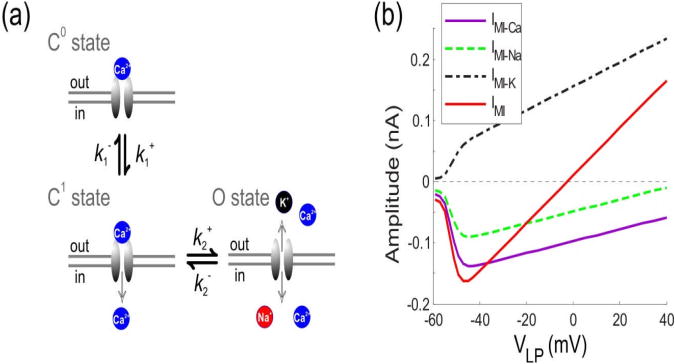
Our hypothesis for MI channel gating is inspired in part by the mechanism of Ca²⁺-dependent inactivation of L-type Ca²⁺ channels (Babich et al. 2007; Yue et al. 1990; Olcese 2007). Namely, we assume in our model that channel state C⁰ has the highest affinity for Ca²⁺, so its pore is completely blocked by Ca²⁺, leading to zero cation permeability. Channel state C¹ has lower but significant Ca²⁺ affinity, allowing only Ca²⁺ ions to pass through upon their binding to the channel pore selectivity site. Finally, state O has very low Ca²⁺ affinity, allowing unrestricted flow of Na+ and K⁺ as well as Ca²⁺ through this channel (see Figure 4(a)).

Figure 4. Modulatory I_MI channel gating in model II.

(a) Schematic diagram of transitions between states C⁰, C¹, O of the MI channel. Channel state C⁰ has the highest affinity for Ca²⁺ and the channel pore is completely blocked by Ca²⁺, leading to zero cation permeability. Channel state C¹ has lower but significant Ca²⁺ affinity, allowing some Ca²⁺ ions to pass through upon their binding to the channel pore selectivity site but with no permeability to Na⁺ and K⁺. Channel state O has very low Ca²⁺ affinity, allowing unrestricted flow of Na⁺ and K⁺. (b) The maximum amplitude of Ca²⁺(I_{MI − Na}(nA): magenta curve), Na⁺(I_{MI − Na}(nA): green dashed curve) , K⁺(I_{MI − Na}(nA): black dash-dotted curve), and the total MI current (I_MI(nA): red curve) influx through the modulatory channel I_MI when the presynaptic cell is depolarized from the resting potential −60mV. The influx is measured in response to the last pulse of the five pulses train. The maximum influx of Ca²⁺ and I_MI occurs at around −40mV.

Because both states C¹ and O are assumed to have non-zero permeability to Ca²⁺, and because only Ca²⁺ currents are responsible for synaptic response, for simplicity we combined these two states into a single open state x when calculating the effect of this channel on Ca²⁺ entry, with the transition between the open and closed states governed by a constant backward rate and a voltage-dependent forward rate given by:

$$k^{+}(V)=\frac{1}{1+\text{exp}(-\frac{V+V^{+}}{S^{+}})}{\mathit{\text{ms}}}^{-1}$$

The time constant of the MI current activation is given by the reciprocal of the sum of the forward and backward rates. We find that this time constant is one of the most critical parameters in the model, and that the slow time scale of this gating for small stimulation amplitude is the main factor causing facilitation in the proctolin conditions at low presynaptic stimulation amplitude.

Equations describing MI channel gating yield standard first-order activation kinetics:

$$\frac{\mathit{\text{dx}}}{\mathit{\text{dt}}}=k^{+}(1-x)-k^{-}x=(k^{+}+k^{-})(\frac{k^{+}}{k^{+}+k^{-}}-x)=\frac{x_{\infty }\left(V\right)-x}{{\tau }_{\infty }\left(V\right)}$$ (9)

where x is the fraction of I_MI channels in forms C¹ and O. The Ca²⁺ influx through the MI channel is then given by

$$I_{\mathit{\text{MI}}-\mathit{\text{Ca}}}={\overline{g}}_{\mathit{\text{MI}}}x(V-V_{\mathit{\text{Ca}}})$$ (10)

where V_Ca = 100mV is the equilibrium potential of Ca²⁺, and ḡ_MI is the maximal conductance of the MI channel.

In this model there are two sources of Ca²⁺ influx, the principal Ca²⁺ channels and the MI channels, so the calcium concentration [Ca²⁺]_i in the presynaptic LP neuron is

$$\frac{d{[{\mathit{\text{Ca}}}^{2+}]}_i}{\mathit{\text{dt}}}=-\frac{{[{\mathit{\text{Ca}}}^{2+}]}_i}{{\tau }_{\mathit{\text{Ca}}}}-\lambda I_{\mathit{\text{Ca}}}-\lambda I_{\mathit{\text{MI}}-\mathit{\text{Ca}}}$$ (11)

where τ_Ca and λ are same as in model I. In contrast to model I, the activation time constant τ_m of I_Ca is fixed to the same value as in control state (c.f. Eq. 7 in model I). Therefore, in this model the principal Ca²⁺ channels are unaffected by proctolin and proctolin targets MI channels only, which play the main role in the proctolin-induced change of synaptic dynamics.

To examine whether our model of the MI channel is consistent with previously published results on the voltage-dependence of this channel, we modeled the currents due to the flux of other cations (Na⁺ and K⁺) through this channel as well. The total current through the channel would be the sum of the currents due to Na⁺, K⁺ and Ca²⁺. Figure 4(b) shows the maximum amplitude of I_MI due to Ca²⁺ (I_MI−Ca, magenta), Na⁺, (I_MI−Na green), K⁺ (I_MI−K, black), as well as the total MI current (I_MI, red) as a function of the holding membrane potential. The maximum amplitude of each component of I_MI depends on the stimulation voltage; the total current reaches its maximum influx at around −40 mV, consistent with previously reported experimental results (Golowasch and Marder 1992). Note that this figure shows the steady state maximum amplitude of current flux produced by voltage pulses and does not use the assumption that the C¹ and O states are collapsed into one state.

The proposed MI channel model assumes that the slow changes in the conformational state of the MI channel generate a gradual increase of Ca²⁺ influx into the presynaptic terminal through the MI channels in the C¹ state (Fig. 4(a)), which is qualitatively similar to the increase in Ca²⁺ obtained in the model I. The synaptic response caused by I_MI gating exhibits facilitation if the Ca²⁺ influx through modulatory channels constitutes a considerable fraction of the total voltage-gated Ca²⁺ influx. This assumption leads to experimentally testable predictions, as described in the discussion.

As with model I, to obtain proper fits for the actions of proctolin in model II, we used an optimization algorithm to fit the synaptic output in both control and proctolin conditions and with presynaptic amplitudes of 20mV and 40mV. A total of 198 randomly-seeded parameter sets were optimized and the overall range of parameter distributions for the fits is shown in Fig. 5. The parameters that were relatively tightly constrained included (as in model I) the midpoint of the Ca⁺⁺ current activation curve and K_Ca, the calcium affinity of neurotransmitter release (Fig. 5(a)).

As in model I, there was no global relationship among parameter sets that provided best fit values in this model (two examples shown in Fig. 5(a)). Also, as in model I, few parameter pairs showed strong pair-wise correlations. The negative correlations included the midpoint and slope of the Ca²⁺ current activation curve and the midpoint and slope of the MI current activation (Fig 5(b)), indicating that the shift of the midpoint of the activation curve to the right was correlated with an increase in its slope.

Figure 6 shows the effect of proctolin in model II for one optimized parameter set, tested at two different amplitudes of presynaptic LP neuron stimulation. For any presynaptic pulse amplitude, [Ca²⁺]_i was higher in proctolin than in control state due to Ca²⁺ entry through the MI channels (I_MI−Ca) whereas Ca²⁺ entry through Ca²⁺ channels (I_Ca) remained unmodulated and unchanged. For high-amplitude (40 mV) presynaptic stimuli, the dominant part of Ca²⁺ influx was through the principal Ca²⁺ channels and therefore synaptic response still showed depression, as in the control state, despite the small gradual increase in I_MI−Ca. However, for the low-amplitude (20 mV) presynaptic stimulation, I_MI−Ca had more influence on total Ca²⁺ entry, resulting in the gradual increase of [Ca²⁺]_i in presynaptic terminal and the change of synaptic dynamics from depression to facilitation. Note that, in this model, accumulation of [Ca²⁺]_i over multiple pulses depended on the slow I_MI−Ca deactivation time constant (Fig. 6(f)) or, equivalently, on a small value of k⁻. Although we did not allow the value of this rate constant to go below 0.1 s⁻¹ in our simulations, in all parameter sets k⁻ converged to a value very close to this lower limit during optimization (and hence it is not shown in Fig. 5(a)).

Figure 6. Effects of proctolin in model II on LP to PD synaptic transmission for a sample parameter set.

The response of the model with the parameter set shown in red in Fig. 5(a) to trains of low- and high-amplitude pulses in control and proctolin is compared to a biological recording (green traces) of the IPSPs in the PD neuron in one experiment (same as Fig. 3). (a) The model response to low-amplitude (20 mV) pulses in the presynaptic LP neuron in control shows no significant IPSP in the PD neuron. (b) The model response to high-amplitude (40 mV) presynaptic pulses shows synaptic depression in control. (c) A switch to synaptic facilitation by proctolin. A gradual increase of [Ca²⁺]_i in presynaptic terminal due to the Ca²⁺ entry through MI channels allows for observed facilitation. (d) Although the increase in [Ca²⁺]_i due to the MI channels is still present, the dominant effect on [Ca²⁺]_i is due to I_Ca, resulting in depression as in control. (e) Steady-state activation of I_Ca in control and in proctolin. Proctolin shifts the activation curve to the left and changes its slope, which leads to enhanced synaptic strength of the LP to PD synapse in the biological range. (f) Activation time constant of I_Ca in control and in proctolin. Parameter values are: K_Ca = 1.7μM, ḡ_syn = 10nS / μM⁴, ḡ_Ca = 37.4nS, g_m = 7.4nS, g_MI = 2.68nS; τ_h = 1.23s, τ_Ca = 9.57ms, τ_m = 14.3ms, V_h = 120mV, S_h = 49.8mV, V_m = 41.1mV, S_m = 1.91mV, V⁺ = 9.45mV, S⁺ = 4.44mV

Discussion

Neuromodulators can change synaptic strength by modifying either presynaptic transmitter release or the postsynaptic receptor response (Johnson and Harris-Warrick, 1997). Our previous experimental findings indicate that the enhancement of the LP to PD synapse by proctolin is correlated with an increase in a presynaptic inward current (Zhao et al. 2011). This inward current is blocked by Mn²⁺, suggesting that it is a Ca²⁺ current, and its accumulation over multiple presynaptic voltage pulses is strongly correlated with the facilitation of the postsynaptic IPSP. The current modeling study therefore focused only on presynaptic effects in accordance with this result and other experimental evidence (Zhao et al. 2011).

To explore the mechanisms underlying the effects of proctolin on the short-term dynamics of the LP to PD synapse, we used computational modeling to examine two alternative hypotheses to find the most parsimonious explanation for the proctolin-mediated modulation of this synapse. Both models assume that the observed changes in synaptic properties are caused by changes in intracellular Ca²⁺ dynamics in the presynaptic LP neuron. Each of the two models reproduces facilitation at low presynaptic voltages, explaining it by the gradual increase in Ca²⁺ concentration in the presynaptic terminal due to the changes of Ca²⁺ influx from pulse to pulse through I_Ca and I_MI channels, respectively. Additionally, in both models it is important for these channels to be close to the presynaptic sites of transmitter release for the mechanisms described to work.

Model I is based on the ideas put forth in our earlier modeling study in which we examined the potential for intracellular Ca²⁺ ion accumulation for producing the synaptic facilitation observed in the presence of proctolin (Zhou et al. 2007). In that study, we described the switch from depression to facilitation using two low-threshold and one high-threshold Ca²⁺ currents which, as shown in the current study, can be accomplished with a single Ca²⁺ current. The simplification of the model in the current study facilitated a direct comparison of the mechanisms underlying the neuromodulation of synaptic plasticity.

It is known that the neuromodulator dopamine exerts its action partially by modulating calcium currents in pyloric neurons (Johnson et al. 2003). Enhancement or reduction of I_Ca is consistent with dopamine-induced synaptic strength changes. Similarly, one possible explanation of proctolin-induced synaptic strength changes is via modulation of presynaptic, I_Ca which is captured by the Ca²⁺ channel model (model I). The modulatory channel model (model II) is dependent on Ca²⁺ influx through both a Ca²⁺ channel and a proctolin-activated non-specific cation channel. Results of Stout et al. (1996) suggest that there is a glutamate-induced Mg²⁺ influx through the NMDA receptor ion channel. The proctolin-modulated MI channels are similar to NMDA receptor channels in that they are believed to be partially blocked by Ca²⁺ at low membrane potentials (Golowasch and Marder 1992). This led us to our second hypothesis that the modulation of the LP to PD synapse may be caused by the voltage-sensitive changes in Ca²⁺-permeability of the MI channels which has some recent experimental support (Gray and Golowasch 2011).

Although both models successfully reproduce the observed dynamic changes in the LP to PD synapse by proctolin, the two models predict different voltage dependence of the total steady-state Ca²⁺ current, which can be verified experimentally. In particular, experiments that combine Ca²⁺ imaging with Cd²⁺ block (which, unlike Mn²⁺, does not affect I_MI (Golowasch and Marder 1992)) of the principal voltage-dependent calcium channels may reveal changes in the Ca²⁺ permeability of the modulatory channels.

Note that the two proposed models make distinct predictions for the interaction between intrinsic and synaptic properties that determines neuronal network activity. Model I may only be relevant for the LP to PD synapse, because proctolin may only modulate local Ca²⁺ channels at this particular synapse, and may have no effect on other synapses in pyloric network or even other synapses from the same presynaptic LP neuron, for example the LP to PY synapse (Mamiya and Nadim 2005). Further, if other neuromodulators do not modulate presynaptic Ca²⁺ channels at this synapse, then the described results are specific to the effect of proctolin on the LP to PD synapse only. On the other hand, model II is likely to be applicable not only to the LP-PD synapse but also to other synapses in the pyloric network, because proctolin activates I_MI in other neurons of the same circuit. Moreover, other neuromodulators such as RPCH and CCAP are also known to activate MI channels (Swensen and Marder 2000). If model II is valid, a similar modulatory effect on synaptic dynamics may be observed throughout the network and may be subserved by a variety of modulatory substances.

The parameter values in the two models were set by optimizing the fit between model and data, which accomplishes several goals. First, it leads to a more thorough parameter-sensitivity analysis, allowing a more thorough exploration of parameter sets that are consistent with experimental observations. Preceding the parameter optimization with random parameter search significantly improves such sampling of parameter space. More importantly, the optimization allows one to establish or validate the mechanism by which elements of a chosen model capture the observed features of data, in this case depression or facilitation under control conditions or in the presence of proctolin. For instance, we hypothesized that model I would reproduce the observed facilitation in proctolin for low-amplitude stimulation if proctolin were to shifts the Ca²⁺ current activation to more negative potentials, and simultaneously change its activation time constant. This was substantiated by the parameter optimization, since Figure 2(a) shows that parameters that were most tightly constrained by data fit optimization correspond to the I_Ca half-activation potentials in control and proctolin, V_m and ${\mathit{\text{V}}}_{\mathit{\text{m}}}^{\mathit{\text{p}}}$, as well as the control potential of activation time constant in proctolin, $V_{\tau }^p$. Similarly, in model II we found that optimization always led to a decrease in the value of k⁻ to its allowed bottom bound of 0.1 s⁻¹, indicating that the only mechanism by which model II can explain facilitation in proctolin for low-amplitude stimulation is the gradual growth of the I_MI−Ca current caused by its slow de-activation. This conclusion was further verified by examining the time traces of simulated PD potential and I_MI−Ca for all optimized parameter sets.

Short-term dynamics of synaptic transmission have been modeled in a number of synapses subserving a variety of activities (Abbott et al. 1997; Hermann et al. 2009; Gundlfinger et al. 2007; Markram and Tsodyks 1996; Tsodyks et al. 1998). The basic feature of most of these models is that vesicle release from a readily releasable pool is generally considered crucial in explaining short-term plasticity. The classic presynaptic vesicle depletion model is often used to explain depression dynamics (Thies 1965; von Gersdorff et al. 1997; Wu and Betz 1998) whereas calcium-dependent transmitter release is usually invoked to model facilitation (Bertram et al. 1996; Matveev et al. 2006). Some studies at a large mammalian central synapse, the calyx of Held in the rat medial nucleus of the trapezoid body, indicate that regulation of voltage-gated Ca²⁺ channels is important in mediating short-term plasticity. For instance, inactivation of presynaptic Ca²⁺ currents is a major mechanism underlying short-term depression for a wide range of stimulation conditions (Xu and Wu 2005) whereas the facilitation of I_Ca mediated in a Ca²⁺-dependent manner (Borst and Sakmann 1998; Cuttle et al. 1998; Tsujimoto et al. 2002) contributes significantly to short-term facilitation (Inchauspe et al. 2004; Ishikawa et al. 2005; Xu and Wu 2005).

The mathematical models of neuromodulation of short-term synaptic dynamics developed in this paper are minimal in the sense that the presynaptic I_Ca is incorporated into a combined pre- and postsynaptic model using a minimal set of assumptions consistent with experimental findings. The advantage of this minimal approach is that the resulting models can be more easily tested with further experimentation. The small number of equations makes these models amenable to network simulations and the minimal implementation highlights those features of the presynaptic Ca²⁺ influx through Ca²⁺ or modulatory channels that play an important role in synaptic dynamics. Furthermore, our study demonstrates the plausibility of the hypothesis that neuromodulation of non-specific cation channels other than the principal presynaptic Ca²⁺ channels may influence synaptic release and therefore postsynaptic potentials. We note that non-specific ion channels show permeability to Ca²⁺ ions in a variety of systems, and therefore this finding has broader implications for potential mechanisms of neuromodulation of synaptic dynamics.