Quantification of cellular penetrative forces using lab-on-a-chip technology and finite element modeling

Abstract

Tip-growing cells have the unique property of invading living tissues and abiotic growth matrices. To do so, they exert significant penetrative forces. In plant and fungal cells, these forces are generated by the hydrostatic turgor pressure. Using the TipChip, a microfluidic lab-on-a-chip device developed for tip-growing cells, we tested the ability to exert penetrative forces generated in pollen tubes, the fastest-growing plant cells. The tubes were guided to grow through microscopic gaps made of elastic polydimethylsiloxane material. Based on the deformation of the gaps, the force exerted by the elongating tubes to permit passage was determined using finite element methods. The data revealed that increasing mechanical impedance was met by the pollen tubes through modulation of the cell wall compliance and, thus, a change in the force acting on the obstacle. Tubes that successfully passed a narrow gap frequently burst, raising questions about the sperm discharge mechanism in the flowering plants.

Tip-growing cells such as neurons, fungal hyphae, root hairs, and pollen tubes have the remarkable ability to follow external guidance cues and to penetrate surrounding living tissues or abiotic matrices. The purpose of this invasive growth activity depends on the cell type and ranges from exploring the environment with the goal of procuring nutrients and water (fungi, root hairs) to establishing contact between remote locations in the organism (neurons) and delivering gametes (pollen tubes). The common challenge encountered by tip-growing cells is the necessity to overcome the mechanical impedance of the tissue or matrix to be penetrated. Two complementary strategies generally are used, typically in combination: the cell produces enzymes or other agents to soften or dissolve the mechanical obstacle in its path, and/or the cell uses mechanical force to penetrate or displace the substrate. Whereas in animal cells the force required for a cell to migrate and invade is generated by the cytoskeleton, either by way of motor proteins (1) or by polymerization of the cytoskeletal filaments proper (2, 3), in plant and fungal cells any pushing force is generated by the internal turgor pressure. This difference is consistent with the fundamentally different mechanics of the growth process in walled cells. Fungal hyphae and plant cells are surrounded by a polysaccharidic cell wall, and all morphogenetic processes necessitate a mechanical deformation of this stiff extracellular matrix. The driving force for this process is supplied by the turgor pressure (4), and only if the cell’s own wall is pliable enough to yield to the turgor pressure can force be exerted onto the surrounding substrate. In tip-growing cells, the turgor pressure has been determined to be between 0.4 and 0.8 MPa for fungal hyphae (5, 6) and 0.1–0.4 MPa for pollen tubes (7). Although the cytoskeleton plays an important role in plant and fungal cell morphogenesis by regulating where and when cell wall components are deposited (8), cytoskeletal polymerization activity is not involved directly in the force generation required for cellular growth or invasive activities (9).

Because of the predominantly invasive lifestyle of fungi and oomycetes and the direct correlation between the efficiency of this behavior and pathogenicity, the mechanism of invasive growth in these organisms has been studied in detail (9–13). More than a century ago, the invasive force of fungal hyphae was measured using a gold membrane as mechanical resistance (14); more recently, a strain gauge (15), an optical wave guide (13, 16), and optical tweezers (17) have been used for this purpose. However, the invasive ability of tip-growing cells in plants remains largely unexplored. Pollen tubes have been investigated using different concentrations of an agarose-stiffened growth matrix (18), but no quantitative values for invasive force generation by this or other tip-growing plant cells had been reported. Our goal was to address this lack of knowledge for the pollen tube, the fastest growing cell in the plant body, whose invasive lifestyle is the fundamental underpinning of sexual reproduction in flowering plants.

The pollen tube is a tubular protrusion formed by the pollen grain upon landing on a receptive stigma. Its function is to deliver the male gametes from the pollen grain (male gametophyte) to the female gametophyte located in the ovules of the flower. The pollen tube therefore is the crucial link between the sexual partners during the reproduction process in higher plants, and its successful elongation growth is pivotal for fertilization and seed set. The distance the pollen tube must cover is species dependent and may be several tens of centimeters. Given that speed is a direct competitive selection factor for fertilization success, pollen tube growth rates are rather impressive at up to 1 cm/h (19, 20). Albeit with somewhat reduced growth rates, pollen tube growth can be triggered easily in an in vitro setup, and the resulting cellular shape and morphogenesis are virtually identical to the in situ situation (21).

To find its path to the ovule, the pollen tube has to invade a series of tissues composing the pistil of the receptive flower (22). Starting from the stigmatic tissue on which it lands, it subsequently must penetrate the transmitting tissue, a cellular mass located within the central canal of the style that connects the stigma to the ovary (23). Upon reaching the ovary, the pollen tube passes onto the internal surface of the placenta. It follows guidance cues emitted by the female gametophyte to embark on the funiculus, a stalk attaching the ovule to the placenta, and then targets the micropyle, an opening in the teguments enveloping the ovule (Fig. S1). Upon invading the micropyle, the pollen tube has to cross the nucellus, a tissue layer surrounding the female gametophyte, and then come in contact with the synergids, two cells adjacent to the egg cell. Here, the tube penetrates the filiform apparatus of one of the synergids, bursts open at its apex, and releases the two sperm cells, one of which moves toward the egg cell and fertilizes it to yield the zygote and future embryo (24). The other sperm cell fuses with the diploid central cell of the female gametophyte to form an accessory zygote that subsequently develops into the endosperm, a tissue that nourishes the growing embryo during its development.

As the pollen tube grows, the most mechanically challenging situations likely are the entry through the cuticle covering the stigmatic papillae (if present), passage through the transmitting tissue, entry into the micropyle, and penetration of the synergids. Depending on the species, the transmitting tissue may be a lining surrounding a hollow canal, leaving ample, mucus-filled space in which the tube can elongate. In many species, however, this canal is filled completely with the transmitting tissue and the tube has to invade and dilate the apoplastic space between the cells composing this tissue (23). Transmission electron microscopy has shown that the space between the cells typically is narrower than what would be required for the tube to pass unhindered (25, 26). Depending on the plant species, pollen tube invasion is facilitated by digestive enzymes that soften the apoplast and are secreted either by the pollen tube (27) or by the pistillar cells themselves (28), or the transmitting tissue is triggered to undergo programmed cell death (29). However, it is unlikely that either of these processes will liquefy the substrate completely. Therefore, it is reasonable to assume that the pollen tube exerts an invasive force. From a mechanical point of view, the process of pollen tube elongation when forcing through the apoplast is similar to that of a balloon catheter used for angioplasty, the widening of a narrow blood vessel to prevent heart infarct.

To quantitatively assess the invasive ability of the pollen tube, we adapted a previously developed lab-on-a-chip (LOC) called the TipChip (30–32). In the TipChip, pollen tubes are guided to elongate through narrow microchannels specifically designed to accommodate testing devices such as mechanical obstacles along its path. Although use of a conventional strain gauge technically is possible, we did not opt for it in the present setup, because a perpendicularly placed force sensor is known to underestimate the invasive force of tip-growing cells as the result of a cellular shape change upon orthogonal contact of the elongating cell with the flat surface of the strain gauge (10). Even more importantly, rather than presenting flat, perpendicular obstacles, the apoplast separating the cells in the pollen tube’s path consists of narrow gaps. Therefore, we designed the microchannels with a series of narrow gaps through which the pollen tubes had to squeeze to continue their elongation. This geometry more accurately represents the microstructure of the in vivo growth environment within the stylar tissue and the physical constraints in the path of pollen tube elongation (Fig. S1). The deformation of the sidewalls forming the microscopic gaps, together with the physical properties of the polydimethylsiloxane (PDMS) material used, allowed us to determine the dilating force exerted by the penetrating pollen tube in the direction normal to the contact surface with the microgap sidewall. Different gap sizes were used to test the pollen tube behavior and its limitations in terms of gap navigation.

Results

Design of the LOC and Quantification of Pollen Tube Behavior.

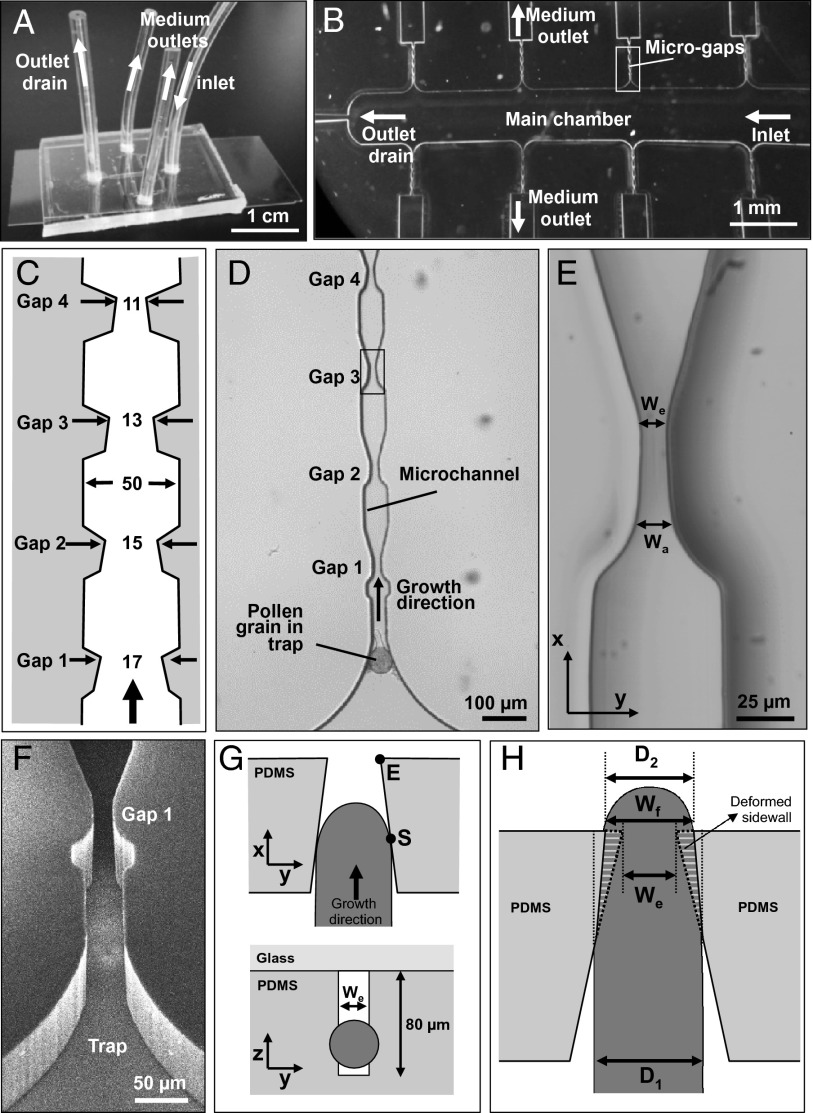
To challenge elongating pollen tubes with a precisely calibrated microstructure resembling the microarchitecture of the pistillar tissue, a modular LOC developed earlier, the TipChip (31), was adapted to expose pollen tubes of Camellia japonica to microscopic gaps. The microfluidic network of the TipChip consists of a distribution chamber, into which pollen grains are injected, and serially arranged microchannels along which the pollen tubes grow (Fig. 1). The entire microfluidic network has a depth of 80 µm to allow the pollen grains (diameter, 60 µm) to move freely while preventing their stacking in the z-direction (perpendicular to the planar orientation of the microfluidic network). Laminar flow within the distribution chamber is used to transport the pollen grains to the entrances of the microchannels where the grains are trapped. Excess pollen grains are evacuated through an outlet at the far end of the distribution chamber. Upon germination, the elongating pollen tubes are guided through the microchannel (width, 50 µm) and thus may be exposed to mechanical obstacles. These obstacles are positioned at least 100 µm from the microchannel entrance to ensure normal and unimpeded germination of the grain and initial tube growth. In the present setup, the microchannels were designed to feature four narrow gaps alternating with stretches of normal microchannel (Fig. 1 C and D). These microgaps were shaped as vertical slits with a constant height of 80 µm and tapered sidewalls that narrow linearly over a distance of 40 µm from initial width W_a to the narrowest part of the opening W_e. W_e was set to be slightly smaller than the size of the average Camellia pollen tube diameter (D₁) for the first gap and increasingly smaller for the three subsequent gaps. Each subsequent gap was set to be 2 µm narrower than the previous gap. The two designs used here started at a gap size of either W_e = 17 µm or 16 µm ending with W_e = 11 µm or 10 µm, respectively, for the fourth gap. In the y–z plane, a microgap of 11-µm width has a rectangular shape of 11 × 80 µm (Fig. 1F).

Fig. 1.

Experimental setup for the exposure of pollen tubes to microgaps and geometry of interaction. (A) Macro photograph of the TipChip illustrating arrangements of inlet and outlets. (B) Micrograph showing the geometry of the microfluidic network. (C) Dimensions of the microchannel with repeated narrow regions (microgaps). Numbers are in micrometers; the drawing does not reflect the aspect ratio. (D) Bright field micrograph of the geometry of a microchannel comprising the channel entrance with a trapped pollen grain and four subsequent gaps. (E) Close-up micrograph of a microgap indicated in D, showing an opening with W_a and W_e. (F) Scanning electron micrograph of the entrance of a microchannel and the first microgap viewed from an oblique angle. (G) Simplified schematic views of the interaction between an elongating pollen tube (dark gray) and a microgap. The pollen tube initially is in contact with both tapered sidewalls forming the microgap at point S. The microgap is formed as a rectangular, slit-shaped opening (white) in the PDMS material (light gray). (H) The passing pollen tube deforms the PDMS sidewalls of the gap to change the gap width at the narrowest section from W_e to W_f. During passage through the gap, the original width of the pollen tube D₁ temporarily is reduced to D₂ but typically widens after passing the gap.

Pollen tubes growing toward a microgap hit the sidewall at the starting point S (Fig. 1G). To continue growing, the tubes had to either apply a penetrating force wedging normal to the sidewalls (dilating force) and deform them, or form narrower tubes (constriction in the y direction, perpendicular to the long axis of the tube). The pollen tubes exited the microgap at end point E to return into the standard microchannel width with 50 µm (Fig. 1 C, D, and H). The interaction between the pollen tube and the sidewalls resulted in the deformation of the sidewalls, an apparent reduction in pollen tube diameter, or a combination of both. When W_f equaled W_e, the sidewall was not deflected and the pollen tube decreased in width to fit the size of the gap. In contrast, the width of the pollen tube did not change; instead, the sidewall was deflected when W_f equaled D₁. The tapered shape of the microgap ensured that the pollen tube did not change growth direction to avoid the obstacle, a phenomenon commonly observed when obstacles are presented perpendicular to the growth direction of pollen tubes (18) and fungal hyphae (10). The interaction between pollen tube and microgap was assessed by determining the change in the pollen tube width and the deflection of the PDMS sidewall forming the gap.

Navigation Through Microgaps.

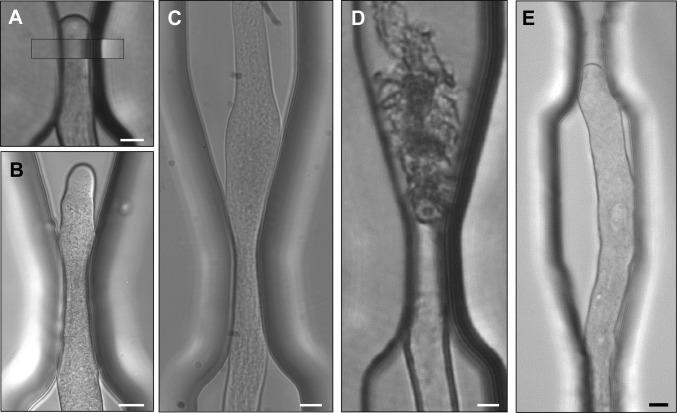
The unimpeded growth rate of Camellia pollen tubes along the microchannels varied between 4 and 11 µm/min. The diameter of the unchallenged pollen tubes ranged from 13 to 21 µm, and depending on the individual diameter, the first and/or second microgap did not pose a mechanical obstacle for the respective tube. Four different types of behavior were observed upon the pollen tubes’ encounter with narrower gaps: (i) The pollen tube passed through the gap without being deformed visibly, but by deforming the PDMS sidewalls (n = 20) (Fig. 2A). (ii) The pollen tube passed through the gap by changing cell shape (n = 5). The reduction in tube width observed microscopically might be either a true reduction in the diameter of the circular cross-section or a local transition from round to oval. The apparent reduction in width was temporary, and upon emerging into a wide portion of the microchannel, it typically returned to the original cell width (Fig. 2B) or became significantly wider than the original tube (Fig. 2C). This widening was temporary, and the tube eventually returned to its original diameter. (iii) The pollen tube passed the gap, and upon entering the wider portion of the channel, it burst (n = 8) (Fig. 2D and Movie S1). (iv) The pollen tube stalled in the gap (n = 5) (Fig. 2E). The fact that individual pollen tubes behaved differently during gap passage demonstrates that the material properties of the PDMS used here were appropriate to assess the mechanical force generation of Camellia pollen tubes. If all tubes had passed the gaps without effect on tube shape, this would indicate that the PDMS material was too soft to present an obstacle. If the gap walls were never deformed by the passing tubes, the PDMS material would have been too hard. Both situations would have prevented the calculation of the dilating force.

Fig. 2.

Different types of pollen tube behavior during passage through a microgap. (A) The pollen tube deflects the sidewalls almost completely to maintain its diameter. (Inset) Same position of the undeformed microgap before the invasion of the pollen tube. (B) The pollen tube becomes narrower in the y-direction to pass the gap and widens to the original diameter after passage. (C) The pollen tube becomes wider than the original tube after passing the gap, but eventually returns to the original diameter. (D) Following passage through the gap, the pollen tube bursts. (E) The pollen tube stalls and cannot pass through the gap. The buckling indicates that a force is exerted against the wall of the gap. Bars: 10 µm (bar in A applies to A–D).

To determine whether the different types of behavior might be correlated with a particular ratio between pollen tube diameter and gap size, these parameters were plotted (Fig. 3A). The plot clearly indicates that at a pollen tube diameter/gap size ratio ≤1.20, the pollen tube could pass without a lasting effect on its shape or growth rate. At a ratio between 1.20 and 1.33, the pollen tube passed, but either it burst after emerging from the gap or its diameter was altered temporarily. A ratio >1.33 prevented the pollen tube from passing and caused it to stall. The pollen tubes that successfully navigated the gap generally displayed a reduced growth rate while passing through the narrow portion (Fig. 3B). The growth rate increased again after emerging from the gap but within the critical ratio range of 1.20–1.33; this acceleration frequently led to bursting (Fig. 3).

Fig. 3.

Behavior of pollen tubes during passage through a microgap. (A) Effect of the ratio between pollen tube diameter and gap width on pollen tube behavior. Between ratios of 1.00 and 1.20, the pollen tubes deform the gap to pass almost without narrowing their diameter (green ▲). Below this ratio, the pollen tube diameter is reduced (light blue ◇) and frequently the tubes burst upon returning to the original diameter following gap passage (solid blue ◆). At a ratio of 1.33 and below, the tubes stall and cannot pass the gap (red ■). Each data point represents one interaction between a pollen tube and a microgap. (B) Change in growth rate during microgap passage. Upon encountering the gap at point S, the tube slows considerably but shows a constant growth rate despite the continuously narrowing gap. After exiting the narrowest region at point E, it starts growing faster but bursts soon after.

Male Germ Unit.

The male germ unit of the pollen tube consists of the vegetative nucleus and the two sperm cells surrounded by a double membrane (Fig. S2). These structures are connected physically to each other (33) and are moved forward in the elongating tube guided by the microtubule cytoskeleton of the vegetative cell (34). Our observations show that in Camellia pollen tubes, the vegetative nucleus was closer to the tip than the sperm cells, with a distance of ∼60–80 µm from the apex, whereas the sperm cells were located immediately adjacent in distal direction with their nuclei at ∼120 µm and 155 µm away from the tip. During normal growth, these distances were kept very stable. During passage through a narrow gap, the vegetative nucleus occasionally had difficulty passing the narrow passage after the pollen tube tip had grown through it successfully (Fig. S2). The nucleus could turn or twist to pass the gap, but this might have entailed a delay in forward movement relative to the velocity of the growing tip. In these cases, once the vegetative nucleus cleared the gap, it usually increased its speed forward to regain its normal distance from the tip (Movie S2). Importantly, when pollen tube bursting was induced by passage through a narrow gap, the male germ unit might have been stuck behind the gap instead of being ejected (Fig. S2).

Finite Element Simulation.

Whereas tubes with a size ratio of 1.2 or higher coped with the slit-shaped microgap by changing their shape, those with ratios between 1.0 and 1.2 could penetrate the gap without significant changes to their shape, deforming the tapered PDMS sidewalls instead (Fig. 3A). This demonstrates that pollen tubes can exert a dilating force in the radial direction that ensures maintenance of the cell shape against forces exerted by the surrounding pistillar tissue. To quantify this dilating force, we modeled the interaction between pollen tube and microgap using finite element analysis.

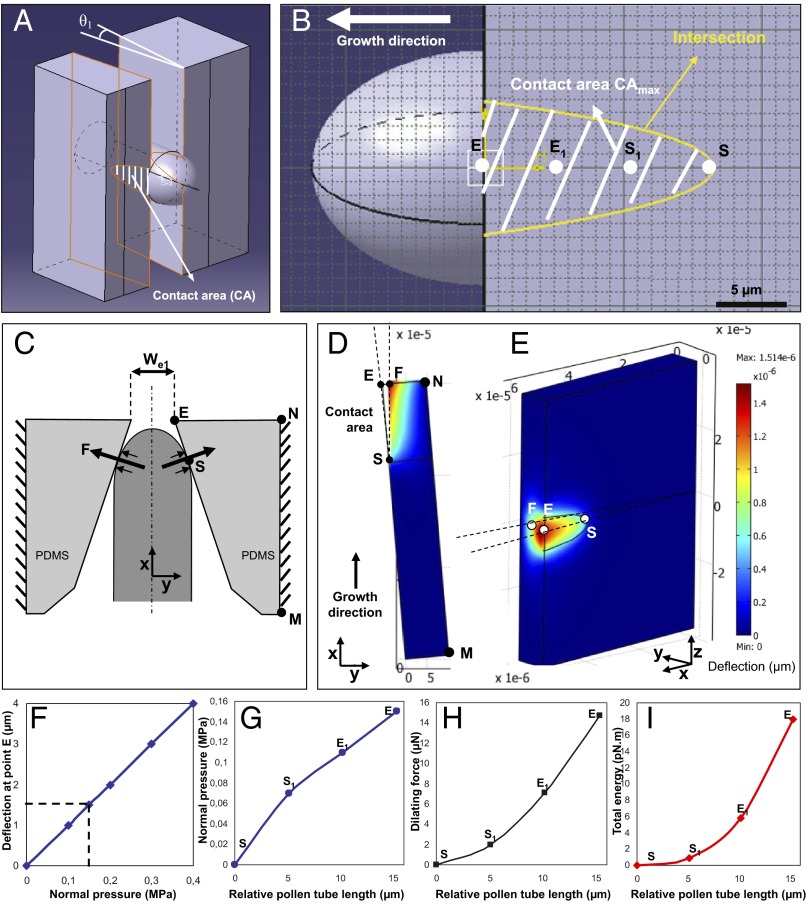
First, the actual contact area between the pollen tube and the microgap during growth was established. This was based on the geometry observed when pollen tubes passed a gap without a detectable change in tube diameter. It was assumed that the maximum contact area is achieved when the hemisphere-shaped tip has passed the gap and the cylindrical tubular portion is in contact with the gap wall. The tube therefore was represented as a cylinder with a constant diameter of 17 µm (Fig. 4B). The microgap is modeled as a 3D structure with tapered sidewalls with a starting width of 20 µm, which narrows to 14 µm (Fig. 4 A and C). The intersection of the cylindrical tube and the tapered sidewall of the microgap is determined using computer-aided design software (AutoCAD 2007). Projection of the contact surface on the sidewall plane [contact area (CA)] when the dome has completely passed through the microgap is shown in Fig. 4B.

Fig. 4.

Finite element model for the simulation of force exertion by the pollen tube on the sidewalls of the microgap. (A) Three-dimensional representation indicating the contact surface between the pollen tube and microgap when the pollen tube is in maximum contact with the sidewall. (B) Position of four reference points on the contact area, starting with point S upon initial contact and ending with point E, the exit of the gap. Points S₁ and E₁ are two sample points equally spaced between S and E. (C) Top view of the simulated geometry, indicating the orientation of the force vectors. (D and E) Top view (D) and 3D view (E) of sidewall deflection at effective pressure P = 0.15 MPa. The color code represents the deflection of the PDMS material. (F) Effect of varying effective pressure on sidewall deflection at point E as simulated by the finite element model. (G) Normal pressure required for sidewall deformation during pollen tube passage through the gap. (H) Dilating force F required for sidewall deformation during pollen tube passage through the gap. (I) Total energy required for sidewall deflection during pollen tube passage through the gap. (G–I) The values are plotted as a function of the pollen tube length, measured relative to the initial length of the tube at the moment of first contact with the microgap wall.

To model the effect of the dilating force exerted by the pollen tube on the PDMS sidewall, finite element modeling was used. In this model, identical pressure is applied throughout the contact area at a given instant of growth. As the tube grows, the contact area increases and a different pressure is applied throughout the new contact area (Fig. 4C). During the advancement of the hemisphere-shaped pollen tube apex into the narrow region of the gap, the contact area increases (in both z and x directions) from zero to the maximum value CA_max at which the PDMS deforms sufficiently to allow passage of the cylindrical portion of the tube through the microgap. Based on published values for Young’s modulus of PDMS material (35) and the measured sidewall deformation required to permit pollen tube passage, the normal pressure exerted on the sidewall and the resulting dilating force are calculated. The induced dilating force (F) shown in Fig. 4 changes from zero at initial contact to a maximum value of F_max, corresponding to the maximum contact area CA_max when the tip exits the gap at point E (Fig. 4B).

An engineering stress–strain relationship is used to extract the dilating force. Assuming small deflections, Navier’s equation for static analysis was used to measure the PDMS deflection under pollen tube pressure (36). To solve the governing Navier equation for the presented interaction model, finite element static analysis is implemented using COMSOL Multiphysics 3.5 software (SI Text). As the boundary condition for finite element modeling analysis, the microgap along the MN line is the fixed support (Fig. 4C). The normal pressure P is applied to the contact area (Fig. 4 D and E). An isotropic material model with a Young modulus of E = 1 MPa and a Poisson ratio of ν = 0.4 is chosen for the PDMS (35). The geometry of the 3D microgap was meshed using quadratic Lagrange elements. The deflection of the PDMS microgap at point E is estimated for various normal pressures P (Fig. 4F) to determine the pressure at the surface that is required for pollen tube passage. The simulations show that a deflection of 1.5 µm at point E requires a uniformly distributed contact pressure of 0.15 MPa (Fig. 4F).

Based on the estimated pressure, dilating force F is extracted using boundary integration over the contact area. At the moment of maximum contact, when the tube reaches the narrowest region of the gap, the total contact area is 98 µm². At this point, F is predicted to be 14.7 µN (Fig. 4H). Because the microscopic quantification of the PDMS deflection is limited by the optical resolution of the microscope, we used the FEM model to determine the effect of measuring imprecision on the calculated force. For a noise of ±0.2 µm in detecting the PDMS deflection, the force changes by ±2.7 µN. The simulations show that before the moment of maximal contact, the normal pressure P necessary to deflect the PDMS material increases in an approximately linear manner as a consequence of the linearly narrowing gap (Fig. 4G). In contrast, the dilating force F increases nonlinearly, consistent with the nonlinear increase in the contact area between tube and gap wall (Fig. 4H). Based on the dilating force and the deflection of the wall, the corresponding total energy required to deflect the microgap may be calculated using integration over the volume of PDMS material displaced by the pollen tube (37). Similar to the dilating force, the total energy required for the pollen tube to overcome the resistance of one sidewall during gap passage increases nonlinearly (Fig. 4I).

Discussion

Tip-growing cells such as neurons, fungal hyphae, root hairs, and pollen tubes, have the formidable task of invading surrounding tissues or other substrates. The purpose of this invasive activity differs among the cell types, but the common challenge for all these cells is the necessity to navigate mechanical obstacles and exert force to displace and penetrate the surrounding matrix. In the case of the pollen tube, this invasive behavior serves to deliver the gametes to their destination; therefore, unlike the other tip-growing cell types, the pollen tube functions as a catheter-like delivery system. This requires not only an invasive force but also the protection of the contents to be transported, the male germ unit. It is crucial that the pollen tube remain tubular, because a kink or collapse in the cylindrical tube shape would prevent passage of the sperm cells. This requires the exertion of pressure to prevent the tube from collapsing under external load. Therefore, rather than comparing the invading pollen tube with a solid object, such as a needle, the mechanical analog of a pollen tube is a balloon catheter conventionally used to widen blocked arteries during angioplasty. To assess the behavior of the pollen tube when faced with an obstacle, we presented elongating tubes with a structural feature resembling those it encounters in planta—the apoplast and narrow intercellular spaces of the pistillar tissues. Our observations demonstrate that the tube does not avoid a narrow opening but proceeds by penetrating it. An elastic opening causing moderate size constraint was deformed completely during passage, but narrower slits caused a reduction in pollen tube width. If this constriction was too narrow, the passage of the male germ unit indeed was jeopardized and, if not blocked, slowed at least temporarily. In this context, it is intriguing to note that the diameter of the pollen tube seems to be hardwired into the pollen tubes of a particular species, illustrated by the fact that tube diameter varies significantly between species (with 5 µm in Arabidopsis and 17 µm in Camellia) but only to a small degree within a given species. The return of the Camellia pollen tube to its previous diameter after a size change induced by gap passage indicates the endogenous control of cell shape that ensures the successful transport of the male germ unit without its getting stuck. The precise mechanism controlling pollen tube diameter is subject to numerous biological and modeling approaches (38, 39), but how species-specific differences can be explained warrants further research.

The observed bursting events after microgap passage open an intriguing avenue to a possible mechanism for sperm cell release in plants. During successful fertilization, the two immotile sperm cells carried by the pollen tube are released by bursting once the pollen tube enters the female gametophyte. Bursting therefore is a crucial and final event in the life of a pollen tube. It must occur for fertilization to happen, but it must not occur precociously, before the female gametophyte is reached. Several agents involved in intergametophyte signaling and attraction of pollen tubes were identified recently (24, 40); however, the physiological mechanisms leading to pollen tube burst and thus sperm discharge remain elusive. Based on our observations, one might propose that a simple mechanical signal, an opening that is narrower than the tube diameter, might represent a trigger mechanism. These putative narrow openings might be represented by the micropyle (the opening in the teguments surrounding the ovule), the intracellular spaces in the nucellus (the cell layer surrounding the female gametophyte), or the invaginations forming the filiform apparatus of the synergids (Fig. S1). However, several of our findings speak against this hypothesis. The range in size ratios that seems to be conducive to bursting is very narrow—between 1.20 and 1.33. At ratios lower than 1.20, the tube simply grows through the gap and beyond without bursting; at ratios higher than 1.33, the tube stalls. Given that there is a certain variability of pollen tube diameter within a single pollen batch, a particular gap size in the ovular structure would allow successful delivery of sperm cells by only a subset of pollen tubes that have the correct diameter relative to the gap size. Because there is no obvious advantage for an ovule to practice exclusion based on pollen tube size, this method does not seem biologically relevant and the search for chemical or proteic triggers remains an urgent quest (24, 40). Second, even if the tube bursts following successful passage of a narrow gap with the appropriate size ratio, the male germ unit does not necessarily pass the narrow gap and might not be ejected from the tube upon burst, as shown in Fig. S2. This further reinforces the notion that a mechanical constraint is unlikely to be involved in sperm discharge in plants. However, even if sperm discharge does not rely on a mechanical trigger, the fact that a tight grip around the tube does result in sperm release illustrates that plant cells perceive and respond to mechanical stimuli.

The precisely defined geometry and known mechanical properties of the material used for the microgaps in the TipChip allowed us to calculate the effective pressure exerted by the pollen tubes using finite element methods. We determined that a maximum pressure of 0.15 MPa is exerted on the gap walls at point E, when the tube has reached the narrowest point of the gap. Any force the pollen tube exerts—whether normal to the laterally placed gap or in the direction of the unidirectional growth—is generated by the turgor pressure that therefore poses the upper limit. The turgor pressure of Camellia pollen tubes is not known, but in lily pollen tubes an average turgor pressure of 0.2 MPa has been determined (7). Our estimated normal pressure thus is on the same order of magnitude but somewhat lower. In this context, it is important to point out that although the hydrostatic turgor pressure provides an upper limit to the force exerted by the pollen tube, the pressure transmitted to the outside of the cell generally is far below this value. In fungal hyphae, the effective pressure calculated from the invasive force typically amounts to only 10% of the turgor pressure (10, 11). The reason for this is that the hydrostatic turgor pressure in the cell is not exerted against the external substrate unless the wall relaxes and has some freedom to expand. Only in some environmental conditions was this fraction found to increase to up to 54% in fungal hyphae (41). The fact that our value of 0.15 MPa for the normal pressure in Camellia pollen tubes is very close to the typical turgor pressure of pollen tubes of similar size [lily, 0.2 MPa (7)] suggests that the compliance of the cell wall in the apical region of the pollen tube is very high compared with the fungal hyphae measured so far, thus releasing much of the turgor-induced pressure to the outside, enabling optimal force exertion. Because the cell wall at the very tip of the tube likely is even softer than that at the flanks involved in the dilating force (38), it may be assumed that the force exerted in the direction of elongation is even higher than the dilating force. However, confirmation of this notion warrants further investigation and a different mechanical test assay (16).

During elongation growth, the cell wall material at the pollen tube apex yields constantly, but in a controlled manner, to the turgor that serves as a driving force for its stretching (38, 42, 43). It is thought that tip-growing cells can adapt their invasive force to the growth conditions by changing the compliance of the cell wall, but experimental evidence for this ad hoc modulation has been elusive. Intriguingly, a detailed analysis of the behavior of the Camellia pollen tube during gap passage provides evidence for this notion. The finite element simulations showed that during the interaction between the advancing pollen tube tip and gap walls, the total energy required to overcome the sidewall resistance increases nonlinearly with the contact area. Because the time course plots of the growth rate did not indicate a significant drop in the growth rate between the moment of initial contact with the gap walls and the moment the tube has reached the narrowest part of the obstacle, the energy dissipated in the deforming PDMS structure should be compensated for either by increasing the turgor pressure or by softening the cell wall. The observation that numerous tubes burst after gap passage is consistent with both mechanisms and hence does not allow discrimination between them. However, finite element modeling has shown that an increase in turgor does not cause a change in tube diameter, whereas a reduction in Young’s modulus in the apical cell wall would cause the tube to grow with a widened diameter (38). The temporary widening of the tube after gap passage (Fig. 2C) therefore supports the notion that rather than a change in turgor, the tube copes with increasing mechanical impedance by increasing the compliance of its wall. This behavior is akin to the bursting of hyphae exposed to a temperature shock. This failure was purported to occur as a result of a sudden change in the relationship between cell wall properties and turgor pressure (10).

Materials and Methods

Pollen Collection and Germination.

Pollen grains of C. japonica were collected from a plant in the Montreal Botanical Garden, dehydrated on anhydrous silica gel overnight, and stored in gelatin capsules at −20 °C. Before use, the pollen was rehydrated in a humid chamber at room temperature for at least 30 min. A few micrograms of pollen were suspended in growth medium containing 2.54 mM Ca(NO₃)₂·4H₂O, 1.62 mM H₃BO₃, 1 mM KNO₃, 0.8 mM MgSO₄·7H₂O, and 8% sucrose (wt/vol) (44). When the grains started germinating, the pollen suspension was introduced into the LOC.

Fabrication of the Microfluidic Device.

The LOC was fabricated as detailed in refs. 30, 31 and in SI Text.

Microscopy.

Bright field imaging of microgap structure was done on a Nikon Eclipse 80i inverted microscope equipped with an Infinity 1 digital CCD camera and infinity analyzer software. Samples were observed either with a Zeiss Imager Z1 microscope equipped with a Zeiss AxioCam MRm Rev.2 camera and AxioVision Release 4.5 software or with a Nikon Eclipse TE2000-U inverted microscope equipped with a Roper fx cooled CCD camera and ImagePro (Media Cybernetics) software. Scanning electron micrographs were taken with an FEI Quanta 200 scanning electron microscope operating at 15 kV.