Abstract
Genetic and other scientific studies routinely generate very many predictor variables, which can be naturally grouped, with predictors in the same groups being highly correlated. It is desirable to incorporate the hierarchical structure of the predictor variables into generalized linear models for simultaneous variable selection and coefficient estimation. We propose two prior distributions: hierarchical Cauchy and double-exponential distributions, on coefficients in generalized linear models. The hierarchical priors include both variable-specific and group-specific tuning parameters, thereby not only adopting different shrinkage for different coefficients and different groups but also providing a way to pool the information within groups. We fit generalized linear models with the proposed hierarchical priors by incorporating flexible expectation-maximization (EM) algorithms into the standard iteratively weighted least squares as implemented in the general statistical package R. The methods are illustrated with data from an experiment to identify genetic polymorphisms for survival of mice following infection with Listeria monocytogenes. The performance of the proposed procedures is further assessed via simulation studies. The methods are implemented in a freely available R package BhGLM (http://www.ssg.uab.edu/bhglm/).
Keywords: Adaptive Lasso, Bayesian inference, Generalized linear model, Genetic polymorphisms, Grouped variables, Hierarchical model, High-dimensional data, Shrinkage prior
1. Introduction
Scientific experiments routinely generate very many highly correlated predictor variables for complex response outcomes. For example, genetic studies of complex traits (e.g. QTL (quantitative trait loci) mapping and genetic association analysis) usually genotype numerous genetic markers across the entire genome, with closely linked markers being nearly collinear. The main goals of such studies are to identify which predictor variables are associated with responses of interest and/or to predict outcomes of new individuals using all the predictor variables. To control for potential confounding effects, it is desirable to simultaneously fit as many predictors as possible in a model. Due to high-dimensional and correlated structure, however, classical generalized linear models are usually nonidentifiable, and thus a variety of penalization methods and Bayesian hierarchical models have been proposed to solve the problem.
Penalization approach introduces constraints (or penalties) on the coefficients and estimates the parameters by maximizing the penalized objective function (Hastie, Tibshirani and Friedman, 2001). A promising penalization method is the Lasso of Tibshirani (1996), which uses the L1-penalty, , where λ(≥ 0) is the tuning parameter controlling the amount of penalty. Bayesian approach places prior distributions on the coeffificients and summarizes posterior inference using MCMC algorithms or by finding posterior modes (Gelman et al., 2003). A commonly used prior distribution is the double-exponential distribution, , where λ (≥ 0) is the shrinkage parameter controlling the amount of shrinkage (Park and Casella, 2008; Tibshirani, 1996a, b; Yi and Xu, 2008). Under this prior, the posterior modes of the coefficients correspond to the Lasso estimates (Park and Casella, 2008; Tibshirani, 1996a). Another widely used prior distribution is the Student-t distribution, p(βj) = tv(0,s2), with the degrees of freedom ν and the scale s controlling the amount of shrinkage (Gelman et al., 2008; Yi and Xu, 2008). The family of the Student-t distributions includes various distributions as special cases, for example, Normal βj ~ N(0, s2) (ν = ∞), Jeffreys’ prior βj ∝ 1/|βj| (ν = s = 0) and Cauchy (ν = 1). One remarkable feature of the above distributions is that they can be expressed as scale mixtures of normal distributions (Park and Casella, 2008; Yi and Xu, 2008). This hierarchical formulation leads to the development of straightforward MCMC and Expectation-Maximization (EM) algorithms (Figueiredo, 2003; Gelman et al., 2008; Kyung et al., 2010; Park and Casella, 2008; Yi and Banerjee, 2009; Yi and Xu, 2008).
The above approaches have shown excellent performance in many situations, however they have some limitations. First, the Lasso (also Student-t) uses a unique tuning parameter to equally penalize all coefficients, and thus can either include a number of irrelevant variables or over-shrink large coefficients. This is particularly critical for sparse high-dimensional data (as in most genetic studies) where among hundreds or thousands of variables only a few have detectable effects. To address this issue, Zou (Zou, 2006) introduced the adaptive Lasso that uses a weighted L1-penalty , where with being some preliminary estimate of βj such as the least-squares estimate. The intuition of the adaptive lasso is to use different penalty parameters for different coefficients and thus differently shrink coefficients. Although theoretically attractive, the practical performance of the adaptive Lasso heavily depends on the quality of the initial estimates. Secondly, some previous methods cannot appropriately address the hierarchical structures of predictor variables. To accommodate the grouping structure, several group approaches based on composite penalties have been proposed. Both the inner and outer penalties can take multiple forms, including ridge, Lasso, elastic net and others. If the inner penalty is ridge as with group Lasso, then the approaches have an “all in or all out” property for variables within the same groups. If the inner penalty is Lasso-type, then two level selection may be achieved. Despite theoretical effectiveness of such methods, they may suffer a high computational cost.
In this article, we adopt a Bayesian approach and propose hierarchical prior distributions for high-dimensional generalized linear models with grouped predictor variables. We express our hierarchical priors as scale mixtures of normal distributions: , or , and assume that the scale parameters (or λj) or further follow gamma distributions with unknown group-specific hyperparameters. The variable-specific scale parameters are similar in spirit to the variable-specific penalties in the adaptive Lasso of Zou (2006), but they can be easily estimated in our Bayesian framework. Similar Bayesian approaches have been proposed. Griffin and Brown (2010) (Griffin and Brown, 2010) and Leng et al. (2010) (Leng, Minh Ngoc Tran and Nott, 2010) have generalized the Bayesian Lasso by including variable-specific scale parameters in the exponential prior with gamma mixing distributions. Sun et al. (2010) (Sun, Ibrahim and Zou, 2010) and Armagan et al. (2010) (Armagan, Dunson and Lee, 2010) assume the parameters λj rather than in the exponential prior to follow gamma distributions and show that this treatment induces simpler posterior distributions facilitating study of properties and implementation. Carvalho et al. (2009, 2010) (Carvalho, Polson and Scott, 2009, 2010) proposed the horseshoe prior that is similar to our prior with . More recently, Lee et al (2012) (Lee et al., 2012) discussed the use of Bayesian sparity priors obtained through hierarchical mixtures of normals for the analysis of genetic association. However, these previous methods either prefix the hyperparameters in gamma distributions or have not considered grouped variables. Our hierarchical priors consist of both the group-specific and variable-specific parameters, and thus not only adopt different shrinkage for different coefficients and different groups but also providing a way to pool the information within groups.
To develop our algorithms for fitting generalized linear models with the proposed hierarchical prior distributions, we first derive the conditional posterior distributions for all parameters. These posterior distributions may allow us to implement MCMC algorithms. In this paper, however, we focus on much faster EM algorithms for finding posterior modes. We incorporate our EM algorithms into the usual iteratively weighted least squares (IWLS) for fitting classical generalized linear models as implemented in the general statistical package R. This strategy allows us to take advantage of the existing algorithm and leads to stable and flexible computational tools.
The rest of the paper is organized as follows. We first introduce hierarchical generalized linear models with grouped variables in Section 2 and then describe the hierarchical prior distributions in Section 3. We derive our EM-IWLS algorithms for fitting the hierarchical GLMs with the proposed priors in Section 4 and describe the implementation in R in Section 7. In Section 6, we discuss the relationship between the proposed models and existing approaches. Section 7 illustrates the methods with data from an experiment to identify genetic polymorphisms for survival of mice following infection with Listeria monocytogenes. Section 8 demonstrates the performance of the proposed procedures via simulation studies. Finally, some concluding remarks and potential extensions are discussed in Section 9.
2. Hierarchical Generalized Linear Models with Grouped Predictors
We consider the problem of variable selection and coefficient estimation in generalized linear models with a large number of coefficients or highly correlated predictor variables. The observed values of a continuous or discrete response are denoted by y = (y1, ⋯, yn). We assume that the predictor variables can be divided into K groups, Gk, k =1, ⋯, K, and the k-th group Gk contains Jk variables, where K ≥ 1 and Jk > 1. There may be multiple ways of defining the groups. In genetic studies, for example, we can use genomic regions or candidate genes, or the types of the effects (e.g., additive and dominance effects) to construct groups. We also include in the model some variables (e.g., gender indicator, age, etc.) that do not belong to any groups.
A generalized linear model consists of three components: the linear predictor η, the link function h, and the data distribution p (Gelman et al., 2003; McCullagh and Nelder, 1989). The linear predictor for the i-th individual can be expressed as
| (1) |
where β0 is the intercept, xij and zij represent observed values of ungrouped and grouped variables, respectively, βj is a coefficient, the notation j ∈ Gk indicates the group of variable j, Xi contains all variables, and β is a vector of all the coefficients and the intercept. For simplicity, we denote Xi = (1, xi1, ⋯, xiJ) and β = (β0, β1, ⋯, βJ)′, where is the total number of variables.
The mean of the response variable is related to the linear predictor via a link function h:
| (2) |
The data distribution is expressed as
| (3) |
where φ is a dispersion parameter, and the distribution p(yi|Xi,β,φ) can take various forms, including Normal, Gamma, Binomial, and Poisson distributions. Some GLMs, for example the Poisson and the Binomial models, do not require a dispersion parameter; that is, φ is fixed at 1.
Generalized linear models with many coefficients or highly correlated variables can be nonidentifiable classically. An approach to overcoming the problem is to use Bayesian inference. We use a hierarchical framework to construct priors for coefficients. At the first level, we assume an independent normal distribution with mean 0 and variable-specific variance for each coefficient βj :
| (4) |
The variance parameters directly control the amount of shrinkage in the coefficient estimates; if , the coefficient βj is shrunk to zero, and if , there is no shrinkage. Although these variances are not the parameters of interest, they are useful intermediate quantities to estimate for easy computation of the model.
We treat the variances as unknowns and will further assign prior distributions to them as discussed in the next sections. Enough data is available to estimate the intercept β0 and the dispersion parameter φ. Thus, we can use any reasonable non-informative prior distributions for these two parameters; for example, with set to a large value, and p(logφ) ∝ 1.
3. Hierarchical Adaptive Shrinkage Priors for Variance Parameters
The prior distributions for the variance parameters play a crucial role on variable selection and coefficient estimation. We consider two types of priors; the first is the half-Cauchy distribution for τj, and the second is the exponential prior distribution for .
3.1. Half-Cauchy prior distribution for τj
A half-Cauchy distribution can be expressed as
| (5) |
which has a peak at zero and a scale parameter αk[j], where the subscript k[j] indexes the group k that the j-th predictor belongs to. The scale parameter controls the amount of shrinkage in the variance estimates; small scales force most of the variances close to zero (Gelman, 2006). For grouped variables, we treat the scale parameters αk[j] as random variables and assign a noninformative prior distribution on the logarithmic scale, p(log αk[j]) ∝ 1. The common scale αk[j] induces a common distribution for variables within a group. For ungrouped variables, we cannot estimate the scale and thus preset αk[j] to a known value (say αj = 1).
There is no direct way to fit the model with the above half-Cauchy prior. Therefore, we use the hierarchical formulation of the half-Cauchy distribution. The half-Cauchy variable can be expressed as the product of the absolute value of a normal random variable with variance and the square root of an inverse-χ2 variable with degree-of-freedom 1 and scale 1, i.e., τj =|sj|ηj, where and . For computational simplicity, we deal with rather than τj and express the prior distribution of hierarchically:
| (6) |
where ν = 1, a = 0.5, and . We describe the computational algorithm for arbitrary values of ν and a in the next section. The half-Cauchy prior distribution corresponds to ν = 1 and a = 0.5, and is free of user-chosen hyperparameters.
3.2. Exponential prior distribution for
The second prior distribution assumes that the variances follow exponential or equivalently gamma distributions with variable-specific hyperparameters sj :
| (7) |
The hyperparameter sj controls the amount of shrinkage in the variance estimate; a large value of sj forces the variance closer to zero. We treat the hyperparameters sj as random variables with the Gamma hyper-prior distributions:
| (8) |
where the subscript k[j] indexes the group k that the j-th predictor belongs to, and a and bk[j] are two hyperparameters. As shown later, placing the gamma prior on sj rather than leads to a simpler posterior distribution of sj that is independent of the variance and thus facilitates computation.
As default, we set a = 0.5. Theoretically, we need not worry so much about how to select a, because the shrinkage can be determined by bk[j] and thus the hyperparameter a has less effect on inference. For ungrouped variables, we preset bk[j] to a known value (say bk[j] = 0.5). For grouped variables, we treat the scale parameters bk[j] as unknown parameters and assign a noninformative prior distribution on the logarithmic scale of bk[j], i.e., p(log bk[j]) ∝ 1.
The above prior distributions include group-specific parameters bk and variable-specific parameters sj. The group-specific parameters provide a way to pool the information among variables within a group and also to induce different shrinkage for different groups, while the variable-specific parameters allow different shrinkage for different variables. Indeed, as we will see in later numerical experiments, the estimates of bk for groups which include no important variables will be much different from those with important variables, and the estimates of sj for zero βj will be different from those for nonzero βj.
Conditional on the scale parameters sj, the hierarchical priors (6) and (7) induce the Student-t distributions and the double-exponential distributions βj ~ DE(0, sj) on the coefficients, respectively. Hereafter, we refer these two prior distributions as to hierarchical t and hierarchical double-exponential distributions, respectively. For the hierarchical t prior, we use the hierarchical Cauchy distribution as a default choice (i.e., setting ν = 1).
4. EM-IWLS Algorithm for Model Fitting
We fit the above hierarchical generalized linear models by estimating the marginal posterior modes of the parameters (β,φ). We modify the usual iterative weighted least squares (IWLS) for fitting classical GLMs and incorporate an EM algorithm into the modified IWLS procedure. The EM-IWLS algorithm increases the marginal posterior density of the parameters (β,φ) at each step and thus converges to a local mode. Our EM algorithm treats the unknown variances and the hyperparameters sj and bk[j] as missing data and estimates the parameters (β,φ) by averaging over these missing values. At each step of the iteration, we replace the terms involving the parameters (β,φ) and the missing values (, sj, bk[j]) by their conditional expectations, and then update the parameters (β,φ) by maximizing the expected value of the joint log-posterior density,
| (9) |
4.1. Conditional posterior distributions and conditional expectations
For the E-step of the algorithm, we take the expectation of the above joint log-posterior density with respect to the conditional posterior distributions of the variances and the hyperparameters. For the hierarchical t prior distribution, the conditional posterior distributions are
| (10) |
| (11) |
| (12) |
Therefore, we have the conditional expectations
| (13) |
| (14) |
| (15) |
For the hierarchical double-exponential prior distribution, the conditional posterior distributions are
| (16) |
| (17) |
| (18) |
Therefore, we have the conditional expectations
| (19) |
| (20) |
| (21) |
It is worth noting that under the hierarchical double-exponential prior the posterior p(sj|βj,bk[j]) is independent of the variance , which may speed up convergence.
4.2. Estimating (β,φ) conditional on the prior variances
Since only the terms include both the parameters and the missing values, only the conditional expectations directly affect the M-step. Given the prior variances , j = 0, ⋯, J, we thus estimate (β,φ) by fitting the generalized linear model with a normal prior distribution for the coefficients the generalized linear model yi ~ p(yi | Xi,β,φ) with the normal priors (Gelman et al., 2008; Yi and Banerjee, 2009; Yi, Kaklamani and Pasche, 2011). Following the usual iteratively weighted least squares (IWLS) algorithm for fitting generalized linear models (as implemented in the glm function in R), we approximate the generalized linear model likelihood p(yi | Xi,β,φ) by the weighted normal likelihood
| (22) |
where the ‘normal response’ zi and ‘weight’ wi are called the pseudo-response and pseudo-weight, respectively. The pseudo-response and pseudo-weight are calculated by
| (23) |
where , , L′(yi | ηi) = dL(yi | ηi)/dηi, L″(yi | ηi) = d2L(yi | ηi)/dηi2, and is the current estimate of β.
The prior can be incorporated into the weighted normal likelihood as an ‘additional data point’ 0 (the prior mean) with corresponding ‘explanatory variables’ equal to 0 except xj which equals 1 and a ‘residual variance’ (Gelman et al., 2003; Gelman et al., 2008). Therefore, we can update β by running the augmented weighted normal linear regression
| (24) |
where is the vector of all zi and all (J + 1) prior means 0, is constructed by the design matrix X of the regression and the identity matrix I(J+1), and is the diagonal matrix of all pseudo-weights and prior variances. With the augmented X*, this regression is identified and thus the resulting estimate is well defined and has finite variance, even if the original data are high-dimensional and have collinearity or separation that would result in nonidentifiability of the classical maximum likelihood estimate (Gelman et al., 2008). Therefore, we obtain the estimate of β, , and its variance . If a dispersion parameter, φ, is present, we can update φ at each step of the iteration by
| (25) |
4.3. EM-IWLS algorithm and inference
In summary, the EM-IWLS algorithm can be described as follows:
Start with a crude parameter estimate.
-
For t = 1, 2, ⋯ :
E-step: Calculate the conditional expectations- for the hierarchical t prior, or for the hierarchical double-exponential prior
M-step:- Based on the current value of β, calculate the pseudo-data and the pseudo-weights .
- Update β by running the augmented weighted normal linear regression.
- If φ is present, update φ.
We choose the starting values of the parameters as follows. An initial estimate to the linear predictor η is found by the standard method as implemented in the R function glm (This standard method is not affected by the number of variables and can be safely used in high-dimensional settings). With the initial linear predictor, we can obtain initial values for the pseudo-response and the pseudo-weight, zi and wi, from Equation (22). We set the starting value of φ (if present) to 1, and the variances to 1 for all the predictors except for the intercept for which is prefixed at a large value (say 1010). This initial value of corresponds to first setting initial values for the hyperparameters bk to be 0.5 or 0.125 for the hierarchical t or double-exponential priors, respectively, and then taking the prior means for the scale parameters sj and the variances . These hyperparameter values lead to a weakly informative prior on the coefficients, and could be reasonable. With the initial values of the pseudo-response and the pseudo-weight zi and wi and the variances , the estimate of β is obtained by the augmented weighted normal linear regression (23). From these starting values, the EM-IWLS algorithm can converge rapidly.
We apply the criterion in the R function glm to assess convergence, i.e., |d(t)−d(t−1)|/(0.1+|d(t)|)< ε, where d(t) = −2 log p(y |Xβ(t),φ(t)) is the estimate of deviance at the tth iteration), and ε is a small value (say 10−5). At convergence of the algorithm, we obtain the latest estimates () and the covariance matrix . As in the classical framework, the p-values for testing the hypotheses H0: βj = 0 can be calculated using the statistics , which approximately follows a standard normal distribution or a Student-t distribution with n degrees of freedom, if the dispersion φ is fixed in the model or estimated from the data, respectively.
4. Relationship with Existing Methods
The Bayesian GLMs with the hierarchical t and double-exponential priors includes various previous methods in the literature as special cases. The EM-IWLS algorithm described above can be easily adapted to fit these existing models.
The hierarchical t prior with sj = ∞ and the double-exponential prior with sj = 0 correspond to a flat distribution. Placing flat priors on all βj corresponds to classical models, which are usually non-identifiable for high-dimensional data. Our framework has the flexibility of setting flat priors to some predictors (e.g., relevant covariates) that perform no shrinkage;
Atνj = ∞, the t prior is equivalent to a normal distribution , which leads to a ridge regression when setting a common scale sj ≡ s ;
For the hierarchical t prior, setting νj = sj = 0 corresponds to placing Jeffreys’ prior on each variance, , which is equivalent to a flat prior on log , leading to improper priors . For the hierarchical double-exponential prior, setting a = bk = 0 in the Gamma hyper-prior distribution (8) leads to the Normal-Jeffrey’s prior on βj (Armagan et al., 2010);
Setting a common scale parameter to all variables, sj ≡ s , leads to the Bayesian lasso or t models discussed in Park and Casella (2008) and Yi and Xu (2008);
Ignoring the group structure but using variable-specific scale parameters sj leads to the Bayesian adaptive lasso described in Leng et al. (2010).
6. Implementation
We have created an R function bglm for setting up and fitting the Bayesian hierarchical generalized linear models. As described above, the Bayesian hierarchical generalized linear models include various models as special cases, and thus the R function bglm can be used not only for general data analysis but also for high-dimensional data analysis using various prior distributions. Our computational strategy is based on extending the well-developed IWLS algorithm for fitting classical GLMs to our Bayesian hierarchical GLMs. The IWLS algorithm is executed in the glm function in R (http://www.r-project.org/). The bglm function implements the EM-IWLS algorithm by inserting the E-step for updating the missing values (i.e., the variances and the hyperparameters sj and bk[j]) and the steps for calculating the augmented data and the dispersion parameter into the IWLS procedure in the glm function, and includes all the glm arguments and also some new arguments for the hierarchical modeling. We have incorporated the bglm function into the freely available R package BhGLM (http://www.ssg.uab.edu/bhglm/).
7. Applications
We illustrate the methods by analyzing the mouse data of (Boyartchuk et al., 2001). This dataset consisted of 116 female mice from an intercross (F2) between the BALB/cByJ and C57BL/6ByJ strains. Each mouse was infected with Listeria monocytogenes. Approximately 30% of the mice recovered from the infection and survived to the end of the experiment (264 hours). We denoted the survival status for the i-th animal by yi (= 0 or 1 if the i-th animal was dead or alive, respectively). The mice were genotyped at 133 genetic markers spanning 20 chromosomes, including two at the X chromosome. The numbers of markers on an autosome range from 4 to 13. The goal of the study was to identify markers that are significantly associated with the survival status and to estimate the genetic effects of these markers. The single-marker analysis has been previously applied to this data set, identifying significant QTL on chromosomes 5 and 13 (Boyartchuk et al., 2001). As shown below, our hierarchical model analyses detected additional significant QTL.
For each autosomal marker which consists of three genotypes, we constructed two main-effect variables, the additive and the dominance, using the Cockerham genetic model; the additive predictor is defined as xa = −1 × Pr(aa) + 0 × Pr(Aa) + 1 × Pr(AA) and the dominance predictor as xd = −0.5 × [Pr(aa) + Pr(AA)] + 0.5 × Pr(Aa), where Pr(aa), Pr(AA) and Pr(Aa) are probabilities of homozygotes aa, AA and heterozygote Aa, respectively. For observed genotypes, one of these probabilities equals 1. The resulting 262 main-effect variables were clustered into 38 groups based on their located chromosomes and effect types (i.e., additive or dominance). Each marker at the X chromosome consists of two genotypes. Therefore, we defined a binary variable for each of these markers and treated these variables as ungrouped. The genotype data contains ~ 11% missing values. We calculated the genotypic probabilities of missing marker genotypes conditioning on the observed marker data, and then used these conditional probabilities to construct additive and dominance predictors (Yi and Banerjee, 2009).
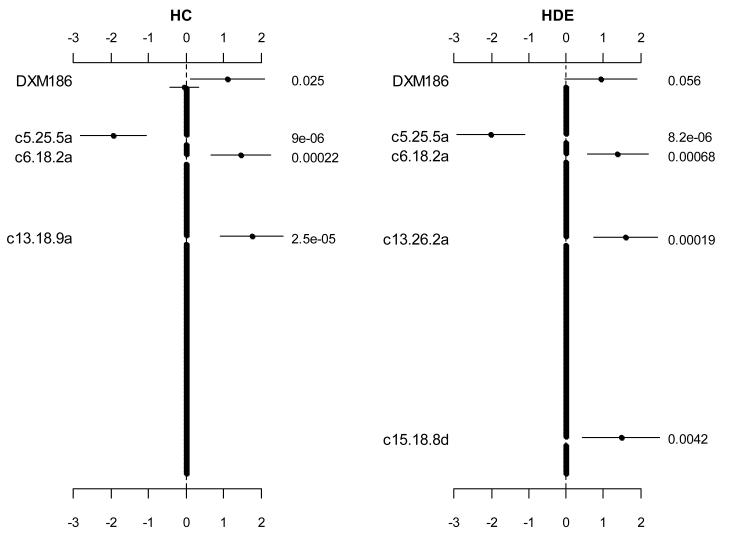
We used logistic models with the proposed prior distributions to simultaneously fit all the variables. Figure 1 displays the coefficient estimates, standard errors, and p-values for all the variables. The two analyses obtained fairly similar results, identifying four or five effects significantly associated with the survival status and shrinking all other effects to zero. Although the two models detected different additive predictors on Chromosome 13 (i.e., c13.18.9a or c13.26.2a), these two variables were strongly correlated (r2 = 0.87). The model with the hierarchical double-exponential prior detected an additional dominance predictor located on Chromosome 15.
Figure 1.
Jointly fitting two effects of markers (DXM186 and DXM64) on the X chromosome and 262 main effects of 131 markers on 19 autosomes using the hierarchical logistic models with the two prior distributions, hierarchical Cauchy (HC) and hierarchical double-exponential (HDE). The points, short lines and numbers at the right side represent estimates of effects, ± 2 standard errors, and p-values, respectively. Only effects with p-value < 0.06 are labeled. The notation, e.g., c5.25.5a, indicates the additive predictor of the marker located at 25.5 cM on chromosome 5.
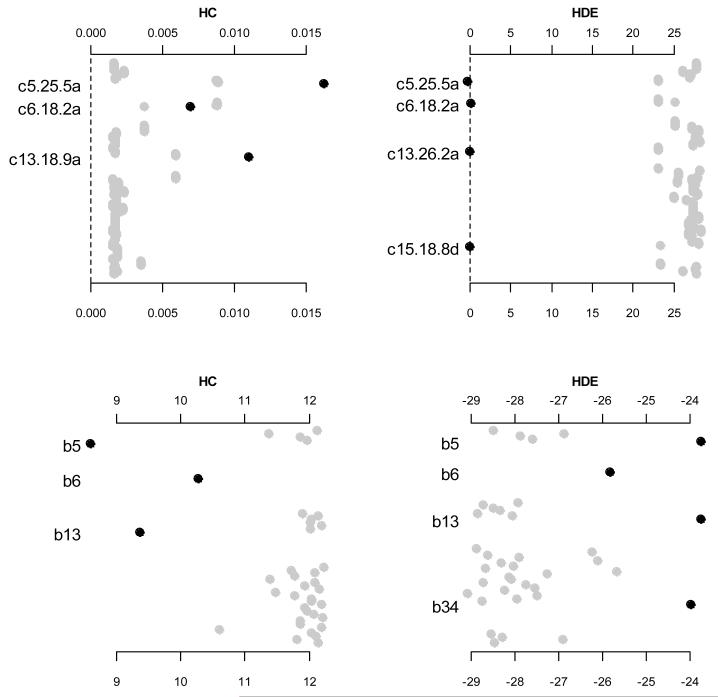
Figure 2 shows the estimates of hyper-parameters sj and bk for the grouped variables. For the hierarchical Cauchy prior, larger sj and smaller bk would induce weaker shrinkage on the corresponding coefficients. As can be seen in Figure 2, the estimates of sj for the detected variables (i.e., c5.25.5a, c6.18.2a and c13.18.9a) were larger than those of other variables, and the estimates of b5, b6 and b13 were much smaller than other bk’s. For the hierarchical double-exponential priors, smaller sj and larger bk are expected to yield weaker shrinkage on the corresponding coefficients. Figure 2 clearly shows that the detected variables had much smaller estimates of sj, and the groups including significant effects had much larger estimates of bk. Therefore, allowing variable-specific parameters sj and group-specific parameters bk enable us to achieve hierarchically adaptive shrinkage on the coefficients.
Figure 2.
Estimates of hyper-parameters of grouped variables for the two prior distributions, hierarchical Cauchy (HC) and hierarchical double-exponential (HDE). The top panels are the estimates of sj and log(sj), and the bottom panels are the estimates of log(bk), for hierarchical Cauchy and hierarchical double-exponential priors, respectively. Only terms corresponding to effects with p-value < 0.05 are labeled and blacked. The notation, e.g., c5.25.5a, indicates the additive predictor of the marker located at 25.5 cM on chromosome 5.
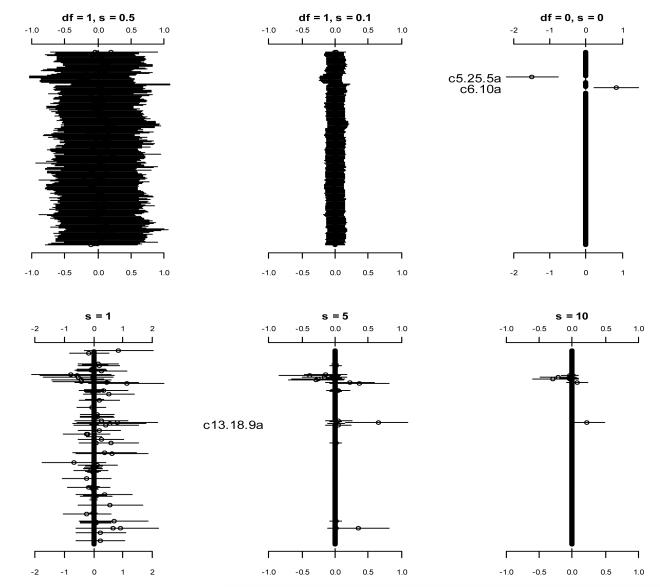
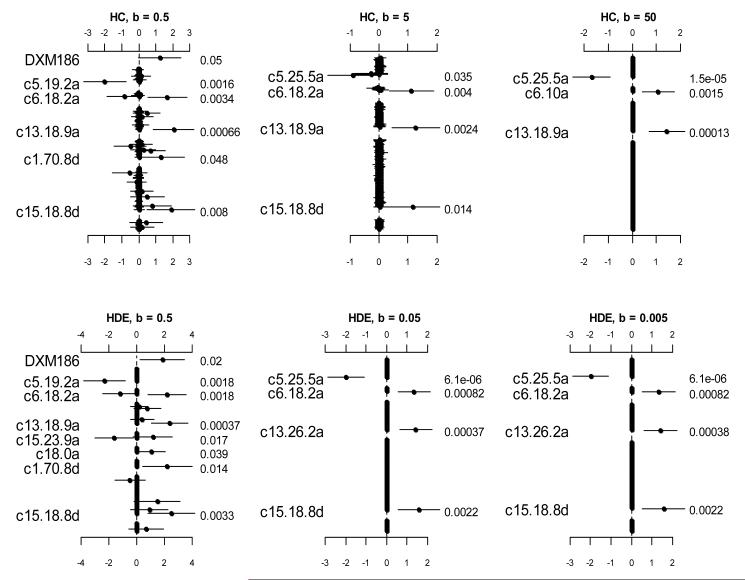
For comparison purposes, we analyzed the data using the prior distributions with fixed values of hyper-parameters. Figure 3 displays the results from the logistic models with the prior distributions and with several fixed values of s2. These prior distributions lead to the existing models described earlier. All these analyses were clearly unsatisfactory, failing to detect the strong signals that were found previously. Figure 4 shows the analyses using the prior distributions with fixed values of bk but unknown variable-specific parameters . Since hyper-parameters that are deeper in the hierarchy have less effect on inference (Leng et al., 2010), some of these analyses could yield results similar to the previous findings. However, the choice of the parameters bk largely affect the results.
Figure 3.
Analyses using the prior distributions (the top panels) and (the bottom panels) with fixed values of s2. The points and short lines represent estimates of effects and ± 2 standard errors, respectively. Only effects with p-value < 0.05 are labeled.
Figure 4.
Analyses using the hierarchical Cauchy (HC) and hierarchical double-exponential (HDE) with fixed values group-specific parameters bk but unknown variable-specific parameters . The points, short lines and numbers at the right side represent estimates of effects, ± 2 standard errors, and p-values, respectively. Only effects with p-value < 0.05 are labeled.
8. Simulation Studies
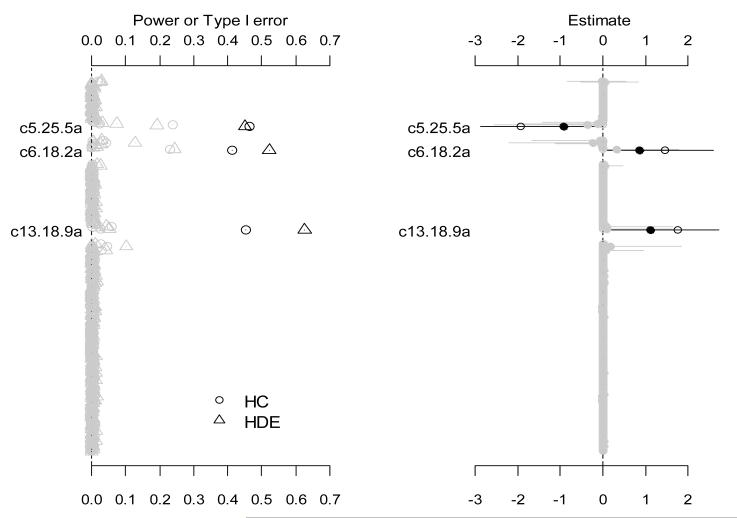
We used simulations to validate the proposed models and algorithm and to study the properties of the method. We compared the proposed method with several alternative models. Our simulation studies used the real genotype data in the above mouse survival study of Listeria monocytogenes, and generated a binary response yi for each of 116 mice from the binomial distribution Bin(1, logit−1(Xiβtrue)) conditional on the assumed ‘true’ coefficients βtrue, where Xi was constructed as in the above real data analysis. The ‘true’ coefficients βtrue were set based on the fitted logistic model with the hierarchical Cauchy prior (see the left panel of Figure 1), equaling the estimated values for the intercept and the detected predictors, c5.25.5a, c6.18.2a and c13.18.9a, and 0 for the others. For each situation, 1000 replicated datasets were simulated. We calculated the frequency of each effect estimated as significant at the threshold level of 0.05 over 1000 replicates. These frequencies corresponded to the empirical power for the simulated non-zero effects and the type I error rate for other coefficients, respectively. We also examined the accuracy of estimated coefficients by calculating the mean and 95% interval estimates.
For each simulated dataset, we simultaneously fitted all the 264 main-effect variables using logistic linear models with the proposed prior distributions. As in the real data analysis, the variables were clustered into 38 groups. As shown in the left panel of Figure 5, the three non-zero effects were detected with higher power than all other effects. Given the small sample size and the relatively large number of predictors, these powers are reasonable. The model with the hierarchical double-exponential prior generated higher power for two of the three simulated effects. The type I error rates for effects on chromosomes without simulated non-zero effects were close to zero. For chromosomes 5, 6 and 13, however, there were several non-simulated effects detected with non-zero type I error rates. This may be expected because these variables were highly correlated with the non-zero variables. The right panel of Figure 5 shows the assumed values, the estimated means and the 95% intervals of all coefficients for the analysis with the hierarchical double-exponential prior. The estimates of all effects were accurate; the estimated means overlapped the simulated values.
Figure 5.
The left panel shows the frequency of each effect estimated with p-value smaller than 0.05 over 1000 replicates with the two prior distributions, hierarchical Cauchy (HC) and hierarchical double exponential (HDE). The right panel shows the assumed values (circles), the estimated means (points) and the 95% intervals (short lines). Only effects with non-zero simulated value are labeled and blacked. The notation, e.g., c5.25.5a, indicates the additive predictor of the marker located at 25.5 cM on chromosome 5.
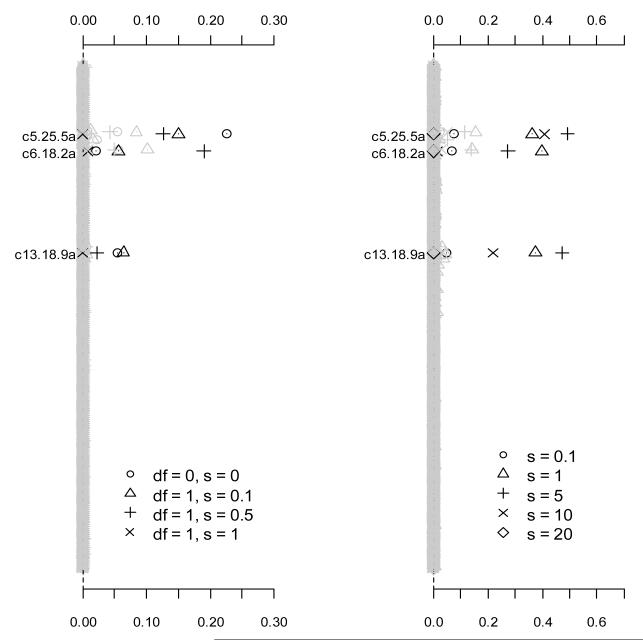
We then analyzed the simulated datasets using logistic regressions with the prior distributions and with several fixed values of sj. As shown in Figure 6, these analyses generated lower power than the proposed hierarchical prior distributions for all the simulated effects. With an inappropriate choice of the hyper-parameter, these alternative priors had no power to detect the simulated effects.
Figure 6.
Frequency of each effect estimated with p-value smaller than 0.05 over 1000 replicates using the prior distributions (the left panel) and (the right panel) with fixed values of sj. Only effects with non-zero simulated value are labeled and blacked. The notation, e.g., c5.25.5a, indicates the additive predictor of the marker located at 25.5 cM on chromosome 5.
9. Discussion
We have proposed two prior distributions, hierarchical Cauchy and double exponential distributions, for simultaneous variable selection and coefficient estimation in high-dimensional generalized linear models. The hierarchical priors include both variable-specific and group-specific tuning parameters. Numerical results showed that our methods can impose different shrinkage for different coefficients and different groups, and hence allow reliable estimates of parameters and increase the power for detection of important variables. Although both the two proposed priors perform well, we found that with the double exponential distribution the power for detection of important variables is usually higher, and the algorithm converges more rapidly. Therefore, we recommend the hierarchical double exponential model as default in high-dimensional data analysis. The proposed algorithm extends the standard procedure for fitting classical generalized linear models in the general statistical package R to our Bayesian models, leading to the development of stable and flexible software. Although a fully Bayesian computation that explores the posterior distribution of parameters provides more information, our mode-finding algorithm quickly produces all results as in routine statistical analysis.
The key to Bayesian hierarchical modeling is to express shrinkage prior distributions as scale mixtures of normals with unknown variable-specific variances (Kyung et al., 2010; Park and Casella, 2008; Yi and Xu, 2008). We have used this hierarchical formulation to obtain our adaptive shrinkage priors and to develop our algorithms. Kyung et al. (2010) and Leng et al. (2010) have showed that various penalized likelihood methods, including the elastic net (Zou and Hastie, 2005), the group Lasso (Yuan and Lin, 2006), and the composite absolute penalty (Zhao, Rocha and Yu, 2009), can be expressed as Bayesian hierarchical models by assigning certain priors on these variances. Our hierarchical priors can be incorporated into various Lasso methods, leading to new Bayesian hierarchical models.
Our computational algorithms also take advantage of the hierarchical formulation of the prior distributions. Given the variances , the normal priors on the coefficients can be included in the model as additional ‘data points’, and thus the coefficients can be estimated using the standard iterative weighted least squares, regardless of the specific prior distributions on the variances. The conditional expectations of the variances and other hyperparameters are independent of response data, and thus the same updating scheme can be used to update the variances and hyperparameters regardless of the response distribution. Therefore, our approach can be straightforwardly applied to a broad class of models. An alternative approach does not require the introduction of these variances (Hans, 2009; Sun et al., 2010). However, it has the disadvantage that the step for updating the coefficients is complicated. As a result, the approach is less extendable.
We describe our algorithm by simultaneously estimating all coefficients β. This can be referred to as the all-at-once algorithm. This method can be very fast when the number of variables is not very large (say J < 1000) and has the advantage of accommodating the correlations among all the variables. However, it can be slow or even cannot be implemented when the number of variables is large (say J > 2000) due to memory storage and convergence problems. We can extend the algorithm to update all coefficients at a group given all the others, referred to as the group-at-time algorithm. At each of the iteration, the group-at-time algorithm proceeds by cycling through all the groups of parameters and treats the linear predictor of all other groups as an offset in the model. This method updates coefficients in a conditional manner, significantly reducing the number of parameters in each M-step, and thus can deal with large number of variables.
Acknowledgments
We are grateful for Dr. Jun Liu for his suggestions and comments. This work was supported in part by the research grants: NIH 5R01GM069430-07 and R01CA142774.
References
- Armagan A, Dunson D, Lee J. Bayesian generalized double Pareto shrinkage. Biometrika. 2010 [PMC free article] [PubMed] [Google Scholar]
- Boyartchuk VL, Broman KW, Mosher RE, D’Orazio SE, Starnbach MN, Dietrich WF. Multigenic control of Listeria monocytogenes usceptibility in mice. Nat Genet. 2001;27:259–260. doi: 10.1038/85812. [DOI] [PubMed] [Google Scholar]
- Carvalho C, Polson N, Scott J. Handling sparsity via the horseshoe. JMLR: W&CP 5. 2009 [Google Scholar]
- Carvalho C, Polson N, Scott J. The horseshoe estimator for sparse signals. Biometrika. 2010;97:465–480. [Google Scholar]
- Figueiredo MAT. Adaptive Sparseness for Supervised Learning. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2003;25:1150–1159. [Google Scholar]
- Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Analysis. 2006;1:515–533. [Google Scholar]
- Gelman A, Carlin J, Stern H, Rubin D. Bayesian data analysis. Chapman and Hall; London: 2003. [Google Scholar]
- Gelman A, Jakulin A, Pittau MG, Su YS. A weakly informative default prior distribution for logistic and other regression models. Annals of Applied Statistics. 2008;2:1360–1383. [Google Scholar]
- Griffin JE, Brown PJ. Technical report. IMSAS, University of Kent; 2010. Bayesian adaptive lassos with non-convex penalization. [Google Scholar]
- Hans C. Bayesian lasso regression. Biometrika. 2009;96:835–845. [Google Scholar]
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning; Data Mining, Inference and Prediction. Springer-Verlag; NewYork: 2001. [Google Scholar]
- Kyung M, Gill J, Ghosh M, Casella G. Penalized Regression, Standard Errors, and Bayesian Lassos. Bayesian Analysis. 2010;5:369–412. [Google Scholar]
- Lee A, Caron F, Doucet A, Holmes C. Bayesian Sparsity-Path-Analysis of Genetic Association Signal using Generalized t Priors. Statistical Applications in Genetics and Molecular Biology. 2012;11:1544–6115. doi: 10.2202/1544-6115.1712. [DOI] [PubMed] [Google Scholar]
- Leng C, Minh Ngoc Tran, Nott D. Bayesian Adaptive Lasso. 2010. Arxiv preprint arXiv:1009.2300. [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. Chapman and Hall; London: 1989. [Google Scholar]
- Park T, Casella G. The Bayesian Lasso. Journal of the American Statistical Association. 2008;103:681–686. [Google Scholar]
- Sun W, Ibrahim J, Zou F. Genomewide multiple-loci mapping in experimental crosses by iterative adaptive penalized regression. Genetics. 2010;185:349–359. doi: 10.1534/genetics.110.114280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression Shrinkage and Selection Via the Lasso. Journal of the Royal Statistical Society. Series B. 1996a;58:267–288. [Google Scholar]
- Tibshirani R. Regression Shrinkage and Selection Via the Lasso. Journal of the Royal Statistical Society. Series B. 1996b:267–288. [Google Scholar]
- Yi N, Banerjee S. Hierarchical generalized linear models for multiple quantitative trait locus mapping. Genetics. 2009;181:1101–1113. doi: 10.1534/genetics.108.099556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Kaklamani VG, Pasche B. Bayesian analysis of genetic interactions in case-control studies, with application to adiponectin genes and colorectal cancer risk. Ann Hum Genet. 2011;75:90–104. doi: 10.1111/j.1469-1809.2010.00605.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi N, Xu S. Bayesian LASSO for quantitative trait loci mapping. Genetics. 2008;179:1045–1055. doi: 10.1534/genetics.107.085589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M, Lin Y. Model Selection and Estimation in Regression with Grouped Variables. Journal of the Royal Statistical Society, Series B. 2006;68:49–67. [Google Scholar]
- Zhao P, Rocha G, Yu B. The composite absolute penalties family for grouped and hierarchical variable selection. Ann. Statist. 2009;37:3468–3497. [Google Scholar]
- Zou H. The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B. 2005;67:301–320. [Google Scholar]