The authors used a mathematical model to simulate the use of the test-and-treat policy for control of human immunodeficiency virus/AIDS in Los Angeles County. They found the significant epidemiologic benefits predicted by the model are counterbalanced by substantial increases in multidrug resistance.
Keywords: HIV/AIDS, test and treat, antiretroviral therapy, drug resistance, mathematical model
Abstract
Background. There is evidence to suggest that antiretroviral therapy (ART) and testing for human immunodeficiency virus (HIV) reduce the probability of transmission of HIV. This has led health officials across the United States to take steps toward a test-and-treat policy. However, the extent of the benefits generated by test-and-treat is debatable, and there are concerns, such as increased multidrug resistance (MDR), that remain unaddressed.
Methods. We developed a deterministic epidemiologic model to simulate the HIV/AIDS epidemic for men who have sex with men (MSM) in Los Angeles County (LAC). We calibrated the model to match the HIV surveillance data from LAC across a 10-year period, starting in 2000. We then modified our model to simulate the test-and-treat policy and compared epidemiologic outcomes under the test-and-treat scenario to the status quo scenario over the years 2012–2023. Outcome measures included new infections, deaths, new AIDS cases, and MDR.
Results. Relative to the status quo, the test-and-treat model resulted in a 34% reduction in new infections, 19% reduction in deaths, and 39% reduction in new AIDS cases by 2023. However, these results are counterbalanced by a near doubling of the prevalence of MDR (9.06% compared to 4.79%) in 2023. We also found that the effects of increasing testing and treatment were not complementary.
Conclusions. Although test-and-treat generates substantial benefits, it will not eliminate the epidemic for MSM in LAC. Moreover, these benefits are counterbalanced by large increases in MDR.
(See the Editorial Commentary by Jena on pages 1797–9.)
Recent evidence suggests that antiretroviral therapy (ART) reduces the probability of human immunodeficiency virus (HIV) transmission, particularly if initiated at early stages of the disease [1–3]. Evidence also suggests that testing HIV positive causes dramatic reductions in sexual activity levels, which also reduces HIV transmission probability [4, 5]. In light of this evidence, health officials across the United States are taking steps toward scaling up testing programs and recommending immediate ART initiation to individuals testing positive, regardless of CD4 cell count [6]. Some argue a “test-and-treat” policy could lead to elimination of the HIV epidemic [7–9].
Although reasons exist for optimism regarding the role of increased testing and treating in HIV prevention agendas, some concerns remain unaddressed. One important concern is that increased ART use creates more multidrug-resistant strains, which might limit the benefits of test-and-treat [10]. Treatment resistance already poses a major public health problem in the United States [11]. Therefore, determining how to implement test-and-treat policies where HIV prevention is maximized and multidrug resistance (MDR) prevalence is minimized is important.
Previous mathematical models that simulate the impact of scaling up test-and-treat policies show mixed results. Some find dramatic benefits [7, 12], whereas others find only modest effects [13–15]. There is also evidence from a natural experiment suggesting that some model results may be exaggerated [16]. The discrepancy in model findings reflects the sensitivity of test-and-treat outcomes to differing underlying assumptions about HIV prevalence, proportion of undiagnosed cases, risky sexual behavior, and other population or location-specific parameters [17, 18]. This highlights the critical need to calibrate mathematical models to mimic real-world HIV prevalence and incidence trends [19]. Additionally, none of these articles explicitly addresses potential effects of test-and-treat policies on the spread of MDR. However, an earlier strand of literature examining expanded ART use addresses this issue and reports mixed findings. Some find that increasing the percentage of people using ART would substantially reduce the HIV epidemic's severity even in the presence of high ART resistance levels [9, 20]. However, the authors note that emergence of highly transmissible resistant strains of HIV can significantly reduce the benefits of expanded use of ART [9]. Baggaley et al found that controlling sub-Saharan African HIV epidemics through treatment is ineffective, as increasing the proportion on treatment increases the emergence and spread of drug resistance [21]. Others find that benefits from expanded ART use are counterbalanced by modest increases in risky sexual behavior [21–23].
Our study contributes to this literature by using a mathematical model to simulate effects of increased testing and early initiation of treatment for men who have sex with men (MSM) in Los Angeles County (LAC). No previous study has focused on test-and-treat in LAC. In the United States, LAC has the largest incidence of HIV, and MSM account for 82% of all people living with HIV/AIDS (PLWHA) [24, 25]. We calibrate our model using HIV surveillance data from LAC for the years 2000 to 2009. Following calibration, we manipulate parameters relating to test-and-treat to simulate alternate test-and-treat policy scenarios. To assess the individual and complementary effects of testing and treating on epidemiologic outcomes, the intensity of both testing and treatment rates are varied. Finally, we also assess how the intensity of each mechanism affects the portion of the population with MDR. The results could help inform policy makers on best approaches for the test-and-treat policy and where to focus future HIV prevention efforts.
METHODS
Study Design
To model the LAC HIV/AIDS epidemic, we calibrate a deterministic epidemiologic model to match LAC's HIV surveillance data across a 10-year period (2000–2009). We obtain the set of model parameters that best reproduce the observed HIV/AIDS prevalence trends for MSM. We then modify our model to investigate effects of the test-and-treat policy whereby HIV testing rates are increased and newly diagnosed HIV-positive individuals are immediately treatment eligible. We focus on the MSM population because they represent >82% of PLWHA in LAC, and their biological and behavioral characteristics are likely to differ from those of heterosexuals (see the Supplementary Appendix for more detail).
Model Structure
We construct a compartmental HIV transmission model. Our model structure follows the general approach used in previous HIV transmission models, and in particular that used by Smith et al [11]. Our model considers the dynamics in the era of triple therapy and therefore considers dynamics of acquired and transmitted MDR.
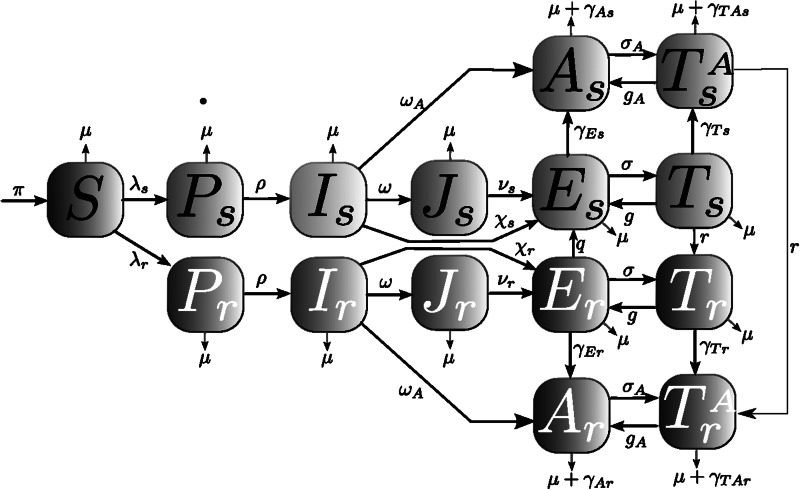
Figure 1 displays our compartmental HIV model, whereby individuals in our population progress over the different stages of the infection. Under status quo, treatment eligibility is based on standard Centers for Disease Control and Prevention guidelines: advanced disease and/or CD4 cell count <350 cells/μL, which, although lower than current treatment guidelines, was the guideline for most of the calibration years. The model is integrated numerically and tracks the dynamics of the population in each compartment as it changes over time.
Figure 1.
Human immunodeficiency virus (HIV) transmission model: individuals in our model are divided into 8 key HIV infection statuses: susceptible or HIV negative (S), infected in the primary stage of infection (P), infected and unaware of being infected (I), diagnosed infected but not treatment-eligible (J), infected and treatment-eligible (E), treated but no progression to AIDS (T), progression to AIDS but not treated (A), and progression to AIDS and treated (TA). We distinguish between infected individuals with drug-sensitive HIV strain (subscript s) from those infected with the multidrug-resistant HIV strain (subscript r).
Key Input Parameters and Ranges
Our model includes 34 parameters, for which we provide uncertainty ranges based upon literature review, expert opinion, and our subjective range assessment (Supplementary Tables 4–8). Key parameters for this study include the rate at which treatment-eligible individuals initiate and adhere to treatment (σ), the rate at which unaware HIV-positive individuals get tested for HIV (ω), the rate at which MDR is acquired for people on treatment (r), and the probability of HIV transmission per sexual partnership (β). To account for different infectiousness levels and risky sexual activity at different disease stages, the β parameter is unique for each model compartment. A key model assumption is that HIV-positive individuals, aware of their serostatus, significantly reduce risky behavior; we account for this by ensuring the sampling range of β for stage J is 56%–76% lower than the sampling range of β for stage I [4].
Surveillance Data
The surveillance data we use, as a reference to calibrate our model, were taken from LAC semiannual surveillance reports from 2008 to 2010. The surveillance data provide annual numbers of PLWHA by transmission group for the years 2000–2009. These reports differentiate HIV-positive individuals from those with AIDS, and we distribute these stages accordingly in our model (Supplementary Appendix, section 4).
Model Calibration
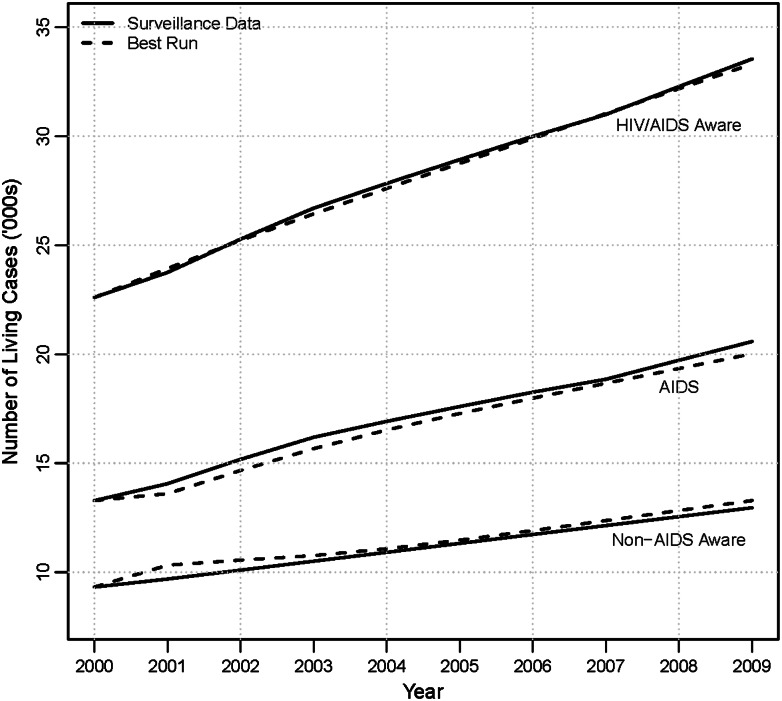
In this section, we briefly summarize how we calibrate the model; more details on the calibration are provided in the Supplementary Appendix, section 5. To calibrate our model, we use a Latin hypercube sampling (LHS) method and match the model output to LAC surveillance data from 2000 to 2009. We first run 500 000 LHS simulations based on parameter ranges from the prior literature. Next, we drop simulations that do not match prior estimates of the proportion of PLHWA who are unaware of their HIV status [26], and MDR prevalence [11, 27]. Finally, we select the top 1000 simulations that best match estimates of total numbers of PLHWA in LAC surveillance data for the years 2000 to 2009. We use these simulations to create narrower parameter ranges and run an additional 500 000 LHS simulations. As before, we drop simulations that do not match prior estimates of the proportion of PLHWA who are unaware of their HIV status and MDR prevalence. In addition, we only retain simulations where predicted AIDS cases and non-AIDS HIV-aware cases are both <5% different from the 2009 surveillance data. Finally, of the remaining simulations, we choose the simulation that best matches the total number of PLHWA in LAC surveillance data for the years 2000–2009. We label this as the “Best Run” and use the parameters produced by this run as the main model parameters. Figure 2 compares results from the “Best Run” simulation to the surveillance data.
Figure 2.
Calibration results. As shown, our calibrated model can accurately predict trends in number of AIDS and non-AIDS human immunodeficiency virus–aware cases in Los Angeles County for the years 2000–2009. Abbreviation: HIV, human immunodeficiency virus.
Test-and-Treat Model
To simulate the test-and-treat policy, we extend the HIV model described above by incorporating 2 additional compartments, TJs and TJr, representing the nondrug resistant and drug-resistant infected individuals who initiate treatment early prior to CD4 counts falling below eligibility guidelines (Supplementary Figure 5). The J to TJ path, σtj , represents the early treatment initiation rate for infected individuals with a CD4 cell count >350 cells/μL. We assume compartment TJ's risk of transmission is 96% lower than the risk of compartment J's transmission [1].
Testing rates and rates at which people begin treatment are key for test-and-treat policy outcomes. We test a range of parameter combinations to assess how more aggressive testing and more aggressive treatment individually and jointly impact HIV-related outcomes.
Our baseline test-and-treat simulation assumes the following: (1) The expected time to treatment initiation for those with CD4 cell counts above the threshold of 350 cells/μL is the same as for those with CD4 count below this threshold; (2) the average duration for undiagnosed PLWHA to get tested changes from 4.4 years to 1 year. In addition to our baseline scenarios, we provide a range of other scenarios that combine different testing and treatment intensity levels.
In LAC, achievable increases in testing and treatment levels are unclear. To estimate feasibility, we calculate new diagnoses and new people initiating treatment after the first year, which serves as a proxy for effort and resources put toward the policy. Table 1 presents new HIV diagnoses and new people beginning treatment during the first year of the test-and-treat policy with alternative scenarios of testing and treatment intensity. Our baseline scenario (test every 1 year and treatment initiation 2.5 years after diagnosis) results in a 115% increase in new diagnoses and a 36% increase in new people initiating treatment during the first year compared to the status quo. The most aggressive strategy we simulate assumes annual testing and treatment initiation 6 months after becoming eligible. This results in increases of 114% and 156%, respectively. The least aggressive strategy we simulate, which assumes testing every 4.4 years and treatment initiation 2.5 years after becoming eligible (simply a change in the treatment eligibility guidelines), still results in an 18% increase in new people initiating treatment in the first year compared to the status quo. This is explained by the new treatment guidelines that allow people to become eligible immediately after diagnosis rather than waiting until they have a CD4 cell count <350 cells/μL.
Table 1.
First-Year Effects of the Test-and-Treat Policy on HIV Diagnoses and Treatment Initiation With Different Levels of Testing and Treatment Intensity Compared to the Status Quo
| Scenario | New HIV Diagnosis in First Year (% Change From Status Quo) | New People Initiating Treatment in First Year (% Change From Status Quo) |
|---|---|---|
| Status quo | 4437 | 5696 |
| Treatment 2.5 ya | ||
| Test every 1 yb | 9537 (115%) | 7724 (36%) |
| Test every 2 y | 7576 (71%) | 7317 (28%) |
| Test every 3 y | 6689 (51%) | 7154 (26%) |
| Test every 4.4 ya | 4433 (0%) | 6732 (18%) |
| Treatment 1 y | ||
| Test every 1 y | 9514 (114%) | 11 248 (97%) |
| Test every 2 y | 7562 (70%) | 10 343 (82%) |
| Test every 3 y | 6678 (51%) | 9973 (75%) |
| Test every 4.4 ya | 4427 (0%) | 9071 (59%) |
| Treatment 6 mo | ||
| Test every 1 y | 9485 (114%) | 14 562 (156%) |
| Test every 2 y | 7544 (70%) | 13 175 (131%) |
| Test every 3 y | 6663 (50%) | 12 596 (121%) |
| Test every 4.4 ya | 4419 (0%) | 11 198 (97%) |
a Current duration based on model calibration.
b Baseline scenario.
Sensitivity Analysis
We first conduct a 1-way sensitivity analysis to determine how the model results are impacted by each parameter individually. In particular, we reestimate the model by varying each parameter by 10% above and below the baseline values, while holding all other parameters fixed. We used these new parameter values to estimate effects of test-and-treat on new infections and MDR. This allows us to understand which parameters most influence our results. We also conduct a multivariate sensitivity analysis by resampling 100 000 parameter sets from the parameter range above. We use estimates from this analysis to report the 95% confidence interval for our baseline test-and-treat results (Supplementary Appendix, section 7).
RESULTS
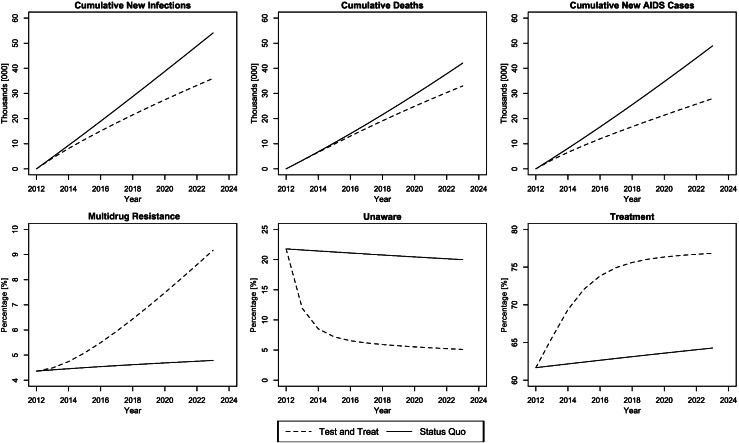
Figure 3 displays results under the baseline test-and-treat scenario compared to the status quo. The baseline test-and-treat scenario represents a 115% increase in the number of first-year diagnosed HIV cases and a 36% increase in the number of PLWHA treated in the first year (Table 1). Figure 3 shows that the percentage of the population that is unaware reduces over a 10-year period from 20% in 2013 to approximately 5% in 2023, and the percentage of PLWHA on ART increases from 62% in 2013 to approximately 76% in 2023. Over these 10 years, the dramatic changes in testing and treatment lead to large reductions in new infections (34%; 95% confidence interval [CI], 30%–37%), deaths (19%; 95% CI, 17%–21%), and new AIDS cases (39%; 95% CI, 36%–41%). However, contrasting these benefits, the MDR prevalence nearly doubles to 9% by 2023 (95% CI, 7.8%–10.2%).
Figure 3.
Baseline test-and-treat scenario compared to the status quo.
Table 2 presents epidemiologic outcomes for all simulated scenarios. Our baseline scenario results in a substantial reduction in all epidemiologic measures. The most aggressive strategy, testing annually and treatment initiation after 6 months, increases new diagnoses by 114% and treatment by 156% in the first year (Table 1). This strategy also creates a 47% reduction in new infections, a 28% reduction in deaths, and a 64% reduction in new AIDS cases by 2023. However, under this scenario, the portion of PLWHA with MDR nearly triples to 13.7% in 2023. The least aggressive strategy we simulated, testing every 4.4 years and treatment initiation after 2.5 years—essentially just a change in treatment eligibility guidelines—still yields a 6% reduction in new infections, a 6% reduction in deaths, and an 11% reduction in new AIDS cases, with only a 1.3% increase in MDR.
Table 2.
Epidemiologic Outcomes Under Different Test-and-Treat Intensity Levels Compared to the Status Quo
| Cumulative From 2013 to 2023 |
% of Total HIV/AIDS Population in 2023 |
||||
|---|---|---|---|---|---|
| Scenario | New Infections (% Reduction) | Deaths (% Reduction) | New AIDS cases (% Reduction) | % Multidrug Resistant | % Unaware |
| Status quo | 54 067 | 42 083 | 48 907 | 4.79% | 20.0% |
| Treatment 2.5 ya | |||||
| Test every 1 yb | 35 795 (34%) | 34 127 (19%) | 29 824 (39%) | 9.06% | 4.50% |
| Test every 2 y | 39 707 (27%) | 36 079 (14%) | 34 131 (30%) | 8.19% | 7.37% |
| Test every 3 y | 42 249 (22%) | 37 417 (11%) | 37 190 (24%) | 7.64% | 9.45% |
| Test every 4.4 ya | 50 676 (6%) | 39 748 (6%) | 43 350 (11%) | 6.07% | 18.51% |
| Treatment 1 y | |||||
| Test every 1 y | 31 251 (42%) | 30 237 (28%) | 22 152 (55%) | 11.90% | 3.67% |
| Test every 2 y | 35 271 (35%) | 31 890 (24%) | 25 709 (47%) | 10.77% | 6.14% |
| Test every 3 y | 37 935 (30%) | 33 015 (22%) | 28 246 (42%) | 10.05% | 7.97% |
| Test every 4.4 ya | 47 226 (13%) | 35 610 (15%) | 34 763 (29%) | 7.85% | 16.57% |
| Treatment 6 mo | |||||
| Test every 1 y | 28 489 (47%) | 27 807 (34%) | 17 642 (64%) | 13.70% | 3.20% |
| Test every 2 y | 32 373 (40%) | 29 172 (31%) | 20 517 (58%) | 12.51% | 5.39% |
| Test every 3 y | 34 957 (35%) | 30 084 (29%) | 22 536 (54%) | 11.75% | 7.02% |
| Test every 4.4 ya | 44 589 (18%) | 32 633(22%) | 28 737 (41%) | 9.22% | 15.18% |
Abbreviation: HIV, human immunodeficiency virus.
a Current duration based on model calibration.
b Baseline scenario.
Table 2 also shows the 2 mechanisms, testing and treating, are not complementary. We see roughly equal benefits from increasing testing rates regardless of treatment initiation rates and vice versa. For example, under the least aggressive treatment strategy (average duration to treatment of 2.5 years), there is an additional 28% reduction in new infections, whereas under the most aggressive treatment strategy (average duration to treatment of 6 months), there is an additional 29% reduction. Similarly, a change from the least aggressive treatment strategy to the most aggressive treatment strategy adds roughly the same benefit under all levels of testing intensity.
We also examined scenarios without early treatment guidelines implemented (ie, only increasing testing rates). This allows analysis of how much test-and-treat benefit is derived from early treatment and how much comes from increasing testing (Supplementary Table 17). We find that without any change to treatment guidelines and only increasing testing, we get about half the epidemiologic benefits, while MDR remains stable.
Sensitivity Analysis
Overall, our results are rather stable, with the largest impact of any 10% change in our baseline parameters resulting in only a 1.82 percentage point change in new infections. We find new infections are most sensitive to the parameters that represent sexual behavior (ie, the transmissibility parameters and number of partners).
For MDR, we find that our results are most sensitive to the rate of resistance parameter (r). Similar to new infections, the results for MDR were rather stable; the largest impact of any 10% change in our baseline parameters results in a .45 percentage point change in MDR prevalence. A complete description and results of the multivariate sensitivity analysis used for confidence intervals is found in section 7 of the Supplementary Appendix.
We also ran an additional simulation using our best parameter estimates from the clinical literature without any calibration. Under this scenario, we find percentage reductions in deaths and new AIDS cases due to test-and-treat to be underestimated by 6.45 percentage points and 14.32 percentage points, respectively, whereas percentage reductions in new infections remain relatively stable. Absolute reductions in all outcomes are significantly underestimated (Supplementary Appendix, section 7.4).
Also, because there are no data on the relative reduction in infectiousness due to ART for MSM—data are for discordant couples—we test the sensitivity of our assumption of a 96% reduction in infectiousness from ART using the upper and lower ends of the Cohen et al 95% confidence interval, 99% and 73% reductions, respectively [1]. We also conduct a third simulation assuming a 50% reduction for additional contrast. We find that assumptions about this parameter have only a modest influence on our results (Supplementary Appendix, section 7.3).
DISCUSSION
We calibrated our model to accurately predict trends in HIV/AIDS prevalence in LAC from 2000 to 2009. We used this model to evaluate the effects of the test-and-treat policy in LAC. The results show that the test-and-treat policy can generate substantial reductions in new infections, death, and new AIDS cases. However, contrary to Granich et al, even the most aggressive test-and-test policy does not eliminate the HIV epidemic [7]. These findings are consistent with those of Long et al, Walensky et al, and Sorensen et al, who find only modest policy effects when modeling the epidemic in the United States [13–15].
We also find that the epidemiologic benefits of test-and-treat are counterbalanced by large MDR increases. It is unclear to what extent increases in MDR will affect the course of the HIV epidemic. Consistent with Velasco-Hernandez et al [9] and Lima et al [20], we show that even when MDR increases 3-fold, increasing treatment rates still brings epidemiologic benefits in the short run. Even when we simulate the model far into the future and MDR prevalence approaches 23%, the policy is still beneficial (Supplementary Appendix, section 9). However, in the long run it is possible new forms of MDR evolve with higher resistance intensity or greater transmissibility, which could exacerbate MDR consequences. Conversely, it is also possible that MDR could be mitigated by the invention of new variants of drugs that are less susceptible to resistance. With such uncertainty about the course of MDR, it is unclear whether benefits from increasing test-and-treat outweigh costs of increasing MDR. If policy makers are risk-averse, a more cautious approach to HIV prevention might involve more focus on testing without changing treatment guidelines to cover early-stage HIV. We find that by simply increasing testing rates, we derive roughly half the benefits of the full test-and-treat policy with no MDR increase. Results also suggest that benefits of increasing testing rates and treatment rates occur independently, suggesting that implementation need not occur in unison.
Our model has its limitations. First, mathematical models are only as good as the available data used for the parameters and calibration. We rigorously calibrated our model to very accurately match LAC surveillance data and we show that if we had not calibrated and instead simply chosen parameters based on clinical literature, we would have underestimated the benefits of test-and-treat. However, many of our parameters are difficult to measure, and HIV surveillance data used for calibration itself might have measurement error. Second, our model is not stratified by risk, ethnicity, or age. Future models should attempt to achieve more granularity. Third, our model does not consider the use of preexposure prophylaxis. Recent US Food and Drug Administration approval of Truvada for preexposure prophylaxis may play an important role in future HIV incidence and drug resistance. Fourth, our simulations do not fully explore the implications of behavior among people who initiate treatment early. The possibility exists that early treatment will result in increased risky behavior in HIV-positive and susceptible populations because transmission is less likely. Another possibility is that people who initiate early-stage treatment are less likely to fully adhere to treatment; this could increase the acquired MDR rate, although the precise relationship between adherence and MDR is unknown. In summary, behavioral changes may mitigate the benefits of test-and-treat, and future research should explore implications of these behavioral changes. Fifth, we omit costs from our model, which precludes us from identifying the optimal combination of testing and treating. Future research should include a cost-effectiveness analysis of alternate test-and-treat policy options to identify the optimal policy. Understanding budgetary and scaling-up constraints of alternate prevention programs would provide insight on where to focus future prevention efforts.
Supplementary Data
Supplementary materials are available at Clinical Infectious Diseases online (http://cid.oxfordjournals.org/). Supplementary materials consist of data provided by the author that are published to benefit the reader. The posted materials are not copyedited. The contents of all supplementary data are the sole responsibility of the authors. Questions or messages regarding errors should be addressed to the author.
Notes
Financial support. This work was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (grant number R01HD054877). The funding source had no role in the design or conduct of this study.
Author contributions. All authors, and especially R. V. and E. D., contributed to the design of the deterministic epidemiologic model. N. S., Z. W., and R. V. contributed to the writing of the manuscript. Z. W., A. J., and E. D. contributed to the literature review and generation of parameter ranges. A. J. calculated the initial conditions and the model baseline. Z. W. and N. S. created all manuscript tables. E. D., Z. W., and A. J. created all tables and figures in the Supplementary Appendix. All authors contributed to the study design, model calibration, and writing of the Supplementary Appendix.
Potential conflicts of interest. All authors: No reported conflicts.
All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.
References
- 1.Cohen MS, Chen YQ, McCauley M, et al. Prevention of HIV-1 infection with early antiretroviral therapy. New Engl J Med. 2011;365:493–505. doi: 10.1056/NEJMoa1105243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Del Romero J. Combined antiretroviral treatment and heterosexual transmission of HIV-1: cross sectional and prospective cohort study. BMJ. 2010;340 doi: 10.1136/bmj.c2205. c2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Donnell D, Baeten JM, Kiarie J, et al. Heterosexual HIV-1 transmission after initiation of antiretroviral therapy: a prospective cohort analysis. Lancet. 2010;375:2092–8. doi: 10.1016/S0140-6736(10)60705-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marks G, Crepaz N, Senterfitt JW, Janssen RS. Meta-analysis of high-risk sexual behavior in persons aware and unaware they are infected with HIV in the United States: implications for HIV prevention programs. JAIDS. 2005;39:446–53. doi: 10.1097/01.qai.0000151079.33935.79. [DOI] [PubMed] [Google Scholar]
- 5.Marks G, Crepaz N, Janssen RS. Estimating sexual transmission of HIV from persons aware and unaware that they are infected with the virus in the USA. AIDS. 2006;20:1447–50. doi: 10.1097/01.aids.0000233579.79714.8d. [DOI] [PubMed] [Google Scholar]
- 6.Department of Health and Human Services. 2011. Guidelines for the use of antiretroviral agents in HIV-1-infected adults and adolescents. Available at: http://aidsinfo.nih.gov/ContentFiles/AdultandAdolescentGL.pdf . Accessed 10 August 2012. [Google Scholar]
- 7.Granich RM, Gilks CF, Dye C, De Cock KM, Williams BG. Universal voluntary HIV testing with immediate antiretroviral therapy as a strategy for elimination of HIV transmission: a mathematical model. Lancet. 2009;373:48–57. doi: 10.1016/S0140-6736(08)61697-9. [DOI] [PubMed] [Google Scholar]
- 8.Montaner JS, Hogg R, Wood E, et al. The case for expanding access to highly active antiretroviral therapy to curb the growth of the HIV epidemic. Lancet. 2006;368:531–6. doi: 10.1016/S0140-6736(06)69162-9. [DOI] [PubMed] [Google Scholar]
- 9.Velasco-Hernandez JX, Gershengorn HB, Blower SM. Could widespread use of combination antiretroviral therapy eradicate HIV epidemics? Lancet Infect Dis. 2002;2:487–93. doi: 10.1016/s1473-3099(02)00346-8. [DOI] [PubMed] [Google Scholar]
- 10.Garnett GP, Baggaley RF. Treating our way out of the HIV pandemic: could we, would we, should we? Lancet. 2009;373:9–11. doi: 10.1016/S0140-6736(08)61698-0. [DOI] [PubMed] [Google Scholar]
- 11.Smith RJ, Okano JT, Kahn JS, Bodine EN, Blower S. Evolutionary dynamics of complex networks of HIV drug-resistant strains: the case of San Francisco. Science. 2010;327:697–701. doi: 10.1126/science.1180556. [DOI] [PubMed] [Google Scholar]
- 12.Charlebois ED, Das M, Porco TC, Havlir DV. The effect of expanded antiretroviral treatment strategies on the HIV epidemic among men who have sex with men in San Francisco. Clin Infect Dis. 2011;52:1046–9. doi: 10.1093/cid/cir085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Long EF, Brandeau ML, Owens DK. The cost-effectiveness and population outcomes of expanded HIV screening and antiretroviral treatment in the United States. Ann Intern Med. 2010;153:778–89. doi: 10.1059/0003-4819-153-12-201012210-00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Walensky RP, Paltiel AD, Losina E, et al. Test and treat DC: forecasting the impact of a comprehensive HIV strategy in Washington DC. Clin Infect Dis. 2010;51:392–400. doi: 10.1086/655130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sorensen SW, Sansom SL, Brooks JT, et al. A Mathematical model of comprehensive test-and-treat services and HIV incidence among men who have sex with men in the United States. PLoS One. 2012;7:e29098. doi: 10.1371/journal.pone.0029098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wilson DP. HIV treatment as prevention: natural experiments highlight limits of antiretroviral treatment as HIV prevention. PLoS Med. 2012;9:e1001231. doi: 10.1371/journal.pmed.1001231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dodd P, Garnett G, Hallett TB. Examining the promise of HIV elimination by ‘Test and Treat. AIDS. 2010;24:729–35. doi: 10.1097/QAD.0b013e32833433fe. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Eaton JW, Johnson LF, Salomon JA, et al. HIV treatment as prevention: systematic comparison of mathematical models of the potential impact of antiretroviral therapy on HIV incidence in South Africa. PLoS Med. 2012;9:e1001245. doi: 10.1371/journal.pmed.1001245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Delva W, Wilson DP, Abu-Raddad L, et al. HIV treatment as prevention: principles of good HIV epidemiology modelling for public health decision-making in all modes of prevention and evaluation. PLoS Med. 2012;9:e1001239. doi: 10.1371/journal.pmed.1001239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lima VD, Johnston K, Hogg RS, et al. Expanded access to highly active antiretroviral therapy: a potentially powerful strategy to curb the growth of the HIV epidemic. J Infect Dis. 2008;198:59–67. doi: 10.1086/588673. [DOI] [PubMed] [Google Scholar]
- 21.Baggaley RF, Garnett GP, Ferguson NM. Modelling the impact of antiretroviral use in resource-poor settings. PLoS Med. 2006;3:e124. doi: 10.1371/journal.pmed.0030124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Blower SM, Gershengorn HB, Grant RM. A tale of two futures: HIV and antiretroviral therapy in San Francisco. Science. 2000;287:650–4. doi: 10.1126/science.287.5453.650. [DOI] [PubMed] [Google Scholar]
- 23.Law MG, Prestage G, Grulich A, Van de Ven P, Kippax S. Modelling the effect of combination antiretroviral treatments on HIV incidence. AIDS. 2001;15:1287–94. doi: 10.1097/00002030-200107060-00011. [DOI] [PubMed] [Google Scholar]
- 24.Centers for Disease Control and Prevention. HIV surveillance report. 2009. Available at: http://www.cdc.gov/hiv/surveillance/resources/reports/2011report . Accessed 28 March 2012.
- 25.LADHSP. Program brief: HIV prevention through care and treatment. 2012. Available at: http://ph.lacounty.gov/aids/ . Accessed 9 May 2012. [Google Scholar]
- 26.Centers for Disease Control and Prevention. HIV/AIDS facts October 2008. 2006. New estimates of U.S. HIV prevalence, Available at: http://www.cdc.gov/hiv/topics/surveillance/ . Accessed 12 April 2012. [Google Scholar]
- 27.van de Vijver DAMC, Wensing AMJ, Boucher CAB. The epidemiology of transmission of drug resistant HIV-1. 2007. pp. 17–36. HIV Sequence Compendium 2007 . [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.