A valid formulation of the analysis of noninferiority trials under random effects meta-analysis

Abstract

A noninferiority (NI) trial is sometimes employed to show efficacy of a new treatment when it is unethical to randomize current patients to placebo because of the established efficacy of a standard treatment. Under this framework, if the NI trial determines that the treatment advantage of the standard to the new drug (i.e. S−N) is less than the historic advantage of the standard to placebo (S−P), then the efficacy of the new treatment (N−P) is established indirectly. We explicitly combine information from the NI trial with estimates from a random effects model, allowing study-to-study variability in k historic trials. Existing methods under random effects, such as the synthesis method, fail to account for the variability of the true standard versus placebo effect in the NI trial. Our method effectively uses a prediction interval for the missing standard versus placebo effect rather than a confidence interval of the mean. The consequences are to increase the variance of the synthesis method by incorporating a prediction variance term and to approximate the null distribution of the new statistic with a t with k−1 degrees of freedom instead of the standard normal. Thus, it is harder to conclude NI of the new to (predicted) placebo, compared with traditional methods, especially when k is small or when between study variability is large. When the between study variances are nonzero, we demonstrate substantial Type I error rate inflation with conventional approaches; simulations suggest that the new procedure has only modest inflation, and it is very conservative when between study variances are zero. An example is used to illustrate practical issues.

1. INTRODUCTION

Clinical trials that employ a noninferiority (NI) design have become increasingly common; the aim is to demonstrate that a new drug's inferiority to a standard drug does not exceed some acceptable amount and hence the new drug is “non-inferior” to the standard. An NI design could be used when the primary question is truly how a new agent compares to a standard; a new drug may be less toxic or less expensive, so that a small loss in efficacy might be a reasonable trade-off. But, in the regulatory environment, in order for a drug to be licensed, superiority to placebo must be demonstrated, thus, the NI design is typically used when the primary goal is to determine if a new drug is superior to a “missing” placebo arm that is unallowable for ethical reasons. Historic data are first used to estimate the treatment effect of the standard drug to placebo; if the NI trial shows the treatment advantage of the standard drug to the new drug is less than this historic estimate, the new drug “must” have been better than placebo and efficacy of the new drug to placebo is demonstrated, albeit indirectly. Many authors have discussed this paradigm; see the following general discussions: Fleming (2008), D'Agostino and others (2003), Hung and others (2003).

Two statistical methods for analysis of this design and paradigm have been in use for at least the past decade (Food and Drug Administration (FDA) 2010; Fleming, 2008; Snapinn, 2004). Our discussion assumes that multiple placebo controlled trials of the standard drug exist, so that a meta-analysis (MA) can be performed. One method, “95–95,” first computes the 95% confidence interval of the mean of the standard versus placebo treatment effect from the MA and selects the lower bound known as M1. If the 95% confidence interval of New versus Standard effect in the NI trial lies above − M₁, then NI is concluded, so the new drug is deemed superior to placebo. Recently issued draft guidance from the FDA (Food and Drug Administration, 2010) recommends this approach; the document notes that this is conservative statistically under certain assumptions, but argues this conservatism is an appealing remedy for all the uncertainties in applying historic data. The second procedure, known as the synthesis method, estimates the new minus placebo treatment effect by combining the standard minus placebo treatment effect in the MA with the new minus standard treatment effect in the NI (Hasselblad and Kong, 2001). The corresponding variance of the estimate is the sum of the variance of the MA treatment effect (standard minus placebo, i.e. S−P) and the NI effect (new minus standard, i.e. N−S).

Rothmann and others (2003) recommend estimating the overall effect of the standard in the MA by either a fixed effects model or a random effects model, choosing “whichever is more appropriate” to the setting. Under a random effects model, the estimate of the overall treatment effect of the standard drug incorporates the trial to trial variability of the treatment effect; the variance associated with this treatment effect is likewise impacted. These estimates are then used in both the “95–95” and the synthesis procedures. However, the variance estimate only measures how well the overall treatment effect has been estimated in the MA. It fails to reflect the fact that the NI study should draw its own random true treatment effect of the standard to the missing placebo. An extreme hypothetical example illustrates the problem with this approach: imagine an MA with an infinite number of historic trials, each of infinite size, where the true mean S–P treatment effect is 10 but varies from study to study with standard deviation 2. Thus, the effect would be estimated as 10, with no sampling error, then either of the above procedures would boil down to the following: if the N–S treatment effect in the NI trial is significantly >−10, we would conclude that the new drug is better than placebo. But, the NI study has its own true standard versus placebo effect; if this is 7, for example, then the above test would lead too often to false conclusions of efficacy. Even if we knew the overall treatment effect of the standard versus placebo exactly, we would still need to account for the uncertainty of this effect in the current NI trial.

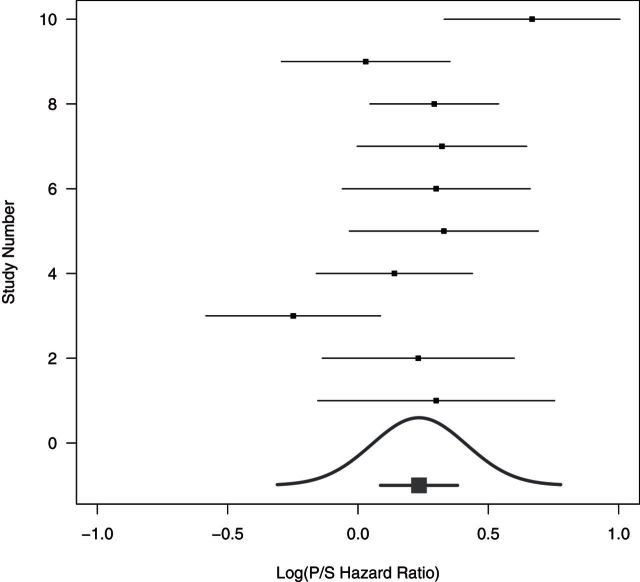
If we have n observations of some random variable X, and we want to predict the next value X, we do not compute the confidence interval on the mean, we, instead, compute the larger prediction interval. The NI trial is analogous, logically we should use a prediction perspective for the missing placebo effect. That is, we need to consider the distribution of the missing (S–P) treatment effect in the new trial not just the overall mean treatment effect. In the new trial, the patients may be a bit sicker or less responsive to treatment. Figure 1, based on an example described later, provides a graphical representation of this idea. There are 10 historic trials each with a treatment effect estimate of the log hazard ratio (HR) of standard versus placebo. These are plotted with trial-specific confidence intervals. A confidence interval for the mean is given at the bottom. An estimated distribution of the study-specific treatment effects is also given at the bottom and there is approximately a 10% chance that in a future study, the study-specific S–P treatment effect would be less than zero, indicating that placebo is better than standard.

Fig. 1.

The 10 historic log HRs (Placebo/Standard) along with treatment effect confidence intervals. The confidence interval for the mean log HR is the short line with the thick square near the bottom line, while the estimated distribution of true (Placebo/Standard) treatment effects is given by the Gaussian curve. Data from “Example 4” of FDA Guidance draft discussed in Section 7.

This paper proposes methodology that incorporates the prediction interval concept (we note that Rothmann and others, 2012 briefly describe a very similar approach in their book (p. 108–109), which appeared after our paper was submitted). We will show that if the historic studies and the NI study are all truly consistent with a random effects model, then our procedure will have approximately correct Type I error rate, whereas existing methods, even the “conservative” 95–95 method, can lead to substantial inflation of the Type I error rate. We present a re-analysis of an NI study evaluating a treatment for metastatic colorectal cancer, based on a 10-study MA. The results using our approach are qualitatively different from the standard procedures.

2. MAIN MODEL

Let Y_Si, Y_Pi, and Y_Ni be random variables representing the (possibly unobserved) summary statistics for the standard arm, placebo arm, or new treatment arm, respectively, from the ith trial, where i = 0 indexes the NI trial and i = 1,…,k indexes the k historic trials. Examples of summary statistics include the mean of a continuous variable, the log rate of an event, the log odds ratio for an event, or some other approximately normally distributed measure. We observe Y_S0 and Y_N0 from the NI trial, and the Y_Si and Y_Pi from the i = 1,…,k historic trials. The value Y_P0 represents the summary statistic from an unobserved “phantom” placebo arm in the NI study, while Y_Ni for i = 1,…,k represent the unobserved summary statistic from a “phantom” arm of the new treatment for the ith historic trial.

We assume a standard random effects formulation for the three summary measures:

where A = P,S, or N and i = 0,1,…,k. The variable β_A represents the overall true mean effect of the arm, b_Ai represents the random deviations from the mean for the ith study, and ϵ_Ai represents within study errors assumed to be independent normal with variance σ_Ai².

We work mainly with the Y_A − Y_B differences, where A,B = N,P, or S, and define the treatment effect of A relative to B as Δ_AB = β_A − β_B, letting δ_ABi = b_Ai − b_Bi and e_ABi = ϵ_Ai − ϵ_Bi. We write the estimated treatment effects as

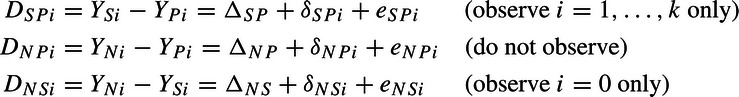and for an arbitrary pair A,B, we have δ_ABi∼N(0,τ_AB²) and e_ABi∼N(0,σ_ABi²), where σ_ABi² = σ_Ai² + σ_Bi². Let ρ be the correlation between δ_SPi and δ_NPi, and we will not need notation for the other correlations.

In the ith historic trial, the SP treatment effect is Δ_SP + δ_SPi. Here, Δ_SP is the average effect over all studies, whereas δ_SPi is the deviation from that average for study i. For example, patients in study i may be a bit sicker than in other studies and the benefit of S over P may be greater for the sickly, thus δ_SPi might be larger than zero. The parameter τ_SP² is the variance of these SP deviations over the historic studies. Similarly, in the NI trial, the NS treatment effect is Δ_NS + δ_NS0.

The fundamental problem of this paper is that we are interested in the NP treatment effect from a study, but D_NPi is not observed in any trial. From the model, we know that conditionally, D_NS0|δ_NS0∼N(Δ_NS + δ_NS0,σ_NS0²), and unconditionally,

(2.1)

From the historic trials, we use a weighted mean of the D_SPi. Let

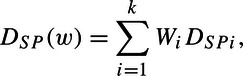where 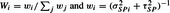. So that if the variances were known, then

(2.2)

where

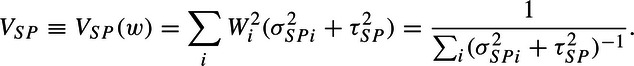Combining (2.1) and (2.2), along with the identities Δ_NP = Δ_NS + Δ_SP and δ_NPi = δ_NSi + δ_SPi, and the independence between the historic and NI studies, we get (assuming known variances)

(2.3)

Additionally, by using standard results for conditional normal random variables, we show in Section 1 of the supplementary material available at Biostatistics online that under the strong null that the new treatment is identical to placebo in all k+1 studies, and assuming known variances that

(2.4)

3. TESTING THAT NEW TREATMENT EQUALS PLACEBO

3.1. Testing with known variances

There are two ways to derive a test that the new treatment effect equals the placebo effect. First, we can test whether over all studies the new treatment is better on average than placebo. That is, formally test the null that H₀:Δ_NP = 0. Alternatively, we can test whether the new treatment would have been better than placebo in study 0. That is, formally test the null that H₀^δ:Δ_NP + δ_NP0 = 0.

Under the strong null that the new is identical to placebo (so that τ_NS² = τ_SP²), we see that assuming known variances, we can derive the same standard normal test statistic, T, under either H₀ (see (2.3)) or H₀^δ (see (2.4)), where

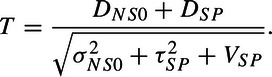(3.5)

In the first situation under H₀, D_NS0 is a poor estimator of Δ_NS and has variance of σ_NS0² + τ_NS², while in the second situation under H₀^δ, D_NS0 is a poor estimator of Δ_NS + δ_NP0 and has null variance of σ_NS0² + τ_SP².

3.2. Testing with unknown variances

In practice, we must estimate the weights, w, as well as the variances used in the denominator of T, V_NP(w)≡V_NP = V_SP + σ_NS0² + τ_SP². In general, we will use the hat notation to denote that all the variances in an expression are replaced by estimates. For example,

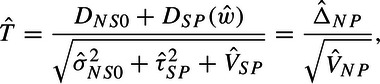(3.6)

where ${\widehat{\Delta }}_{NP}=D_{NS0}+D_{SP}\left(\widehat{w}\right)$; the study-specific variance estimates, ${\widehat{\sigma }}_{NS0}^2$ and ${\widehat{\sigma }}_{SPi}^2$, are estimated from within the appropriate study; and ${\widehat{\tau }}_{SP}$ is the Paule and Mandel (1982) MA variance estimator (details in Section 2 of the supplementary material available at Biostatistics online).

The impact of the estimation of those variances on the distribution of $\widehat{T}$ needs to be incorporated. If σ_SPi² and σ_NS0² are tiny compared to τ_SP², then we can treat those variances as zero, so that W_i is approximately 1/k for all i, and ${\widehat{\tau }}_{SP}^2$ approximately reduces to the sample variance of the D_SPi (see Section 2 of the supplementary material available at Biostatistics online). Under tiny σ_SPi² and σ_NS0², we also have V_SP≈τ_SP²/k, so that analogous to the standard derivation of the t-test, one can show that $\widehat{T}$ is approximately distributed t with k−1 degrees of freedom. Section 3 of the supplementary material available at Biostatistics online gives a fairly general estimate of degrees of freedom requiring fewer assumptions but giving a more variable degrees of freedom estimator. Stabilization of that variable estimator leads back to the k−1 degrees of freedom estimator. Thus, comparing $\widehat{T}$ to a t distribution with k−1 degrees of freedom is our recommended approach and will be called the full random effects (FRE) test.

We briefly mention an alternate approach. There has been considerable work on making inferences from the random effects model identical to our standard versus placebo MA model when the σ_SPi are not assumed equal (see review of Sutton and Higgins, 2008). We incorporate one of those methods, the one described in Hartung (1999), into our problem and describe the results in the supplementary material available at Biostatistics online Section 4. Unfortunately, similar to the simulations in Hartung (1999), our simulations show that the Type I error is often anti-conservative (with 0.025 nominal values as large as 0.05); thus, we do not recommend this approach.

3.3. Proposed method compared to conventional ones

We compare the FRE test to the traditional methods of analysis when they are based on MAs with random effects (see, e.g. Food and Drug Administration, 2010). The synthesis method uses

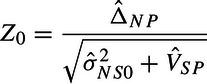as a test statistic. Z₀ eliminates ${\widehat{\tau }}_{SP}^2$ from the denominator of $\widehat{T}$ and thus $\left|Z_0|\ge |\widehat{T}\right|$. The two approaches differ because our goal is to reconstruct the missing placebo arm in the current NI trial, while the synthesis method compares the NS effect in the NI trial to the average SP effect over all historic studies. Additionally, the synthesis method uses a standard normal null, while the FRE uses a t_{k − 1}. Under a fixed effects approach τ_SP² is known to be zero and both $\widehat{T}$ and Z₀ reduce to the same statistic which can be compared to a standard normal null. Finally, Snapinn (2004) shows that the 95–95 method reduces to comparing

to a standard normal distribution. This is smaller in absolute value than Z₀ but can be larger or smaller than $\widehat{T}$ in absolute value. As with the synthesis method, a standard normal null is used.

4. SIMULATIONS

We simulate rejection rates under the null for the various procedures. We assume Δ_SP = 1 and further assume that each patient's outcome follows a normal distribution with true standard deviation, ϕ, of 2.15 or 5 (to clarify, the notation ϕ relates to previously introduced notation such that σ² = 2ϕ²/n, where n is a per group sample size). We let k equal 2, 3, 5, or 10, and we let τ_SP equal 0, 0.3, 0.7, or 1. The per group sample sizes in the historic studies vary uniformly from 50 to 150 (e.g. when k=5, the sample sizes are 60, 80, 100, 120, and 140), and the per group sample size in the NI trial is 350. These parameters are chosen, in part, to yield standard errors that are similar to those seen in a later section, except scaled so that Δ_SP = 1. The correspondence occurs with the true standard deviation, ϕ, of 5 and τ_SP of 0.7. We also include a standard deviation of 2.15 as this corresponds to 90% power in each historic study, which may be more typical in practice. Note that our simulation results apply more widely; for example, our simulation results with ϕ of 5 and τ_SP of 0.3 also apply to the following set of parameters: Δ_SP = 5, ϕ of 25, and τ_SP of 1.5. All parameter combinations are simulated with 100,000 replications. For each replication, we simulate an MA and an NI trial; that is, we generate k treatment effects with corresponding standard errors and an NI trial treatment effect. The results are shown in Table 1, where the nominal rate is 0.025.

Table 1.

Simulations of rejection rates under the null (for nominal one-sided 0.025 level), and 10th, 50th, and 90th percentiles of $\widehat{\tau }$ as a function of standard deviation, φ, k, and τ_SP

		${\widehat{\tau }}_{\text{SP}}$				Rejection rates
φ	k	τSP	τ(0.10)	τ(0.50)	τ(0.90)	Synthesis	95–95	FRE
2.15	2	0.0	0.00	0.00	0.41	0.020	0.002	0.000
2.15	2	0.3	0.00	0.00	0.64	0.089	0.036	0.000
2.15	2	0.7	0.00	0.41	1.22	0.175	0.120	0.000
2.15	2	1.0	0.00	0.63	1.69	0.198	0.153	0.001
2.15	3	0.0	0.00	0.00	0.36	0.021	0.002	0.000
2.15	3	0.3	0.00	0.18	0.58	0.095	0.038	0.003
2.15	3	0.7	0.00	0.56	1.12	0.173	0.115	0.024
2.15	3	1.0	0.14	0.81	1.56	0.192	0.144	0.027
2.15	5	0.0	0.00	0.00	0.31	0.021	0.002	0.002
2.15	5	0.3	0.00	0.24	0.52	0.109	0.044	0.025
2.15	5	0.7	0.24	0.63	1.03	0.191	0.125	0.035
2.15	5	1.0	0.44	0.90	1.43	0.211	0.153	0.031
2.15	10	0.0	0.00	0.00	0.25	0.024	0.003	0.008
2.15	10	0.3	0.00	0.28	0.46	0.131	0.059	0.036
2.15	10	0.7	0.42	0.67	0.93	0.231	0.155	0.030
2.15	10	1.0	0.64	0.96	1.30	0.253	0.187	0.027
5.00	2	0.0	0.00	0.00	0.96	0.020	0.002	0.000
5.00	2	0.3	0.00	0.00	1.08	0.035	0.007	0.000
5.00	2	0.7	0.00	0.00	1.49	0.089	0.036	0.000
5.00	2	1.0	0.00	0.41	1.90	0.127	0.069	0.000
5.00	3	0.0	0.00	0.00	0.84	0.020	0.002	0.000
5.00	3	0.3	0.00	0.00	0.95	0.038	0.007	0.000
5.00	3	0.7	0.00	0.42	1.35	0.097	0.039	0.004
5.00	3	1.0	0.00	0.73	1.73	0.132	0.068	0.010
5.00	5	0.0	0.00	0.00	0.71	0.021	0.002	0.002
5.00	5	0.3	0.00	0.00	0.82	0.042	0.007	0.005
5.00	5	0.7	0.00	0.57	1.21	0.109	0.045	0.025
5.00	5	1.0	0.00	0.87	1.57	0.149	0.079	0.034
5.00	10	0.0	0.00	0.00	0.58	0.022	0.003	0.007
5.00	10	0.3	0.00	0.23	0.70	0.050	0.012	0.019
5.00	10	0.7	0.00	0.65	1.07	0.131	0.059	0.037
5.00	10	1.0	0.43	0.94	1.41	0.177	0.098	0.036

While the synthesis method has appropriate Type I error when τ_SP = 0, this inflates dramatically as τ_SP increases. The 95–95 method, which is generally viewed as conservative, is indeed conservative when τ_SP = 0, but even this procedure is associated with large inflation as τ_SP grows. For both these methods, the inflation gets slightly worse as k increases and is clearly worse for the smaller value of the standard deviation ϕ. The Type I error for the new FRE statistic is much closer to the nominal level, although it has some relatively modest inflation in some of the parameter combinations (this inflation would not occur had the simulation been done with equal sample sizes across the studies). Furthermore, the rejection rates for the FRE procedure are sometimes well below 0.025 when τ_SP = 0 or when both τ_SP and k are small. We believe this conservatism is inherent that this is the price one must pay for the test procedure to have correct Type I error for any possible value of τ_SP. Finally, the range of values for ${\widehat{\tau }}_{SP}$ illustrate the imprecision of these estimates.

We do not present simulation results comparing the approaches for power, as the previous simulations indicate that the synthesis and 95–95 methods do not control the Type I error rate if there is a possibility that τ_SP is greater than zero and are thus not viable under full random effects. In the next section, we present a power formula for the new procedure.

5. PREDICTION INTERVAL, POWER, AND CHOICE OF STUDY DESIGN

When planning an NI study, we would have results from the completed MA already at hand. Typically, we will want to calculate a prediction interval for Δ_SP + δ_SP0 as well as the power of the NI trial to detect a difference between the new treatment and placebo. Formulas are derived in Section 5 of the supplementary material available at Biostatistics online. An approximate 100(1 − α)% prediction interval for Δ_SP + δ_SP0 is given by

(5.7)

Power can be calculated by

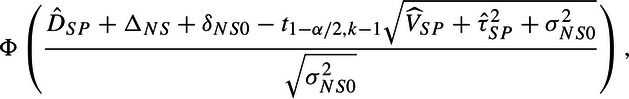(5.8)

where ϕ is the standard normal cumulative distribution (We note that this power formula could also be reformulated as a function of τ_NS² using (2.3). Under this approach, the δ_NS0 term is eliminated, and τ_NS² would be added to σ_NS0² in the denominator.). If an MA leads to a prediction interval (see (5.7)) that straddles the null, then the numerator (5.8) is less that 0 (under the usual assumption that Δ_NS + δ_NS0 = 0) and power for our test procedure would be <50%, even with an infinitely sized NI trial unless the new drug could be assumed to be better than the standard. If that were the case, the usual test of superiority of new over standard might be more powerful. So, if confronted with a wide prediction interval, it would be prudent to evaluate the power under both these approaches to determine the most efficient strategy.

We note that under our random effects, the power formulas for the existing approaches mimic (5.8), except that, when α=0.05, the negative term in the numerator is replaced by 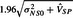for synthesis and 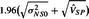for 95–95. When using the synthesis or 95–95 procedures if the confidence interval from the MA straddles the null value, then the power will be <50%, which, of course, will occur much less frequently than the prediction interval straddling the null.

Thus, the implication of using a true random effects approach is that some MAs, which would have supported an NI trial using the previous procedures, will no longer do so. And, even where the NI is still supported, the sample size requirements will typically be greater and often substantially so.

There are, however, some plausible scenarios where the required sample size for the new procedure is lower than the 95–95 method which is currently recommended because of its supposed conservatism. As a rough rule of thumb, this generally occurs when ${\widehat{\tau }}_{SP}=0$ and k is at least six. As k further increases, as long as ${\widehat{\tau }}_{SP}$ is sufficiently small, the required sample size for the new procedure is likely to be smaller than that of 95–95. Similarly, when ${\widehat{\tau }}_{SP}=0$, and k gets large, the new procedure and the synthesis method converge.

6. TESTING THAT NEW TREATMENT IS A FACTOR OF STANDARD

We assume that the new treatment acts like a dilution or concentration of the standard treatment. This assumption implies that the new treatment cannot be worse than placebo. Although this is restrictive, it does allow us to model some key cases. In terms of the parameters in our model, this means that Δ_NP = γΔ_SP and δ_NPi = γδ_SPi for i = 0,1,…,k. If γ < 1, then this represents the new treatment acting like a diluted (i.e. weakened) standard and if γ>1 this represents the new treatment acting like a concentrated (i.e. stronger) standard. This assumption implies that τ_NP² = γ²τ_SP² and ρ = 1, so that τ_NS² = (1 − γ)²τ_SP²6. The value γ = 0 reduces to a null hypothesis model where the new treatment acts like placebo. When γ = 1 this means that the new treatment is acting exactly like the standard treatment, and we see that the last term drops out of V_NP. When 0 < γ < 1, then the new treatment retains γ of the standard effect.

Ideally, we want to estimate γ and test that it is greater than some factor, say γ₀ = 0.5. We consider testing H₀:γ = γ₀. Using the assumptions above, under the null hypothesis since Δ_NS0 = Δ_NP0 − Δ_SP0 = Δ_SP0(γ₀ − 1), then D_NS0∼N( − Δ_SP0(1 − γ₀),σ_NS0² + (1 − γ₀)²τ_SP²). Therefore, under the null that γ = γ₀, D_NS0 + (1 − γ₀)D_SP∼N(0,V_γ0), where V_γ0 = (1 − γ₀)²V_SP + σ_NS0² + (1 − γ₀)²τ_SP². Let $\hat{V}{\gamma }_0$ be V_γo with the estimators for σ_SPi² and τ_SP² replacing their values. We can then perform the hypothesis test by assuming, similarly to Section 3, that

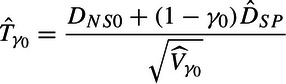is distributed t with k − 1 degrees of freedom.

We can get confidence intervals for γ by inverting the hypothesis tests. In other words, the 95% confidence interval is the values of γ₀ which would fail to reject the two-sided point null hypothesis that H₀:γ = γ₀. Further we can use a median unbiased estimator using the confidence intervals. Specifically, define $\widehat{\gamma }$ as the value of γ₀ such that the one-sided p value is 0.5 (see, e.g. Read, 2006).

7. EXAMPLE

7.1. Original data

The FDA presents several examples as part of their new Guidance on NI trials (Food and Drug Administration, 2010). In this section, we present our re-analysis of their “Example 4,” which considers NI trials designed to assess the efficacy of Xeloda, an oral fluorpyrimidine, as a first-line treatment of metastatic colorectal cancer. An early treatment 5-fluoracil (5-FU), an infusional fluoropyrimidine, had not been proven to have efficacy in survival in this setting. However, a combination product, 5-fluorouracil with leucovorin (5-FU + LV) had a demonstrated survival advantage, and this regimen was the standard of care at the time the NI trials were designed. Numerous randomized trials of 5-FU + LV versus 5-FU alone were conducted, and the FDA Guidance summarized the 10 studies used in the MA which supported the use of the NI trials. As the FDA Guidance notes, since 5-FU may have some efficacy, this MA may lead to a conservative estimate of the 5-FU + LV treatment effect. Thus, even though 5-FU is not a placebo, for the purposes of our discussion, we hereafter refer to 5-FU as “Placebo,” 5-FU + LV as “Standard,” and Xeloda as “New.” The summary of the trials that comprise this previous MA is seen in Fig. 1 and Table 2, adapted from Table 8 on page 54 of the FDA Guidance (Food and Drug Administration, 2010). Of course, a licensure decision involves many aspects that are not touched upon in this section, and we use Example 4 only to illustrate how our method could be used. Furthermore, as already noted, we treat the 5-FU as a placebo in the analysis; if this regimen had some activity, our analysis would be conservative. Thus, our analysis might be viewed as providing an upper bound on the p value for NI.

Table 2.

The “Placebo”/“Standard” hazard ratios of 10 MA studies as presented in FDA Guidance Example 4; the “New”/“Standard” HR is also shown for the corresponding noninferiority(NI) Study 2 (Food and Drug Administration, 2010)

Study	Hazard ratio	Log hazard ratio	SE (log hazard ratio)
MA 1	1.35	0.301	0.232
MA 2	1.26	0.235	0.188
MA 3	0.78	–0.253	0.171
MA 4	1.15	0.143	0.153
MA 5	1.39	0.329	0.185
MA 6	1.35	0.300	0.184
MA 7	1.38	0.324	0.166
MA 8	1.34	0.294	0.126
MA 9	1.03	0.0296	0.165
MA 10	1.95	0.670	0.172
NI 0	0.92	–0.0844	0.0867

We present the summary statistics associated with this MA, using a random effects model in Table 3. We note that all calculations are done on the log HR scale. The MA has two outlying studies, the third trial with an HR estimate of 0.78, and the final trial with an estimate of 1.95. Our re-analysis focuses exclusively on the second NI study of “Example 4” presented in the Guidance; Table 2 includes the results of this trial. Our point estimate of the log HR for Placebo/New is 0.318 (i.e. the numerator of the new test statistic), with the corresponding HR estimate of 1.375.

Table 3.

Summary of MA results from FDA Guidance Example 4 (Food and Drug Administration, 2010)

Scale	${\widehat{D}}_{\text{SP}}$		${\widehat{\tau }}_{\text{SP}}$	95% confidence interval	95% prediction interval
Log HR	0.234	0.075	0.165	(0.086, 0.382)	( – 0.176, 0.644)
HR	1.264	—	—	(1.09, 1.46)	(0.84, 1.90)

Table 4 provides the results associated with the three methods of analysis (see rows labeled “ALL” data), where one-sided p values <0.025 are considered statistically significant. The synthesis method is highly significant, the 95–95 is just barely significant, and the new FRE test is not statistically significant. Under the assumption that the observed estimates for Δ_SP and τ_SP match the true parameters, the penultimate row of Table 1 provide the approximate Type I error for the three procedures. These rejection rates are 0.037, 0.059, and 0.131, for FRE, 95–95, and synthesis, respectively, where 0.025 is the nominal level. Thus, although there is some relatively modest inflation for the FRE procedure, the inflation is significant for 95–95 and very substantial for synthesis.

Table 4.

Summary of tests of “New” compared to “Placebo”: hazard ratios are “Placebo”/“New”; all values are in terms of Log(HR) except where noted (From FDA Guidance Example 4, NI Study 2; Food and Drug Administration, 2010). Results shown using all data and again omitting MA Study 3

Data	Method	Treatment effect	SE	95% CI Log HR	95% CI HR	Statistic	One-sided p value
All	FRE	0.318	0.201	( – 0.136, 0.773)	(0.87, 2.17)	1.59	0.074
All	95–95	0.318	0.162	(0.001, 0.636)	(1.00, 1.89)	1.97	0.025
All	Synthesis	0.318	0.115	(0.093, 0.544)	(1.10, 1.72)	2.77	0.003
Omits MA 3	FRE	0.370	0.112	(0.112, 0.628)	(1.12, 1.87)	3.31	0.005
Omits MA 3	95–95	0.370	0.145	(0.087, 0.654)	(1.09, 1.92)	2.56	0.005
Omits MA 3	Synthesis	0.370	0.104	(0.166, 0.574)	(1.18, 1.78)	3.55	0.0002

As the prediction interval straddles the null, this NI trial is very underpowered for the FRE test. Consider the case where we assume that the new is exactly equivalent to the standard, then the power is near zero for both the FRE test and for the usual new versus standard superiority test. Even if we assume that the new drug is 50% more efficacious than the standard, then the power would be only 0.12 for the FRE procedure and 0.27 for the usual new versus standard superiority test. Thus, in practice, if we were charged with designing a trial to determine efficacy of the new drug, and we assume a random effects model, a larger advantage of the new drug to the standard would need to be assumed to have adequate statistical power. Indeed, one might opt to consider the usual superiority comparison of new to standard as the primary analysis. If the new treatment is likely to have similar efficacy to the standard, then the study designers would need an alternate study paradigm to test efficacy of the new treatment.

In order to illustrate some alternate examples, we re-analyze the NI trial above, but where the MA is based on subsets of the original 10.

7.2. Subset of original data with statistically significant result

The above example yields a prediction interval that straddles the null, and the NI study test is not statistically significant. Simply to illustrate, we repeat the analysis, but this time omitting the third historic trial, to present an example with a statistically significant result using our approach. This historic study has a large impact on the MA; and if it had never been conducted, the MA of the remaining nine trials would have led to 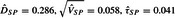, and the prediction interval for the HR is (1.13, 1.57). This MA result would lead to a much higher power for the new test procedure in the NI trial compared to the previous example; with the assumption that the new treatment has the same true efficacy as the standard in the NI trial, the power would be 0.63, and with a 50% improvement in treatment effect over the standard, the power approaches 100%; the corresponding powers for testing superiority of new to standard would be much lower. Under this artificial scenario, the results of the NI trial would yield a p value of 0.0053 for the test of efficacy of new versus placebo. Table 4 exhibits the results for the three procedures (see the rows labeled “Omits MA 3”); it is interesting to note that the p values for the new FRE procedure and for 95–95 are now identical. (If we further exclude the other outlying trial, MA10, the p value for FRE would be 0.009 and for the 95–95 would be 0.013.)

If we believed that the new drug were a dilution of the standard, such that we could assume the model described in Section 6, we could evaluate γ, the factor of the standard. The test of 50% retention would have a p value of 0.021, $\widehat{{\gamma }_0}$ would be 1.30, and the lower bound of the confidence interval would be 0.551. Thus, if the third historic trial did not exist, one could conclude the new drug is superior to placebo and that it retains at least 55.1% of the benefit of the standard regimen if the new treatment is a dilution of the standard.

8. DISCUSSION

NI studies have substantial vulnerabilities beyond the issues focused upon in this paper. These trials rely on “constancy”; that is, the design and underlying conditions of the NI trial must be completely consistent with the historic studies and that the treatment effect remains unchanged over time (Fleming, 2008; Food and Drug Administration, 2010). If the constancy assumption is not met, there is no statistical procedure that gives the correct Type I error rate. Some authors have advocated “discounting,” a sort of fudged conservatism, as a means to deal with any potential inconsistencies. This is the basis for the common use of the 95–95 method, which is known to be conservative under the fixed effects model when there is constancy. Under the random effects model with constancy, our procedure will have approximately the correct Type I error rate, while existing methods can lead to substantial inflation of the Type I error rate, even the 95–95 method that is thought to be conservative. If there is good reason to question the constancy assumption and there is little ability to quantify deviations from this assumption, we strongly recommend employing innovative superiority trial designs instead of NI trials. We see no contradiction between the constancy assumption and a random effects model, as long as the distribution of true treatment effect of the standard remains constant over time. In a setting where constancy is a reasonable assumption, and a random effects model is needed, we recommend using our procedure. Indeed, we believe that it typically would be difficult to justify an assumption of fixed effects a priori.

Our focus is on the comparison of the new drug to placebo. In the regulatory environment, this is an essential requirement; however, sometimes, similar efficacy to the comparison drug is also important to show, and this can lead to a more stringent standard (see Food and Drug Administration, 2010 and Snapinn and Jiang, 2008 for perspectives). This goal can be incorporated into the analysis, and one approach that may be appropriate is discussed in Section 6. On the other hand, there are public health settings where the goal of an NI trial only relates to the comparison of the two established drugs being studied, and our method is not relevant to that setting.

Selection of studies to include in the MA obviously strongly impacts our method. As seen in the example, when one outlying historic study out of 10 was omitted, the one-sided p value dropped from 0.074 to 0.005. These sorts of sensitivity analyses are especially important with the new procedure. If an effective argument can be made that a particular trial does not really fall in the population of studies of interest, then this study should be omitted from the MA. Of course, such arguments, even if made prior to conducting the NI trial, may be self-serving.

Our method assumes normality of several processes including the distribution of the random effects of the studies. For standard parameter estimation and inference, the central limit theorem ensures that departures from the distributional assumptions on the errors generally do not overly influence the results. On the contrary, prediction of effects is not as robust to departures from distributional assumptions (see McCulloch and Neuhaus, 2011). Thus, it would be useful to employ some sensitivity analyses. One possible strategy would be to re-analyze the data using a parametric bootstrap, where one bootstraps the δ_SPi values using some non-normal distribution.

If one knew the true value of τ_SP, one could modify our test statistic, by replacing the estimate with the known value and obtaining the p value from a standard normal instead of a t-distribution. So, as another type of sensitivity analysis, we can compute this p value for all possible values of τ_SP. This allows us to determine the maximum value of τ_SP that yields statistical significance, where such value exists. This analysis can provide important context in situations where the MA leads to an estimate of τ_SP that seems questionable. In addition, this approach is perhaps the most straightforward way to handle the situation of a single historic study.

The practical consequences of using our new method compared to the existing approaches are significant. For example, unlike the analysis presented in Section 7, there will sometimes be only two or three placebo control trials, which could often lead to insufficient power with our method. For this and other reasons, this full random effects approach will sometimes lead to the inability to design an NI trial with adequate power and will sometimes require much larger studies when NI studies can be properly powered. However, this is much better than observing a spurious result. If the fixed effects model really is true, and we apply our method, even where we correctly estimate τ to be zero, the new procedure would have the same test statistic as the synthesis method but will have a larger p value because it employs a t-distribution instead of a standard normal. These unfortunate losses in efficiency have to be weighed against the reverse situation, where the random effects model is true, and we have inflated Type I error rate with the existing procedures. That is, protecting against inflated Type I error rate under random effects leads to less efficiency when the effects are not random. We do not think the poor power is a weakness of our method, but rather a reflection that unless there are a sizeable number of historic studies or some clear-cut rationale for fixed effects, it is inherently difficult to have good statistical power with valid inference.

In the regulatory arena, patient level data would not typically be available for the MA because of proprietary considerations. However, Piedbois and Buyse (2004) describe the many advantages of individual data and call on regulatory agencies to promote this approach. Given the importance of reliable MA results to our NI procedure, such data, if available, would be helpful. Furthermore, when our approach is not feasible, we encourage consideration of an alternate strategy. One could determine the effect of baseline covariates, preferably at the individual level, on the standard versus placebo treatment effect in some rigorous manner, such that the default assumption of a pure random effects model is less necessary. For example, if we can learn from the historic trials that patients with a particular risk factor have a much larger treatment effect than those without; this information could improve our ability to predict what the standard versus placebo effect would be in the NI trial and may minimize or eliminate random study-to-study variability. This strategy could lead to much more efficient analyses of NI trials than the full random effects approach.

We urge designers of NI clinical trials to recognize that the methods in current use can lead to false conclusions of efficacy when there are true random effects. We believe our procedure represents an important advance in this arena.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

The previous version had some errors with the equations. These have now been corrected. The authors apologize for these errors.