Sodium and calcium mechanisms of rhythmic bursting in excitatory neural networks of the pre-Bötzinger complex: a computational modelling study

Abstract

The neural mechanisms generating rhythmic bursting activity in the mammalian brainstem, particularly in the pre-Bötzinger complex (pre-BötC), which is involved in respiratory rhythm generation, and in the spinal cord (e.g. locomotor rhythmic activity) that persist after blockade of synaptic inhibition remain poorly understood. Experimental studies in rodent medullary slices containing the pre-BötC identified two mechanisms that could potentially contribute to the generation of rhythmic bursting: one based on the persistent Na⁺ current (I_NaP), and the other involving the voltage-gated Ca²⁺ current (I_Ca) and the Ca²⁺-activated nonspecific cation current (I_CAN), activated by intracellular Ca²⁺ accumulated from extracellular and intracellular sources. However, the involvement and relative roles of these mechanisms in rhythmic bursting are still under debate. In this theoretical/modelling study, we investigated Na⁺-dependent and Ca²⁺-dependent bursting generated in single cells and heterogeneous populations of synaptically interconnected excitatory neurons with I_NaP and I_Ca randomly distributed within populations. We analysed the possible roles of network connections, ionotropic and metabotropic synaptic mechanisms, intracellular Ca²⁺ release, and the Na⁺/K⁺ pump in rhythmic bursting generated under different conditions. We show that a heterogeneous population of excitatory neurons can operate in different oscillatory regimes with bursting dependent on I_NaP and/or I_CAN, or independent of both. We demonstrate that the operating bursting mechanism may depend on neuronal excitation, synaptic interactions within the network, and the relative expression of particular ionic currents. The existence of multiple oscillatory regimes and their state dependence demonstrated in our models may explain different rhythmic activities observed in the pre-BötC and other brainstem/spinal cord circuits under different experimental conditions.

Introduction

Synchronised neural oscillations are generated in the brain by central pattern generators, which are centrally located neural networks that control rhythmic movements, such as walking, swimming, breathing, and chewing (Cohen et al., 1988; Stain et al., 1999; Gossard et al., 2010). Although synaptic inhibition plays a considerable role in these behaviours, the basic rhythmic activity in the corresponding structures usually persists after pharmacological blockade of inhibition. This was demonstrated in isolated rodent spinal cord preparations (Cowley & Schmidt, 1995) and medullary slices containing the pre-Bötzinger complex (pre-BötC, Feldman & Smith, 1989; Ramirez et al., 1996), which is the medullary structure involved in respiratory rhythm generation (Smith et al., 1991; Rekling & Feldman, 1998; Gray et al., 2001). However, the neural mechanisms underlying the generation of these important rhythms remain largely unknown.

Butera et al. (1999a,b) suggested that the population bursting observed in the pre-BötC in vitro arises from the persistent (slowly inactivating) Na⁺ current (I_NaP) in pre-BötC neurons and excitatory synaptic interactions within populations of these neurons. The presence of I_NaP in the pre-BötC has been confirmed (Del Negro et al., 2002a; Rybak et al., 2003a; Koizumi & Smith, 2008), and the pre-BötC rhythmic activity in medullary slices from neonatal rats could be abolished by the I_NaP blocker riluzole (Rybak et al., 2003b; Koizumi & Smith, 2008). Alternatively, Thoby-Brisson & Ramirez (2001), using medullary slices from mice at postnatal days 6–12 (P6-P12), found two distinct types of intrinsically bursting cells (bursters) in the pre-BötC whose bursting was, respectively, sensitive and insensitive to the Ca²⁺ current blocker Cd²⁺. Later, Peña et al. (2004) found that the Cd²⁺-sensitive bursters were riluzole-insensitive, whereas most of the Cd²⁺-insensitive ones were riluzole-sensitive. Furthermore, rhythmic activity in the Cd²⁺-sensitive bursters could be blocked by flufenamic acid (FFA), a pharmacological blocker of the Ca²⁺-activated nonspecific cation current (I_CAN, Del Negro et al., 2005), suggesting that both I_NaP and I_CAN are involved in bursting generated in the pre-BötC. The role of I_CAN in this bursting was further investigated by Del Negro and collaborators (Pace et al., 2007; Pace & Del Negro, 2008; Rubin et al., 2009), who suggested a metabotropic mechanism for synaptic activation of I_CAN.

However, the involvement and specific roles of these mechanisms in experimentally observed bursting activities remain controversial, and require special investigations. In this modelling study, we consider the intrinsic Na⁺-dependent and Ca²⁺-dependent bursting generated in single cells and heterogeneous populations of excitatory neurons with I_NaP and the voltage-gated Ca²⁺ current (I_Ca) randomly distributed across neurons in the populations. We study the possible roles of synaptic interactions, ionotropic and metabotropic synaptic mechanisms, intracellular Ca²⁺ release and the Na⁺/K⁺ pump in the cellular and network rhythmic bursting. We show that heterogeneous populations of excitatory neurons can generate rhythmic bursting dependent on I_NaP and/or I_CAN, or independent of both, and that the involvement of each mechanism may depend on the neuronal excitation, strength of synaptic interactions, and expression of particular ionic channels. We therefore suggest that the rhythmic bursting activity discovered in the pre-BötC in vitro is state-dependent, and hence, depending on the state, the pre-BötC can operate in multiple oscillatory regimes involving different I_NaP-dependent and/or I_CAN-dependent mechanisms. We also support the previous suggestion that the electrogenic Na⁺/K⁺ pump can play an important role in the generation of this rhythmic bursting by performing the burst-terminating function in multiple regimes of oscillations. The results of this theoretical/modelling study provide important insights into various rhythmic activities observed in the pre-BötC and other brainstem and spinal cord circuits.

Methods

Model description

The conductance-based single-compartment model of a single neuron was developed in the Hodgkin–Huxley style. The neuronal membrane potential (V) is defined by a set of membrane ionic currents:

$$C\cdot \frac{\mathrm{d}V}{\mathrm{d}t}=-I_{\mathrm{Na}}-I_{\mathrm{NaP}}-I_{\mathrm{K}}-I_{\mathrm{Ca}}-I_{\mathrm{CAN}}-I_{\mathrm{Pump}}-I_{\mathrm{L}}-I_{\mathrm{SynE}},$$ (1)

where C is neuronal membrane capacitance and t is time. The ionic currents in the model include fast Na⁺ (I_Na with the maximal conductance ${\stackrel{‒}{g}}_{\mathrm{Na}}$), persistent (or slowly inactivating) Na⁺ (I_NaP with the maximal conductance ${\stackrel{‒}{g}}_{\mathrm{NaP}}$), delayed rectifier K⁺ (I_K with the maximal conductance ${\stackrel{‒}{g}}_{\mathrm{K}}$), high-voltage-activated Ca²⁺ (I_Ca with the maximal conductance ${\stackrel{‒}{g}}_{\mathrm{Ca}}$), Ca²⁺-activated nonspecific cation (I_CAN with the maximal conductance ${\stackrel{‒}{g}}_{\mathrm{CAN}}$), Na⁺/K⁺ pump (I_Pump), leakage (I_L with the constant conductance g_L) and excitatory synaptic (I_SynE) currents. These currents, except for I_Pump, are described as follows:

$$\begin{array}{cc}\hfill & I_{\mathrm{Na}}={\stackrel{‒}{g}}_{\mathrm{Na}}\cdot m_{\mathrm{Na}}^3\cdot h_{\mathrm{Na}}\cdot (V-E_{\mathrm{Na}});\hfill \\ \hfill & I_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{NaP}}\cdot m_{\mathrm{Nap}}\cdot h_{\mathrm{Nap}}\cdot (V-E_{\mathrm{Na}});\hfill \\ \hfill & I_{\mathrm{K}}={\stackrel{‒}{g}}_{\mathrm{K}}\cdot m_{\mathrm{K}}^4\cdot (V-E_{\mathrm{K}});\hfill \\ \hfill & I_{\mathrm{Ca}}={\stackrel{‒}{g}}_{\mathrm{Ca}}\cdot m_{\mathrm{Ca}}\cdot h_{\mathrm{Ca}}\cdot (V-E_{\mathrm{Ca}});\hfill \\ \hfill & I_{\mathrm{CAN}}={\stackrel{‒}{g}}_{\mathrm{CAN}}\cdot m_{\mathrm{CAN}}\cdot (V-E_{\mathrm{CAN}});\hfill \\ \hfill & I_{\mathrm{L}}=g_{\mathrm{L}}\cdot (V-E_{\mathrm{L}});\hfill \\ \hfill & I_{\mathrm{SynE}}=g_{\mathrm{SynE}}\cdot (V-E_{\mathrm{SynE}}),\hfill \end{array}$$ (2)

where E_Na, E_K, E_Ca, E_CAN, E_L and E_SynE are reversal potentials of the corresponding channels:

$$\begin{array}{cc}\hfill & E_{\mathrm{Na}}=(R\cdot T∕F)\cdot \ln ({\mathrm{Na}}_{\mathrm{o}}∕{\mathrm{Na}}_{\mathrm{i}});\hfill \\ \hfill & E_{\mathrm{K}}=(R\cdot T∕F)\cdot \ln ({\mathrm{K}}_{\mathrm{o}}∕{\mathrm{K}}_{\mathrm{i}});\hfill \\ \hfill & E_{\mathrm{Ca}}=(R\cdot T∕2F)\cdot \ln ({\mathrm{Ca}}_{\mathrm{o}}∕{\mathrm{Ca}}_{\mathrm{i}});\hfill \\ \hfill & E_{\mathrm{CAN}}=0;E_{\mathrm{L}}=-68\mathrm{mV};E_{\mathrm{SynE}}=-10\mathrm{mV}.\hfill \end{array}$$ (3)

In the above equations: R = 8.314 J/(mol K) is the universal gas constant; T = 308 K is the temperature; and F = 96.485 kC/mol is the Faraday constant. This makes R · T/F = 26.54 mV. Na, K and Ca represent the concentrations of Na⁺, K⁺, and Ca²⁺, respectively. The subscripts ‘o’ (or ‘out’) and ‘i’ (or ‘in’) indicate the concentrations of these ions outside and inside the cell, respectively. In our model: Na_o = 120 mm; Ca_o = 4 mm; K_o = 4 mm; K_i = 140 mm; and Na_i and Ca_i were considered to be dynamical variables. Therefore, the K⁺ reversal potential was constant, E_K = −94 mV, whereas E_Na and E_Ca varied according to Eqn 3: E_Na = 26.54 · ln(120/Na_i) mV and E_Ca = 13.27 · ln(4/Ca_i) mV. The membrane capacitance value was set to C = 36 pF (Rybak et al., 2007; Smith et al., 2007).

Activation (m) and inactivation (h) variables for most ionic channels are described as:

$${\tau }_y\left(V\right)\cdot \frac{\mathrm{d}y}{\mathrm{d}t}=\left(y_{\infty }\right(V)-y);y=\{m,h\}.$$ (4)

For I_Na and I_NaP, steady-state activation (m_∞) and inactivation (h_∞) and their time constants are described as:

$$\begin{array}{cc}\hfill y_{\infty }\left(V\right)& =1∕(1+\exp (-(V-V_{y1∕2})∕k_y\left)\right);\hfill \\ \hfill {\tau }_y\left(V\right)& ={\tau }_{y\max }∕\cosh (-(V-V_{\tau y1∕2})∕k_{\tau y}).\hfill \end{array}$$ (5)

The parameters for these currents are shown in Table 1. The formal descriptions of channel kinetics and the corresponding parameters were derived from previous experimental (Rybak et al., 2003a) and modelling (Rybak et al., 2007; Smith et al., 2007) studies.

Table 1.

Ionic currents and channel kinetics parameters

Current	Parameters
Fast Na+	${\stackrel{‒}{g}}_{\mathrm{Na}}=150\mathrm{nS}$
I Na	Vm1/2 = −43.8 mV, km = 6 mV, τm max = 0.25 ms, Vτm1/2 = −43.8 mV, kτm = 14 mV
	Vh1/2 = −67.5 mV, kh = −10.8 mV, τh max = 8.46 ms, Vτh1/2 = −67.5 mV, kτh = 12.8 mV
Persistent	${\stackrel{‒}{g}}_{\mathrm{NaP}}\in [0,5]\mathrm{nS}$
Na+	Vm1/2 = −47.1 mV, km = 3.1 mV, τm max = 1 ms, Vτm1/2 = −47.1 mV, km = 6.2 mV
I NaP	Vh1/2 = −60 mV, kh = −9 mV, τh max = 5000 ms, Vτh1/2 = −60 mV, kτh = 9 mV
	In the case of non-inactivating INaP, h = constant = 0.4
K+ delayed rectifier	${\stackrel{‒}{g}}_K=160\mathrm{nS}$
I K	Aα = 0.01, Bα = 44 mV, kα = 5 mV, Aβ = 0.17, Bβ = 49 mV, kβ = 40 mV
Ca2+	${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.01]\mathrm{nS}$
I Ca	Vm1/2 = −27.5 mV, km = 5.7 mV, τm = 0.5 ms
	Vh1/2 = −52.4 mV, kh = −5.2 mV, τh = 18 ms
Ca2+-activated nonspecific ICAN	${\stackrel{‒}{g}}_{\mathrm{CAN}}=1\mathrm{nS}$ (in the case of sigh simulation, ${\stackrel{‒}{g}}_{\mathrm{CAN}}=3\mathrm{nS}$)
	KCAN = 0.00074 mm, n = 0.97
Na+/K+pump IPump	RPump = 200 pA, Naieq = 15 mm, KP = 15 mm
Leakage IL	$g_{\mathrm{L}}\in [2,3]\mathrm{nS}$

For the non-inactivating K⁺ delayed rectifier current (I_K):

$$\begin{array}{cc}\hfill m_{\infty }& ={\alpha }_{\infty }∕({\alpha }_{\infty }+{\beta }_{\infty });\hfill \\ \hfill {\tau }_{\infty }& =1∕({\alpha }_{\infty }+{\beta }_{\infty }),\hfill \end{array}$$ (6)

where

$$\begin{array}{cc}\hfill {\alpha }_{\infty }& =A_{\alpha }\cdot (V+B_{\alpha })∕(1-\exp (-(V+B_{\alpha })∕k_{\alpha });\hfill \\ \hfill {\beta }_{\infty }& =A_{\beta }\cdot \exp (-(V+B_{\beta })∕k_{\beta }).\hfill \end{array}$$ (7)

These channel kinetics and the corresponding parameter values, shown in Table 1, were derived from previous models (Huguenard & McCormick, 2004; Rybak et al., 2007; Smith et al., 2007).

The parameters for steady-state activation (m_∞) and inactivation (h_∞) of I_Ca are shown in Table 1. This channel description and parameters were accepted from previous models (Rybak et al., 2007; Smith et al., 2007), and had been initially derived from experimental studies of Elsen & Ramirez (1998).

I_CAN has instantaneous activation, which depends on Ca_i and is voltage-independent:

$$m_{\mathrm{CAN}}=1∕(1+{(K_{\mathrm{CAN}}∕{\mathrm{Ca}}_{\mathrm{i}})}^n),$$ (8)

where K_CAN represents the half-activation concentration of Ca_i, and n is the Hill coefficient. These parameters in Table 1 are taken from Toporikova & Butera (2011).

The description of the Na⁺/K⁺ pump is taken from Li et al. (1996), with parameters as in Rubin et al. (2009):

$$I_{\mathrm{Pump}}=R_{\mathrm{Pump}}\cdot \left(\phi \right({\mathrm{Na}}_{\mathrm{i}})-\phi ({\mathrm{Na}}_{\mathrm{ieq}}\left)\right),$$ (9)

where, $\phi \left(x\right)=x^3∕(x^3+K_{\mathrm{P}}^3)$, R_Pump is the maximal pump current, Na_ieq is equilibrium intracellular Na⁺ concentration, and K_P is the pump parameter (Table 1).

The dynamics of the total intracellular Ca²⁺ concentration within the cell (Ca_tot) are described as follows:

$$\frac{{\mathrm{dCa}}_{\mathrm{tot}}}{\mathrm{d}t}=-{\alpha }_{\mathrm{Ca}}\cdot I_{\mathrm{Ca}}-{\mathrm{Ca}}_{\mathrm{i}}∕{\tau }_{\mathrm{Ca}}.$$ (10)

In the right part of this equation, the first term represents Ca²⁺ influx from the extracellular space through voltage-gated Ca²⁺ channels, and the second term represents the membrane Ca²⁺ pump, which extrudes free intracellular Ca²⁺ (Ca_i) from the cytoplasm (Li & Rinzel, 1994).

The dynamics of the intracellular concentration of free Ca²⁺ ([Ca²⁺]_in, Ca_i) are described by the following differential equation (Li & Rinzel, 1994; Toporikova & Butera, 2011):

$$\frac{{\mathrm{dCa}}_{\mathrm{i}}}{\mathrm{d}t}=-{\alpha }_{\mathrm{Ca}}\cdot I_{\mathrm{Ca}}-{\mathrm{Ca}}_{\mathrm{i}}∕{\tau }_{\mathrm{Ca}}+f_{\mathrm{Ca}}\cdot (J_{\mathrm{ERin}}-J_{\mathrm{ERout}}).$$ (11)

In Eqns 10 and 11: α_Ca is the conversion factor between current and rate of concentration change), and τ_Ca is the time constant for the Ca²⁺ pump (α_Ca = 2.5 × 10⁻⁵ mm/fC and τ_Ca = 500 ms). In Eqn 11, J_ERin represents the flux of Ca²⁺ per unit volume from the endoplasmic reticulum (ER) into the cytoplasm, J_ERout represents the flux of Ca²⁺ per unit volume from the cytoplasm into the ER, and f_Ca is the ratio of free to bound Ca²⁺ in the cytosol (f_Ca = 2.5 × 10 ⁻⁵).

The flux per unit volume of Ca²⁺ from the ER to the cytoplasm is hypothesised to be mediated by the inositol triphosphate (IP3) receptor (IP3R), which is modelled as:

$$J_{\mathrm{ERin}}=\left[L_{\mathrm{IP}3R}+P_{\mathrm{IP}3R}\cdot \left(\frac{{\mathrm{Ca}}_i}{{\mathrm{Ca}}_i+K_a}\cdot \frac{IP3}{IP3+K_{\mathrm{I}}}\cdot l^3\right)\right]\cdot ({\mathrm{Ca}}_{\mathrm{ER}}-{\mathrm{Ca}}_i),$$ (12)

where IP3 represents the intracellular concentration of IP3, which, in our simulations, is considered to be constant (IP3 = 0.5 × 10⁻³ mm unless otherwise indicated). Also in this equation: L_IP3R is the leak constant of IP3R (L_IP3R = 0.37/ms); P_IP3R characterises the permeability of the IP3 channels (P_IP3R = 31 000/ms); and K_α and K_I are the dissociation constants (K_α = 0.4 × 10⁻³ mm; K_I = 10⁻³ mm). The values of these parameters have been drawn from Toporikova & Butera (2011). The Ca²⁺-dependent IP3 gating variable (l) and the Ca²⁺ concentration in the ER (Ca_ER) are described as follows:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}l}{\mathrm{d}t}& =A\cdot (K_{\mathrm{d}}-l\cdot ({\mathrm{Ca}}_{\mathrm{i}}+K_{\mathrm{d}}\left)\right);\hfill \\ \hfill & {\mathrm{Ca}}_{\mathrm{ER}}=({\mathrm{Ca}}_{\mathrm{tot}}-{\mathrm{Ca}}_{\mathrm{i}})∕{\sigma }_{\mathrm{Ca}},\hfill \end{array}$$ (13)

where A is a conversion factor, K_d is the dissociation constant for IP3 inactivation, and σ_Ca is the ratio of cytosolic to ER volume. The following parameter values have been used: A = 5 mm/ms; K_d = 0.4 × 10⁻³ mm; σ_Ca = 0.185 (Toporikova & Butera, 2011).

The flux per unit volume of Ca²⁺ into the ER from the cytoplasm is hypothesised to be mediated by an ER membrane pump representing the sarcoplasmic/endoplasmic reticulum Ca²⁺-ATPase (SERCA):

$$J_{\mathrm{ERout}}=V_{\mathrm{SERCA}}\cdot {\mathrm{Ca}}_{\mathrm{i}}^2∕(K_{\mathrm{SERCA}}^2+{\mathrm{Ca}}_{\mathrm{i}}^2)$$ (14)

where V_SERCA = 0.4 mm/ms is the maximal flux through the SERCA pumps, and K_SERCA = 0.2 × 10⁻³ mm (Toporikova & Butera, 2011).

Na_i is governed by the following differential equation:

$$\frac{{\mathrm{dNa}}_{\mathrm{i}}}{{\mathrm{d}}_t}=-{\alpha }_{\mathrm{Na}}\cdot (I_{\mathrm{Na}}+I_{\mathrm{NaP}}+I_{\mathrm{CAN}}+3\cdot I_{\mathrm{Pump}}),$$ (15)

where α_Ca = 5 × 10⁻⁵ mm/fC is the conversion factor.

The total synaptic conductance of each neuron i (g_SynEi) includes two components: one, g_tonic, that characterises an external tonic excitatory drive to the neuron, and another characterising excitatory synaptic inputs from all N neurons of the population (including itself):

$$g_{\mathrm{SynE}i}\left(t\right)=g_{\mathrm{tonic}}+\sum _{j=1}^N{w}_{ji}\cdot \sum _{t_{k_j}<t}\exp (-(t-t_{kj})∕{\tau }_{\mathrm{SynE}})$$ (16)

According to this equation, each spike of neuron j triggering a postsynaptic current in neuron i at time t_kj increases the excitatory synaptic conductance in neuron i by w_ji, which represents the weight of the synaptic connection from neuron j to neuron i. τ_SynE = 5 ms is the decay time constant. In our simulations, each neuron in the population received the same external drive g_tonic ∈ [0, 1.2] nS, and the weights of its synaptic inputs were normally distributed by use of the assigned average weight $\stackrel{‒}{w}$ ($\stackrel{‒}{w}\in [0,0.2]$) nS and the variance σ_w = 0.2 · $\stackrel{‒}{w}$.

A population of N = 50 neurons with all-to-all connections was simulated. The heterogeneity of neurons within the population was provided by the uniformly distributed maximal conductance of leakage, persistent Na⁺ and Ca²⁺ channels. The leakage conductance was uniformly distributed within a range g_L ∈ [2, 3] nS, which was selected on the basis of the experimental measurements of input resistance in neurons of the rostral ventrolateral medulla and the pre-BötC (500 MΩ in Mazza et al., 2000 and 430 MΩ in Del Negro et al., 2002a; see also Koizumi et al., 2008). The persistent Na⁺ conductance was distributed within a range ${\stackrel{‒}{g}}_{\mathrm{NaP}}\in [0,5]\mathrm{nS}$, which was based on experimental measurements of this conductance in rostral ventrolateral medulla and pre-BötC neurons (Rybak et al., 2003a). The Ca²⁺ conductance was distributed within a range ${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.01]\mathrm{nS}$, unless a different range is stated in the text. To apply these distributions, a random number generator from the standard library of the Intel C++ compiler was used. To initialise a particular conductance value, a random four-byte integer number (i.e. from 0 to 2³²) was generated and divided by 2³². This provided us with a random number x, uniformly distributed in the [0, 1] interval. Then, if a randomised parameter g (e.g. one of the above maximal conductances) should be uniformly distributed within a range g ∈ [a, b], we calculated g = a + x · (b − a), which served as a particular g value.

The weights of synaptic interactions were also distributed (by use of a standard normal distribution; see above). The total synaptic input to each neuron from other neurons in the population can be characterised by $N\cdot \stackrel{‒}{w}$. The initial conditions for membrane potentials, intracellular Ca²⁺ and Na⁺ concentrations and channel conductances were chosen by use of a uniform distribution within the physiologically realistic ranges of values for each variable, and a settling period of 10–20 s was allowed in the performed or testing simulations to ensure that the results are independent of initial conditions. Most simulations were repeated 10–20 times, and they demonstrated qualitatively similar behaviour for all values of distributed parameters and initial conditions.

Data analysis and representation

Spike timing in individual neurons was detected when the neuron membrane potential crossed a threshold (−35 mV) from below. The activity of the population was defined as the average number of spikes generated by one neuron of the population per time unit. To determine this value, the total number of spikes generated by all neurons of the population during the selected time bin (usually 20 ms) was calculated and then normalised by the number of neurons and bin size.

At the single-neuron level, the record of interspike intervals was analysed to identify bursting. Owing to the complex nature of the bursting found in our model, which includes such things as mixed-mode oscillations and tonic-like activity preceding bursts, we found that a simple threshold based on a fixed interval was not enough to distinguish interburst intervals from interspike intervals. We therefore used an algorithm that defined an interburst interval as an interspike interval that is at least twice as long as the subsequent interval, and greater than the preceding interval. This interval was summed together with all preceding intervals that did not meet this condition to define bursting period. We found this to be an effective algorithm that is relatively free from artefacts, but if any doubt existed about whether a burst defined by the algorithm was genuine, e.g. near the transition between bursting and tonic spiking, the record of the interspike intervals was first examined, and if this was not enough to make a determination, a simulation was run, the membrane potential was recorded, and the type of neuronal activity (bursting or tonic) and the bursting period (in case of bursting) were determined by visual inspection of the membrane potential trace.

At the network activity level, a time series of the integrated activity was generated, and the average activity was calculated. To recognise bursts, we introduced a threshold that was defined as a fraction of the average activity. It turned out that the boundaries of the areas of bursting were insensitive to changes of the threshold in the 10–50% range, creating a basis for reliable detection of bursting. A level of 20% of the average activity was finally accepted for the threshold. Time moments when the activity of the population crossed the threshold from below were considered as burst onset times. The time interval between two consecutive onsets was defined as a burst period.

We constructed scatter plots that can be interpreted as maps of the bursting regions in a two-dimensional (2D) space of parameters (Figs 2A–C, and 4A and B, 8A–D, and 11) in the following way. A simulation was run for a fixed value of the parameter on the y-axis (${\stackrel{‒}{g}}_{\mathrm{NaP}}$, ${\stackrel{‒}{g}}_{\mathrm{CAN}}$, or $N\cdot \stackrel{‒}{w}$), in which the parameter on the x-axis (g_tonic) was slowly varied over some fixed interval known to contain the bursting region, and interspike intervals (single neuron) or integrated activity (network) were recorded. The burst recognition algorithms described above were applied to the records, giving the period of each burst cycle, and the average value of g_tonic over which the burst occurred. By running multiple simulations for incrementally different values of the y-parameter, and analysing the data as described, we generated a 2D scatter plot of dots corresponding to bursts in which the colour of each dot corresponded to the period of the burst cycle containing that burst. We chose the rate of change of g_tonic to be slow enough so that any halving of this rate would have no noticeable effect on the boundaries and the colour of the plot. In practice, we found that a total time of 2000 s for a 1 nS change in g_tonic was sufficient. To further confirm the accuracy of this technique, we compared our results with results obtained by running a number of simulations at different fixed values of g_tonic in which the initial transient phase is eliminated by discarding the first 10 bursts, and the period is calculated by taking the average of the next 10 bursts. We found no noticeable differences between the values of period or the boundaries of the transitions between different oscillatory regimes obtained with this method and with our method. Some graphs (e.g. Figs 2A1–C1 and D, and 4A1 and B1 and C) were explicitly built by use of the average values of the period obtained with the latter method.

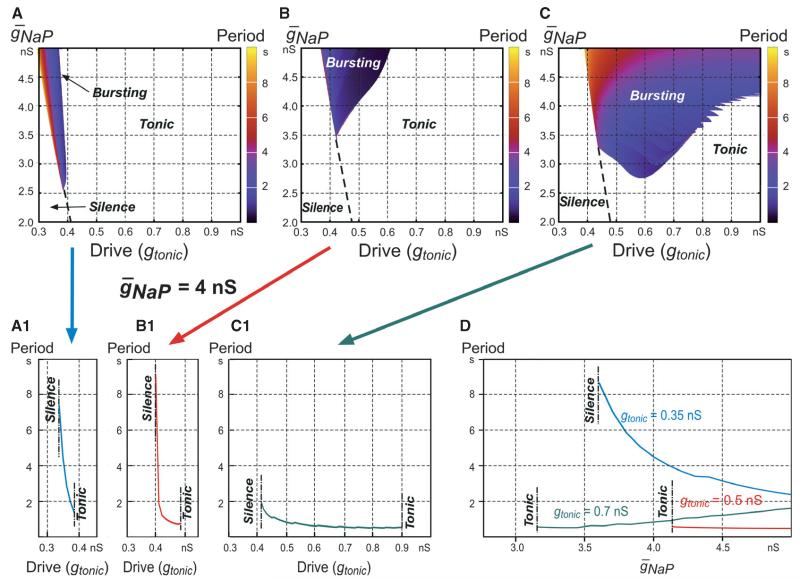
Fig. 2.

Bursting regimes for the three I_NaP-dependent models shown in Fig. 1. (A–C) Regions of silence, bursting (coloured) and tonic activity in the 2D space (${\stackrel{‒}{g}}_{\mathrm{NaP}}$, g_tonic) for the models shown in Fig. 1A–C. The bursting period in each plot is indicated by colour (see key on the right of each diagram). (A1–C1) The dependence of bursting period on excitatory drive (g_tonic) for the three models that correspond to plots A–C, respectively (indicated by arrows), at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=4\mathrm{nS}$. (D) The dependence of bursting period on ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ for the first (at g_tonic = 0.35 nS, blue curve), second (at g_tonic = 0.5 nS, red curve) and third (at g_tonic = 0.7 nS, green curve) models with I_NaP-dependent bursting that correspond to plots A–C, respectively.

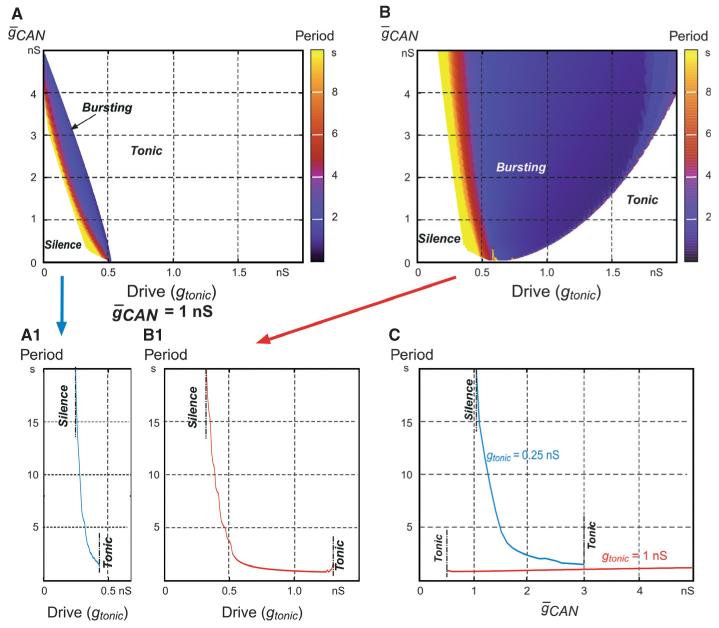
Fig. 4.

Bursting regimes for the two I_Ca/I_CAN-dependent models shown in Fig. 3. (A and B) Regions of silence, bursting (coloured) and tonic activity in the 2D space (${\stackrel{‒}{g}}_{\mathrm{CAN}}$, g_tonic) for the models shown in Fig. 3A and B. The bursting period in each plot is indicated by colour. (A1 and B1) The dependence of bursting period on excitatory drive (g_tonic) for the two models that correspond to plots A and B, respectively (indicated by arrows), at ${\stackrel{‒}{g}}_{\mathrm{CAN}}=1\mathrm{nS}$. (C) The dependence of bursting period on ${\stackrel{‒}{g}}_{\mathrm{CAN}}$ for the first (at g_tonic = 0.25 nS, blue curve) and second (at g_tonic = 1 nS, red curve) models that correspond to plots A and B, respectively.

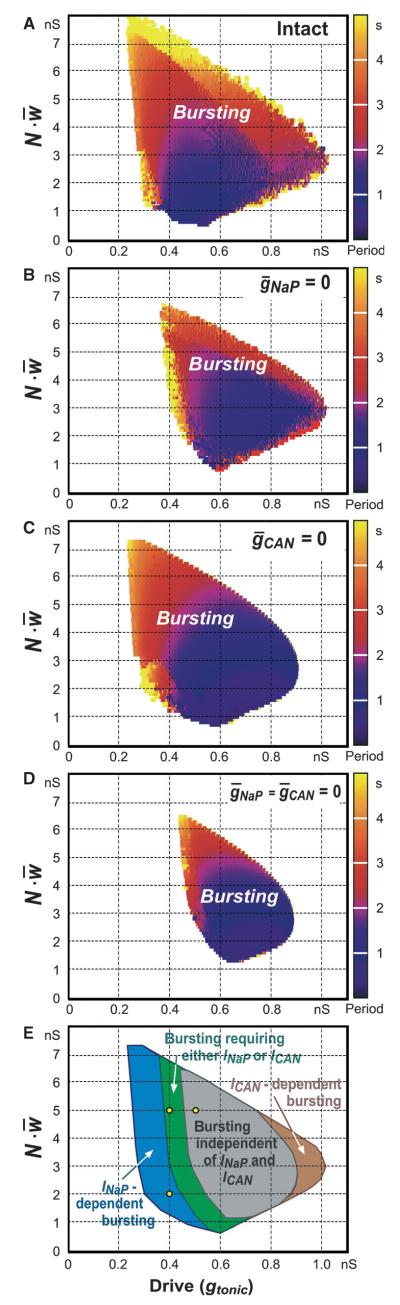
Fig. 8.

Population bursting in the 2D parameter space (g_tonic, $N\cdot \stackrel{‒}{w}$) for the intact network (A) and when ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (B), or ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (C), or ${\stackrel{‒}{g}}_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (D). The bursting period in A–D is represented by colour (see key on the right of each diagram). The results are summarised in E, where types of bursting involving different mechanisms are distinguished by colour. The region for I_NaP-dependent population bursting is shown in blue (this region is not present in B and D); the region in which population bursting may be based on either I_NaP or I_CAN is shown in green (this region is not present in D); the region in which population bursting may exist without both of these currents is shown in grey (this region corresponds to that shown in D); an additional region (brown) represents unstable Ca²⁺-dependent and I_CAN-dependent bursting. All diagrams (A–E) refer to a single simulated population (based on a particular distribution of parameters shown in Fig. 5) – the same as was used to obtain the results shown in Figs 6 and 7. Simulations of other populations (resulting from the re-initialisation of the randomised parameters within the same ranges and distributions) resulted in qualitatively similar diagrams without significant shifting of borders between the bursting areas or other critical differences. Statistical analysis and averaging of data from multiple simulations with parameter re-initialisation was not performed. The three yellow points in E correspond to the three regimes shown in Fig. 7A1–A3, B1–B3, and C1–C3, respectively. See text for details.

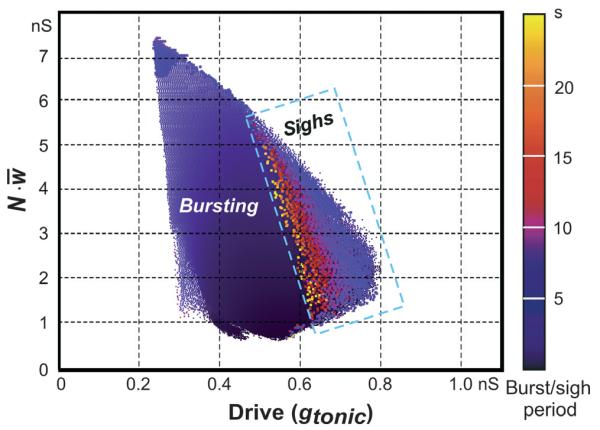
Fig. 11.

A map of sigh-like bursting. The original 2D plot shows the periods of regular bursting (represented by colour) in the (g_tonic, $N\cdot \stackrel{‒}{w}$) space. A rectangle indicating the periods of sigh-like bursts (using the same colour representation) is superimposed on the 2D plot of the regular burst periods. This figure shows that sigh-like bursting appears at high values of drive at the end of the regular bursting area just before the transition from bursting to asynchronous population activity.

All simulations were performed with custom-written C++ software for a Linux-based operating system, which ran locally on a six-core workstation in the laboratory or remotely on the high-performance parallel cluster Biowulf at the National Institutes of Health, Bethesda, MD, USA (http://biowulf.nih.gov).

Results

The intrinsic Na⁺-dependent and Ca²⁺-dependent mechanisms for single-neuron bursting

Bursting mechanisms involving I_NaP

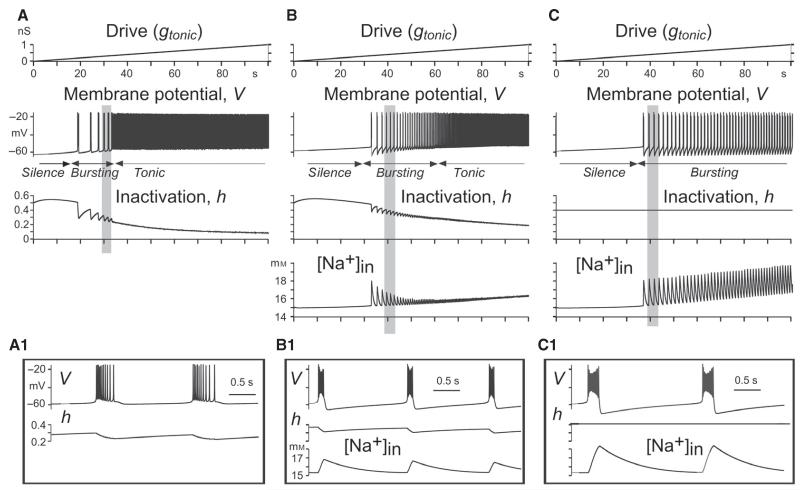
The presence of a persistent (i.e. non-inactivating) Na⁺ current is not enough for a neuron to generate intrinsic bursting; there needs to be an additional burst-terminating mechanism. In the well-known model of an I_NaP-dependent bursting neuron by Butera et al. (1999a; Model 1), the burst-terminating mechanism was based on the slow inactivation of the persistent Na⁺ channels themselves (as represented by the h_NaP variable in the equation for I_NaP in Eqn 2). The other proposed burst-terminating mechanisms were based on the slowly activating, voltage-dependent (e.g. Butera et al., 1999a; Model 2) or [Ca²⁺]_in-dependent (e.g. El Manira et al., 1994; Ryczko et al., 2010) K⁺ currents. In the present study, we proposed and investigated another potential burst-terminating mechanism, based on the activity-dependent accumulation of Na⁺ within the cell, and subsequent activation of the electrogenic Na⁺/K⁺ pump (I_Pump; see Eqn 9) removing the intracellularly accumulated Na⁺.

In our single-neuron simulations of Na⁺-dependent bursting, all possible effects of Ca²⁺-dependent mechanisms were eliminated by setting ${\stackrel{‒}{g}}_{\mathrm{Ca}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$. Three single-neuron models exhibiting I_NaP-dependent bursting were studied, which differed by the burst-terminating mechanisms operating in the models (Figs 1 and 2). The first model (Figs 1A and A1, and 2A and A1) was qualitatively similar to the classical Butera model (Butera et al., 1999a; Model 1), but with parameter values drawn from previous experimental measurements (Rybak et al., 2003a). Burst termination in this model was based on the slow inactivation of I_NaP. In this case in Eqn 1, I_Ca = I_CAN = I_Pump = 0, and h_NaP changed in accordance with Eqns 4 and 5. In the second model (Figs 1B and B1, and 2B and B1), in addition to the slowly inactivating I_NaP (as in the first model), we incorporated the burst-terminating mechanism based on the intracellular accumulation of Na⁺ (Eqn 15 at I_CAN = 0) followed by intracellular Na⁺ concentration ([Na⁺]_in)-dependent activation of the Na⁺/K⁺ pump (I_Pump, Eqn 15]. In the third neuron model (Figs 1C and C1, and 2C and C1), I_NaP was considered to be non-inactivating (by setting h_NaP = constant = 0.4; see Table 1), and burst termination was based entirely on the Na⁺/K⁺ pump. Not only did this Na⁺/K⁺ pump-based mechanism cause burst termination, but its relaxation was also involved in the recovery of the membrane potential during the interburst interval, leading to the onset of the next burst.

Fig. 1.

Simulation of I_NaP-dependent bursting by the use of three single-neuron models with different burst-terminating mechanisms. In the first model (A), burst termination was based on the slow inactivation of the persistent Na⁺ channels. In the second model (B), there were two burst-terminating mechanisms: one based on the slow inactivation of I_NaP (as in the first model), and the other based on intracellular Na⁺ accumulation and subsequent activation of the Na⁺/K⁺ pump. In the third model (C), the [Na⁺]_in-dependent Na⁺/K⁺ pump burst-terminating mechanism (as in the second model) operated alone without I_NaP inactivation. In all three models, ${\stackrel{‒}{g}}_{\mathrm{Ca}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$. Each column shows the neuron response (changes in the membrane potential at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=5\mathrm{nS}$ and g_L = 2.5 nS) to the slow ramp increase of input synaptic drive (shown at the top) and the dynamic changes in the relevant variables (h and [Na⁺]_in. Insets A1, B1 and C1 (from A, B, and C, respectively, highlighted in grey) show the shape of the generated bursts and the changes in the relevant variables. See text for details.

These models were comparatively investigated with respect to their response to tonic excitatory drive (g_tonic), which was elevated slowly from 0 to 1 nS to sweep a range of baseline membrane potentials (Figs 1A–C and A1–C1). In each model, the neuron started rhythmic bursting when the drive exceeded some model-specific threshold (Figs 1A–C, and 2A–C, and A1–C1), and the frequency of this bursting increased (bursting period decreased) with increasing g_tonic. Then, when the drive exceeded another model-specific threshold, the neuron switched from rhythmic bursting to tonic spiking (Figs 1A and B, and 2A–C and A1–C1).

Figure 2A–C, shows respectively the bursting regions for each model represented in the 2D space of parameters (${\stackrel{‒}{g}}_{\mathrm{NaP}}$, g_tonic), in which bursting period is indicated by colour. It can be seen that the burst-terminating mechanism based on an Na⁺/K⁺ pump alone provided a significantly larger area of bursting in the above parameter space than in the two other models (Fig. 2A–C and A1–C1), and the smallest bursting area was in the case when burst termination was provided by the voltage-dependent I_NaP inactivation alone (Fig. 2A and A1).

The other interesting difference between the models is the dependence of burst frequency on ${\stackrel{‒}{g}}_{\mathrm{NaP}}$. Specifically, when ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ is decreasing (at a constant g_tonic) to simulate the effect of I_NaP blockers (that is, when we move vertically downwards within bursting areas in Fig. 2A–C or from right to left in Fig. 2D), the burst frequency is: (i) decreasing in the first model (the bursting period is increasing, as seen in Fig. 2A, where the colour representing the bursting period changes from blue–violet to red–yellow, and explicitly in Fig. 2D); (ii) staying almost constant in the second model (Fig. 2B and D); and (iii) increasing in the third model (the bursting period is decreasing, as seen in Fig. 2C, where, the colour changes from yellow–red to violet–blue, and explicitly in Fig. 2D).

It might seem paradoxical that the model with two burst-terminating mechanisms has a smaller bursting region than the model with only I_Pump, but this can be understood by the effect of I_NaP on [Na⁺]_in. As g_tonic is increased and the neuron in the second model becomes increasingly depolarised, I_NaP is progressively inactivated, so that its contribution to intracellular Na⁺ accumulation during the active phase decreases (compare [Na⁺]_in in Fig. 1B1 to that in C1), and burst-terminating I_Pump becomes progressively weaker.

There is also an interesting issue concerning the different effects of the I_NaP suppression used to simulate the possible effects of riluzole (i.e. a decrease in ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ at a constant excitatory drive, which would correspond to a vertical downwards shift from bursting regions in each 2D plot in Fig. 2A–C and a right-to-left shift in Fig. 2D). It can be seen that, in the first model (Fig. 2A and D, blue curve), this ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ reduction can only cause a switch from bursting to silence, whereas in the second and third models containing the Na⁺/K⁺ pump (Fig. 2B and C), the result depends on the drive. At low drive, this I_NaP suppression also produces a switch from bursting to silence, but at higher drive, it causes a switch from bursting to tonic spiking in the majority of the bursting region in each of these models (see examples in Fig. 2D, red and green curves, respectively).

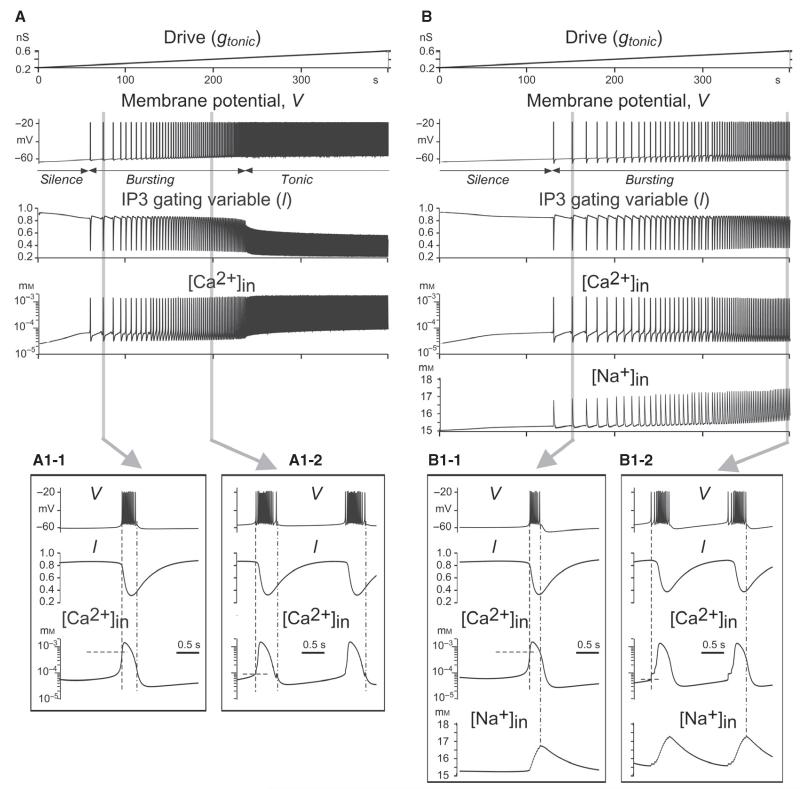
Bursting involving I_Ca and I_CAN

This component of the study was motivated by the experimental and modelling studies of Del Negro and his collaborators (Crowder et al., 2007; Pace et al., 2007; Pace & Del Negro, 2008; Krey et al., 2010; Dunmyre et al., 2011), as well as Toporikova & Butera (2011), and focused on simulation of an I_CAN-dependent bursting mechanism. To exclude the effect of I_NaP, in all models considered here we set ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$. In these models, I_CAN was activated by intracellular Ca²⁺, whose accumulation was provided by the IP3-dependent Ca²⁺ release from intracellular stores (Eqns 11–14). This process in our models critically depended on Ca²⁺ influx through voltage-gated Ca²⁺ channels (i.e. by I_Ca), which provided an initial [Ca⁺²]_in inducing a nonlinear positive feedback mechanism known as Ca²⁺-induced Ca²⁺ release (CICR). Both the input synaptic activation (provided by synaptic drive) and the [Ca²⁺]_in-dependent activation of I_CAN contributed to the initial membrane depolarisation (burst onset), and their contributions depended on the input synaptic activation. Two burst-terminating mechanisms were considered. One mechanism involved Ca²⁺-dependent inactivation of IP3R (regulated by the gating variable l; see Eqn 13), leading to the reduction of [Ca²⁺]_in and deactivation of I_CAN (see Toporikova & Butera, 2011). The second mechanism was based on the activity-dependent accumulation of intracellular Na⁺ followed by the [Na⁺]_in-activated I_Pump, i.e. the same Na⁺/K⁺-based mechanism as in the second and third I_NaP-based models described above. However, in contrast to the I_NaP-based models, the accumulation of intracellular Na⁺ in these models was mainly provided by I_CAN (and partly by I_Na), but not by I_NaP, as ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (see Eqn 15).

In order to investigate the effect of these burst-terminating mechanisms, two distinct models were considered: one with burst termination based entirely on the Ca²⁺-dependent inactivation of IP3R without involvement of the Na⁺/K⁺ pump (Figs 3A and A1-1 and A1-2, and 4A and A1), and the other with both mechanisms (based on Ca²⁺-dependent IP3R inactivation and Na⁺/K⁺ pump activation) contributing to burst termination (Figs 3B and B1-1 and B1-2, and 4B and B1).

Fig. 3.

Simulation of I_Ca-dependent and I_CAN-dependent bursting by the use of two single-neuron models with different burst-terminating mechanisms. In the first model (A), burst termination was based on Ca²⁺-dependent IP3R inactivation (see the traces for IP3R gating variable l and [Ca²⁺]_in). In the second model (B), there were two burst-terminating mechanisms: one based on Ca²⁺-dependent IP3R inactivation (as in the first model), and the other based on intracellular Na⁺ accumulation (see [Na⁺]_in traces) and subsequent activation of the Na⁺/K⁺ pump. In both models, ḡ_NaP = 0. Each column shows the neuron response (changes in the membrane potential at ${\stackrel{‒}{g}}_{\mathrm{Ca}}=0.01\mathrm{nS}$, ${\stackrel{‒}{g}}_{\mathrm{CAN}}=1\mathrm{nS}$, and g_L = 2.5 nS) to the slow ramp increase of input synaptic drive (shown at the top). Insets A1-1, A1-2, B1-1 and B1-2 (from A and B traces, respectively, highlighted in grey) show the shapes of generated bursts and the changes in relevant variables. See text for details.

Figure 3A and B shows the response of each model to g_tonic, slowly increasing from 0.2 to 0.6 nS. Similarly to the I_NaP-based models described above, both of these models showed a progression over the three regimes of silence, bursting and tonic spiking as drive was increased (Figs 3A and B, and 4A and B), and the burst frequency increased in the bursting regime with increasing g_tonic (Figs 3A and B, and 4A, B, A1 and B1). The insets in Fig. 3A1-1 and B1-1 show burst details in each model at relatively low values of drive, whereas the insets in Fig. 3A1-2 and B1-2 show burst details in these models at higher values of drive. At low drives (Fig. 3A1-1 and B1-1), the initial increase in [Ca²⁺]_in through I_Ca and the CICR mechanism precedes membrane depolarisation and burst onset (indicated by the vertical dashed line). This accumulated intracellular Ca²⁺ activates I_CAN, which, in turn, produces the membrane depolarisation and burst onset. In contrast, at higher drives (Fig. 3A1-2 and B1-2), the initial membrane depolarisation is provided by the dynamics of synaptic input (i.e. drive) and I_Pump (which decreases during the preceding interburst interval), and hence the onset of the burst (indicated by the dashed line) precedes the [Ca²⁺]_in-dependent I_CAN activation. This can also explain a clear difference in the intraburst spike pattern between the corresponding bursts (a decreasing spike frequency at lower drives vs. an initial ramp increase in spike frequency within the burst at higher drives, Fig. 3B1-1 vs. B1-2). Although I_CAN does not play a leading role in burst initiation at higher drives, it contributes to the above patterning of intraburst spikes (the initial ramp in spike frequency) in both models. In addition, I_CAN is critical for burst termination in both models, as described below.

The above insets demonstrate the differences between the two models in burst termination. In the first model (Fig. 3A1-1 and A1-2), burst termination (controlled by IP3R inactivation defined by l) occurs when [Ca²⁺]_in drops below the threshold for I_CAN activation (indicated by the dot-dashed line). In the second model (Fig. 3B1-1 and B1-2), burst termination is mostly provided by the I_CAN-dependent intracellular accumulation of Na⁺ followed by [Na⁺]_in-dependent activation of the Na⁺/K⁺ pump (I_Pump, see the vertical dot-dashed line, showing that bursts are terminated not when [Ca²⁺]_in drops below the half-activation concentration for I_CAN, as in Fig. 3A1-1 and A1-2, but when [Na⁺]_in reaches its maximum).

Figure 4A and B shows maps of the bursting regions for the two models in the 2D space of (${\stackrel{‒}{g}}_{\mathrm{CAN}}$, g_tonic), in which the bursting period is indicated by colour. In each bursting region, burst frequency increased with drive (see also Fig. 4A1 and B1). The most important difference between these two models is that the second model has a significantly wider region of bursting in the (${\stackrel{‒}{g}}_{\mathrm{CAN}}$, g_tonic) plane. The main conclusion here is that the Na⁺/K⁺ pump-dependent burst-terminating mechanism greatly increases the area of the bursting region in the parameter space.

The other interesting difference between the models concerns the different effects of I_CAN suppression simulating the possible effect of FFA (implemented as a decrease in g_CAN at a constant drive, i.e. a vertical downwards shift from the bursting regions in each 2D plot or a right-to-left shift in Fig. 4C). In the first model (Fig. 4A1 and C, blue curve), this ${\stackrel{‒}{g}}_{\mathrm{CAN}}$ reduction would only cause a switch from bursting to silence, whereas in the second model, the result depends on the drive. At low drive, this I_CAN suppression would also produce a switch to silence, but at higher drive (roughly to the right of 0.6, i.e. in the majority of the bursting region) it would cause a switch from bursting to tonic spiking (Fig. 4B1 and C, red curve).

Modelling a heterogeneous neural population with randomly distributed ${\stackrel{‒}{g}}_{NaP}$, ${\stackrel{‒}{g}}_{Ca}$, and g_L

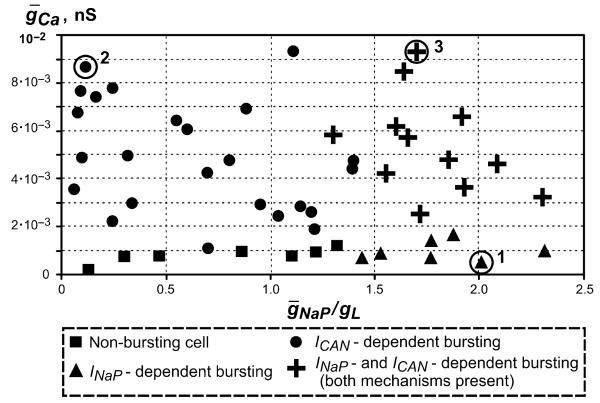
Experimental studies in neonatal/juvenile mouse in vitro slice preparations have demonstrated that I_NaP-mediated and I_Ca/I_CAN-mediated mechanisms may coexist in the pre-BötC (e.g. Peña et al., 2004). Therefore, our objective in this part of the study was to investigate how the different intrinsic mechanisms considered above operate together within a heterogeneous population of neurons with mutual excitatory synaptic interactions. A population of 50 neurons was simulated. The values of ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ and g_L assigned to each neuron of the population were randomly selected from the following ranges: ${\stackrel{‒}{g}}_{\mathrm{NaP}}\in [0,5]\mathrm{nS}$, g_L ∈ [2, 3] nS, and ${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.01]\mathrm{nS}$ (see Methods). The results of particular parameter distributions are shown in Fig. 5. In this figure, each of the 50 neurons is represented by a symbol in the 2D space of (${\stackrel{‒}{g}}_{\mathrm{Ca}}$, ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L). The intrinsic bursting properties of each neuron in the population depended on the particular values of these parameters assigned from their random distributions. The ratio ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L effectively defines the essential biophysical conditions for I_NaP-dependent bursting (Butera et al., 1999a; Purvis et al., 2007), whereas the Ca²⁺-dependent mechanism activating I_CAN was linked in our model to ${\stackrel{‒}{g}}_{\mathrm{Ca}}$.

Fig. 5.

Bursting properties of neurons within a 50-neuron population with randomly distributed ${\stackrel{‒}{g}}_{\mathrm{NaP}}$, g_L, and ${\stackrel{‒}{g}}_{\mathrm{Ca}}$. Synaptic interactions between all neurons were set to zero (uncoupled case). The maximal conductance of persistent Na⁺, leakage and Ca²⁺ currents were uniformly distributed within the following ranges: ${\stackrel{‒}{g}}_{\mathrm{NaP}}\in [0,5]\mathrm{nS}$, g_L ∈ [2, 3] nS, and ${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.01]\mathrm{nS}$ (see Methods). Each neuron is represented by a symbol (triangle, filled circle, cross, or square) in the 2D space of (${\stackrel{‒}{g}}_{\mathrm{Ca}}$, ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L) located in accordance with the particular values of these parameters in this neuron assigned from the random distributions. Symbols indicate the types of bursting expressed in each neuron in the uncoupled case. One representative neuron of each bursting type, indicated by the circles around the corresponding symbol and the number 1, 2, or 3, respectively, was used for description of its firing under the different conditions shown in the following figures (Figs 6 and 7). See text for details.

To test the ability of each neuron in the population to generate intrinsic bursting activity, we first uncoupled all neurons by removing all synaptic interactions between the neurons (by setting all w_ji = 0), and then tested the response of each neuron to slow ramp increases of excitatory drive (as with the single-neuron modelling above). In order to identify the bursting mechanism involved, we repeated this under conditions when either ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ or ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$, or ${\stackrel{‒}{g}}_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$). In Fig. 5, all neurons exhibiting I_NaP-dependent bursting (i.e. those whose bursting persisted at some level of drive at ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$, but was abolished at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$) are represented by triangles, which are mostly located in the area corresponding to the relatively high values of ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L and lower values of ${\stackrel{‒}{g}}_{\mathrm{Ca}}$. The neurons whose bursting was dependent on I_CAN are represented by the filled circles. The bursting in these neurons persisted at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$, but could be abolished at ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$; these neurons are located in the area corresponding to the higher values of ${\stackrel{‒}{g}}_{\mathrm{Ca}}$ and relatively lower values of ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L. The neurons represented by crosses could express bursting based on any of the above mechanisms; that is, their bursting could be abolished only if ${\stackrel{‒}{g}}_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$. It is not surprising that these neurons are located in the area corresponding to the higher values of both ${\stackrel{‒}{g}}_{\mathrm{Ca}}$ and ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L. Finally, the neurons unable to express bursting under any condition are represented by squares, and are located in the area corresponding to the lower values of both ${\stackrel{‒}{g}}_{\mathrm{Ca}}$ and ${\stackrel{‒}{g}}_{\mathrm{NaP}}$/g_L.

Figure 5 shows that, at the ranges assigned for random distribution of ${\stackrel{‒}{g}}_{\mathrm{NaP}}$, g_L, and ${\stackrel{‒}{g}}_{\mathrm{Ca}}$, the 50-neuron population of uncoupled neurons contained 43 potential bursters (86%; this includes all cells except those represented by rectangles). For comparison, Koshiya & Smith (1999) reported that 70% of inspiratory cells in the pre-BötC maintained bursting (most likely I_NaP-dependent) in neonatal rat slices after neuron uncoupling by 6-cyano-7-nitroquinoxaline-2,3-dione application, which is close to the percentage of bursters in our simulation. The ranges used for ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ and g_L distributions (justified in Methods) resulted in 19 (38%) neurons that could intrinsically generate bursting after blockade of I_Ca (i.e. at ${\stackrel{‒}{g}}_{\mathrm{Ca}}=0$); these are the neurons shown in Fig. 5 by triangles and crosses together. The percentage of these bursters in the model looks plausible, given the account of the percentage of I_NaP-dependent bursters estimated in slices from neonatal rats (60%, Koizumi & Smith, 2008) and the percentage of Cd²⁺-insensitive bursters found in slices from P11–15 mice (29%, Peña et al., 2004). This provided additional support for the distribution ranges of ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ and g_L used in our model. Unfortunately, no experimental data were found to justify an advanced assignment of the range for ${\stackrel{‒}{g}}_{\mathrm{Ca}}$ distribution. The use of ${\stackrel{‒}{g}}_{\mathrm{Ca}}\le 0.001\mathrm{nS}$ led to the absence of I_Ca/I_CAN-dependent busters in the population. Setting a range of ${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.01]\mathrm{nS}$ (as in the simulation shown in Fig. 5) resulted in 24 cells (48%) whose bursting critically depended on I_CAN (cells represented by circles). This value substantially exceeded the percentage of Cd²⁺-sensitive bursters estimated by Peña et al. (2004) for P6–10 mice (9.5%). However, Cd²⁺-sensitive pacemakers were found to be almost absent in neonatal mice (0.6%), and their number tended to increase with age (Del Negro et al., 2005). According to our estimation, the percentage of I_Ca/I_CAN-dependent busters of ~9.5% (estimated by Peña et al.) could be achieved in the model if ${\stackrel{‒}{g}}_{\mathrm{Ca}}$ was distributed within the interval ${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.0012]\mathrm{nS}$. Nevertheless, our ultimate goal was to perform a general theoretical investigation, rather than to meet the experimentally estimated percentages of potential bursters in the uncoupled case, and in most simulations described below we used ${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0,0.01]\mathrm{nS}$, as shown in Fig. 5.

Figure 6A1–C1, and A2–C2 and A3–C3 shows the behaviour of one representative neuron of each type (indicated in Fig. 5 by the circles around the corresponding symbols and the numbers 1, 2, and 3, respectively) under control conditions (Fig. 6A1, A2 and A3, respectively), and after assigning ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 6B1, B2 and B3, respectively) or ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 6C1, C2 and C3, respectively). Specifically, neuron 1 (Figs 5 and 6A1) with the I_NaP-dependent bursting mechanism did not express bursting when ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 6B1), but maintained bursting at ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 6C1). Neuron 2 (Figs 5 and 6A2) with the I_CAN-dependent bursting mechanism did not express bursting at ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 6C2), but maintained bursting at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 6B2). Neuron 3 (Figs 5 and 6A3) with both bursting mechanisms expressed bursting if either ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 6C3) or ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 6B3), which could be blocked only if ${\stackrel{‒}{g}}_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (not shown). As mentioned in the Introduction, both riluzole-sensitive and Cd²⁺-sensitive pacemaker neurons have been identified in the pre-BötC in vitro (Peña et al., 2004). In this connection, we suggest that neuron 1 simulates the riluzole-sensitive, Cd²⁺-insensitive pacemaker neuron (Fig. 6A4–C4), whereas neuron 2 may simulate the Cd²⁺-sensitive pacemaker (Fig. 6A5–C5).

Fig. 6.

Firing behaviour of the uncoupled representative neurons with different values of ${\stackrel{‒}{g}}_{\mathrm{NaP}}$, ${\stackrel{‒}{g}}_{\mathrm{Ca}}$, and g_L. A1–C1, A2–C2 and A3–C3 show the behaviour of one representative neuron of each type (indicated in Fig. 5 by the circles around the corresponding symbol and the number 1, 2, and 3, respectively) under control conditions (A1, A2, and A3, respectively), and after blocking I_NaP (${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ in B1, B2, and B3, respectively) or I_CAN (${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ in C1, C2, and C3, respectively). Specifically, neuron 1 (A1–C1; see also Fig. 5) with the I_NaP-dependent bursting mechanism did not express bursting when ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (B1, exhibiting a switch to tonic spiking with an increase in excitatory drive), but maintained bursting activity at ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (C1). Neuron 2 (A2–C2; see=also Fig. 5) with the I_CAN-dependent bursting mechanism did not express bursting when ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (C2), but maintained bursting activity at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (B2). Neuron 3 (A3–C3; see also Fig. 5) with both bursting mechanisms; this neuron expressed bursting when either ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (C3) or ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (B3), which could be blocked only if ${\stackrel{‒}{g}}_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (not shown). A4–C4 show an isolated riluzole-sensitive, Cd²⁺-insensitive intrinsically bursting ‘pacemaker neuron recorded in the pre-BötC in vitro after pharmacological blockade of excitatory and inhibitory synaptic transmission (cocktail, A4), and after application of riluzole (B4) and Cd²⁺ (C4, modified from Peña et al., 2004, fig. 3, with permission). A5–C5 show an isolated riluzole-insensitive, Cd²⁺-sensitive intrinsic burster before (cocktail, A4) and after application of riluzole (B5) and Cd²⁺ (C5, also from Peña et al., 2004; Fig. 3). See text for details.

Behaviour of the fully interconnected network

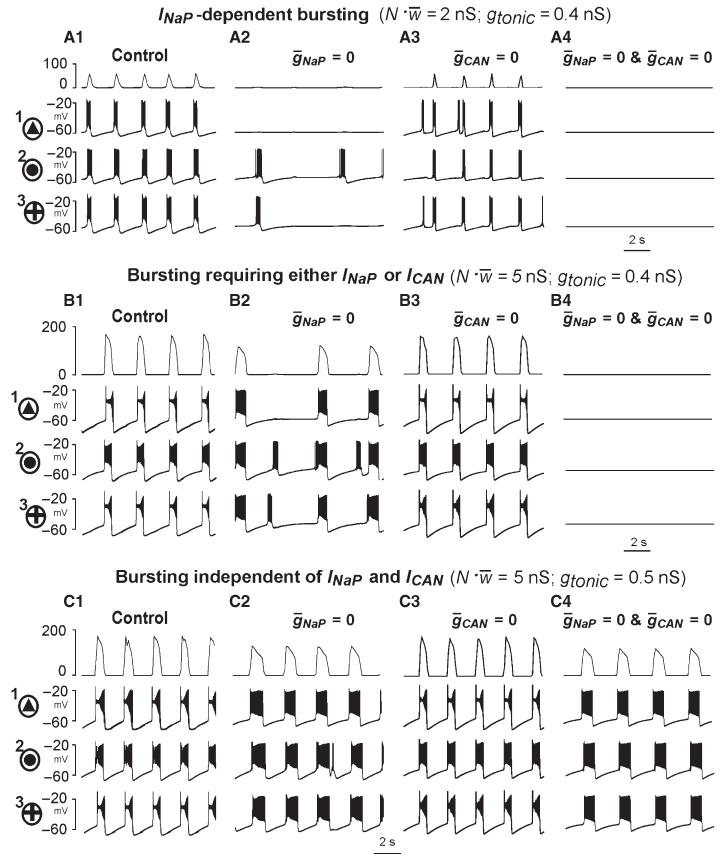
With mutually excitatory synaptic interactions, the neural populations with distributed parameters (e.g. as shown in Fig. 5) were able to generate synchronised rhythmic bursting activity. We studied the activity of the population with parameters distributed as in Fig. 5, with all-to-all excitatory connections with the average synaptic weight $\stackrel{‒}{w}$ ($\stackrel{‒}{w}\in [0,0.2]\mathrm{nS}$, see Methods). Figure 7 shows the integrated population activity (upper trace in each panel) and the traces of the membrane potential of the three neurons identified in Figs 5 and 6 as neurons 1, 2, and 3, under control conditions (Fig. 7A1–C1) and after simulated blockade of I_NaP (${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$; Fig. 7A2–C2) or I_CAN (${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$; Fig. 7A3–C3), or both currents (g_NaP = 0 and g_CAN = 0; Fig. 7A4–C4). Figure 8A–D shows the bursting regions in the plane of (g_tonic, $N\cdot \stackrel{‒}{w}$) corresponding to the intact network (Fig. 8A) and when either ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 8B) or ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 8C) or (${\stackrel{‒}{g}}_{\mathrm{NaP}}={\stackrel{‒}{g}}_{\mathrm{CAN}}=0$, Fig. 8D). The diagram in Fig. 8E summarises the results shown in Fig. 8B–D.

Fig. 7.

Rhythmic bursting activity generated by the 50-neuron population with mutual excitatory synaptic interconnections. Each panel shows the integrated population activity represented by the average histogram of neuronal activities [upper trace, y-axis represents an average histogram of population activity in spikes/(neuron ·s), bin size = 20 ms] and the membrane potential traces of three neurons, indicated in Figs 5 and 6 as neurons 1, 2, and 3, respectively. The top row (A1–A4) shows I_NaP-dependent bursting that occurs in the population at relatively low levels of both neuronal interaction ($N\cdot \stackrel{‒}{w}=2\mathrm{nS}$) and drive (g_tonic = 0.4 nS). The middle row (B1–B4) shows population bursting requiring either I_NaP or I_CAN that occurs with increased neuronal interactions ($N\cdot \stackrel{‒}{w}=5\mathrm{nS}$) at the same level of drive (g_tonic = 0.4 nS). The bottom row (C1–C4) shows population bursting independent of I_NaP and I_CAN that occurs at higher levels of interaction ($N\cdot \stackrel{‒}{w}=5\mathrm{nS}$) and drive (g_tonic = 0.5 nS). The first column (A1–C1) shows the population activity and activities of the identified neurons 1, 2 and 3 under control conditions; the second column (A2–C2) shows the simulated effects of I_NaP blockade (${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$) on the population and single-neuron bursting in the three cases of drive and neuronal interaction described above; the third column (A3–C3) shows the simulated effects of I_CAN blockade (${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$) on the population and single-neuron bursting for the same three cases; the fourth column (A4–C4) shows the simulated effects of blockade of both I_NaP and I_CAN (${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ and ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$). See text for details.

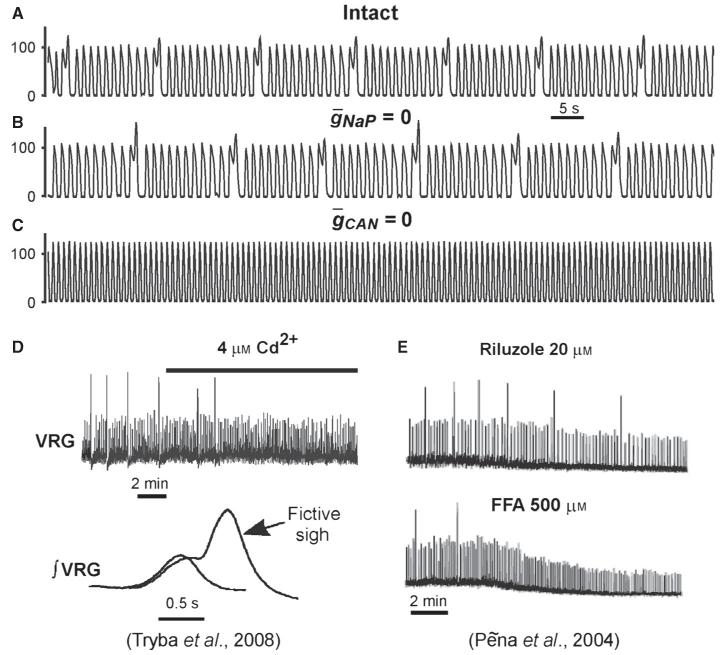
Our simulations showed that when both the external excitatory drive and the total network input to each neuron were relatively weak [e.g. g_tonic = 0.4 nS, $N\cdot \stackrel{‒}{w}=2\mathrm{nS}$, as in Fig. 7A1–A4, which corresponds to the point (0.4, 2) nS indicated in Fig. 8E by the small yellow circle], the network generated I_NaP-dependent population bursting that could be abolished by setting ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 7A2), despite the presence of unsynchronised rhythmic bursting in a few neurons (e.g. neurons 2 and 3). This type of bursting corresponds to the I_NaP-dependent (blue) bursting region in Fig. 8E.

An increase in the total network synaptic input to each neuron at the same g_tonic (e.g. from $N\cdot \stackrel{‒}{w}=2$ to $N\cdot \stackrel{‒}{w}=5\mathrm{nS}$, simulating an increase in the number of neurons in the population; Fig. 7B1–B4), which corresponds to the point (0.4, 5) nS (indicated in Fig. 8E by another small yellow circle), allowed the population to maintain (I_CAN-dependent) population bursting at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ (Fig. 7B2): this bursting could be abolished only if both ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ and ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 7B4). The same type of bursting could be obtained by increasing drive (e.g. g_tonic = 0.5 nS) while keeping a low level of excitatory synaptic interactions within the network ($N\cdot \stackrel{‒}{w}=2\mathrm{nS}$, not shown). This type of bursting, requiring the presence of=either I_NaP or I_CAN, corresponds to the green region in Fig. 8E.

A further increase of excitatory drive, e.g. by setting g_tonic = 0.5 nS at $N\cdot \stackrel{‒}{w}=5\mathrm{nS}$ as in Fig. 7C1–C4 (corresponding to the point (0.5, 5) nS indicated in Fig. 8E by the third small yellow circle), allowed for population bursting independent of both I_NaP and I_CAN (see Figs 7C4 and 8D, and the grey region in Fig. 8E). In this case, relatively strong excitatory synaptic interactions within the population provided burst initiation and then its termination via intracellular Na⁺ accumulation and Na⁺/K⁺ pump activation). Note that setting ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ to simulate the suppression of only I_CAN could not stop population bursting in the above three cases (see Fig. 7A3–C3). Unstable, irregular I_CAN-dependent bursting could only exist at very high drive values with a moderate level of $N\cdot \stackrel{‒}{w}$ (see Fig. 8B and the brown region in Fig. 8E), and the biological plausibility of this bursting is questionable.

Synchronised Ca²⁺ oscillations and sigh-like rhythmic activity

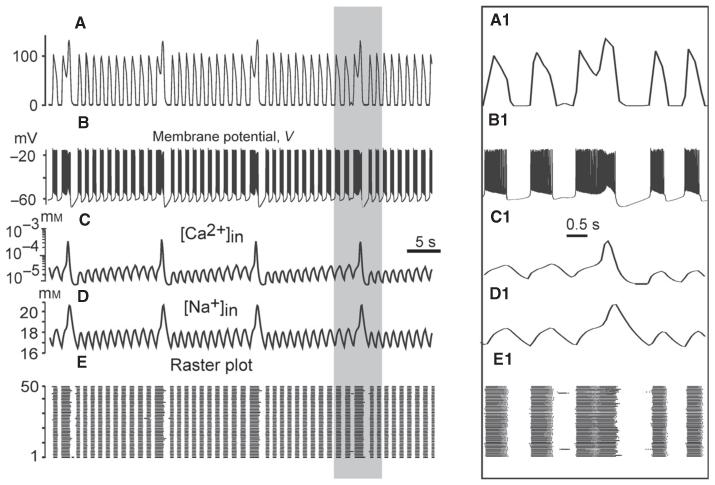
Under certain conditions, the model was capable of generating an additional slow sigh-like bursting activity with augmented amplitude arising from low-frequency Ca²⁺ oscillations synchronised over the population. In the simulations presented here, we narrowed the allowed ranges of parameters in the random distributions of the maximal Ca²⁺ and leak conductances (${\stackrel{‒}{g}}_{\mathrm{Ca}}\in [0.0006,0.0007]\mathrm{nS}$ and g_L ∈ [2.25, 2.75] nS). In addition, we increased both the IP3 concentration (IP3 = 1.5 × 10⁻³ mm) and the maximal conductance for I_CAN channels (${\stackrel{‒}{g}}_{\mathrm{CAN}}=3\mathrm{nS}$). The results of simulations at g_tonic = 0.7 nS and $N\cdot \stackrel{‒}{w}=2.5\mathrm{nS}$ are shown in Fig. 9. These simulations demonstrate the emergence of higher-amplitude, low-frequency bursts that appeared periodically at the top of the regular bursts (Fig. 9A and A1). Figure 9C shows the low-amplitude [Ca⁺²]_in transients occurring in each neuron during regular bursts, which were subthreshold for the CICR mechanism. The slow background accumulation of intracellular Ca²⁺ in each neuron finally resulted in synchronised CICR producing low-frequency, high-amplitude [Ca⁺²]_in transients, which, through synchronous activation of I_CAN, produced higher-amplitude bursts emerging at the top of the regular bursts (Fig. 9A and B), forming distinctive biphasic burst shapes (Fig. 9A1) and delaying the onset of the next regular bursts (Fig. 9A, B, E, A1, B1 and E1). These bursts were qualitatively similar to the ‘fictive sighs’ that have been previously described by Ramirez and his collaborators (Lieske et al., 2000; Peña et al., 2004; Tryba et al., 2008, e.g. see Fig. 10D and E). As relatively high drives were used, the regular bursting was independent of both I_NaP and I_CAN (see the previous section), and hence was not abolished at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ or ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 10B and C). However, assigning ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (or ${\stackrel{‒}{g}}_{\mathrm{Ca}}=0$, not shown) fully removed the slow sigh-like oscillations (Fig. 10C), confirming that the generation of sigh-like bursts in our model is I_Ca/I_CAN-dependent.

Fig. 9.

Simulation of sigh-like rhythmic bursting. (A) An example of rhythmic population bursting with higher-amplitude, low-frequency sigh-like bursts emerging at the top of regular bursts. The trace shows integrated population activity represented by the average histogram of neuronal activity (bin size = 20 ms). (B) Membrane potential changes in one neuron of the population. (C and D) Changes in [Ca²⁺]_in and [Na⁺]_in, respectively, in the same neuron; both values show high-amplitude oscillations synchronised with the ‘sighs’. (E) Raster plot of all 50 neurons of the population (each row corresponds to one neuron whose spikes are represented by dots). (A1–E1) The expanded insets indicated in A–E by the grey rectangle.

Fig. 10.

Effects of I_NaP and I_CAN suppression on the sigh-like activity. (A–C) Population bursting with the sigh-like activity under control conditions (intact, A), after simulated blockade of I_NaP (${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$, B), and after blockade of I_CAN (${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$, C). Note that blocking I_NaP did not affect population activity, whereas blocking I_CAN suppressed ‘sighs’. See text for details. (D) Fictive sighs recorded from a neonatal mouse medullary slice preparation containing the pre-BötC in vitro. The top trace shows that application of Cd²⁺ to block Ca²⁺ currents suppressed fictive sighs without affecting regular bursting; the bottom trace shows the emergence of a fictive sigh on the top of the regular burst (from Tryba et al., 2008, fig. 1, with permission). (E) Another example of fictive sighs from the slice preparation demonstrating that the application of riluzole to block I_NaP did not suppress sighs (and regular bursts), whereas application of FFA to block I_CAN fully abolished sighs without affecting regular bursts (from Peña et al., 2004, fig. 7, with permission).

Figure 11 presents a colour-coded 2D plot showing the period of regular bursting (represented by colour) in the (g_tonic, $N\cdot \stackrel{‒}{w}$) plane. A rectangle indicating the period of sigh-like bursts (using the same colour representation) is superimposed on the 2D plot of the regular burst periods. This figure shows that the sigh-like bursting appears at high values of excitatory drive at the end of the regular bursting region, just before the transition from bursting to asynchronous population activity. Furthermore, in the sigh-like bursting regime, the frequency of the sigh-like bursts increases with increasing g_tonic.

Discussion

State/preparation dependence of I_NaP-dependent and I_CAN-dependent bursting

The major objective of this study was to consider the possible mechanisms generating synchronised rhythmic bursting activity in large-scale neural populations with mutual excitatory synaptic interactions and randomly distributed intrinsic neuronal properties that have been previously found or proposed to contribute to the population bursting observed under different experimental conditions. Although most of the experimental data used, and the corresponding simulations performed, in this study concern the generation of population rhythmic bursting in the medullary pre-BötzC in vitro, some of the results described herein may also be relevant to the generation of population bursting activities in other areas of the brain, including the mammalian spinal cord. Despite more than two decades of intensive investigation, the neural mechanisms responsible for rhythmic bursting in the pre-BötC in vitro remain poorly understood, and continue to be widely debated in the literature. The wide spectrum of opinions (explicitly or implicitly supported by experimental data in some preparations) range from the suggestion of a critical role of I_NaP in pre-BötC bursting (Butera et al., 1999a; Del Negro et al., 2002a; Rybak et al., 2003b; Koizumi & Smith, 2008) to the complete rejection of the role of this current (Del Negro et al., 2002b, 2005), and an opposite suggestion of the critical involvement of I_CAN synaptically activated via ionotropic or metabotropic (or both) mechanisms (Crowder et al., 2007; Pace et al., 2007; Pace & Del Negro, 2008; Krey et al., 2010). In this modelling study, we addressed these seemingly conflicting concepts and data, and attempted to integrate them and investigate them in a common computational framework. In contrast to previous computational models investigating the possible roles of I_NaP-dependent and I_CAN-dependent bursting mechanisms, in which these currents were included together in the same model of single pre-BötC neurons (Rubin et al., 2009; Dunmyre et al., 2011; Toporikova & Butera, 2011), we mainly considered models of heterogeneous neural populations, in which key neuronal biophysical properties defining these bursting mechanisms were randomly distributed across neurons of the population. Therefore, after the initial random distribution of persistent Na⁺, Ca²⁺ and leak conductances, the entire neural population contained subpopulations of neurons whose intrinsic bursting activity (when synaptically uncoupled) critically depended on either I_NaP, or I_CAN, or both of these currents, or could not be evoked at all (Figs 5 and 6), which is consistent with the existing experimental data (e.g. Thoby-Brisson & Ramirez, 2001; Peña et al., 2004, see Fig. 6A4–C4 and A5–C5).

In the coupled case (with all-to-all excitatory synaptic interactions), we have shown that, depending on the general level of neuronal excitation in the network (defined by external tonic excitatory drive to all neurons) and the strength of synaptic interactions within the population (defined by the size of the network and synaptic weights), the population can generate bursting activity that critically depends on I_NaP or on I_CAN, or is independent of both of these currents (Figs 7 and 8, and specifically Fig. 8E). We consider this to be an important result of our study that may resolve the long-standing debate about which of the intrinsic mechanisms proposed from different studies and preparations, I_NaP-dependent or I_CAN-dependent, is necessary and is not necessary for rhythm generation in the pre-BötC in vitro.

In this regard, the conclusion from our simulations is that the necessity of these currents for the generation of this rhythmic activity is not absolute but depends on many factors, including the neuronal excitability, network size (number of neurons), and strength of excitatory synaptic interactions. The necessity of I_NaP and I_CAN for rhythm generation in the pre-BötC in vitro may also depend on the experimental preparation, animal type (rat or mouse) and age (reflecting developmental differences in the expression of neuronal ionic channels), thickness of the slices used (reflecting numbers of interacting neurons and their synaptic connections, as well as sources of tonic excitation), and experimental conditions, such as the metabolic state and extracellular ionic concentrations. Specifically, the suggestion of an essential role of I_NaP for generation of bursting activity in the pre-BötC in vitro came from experimental studies performed on thin (200–350-μm) medullary slices and pre-BötC island preparations from neonatal rats (Koshiya & Smith, 1999; Johnson et al., 2001; Koizumi & Smith, 2008), whereas the Cd²⁺-sensitive (riluzole-insensitive) rhythmic bursting and its coexistence/cooperation with the I_NaP-dependent (riluzole-sensitive) bursting were found in much thicker medullary slices (550–700 μm) from older mice (e.g. Lieske et al., 2000; Thoby-Brisson & Ramirez, 2001; Peña et al., 2004). In this connection, our simulations give an example of how an increase in the population size or interactions (i.e. an increase in $N\cdot \stackrel{‒}{w}$) at a relatively constant excitability (g_tonic) can cause a transition from I_NaP-dependent bursting (abolished at ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$, simulating the effect of riluzole; Fig. 7A2 and A4) to bursting activity involving neuronal and excitatory synaptic mechanisms, which can be abolished only if both of the currents are blocked (Fig. 7B2–B4; see also a corresponding representation in Fig. 8E). A similar transition can be produced by an increase in neuronal excitation (g_tonic) while the total synaptic weight is kept constant (see Fig. 8E). Moreover, our simulations have shown that, at high g_tonic, population bursting can be generated even if both I_NaP and I_CAN are blocked (see the grey region in Fig. 8E). In our opinion, this modelling result is consistent with, and may provide an explanation for, the experimental findings of Del Negro et al. (2005), who showed that, after rhythmic bursting in the pre-BötC was blocked by both FFA and riluzole, it could be restored by substance-P, a neuromodulator that can produce strong neuronal excitation by mechanisms not involving I_NaP or I_CAN (e.g. Peña & Ramirez, 2004; Koizumi & Smith, 2008).

I_NaP-dependent bursting

It should be clearly understood that a truly persistent (non-inactivating) I_NaP cannot produce rhythmic bursting at the cellular or network levels by itself without additional mechanism(s) providing burst termination. In the classical model of Butera et al. (1999a, Model 1) and in many later models (e.g. Rybak et al., 2003b; Dunmyre et al., 2011; Toporikova & Butera, 2011), burst termination was based on the slow voltage-dependent inactivation of g_NaP conductance (h_NaP variable). This mathematically elegant idea, however, does not have direct experimental support, as the slow I_NaP inactivation has not yet been characterised in detail in pre-BötC excitatory neurons. Moreover, modelling studies have shown that the I_NaP-dependent bursting based on the slow voltage-dependent inactivation of I_NaP exists in a limited range of neuronal excitability or input excitatory drive (Butera et al., 1999a; see also Fig. 2A), at least at the single-neuron level, although the dynamic range is somewhat extended in heterogeneous excitatory networks (Butera et al., 1999b; Purvis et al., 2007). Therefore, even if the slow voltage-dependent inactivation of I_NaP exists, it is unlikely that it could represent the only mechanism for burst termination; other voltage-dependent, or [Ca²⁺]_in-dependent, or [Na⁺]_in-dependent mechanisms could be involved or critically contribute to burst termination.

Several proposals have been made concerning other potential burst-terminating mechanisms, including mechanisms based on: (i) slowly activating voltage-dependent K⁺ current (e.g. Butera et al., 1999a; Model 2) or Ca²⁺-activated K⁺ current (suggesting accumulation of intracellular Ca²⁺ during bursts via high voltage-activated Ca²⁺ currents (e.g. El Manira et al., 1994; Bevan & Wilson, 1999; Ryczko et al., 2010); (ii) Na⁺-activated K⁺ currents (e.g. Yuan et al., 2003; Wallen et al., 2007; Krey et al., 2010); and (iii) activation of the Na⁺/K⁺ electrogenic pump (e.g. Ballerini et al., 1997; Darbon et al., 2003; Del Negro et al., 2009; Krey et al., 2010). The two latter mechanisms suggest an important role of intracellular Na⁺ accumulation during bursts. However, slowly activating K⁺ channels have not been characterised so far in the mammalian brainstem/spinal cord, and Ca²⁺-activated K⁺ channels have been found to be unnecessary for rhythm generation in vitro in both the pre-BötC (Onimaru et al., 2003; Zavala-Tecuapetla et al., 2008) and isolated spinal cord of rodents (Ballerini et al., 1997). Hence the [Na⁺]_in-dependent burst-terminating mechanisms, such as those involving activation of the Na⁺/K⁺ pump, currently look most plausible, and this is supported by experimental studies on both the pre-BötC (Krey et al., 2010) and isolated spinal cord (Ballerini et al., 1997).

In this study, we compared three single-neuron models capable of generating I_NaP-dependent bursting that differed by the operating burst-terminating mechanisms. In the first model, burst termination was based on the slow inactivation of I_NaP (Fig. 1A and A1), as in the original Butera et al. (1999a) model (Model 1). In the second model, burst termination was provided by both the slow inactivation of I_NaP (as in the first model) and the Na⁺/K⁺ pump activated by intracellular Na⁺ accumulating during bursts (Fig. 1B and B1). In the third model, the Na⁺/K⁺ pump-based burst-terminating mechanism operated alone without I_NaP inactivation; that is, I_NaP was considered to be non-inactivating (Fig. 1C and C1). We found that the contribution of the Na⁺/K⁺ pump to the I_NaP-based bursting as a part of the burst-terminating mechanism significantly increases the range of neuronal excitability (external drive) in which I_NaP-based bursting exists (Fig. 2A–C and A1–C1).

An additional point of difference between the first model of Butera et al. (1999a), and the second and third models incorporating the Na⁺/K⁺ pump, is that each of the latter models has a wide area of bursting in which a reduction in ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ at constant g_tonic produces a switch from bursting to tonic spiking (see Fig. 2B–D), which can explain how riluzole-sensitive intrinsic bursters can become tonically spiking after application of riluzole (see Fig. 6B4 and Peña et al., 2004). This feature is incompatible with the first model, in which burst termination is based only on I_NaP inactivation (Fig. 2A and D).

The other interesting difference between the three models concerns the dependence of bursting frequency in these models on ${\stackrel{‒}{g}}_{\mathrm{NaP}}$. With decreasing ${\stackrel{‒}{g}}_{\mathrm{NaP}}$ at a constant g_tonic (to simulate the effects of pharmacological blockade of I_NaP, e.g. by riluzole), the burst frequency decreased in the first model (Fig. 2A and D), was relatively constant in the second model (Fig. 2B and D), and increased in the third model (Fig. 2C and D). Thus, our model predicts that such differences can be used experimentally to test for the presence of these burst-terminating mechanisms and to potentially distinguish them. These features also suggest that the effect of blocking I_NaP by riluzole on burst frequency may depend not on I_NaP activation as such, but rather on the operating burst-terminating and recovery mechanisms, and hence the change in burst frequency with I_NaP suppression cannot be considered as an argument for or against the critical role of I_NaP in the generation of bursting, as proposed by some authors (Del Negro et al., 2002b, 2005).

I_CAN-dependent bursting

The essential role of I_CAN in rhythm generation in the pre-BötC in vitro has been suggested as a plausible alternative to I_NaP-dependent mechanisms. Specifically, a metabotropic mechanism has been hypothesised, suggesting that synaptically activated metabotropic glutamate receptors (mGluRs) explicitly trigger IP3-mediated intracellular Ca²⁺ release, which in turn activates I_CAN (Pace et al., 2007; Pace & Del Negro, 2008).

An important issue in this hypothesised mechanism concerns the onset of bursting, i.e. the initial membrane depolarisation that initiates spiking. Do synaptically activated mGluRs directly evoke IP3-dependent intracellular Ca²⁺ release leading to intracellular Ca²⁺ accumulation, which in turn activates I_CAN, providing membrane depolarisation initiating the burst (metabotropic burst-initiating mechanism), or does the synaptic activation by ionotropic mechanisms explicitly cause a necessary membrane depolarisation, which evokes IP3-dependent intracellular Ca²⁺ release that activates I_CAN?

In the former case (metabotropic burst-initiating mechanism), we should expect a critical role of mGluR activation, which is not supported by recent studies showing that bursting in the pre-BötC network persists following the blockade of group I mGluRs (Ben-Mabrouk et al., 2012). In this case, we should also expect dynamic (phasic) changes of IP3 production within a time scale compatible with the temporal characteristics of bursting. Although it has been shown that transient stimulation of glutamate receptors can induce Ca²⁺-activated currents (e.g. Berridge, 1998; Anwyl, 1999), this effect occurs on a time scale of hundreds of milliseconds or slower, which is not compatible with the temporal characteristics of burst initiation considered here. Therefore, the dynamic IP3 changes as such probably do not play a major/critical role here, and may be ignored. The IP3 changes, however, may be important in slower processes; for example, they can mediate the effects of neuromodulators.

In the latter case (ionotropic burst-initiating mechanism), the synaptically evoked membrane depolarisation by glutamate receptor activation can activate voltage-gated Ca²⁺ currents, providing an initial accumulation of intracellular Ca²⁺. The latter can initiate the IP3-dependent CICR mechanism (Berridge, 1998). For this reason, the latter mechanism does not necessarily require changes in the IP3 concentration. In this connection, Pace & Del Negro (2008) have confirmed a critical involvement of both the influx of Ca²⁺ through voltage-gated Ca²⁺ channels and the CICR-based mechanism in the activation of I_CAN in pre-BötC bursting at the single-neuron level. Here, it is worth recalling that the idea of an important role of I_CAN in the pre-BötC bursting was earlier proposed by Peña et al. (2004), who demonstrated that rhythmic activity in the Cd²⁺-sensitive intrinsic bursters could be blocked by the I_CAN blocker FFA, and that combined application of riluzole and FFA abolished rhythmic bursting in the pre-BötC. Later, Pace et al. (2007) reported that even application of FFA alone (without riluzole) could stop the rhythm in the slice, hence suggesting that I_CAN alone (i.e. without I_NaP) could be sufficient for bursting in the pre-BötC. However, the possible nonspecific effects of FFA at the concentration used (300 μm) do not warrant this conclusion, especially as FFA at such a high concentration has also been shown to affect Na⁺ channels, by reducing Na⁺ current availability and slowing down Na⁺ channel inactivation (Yau et al., 2010).

However, the important finding of Peña et al. (2004) was that Ca²⁺ influx through voltage-gated Ca²⁺ channels was actually necessary for I_CAN-dependent bursting, as the latter could be abolished by the Ca²⁺ current blocker Cd²⁺. This allows the suggestion that the [Ca²⁺]_in necessary for I_CAN activation is actually provided by voltage-gated Ca²⁺ currents, either directly (through Ca²⁺ influx via voltage-gated Ca²⁺ channels) or indirectly via IP3-dependent CICR mechanisms, which, in any case, contradicts a pure metabotropic (based on mGluR activation) concept. This suggestion has been explicitly implemented in our model, in which I_CAN-dependent bursting can be abolished in both cases, when either ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ or ${\stackrel{‒}{g}}_{\mathrm{Ca}}=0$, which is consistent with the results of both Peña et al. (2004) and Pace & Del Negro (2008).

Modelling low-frequency, high-amplitude sigh-like bursting

Increases in both IP3 concentration and I_CAN (both were tripled) accompanied by a lowering of I_Ca conductance and a narrowing of its distribution allowed our model to generate higher-amplitude, low-frequency bursts emerging periodically on the top of regular network bursts (Figs 9 and 10). These slow oscillations appeared very similar to the ‘fictive sighs’ described previously by Ramirez and his collaborators (Lieske et al., 2000; Peña et al., 2004; Tryba et al., 2008). In our model, with the above augmentation of IP3/I_CAN, the sigh-like activity emerged at a high level of external drive (or neuronal excitability, see Fig. 11), when the regular bursting became independent of both I_NaP and I_CAN. Therefore, the regular bursting persisted when ${\stackrel{‒}{g}}_{\mathrm{NaP}}=0$ and/or ${\stackrel{‒}{g}}_{\mathrm{CAN}}=0$ (Fig. 10B and C), whereas the sigh-like bursts were eliminated= during simulated suppression of I_CAN (Fig. 10C) or I_Ca, confirming that the sigh-like bursting in our model critically depends on both I_CAN and I_Ca. On the other hand, the sigh-like bursting in the model represents a network phenomenon, because no sigh-like bursts were seen in the activity of any neuron (at any drive) if the neurons were uncoupled by setting all w_ij = 0 (not shown). These modelling results look consistent with the previous experimental data showing that both Cd²⁺ (I_Ca blocker, Lieske et al., 2000; Tryba et al., 2008, see Fig. 10D) and FFA (I_CAN blocker, Peña et al., 2004, see Fig. 10E) could remove sighs generated in the medullary slices (or even slice islands) containing the pre-BötC without suppressing regular (high-frequency, low-amplitude) bursting activity in these slices. It is possible that a low concentration of Cd²⁺ (20 μm) used in the experiments of Lieske et al. (2000) and Tryba et al. (2008) removed sighs via a reduction of synaptic interactions in the network, as suggested by Lieske & Ramirez (2006). However, the results of our simulations allow a different explanation for sigh suppression by low Cd²⁺ concentrations: such low concentration of Cd²⁺ could be enough to block relatively weak I_Ca in pre-BötC neurons, which (when not blocked) is sufficient to initiate the CICR mechanism, leading to slow accumulation of intracellular Ca²⁺ to activate I_CAN involved in the generation of sighs (see Fig. 9C). Pharmacological blockade of I_CAN by FFA was experimentally demonstrated by Peña et al. (2004) (see Fig. 10E). Although they used a relatively high concentration of FFA (500 μm), which might not be selective enough for I_CAN to allow conclusions to be drawn about the necessity for I_CAN, the authors stated that the effect of FFA could be mimicked by 100 μm lanthanum, another blocker of I_CAN (Peña et al., 2004).

Besides sharing a similarity in appearance and pharmacological suppression, the sigh-like bursting in our model has many of the characteristic features of experimentally recorded ‘fictive sighs’, such as their biphasic profile as they are triggered by regular bursts, their duration of ~1 s, an increased delay in the onset of the next bursts after sighs (Lieske et al., 2000; Peña et al., 2004; Tryba et al., 2008; see Fig. 10 A and D), and the frequency of sigh-like bursts as reported in some recent studies (Doi & Ramirez, 2010). However, we were unable to obtain regular sigh-like oscillations in our model with periods larger than 25–30 s (with the parameters chosen) that were observed in other experimental studies (e.g. Lieske et al., 2000; Peña et al., 2004; Tryba et al., 2008); further reduction of g_tonic in all neurons allowed the model to produce intersigh intervals of up to 1–2 min, but these intervals (and the sigh-like bursting activities) were very irregular. Therefore, additional coordinated experimental, modelling and analytical studies are required to improve the model, find a correct set of parameters, and carefully verify whether this modelling phenomenon (and its mechanisms) relate to, and may provide a plausible explanation for, the ‘sighs’ observed in the pre-BötC in vitro. In particular, our model predicts that CICR may occur in pre-BötC neurons primarily during the sigh bursts, suggesting an interaction between purely network and intrinsic cellular processes in producing the sighing rhythm.

Burst-terminating mechanisms and the ‘group-pacemaker’ hypothesis

The burst-terminating mechanism that is critical for bursting in the largest part of the bursting regions determined in the present model (Fig. 8) is based on strong accumulation of intracellular Na⁺ followed by activation of the Na⁺/K⁺ pump. Another [Na⁺]_in-dependent burst-terminating mechanism could be based on an Na⁺-activated K⁺ current (Yuan et al., 2003; Wallen et al., 2007; Krey et al., 2010), which was not considered in the present model. The plausibility of [Na⁺]_in-dependent burst termination in pre-BötC bursting in vitro, and specifically the plausibility of the Na⁺/K⁺ pump-based mechanism, has been indirectly supported by recent experimental studies (Krey et al., 2010), and requires further investigation. According to our model, the intracellular Na⁺ accumulation can be provided by several cellular mechanisms, such as those involving I_NaP and I_CAN, or network interactions, which, if they are strong enough (defined by $N\cdot \stackrel{‒}{w}$), could allow intracellular Na⁺ accumulation via neuronal depolarisation and fast Na⁺ currents (I_Na, see Eqn 15), sufficiently to activate the Na⁺/K⁺ pump-dependent burst-terminating mechanism. Correspondingly, our simulations have demonstrated a large region in the (g_tonic, $N\cdot \stackrel{‒}{w}$) parameter space where bursting can occur even if I_NaP = I_CAN = 0 (Fig. 8D or grey area in Fig. 8E). Interestingly, this emergent, network interaction-dependent bursting (which cannot be generated by single neurons) may reflect a so-called group-pacemaker mechanism (Rekling & Feldman, 1998). In this case, such a group-pacemaker bursting mechanism would provide burst initiation by recurrent excitation via excitatory synaptic network interactions and burst termination by an Na⁺/K⁺ pump-dependent burst-terminating mechanism in each neuron. Moreover, generation of such group-pacemaker bursting does not need I_CAN, nor does it require any additional neuronal/network properties, such as the depolarisation block and associated transient depression of network synaptic interactions suggested by Rubin et al. (2009).

Comparison with other related models

Three computational models have been previously developed to simulate the I_CAN-dependent bursting and the possible coexistence of, and interactions between, I_CAN-dependent and I_NaP-dependent oscillations in the pre-BötC (Rubin et al., 2009; Dunmyre et al., 2011; Toporikova & Butera, 2011). These models have provided important insights into previously hypothesised bursting mechanisms, and some formal descriptions from these models were explicitly used in our model. Nevertheless, there are several critical points concerning conceptual and technical differences between our model and these models that need to be considered and discussed.

In the model of Rubin et al. (2009), the recurrent synaptic excitation evokes IP3-dependent intracellular Ca²⁺ accumulation from intracellular stores. Although the authors use a parameter that explicitly connects intracellular Ca²⁺ accumulation with synaptic activation, the metabotropic mechanism behind this process is not explicitly modelled. The accumulated intracellular Ca²⁺ activates I_CAN, which then evokes membrane depolarisation, initiates the neuronal burst, and finally produces the population burst via the recurrent excitatory interactions. This current also initiates accumulation of intracellular Na⁺. The I_CAN-produced membrane depolarisation causes voltage-dependent spike inactivation, which diminishes recurrent excitation, causing a short-term depression of excitatory transmission (depolarisation block), hence suppressing intracellular Ca²⁺ accumulation from intracellular stores. The kinetics of IP3 receptor activation/inactivation, which could also provide burst termination (see Toporikova & Butera, 2011, and our model herein), were not considered. Finally, the [Na⁺]_in-activated Na⁺/K⁺ pump was included in the model to contribute to burst termination and support the transient quiescent state in the network. Importantly, as burst initiation here critically depends on recurrent excitation within the network, this model was considered as the first model of a group-pacemaker bursting mechanism operating in the pre-BötC. This model, however, has several important limitations. First, it proposes pure metabotropic activation of I_CAN and ignores a possible role of voltage-gated Ca²⁺ currents and CICR, which is not supported experimentally (Pace & Del Negro, 2008; Ben-Mabrouk et al., 2012). Therefore it cannot reproduce and explain the Ca²⁺-dependent, Cd²⁺-sensitive bursting demonstrated experimentally by Ramirez and collaborators (Thoby-Brisson & Ramirez, 2001; Peña et al., 2004). Second, this model ignores the possible generation of I_NaP-dependent bursting (Rybak et al., 2003b; Peña et al., 2004; Koizumi & Smith, 2008). Therefore, full blockade of I_CAN (setting I_CAN = 0) should completely stop bursting, which contradicts the experimental data (Peña et al., 2004). For some reason, only the I_CAN contribution to intracellular Na⁺ accumulation was considered in this model, whereas the possible contribution of Na⁺ currents (both fast I_Na and persistent I_NaP) was not taken into account.

An important problem with this model involves the issue of external control of population bursting. The current view is that the frequency and/or amplitude of network oscillations are usually controlled by drives from other neural sources providing tonic synaptic input. In this connection, this model has no mechanisms controlling intracellular Ca²⁺ accumulation induced by synaptic drives from external sources. Depolarisation block does not help here, because this mechanism only applies to synaptic interactions within the network. Therefore, any tonic excitatory synaptic input from an external source would result in constantly increasing intracellular Ca²⁺ accumulation, leading to cellular hyperactivation, which has not been investigated.

An additional problem in the Rubin et al. model relates to the possible overestimation of the voltage-dependent spike inactivation (depolarisation block) mechanism, which, in this model, is necessary to suppress recurrent excitation and initiate burst termination. There is often reactivation of the spiking (after the transient spike inactivation) in the latter half of the burst, which must be overcome by some other burst-terminating mechanism than that incorporated in the model. In our model, some neurons in the network also exhibited transient partial spike inactivation during the burst under some conditions with strong phasic synaptic input (e.g. see Fig. 7B1, B3, C1 and C3), as observed experimentally in some neuronal recordings, but this phenomenon did not contribute significantly to population burst termination in our network model.

Dunmyre et al. (2011) extended the model described above by including I_NaP and considering the behaviour of a self-coupled single neuron by varying ${\stackrel{‒}{g}}_{\mathrm{CAN}}$ and ${\stackrel{‒}{g}}_{\mathrm{NaP}}$, the conductances of I_CAN and I_NaP, respectively. By varying these conductances, the authors obtained a spectrum of activity patterns, including quiescence, tonic spiking, and two types of bursting, which were classified on the basis of whether depolarisation block was present or not. The authors elucidated the mechanisms underlying each behaviour, as well as the transitions between the corresponding regimes with the occurrence of bistability. The obvious advantage of this model is that it allows for I_NaP-dependent (I_CAN-independent) bursting in some region of the parameter space. As in the Rubin et al. (2009) model, only I_CAN could provide intracellular Na⁺ accumulation, and I_Na and I_NaP did not contribute to this process. Setting I_CAN = 0 reduces this model to the Butera et al. (1999a) model with a narrow area of bursting in the parameter space. Also as in the Rubin et al. (2009) model, this model suggests metabotropic activation of I_CAN, and possible roles of voltage-gated Ca²⁺ currents and CICR have not been considered. Hence, it also could not reproduce and explain Ca²⁺-dependent, Cd²⁺-sensitive bursting (Thoby-Brisson & Ramirez, 2001; Peña et al., 2004). The problem with the possible neuron behaviour under conditions of external (not recurrent) synaptic input (see above) also remained unsolved. Furthermore, just a single self-exciting neuron was considered in this model, and not the behaviour of a population of such neurons. All of the possible issues concerning synchronisation of neuronal activity within populations of such neurons with randomised parameters were not addressed in the Dunmyre et al. model.

Toporikova & Butera (2011) have developed a two-compartment model of a single pre-BötC neuron with two independent bursting mechanisms: an I_NaP-dependent mechanism with burst termination based on I_NaP slow inactivation, operating in the soma, and an IP3-dependent and I_CAN-dependent mechanism operating in the dendritic compartment. In contrast to the models described above, the authors of this model incorporated and simulated more realistic and detailed kinetics of the [Ca²⁺]_in-dependent and IP3-dependent intracellular Ca²⁺ release, which can produce both CICR and endogenous [Ca²⁺]_in oscillations (which we explicitly incorporated in our model; see Methods). However, their modelling focused on investigating neuronal behaviour in response to current injection in the soma, and the possible effects of neuromodulators that can control cellular activity via IP3. Hence, synaptic input to the neuron was not considered. Thus, this model did not consider possible interactions between synaptic activation and IP3/I_CAN dynamics, or a possible role of voltage-gated Ca²⁺ currents, the dynamics of [Na⁺]_in, and a possible role of the Na⁺/K⁺ pump. The burst-terminating mechanism in this model relies on Ca²⁺-dependent inactivation of intracellular Ca²⁺ release operating in a very narrow parameter space supporting bursting. Moreover, although the model has, importantly, demonstrated that a single neuron can generate Ca²⁺-dependent (and I_NaP)-dependent bursting, the possible behaviour of a population of such cells with mutual excitatory synaptic interconnections and distributed parameters was not simulated and investigated in this study. The ability of such an excitatory network to produce synchronous population bursting is questionable, because endogenous Ca²⁺ oscillations generated in different neurons would not synchronise, as the single-neuron model proposed does not have a mechanism by which synaptic inputs could affect (and hence synchronise) Ca²⁺ dynamics in each neuron.

The model of a single neuron built in our study incorporated several key features of the above models, including some mathematical formulations and particular parameters (see Methods). Specifically, the formal description of the Na⁺/K⁺ pump was adapted from Rubin et al. (2009) and Dunmyre et al. (2011) (originally from Li et al., 1996), and the description of IP3-dependent Ca²⁺ dynamics and I_CAN were taken from Toporikova & Butera (2011). We additionally incorporated in the single-neuron model a voltage-gated I_Ca providing initial accumulation of intracellular Ca²⁺ from the extracellular space and initiating the CICR process. This made the ionotropic mechanism of synaptic activation more important than the metabotropic mechanism (simulated by Rubin et al. and Dunmyre et al.), and allowed a normal neuron response to external synaptic inputs. This also allowed us to simulate the Ca²⁺-dependent bursters and reproduce the effect of Cd²⁺ on bursting activity in these neurons (Thoby-Brisson & Ramirez, 2001; Peña et al., 2004). Also, in contrast to the Rubin et al. and Dunmyre et al. models, the accumulation of intracellular Na⁺ in our model takes into account both fast I_Na and persistent I_NaP. Hence, the major [Na⁺]_in-dependent burst-terminating mechanism (based on the Na⁺/K⁺ pump) can operate independently of burst initiation, whether the latter is provided by I_CAN, or I_NaP, or synaptic interactions in the network driving activation of the fast I_Na.

The other important feature of our model, distinguishing it from other models, is that it principally considers a strong population heterogeneity resulting from distributed intrinsic neuronal properties, which allowed us to investigate the behaviour of a population of cells with distinct properties and to reproduce many experimental data showing the effects of specific pharmacological blockers on the activity of pre-BötC neurons in the intact (coupled) and uncoupled (after blockade of synaptic transmission) cases, as described in Results.

Model limitations and modelling predictions

Like any other model, our model has a number of limitations that could affect our conclusions. Specifically, we have only considered networks with all-to-all excitatory interactions, and have not simulated physiologically more realistic networks with sparser connections between the neurons. We have only considered single-compartment models of single neurons, although a consideration of two-compartment and multi-compartment neuronal models with ionic channels and other cellular properties distributed over neuronal compartments could potentially provide other single-neuron and network behaviours that are not available with the single-compartment representation.

One of the predictions of our model is that the rhythm-generating mechanism operating in the pre-BötC excitatory network (I_NaP-dependent, or I_Ca/I_CAN-dependent, or independent of both) is state-dependent. It specifically depends on the general level of neuronal excitation in the network (provided by external excitatory drive) and the strength of synaptic interactions within the network. Hence, the critical involvement of a particular cellular mechanism in the population bursting may depend on the particular conditions, e.g. those defining the average neuronal excitation in the network. Specifically, blocking I_NaP could effectively abolish the population bursting generated at a lower level of neuronal excitation in the network (e.g. at a lower concentration of extracellular K⁺ used to produce the rhythm), whereas at a higher level of neuronal excitation the cessation of the population rhythm would require suppression of both I_NaP and I_CAN, and, even after that, according to our model prediction, the population bursting can be recovered by a subsequent further increase in neuronal excitation in the network (see Fig. 8E).

We also note that many of our results are based on the assumption that free intracellular sodium ions are accumulated during cellular activity (i.e. during bursts) and activate an [Na⁺]_in-dependent burst-terminating mechanism operating in each cell independently of the source of intracellular Na⁺ accumulation. We also suggest that this [Na⁺]_in-dependent burst-terminating mechanism is connected with the activation of the Na⁺/K⁺ pump. Moreover, at a high level of excitatory synaptic interactions in the network, bursting can occur without I_NaP and I_CAN (see Fig 8D and grey area in Fig. 8E). However, such bursting, which is based entirely on excitatory neural interactions and the Na⁺/K⁺ pump-dependent burst termination, can occur only at a sufficiently high strength of synaptic interactions (as defined by $N\cdot \stackrel{‒}{w}$; see Fig 8D and E), and thus may not occur in networks with sparse or weak interconnections (low $N\cdot \stackrel{‒}{w}$). Note that a similar model and concept can, in principle, be developed with another [Na⁺]_in-activated burst-terminating mechanism based on an [Na⁺]_in-activated K⁺ current, which could perform a function similar to that of the Na⁺/K⁺ pump in the current model. However, despite some indirect support (Krey et al., 2010), these [Na⁺]_in-activated mechanisms remain highly hypothetical, and are considered to be model predictions requiring more thorough experimental investigations and testing.

In summary, we suggest that our analysis represents an important step forward in understanding the integration at the network level of a number of currently proposed cellular and network properties for the generation of Na⁺-dependent and Ca²⁺-dependent rhythms in the pre-BötC, and possibly in other brainstem or spinal networks.

Abbreviations

[Ca²⁺]_in

intracellular Ca²⁺ concentration

CICR

Ca²⁺-induced Ca²⁺ release

ER

endoplasmic reticulum

FFA

flufenamic acid

IP3

inositol triphosphate

IP3R

inositol triphosphate receptor

mGluR

metabotropic glutamate receptor

[Na⁺]_in

intracellular Na⁺ concentration

P

postnatal day

pre-BötC

pre-Bötzinger complex

SERCA

sarcoplasmic/endoplasmic reticulum Ca²⁺-ATPase

2D

two-dimensional