Simulation and modeling of crowding effects on the thermodynamic and kinetic properties of proteins with atomic details

Abstract

Recent experimental studies of protein folding and binding under crowded solutions suggest that crowding agents exert subtle influences on the thermodynamic and kinetic properties of the proteins. While some of the crowding effects can be understood qualitatively from simple models of the proteins, quantitative rationalization of these effects requires an atomistic representation of the protein molecules in modeling their interactions with crowders. A computational approach, known as postprocessing, has opened the door for atomistic modeling of crowding effects. This review summarizes the applications of the postprocessing approach for studying crowding effects on the thermodynamics and kinetics of protein folding, conformational transition, and binding. The integration of atomistic modeling with experiments in crowded solutions promises new insight into biochemical processes in cellular environments.

Introduction

The idea that the crowded conditions of cellular environments can significantly affect the biophysical properties of proteins and nucleic acids, promoted by Minton and others (Zimmerman and Minton 1993; Kornberg 2000; Ellis 2001; Zhou et al. 2008), is now bearing many fruits. The biophysical community is largely convinced of the affirmative answer to the question of whether macromolecular crowding makes important contributions to cellular functions, and is now working on the characterization and quantification of these contributions, as well as on developing tools and techniques for modeling these contributions experimentally, theoretically, and through simulation (Elcock 2010). This review focuses on recent progress in our understanding of macromolecular crowding achieved through molecular simulations, with a particular focus on the effects of crowding, calculated through an approach known as postprocessing (Qin and Zhou 2009; Qin et al. 2010), on the thermodynamics and kinetics of protein folding, conformational transition, and binding.

Many experimental studies have been directed at measuring the degree to which crowding agents affect the folding, conformational transition and binding equilibria (Qu and Bolen 2002; Spencer et al. 2005; Roberts and Jackson 2007; Batra et al. 2009a, b; Phillip et al. 2009; Dhar et al. 2010; Miklos et al. 2011; Denos et al. 2012), often spurred by Minton’s predictions of significant crowder-induced stabilization of the compact states over the more open states (Minton 1981, 1998, 2000, 2005). The predictions are largely based on the scaled particle theory (Lebowitz and Rowlinson 1964) for the free energy of transferring a test protein into crowders, all of which are modeled as convex hard particles. The experimental results have often validated the qualitative aspect of Minton’s predictions, but the observed magnitudes of crowding effects are usually smaller than anticipated. Moreover, the subtle and complicated influences of crowding agents revealed by some experiments, such as a dependence on the chemical nature of the crowders (Batra et al. 2009b; Miklos et al. 2011; Denos et al. 2012), seem to be beyond the scope of simple theoretical models. Recent experiments on the kinetics of protein folding and binding under crowded conditions (Kuttner et al. 2005; Schlarb-Ridley et al. 2005; Ai et al. 2006; Yuan et al. 2008; Phillip et al. 2009, 2012a; Denos et al. 2012) pose additional challenges, since the effects of crowders on the thermodynamics and dynamics of test proteins can potentially oppose each other, leading to a net effect on the kinetics that is even more moderated than that on the equilibria (Zhou 2004; Qin et al. 2012).

Molecular simulations have further enriched our understanding of protein folding, conformational transition, and binding under crowding conditions. Earlier studies took the direct simulation approach (horizontal paths in Fig. 1a), i.e., as in an in vitro experiment, the test protein(s) in a biochemical process of interest and the crowders are simulated together (Fig. 1b). Because the simulation had to include a large number of crowder molecules and was designed to model rare transitions between stable states along the biochemical process, the test protein(s) by necessity was (were) represented at the coarse-grained level (e.g., one bead per residue) (Cheung et al. 2005; Minh et al. 2006; Kim et al. 2010; Mittal and Best 2010). The alternative, postprocessing approach (vertical paths in Fig. 1a) (Qin and Zhou 2009; McGuffee and Elcock 2010; Qin et al. 2010) circumvents the modeling of rare transitions between stable states and has allowed the test proteins to be represented at the all-atom level (Fig. 1c). Such atomistic modeling enables more quantitative interrogation by and closer integration with experimental studies of crowding effects, hopefully leading to new insight into biochemical processes in cellular environments.

Fig. 1.

Two different approaches for modeling biochemical reactions under crowding. a The direct simulation approach follows the horizontal paths, whereas the postprocessing approach follows the vertical paths, illustrated on the folding process of cytochrome b₅₆₂. The same free energy difference (ΔΔG), here representing the effect of crowding on the folding free energy, is obtained by following either the horizontal paths (ΔΔG = ΔG _f – ΔG _f0) or the vertical paths (ΔΔG = Δμ _F – Δμ _U) (Zhou et al. 2008). b In the direct simulation approach, the folding transition is followed in the presence of crowders. c In the postprocessing approach, only the folded state and the unfolded state are simulated, not their inter-conversion, and the simulations are done in the absence of crowders (Qin and Zhou 2009). Snapshots of the folded (unfolded) protein are then fictitiously inserted into the crowders to calculate Δμ _F (Δμ _U)

Modeling crowding by direct simulations

Using direct simulations, Cheung et al. (2005) studied the folding stability and kinetics of the 34-residue all-β WW domain in the presence of purely repulsive spherical crowders. The WW domain was coarse-grained to two beads per residue (representing the Cα atom and the center of mass of the side chain), with a Go-like potential (Ueda et al. 1978) in which only native interactions were retained. At a crowder volume fraction (ϕ) of 0.25, the melting temperature was increased by as much as 24 °C. In contrast to the crowding effect on folding stability, the folding rate constant (k _f) exhibited a non-monotonic dependence in ϕ, reaching a maximum of a threefold increase at ϕ = 0.1 (relative to the crowder-free situation) and then slowing down to a 1.8-fold increase. Cheung et al. (2005) attributed the latter slowing down to restricted conformational fluctuations needed for the folding transition.

A similar model was adopted by Mittal and Best (2010) to study the effect of crowding on the folding free energy surfaces of three small proteins. The potentials of mean force along the fraction of native contacts were obtained by umbrella sampling. For each protein, crowding increased the free energy of the unfolded state well relative to that of the folded state well. Also using direct simulations, Minh et al. (2006) studied the effect of crowding on the flap opening equilibrium of the HIV-1 protease dimer. The opening motion is essential for substrate and inhibitor binding. These researchers found that repulsive crowders decreased the flap-open population.

Feig and Sugita (2012) recently carried out all-atom explicit solvent molecular dynamics simulations of chymotrypsin 2 (CI2) in the presence of either lysozyme or bovine serum albumin as crowders. These simulations were motivated by the experiments of Miklos et al. (2011), who used nuclear magnetic resonance-detected amide proton exchange to probe residue-level local stability, i.e., the stability of individual residues to withstand opening up for hydrogen/deuterium exchange (Englander and Kallenbach 1983). Opening of the residues with the highest local stability involves global unfolding; hence, the highest local stability corresponds to the folding stability. The experiments showed that the protein crowders decreased the local stability of many of the monitored CI2 residues and the folding stability, in contrast to an increase in folding stability by polymer crowders on CI2 and on a number of other proteins. Miklos et al. (2011) attributed the decreased local and folding stability to attractive interactions between the test protein and the crowder protein molecules. The work of Feig and Sugita (2012) corroborated this attribution, in that the residues showing decreased local stability largely overlap with residues showing increased conformational fluctuations in the simulations in the presence of the protein crowders. It should be noted that the simulations of the Feig and Sugita (2012) probe nanosecond fluctuations in the folded state, whereas the experiments of Miklos et al. (2011) present measurements on the equilibria between the folded state and the locally or globally unfolded state. A re-analysis of these measurements has now suggested experimental temperature as a contributing factor for the observed differences, and that all of the data can be explained by a unified mechanism of action for protein and polymer crowders (Zhou 2013).

Postprocessing approach: strategy and implementation

Instead of following the horizontal paths of Fig. 1a to obtain ΔΔG, the effect of crowding on the free energy change of the test protein(s) in a biochemical process (folding, conformational change, or binding), in the postprocessing approach we follow the vertical paths. That is, we calculate the free energy for transferring, from a dilute solution to a crowded solution, the protein(s) either in the reactant state or the product state (Qin and Zhou 2009; Qin et al. 2010). By closing a thermodynamic cycle, the difference between the two transfer free energies is the same as the ΔΔG between the two horizontal paths, but we avoid simulating rare transitions along the horizontal paths.

To implement the postprocessing approach, we carry out separate simulations for the test proteins(s) in the reactant state and in the product state, without any crowders. The latter condition allows the test proteins to be represented at the all-atom level and the simulations to be done in an explicit solvent. A separate simulation of the crowder molecules is also carried out to generate a configurational ensemble for the crowded solution and can be used for the transfer of many test proteins.

To calculate the transfer free energy (∆μ) of the test protein(s) in a given state, we take snapshots from the simulation in that state and fictitiously insert them into the crowded solution (Fig. 1c). If the effective interaction energy between a test protein and the crowders is U(X, R, Ω), where X, R, and Ω represent the conformation, position, and orientation, respectively, of the test protein, then ∆μ is given by

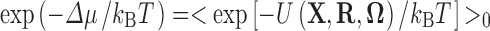1

where k _B is Boltzmann’s constant, T is the absolute temperature, <···>₀ means averaging over the conformation, position, and orientation of the test protein and over the configurations of the crowders, and the subscript “0” emphasizes the fact that the protein conformations are those sampled in the absence of crowders. Postprocessing is simply a form of Widom’s insertion method (Widom 1963). For the purely repulsive interaction between crowders and test proteins, U(X, R, Ω) is either 0, when the test protein does not clash with crowders, or infinite, when a clash occurs. Correspondingly, exp [−U(X, R, Ω)/k _B T] is either 1 or 0, and the average on the right-hand side of Eq. (1) is the clash-free or allowed fraction (f) of attempts to insert the test protein into the crowded solution.

The allowed fraction of insertion can be simply calculated by repeatedly inserting the test protein into the crowded solution and testing for clash, but we have designed an algorithm to speed up the calculation for spherical crowders (Qin and Zhou 2009). Briefly, we take one crowder particle and identify all of the grid points at which the placement of the test protein (in a given conformation and orientation) results in clash. We then copy all the “clashing” grid points to each crowder particle in the crowded solution (in a given crowder configuration). The allowed fraction of insertion is finally given by the fraction of grid points that are not part of the clashing grid points of any crowder particle. The calculation needs to be repeated for other test protein conformations and orientations and other crowder configurations to obtain the appropriate average.

Because the calculation needs to be repeated many times, we further developed an alternative, faster way of calculating the transfer free energy (Qin and Zhou 2010). We were guided by the observation that the transfer free energies calculated by our insertion algorithm can be fitted to the scaled particle theory with the radius, surface area, volume of the test protein as free parameters; the fitted values of these parameters are more or less those expected from the structure of the protein (Batra et al. 2009a; Qin and Zhou 2009). Mittal and Best (2010) confirmed this observation in their subsequent study. Essentially, our calculation for the transfer free energy can be viewed as a generalization of the fundamental measure theory (Rosenfeld 1989; Oversteegen and Roth 2005), which itself is a generalization of the scaled particle theory. Our generalized fundamental measure theory (GFMT) predicts the transfer free energy as

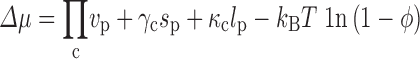2

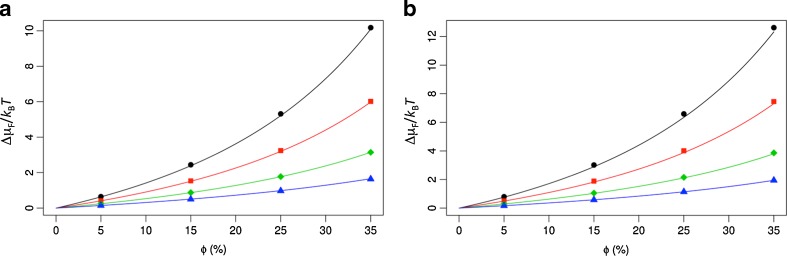
where v _p, s _p, and l _p are the volume, surface area, and linear size, respectively, of the test protein, and П_c, γ _c, and κ _c are the osmotic pressure, surface tension, and bending rigidity, respectively, of the crowded solution. The latter crowder-only quantities are determined by the volume, surface area, and radius of the crowders. The geometric quantities v _p, s _p, and l _p of the test protein are essentially defined by its crowder-excluded surface (represented at the all-atom level). Note that the crowder-excluded surface depends on the crowder radius and is not convex. Figure 2 illustrates the good agreement between the GFMT transfer free energies and those calculated by the insertion algorithm.

Fig. 2.

Comparison of the generalized fundamental measure theory (GFMT) results and those calculated by the insertion algorithm (Qin and Zhou 2009) for the transfer free energies of cytochrome b₅₆₂ in the folded state (a) and unfolded state (b). The results by the insertion algorithm are shown as circles, squares, diamonds, and triangles for crowders with radii of 15, 20, 30, and 50 Å, respectively; the corresponding GFMT results are shown as curves. These results were calculated in Qin and Zhou (2010), but there only the difference between Δμ _F and Δμ _U was shown. The GFMT calculations yielded values of 21.1, 21.4, and 21.8 Å for the linear size (l _p) of cytochrome b₅₆₂ in the folded state when the crowder radii were 15, 30, and 50 Å, respectively; the corresponding values of l _p were 24.5, 25.4, and 25.9 Å in the unfolded state. Note that these values corresponding to different crowder radii were obtained from the same set of protein conformations (either in the folded or unfolded state) generated without crowders

Validation against direct simulations

In essence the postprocessing approach yields the transfer free energy by using the protein conformations sampled in the absence of crowders and reweighting them according to the would-be protein-crowder interaction energy. Of course, the important conformational region will necessarily shift due to the presence of crowders. The postprocessing calculation is exact if the conformational space of the protein is exhaustively sampled so as to cover the important conformational region in the presence of crowders. In practice, however, can conformations be adequately sampled to ensure accurate calculation by the postprocessing approach? An important test case is whether the conformations sampled in the absence of crowders through the direct simulation approach can be used to predict crowding effects.

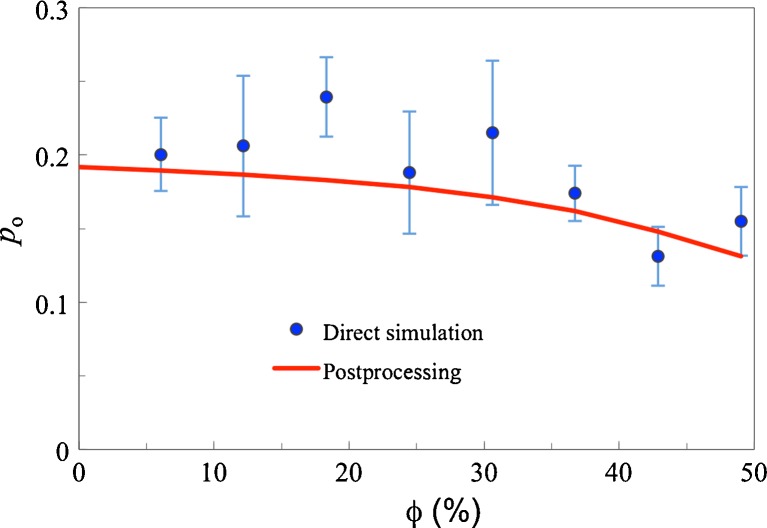
We recently addressed such a test case (Qin et al. 2010). Using the simulation code of Minh et al. (2006) we extended their study of the effect of crowding on the flap opening equilibrium of the HIV-1 protease dimer. The values of the flap-open probability (p _o) calculated using the direct simulation approach at 8 volume fractions of 30-Å crowders are shown in Fig. 3 as circles. p _o shows a small but distinct decrease with increasing ϕ. Using only the conformations sampled in the absence of crowders and applying postprocessing, we reproduced the direct simulation results very well (curve in Fig. 3). While the direct simulation results have significant statistical errors (as estimated by the variation among 6 repeat simulations), the statistical errors of the postprocessing approach on the crowding effect are negligible. The significant reduction in statistical errors comes about because averaging over protein position and orientation and over crowder configuration is effectively exhaustive in the postprocessing approach (Qin and Zhou 2009).

Fig. 3.

Postprocessing predictions (curve) and direct simulation results (circles) for the HIV-1 protease dimer flap-open probability under crowding, taken from Qin et al. (2010). Error bars in the direct simulation results represent variations among 6 repeat simulations. The postprocessing results are predicted according to 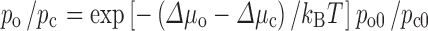, where p _o and p _c are the flap-open and flap-close probabilities under crowding, p _o0 and p _c0 are the counterparts in the absence of crowding, and ∆μ _o and ∆μ _c are the transfer free energies of the open and closed conformational ensembles

In the postprocessing approach, the same conformations, sampled in the absence of crowders, are used for different crowding conditions, such as the different volume fractions of the 30-Å crowders (Fig. 3) or for crowders with other sizes. For 100-Å crowders, the decrease in p _o with increasing ϕ becomes negligible. The latter prediction explains the experimental observation that 6 % Ficoll400 (with a Stokes radius of approx. 100 Å) did not result in a discernible change in the distribution of the inter-flap distance (Galiano et al. 2009). Using the postprocessing approach, we have also been able to reproduce Mittal and Best’s (2010) direct simulation results for the folding free energy surfaces of three small proteins under crowding (Qin et al. 2013).

From theymodynamics to kinetics

In addition to equilibrium properties, the postprocessing approach can be applied to model crowding effects on kinetic properties. In general, the rate constant of a biochemical reaction is determined by the energetics and dynamics of the biomolecule(s) involved (Zhou 2010). The rate constant under crowding can be modeled by accounting for the effects of crowding on these energetic and dynamic properties (Zhou 2004; Qin et al. 2012).

The rate constant for a unimolecular reaction, such as a folding or unfolding process or a conformational transition, can generally be expressed as (Zhou 2010)

3

where ∆G ^‡ is the activation energy (i.e., difference in free energy between the transition state and the reactant state), and A is a prefactor dictated by the dynamics, which can be described as diffusive for most biochemical reactions, along the reaction coordinate. Both internal dynamics and the solvent microviscosity can contribute to the effective diffusion constant along the reaction coordinate (Ansari et al. 1992). In principle, crowding can affect both ∆G ^‡ and the prefactor A. The effect of crowding on ∆G ^‡ can be calculated by the postprocessing approach, just as described above for the free energy difference between two stable states, provided that we can sample the transition state (in the absence of crowders) in addition to the reactant state.

The effect of crowding on A depends on the extent to which the reaction coordinate is exposed to crowders. In one extreme, the motion leading to the transition state involves only residues that are shielded from crowders, then A should be relatively independent of crowding (Yuan et al. 2008). As another example, the folding rate constant of a small protein calculated by Mittal and Best (2010) through simulations was consistent with that predicted when only the effect of crowding on the free energy surface was taken into consideration. In the other extreme, the rate-limiting step involves large-scale relative motion between domains or large fragments of the protein; in this case, crowders will affect A by changing the microviscosity. (Note that, for macromolecular crowders, the microviscosity is usually much less than the bulk viscosity.) If the relative translational diffusion constant of the domains changes from D ₀ to D under crowding, then we expect the prefactor to change in proportion:

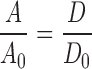4

In general, we expect the effect of crowding on A to fall between the above two extremes.

Protein–protein binding can be reaction-limited, diffusion-limited, or between these two regimes. In the reaction-limited regime, the rate-limiting step is the crossing of an energy barrier, much like in a unimolecular reaction. This may involve conformational rearrangement of one of both proteins during the binding process. The effect of crowding on the binding rate constant in the reaction-limited regime can be modeled very similarly to what is described above for unimolecular reactions.

For binding in the diffusion-controlled regime, we have developed a computational method known as the transient-complex theory for predicting the rate constant (Alsallaq and Zhou 2008; Qin et al. 2011). The transient complex refers to an intermediate in which the two proteins have near-native separation and relative orientation but have yet to form most of the short-range native interactions. The association rate constant is predicted as

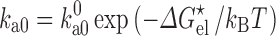5

where 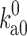is the basal rate constant, i.e., the rate constant for reaching the transient complex by unbiased diffusion, and the Boltzmann factor (with 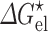denoting the electrostatic interaction energy in the transient complex) accounts for the biasing contribution of long-range electrostatic interactions in the diffusional approach to the transient complex. We have now extended the transient-complex theory to account for the effects of crowding (Qin et al. 2012). Crowding modifies the basal rate constant (from 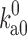to 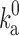) by changing the microviscosity and induces an effective interaction energy (∆∆G _c) between the proteins. Therefore

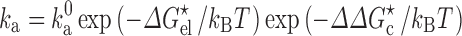6

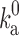can be estimated in analogy to Eq. (4):

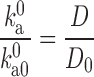7

where D ₀ and D now represent the relative translational diffusion constants of the two proteins without and with crowding. 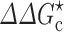can be calculated by our postprocessing method.

Applications: interrogation by experiments

The all-atom representation of test proteins, afforded by the postprocessing approach, makes the modeling of crowding more realistic and reduces the number of adjustable parameters in comparison with experiments. In particular, one no longer has the freedom of adjusting the size of a test protein. Therefore, the interrogation by experiments becomes more quantitative. Below we summarize several applications of the postprocessing approach in modeling the effects of crowding on the thermodynamics and kinetics of protein folding, conformational transition, and binding.

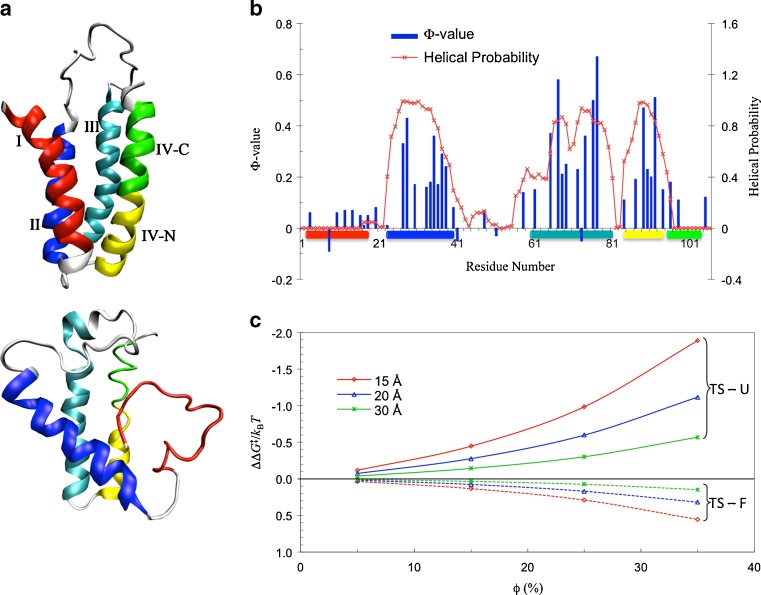
Ai et al. (2006) used the ¹⁵N relaxation dispersion technique to determine the folding and unfolding rate constants (k _f and k _u) of cytochrome b₅₆₂ in the absence and presence of 85 g/l PEG 20 K. At 25 °C they observed that crowding caused a 45 % increase in k _f and a very small 6 % decrease in k _u. To quantitatively rationalize these results, we carried out simulations to unfold cytochrome b₅₆₂, a four-helix bundle protein, by high temperature (Tjong and Zhou 2010). The order of melting of the helices in the simulations was consistent with previous experimental observations (Zhou et al. 2005), leading us to identify the transition-state ensemble as comprising conformations in which helices II, III, and IV-N are partially folded and helices I and IV-C are unfolded (Fig. 4a). The probabilities of individual residues in the helical state (Fig. 4b), calculated on the putative transition-state ensemble, correlated well with experimental Φ-values (Zhou et al. 2005), which measure the extent to which native interactions are formed in the transition state. Applying the postprocessing approach to these conformational ensembles of the folded state, transition state, and unfolded state generated in simulations without crowders, we calculated the effects of crowding on the activation energies for folding and unfolding (Fig. 4c). With a crowder size (20 Å) and volume fraction (15 %) approximating the experimental condition (PEG 20 K at 85 g/l), we found a decrease of 0.28k _B T in the folding activation energy and an increase of 0.08k _B T in the unfolding activation energy. Assuming that the prefactor A is unaffected by crowding, as can be justified according to the preceding section, we would predict a 32 % increase in k _f and a 8 % decrease in k _u, which is in good agreement with the experimental values.

Fig. 4.

The folding transition state of cytochrome b₅₆₂ and effects of crowding on its folding and unfolding activation energies, taken from Tjong and Zhou (2010). a Top The folded state, with helical segments color coded and labeled; bottom a representative conformation of the transition-state ensemble. b Comparison of the residue helical probabilities calculated on the transition-state ensemble with experimental Φ-values (Zhou et al. 2005). c Postprocessing results for the effects of crowding on the folding activation energy (curves labeled TS – U) and the unfolding activation energy (curves labeled TS – F). Results for three crowder radii are shown by the curves in different colors

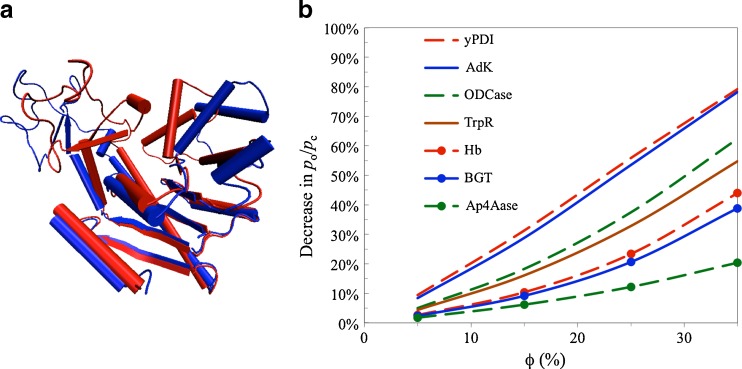
Expanding on our study of crowding effects on the HIV-1 protease dimer flap open equilibrium (Qin et al. 2010), we used the postprocessing approach to study how crowding affects the equilibria and transition rates between open and closed conformations of seven proteins, including adenylate kinase (Fig. 5a) (Dong et al. 2010). For each protein, explicit-solvent molecular dynamics simulations of the open and closed states were separately run, and snapshots were taken to calculate the transfer free energies (∆μ _o and ∆μ _c). In the presence of 15-Å crowders with a 35 % volume fraction, the open-to-closed probability ratio (p _o/p _c) decreased by 78 % for adenylate kinase. This prediction is consistent with a subsequent experimental study using TMAO as the crowding agent (Nagarajan et al. 2011). Among the seven proteins that we studied, the effects of crowding were reduced when the conformational difference between the open and closed state was less (Fig. 5b). We also calculated the effects of crowding on the potentials of mean force along the open-close reaction coordinate, which suggested that crowding could affect the conformational transition rates.

Fig. 5.

Effects of crowding on the conformational transition of seven proteins, taken from Dong et al. (2010). a Conformational difference between the open (blue) and closed (red) forms of adenylate kinase (Adk), one of the seven proteins studied. b Decreases in the open-to-closed probability ratios of the seven proteins by crowding. The crowder radius was 15 Å

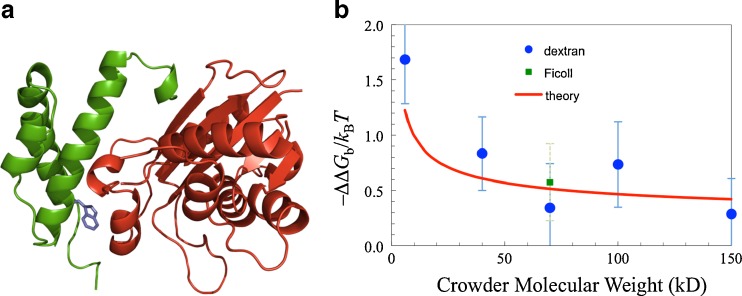
We carried out experiments to measure the effects of crowding on the binding affinity of the ε and θ subunits of Escherichia coli DNA polymerase III (Fig. 6a) (Batra et al. 2009a). Dextran of various molecular weights and Ficoll70 were used as crowding agents, and both were found to increase the binding affinity (Fig. 6b). At the same crowder concentration (100 g/l), the effect of dextran apparently tapered as the molecular weight increased. The experimental results were quantitatively rationalized when 100 g/l dextran with molecular weight W (in kDa) was modeled as crowder with a fixed 15 % volume fraction and radius given by 8.26W ^1/3 Å (Fig. 6b).

Fig. 6.

Effects of crowding on the binding affinity of the DNA polymerase III ε and θ subunits. a Structure of the ε-θ complex. ε and θ are given in red and green, respectively. A tryptophan introduced in the interface as a fluorescence probe is shown. b Experimental (symbols) and theoretical (curve) results for the effects of crowding on the binding free energy

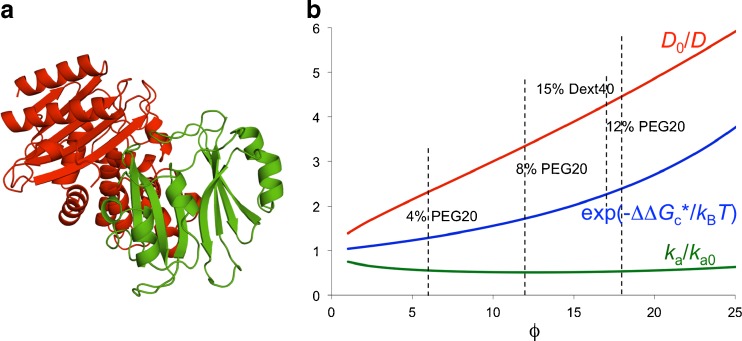
In a joint experimental-computational study with the Schreiber group, we recently determined the effects of PEG 20 K and dextran 40 K on the association rate constant of two proteins, TEM-1 and BLIP (Fig. 7a) (Phillip et al. 2012a). The association rate constant was essentially unaffected by 4, 8, and 12 % PEG 20 K or 15 % dextran 40 K. We rationalized this observation by our transient-complex theory extended for crowding (Fig. 7b). PEG 20 K at 4–12 % was estimated to slow down the relative diffusion of the two proteins by two- to fivefold. Modeling PEG 20 K as a 20-Å crowder with a volume fraction proportional to the weight fraction, we calculated the crowder-induced interaction energy, 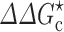, to be −0.3k _B T to −0.9k _B T, corresponding to a 1.3- to 2.4-fold rate enhancement. These two opposing factors together lead to the observed null effect of crowding (Fig. 7b). Similar results were obtained for 15 % dextran 40 K (Fig. 7b).

Fig. 7.

Effects of crowding on the association rate constant of TEM1 and BLIP, adapted from Phillip et al. (2012a). a Structure of the TEM1-BLIP complex. TEM1 and BLIP are given in red and green, respectively. b ϕ dependences of the relative translational diffusion constant (D), the effective interaction energy (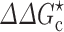), and the association rate constant (k _a), calculated for PEG 20 K. PEG 20 K was modeled as a polymer for D and as a 20-Å crowder for 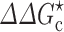; the correspondence between three PEG weight fractions and volume fractions is indicated by vertical lines. Dextran 40 K at 15 % results in a fourfold slowing down in relative diffusion and, when modeled as a 30-Å crowder, leads to a 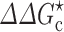that translates into a 2.3-fold rate enhancement

Conclusion

With the ability to represent proteins with atomistic details, we are now much closer in making quantitative predictions on the effects of crowding on the thermodynamics and kinetics of protein folding, conformational transition, and binding. To date, the crowders have only been modeled crudely, mostly as spherical particles with purely repulsive interactions. More sophisticated crowders, with residue-level details and compositions approaching those of bacterial cells, have become computationally feasible (Ando and Skolnick 2010; McGuffee and Elcock 2010; Mereghetti et al. 2010). Combined with the power of the postprocessing approach, we can start to predict, with some confidence, thermodynamic and kinetic properties under in vivo crowding conditions. Integrated with experimental studies (Ghaemmaghami and Oas 2001; Ignatova and Gierasch 2004; Ebbinghaus et al. 2010; Phillip et al. 2012b), we will soon be able to gain new insight into biochemical processes in cellular environments. It will be of particular interest to address questions such as whether protein sequences are tuned for folding or binding in particular cellular compartments.