Consequences of Common Data Analysis Inaccuracies in CNS Trauma Injury Basic Research

Abstract

The development of successful treatments for humans after traumatic brain or spinal cord injuries (TBI and SCI, respectively) requires animal research. This effort can be hampered when promising experimental results cannot be replicated because of incorrect data analysis procedures. To identify and hopefully avoid these errors in future studies, the articles in seven journals with the highest number of basic science central nervous system TBI and SCI animal research studies published in 2010 (N=125 articles) were reviewed for their data analysis procedures. After identifying the most common statistical errors, the implications of those findings were demonstrated by reanalyzing previously published data from our laboratories using the identified inappropriate statistical procedures, then comparing the two sets of results. Overall, 70% of the articles contained at least one type of inappropriate statistical procedure. The highest percentage involved incorrect post hoc t-tests (56.4%), followed by inappropriate parametric statistics (analysis of variance and t-test; 37.6%). Repeated Measures analysis was inappropriately missing in 52.0% of all articles and, among those with behavioral assessments, 58% were analyzed incorrectly. Reanalysis of our published data using the most common inappropriate statistical procedures resulted in a 14.1% average increase in significant effects compared to the original results. Specifically, an increase of 15.5% occurred with Independent t-tests and 11.1% after incorrect post hoc t-tests. Utilizing proper statistical procedures can allow more-definitive conclusions, facilitate replicability of research results, and enable more accurate translation of those results to the clinic.

Introduction

Much of the progress in the development of successful treatments after traumatic brain injury (TBI) and spinal cord injury (TBI and SCI, respectively) depends on a solid foundation of published, replicable research studies. Because this progress is built upon earlier studies, it can be slowed by the inability to replicate results reported previously. Although there are rigorous standards and guidelines for experimentation and publication in place, one potential reason for failures of replication is related to inaccuracies in the interpretation of reported experimental results and, in turn, the use of data analysis procedures that lack the rigor (i.e., statistical power) necessary to ensure confidence and replicability.

For many years, there has been much discussion over the lack of proper statistical procedures used in basic science medical journals.^1–6 These errors can lead to both overestimation of significant effects and inappropriate interpretations of reported experimental results, thus affecting the ability to produce similar results reported in previous publications.^4,6–9

Instructions to authors provide procedures for journal publication, which are primarily for consistency. There is little statistical guidance offered in the Instructions For Authors of most major journals.¹⁰ The peer review process and, ultimately, journal editors are responsible for assessing the merits of a study.^4,11,12 However, few reviewers or editors have the expertise to evaluate the rigor and statistical power of many statistical procedures.^14,15 In an effort by the American Physiological Society (APS) to improve statistical reporting in its basic life science journals, guidelines for reporting statistics were included in its instructions for authors.¹⁶ Regrettably, a follow-up study in 2007 revealed that the effort met with limited success and had been largely ineffective in correcting the problem.¹⁷

An awareness of the most common mistakes should help researchers avoid them. Application of rigorous analytic procedures will improve the overall quality of publications in TBI and SCI research and improve the accuracy and interpretability of the results. The first aim of this study was to explore the scope of statistical errors in SCI animal research and determine which errors occur most frequently. The second and primary aim of this study was to estimate the probable rate of “false positive” significant effects reported in the literature that the data analysis errors would produce. The present study describes the effects of data analysis choices by illustrating the effect of appropriately rigorous analysis on the number of significant differences in previously published data sets.

Methods

Journal article compilation

Journals with the highest number of basic science SCI animal studies in 2010 were identified after a database search of “spinal cord injury” for the year “2010.” The initial search resulted in seven journals with the highest number of articles, from 44 to 10 in the second to sixth journals; however, there were over 100 articles in the first journal. These were found to be mostly human studies, and thus a second search added “rats” or “mice” to the search parameter for this journal that resulted in a list (N=16) comparable to the other journals' listings.

Description of data analysis errors

Three general types of data analysis errors were tabulated (Table 1). (1) Parametric statistics: Parametric statistical procedures have assumptions for their use and are influenced by factors such as the distribution of the data, sample size, error distribution, and repeated observations.^18,19 (2) Post hoc t-tests: The inappropriate use or lack of post hoc t-tests can affect the number of significant differences obtained. Selection of a post hoc t-test depends upon factors such as the number of comparisons made and correlated observations while also taking into account experiment-wise or per-comparison error rates that can cause type I errors.^2,18,20,21 (3) Parametric versus nonparametric: Application of either type of procedure depends upon consideration of factors such as type of data (e.g., level of measurement), distribution of data (e.g., variability, amount of missing data) as well as sample size.¹⁹ Determining and tabulating the inappropriate use of this item was possible only in cases where detailed descriptions of the data were provided.^4,19

Table 1.

Three Categories of Data Analysis Errors Recorded from 125 Articles in Seven Major Journals with the Most CNS Trauma Injury Animal Research Articles Published in 2010

1	Incorrect parametric tests18
	-Independent t-tests rather than ANOVA
	-Independent t-tests performed without statement of type or correction, if necessary
	(i.e., means with = or ≠variance using the F test for = or ≠variance)
	-Excessive number of Independent t-tests without correction to p-value for performing multiple test comparisons
	-One-way ANOVA rather than Repeated Measures ANOVA with the group factor
	-Multiple one-way ANOVAs rather than two-way ANOVAs (with test for interaction)6
2	Inappropriate or lack of post hoc t-tests after ANOVA
	-Lack of control of error rate in multiple comparisons in instances of very large numbers of comparisons (e.g., Duncan, Student-Newman-Keuls)20,21
	-Dunnett versus non control group; Dunn's post hoc t-test used with three comparisons
3	Parametric versus nonparametric tests19
	-e.g., Independent t-tests rather than a nonparametric t-test (small range category data)

For each article, an error was counted if the improper procedure was observed or, in the case of multiple instances, when a type of mistake occurred a majority of the time in the article. The number of errors across all articles and by error type was tabulated. Overall error rate was calculated as the total number of errors observed divided by the total number of possible occurrences (i.e., number of articles×3 error types).

Consequences of inappropriate data analysis after reanalysis

To determine the effects of the incorrect data analysis procedures observed in the literature survey, it would be necessary to reanalyze the data correctly and compare differences in the results. This is not possible without access to the raw data. Therefore, to directly compare the change in the number of significant effects and demonstrate the consequences that occur from correct and incorrect analyses, the raw data from a variety of published data (large and small, independent and paired, and so forth) from our laboratories was reanalyzed using the most frequently observed incorrect statistical procedures found (Figs. 1 and 2A) and compared to the original results.

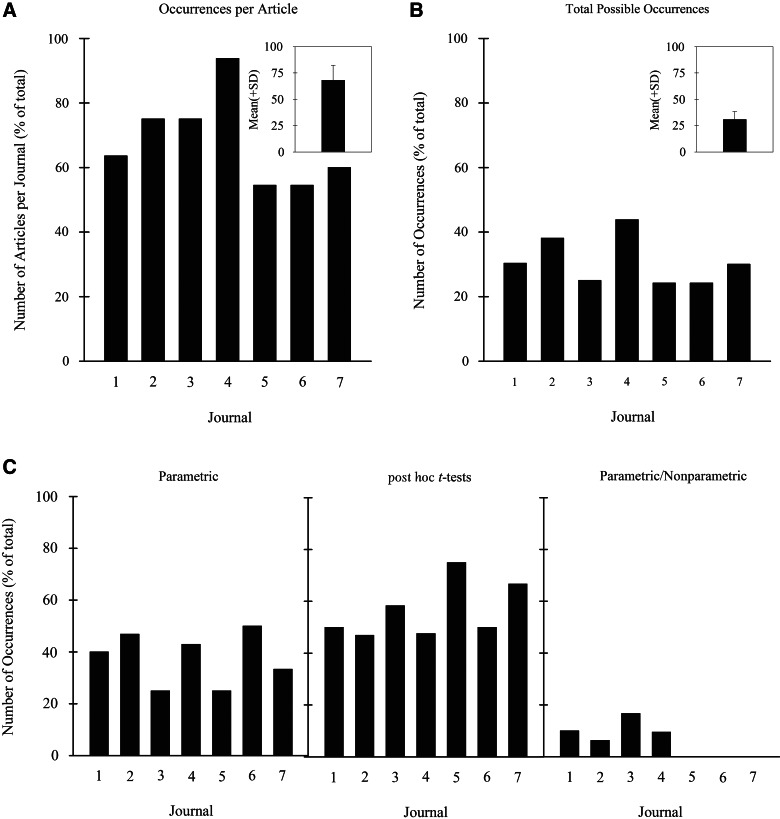
FIG. 1.

Number of occurrences of misapplied statistical procedures observed in the journals is shown for each journal as a percentage of (A) the total number of articles per journal, (B) the three types of statistical procedures, and (C) the total possible number of occurrences. Insets of (A) and (C) equal the average (plus SD) across all the journals. Journals are listed from highest number of articles to lowest.

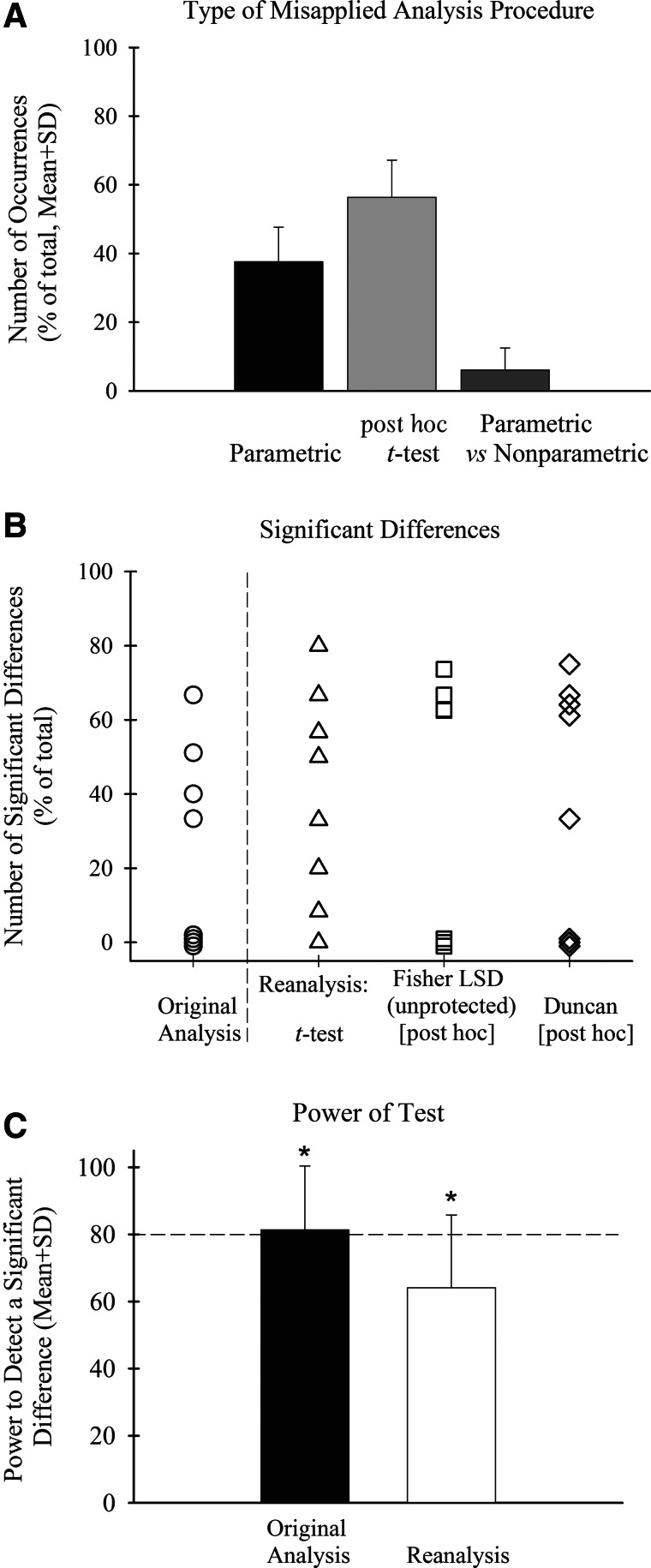
FIG. 2.

Average percentage (plus SD) of misapplied statistical procedures observed in the journals is shown in (A) for each of the three types of statistics. Graph (B) shows a scatter plot of the percentages of significant differences obtained in the original data sets before reanalyses, compared to after reanalysis with Independent t-tests and Fisher's LSD (unprotected) and Duncan's post hoc t-tests. In (C), the results of power analyses to calculate the power associated with the significant differences between the means in the original data sets before reanalysis, compared to after reanalysis, is shown. The dotted line at 80% shows that the power of the original analysis is >80%, which is the probability of correctly rejecting the null hypothesis.

The reanalyzed data were comprised of 31 variables in 11 data sets (Table 2C) from six published articles (see Table 2D for list of references). As can be seen in Table 2, these studies encompassed a wide variety of experimental designs, injury/surgery models, injury severities, spinal cord level (Table 2A), sample size, number of outcome measures (Table 2B), and type of analysis (Table 2C) used in the studies, thus enabling a large number of possible comparisons. In addition to comparing the differences in the number of significant effects, the changes in the number of significant differences were compared also by type of analysis procedure and type of data analyzed. Binomial Proportion tests were used to compare the percentage of data sets with significant differences after reanalysis compared to original results.^18,19 Power analyses were calculated for significant mean comparisons in the original studies and compared with the power of those obtained after reanalysis using an Independent t-test for means with equal variance.²² Data were analyzed using the statistical software package, IBM SPSS Version 19 (IBM Corporation, Armonk, NY).

Table 2.

Variables in Data Sets of Six Published Studies

A
Injury/surgery types	Contusion (4)	Laceration (1)	Injections (1)	Skin incision (1)
Model	NYU (2) (contusion)	LISA (1) (contusion)	Impactor (1)a (contusion)	Glass micropipette (injections)
Level	C7-8 (1)	T9(5); T13 (1)	L1-L2 (1); L3-L4 (1); L5-L6 (1)
Severity	Sham (4–5)	Mild (3)	Mild-Moderate (4)	Moderate (2)
Rodent	Rat (6)	Mice (1)	Rat = Sprague-Dawley	Mice = C57 BL/6

B
Data set outcome measures	Group types	Samples size (n)
Spinal cord counts: (cord sections/genes/cell sizes/markers)	Independent groups, multiple time points (1)	6
	Independent groups (3)	4–12
5 behavior/gait kinematics	Independent groups, multiple time points (1)	9–15
6 behavior/gait kinematics	RM: Speed: multiple time points (1)	9–15
8 behavior (motor/sensory) assessmts	Independent groups (2)	3–4
6 cord imaging measures	Independent groups (1)	3–4
Morphology (spared WM)	Independent groups (1)	3–4

C
Data sets	Original type of analysis	Total possible comparisons in reanalysis
1–6	Repeated measures with a group factor	5 (2), 72 (2), 120 (2)
7–11	Independent groupings	3, 5, 6 (2), 78 (2)

D

^aAn original device.

Beare, J., Morehouse, J.M., DeVries, W., Enzmann, G., Burke, D.A., Magnuson, D.S.K.M., and Whittemore, S.R. (2009). Gait analysis in normal and spinal contused mice using the treadscan system. J Neurotrauma 26, 1–12.

Hill, C.E., Harrison, B.J., Rau, K.K., Hougland, M.T., Bunge, M.B., Mendell, L.M., and Petruska, J.C. (2010). Skin incision induces expression of axonal regeneration-ralated genes in adult rat spinal sensory neurons. J. Pain 11, 1066–1073.

Kim, J.H., Song, S-K., Burke, D.A., and Magnuson, D.S.K. (2010). Comprehensive locomotor outcomes correlate to hyperacute diffusion tensor measures after spinal cord injury in the adult rat. Exp. Neurol. 235, 188–196.

Mozer, A.B., Whittemore, S.R., and Benton, R.L. (2010). Spinal microvascular expression of PV-1 is associated with inflammation, perivascular astrocyte loss, and diminished EC glucose transport potential in acute SCI. Curr. Neurovasc. Res. 7, 238–250.

Saraswat, S., Maddie, M.A., Zhang, Y., Shields, C.B., Hetman, M., and Whittemore, S.R. (2011). Deletion of the pro-apoptotic endoplasmic reticulum stress response effector CHOP does not result in improved locomotor function after severe contusive spinal cord injury. J. Neurotrauma 28, 1–10.

Smith, R., Brown, E., Shum-Siu, A., Whelan, A., Burke, D.A., Benton, R., and Magnuson, D.S.K. (2009). Swim training initiated acutely after spinal cord injury is ineffective and Induces extravasation in and around the epicenter. J. Neurotrauma 26, 1–11.

The summary above lists (A) the surgery/injury and animal details of the six published studies (D) used for reanalysis, (B) details of the type of data reanalyzed, type of groupings compared and sample sizes, and (C) the original type of data analysis performed in the 11 data sets from the six studies with the number of total possible comparisons in the reanalysis. The number of studies involved in the description is shown in parentheses.

Results

Review of 2010 journal articles

A search of journals with the highest number of basic science animal central nervous system (CNS) trauma injury articles (listed in alphabetical order: Brain Research, Experimental Neurology, Journal of Neurochemistry, Journal of Neurology, Journal of Neurotrauma, Neuroscience, and Spinal Cord) resulted in seven journals that contained a total of 142 articles (range: from a high of 44 to a low of 10 articles per journal). Articles were excluded (n=17) if they were not basic science research (i.e., animal care, epidemiological, human, or review) or included coauthors of the present article, yielding a sample of 125 articles (range: maximum of 33 to a low of 10 per journal). Rodents were used in 97.6% of the studies (rat, 74.4%; mice, 23.3%).

Overall, 69.6% (87 of 125) of the articles contained one or more types of data analysis inaccuracies, averaging 68.1% (standard deviation [SD], 14.2%) across all journals (Fig. 1A, inset). The percentage of total possible errors per journal (number of articles×3 types) ranged from 24.2 to 43.8% (overall percentage, 120/375=32.0%; Fig. 1B).

Type of data analysis errors

Of the three general types of errors examined, parametric analysis, post hoc t-test, and parametric versus nonparametric, the first two accounted for 94% of the occurrences. Of these two error types, the higher percentage was associated with inappropriate or lack of post hoc t-tests performed (56.4%; SD, 10.8) and ranged from nearly 50% (SD, 10.8%) to a high of 75% (Figs. 1C [middle] and 2A). The second higher percentage, inappropriate parametric statistics errors, ranged from 25 to 50% (mean, 37.6%; SD, 10.1%; Figs. 1C [left] and 2A). The number of occurrences tabulated for incorrect usage of parametric versus nonparametric statistical analyses was low, representing 6.1% (SD, 6.4%) of the articles (Figs. 1C [right] and 2A). Note that in three of the seven journals, no parametric versus nonparametric errors were recorded. This percentage is greatly underestimated because of the lack of access to some of the details about the raw data needed to determine the appropriateness of using parametric versus nonparametric analyses.

Unexpectedly, the majority of parametric statistical analysis errors were not from the overuse of Independent (Student's) t-tests rather than analysis of variance (ANOVA) but, instead, from the use of one- or two-way ANOVA instead of repeated-measures ANOVA (52.0%; SD, 20.6). Because this result has major implications for functional improvement studies after injury that often include behavioral assessment outcome measures over time (i.e., repeated measures), a more detailed examination of the repeated-measures inaccuracies was undertaken.

Repeated measures

The percentage of articles incorporating a Repeated Measures design equaled 52.0% (SD, 20.6). Among these articles, behavioral assessments (such as in SCI, locomotor: e.g., the Basso, Beattie, Bresnahan Locomotor Rating Scale, the Basso Mouse Scale; sensorimotor: e.g., grid, horizontal ladder, catwalk, kinematics; allodynia [pain] and tactile assessments) represented 71.1% (SD, 17.7) of these studies. Remarkably, 57.7% of behavioral assessment testing over time was not analyzed appropriately using repeated-measures ANOVA procedures. This was observed very frequently in four journals (50, 80, 82, and 100%) and less often in the remaining three (26, 29, and 38%), revealing a bimodal distribution for this occurrence among journals.

Journal instructions for authors

The content in the Instructions For Authors of these seven journals was examined for information pertaining to directions on statistical content and reporting data analysis results.¹⁰ Three journals' instructions included more specific information regarding statistics: One contained a statement to include a statistics subsection, a second included two sentences giving instructions to analyze using “statistical analysis of variance” and to present a measure of variance of SD or standard error, and the third listed four source references for the Guidelines for Reporting Statistics. Instructions in two journals simply stated the results should be reported in a “clear and concise” manner; one instructed authors to report the “findings” and two had no statement about statistics at all.

Reanalysis of previously published data

The data used in the reanalysis represented a wide variety of experimental designs, sample sizes, surgery/injury models, and severities at multiple spinal cord levels using both rats and mice with numerous outcome measures and types of analysis (Table 2). Half of the studies included a Repeated Measures experimental design (Table 2C), matching results in the evaluated literature showing 52% of the journal articles had included this type of experimental design. To achieve results that would be representative of the greatest number of study parameters possible, all reanalyses included as many data sets as possible.

As previously stated, the highest percentage of data analysis errors (56%) was the result of the use of inappropriate or lack of post hoc t-tests. This was followed by a high percentage of incorrect parametric analyses that was observed in nearly 40% of the studies. The published data sets were reanalyzed in the following manner: Five data sets were reanalyzed using one-way ANOVA, followed by the two most often observed incorrect post hoc t-tests, Fisher's least significant difference (LSD; unprotected) and Duncan's tests (data not shown).^18,20,21 The number of significant differences after reanalysis was compared to the number of significant differences in the original analysis. In addition, groups in eight data sets were reanalyzed using Independent t-tests (for means with equal or unequal variance) and compared to the original results. One data set contained a repeated factor with two levels that was analyzed using paired t-tests. For some data sets, it was possible to analyze the data using both one-way ANOVA and t-test procedures.

The original percentage of comparisons with significant differences in the 11 data sets equaled 27.3% (SD, 28.0) overall and ranged from 0 to 67%. A scatter plot of all of the individual results from the original and reanalysis of each data set are shown in Figure 2B. All 18 reanalyses of the 11 data sets (eight t-tests and five one-way ANOVA analyses each using either Fisher's LSD or Duncan's post hoc t-tests) resulted in either no change (2/18=11.1%) or an increase (16/18=88.9%) in the number of significant differences (z=12.0, p<.001, Binomial Proportion test on 16/18 [versus the null hypothesis of no change expected]), compared to the original analysis results. Importantly, there were no instances of fewer significant differences using the incorrect procedures. The number of significant differences equaled 39.1%, compared to the original analyses average of 27.3%, representing an increase of 11.8%. The results of reanalysis using Independent t-tests on eight data sets resulted in a significantly higher percentage of significant differences, increasing from 23.7 to 39.5% (paired t-test, p<.001). This represented an increase of 15.5%. After analyzing the five data sets using one-way ANOVA followed by both Fisher's LSD and Duncan's post hoc t-tests, the percentage of comparisons with significant differences was greatly increased to 60.0% using Duncan's test (SD, 15.8%) and nearly 70% higher using Fisher's LSD test (66.4%; SD, 4.5%), compared to 51.1% in the original analysis of these five data sets. Overall, these analyses (ANOVA and t-test) resulted in a significantly higher number of significant effects in the data sets, compared to the original analyses (t-tests=6/8; z=4.9; p<.001, Binomial Proportion test versus expected proportion of no change; post hoc t-test methods=7/10: 4/5+3/5; z=4.8; p<.001, Binomial Proportion test versus expected proportion of no change).

Injury severity group and behavior outcome measures

Two of the studies used in the reanalysis contained very large data sets. The composition of these two data sets offered a unique opportunity to examine the conditions under which the changes in the number of significant differences occurred in relation to (1) severity of SCI and (2) behavior versus nonbehavior physiological measures. Both large data sets were used to examine, in greater detail, whether the increase in the number of significant differences that resulted when using Fisher's LSD and Duncan's post hoc t-test comparisons had occurred at the same rate for the different injury severity groups compared to the original data analysis results. The second data set offered the ability to examine whether the increase in the number of significant comparisons was the same for both behavior and nonbehavioral outcome measures.

Reanalysis of the injury groups (sham, mild, and moderate) in the first data set using Fisher's LSD post hoc t-tests resulted in an increase in the number of significant differences when the mild injury group was compared to the other injured and sham groups (8.3–12.5%), whereas comparisons to the moderate group resulted in a 4–8% decrease in the number of significant differences. In the second data set, injury group (very mild, mild, mild/moderate, and moderate) mild-injured group comparisons resulted in a 13–27% increase in the number of significant differences, but only 13% in moderate injury group comparisons, compared to original analyses. Comparisons among the injury groups' behavior outcome measures in the second data set revealed large increases in the number of significant effects, especially in the mild injury group (12.5–37.5%). Conversely, in general, the nonbehavior physiological measures showed a small increase in the percentage of significant differences (14.3%).

In sum, both large data sets showed changes in the number of significant differences among the SCI groups using Fisher's LSD and Duncan's post hoc t-tests, compared to the original data analysis results. Increases in the number of significant differences occurred among all injury severity groups, but predominantly in the mild injured groups. Further, results showed that these increased effects occurred at a significantly higher rate in the behavior assessment outcome measures.

Effects on results and conclusions

Some of the increased number of significant effects from the reanalysis of the previously published articles from our laboratories (Table 2D) would have influenced some of the conclusions stated in those articles. For example, conclusions in an article that examined the kinematics of treadmill walking gait characteristics in SCI mice (Beare et al., 2009) discussed the differences between the sham and mild injured groups' measures associated with stride and balance that are important in locomotor recovery (swing phase, rear track width, and toe spread). In this study, before reanalysis, only a few measures revealed differences in gait characteristics between the mild and moderate injury groups. After reanalysis, however, these data analysis procedures led to a 50% increase in the number of significant differences between them. These effects occurred primarily in the faster treadmill speed where there was a reduced sample size because fewer animals were able to perform the task. Thus, the change in results (i.e., more-significant differences) occurred because of the less-restrictive statistical test with a smaller sample size.

Results that are based on considerably smaller sample sizes reduce the power of a test and its reproducibility. For purposes of illustration, power analyses using Independent t-tests were performed on the additional mean pairs that were significant. These results revealed a power of 60.2 and 34.4%, on average, for comparisons at the slower and faster walking speeds, respectively, compared to the power associated with the original reported mean differences that equaled 72.1 and 72.2% for the two speeds, respectively. The conclusions by the authors based on the low-power significant differences likely would have led to expanding their discussion regarding the mild and moderate injury groups and overemphasizing the differences in their walking abilities.

Reanalysis of injury groups' physiological cord measures in another study using diffusion tensor magnetic resonance imaging (DTi) (Kim et al., 2011) resulted in a greater number of significant differences among the groups using the less rigorous data analysis procedures (33.3 versus 42.9%). These effects included the outer and total ventral cord DTi measures that were previously not different among the injury groups in the original article's results. Had these results been significant in the original article, they would have corresponded with the spared white matter outcome measure in their article. Because the motor pathways associated with locomotor recovery are primarily located in the ventral part of the spinal cord, this would have added additional support to the authors' conclusions associated with recovery of spinal tract pathways. This result appears to reveal greater sensitivity of the DTi measures to detect physiological cord measure differences between groups with milder injuries. However, a power analysis examining the power associated with these tests to detect the significant difference between the groups resulted in a power of only 46.3 and 47.5%, respectively. In addition, the effect of reanalysis on the behavioral measures in this study resulted in an even greater increase in the number of significant differences (six more), from 37.5 to 62.5%. The results likely would have altered the conclusions in their discussion regarding the Louisville Swim Scale (LSS) swim and horizontal ladder walking score comparisons among the injury groups. A power analysis on this data revealed a power of 74.2 and 62.3% for the LSS and ladder scores, respectively. The increases in significant differences after the reanalysis that resulted with sample sizes of 3–4 per group in this study and the low power of the reanalyzed mean comparisons in both pairs of power analyses exemplify the need for caution in conclusions made from small sample sizes using less rigorous statistical procedures in both physiological and behavioral measures. Overall, the power of all of the added significant differences of the reanalysis means averaged 68.1% compared to 83.2% for the original mean differences reported in the study.

Another study preceding reanalysis showed significant effects of increased extravasation near the SCI epicenter at 4 mm rostral and caudal to the epicenter after only 8 min of swim training, but not at 6 or 8 mm rostral and caudal (Smith et al., 2009). Based on the more-limited spread of extravasation near the SCI epicenter, the authors suggest that rehabilitative efforts may be compromised because of increased negative effects from secondary injury. After reanalysis, the more distant rostral and caudal locations, relative to the epicenter, also were now significant (6 mm rostral and caudal), a result that would have suggested there was a greater extent of extravasation from the epicenter and thus indicative of greater negative effects from secondary injury. The effect of these added results may have led the authors to make a considerably stronger statement regarding postponement of rehabilitative efforts after injury in humans to minimize secondary injury effects, based on the more widespread effects of extravasation, and would represent a huge effect on the rehabilitation of SCI patients postinjury. However, the power associated with the two additional mean comparisons averaged 75.7%, which is considerably lower than the original significant differences with power values averaging 96.0%.

One data set examined in a fourth study found one additional significant effect after reanalysis of six mean comparisons, and there were no additional significant differences in the remaining two articles that contained small data sets with few group comparisons. Overall, the additional significant effects that were obtained using the reanalysis procedures had a significantly lower average power of 64.1%, compared to the power associated with the originally reported mean comparisons with significant differences that averaged 81.4% (Independent t-test between means with equal variances, p<.005; Fig. 2C).

Discussion

The ability to replicate and build upon previous research is essential for developing successful treatments for TBI and SCI. The lack of rigorous data analysis procedures in some CNS TBI and SCI animal research articles, as illustrated here, potentially could slow that progress.

Results revealed a high occurrence of the types of statistical analysis procedures that result in an overestimation of significant effects compared to the use of more rigorous statistical procedures. These occurrences were observed in 70% of articles, supporting the assertion that this is a growing trend in the medical field.^{1,2,4,6,7,14,23}

The probable error rate was estimated by reanalyzing data from previously published studies. Care was taken in the reanalysis portion of this study to include as many data sets as possible to maximize representation of a wide variety of parameters, such as size (number of variables), surgery/injury, SCI level and severity, type of data (independent, repeated), animal (rodent), and type of outcome measures. Because these data sets comprised a wide variety of variables, it is reasonable to assume the results can be used to approximate the probable degree of error associated with different data analysis procedures and that the injury group and behavioral results can be used to extrapolate effects to current published literature in this field. After reanalysis, it was found that misapplication of the most frequently observed procedures resulted in an overestimation of significant effects averaging approximately 14% and occurred in nearly every reanalysis procedure (16/18=89%), suggesting that these results are likely to be independent of study-type parameters and that successful replication of promising components of these studies would be unlikely.

Based on the reanalysis, the overestimation of significant effects from use of the two most commonly observed post hoc t-tests, Fisher's LSD (uncorrected) and Duncan's tests, increased the number of significant differences by 9 and 15%, respectively. Overestimation of significant effects also results from the use of Independent t-tests, compared to ANOVA procedures. The reanalysis revealed a 16% increase in the number of significant differences from using Independent t-tests. It is already well established that overuse of Independent t-tests can increase the likelihood of Type I errors, resulting in a greater number of significant differences than are actually true.^{6,18,20,21,24} Taken together, these results strongly support efforts to increase the use of more rigorous statistical procedures and appropriate t-tests and post hoc t-test comparisons.^{2,6,14,20,21,25}

Specifically, post hoc t-tests, such as Fisher's LSD, Duncan's multiple-range, and Student Newman-Keuls' tests, are prone to inflating Type I error rates when multiple comparisons are made and are most suited only to a limited number of mean comparisons.^2,18,20,21 However, post hoc t-tests associated with Bonferroni, Tukey and Šidák (e.g., Bonferroni's and Šidák's inequality tests, Tukey's Honestly Significant Difference (HSD), and Tukey-Kramer's test) control the Type I error rate well in multiple comparison tests, but are more conservative and can result in “overcorrection,” leading to missed occurrences of true significant differences.^2,21,25 Dunnett's procedure also controls the Type I error rate, but only when properly used to compare against control means.²⁰ Because it is likely that no single post hoc t-test will be applicable in all experimental situations, alternates have been proposed (e.g., such as Holm's step-down procedure based on Bonferroni's and Šidák's inequality tests and the false error rate procedure) to control the Type I error rate and, in some cases, lessen the conservative disadvantage that sometimes occurs in these latter methods.^21,25,26

The present study increases awareness that the lack of rigorous statistical procedures might have widespread effects in experimental studies because effects were observed in mild SCI groups, in both rats and mice with many behavior function outcome measures and comparisons among injury severity groups, the error rate of the latter reaching nearly 40% (data not shown). Further, results of the reanalysis showing a pronounced effect on behavior outcome measures, compared to nonbehavioral measures, are of great concern for SCI research studies, because a recent trend in the field to use a multi-outcome assessment approach to explore significant improvements in function after SCI has been increasingly advocated.^27–29

An important component of evaluating reported experimental results is the ability to recognize misapplication of data analysis that can potentially result in misleading interpretation of results and a subsequent failure to replicate similar findings.^30,31 Though it is true that reporting, formatting, or display errors do not change the outcome of study results, misleading and inaccurate reporting can greatly influence the perception of the results, exaggerate the true merits of the study,^4,9,10 lead investigators in the wrong direction,^7,31,32 and bias future research based upon it, all contributing to the problems of nonreplication.^{1,3,7–9,23,31,32} One example is the current predominance of reporting small sample sizes with the population statistic (appropriate for N>20) of standard error of the mean, rather than the proper sample measure, the SD. This practice makes the results of the outcome measure appear to have greater consistency within and between samples, which is not present,^1,2,4,7,8,15 leading to overemphasized results from studies with small sample sizes^7,8,15 and increasing the chances of results that are difficult to replicate. As clearly demonstrated by the preponderance of low values obtained in the power analysis on the reanalyzed means with significant differences, some of which had a lower sample size, caution should be used in evaluating results based on less rigorous statistical analysis procedures.

Potential solutions

There are instructions for authors in the Guidelines for Reporting Statistics, as published by the APS.^16,17 The use of statistics reviewers in the peer review process has been suggested to advise reviewers who need assistance with statistical analysis procedures reported in submitted manuscripts.¹¹ They also could assist editors before acceptance,^14–17,23 a practice reported to be instituted for the British Journal of Medicine already.^5,24

Additionally, an important, but often overlooked and underrated, contributing factor to the high percentage of inappropriate statistical procedures performed is the increased availability of desktop and on-line statistical programs. Many of these programs contain only limited, basic statistical procedures, do not teach statistics and are used improperly by investigators who lack expertise, and, often, do not report in the Methods section the statistical program and methods used.^2,4,7,31 A model for reaching biomedical researchers to teach and illustrate sound experimental practices is underway through simultaneous publication of a series of articles in six journals (see Appendix) in an effort designed to improve statistical practices and data presentation in medical journals.^5,23,33

Progress in developing treatments to improve function after injury is an important component of TBI and SCI animal research, but can be achieved only by building upon previous research, which relies on the ability to successfully replicate these findings. A more rigorous approach to statistical data analysis and a more critical evaluation of studies will minimize the potential for misinterpretation of experimental results caused by misapplication of data analysis procedures and programs and help ensure the continuation of promising lines of investigation in the field of CNS trauma research.

Appendix

List of the six journals offering simultaneous publication of series of articles

The Journal of Physiology, Experimental Physiology, The British Journal of Pharmacology, Advances in Physiology Education, Clinical and Experimental Pharmacology and Physiology, and Microcirculation

Additional sources for data and results presentation

In addition to references 4 (Drummond and Tom, 2011), 9 (Doherty and Anderson, 2009), and 1 (Curran-Everett et al., 1998) [Review]:

Ludbrook, J. (2007). Writing intelligible English prose for biomedical journals. Clin. Exp. Pharmacol. Physiol. 34, 508–514.

Ludbrook, J. (2008). Outlying observations and missing values: how should they be handled? Clin. Exp. Pharmacol. Physiol. 35, 670–678.

Additional sources for reviewing manuscripts

In addition to references 11 (Ludbrook, 2003), 12 (Berger, 2006), 13 (Kurusz, 2010), and 15 (Morton, 2009):

Provenzale, J.M., and Stanley, R.J. (2006). A systematic guide to reviewing a manuscript. J. Nucl. Med. Technol. 34, 92–99.

Benos, D.J., Kirk, K.L, and Hall, J.E. (2003). How to review a paper. Adv. Physiol. Educ. 27, 47–52.

Lepak, D. (2009). Editor's comments: what is good reviewing? Acad. Manage. Rev. 34, 375–381.

Acknowledgments

This work was supported by grants from COBRE and GMS (NIH1P30 RR031159-01A1 and GM-8P30GM103507-02; to S.R.W., D.S.K.M., and D.A.B.) and Kentucky Spinal Cord and Head Injury Research Trust (8-7A; to D.S.K.M.).

Author Disclosure Statement

No competing financial interests exist.