Ca²⁺ waves in the heart

Abstract

Ca²⁺ waves were probably first observed in the early 1940s. Since then Ca²⁺ waves have captured the attention of an eclectic mixture of mathematicians, neuroscientists, muscle physiologists, developmental biologists, and clinical cardiologists. This review discusses the current state of mathematical models of Ca²⁺ waves, the normal physiological functions Ca²⁺ waves might serve in cardiac cells, as well as how the spatial arrangement of Ca²⁺ release channels shape Ca²⁺ waves, and we introduce the idea of Ca²⁺ phase waves that might provide a useful framework for understanding triggered arrhythmias. This article is part of a Special Issue entitled ‘Calcium Signaling in Heart’.

1. Introduction

In a charming recollection of his life’s work Natori [1] writes that in 1940s and 50s he and his colleagues observed propagating contractions in skeletal muscle fibers following cessation of repetitive electrical stimulation or application of caffeine. Although at that time Natori did not know their origin, these propagating contractions bore the hallmarks of what we now recognize to be propagating Ca²⁺ waves: they propagated with a velocity of about 30–100 μm/s, they propagated without decrement, they annihilated each other upon collision, and they could be initiated with caffeine. These observations by Natori were perhaps the first, albeit indirect, evidence of Ca²⁺ waves.

In 1970 Ford and Podolsky [2] and Endo et al. [3] discovered, in skeletal muscle, the basic mechanism underlying the generation of Ca²⁺ waves: the regenerative release of Ca²⁺ by the sarcoplasmic reticulum (SR) or Ca²⁺-induced Ca²⁺ release (CICR). Indeed, Endo et al. had observed, similar to Natori, regions of highly shortened sarcomeres that moved slowly from one end of the fiber to the other, which they explained would arise from CICR.

Fabiato [4] just two years later extended the domain of Ca²⁺ waves to single isolated ventricular myocytes. He observed contracted regions that could propagate 20–50 μm within a cell at a velocity of 50–100 μm/s. Based on a series of elegant experiments Fabiato concluded that these regions of propagating contraction reflected an underlying wave of regenerative Ca²⁺ release.

In these early works local sarcomeric contractions served as the Ca²⁺ “indicator”. The advent of exogenous Ca²⁺ indicators such as aequorin enabled direct visualization of Ca²⁺ waves in non-muscle cells such as the fish egg [5] when activated by sperm or local application of a high concentration of Ca²⁺. Gilkey et al. [6] show dramatic images of a ring of aequorin luminescence traversing a spherical egg.

The development of second generation fluorescent indicators with high quantum yield [7] and conjugated to an acetoxymethyl ester, which allowed loading of cells simply by incubation, revolutionized the study of Ca²⁺ dynamics. The first visualization of Ca²⁺ waves in the isolated ventricular myocyte using the newly developed fluorescent indicator (fura-2) was carried out in 1987 by Wier et al. [8].

2. Current state of mathematical models of Ca²⁺ waves

Endo et al. in 1970 had explained the formation and propagation of Ca²⁺ waves in terms of CICR. This classical explanation remains at the core of current understanding of Ca²⁺ waves and all mathematical models of Ca²⁺ waves include CICR. The first mathematical model of Ca²⁺ waves by Backx et al. [9] assumed that Ca²⁺ release occurred continuously in space. Although Backx et al. could not have known it at that time (1989), this assumption was fundamentally wrong. In his seminal 1992 paper [10], Stern resolved the longstanding paradox of graded Ca²⁺ release in the face of CICR by positing that Ca²⁺ release did not occur continuously in space but rather only at discrete sites that were spatially separated from each other. In the following year Cheng et al. [11] published their remarkable discovery of Ca²⁺ sparks, which provided striking experimental support for Stern’s hypothesis that Ca²⁺ release occurs at discrete sites. Confocal imaging [12–17] of fluorescently labeled antibodies to ryanodine receptors (RyRs, the Ca²⁺ release channel of the SR) and electron microscopy [18] provided the structural underpinnings for Stern’s local control hypothesis. These studies showed that the RyRs occurred in discrete clusters arranged in a fairly regular lattice (Fig. 1). The cluster of RyRs forms a Ca²⁺ release unit (CRU, see [18,19]) contains ~70 [14,15] to about 250 [15,18] RyR molecules although the latest estimate based on super-resolution microscopy has put the number to be about 14 [17]. The number of RyRs in a cluster is important because it determines the maximum Ca²⁺ flux, which is an important determinant of whether Ca²⁺ waves can form and propagate.

Fig. 1.

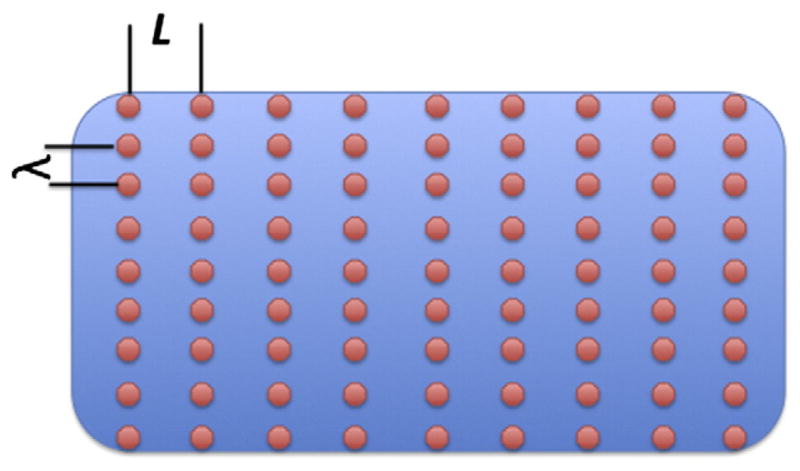
Schematic of CRUs in myocytes. The CRUs are aligned on the z-disk spaced L≈2μm apart. λ is the nearest neighbor distance between CRUs in the plane of the z-disk. λ ranges between ~0.4 and ~1 μm ([14,15,17]).

Most mathematical models for Ca²⁺ waves now assume that CRUs are spatially discrete and all models are of the fire–diffuse–fire type. In fire–diffuse–fire models, Ca²⁺ released from one CRU diffuses to a neighboring CRU triggering regenerative SR Ca²⁺ release. Ca²⁺ wave models differ in the number of dimensions (1-dimensional (1-d), [9,20,21]; 2-d, [22–24]; 3-d, [16,25]; whether release is deterministic [20,21,24,26,27] or stochastic [16,22,25,28]; and whether SR Ca²⁺ concentration is explicitly included in the model [21,29–31] or not [16,22,24,25,28].

Keizer et al. [20,26] developed the first mathematical model of Ca²⁺ waves based on discrete Ca²⁺ release sites. This was a simple 1-d, deterministic, linear diffusion model. In this model a fixed amount of Ca²⁺ was released from one CRU and the adjacent CRU fired if and when the ambient cytoplasmic Ca²⁺concentration ([Ca]_i) exceeded some threshold. Because of its simplicity, the model revealed the factors essential for wave propagation on lattices: the amount of Ca²⁺ released, the threshold or sensitivity of Ca²⁺ release, and the lattice spacing. Later models have underscored the importance of these factors [22,24,25,28].

We later developed the first stochastic model of Ca²⁺ sparks and waves where the probability of a spark occurring depended on the local [Ca]_i [22]. In this 2-d model the CRUs were asymmetrically distributed (2 μm along the longitudinal axis of the myocyte and 0.4 or 0.8 μm along the transverse axis) to match ultrastructural (see references above) and spark data [32]. At the time we undertook this project it seemed like a straightforward modeling problem to generate realistic Ca²⁺ waves from realistic stochastically occurring sparks based on realistic spacing of CRUs. It turned out that our model could satisfy most but not all experimental constraints. So far, no model we know satisfies all known experimental constraints.

Here are the challenges in developing models for Ca²⁺ waves. First, the sensitivity of RyRs to Ca²⁺ appears to be low; estimates range from 15 to 100 μM [33,34]. This means that as a Ca²⁺ wave propagates in the longitudinal direction, [Ca]_i must reach more than about 10 μM in order for the CRUs to have a high probability of firing and thus sustaining the wave propagation. However, this high Ca²⁺ concentration is incompatible with the ~1 μM concentration measured during a wave [35,36].

Second, if the RyR Ca²⁺ sensitivity was assumed to be ~1 μM then models could generate Ca²⁺ waves that raise [Ca]_i to only ~1 μM. However, these models would need to be deterministic and could not use stochastic models of sparks because when the RyR sensitivity is so high, the models become stochastically unstable. That is, such high sensitivity leads to a very high frequency of sparks and the initiation of so many Ca²⁺ waves (like raindrops on a pond) that no well-defined traveling wave can be observed [22,24].

Keller et al. [37] have proposed a “wave front sensitization” mechanism that allows Ca²⁺ waves to propagate with ~1 μM amplitude while still maintaining low Ca²⁺ release sensitivity of the CRUs. Their idea depends on the strong effect of an increased luminal SR Ca²⁺ content has on increasing the sensitivity of Ca²⁺ release [38–44]. Shannon et al. [41] found that the SR fractional release Ca²⁺ release increased slowly and linearly with the SR Ca²⁺ content (free [Ca]_SR and total Ca²⁺) but then rose very steeply when [Ca]_SR exceeded a threshold concentration about 500 μM. (We use the term “threshold” as a convenient shorthand to indicate where the fractional release curve begins to rapidly increase without implying the existence of a discontinuity.) With the wave front sensitization mechanism, Ca²⁺ released at the leading edge of the wave, diffuses through the cytoplasm and is taken up by SR in front of the wave. If the amount of Ca²⁺ taken up causes [Ca]_SR to exceed the threshold then SR Ca²⁺ release occurs thereby maintaining the propagation of the wave. Modeling [29,31] has shown the feasibility of this mechanism but requires that Ca²⁺ diffusion in the SR relative to cytoplasmic diffusion be slow enough so that the build up of [Ca]_SR at the front of the wave is not dissipated by retrograde diffusion. The wave front sensitization mechanism neatly resolves the seemingly incompatible requirements of low RyR Ca²⁺ sensitivity and low Ca²⁺ wave concentration and this mechanism readily explains the long known observation that Ca²⁺ waves occur under conditions that cause SR Ca²⁺ overload [4].

While the wave front sensitization mechanism obviates the need for high cytosolic Ca²⁺ concentrations to maintain wave propagation it still does not clear the way for a self-consistent model of Ca²⁺ waves. The third challenge in developing models of Ca²⁺ waves based on Ca²⁺ sparks is the fundamental lack of an adequate model of Ca²⁺ sparks. Spark models based on relatively small Ca²⁺ currents (I_CRU ~1 pA) through the CRUs produce Ca²⁺ transients of reasonable magnitudes but the spatial spread of the computed spark (the full-width at half maximum, FWHM) is ~1 μm [45,46] about half of what is experimentally observed [32,47,48]. Because the spark image is a 2-dimensional projection of the 3-dimensional sphere (or paraboloid) of Ca²⁺-bound fluorescent indicator, doubling of the FWHM requires the amount of released Ca²⁺ to increase by a factor of ~8 [49]. Larger estimates of I_CRU (~10–20 pA) based on noise analysis [50] or back calculation from the spark properties [49,51,52] produce sparks that have the right FWHM but produce Ca²⁺ waves that have too high average [Ca]_i (~10–100 μM, [22,24,25]).

The problem of needing to use large I_CRU to get sparks with FWHM ~2 μm may stem from a wrong diffusion model. In current spark models, there is no coupling between the movement of Ca²⁺ and other molecules, except through the chemical reactions involving Ca²⁺ and buffers. However, the movement of Ca²⁺ (when measured with respect to a fixed reference frame as in all confocal measurements of sparks) is necessarily coupled to the movement of all other molecules and ions (water and K⁺, for example) to some extent [53,54]. Such coupling might result in a larger spatial spread of Ca²⁺ and Ca²⁺-bound indicator (i.e., a larger spark) for a smaller total amount of released Ca²⁺ than predicted by current linear diffusion models. Diffusion is difficult to model from first principles because the interaction of all species must be considered in writing the conservation equations (mass, momentum, energy). Tan et al. [55] approach the spark width problem differently by assuming that diffusion is non-Fickian. They show that a subdiffusion model can produce sparks of ~2μm width using a current of 2 pA. Although Tan et al. do not specify the physical mechanism underlying anomalous subdiffusion their work is an important call to look more deeply into the mechanism of diffusion not only of Ca²⁺ but all molecular and ionic species in a complex milieu such as the cytoplasm.

3. Physiological Ca²⁺ waves in myocytes

Ca²⁺ waves in mammalian ventricular myocytes are generally viewed as pathological and underlie triggered arrhythmias (see below but see [38] for an alternative viewpoint). Here we examine the role that Ca²⁺ waves may play in the normal functioning of non-mammalian ventricular myocytes, atrial myocytes, and Purkinje cells and how the spatial arrangement of Ca²⁺ release channels could affect cellular function.

3.1. To wave or not to wave

Non-mammalian ventricular myocytes [56] and atrial cells lack t-tubules although rat and mouse atrial cells do have a transverse axial tubular system (TATS) that predominantly runs longitudinally [57–60]. Excitation–contraction (E–C) coupling in these cells is initiated only at the cell periphery (or occasionally at sparsely distributed sites within the cell [60]) where the dihydropyridine receptors CaV1.2 and RyRs are in close apposition [56], Fig. 2. Full activation of myofibrils requires that [Ca]_i reach a sufficiently high level throughout the myocyte within the period of the heartbeat. To achieve full and rapid myofibrillar activation, cells lacking t-tubules could adopt a strategy of being thin or use Ca²⁺ waves that start at the cell surface and propagate radially to the cell center (centripetal waves). Diffusion occurs quickly for short distances so thin cells could depend solely on Ca²⁺ diffusing from the sarcolemmal surface. However, the time scale for diffusion increases quadratically with distance so myofibrils at the core of myocytes with larger cross sections might not be fully activated within the period of the heartbeat. Ca²⁺ waves, which involve diffusion and sequential activation CRUs, change the time scale of activation from a quadratic to a linear function of distance. Moreover, large surface-to-core Ca²⁺ concentration gradients that occur when Ca²⁺ enters only from the surface sarcolemma are reduced with Ca²⁺ waves. Accordingly, we might expect that species with wider cells would have evolved mechanisms that support Ca²⁺ waves. Centripetally propagating Ca²⁺ waves have been observed in guinea pig [61], cat [62], and rat [60,63,64] atrial myocytes.

Fig. 2.

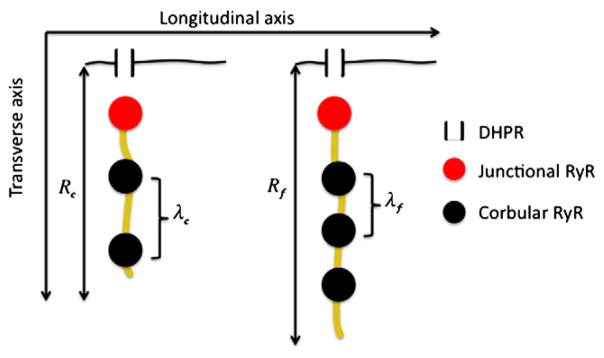
Schematic of spatial distribution of Ca²⁺ handling molecules in chicken (c) and finch (f).

Recent measurements of Perni et al. [56] on lizard, chicken, and finch ventricular myocytes allow us to make rough quantitative estimates that may distinguish between these two strategies. The choice of strategy is constrained by the heart rate, the cross-sectional size of the cell, and Ca²⁺ handling properties. The heart rates (ν) for the lizard, chicken, and finch are, respectively, 40–140, 275, and 500 beats/min. The mean myocyte cross-sectional radii(R) are 2.7 μm, 4.6 μm, and 6.9 μm for the lizard, chicken, and finch. Because Ca²⁺ waves propagate by sequential activation of CRUs, the ability of a myocyte to support a wave and the wave velocity depend on the distance between the CRUs. Perni et al. found the edge-to-edge distances between CRUs (λ) in the corbular/extended SR are 235 nm and 126 nm for the chicken and finch; no datum is given for the lizard. There is insufficient data on Ca²⁺ handling for the chicken and finch to model Ca²⁺ waves so we ask whether these two species are dynamically equivalent. That is, if we suppose a Ca²⁺ wave can propagate in the chicken myocyte at a speed sufficient to activate the cell within the time of its heart beat, then could a Ca²⁺ wave also activate the finch myocyte during period of its heart beat assuming that Ca²⁺ handling were the same in both species? To answer this we adopt the simplest wave propagation model where we suppose that the CRU fires when the ambient [Ca]_i exceeds some threshold. The time (τ) for a diffusive process (for simple linear diffusion) scales quadratically with distance, τ~λ²/D, where λ is a characteristic length and D is the diffusion coefficient. In this case let λ be the edge-to-edge distance between CRUs and we estimate the time between when Ca²⁺ is released from one CRU and when the threshold concentration is reached at the adjacent CRU by τ=βλ²; a more accurate estimate can be found in [65] but this simple formula is sufficient here. The number of CRUs from the cell periphery to the center is n=R/λ. A steadily propagating wave will take time T=nτ=(R/λ)βλ²=Rβλ to travel from the surface to the center. We choose β so that the total time T_c for the chicken matches the observed heart rate. Thus β =(R_cλ_cv_c)⁻¹, where the subscript c refers to the chicken. Perni et al.’s data give β=0.4 s/μm². Let us see if we can recover the time for a wave in the finch myocyte to reach the center, T_f, using this β value. By using the same β value we are assuming that Ca²⁺ handling is identical in the chicken and finch. The wave propagation time is T_f = βR_fλ_f =(0.4 s/μm²)(3.45μm)(0.126μm)=0.17 s. This value is close to the observed heart beat period of 0.12 s, which suggests closer edge-to-edge CRU spacing in the finch had evolved so that a Ca²⁺ wave could propagate throughout the myocyte within the time of the heartbeat.

We can apply a similar analysis to see if the finch could use only the Ca²⁺ that enters through activation of the peripheral couplings on the cell surface. In this case our time scale τ is the characteristic time for the concentration at the center to reach some specified level, τ=βR². We choose β so that τ_c equals the observed chicken heartbeat period τ_c =1/v_c, which gives $\beta ={(v_c{R}_c^2)}^{-1}$. When we use this β to calculate τ_f we get ${\tau }_f=R_f^2/(v_c{R}_c^2)=0.49s$. This value is far larger than the observed period of 0.12 s. The analysis suggests that the finch, because of the myocytes’ large cross section and rapid heart rate, could not survive solely on Ca²⁺ released from CRUs at the peripheral couplings but require Ca²⁺ waves that travel centripetally from surface to center.

Applying the same analysis to the lizard we find that τ_e =0.08 s, which is well below the observed cycle length of 0.43 to 1.49 s. This suggests that because of the low heart rate and the thinness of the cell, the lizard could activate all its myofibrils just from Ca²⁺ coming from the peripheral couplings (provided the quantity of Ca²⁺ in these stores is adequate) obviating the need for Ca²⁺ waves.

These calculations provide a teleological glimpse into how Mother Nature could modify structures to attain her goals. There is a common need in the ventricular and atrial myocyte to activate all myofibrils but in the face of different constraints of force (~R²) and heart rate. If the biochemical machinery (actin, myosin, RyRs, SERCA) is similar in different species then it suggests that adaptation occurs by the (presumably) easier pathway of altering structures (changing number and distances between CRUs) rather than changing the biochemical machinery.

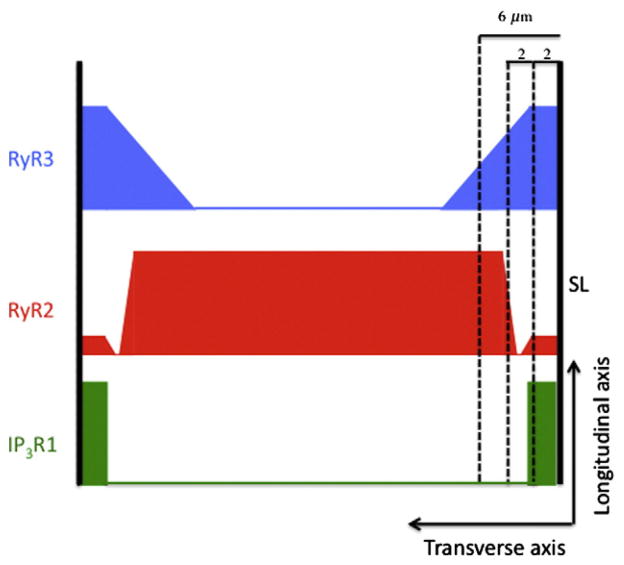
3.2. Layered structure of Ca²⁺ handling molecules in Purkinje and atrial cells

The spatial distribution of type 2 RyRs (RyR2) in both atrial and Purkinje cells in the central (a few μm away from the surface) is fairly represented by the cartoon in Fig. 1. That figure does not depict the more complex layering of different Ca²⁺ handling molecules near the sarcolemmal surface seen in atrial cells [63,66], neonatal myocytes [67–70], and Purkinje cells [71]. The canine Purkinje cell has overlapping concentric layers of IP₃R1, RyR3, and RyR2 [71] shown schematically in Fig. 3. Within 2 μm of the surface is a mixture of RyR1, RyR3, and type 1 IP₃ receptors (IP₃R1), with more RyR3 than RyR2. The layer between 2 and 4 μm from the surface is filled primarily with RyR3 and is virtually devoid of RyR2. From 4 to 6 μm the ratio of RyR2 to RyR3 increases and from 6 μm to the center (about 12–15 μm from the surface, [72]) is filled principally with RyR2 although IP₃R1 is sparsely scattered throughout this region.

Fig. 3.

Layers of RyR3, RyR2, and IP₃R1 in canine Purkinje cells. Redrawn from [71].

In a series of papers Boyden and her colleagues [71–74] have found 3 types of Ca²⁺ waves. One type propagates just along the surface parallel to the cell’s long axis; the second type is a local wavelet that propagates perpendicular to the surface and limited to the subsarcolemmal space, which they define to be within 6 μm of the surface, the furthest extent of RyR3s. The third type, the cell-wide wave, is similar to those seen in ventricular myocytes that propagate longitudinally.

The function the layered structures of IP3R1s and RyRs serve is unknown. Stuyver et al. [71] speculate that the higher Ca²⁺ sensitivity of RyR3s will more readily respond to Ca²⁺ entry through the DHPRs and generate subsarcolemmal wavelets, which can then develop into cell-wide waves. This interpretation must be regarded with caution since the functional properties of RyR3 depend on SR loading [75] and on specific tissue [76]. Application of an IP₃ antagonist reduced the number of wavelets and cell-wide waves [71,74]. This suggests that activation of the IP₃R1s could be enhancing the open probability of individual clusters of RyR2s and/or the diffusive coupling of separate CRUs by locally releasing Ca²⁺ into the subsarcolemmal space.

Rat atrial cells have a somewhat similar layered structure with type 2 IP₃R colocalized with RyR2 at the periphery [63,66]. A 2 μm gap exists between this surface layer of IP₃R2+RyR2 and the central core of RyR2. It is not known whether RyR3 is present in rat atrial cells and whether the 2 μm gap might be filled with RyR3s. Activation of IP₃R2s by IP₃ agonists increased the spark frequency at the periphery and triggered extra diastolic Ca²⁺ transients during pacing [66]. Modeling studies of atrial cells show that the 2 μm gap between the surface layer and central core of RyR2s is a significant barrier to centripetal Ca²⁺ wave propagation [24].

In cat atrial cells activation of IP₃R2 by endothelin generated robust Ca²⁺ waves during pacing and, as with the rat atrial cells, extra diastolic Ca²⁺ release [77]. Interestingly, exposing permeabilized cells to IP₃ or an IP₃ agonist increased spark frequency throughout the myocyte suggesting that, unlike rat atrial cells, IP₃R2s are not restricted to the periphery. Indeed, silencing the RyRs with tetracaine revealed elementary Ca²⁺ release from IP₃R2 throughout the myocyte [77].

The aggregate of these studies suggests an interplay between IP₃Rs and RyRs with the former modulating the probability that the RyRs would generate cell-wide Ca²⁺ waves. Why would this modulation be needed? As discussed earlier, cells without t-tubules must rely on Ca²⁺ released from junctional CRUs at the cell surface and from Ca²⁺ entry from surface DHPRs and Na⁺–Ca²⁺ exchanger (a prominent source of Ca²⁺ in neonatal cells [68,70]) or release from central CRUs presumably as a centripetal wave. It is a geometrical fact that an annulus close to the surface contains a disproportionate share of the cell volume. Therefore, even if Ca²⁺ elevation were restricted to near the surface, a sufficient fraction of the myofibrils might still be activated to meet the contractile demands. However, as the demands for greater contractile force or speed increase the IP₃ signaling pathway might tune the sensitivity of the RyRs, perhaps by triggering IP₃R Ca²⁺ release that raises the local [Ca]_i around the RyRs, and increasing the probability of initiating a cell-wide wave. This scenario might be appealing but we should note that the studies on Purkinje and atrial cells indicate that IP₃ stimulation tended to be proarrhythmic.

A number of important questions remain. What role does RyR3 in the Purkinje cell play? If we looked for RyR3s, would we find them in atrial cells with the spatial distribution seen in Purkinje cells? Canine Purkinje cells have type 1 but not type 2 IP₃Rs [71] whereas the rat atrial cell has type 2. Do the differences in Ca²⁺ inactivation and Ca²⁺ and IP₃ sensitivities between these two types [78] play a functional role in the generating waves? There may be a greater imperative to generate cell-wide waves in Purkinje cells to fully activate myofibrils because their diameter is about twice that of atrial cells [72]. Although Purkinje cells are not devoid of t-tubules the volume density is low compared to that in the ventricles [79] so it is unlikely t-tubules play a significant part in coordinating contraction in these cells. Perhaps the molecular differences in IP₃Rs and RyRs and their spatial distribution in Purkinje and atrial cells might reflect the differing demands for generating Ca²⁺ waves.

4. Ca²⁺ waves and pathology

The elevation of [Ca]_i by Ca²⁺ waves can generate a transient inward current via the Na⁺-Ca²⁺ exchanger and other Ca²⁺ activated currents [80–85]. Depolarization induced by this inward current can sometimes be sufficiently large to trigger an action potential (AP, [73,83,85,86]) in single myocytes. One miscreant myocyte cannot, however, trigger an ectopic beat because it cannot source enough current to depolarize neighboring cells sufficiently to trigger another round of APs. This is the source-sink mismatch problem. Modeling studies show that a very large number of myocytes must synchronously release Ca²⁺ in order for the aggregate to overcome the source-sink mismatch and generate an ectopic beat [87,88]. The number depends strongly on the number of spatial dimensions, the smallest being for 1-dimensional tissue such as Purkinje fibers. Pathological conditions that reduce repolarization reserve or reduce electrical coupling (such as fibrosis) can greatly reduce the number. Still, even for conditions favoring ectopic beat generation, synchronous spontaneous Ca²⁺ release (SCR) must occur in 10,000 or more cells to generate an ectopic beat [87]. These modeling results are consistent with experiments by Katra and Laurita [89] in a canine wedge model showing after depolarizations occur when SCR occurs over a relatively large area (~3×3 mm²). Based on combined optical mapping of Ca²⁺ and membrane potential in whole rabbit hearts, Myles et al. [90] estimated that the number of cells needed to produce a premature ventricular complex (PVC) is ~12,000 in 2-d and ~2×10⁶ in 3-d, close to the model estimates of 8000 and 0.8×10⁶ respectively.

The key question is how to get 10,000 or more cells to spontaneously release Ca²⁺ at about the same time. There are two possible mechanisms: synchronization occurs because cells are coupled, i.e., not acting independently; or cells act independently and happen to all fire at about the same time. Coupling could occur via diffusion of Ca²⁺ through gap junctions but this is unlikely because the probability of cell-to-cell wave propagation is low [91,92]. Cells could be mechanically coupled. SCR that initiates a contraction and relaxation cycle in one myocyte can trigger Ca²⁺ release from myofilaments in a neighboring mechanically coupled myocyte, which could then trigger spontaneous release from the SR [93–95]. The velocity of this mechanically triggered Ca²⁺ and contraction wave is ~1 to 17 mm/s [96], orders of magnitude higher than velocity of Ca²⁺ waves (~100μm/s) generated within a single myocyte by the fire–diffuse–fire mechanism. The very high velocity of these mechanical waves makes them a possible mechanism for synchronizing the spontaneous release of ~10,000 cells. However, in two cited studies [89,90] mechanical movement was arrested so mechanical coupling could not have been the cause of synchronization.

Alternatively, synchronous SCR can also occur without any cell-to-cell coupling, similar to the sudden (within ~1 month) emergence of billions of cicadas every ~17 years. Two ingredients are needed for synchronization to work by this mechanism: a synchronizing event, such as an AP, that simultaneously puts ~10,000 cells into the same starting state and a population of cells that will, in time, independently spontaneously release Ca²⁺. The time between the synchronizing event and when SCR first occurs is called the first latency time and the distribution of these times in the population is the first latency distribution. If the first latency distribution is narrow then spontaneous Ca²⁺ release will occur nearly synchronously in many cells. The important question is what factors control the width of the first latency distribution. There are many possibilities including SR load and RyR restitution time ([97] for review). In an experimental and theoretical study Wasserstrom et al. [92] showed that the first latency distribution becomes narrower with increasing SR Ca²⁺ load. In other words, higher SR Ca²⁺ load leads to more synchronous Ca²⁺ release.

The existence of a synchronizing event allows the definition of a Ca²⁺ “phase wave”. The idea of a phase wave can be illustrated with a line of equidistantly spaced clocks (say 1 m apart) whose initial time is set in proportion to the distance from the origin, say −1 s apart so clock zero starts at 12:00, clock 1 starts at 11:59, etc. If the clocks are allowed to run and we follow the position of the clock hitting the 12:00 mark (the “phase” marker) then it would appear that a wave is propagating at 1 m/s. In a myocyte a phase wave is the apparent propagation of a wave front as CRUs exit from their refractory period and spontaneously release Ca²⁺. A Ca²⁺ phase wave differs from a “diffusion” wave generated by the fire–diffuse–fire mechanism because nothing, Ca²⁺ in particular, is actually diffusing. Because nothing is diffusing, phase waves can go through barriers, can pass through each other without annihilation, and can have infinite velocity.

Phase waves and diffusion waves can coexist but it becomes more sensible to talk about phase waves as the first latency distribution of CRU release becomes increasingly narrow [92]. As the first latency distribution narrows many CRUs fire in close succession that can initiate diffusion waves at multiple sites. As the number of initiation sites increases, it becomes harder to discern diffusion waves, ultimately fusing into a cell-wide synchronous SCR. As Ca²⁺ release becomes more synchronous within the cell, the greater its effectiveness in triggering an AP [81]. Therefore, the notion of phase waves may provide a more useful framework to address the synchronization of spontaneous Ca²⁺ release between cells and within cells.

Ca²⁺ waves have a long history. Ca²⁺ waves are deceptively easy to model, yet models remain fundamentally incomplete. Important questions remain as to the how the spatial distribution of RyRs and IP₃Rs shape the initiation and propagation of Ca²⁺ waves in atrial cells, Purkinje cells, and perhaps in non-mammalian ventricular myocytes. Ca²⁺ diffusion waves are important for activating contraction in atrial, Purkinje, and non-mammalian ventricular myocytes. Ca²⁺ phase waves may be more important for understanding the origins of triggered arrhythmias than Ca²⁺ diffusion waves.