Abstract
The production of images of kinetic parameters is often the ultimate goal of positron emission tomography (PET) imaging. The indirect method of PET parametric imaging, also called the frame-based method (FM), is performed by fitting the time-activity curve (TAC) for each voxel with an appropriate compartment model after image reconstruction. The indirect method is simple and easily implemented, however, it usually leads to some loss of accuracy or precision, due to the use of two separate steps. This paper presents a direct 4-D method for producing 3-D images of kinetic parameters from list mode PET data. In this application, the TAC for each voxel is described by a one-tissue compartment model (1T). Extending previous EM algorithms, a new spatiotemporal complete data space was introduced to optimize the maximum likelihood function. This leads to a straightforward closed-form parametric image update equation. This method was implemented by extending the current list mode platform MOLAR to produce a parametric algorithm PMOLAR-1T. Using an ordered subset approach, qualitative and quantitative evaluations were performed using 2-D (x, t) and 4-D (x, y, z, t) simulated list mode data based on brain receptor tracers and also with a human brain study. Comparisons with the indirect method showed that the proposed direct method can lead to accurate estimation of the parametric image values with reduced variance, especially at low count levels. In the 2-D test, the direct method showed similar bias to the frame-based method but with variance reduction of 23%–60%. In the 4-D test, bias values of both methods were no more than 4% and the direct method had lower variability (coefficient of variation reduction of 0%–64% compared to the frame-based method) at the normal count level. The direct method had a larger reduction in variability (27%–81%) and lower bias (1%–5% for 4-D and 1%–19% for FM) at low count levels. The results in the human brain study are similar with PMOLAR-1T showing lower noise than FM.
Keywords: Expectation maximization, image reconstruction, one-tissue compartment model, parametric imaging
I. Introduction
DYNAMIC positron emission tomography (PET) permits quantification of tracer dynamics. An important goal of much of quantitative brain PET is to produce parametric images of kinetic parameters, such as the uptake rate K1 and the total volume of distribution (VT) [1]. The current data processing path for parametric imaging is to reconstruct a time series of images from measured projection data independently, and then estimate each voxel’s kinetic parameters from the time-activity curve (TAC), typically with a compartmental model. This indirect or frame-based approach requires selection of the duration of each frame, involving a choice between using longer scans with better counting statistics but poor temporal resolution, and shorter scans that are noisy but preserve temporal resolution. Optimal use of the dynamic data requires accurate noise estimates for data weighting; this estimation is challenging for nonlinear iterative reconstruction methods because noise is spatially variant and object dependent [2], [3].
Direct approaches for creation of parametric images have been in the literature for nearly 30 years. In 1984, Snyder [4] developed a list mode expectation-maximization (EM) maximum likelihood (ML) algorithm for estimation of parametric images using an inhomogeneous spatial-temporal Poisson processes and a kinetic compartmental model. Carson and Lange [5] also proposed an EM framework for direct parametric image reconstruction algorithm for a one-tissue model. Subsequently, many direct kinetic estimation methods [6]–[10] for sinogram data have been produced. However, for a high-resolution scanner such as the HRRT [11] with 4.5×109 potential lines of response, list mode data is preferred, since it can reduce the data storage requirements while maintaining the highest resolution by storing the measured attributes of each event in the list. Other direct methods [12]–[20] were developed from linear basis functions, whose temporal model is linear with respect to the parameters. Although such basis functions can describe the TAC, they have no direct physiological meaning and kinetic parameters must still be calculated from the dynamic images, leading again to a two-step process.
The use of kinetic compartment models has a firmer biological basis, and is thus the primary goal of dynamic PET. Tsoumpas et al. [9] and Wang et al. [10] proposed direct parametric image reconstruction methods, whose compartment model is linear (Patlak plot), and is thus limited to irreversible tracers such as FDG. Furthermore, Rahmim et al. [21] proposed a closed-form direct 4-D parametric image estimation method for reversible tracers employing a recently published linear graphical analysis model. Recently, Wang and Qi [22] proposed a generalized direct parametric image reconstruction approach applicable to any kinetic model, which was comprised of two steps for each parameter update (reconstruction of intermediate images and kinetic parameter estimation with accurate weights determined from the derived algorithm).
Here, we present a new EM-based direct 4-D parametric image reconstruction algorithm for list mode data by combining the one-tissue (1T) compartment model into the scanner physical model. ML estimation is a statistically efficient method, i.e., it will asymptotically produce minimum variance unbiased estimators. The indirect methods are intrinsically not ML methods since they do not carry the full statistical characteristics of the frame-based voxel values into the kinetic parameter estimation. Therefore, we hypothesize that the direct method will produce superior results to the indirect methods. Since this algorithm extends the current list mode algorithm MOLAR for parametric imaging, it is called PMOLAR-1T. An initial description of this algorithm has been published previously [23].
This paper is organized as follows. Section II reviews the 1T model. Section III describes the theory of this work, consisting of 1) derivation of the direct 4-D bin-mode parametric reconstruction algorithm, 2) description of our current static list mode emission image reconstruction method, and 3) extension to the direct 4-D list mode reconstruction scheme. Simulation results are shown in Section IV. Discussion and conclusions follow in Sections V and VI.
II. One-Tissue Compartment Model
Compartmental modeling is the most commonly used method for describing the uptake and clearance of radioactive tracers in tissue [24]. The simple one tissue (1T) model describes each voxel with one compartment and is defined by the following ordinary differential equation:
| (1) |
where Cp(t) is the time course of tracer in the arterial plasma (input function, Bq·mL−1), K1 is the rate constant for entry of tracer from blood to tissue (mL·min−1·cm−3), k2 is the constant for return of tracer to blood (min−1), and λ(t) is the tissue concentration in time bin t (Bq·cm−3). The solution to the differential equation is
| (2) |
where “⊗” denotes the convolution operator.
For receptor binding agents, the volume of distribution (VT, mL·cm−3) is the most important parameter [1]; this is defined as the ratio of tracer concentration in tissue to that in plasma at equilibrium and, for the 1T model, is mathematically given by
| (3) |
III. Direct 4-D List Mode Parametric Reconstruction Method
A. Direct 4-D Bin Mode Parametric Reconstruction Method
We extend the notation of Lange and Carson [25] from static mode to dynamic mode and use “bin mode” to illustrate first. The bin size is equal to the time resolution of the list mode data; for the HRRT, the time resolution is 1 ms. Thus, for purpose of notation, it appears that the data are binned into sinograms corresponding to each discrete time bin of the list mode file. In this section, the physical model for the projection measurement Yit of line of response (LOR) i(i = 1,…,I) in time bin t excludes physical factors such as attenuation, normalization, randoms, scatter, and motion (see below for full model) and is given by
| (4) |
where cij is the probability of an emission from voxel j (activity λjt in time bin t) detected in LOR i, Δt is the duration of time bin t, and Li accounts for decay (Li = exp(−(ln 2)t/t1/2), where t1/2 is the half life of the tracer. The bin-mode log-likelihood function for I LORs and T time bins is given by
| (5) |
The activity λjt is assumed to be represented by the 1T model with known input function. Inserting (2) yields
| (6) |
where Δt is the time binning of the plasma data, Pτ = Cp(τ)Δt, and K1j and k2j represent the parameter values at voxel j.
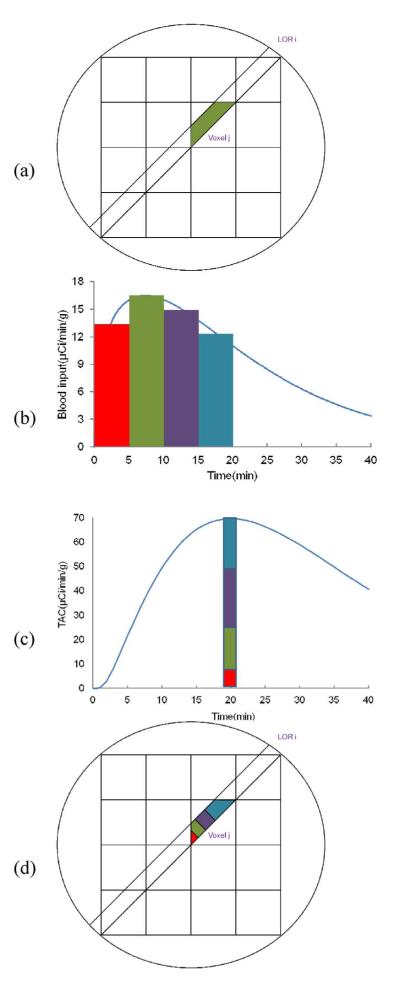
Due to the nonlinearity of the above function with respect to the parameter k2, the maximum likelihood estimate can not be easily obtained, even for the simpler static emission image reconstruction. The expectation-maximization (EM) algorithm is often used in statistics to find maximum likelihood estimates of parameters in probabilistic mixture models, and was first introduced into static emission image reconstruction by Shepp and Vardi [26] and Lange and Carson [25]. The Yi are the incomplete data, and the coupling of the voxels makes it difficult to obtain maximum likelihood estimates directly. The problem can be solved by creating complete data Xij defined as the counts emitted from voxel j collected along LOR i, as shown in Fig. 1(a). This separation of the components of Yi into Xij allows an EM algorithm to be defined and solved.
Fig. 1.
Illustration of static and dynamic complete data spaces. (a) Static spatial complete data (Xij). (b) Plasma input, colors represent different delivery times. (c) Time activity curve and separation of activity based on tracer delivery time. (d) Spatiotemporal complete data (Xijtr). See text for details.
However, in direct 4-D parametric imaging, emission activity of each voxel λjt and the counts Yit collected along LOR i change continuously with time. As described in Section II, the activity λjt in time bin t can be described as the convolution of the plasma input function with an impulse response function (2), i.e., the activity at a given time is a weighted sum of all of the previous input function values. The convolution property indicates that the later a given molecule of tracer is delivered to the tissue, the greater is its contribution to the activity λjt. A simple example is shown in Fig. 1(b), the input function, and Fig. 1(c), the tissue TAC. The activity at time 20 min has four components, with each component derived from the plasma input from different times, denoted with the matching colors. This ability to separate the activity at a given time into its components, based on the arrival time in the plasma, motivates the definition of the complete data space for a 4-D EM algorithm [as shown in Fig. 1(d)], where different colors represents different arrival times). Thus, we define a spatiotemporal complete data space Xijtr as the counts collected along LOR i in time bin t emitted from voxel j and where the tracer input that produced that event was delivered at time τ. For the 1T model, this random variable is
| (7) |
From the complete data definition, the E- and M-steps of the EM algorithm for estimation of the parameters can be derived. In a similar manner to the static EM algorithm, the E-step calculates the expectation of the complete data given measured data Y, and the current kinetic parameters estimates K1 and k2 at iteration n
| (8) |
The M-step maximizes the corresponding conditional complete data likelihood, which, ignoring constant terms is
| (9) |
Taking partial derivatives with respect to K1j, and setting to zero, yields
| (10) |
which leads to the K1j update equation, in terms of k2j
| (11) |
where , the voxel sensitivity. For k2j
| (12) |
The K1j update (11) is inserted into (12), which leads to
| (13) |
The right-hand side of (13) is a function of the measured data and the current parameters (8). The left-hand side is a function only of k2 and the known input function; we define this term as H(k2). This function can be precomputed for a range of k2 values and is found to be monotonically decreasing. Therefore, H is invertible for the 1T model, so H(k2) and the k2j update equation are given by
| (14) |
| (15) |
B. Static List Mode Reconstruction (MOLAR)
The HRRT [11] is a 3-D brain-dedicated scanner with high resolution (2.5–3 mm). It has a total of 119 808 crystals which produce a total of 4.5 × 109 potential LORs, since each of the eight detector panels is in coincidence with the five opposite panels. For this scanner, list mode data is advantageous over sinogram data. First, unless resolution is reduced, sinogram data have a higher storage cost than list mode data due to the very large number of LORs, especially for dynamic PET where high temporal resolution is usually required. Secondly, maintaining the full resolution by not averaging similar LORs provides the ability for accurate physics modeling of individual LOR resolution characteristics such as detector layer and incident angles. In order to fully exploit the HRRT resolution capabilities, we designed and implemented MOLAR, the Motion compensation OSEM List mode Algorithm for Resolution recovery, implemented on a computer cluster [27]. MOLAR, uses an OP-OSEM approach, whereby there are no precorrections to the measured data, thus preserving the Poisson nature of the data. Other features include randoms correction from singles (without delayed coincidences), component-based count-rate dependent normalization, iterative single scatter simulation, and event-by-event motion correction [28]. Let Yit equal the number of prompt coincidences in LOR i in time bin t. The expected value of Yit at iteration n is given by
| (16) |
where Δt is the time bin duration, cijt is the contribution of voxel j to LOR i in time bin t, accounting for geometry, resolution, solid angle, and motion effects. Lit is the product of the decay factor, the live time for this event (based on the block singles rates for this LOR at time bin t) and the isotope branching fraction. Ait is the attenuation factor accounting for the position of LOR i with respect to the attenuating object in time bin t, calculated by projection through a precomputed attenuation image. The normalization term Ni is determined using a count-rate dependent component-based model [29]. Rit is the estimate of the random coincidence rate calculated from block single rates [30]. Sit is the scatter estimate from the single scatter simulation method [31]. For static reconstructions, the list mode algorithm processes only the M prompt coincidence events in each frame
| (17) |
where T is the frame duration and Qj is the voxel sensitivity, with summations over all LORs and over all time bin periods
| (18) |
C. Direct 4-D List Mode Parametric Reconstruction (PMOLAR-1T)
The new direct 4-D parametric imaging method was integrated into the MOLAR algorithm, and called Parametric MOLAR for the one-tissue model (PMOLAR-1T). In this presentation, livetime, randoms, scatter, and motion factors were not included, so the system matrix c and attenuation factor A are constant throughout the entire scan and Lt depends only on decay. The complete data is given by
| (19) |
Following the strategy in Section III-A and converting from bin-mode to list mode indexing, with M prompt coincident events indexed by m, the update equations with attenuation, normalization, and decay factors are
| (20) |
| (21) |
| (22) |
where tm is the time of event m and Ym is always 1 in list mode. In (20), the numerator sums over LORs with measured event, but the denominator sums over all LORs. This term is the equivalent of Q (the sensitivity image) for static MOLAR (18) and is approximated by random sampling of LORs, as in MOLAR [27].
IV. Algorithm Evaluation
To evaluate PMOLAR-1T, 2-D (x,t) and 4-D (x,y,z,t) tests were performed, and results were compared to the indirect frame-based method (FM). In addition, one human brain study was also evaluated.
A. 2-D Evaluation With Simulated Data
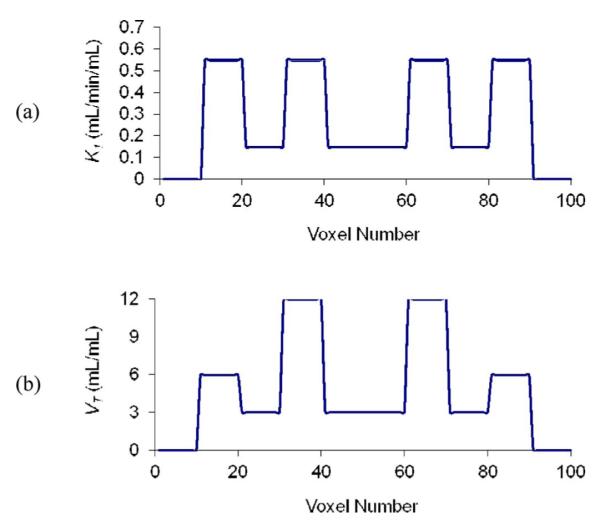
Given the huge computational demand of full 4-D reconstruction, it was deemed useful to initially evaluate the new algorithm with simple 2-D (x,t) data. Tests were performed for the case of a 1-D profile with one hundred voxels, where gray matter (GM, K1 = 0.55 mL·min−1·cm−3, VT = 6 mL·cm−3), white matter (WM, K1 = 0.15 mL·min−1·cm, VT = 3 mL·cm−3) and basal ganglia (BG, K1 = 0.55 mL·min−1·cm−3, VT = 12 mL·cm−3) were simulated. Fig. 2 shows the phantom and its K1 and VT values as a function of position x. These parameter values are typical for receptor ligand kinetics. Fifty 30-min list mode data replicates were created with the forward projection model and a measured input function from the tracer [11C]P943 [32] [Fig. 3(a)] and sampling, resolution, and sensitivity per voxel (Q) comparable to that of HRRT scanner. The system matrix was based on a Gaussian point-spread function with 2.5 mm full-width at half-maximum and voxel size of 1.2 mm. Poisson noise was added to each replicate, corresponding to 6.3 × 105 events. Decay of tracer [11C]P943 was included, but random and scattered events were not included.
Fig. 2.
Numerical phantom used for 2-D (x,t) simulation. (a) K1(x). (b) VT(x).
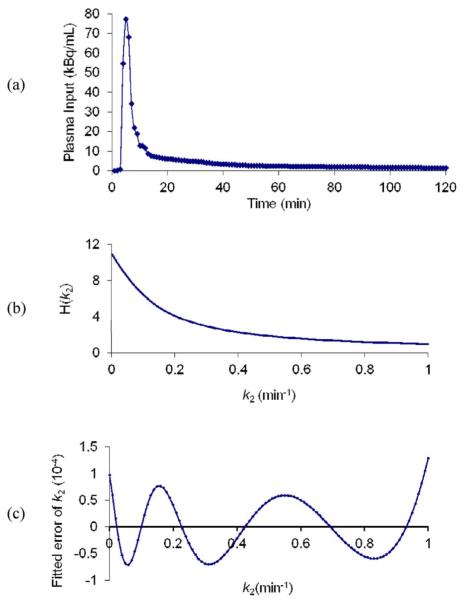
Fig. 3.
(a) Measured plasma input used for simulations. (b) H(k2) (14). (c) Absolute difference between true k2 value and k2 calculated by the fitted polynomial function.
For this algorithm, to update k2, the inverse of H(k2) is required. This was determined by precomputing H(k2) for a range of k2 values. Then, the inverse function was obtained by fitting these values with a log-polynomial function as shown in (23). Since H(k2) is independent of the measured data, it can be computed from the known plasma input data. H(k2) for a 30-min simulation is shown in Fig. 3(b), plotted over the normal physiological k2 range for a brain tracer. The inverse function for this simulation can be well fitted by a fifth-order polynomial function and the absolute fitting error is shown in Fig. 3(c) and is less than 1 × 10−4, i.e., less than 0.01% of the H(k2) values. The average (across x) true K1 and k2 values of all voxels were used as initial guesses for PMOLAR-1T
| (23) |
For the indirect method, data were binned into 30 1-min frames and each frame’s image was reconstructed by MLEM [25], [26] using the mean activity value of the phantom as the initial guess for all frames. To fairly compare the two methods, for the indirect method following reconstruction of each frame, weighted least squares (WLS) fitting with the Levenberg–Marquardt algorithm was used to estimate parameters by minimizing the weighted residual sum of squares (WRSS)
| (24) |
where WRSSj is the WRSS for voxel j, f is the frame index, Wf is the weight for frame f, λjf is the activity for voxel j at frame f, and is the activity for voxel j at frame f given by the model (2). The weights were based on noise equivalent counts (NEC), which in this case corresponded to total true events in each frame
| (25) |
Here, λwb is the mean whole phantom activity.
Region of interest (ROI) values were obtained from the mean values of the three regions (GM, WM, and BG), excluding one voxel from each edge, to minimize the partial volume effect. Thus, GM, WM, and BG regions were evaluated with 18, 34, and 18 voxels, respectively. To measure bias and noise, standard deviation (SD) and mean 1-D profiles were calculated from the reconstructed replicate 1-D profiles. The coefficient of variation (COV) and percent bias was calculated in each ROI as the ratio of average voxel SD to the true value and the ratio of the difference between average and true voxel values to the true value, respectively. These values were assessed as a function of iteration. After 10 iterations, both FM and PMOLAR-1T methods had almost 0% bias for k2 and bias of less than 2% for K1. In this 2-D test, both methods converge quickly and there were minor differences in bias.
Table I shows the percent bias and percent COV for GM, WM, and BG across the 50 replicates for FM and PMOLAR-1T after 60 iterations (no subsets). All bias values were small. Percent bias of PMOLAR-1T was comparable to that of FM, and slightly smaller for VT, which is the most important parameter for brain receptor studies. The advantage of PMOLAR-1T was clearly demonstrated by the COV reduction of 23%–60%.
TABLE I.
2-D Test Results [Mean Percent Bias and COV for GM, WM, BG Over the 50 Replicates by FM and PMOLAR-1T (4-D)]
| Frame | 4D | |||||
|---|---|---|---|---|---|---|
| Bias (%) | COV (%) | Bias (%) | COV (%) | COV reduction (%) | ||
| Kt | GM | 1.1 | 6.0 | 1.1 | 4.0 | 33 |
| WM | −1.6 | 9.2 | −1.6 | 7.1 | 23 | |
| BG | 1.2 | 5.0 | 1.2 | 2.0 | 60 | |
| k 2 | GM | 0.0 | 7.9 | 0.2 | 4.9 | 38 |
| WM | 0.1 | 19.1 | 0.2 | 14.1 | 26 | |
| BG | 0.1 | 11.1 | 0.4 | 8.2 | 26 | |
| V T | GM | 1.3 | 4.3 | 0.9 | 3.3 | 23 |
| WM | 0.6 | 13.1 | −0.4 | 10.0 | 24 | |
| BG | 1.8 | 7.2 | 1.2 | 5.1 | 29 | |
B. 4-D Evaluation With Simulated Data
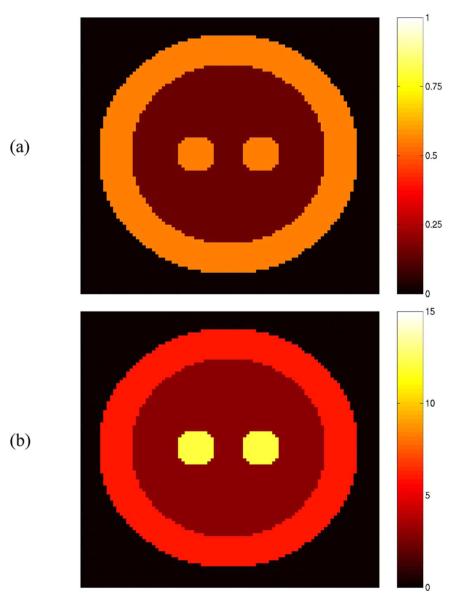
A 10-cm-diameter spherical 3-D phantom (Fig. 4) was created with three regions, corresponding to GM (K1 = 0.55 mL·min−1·cm−3, VT = 6 mL·cm−3), WM (K1 = 0.15 mL·min−1·cm−3, VT = 3 mL·cm−3), and BG (K1 = 0.55 mL·min−1·cm−3, VT = 12 mL·cm−3), with the same plasma input as the 2-D tests. Sixteen 60-min list mode file replicates (each with ~430 M counts, a “normal” count level for an object this size) were simulated with MOLAR by using the forward projection model to compute the expected value for a user-defined number of LORs and then generating Poisson realizations. In the simulations, the measured data did not include effects of livetime, randoms, scatter, or motion, in order to focus on the reconstruction algorithm. Decay (C-11) was included in the simulation. The reconstruction software was executed with an Intel Xeon computer cluster of 16 nodes with each node having 2 CPUs of 3.2 GHz and 2.0 GB memory.
Fig. 4.
The 10-cm-diameter 3-D phantom composed of gray matter (outer rim), white matter (inner region), and Basal Ganglia (central spheres). (a) K1 (mL·min−1cm−3). (b) VT (mL·cm−3).
For comparison, the conventional FM employed MOLAR to reconstruct 21 frames (6 × 30 s, 3 × 60 s, 2 × 120 s, 10 × 300 s) and WLS was used to estimate each voxel’s parameters with weights based on NEC. Both FM and PMOLAR-1T were implemented with ordered subsets (30 subsets, two iterations) based on event order of arrival. Initial reconstruction values (K1 and k2) for PMOLAR-1T were both set as 0.01 and the initial λ of FM was a uniform activity (37000 Bq·mL−1), as in our routine use.
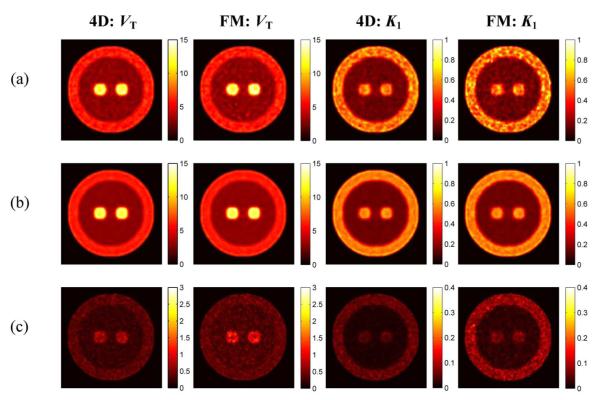
Typical, mean and SD images reconstructed by the two methods are shown in Fig. 5(a), (b), and (c), respectively. The similarity of K1 and VT mean images between FM and PMOLAR-1T indicated that the two approaches result in similar accuracy of the estimates at a normal count level (~430 M counts). However, the FM SD showed this method to be noisier than PMOLAR-1T, which indicated that PMOLAR-1T had better performance.
Fig. 5.
Reconstructed parametric images (VT and K1) by the FM and PMOLAR-1T (4-D) at the normal count level (two iterations, 30 subsets). (a) Typical images. (b) Mean images. (c) Standard deviation images.
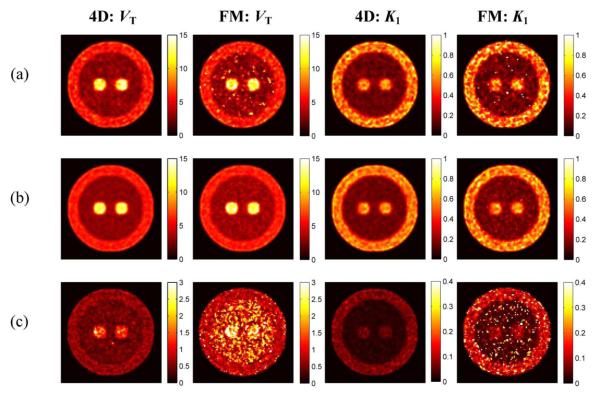
To further compare the two methods, their performance under low count condition (~43 M counts) was assessed by scaling down the original plasma input by a factor of 10 and repeating the simulation. The typical, mean and SD images are shown in Fig. 6. Given the higher noise level in these low-count simulations, the noise reduction in PMOLAR-1T is visually more apparent. This difference is most apparent in the WM (low activity) region.
Fig. 6.
Reconstructed parametric images (VT and K1) by FM and PMOLAR-1T (4-D) at a low-count level (2 iterations, 30 subsets). (a) Typical images. (b) Mean images. (c) Standard deviation images.
To quantitatively compare the two methods, ROIs were placed on the three regions (GM, WM, BG) excluding all voxels within 2.5 mm of the edges of each region, and percent bias and COV of each ROI were calculated from the average voxel mean and SD at the two count levels (as shown in Table II). At the normal count level, the percent bias values of both methods were small, with ≤ 4% for all parameters, although PMOLAR-1T was slightly worse than FM.However,PMOLAR-1T produced lower variability than FM for all parameters and regions (variability reduction of 36%–41% for K1, 59%–64% for k2, and 0%–30% for VT). At the low count level, PMOLAR-1T not only had a larger reduction in variability (44%–67% for K1, 62%–81% for k2, and 27%–65% for VT) but also produced lower percent bias values (1%–5%) than FM (1%–19%) for all parameters and all regions. Consistent with visual inspection, PMOLAR-1T produces its most dramatic advantage over FM in the WM (low activity) region.
TABLE II.
4-D Test Results [Mean Percent Bias and COV for GM, WM, BG Over the 16 Replicates by the FM and PMOLAR-1T (4-D) at Normal and Low Count Levels.]
| Bias (%) | COV (%) | COV reduction (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Regions | BG | WM | GM | BG | WM | GM | BG | WM | GM | |
| K1 (Normal) | 4D | 4 | 2 | 0 | 7 | 10 | 10 | 36 | 41 | 38 |
| FM | 3 | 1 | 1 | 11 | 17 | 16 | ||||
| K1 (Low) | 4D | 4 | 2 | 0 | 10 | 15 | 13 | 44 | 67 | 52 |
| FM | 4 | 10 | 4 | 18 | 46 | 27 | ||||
| k2 (Normal) | 4D | 0 | 4 | 0 | 6 | 8 | 7 | 60 | 64 | 59 |
| FM | 0 | 2 | 0 | 15 | 22 | 17 | ||||
| k2 (Low) | 4D | 1 | 5 | 0 | 11 | 16 | 11 | 62 | 81 | 69 |
| FM | 1 | 19 | 4 | 29 | 83 | 35 | ||||
| VT (Normal) | 4D | 3 | − 1 | 1 | 5 | 7 | 6 | 29 | 30 | 0 |
| FM | 4 | 0 | 1 | 7 | 10 | 6 | ||||
| VT (Low) | 4D | 4 | −1 | 1 | 11 | 15 | 11 | 52 | 65 | 27 |
| FM | 8 | 11 | 3 | 23 | 43 | 15 | ||||
C. 4-D Evaluation With Human Brain Data
One 120-min human [11C]AFM study was performed with list mode acquisition on the HRRT scanner (~20 mCi injection). Since the simulations showed the most substantial performance improvement at low counts, the original data were uniformly undersampled so that the data had only one-sixth the count level of the original study. A 1T model has previously been found to be appropriate for this tracer [33]. In advance of the scan, an arterial catheter was inserted into the radial artery for blood sampling. An automated blood counting system (PBS-101, Veenstra Instruments, Joure, The Netherlands) was used to measure the radioactivity in blood during the first 7 min. Fifteen handdrawn samples were collected at later times. For each sample, plasma was counted in a cross-calibrated gamma counter (1480 WIZARD, PerkinElmer, Waltham, MA). The total plasma curve from ~6 min on was fitted to a sum of exponentials. The unchanged parent compound in plasma was determined using a high performance liquid chromatography (HPLC) assay. The final plasma input function was calculated as the product of the fitted total plasma curve and the fitted HPLC fraction curve. In the conventional FM, MOLAR was employed to reconstruct 33 frames (6 × 30 s, 3 × 60 s, 2 × 120 s, 22 × 300 s) and then weighted least squares estimation was used to estimate each voxel’s parameters with weights based on NEC. Comparable physics corrections including normalization, motion, attenuation, randoms, and scatter were employed for both methods.
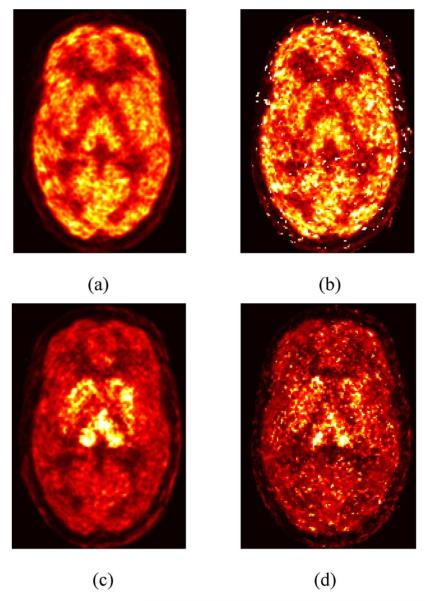
Fig. 7 shows images of K1 and VT created by PMOLAR-1T and FM for the human brain data. The distribution patterns in the two sets of images are similar. However, many high noise voxels exist in the FM images while PMOLAR-1T is less noisy. This is most clearly visualized in the low-activity regions such as white matter, and is also more noticeable in the VT image. The visual differences in low activity regions with human brain data are consistent with those in the simulations.
Fig. 7.
Reconstructed parametric images (VT (scale: 0–60 mL·cm−3) and [scale: 0–1 mL·min−1·cm−3)] by FM and PMOLAR-1T (4-D) (two iterations, 30 subsets) from a human brain study with [11C]AFM. (a) 4-D: K1. (b) FM: K1. (c) 4-D: VT. (d) FM: VT.
V. Discussion
In this work, we proposed a direct 4-D parametric imaging method (PMOLAR-1T) for the 1T compartment model with a novel EM algorithm for list mode data and implemented it in the MOLAR framework. A unique characteristic of this approach is the definition of the complete data space, using temporal partitioning of the events based on the delivery time of each radioactive molecule to the tissue, which echoes the spatial partitioning of events in static EM methods based on the voxel of origin.
1) Comparison With Frame-Based Method
With a measured blood input, list mode replicates were simulated for the 2-D and 4-D tests. In addition, human brain data were used for comparison of these two methods. 2-D results showed that the direct method is slightly better (Table I) than the indirect method. Under the 4-D test, we used a typical frame timing scheme (21 frames: 6 × 30 s, 3 × 60 s, 2 × 120 s, 10 × 300 s) and WLS fitting method with weights based on NEC for FM. NEC is a useful weighting approach for real data since it can be easily implemented.
The two methods were evaluated under our current routine reconstruction protocol (two iterations, 30 subsets). Qualitative and quantitative comparisons at normal and low-count levels showed that PMOLAR-1T can produce accurate estimates (percent bias less than 5%) with lower variability, with a greater improvement at the low count level (up to 81% reduction compared to the frame based method). Although the small sample size could reduce the confidence in the COV reduction shown in Table II, the consistent reduction of COV showed that 4-D has advantages over FM, especially at a low count level.
In addition to the NEC weighting for FM, we also compared the results of PMOLAR-1T with the best possible results that could be achieved by FM. The process for the best case of FM is comprised of the following three steps.
Producing SD images of each frame across replicates in the first step of FM.
Creating noisy TAC replicates for each ROI (GM, WM, and BG) by adding noise to the true TAC with magnitude set to the mean of the SD images for each ROI.
Fitting each noisy TAC by WLS with weights equal to 1/SD2 for each ROI.
The quantitative results showed that PMOLAR-1T can achieve lower variability than the best case of FM. When compared to original FM, the best case of FM had average COV reduction of 8% and 32% for the two direct reconstructed parameters (K1 and k2) in all ROIs at the normal and low count level, respectively, whereas the two COV reductions for PMOLAR-1T were larger: 49% and 63%.
The results with a low-count human brain study showed that PMOLAR-1T and FM can produce parametric images with similar patterns, but with lower noise with PMOLAR-1T.
In these comparisons, it is possible that the frame timing would affect FM bias and variability results, so that further tuning of frame durations for FM could improve the bias/variance behavior of the indirect method. For example, longer frames would have better statistics and pixel values might have a more Gaussian distribution. Low-count frames have also been shown to suffer from bias, however, MOLAR in FM produces little or no bias at low count levels [34]. Since OSEM reconstructions of low-count/short-duration frames can produce non-Gaussian statistics, the WLS method is suboptimal, since WLS assumes a Gaussian distribution for the pixel values. Thus, an ideal frame-based method would require the use of another optimization criterion instead of weighted least square. Such a criterion would ideally also account for variations in quantitative accuracy between frames, since iterative algorithms produce object-dependent resolution at finite iterations, and contrast changes over time. Thus, without the development of such an optimization criterion for FM, it is unlikely that these methods can match the performance of PMOLAR-1T where the accurate statistical model is intrinsic to the algorithm.
2) Convergence
Convergence is an important indicator of performance of a reconstruction algorithm and fast convergence usually means less computation cost. Due to the lack of convergence of OSEM, it is better to evaluate the convergence of FM and PMOLAR-1T with their non-OS (ordered subsets) versions. However, PMOLAR-1T suffers from high computation cost, therefore only the OS versions of both methods were investigated. Bias and COV as a function of iteration (three iterations) with 30 subsets for both methods were computed in the 4-D test at the two count levels (data not shown). At the normal count level, both methods showed low percent bias of ≤ 5%, and PMOLAR-1T values were more stable than those of FM with iteration increasing. Moreover, sample means from PMOLAR-1T showed greater stability with bias of FM sample means increasing substantially at the low count level. For example, in the low activity region (WM) over three iterations, FM had increasing percent bias of 4%, 10%, and 24% for K1, 4%, 19%, and 44% for k2, whereas 4-D had percent bias values of 5%, 2%, and 2% for K1, 7%, 5%, and 5% for k2.
PMOLAR-1T was developed from the method proposed by Carson and Lange [5] with a new higher-dimension complete data space. Generally, PET image reconstruction methods based on the EM algorithm with higher-dimension complete data spaces will converge slower. However, it is worth noting that the parameter space in PMOLAR-1T is smaller than the parameter space for frame-based reconstruction, since PMOLAR-1T does not reconstruct individual frame concentration values. A smaller parameter space will likely lead to faster convergence. Based on these initial results, net convergence speed is comparable for these two methods, although much more evaluation is required.
3) Computation Time
In the current implementation of PMOLAR-1T, we introduced two 2-D look-up tables into the update of so that convolution was not required, but there was extra memory cost for the intermediate variables. Each element of the look-up tables represented values of and for different t and k2. Moreover, PMOLAR-1T is required to read in and process the entire list mode file, as opposed to frame-based reconstructions where the program is executed multiple times using different portions of the list mode file. Although the current code handled the situation where all events could not be stored in memory at one time, more swapping time between disk and memory was needed to handle the entire scan list mode file. Currently, the computation time for the reconstructions of the frame-based method and PMOLAR-1T were 26 and 40 h, respectively, with 16 cluster nodes (each is dual core with 2G CPU and 2GB memory) when processing 430 million events. It is clearly necessary to optimize the PMOLAR-1T code to decrease the total computation time. One approach that would reduce computation time for PMOLAR-1T (and MOLAR) is a GPU implementation of the forward- and backprojections.
4) Randoms and Motion Correction
In MOLAR, randoms are estimated from the coincidence timing window and the block singles rates, stored in the list mode file. The conversion from block to crystal singles rates uses the crystal efficiency data from normalization. Delayed coincidences in the list mode stream are not used in the reconstruction, except to validate the estimates of randoms rate. Motion information is measured with the Polaris and Vicra devices, by tracking infrared reflectors mounted on a “tool” attached to the subject’s head. The measured data are processed into a file with time information and transformation matrix and then correct each event. Both randoms and motion corrections are emission-image independent, so these corrections can be directly applied in PMOLAR-1T as in MOLAR, since they do not affect the Poisson nature of the data.
5) Scatter Correction
Currently, scatter correction is performed on an event-by-event basis using the single scatter simulation (SSS) method [31]. The estimated scatter rate along a LOR is proportional to the sum of the contributions calculated from a random distribution of scatter points within the attenuation volume and depends on the activity image. In conventional frame mode dynamic PET, the SSS method is used in each frame. For each frame, an initial uniform activity image within the measured attenuation volume is defined for scatter computation. This activity distribution is subsequently replaced by the image iteratively determined by MOLAR and the scatter estimate is updated, typically with two updates within the first iteration. In the frame method, each frame’s emission image is static and the LOR scatter rate is time-independent. However, the emission image is time-varying in PMOLAR-1T. Therefore, the SSS method could be directly used in PMOLAR-1T, however, since each voxel’s activity changes over each time bin and scatter should, in theory, also change accordingly, this would lead to highly expensive computation. Therefore, additional SSS approximations are needed for PMOLAR-1T [35].
6) Model Applicability
Direct 4-D assumed that all voxels in the field-of-view can be described by the 1T model. Depending on the tracer, other models might be required. The 4-D method can be directly extended to various kinetic models that use only one nonlinear parameter such as the Simplified Reference Tissue Model (SRTM) [36] with three parameters, or the FDG model with or without a blood volume term (but without k4). Extensions to a model with two nonlinear parameters (such as a model with two tissue compartments) would require a 2-D search instead of the direct function inverse in (21). Note that there are very few examples in the literature of voxel-by-voxel fitting of such a model without substantial regularization to control noise.
Further, although this model may be appropriate in the brain, this might not be true for nonbrain regions, especially if radioactive metabolites enter nonbrain regions. Thus, integration of modeling for regions outside the brain may require a hybrid method where the 4-D model is only applied to brain voxels. An additional correction that would be required for real data is adjustment of the input function for time delay between the site of measurement and the organ of interest. This is conventionally performed by a fit of the whole brain TAC (often just the first few frames) with an additional delay parameter. Thus, in the context of PMOLAR-1T, reconstructions of a few individual early frames may be necessary to estimate this time delay. Further, sensitivity of PMOLAR-1T to other errors in the input function, both deterministic and stochastic, must be evaluated and compared to frame-based methods.
VI. Conclusion
In this paper, we introduced a method called PMOLAR-1T for the direct reconstruction of kinetic parameters from PET list mode data. This approach integrated the one tissue compartment model and the PET physical model and facilitated kinetic parameters estimation with the help of a novel EM algorithm using a new spatiotemporal complete data space. Substantial more evaluation of this algorithm is required including simulations with motion and motion correction, randoms correction and scatter correction and human data evaluations. Careful evaluation of convergence between 4-D and frame-based methods will also be essential for fair comparisons of resolution and noise. In addition, it is necessary to optimize the software to decrease the computation time. Based on the results presented here, we believe that this 4-D EM method is a promising approach to reduce noise in PET parametric images, especially in low-count situations.
Acknowledgments
This work was supported by the National Institute of Neurological Disorders and Stroke under Grant R01NS058360, Clinical and Translational Science Awards under Grant UL1 RR024139 from the National Center for Research Resources (NCRR), National Institutes of Health (NIH) Roadmap for Medical Research and Siemens Medical Systems. Its contents are solely the responsibility of the authors and do not necessarily represent the official review of NCRR or NIH.
Contributor Information
Jianhua Yan, PET Center, Department of Diagnostic Radiology, Yale University, New Haven, CT 06520 USA. He is now with the A*STAR-NUS, Clinical Imaging Research Center, Center for Translational Medicine, Singapore 117599 (yan_jianhua@circ.a-star.edu.sg).
Beata Planeta-Wilson, PET Center, Department of Diagnostic Radiology, Yale University, New Haven, CT 06520 USA.
Richard E. Carson, PET Center, Department of Diagnostic Radiology, Yale University, New Haven, CT 06520 USA.
References
- [1].Innis RB, Cunningham VJ, Delforge J, Fujita M, Gunn RN, Holden J, Houle S, Huang S-C, Ichise M, Iida H, Ito H, Kimura Y, Koeppe RA, Knudsen GM, Knuuti J, Lammertsma AA, Laruelle M, Maguire RP, Mintun M, Morris ED, Parsey R, Price J, Slifstein M, Sossi V, Suhara T, Votaw J, Wong DF, Carson RE. Consensus nomenclature for in vivo imaging of reversibly binding radioligands. J. Cerebral Blood Flow Metabol. 2007;vol. 27:1533–1539. doi: 10.1038/sj.jcbfm.9600493. [DOI] [PubMed] [Google Scholar]
- [2].Wilson DW, Tsui BMW. Noise properties of filtered-back-projection and ML-EM reconstructed emission tomographic images. IEEE Trans. Nucl. Sci. 1993 Aug.vol. 40(no. 4):1198–1203. [Google Scholar]
- [3].Stayman JW, Fessler JA. Regularization for uniform spatial resolution properties in penalized-likelihood image reconstruction. IEEE Trans. Med. Imag. 2000 Jun.vol. 19(no. 6):601–615. doi: 10.1109/42.870666. [DOI] [PubMed] [Google Scholar]
- [4].Snyder DL. Parameter estimation for dynamic studies in emission-tomography systems having list-mode data. IEEE Trans. Nucl. Sci. 1984 Feb.vol. 31(no. 2):925–931. [Google Scholar]
- [5].Carson RE, Lange K. The EM parametric image reconstruction algorithm. J. Am. Stat. Assoc. 1985;vol. 80(no. 389):20–22. [Google Scholar]
- [6].Kamasak ME, Bouman CA, Morris ED, Sauer K. Direct reconstruction of kinetic parameter images from dynamic PET data. IEEE Trans. Med. Imag. 2005 May;vol. 24(no. 5):636–650. doi: 10.1109/TMI.2005.845317. [DOI] [PubMed] [Google Scholar]
- [7].Reader AJ, Matthews JC, Sureau FC, Comtat C, Trebossen R, Buvat I. Iterative kinetic parameter estimation within fully 4-D PET image reconstruction. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2006;vol. 3:1752–1756. [Google Scholar]
- [8].Yetik S, Qi J. Direct estimation of kinetic parameters from the sinogram with an unknown blood function. IEEE Biomed. Img. Symp: Macro Nano. 2006;vol. 1:295–298. [Google Scholar]
- [9].Tsoumpas C, Turkheimer FE, Thielemans K. Study of direct and indirect parametric estimation methods of linear models in dynamic positron emission tomography. Med. Phys. 2008 Apr.vol. 35(no. 4):1299–1309. doi: 10.1118/1.2885369. [DOI] [PubMed] [Google Scholar]
- [10].Wang G, Fu L, Qi J. Maximum a posteriori reconstruction of the Patlak parametric image from sinograms in dynamic PET. Phys. Med. Biol. 2008 Feb.vol. 53:593–604. doi: 10.1088/0031-9155/53/3/006. [DOI] [PubMed] [Google Scholar]
- [11].de Jong HWAM, van Velden FHP, Kloet RW, Buijs FL, Boellaard R, Lammertsma AA. Performance evaluation of the ECAT HRRT: An LSO-LYSO double layer high resolution, high sensitivity scanner. Phys. Med. Biol. 2007 Feb.vol. 52(no. 5):1505–1526. doi: 10.1088/0031-9155/52/5/019. [DOI] [PubMed] [Google Scholar]
- [12].Matthews J, Bailey DL, Price P, Cunningham VJ. The direct calculation of parametric images from dynamic PET data using maximum-likelihood iterative reconstruction. Phys. Med. Biol. 1997 Jun.vol. 42:1155–1173. doi: 10.1088/0031-9155/42/6/012. [DOI] [PubMed] [Google Scholar]
- [13].Meikle SR, Matthews JC, Cunningham VJ, Bailey DL, Livieratos L, Jones T, Price P. Parametric image reconstruction using spectral analysis of PET projection data. Phys. Med. Biol. 1998 Mar.vol. 43:651–666. doi: 10.1088/0031-9155/43/3/016. [DOI] [PubMed] [Google Scholar]
- [14].Nichols TE, Qi J, Asma E, Leahy RM. Spatiotemporal reconstruction of list-mode PET data. IEEE Trans. Med. Imag. 2002 Apr.vol. 21(no. 4):396–404. doi: 10.1109/TMI.2002.1000263. [DOI] [PubMed] [Google Scholar]
- [15].Reader AJ, Sureau FC, Comtat C, Trebossen R, Buvat I. Joint estimation of dynamic PET images and temporal basis functions using fully 4-D ML-EM. Phys. Med. Biol. 2006 Nov.vol. 51:5455–5474. doi: 10.1088/0031-9155/51/21/005. [DOI] [PubMed] [Google Scholar]
- [16].Li Q, Asma E, Ahn S, Leahy RM. A fast fully 4-D incremental gradient reconstruction algorithm for list mode PET data. IEEE Trans. Med. Imag. 2007 Jan.vol. 26(no. 1):58–67. doi: 10.1109/TMI.2006.884208. [DOI] [PubMed] [Google Scholar]
- [17].Verhaeghe J, D’Asseler Y, Vandenberghe S, Staelens S, Lemahieu I. An investigation of temporal regularization techniques for dynamic PET reconstructions using temporal splines. Med. Phys. 2007 May;vol. 34(no. 5):1766–1778. doi: 10.1118/1.2723879. [DOI] [PubMed] [Google Scholar]
- [18].Reader AJ, Sureau FC, Comtat C, Trebossen R, Buvat I. Simultaneous estimation of temporal basis functions and fully 4-D PET images. IEEE Nucl. Sci. Symp. Med. Im. Conf. 2006;vol. 4:2219–2223. doi: 10.1088/0031-9155/51/21/005. [DOI] [PubMed] [Google Scholar]
- [19].Reader AJ, Matthews JC, Sureau FC, Comtat C, Trebossen R, Buvat I. Fully 4-D image reconstruction by estimation of an input function and spectral coefficients. IEEE Nucl. Sci. Symp. Med. Im. Conf. 2007;vol. 4:3260–3267. [Google Scholar]
- [20].Verhaeghe J, Ville DVD, Khalidov I, D’Asseler Y, Lemahieu I, Unser M. Dynamic PET reconstruction using wavelet regularization with adapted basis functions. IEEE Trans. Med. Imag. 2008 Jul.vol. 27(no. 7):943–959. doi: 10.1109/TMI.2008.923698. [DOI] [PubMed] [Google Scholar]
- [21].Rahmin A, Zhou Y, Tang J. Direct 4-D parametric image estimation in reversible tracer binding imaging. J. Nucl. Med. 2009 Jun.vol. 50:137–138. [Google Scholar]
- [22].Wang G, Qi J. Generalized algorithms for direct reconstruction of parametric images from dynamic PET data. IEEE Trans. Med. Imag. 2009 Nov.vol. 28(no. 11):1717–1726. doi: 10.1109/TMI.2009.2021851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Yan J, Wilson BP, Carson RE. Direct 4-D list mode parametric reconstruction for PET with a novel EM algorithm. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2008 Oct.vol. 4:3625–3628. doi: 10.1109/NSSMIC.2008.4774103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Carson RE, Valk PE, Bailey DL, Townsend DW, Maisey MN, editors. Positron Emission Tomography, Basic Science and Clinical Practice. Springer; London, U.K.: 2002. Tracer kinetic modeling in PET. [Google Scholar]
- [25].Lange K, Carson RE. EM reconstruction algorithms for emission and transmission tomography. J. Comput. Assist. Tomogr. 1984 Apr.vol. 8:306–316. [PubMed] [Google Scholar]
- [26].Shepp L, Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imag. 1982 Oct.vol. 1(no. 2):113–122. doi: 10.1109/TMI.1982.4307558. [DOI] [PubMed] [Google Scholar]
- [27].Carson RE, Barker WC, Johnson JL. Design of a motion-compensation OSEM list-mode algorithm for resolution-recovery reconstruction for the HRRT. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2003;vol. 5:3281–3285. [Google Scholar]
- [28].Jin X, Mulnix T, Wilson BP, Gallezot JD, Carson RE. Accuracy of head motion compensation for the HRRT: Comparison of methods. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2009:3199–3202. doi: 10.1109/NSSMIC.2009.5401706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Rodriguez M, Liow JS, Thada S, Sibomana M, Chelikani S, Mulnix T, Johnson CA, Michel C, Barker WC, Carson RE. Count-rate dependent component-based normalization for the HRRT. IEEE Trans. Nucl. Sci. 2007 Jun.vol. 54(no. 3):486–495. [Google Scholar]
- [30].Barker WC, Liow J-S, Zhao Y, Thada S, Iano-Fletcher A, Lenox M, Michel C, Johnson CA, Carson RE. Randoms estimation for list-mode reconstruction for the ECAT HRRT. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2004:3510–3513. [Google Scholar]
- [31].Watson CC. New, faster, image-based scatter correction for 3-D PET. IEEE Trans. Nucl. Sci. 2000;vol. 47:1587–1594. [Google Scholar]
- [32].Gallezot JD, Nabulsi N, Neumeister A, Wilson BP, Williams WA, Singhal T, Kim S, Maguire RP, McCarthy T, Frost JJ, Huang Y, Ding Y, Carson RE. Kinetic modeling of the serotonin 5-HT1B receptor radioligand [11C]P943 in humans. J. Cerebral Blood Flow Metabol. 2010;vol. 30:196–210. doi: 10.1038/jcbfm.2009.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Naganawa M, Wilson BP, Nabulsi N, Ropchan J, Labaree D, Neumeister A, Huang YY, Carson RE. Tracer kinetic modeling of [11C] AFM, a new PET imaging agent for the serotonin transporter. J. Nucl. Med. 2008;vol. 49:118. [Google Scholar]
- [34].Wilson BP, Yan J, Mulnix T, Carson RE. Quantitative accuracy of HRRT list-mode reconstructions: Effect of low statistics. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2008:5121–5124. doi: 10.1109/NSSMIC.2008.4774388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Yan J, Wilson BP, Gallezot JD, Carson RE. Initial evaluation of direct 4-D parametric reconstruction with human PET data. IEEE Nucl. Sci. Symp. Med. Imag. Conf. 2009:2503–2506. doi: 10.1109/NSSMIC.2009.5402049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Lammertsma AA, Hume SP. Simplified reference tissue model for PET receptor studies. Neuroimage. 1996 Dec.vol. 4(no. 3):153–158. doi: 10.1006/nimg.1996.0066. [DOI] [PubMed] [Google Scholar]