Motor primitives and synergies in spinal cord and after injury– the current state of play

Abstract

Modular pattern generator elements, also known as burst synergies or motor primitives, have become a useful and important way of describing motor behavior, albeit controversial. It is suggested that these synergy elements may comprise part of the pattern shaping layers of a McCrea/Rybak two layer pattern generator, as well as being used in other ways in spinal cord. The data supporting modular synergies ranges across species including man and encompasses motor pattern analyses and neural recordings. Recently, synergy persistence and changes following clinical trauma have been presented. These new data underscore the importance of understanding the modular structure of motor behaviors and the underlying circuitry in order to best provide principled therapies and to understand phenomena reported in the clinic. We discuss the evidence and different viewpoints on modularity, the neural underpinnings identified thus far, and possible critical issues for the future of this area.

Introduction

We here review ideas and experimental data related to modularity, in particular motor primitives and muscle synergies, and recent work suggesting the direct clinical relevance of these ideas and data. We will highlight gaps to be filled by the research community which are likely, when filled, to produce new therapeutic information and strategies.

Modular systems have components which may be separated and recombined. Modularity thus implies a compositional set of building blocks with different possible arrangements.^1,2 Interest in motor modularity has grown greatly recently.^3,4 However, the area remains controversial and competing perspectives are presently available on the topic. For example, there are several levels of analysis ––kinematic, muscle, neural, supporting modularity –– and several different sets of ideas about the origins of modularity in each of these. Depending on the perspective, modularity can be seen as a benefit or an impediment to motor control, as a fundamental neural structural feature, as an epiphenomenon of other more fundamental mechanisms, and as offering both clinical opportunities and hindrances. However, it is becoming clear that modularity perspectives at the worst offer a concise shorthand to describe clinical changes and pathology,^5–7 and for this reason alone it is important to gain a better insight into modularity. Our understanding of the processes supporting modular motor control and the spinal segmental implementation of modularity remains sketchy,^8–12 but filling out this understanding will be the only way to resolve the controversies and leverage modular descriptions to clinical benefit.

Definitions and types of modules

Modularity is apparent at several levels of analysis in motor control. Table 1 summarizes many of the levels and descriptions used, and some examples of biomimetic robotic uses of modularity for comparison. Here we unpack this description.

Table 1.

Modularity terminology and relationships among descriptions and units

Marr level of description	Increasingly finer resolution elements of action composition and control					Type of data and description
Task  Behavioral task/Kinematic task/Task planning	Behavior (e.g., Hunt, groom etc.)	Task: (run to capture); akinematic oscillation	Subtask: (swing, stance, foot placement, reach to grasp)	Stroke/kinematic segmentation unit = kinematic stroke or kinematic primitive		Kinematics
Algorithms  Controls/algorithms (kinetics necessary)		Timing, rhythm & sequence	d Force pattern for subtask, possible co-articulation	Force pattern for individual kinematic stroke, possible co-articulation	Unit building block for force patterns. Force-field primitives = kinetic primitives	Kinetics
		bRhythm generator system	cPattern shaping under rhythm generator, descending and sensory control influences or		gBurst synergies = motor primitives = force-field primitive. Unitary burst (or “pulse”) of a synchronous muscle synergy	Muscle patterns
		Rhythm generator system	Pattern shaping system	eTime-varying synergies
Implementation  Implementations/circuitry		Neural oscillator or state chaining system	fNeural switching systems or emergent pattern shaping and sequencing processes		Separated neural premotor drives and burst generation	Neural support
		<=> robotic Dynamical movement primitive (oscillator primitives) or finite state machine	<=> robotic Coupling or selection and switching policy, e.g., finite state machine with time outs	<=> robotic Kinematic primitive and PID controller	<=> robotic Kinetic primitive or multi-joint PD control unit	Sample equivalent idea in biomimetic robotics

Note: Missing from the table are the synergy formulations as optimal controlled subspaces, and controlled/uncontrolled manifolds. The missing terms and models of modularity are harder to relate simply and directly to pattern generation and spinal neural circuits in testable hypotheses. In the table, specific relationships or areas need significant work and are important to understand new data on modularity in stroke and spinal cord injury.

^aThe relations of rhythmic and discrete motion at kinematic and production descriptions remain an area of ambiguity.

^bAs might be expected, rhythm/timing generation mechanisms and circuit location remain insufficiently specified.

^cThe structure of pattern shaping remains difficult and controversial. The separation from rhythm generation is controversial. The composition and modularity of pattern is disputed. Modularity can be considered emergent from network dynamics or based on switching and incorporation of explicit modules.

^dEfficient kinematic and kinetic action may involve co-articulation of modules in sequences and mechanisms should support this contextual adjustment for increasing skill levels in tasks.

^eModules in pattern shaping could be fixed sequences of several bursts, also called time varying synergies, that are explicitly related to kinematic modules such as strokes or cycles. Alternatively, pattern shaping modules could be single bursts, that are not uniquely or closely related to kinematic strokes and cycles (e.g., unit bursts/synchronous synergies that instead relate directly to units of biomechanical modularity such as unitary force-fields, and to neural drive (see ^g below).

^fThe structure of neural switching and pattern sequencing is very poorly understood but is probably crucial to understand processes of co-articulation, merging, splitting, and sequence changes after neural damage and during therapy.

^gNeural underpinning of unit bursts and drive structure are also part of the key to these clinically meaningful processes.

Kinematic descriptions

Early kinematic analyses undertaken by ethologists supported modular constructions, although these ethological descriptions generally faltered as more detailed analysis of execution was considered.¹⁷ Nonetheless, Fentress and Golani,^13,14 and more recently Whishaw,^15,16 have used such kinematic modular analyses to good effect. Kinematic execution modularity has provided the most insight in work on human reach kinematics and its segmentation. As elements of the segmentation, unitary “kinematic strokes” were noted by Viviani and Terzuolo.¹⁸ Explanations for the observed stroke properties were first explored by Hogan and Flash^20,21. In general, the motions of limb end-points exhibit straight paths, and have unimodal bell-shaped tangential velocity profiles. These profiles and the resultant stroke segmentations were consistent with kinematic optimization and were well predicted by an endpoint minimization of jerk.^20,21 For point to point motions, these features are preserved across loads and in different species and environments.^12,22,23 However, likely due to features of biological limb design, the kinematic strokes observed are also consistent with various other kinetic and task optimizations. These other optimizations include minimum torque change and minimized signal dependent noise at the muscle.²⁴ Superposition of collections of kinematic strokes by the central nervous system (CNS) account for various learning, correction, and rehabilitation phenomena.^23,25,27 Flash and colleagues continue to develop better descriptions for similar analyses of more complex 3D kinematics.²⁶

Pattern generation and pattern structure descriptions

Rhythmic motions have repeating forms that can be considered modular. Modular and repeatable controls for rhythmic motions have been evaluated at both kinematic and motor pattern levels. Evaluations at the kinematic level include the research of Schaal and colleagues,^28,29 and Sternad and Hogan.^30,33 Schaal, Ijspeert, and colleagues suggested dynamic primitives in robotics.^31,32 Pattern generation was clearly established by seminal work of Wilson, Grillner, and their successors in both vertebrate and invertebrate animals,³⁴ and suggested that central motor pattern was fundamental.³⁵ Examples of modularity at the pattern generator levels would be unit burst generators for hip flexion and hip extension as examined by Stein and colleagues in turtles.^36–39 The CNS can organize modular patterns underlying behaviors (usually rhythmic), independent of any feedback or patterned input. Identifying the structure of pattern generator circuitry is an ongoing process. While the neural elements comprising the structure of patterned generators are well identified and modeled in simpler vertebrate circuits,^36,40 the topic is significantly less well understood in complex mammalian systems. The biological central pattern generators (CPGs) could represent several types of engineer-style controllers. Neural networks in the CNS could implement dynamic system limit-cycle oscillators. These might be implemented as half center oscillators, as in the original models of Brown and succeeding work. Alternatively, the CPG might represent a kind of finite state machine, one that cycles through its states in the absence of rhythmic inputs. Various pacemaking and burst generating mechanisms in neurophysiology, e.g., in respiration,⁴¹ arguably show some features of such a system. Recent data from the paralyzed decerebrate cat supports a hierarchical hybrid CPG in mammalian hindlimb locomotion: a rhythmic or clocking system layer (constructing timing features and perhaps state sequencing) exerts control on a pattern shaping layer.^42–48 This hybrid framework is also consistent with component motor primitive/synergy elements (see below) and unit burst elements.^36–39

Muscle Synergies

To discover pattern and modularity in unparalyzed animals and humans behaving more broadly, statistical analysis of motor patterns has been used.^7,59–511 In animals ranging from the frog to the intact or injured human being, and in both rhythmic and non-rhythmic behaviors, application of statistical decomposition techniques show a remarkably similar breakdown of muscle activation patterns into modular muscle groups (or synergies or drive motor primitives). Other non-statistical physiological methods also support the modules and analysis results.^52,53 These muscle groups or synergies are activated as unitary synchronous muscle bursts or pulses, either in sequence or simultaneously, across various test paradigms.^51,54–64 They are adjusted and adapted by the CNS in response to the task conditions by selecting among the different synergies, and by changing overall burst amplitudes and onset timings. Dimensionality reduction of the full range of muscle activations that are possible, down to a significantly smaller set of muscle synergies, seems to be the rule. The data are thus consistent with the separate sequencing and control of a small set of premotor drives in each task. The precise structure of the drives has been disputed. Some authors have favored synchronous unit bursts (equivalent to neurophysiological unit burst generators.^{9,51–53,56,,65}), while others have favored time sequences of muscle activations, with the whole sequence acting as an atom or unit of the motor patterns.^60,61,63 Pulses of synergistic activity (or unit burst generators) that act as fundamental building blocks of patterns at spinal levels, added or deleted as units, seem to be favored by most data from both fictive, semi-intact, and intact animal behaviors.^{8,9,36,42,52,53}

Linking muscle synergy to biomechanics - unit bursts as force-field primitives

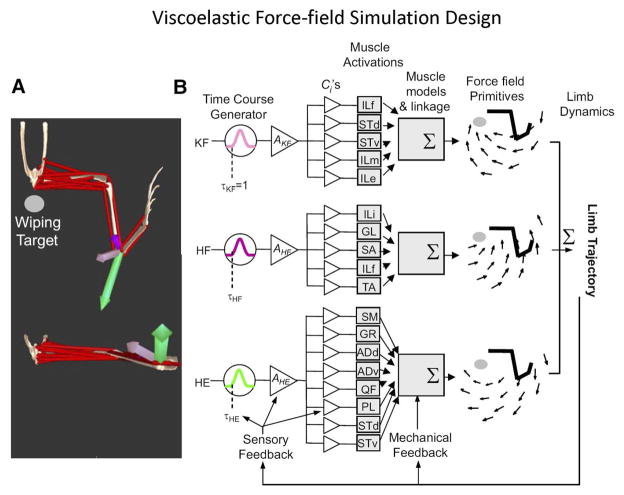
Muscles are intrinsically visco-elastic. The precise mechanical properties vary with activation, history of activation, and shortening or lengthening history. Muscles act in concert via soft tissues, ligament and tendon systems and their moment arms, through the skeletal linkage and its Jacobean properties, to generate forces that can be described as position- and velocity-dependent fields. The simultaneous (synchronous) activation of a collection of muscles produces a well-defined visco-elastic force-field in the limb which modulates with time. This field depends on the initial limb state. In this way force-field descriptions can capture the action of muscle synergies (Fig. 1 and ^66–74). Muscles in a synchronous burst synergy have fixed ratios to each other, matching the ratios of c_is in Figure 1, e.g., see Figure 2. These force-field descriptions show the property of linear vector superposition, which can be demonstrated when fields are combined through electrical stimulation of spinal cord, or during natural drive co-activations.^52,53,65,71 Feedback systems in the spinal cord do not disrupt these visco-elastic force-field structures, but rather seem to support them.⁵³

Figure 1.

Simulating hindlimb wiping with a detailed model of the spinal primitives. (A) The 13 hindlimb muscles forming the biomechanical model are shown as red lines. Colored arrows mark the force directions of the three force primitives at a fixed limb position during the isometric wiping response: KF (knee flexor primitive), light purple; HE (hip extensor primitive), green; HF (hip flexor primitive), dark purple. (B) The framework used to simulate wiping (left to right): each primitive had a time-course generator, representing the premotor drive burst, which output a normalized waveform (peak = 1.0) at time τ. The variable A scaled this waveform, which was then distributed to each of the muscles within the primitive. Each muscle had a muscle-specific variable C that scaled the excitation wave form. The synergy muscle groups generate contractile forces MF that are transmitted through the limb to produce anisometric endpoint force (at one position) or force field FF (when forces are measured across a range of positions). Normalized force fields produced by each primitive are shown in the far right. When the model limb is freed to move, MFs drive the motion of the model. MF values are in turn regulated by the limb motion (i.e., the force–velocity and force–length properties of muscle and stress–strain properties of in series connective tissue alter MF forces). In this version model, sensory feedback from muscles potentially regulate τ A or C. ILf, iliofibularis; STd, semitendinosus dorsal branch; STv, semitendinosus ventral branch; ILm, iliacus median; Ile, iliacus externus; ILi, iliacus internus; GL, gluteus; SA, sartorius; TA, tibialis anticus; SM, semimembranosus; GR, gracilis; ADd, adductor dorsal; ADv, sdductor ventral; QF, quadratus femoris; PL, peroneus longus. Reproduced from Ref. 83, with permission.

Figure 2.

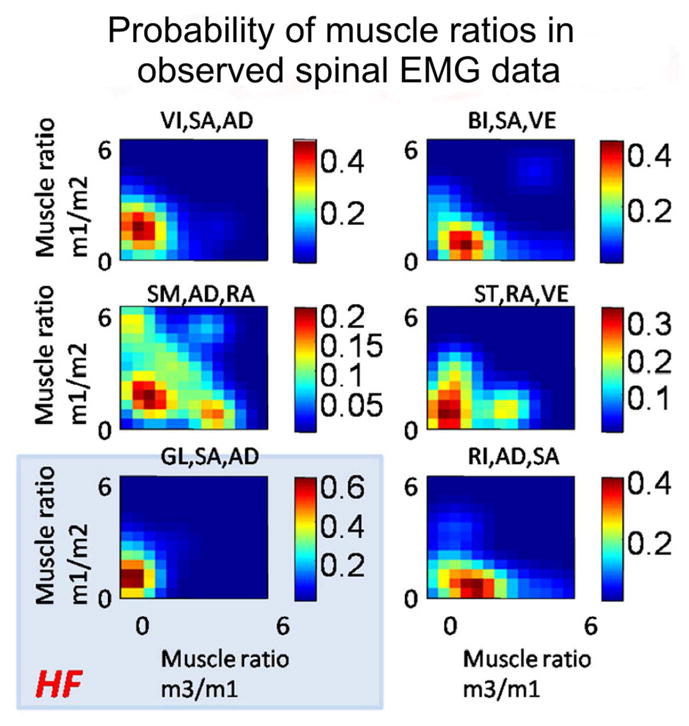
Examining reproducibility of frog primitives. Stability of muscle proportionality ratios in the six main primitives are observed across frogs and across behaviors. The action of the spinal cord across the tested behaviors was to recruit the muscles in fixed ratios and thereby couple muscles so as to generate specific force-field primitives and associated preflex responses. Reflex actions (i.e., feedback effects) modulated these primitives, not individual muscles (see Ref. 53), and thus acted on their component muscles as groups. HF, hip flexor synergy. Muscle Abbrev (nomenclature of Ecker, with equivalent Abbott and Lombard): VI, vastus internus (= iliacus internus); VE, vastus externus (= iliacus externus); BI, biceps (= Iliofibularis); AD, adductor magnus; SA, sartorius; RA, rectus anticus (= quadratus femoris); GL, gluteus. Reproduced from Ref. 83, with permission.

A synergy-driven force-field is a predictable pattern, whether the synergy is activated as a single primitive, as part of a coordinated reflex, or in a voluntary pattern. A ‘force-field motor primitive’ in biomechanics can be associated with a muscle synergy, and corresponds 1:1 to the specific premotor drive bursts (or primitive pulses) occuring in the motor pattern. In effect, the actions of the multiple simultaneously pulsed drives and their associated muscle recruitment effects can be summarized as a sum of the individual muscle biomechanical force effects :

$$F(q,\stackrel{.}{q},t)=\sum _i{A}_i{a}_i(t){\mathrm{\Phi }}_i(q,\stackrel{.}{q})$$ (1)

where q is a configuration vector, F is the total limb force-field, A_i is the amplitude of the activation of the i^th force-field motor primitive, a_i(t) is the normalized activation time course of the ith primitive, and Φ_i is the normalized visoelastic field associated with the ith premotor drive and its collection of associated muscles. This summation has been demonstrated experimentally.^68,69,70,71 Since each field Φ_i consists of the sum of individual muscle fields, this framework naturally extends from an initially constrained low degree of freedom synergies/motor primitives in reflex and pattern generation through to the fullest voluntary use of spinal cord capabilities of the motor system using individuated muscles that are driven independently from one another.

To generate flexible behaviors and action using the individual premotor drive pulses, the pulses may be repeated and staggered in different combinations:

$$F(q,\stackrel{.}{q},t)=\sum _i{A}_{i}a(t+{\tau }_i){\mathrm{\Phi }}_i(q,\stackrel{.}{q})$$ (2)

where τ_i represents the time shift of the ith drive pulse. The point of this brief mathematical excursion is that a matching between Newton’s laws, a compact control framework, and synergy bursts as motor pattern elements is possible and, taken together, this suggests a simple compositional scheme for movement. This framework ably represents spinal generated behaviors and reflexes^53,83 (see Figures 1–3). It also maps cleanly onto the inferred hierarchical control of the pattern shaping systems suggested by McCrea, Rybak and others.

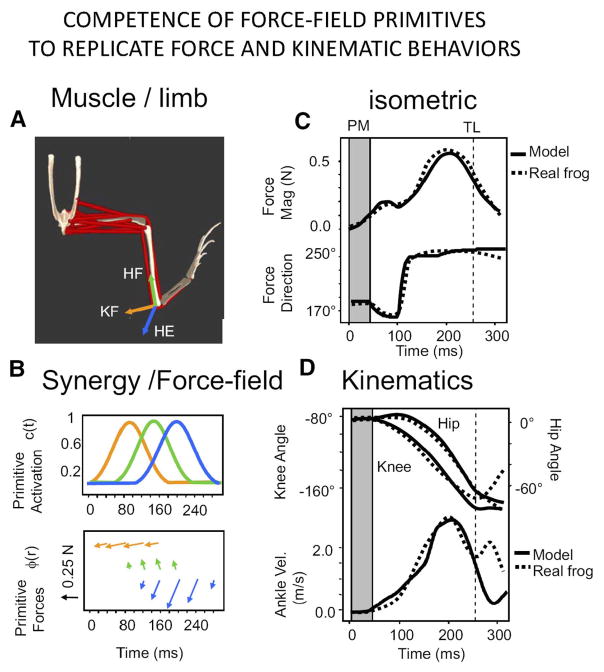
Figure 3.

Simulation results using a framework of primitives. Simulating wiping forces and kinematics with the primitive framework and model frog. (A) Model structure. (B) Activation of muscles as synergies. (C) The isometric force pattern produced by the model frog (solid lines) closely matched the force pattern recorded experimentally (dotted lines). (D) After making minor adjustments to the isometric motor pattern (amplitude scaling the ensemble down slightly) the model frog also reproduced the free limb kinematics of the experimental frog. Without downscaling the forces were too strong, indicating potential feedback adjustment in isometric conditions. The top row shows hip and knee angles. The bottom row shows ankle velocity. Dashed line marks the time of target limb contact in the real frog. The gray area (PM) represents the 40-ms premovement period between EMG onset and motion onset that is observed in real frogs.

Support of motor modularity across species

The kinematic stroke modularity seen in human reaching ²⁵ is also exhibited in octopus reaching^12,76 in a marine environment using very different effector and neural control circuitry. This suggests fundamental aspects of physics, mechanics and task control may be a basis for the structure of kinematic strokes. Similarly, basic postures and stereotypic motions are exhibited in swimming turns, escape (C-start turns) and other kinematic controls.^77,78 Rhythmic kinematics of locomotion in both aquatic, terrestrial and aerial media support common compositional features, this leading Koditschek and Full to the notion of templates and anchors.⁷⁹ Templates represent the lowest order (lowest dimensional) description of the essence of the physical task and its requirements. Anchors are specific hypotheses regarding the neuromuscular and biomechanical controls used for implementation of the template. In their scheme, motor primitives of any kind (kinematic or kinetic) would be the anchors that allow low dimensional and efficient physical task performance.

Motor patterns and muscle/pattern modularity across species

Features of the motor patterns, stereotypic bursting, and synergies supporting both stereotypic and more flexible behaviors are common from invertebrates to man. Examples of common features have been reviewed and remarked on extensively.⁸⁰ Recent work from Lacquaniti, Ivanenko, Dominici and colleagues has shown the similarity of rhythmic pattern construction in guinea fowl, rat, cat and human, and across human development, linking rhythm generation and primitives across species.⁶⁴

Interpreting modular structures: task, algorithm, and implementation

Modularity as exhibited across species in kinematic, kinetic, and motor pattern features could be considered in several ways. The neuroscientist David Marr ⁸¹ suggested considering nested levels of task, algorithm and implementation in analyzing CNS function in behavior. This scheme is useful in modularity because it highlights the points of convergence and divergence in different accounts of modularity. At the task level, modularity may simply represent task features that must be managed as constraints or task affordances in the real world: most locomotion and physical engines employ cyclic features, etc. and often have, in the parlance of Full and Koditschek, similar templates. At the algorithmic level, if task solutions are modular, how is this accomplished computationally? What are the computational anchors? How flexible and general are the algorithms employed in different biological systems, in different tasks, and at different levels of the neuraxis? Control theory as a field has developed numerous principled and powerful ways of constructing and managing controls that often converge on modular solutions, and the field continues to advance rapidly. Complex issues such as problems of degrees of freedom are proving more tractable than originally supposed, though still by no means paper tiger problems that can be ignored.⁸⁴ Optimization methods in control lead to modular solutions.^85–89 It is natural to wonder how much of the biological circuitry represents the implementation of a set of powerful, flexible, and principled control algorithms.^90–97 Alternatively, how much of biological circuitry represents hacks, heuristics, and the historical baggage from evolution? Engineers all recognize that real-world systems are a compromise between what is ideal and what is possible, given the manufacturing, design, material and other costs available. We do not know how best to balance this cost as we think about biology and motor evolution, ontogeny, and learned interactions. Data and simulation results are often consistent with both perspectives.^98,99 It seems that algorithmic flexibility, generality, and learning time must be weighed against the evolutionary pressure to function rapidly (e.g., the wildebeest calf, hatchling sea turtle). The pack-and-go cost of added neural hardware for flexibility in weight and energy consumption must be balanced against other options for using the mass and energy. Some of these kinds of trade-offs are observed in modern consumer technologies such as mobile phones, which also must survive in the marketplace in competition with other choices. Not every phone type is equally smart, or similarly controlled, and each has its niche. While some researchers view modules as built into the neural structure of the CNS by evolution,⁸ others see them as arising from an optimal control implementation operating on the anatomical affordances in the musculoskeletal system. In this last view, modularity arises as an optimal strategy and division of labor by the optimal controller, which parcels task dimensions into a controlled and an uncontrolled manifold, (i.e., different subspaces) with the controlled task operating in low dimensions.^94–96

Some behavioral needs that can always be anticipated are partly embedded in the mechanical design of limbs. De novo neural motor solutions in each generation may waste time and lose access to scarce resources, and be selected against. Further, in biological systems, all requirements for function are not available a priori in early development. Future control needs must be anticipated or learning must be channeled to support the critical functions needed later, beyond the current locally optimal learning. Developmental research supports much pre-structuring of circuits, prior to feedback use.^103–106 Nonetheless, subsequent adaptation and extensibility of behaviors are also needed, and automaton-like behavior is clearly insufficient.^100–102 Optimization and adaptation in adults is essential. Modularity, if well crafted by evolution, should support both early function and later adjustment to conditions and new affordances.

How might the circuitry and algorithms suggested by these different views arise and be supported in the spinal cord? Are they built-in by evolution, learned in child development, or developed denovo in task solutions? In Marr’s scheme,⁸¹ the implementation details of neural systems, where available, may help resolve these conundrums. Current data suggest that different perspectives can be correct, depending on species, age, task, and the specific CNS circuit regions that are examined.

Implementation of spinal primitives and modules –spinal structures

Several lines of investigation support spinal circuits explicitly geared toward modularity. The competence of modular systems is largely established. From the perspective of synergy-based modularity, work in frog, cat, and monkey bears strongly on these issues. In our lab, Corey Hart has demonstrated with single unit extracellular recordings in the frog spinal cord that interneurons with mono- or di-synaptic projections to motor pools replicate the patterns and weightings of synergy drives.¹⁰⁷ Other interneurons showed a range of features that further support the idea that the frog reflex circuitry is organized to drive and control onset timing, amplitude, and combinations of synergy and primitives in spinal reflexes (¹⁰⁷ and unpublished data). Recordings by Berkowitz and colleagues in turtles support similar shared and specialized neural structures that might match with synergy/primitives analyses of motor pattern.^108–110 Behavioral state-dependent control and altered output patterns from a spinal circuit in this case are expected to arise from rearranging the onset timing and combinations of synergy primitives, not from radical alteration of these drive circuits. Within such a framework, duplication of similar projecting drive circuit neurons for specialized use in various contexts could occur. Specialized drive systems that contribute to reaching were characterized in the work of Alstermark and colleagues on the C3–C4 interneuron systems (reviewed by Alstermark and Isa, ¹¹¹). The precise premotor drive and motoneuron projection patterns of these neurons are not sufficiently characterized to show whether there are truly discrete sets of modular drive projections, but the roles and even genetic developmental processes of the C3–C4 systems in mice, cats, and monkeys are now beginning to yield to modern methods.¹¹² The work of Seki and colleagues, recording in monkey spinal cord, also supports possible modular groupings in upper limb controls.¹¹³ Taken together, these studies all represent modern extensions of the modular ideas initiated by Hall, Brown and Sherrington.¹²¹ In mouse CPG, the extensive data from the combination of physiological and genetic dissection of the interneuron systems may in future be related to ideas of modular spinal organization¹⁰⁷ and to hierarchical pattern generator organization.^42,43 The explicit linkages of developmental mechanisms, genetics, and resulting interneuron form and projection details remain to be determined but will surely yield to this powerful strategy.

Learning and subsuming spinal modular structure through development

A scaffold of basic infrastructure for modular control and pattern generation is likely to be common across tetrapods. Through development this may be put into use very rapidly, or more gradually shaped by learning. Dominici and colleagues have recently performed an analysis and comparison of human and cross-species development of locomotion.⁶⁴ Their data support the idea that the basic modular pattern generation of tetrapods is, in man, gradually specialized for bipedalism through development. The quadrupedal infrastructure is refined: some is preserved and some is modified to satisfy the novel biomechanical constraints of bipedalism. Their account is very much in keeping with a hybrid perspective of evolutionarily embedded bootstrap circuitry, onto which novel extensions and optimizations are layered. ^8,114 In some instances the older circuits are subsumed to form elements of the new control, but in others instances these may be reshaped or replaced to satisfy the novel needs.

This is consistent with the points emphasized by Valero-Cuevas and colleagues, namely that neural modularity constraints will both support and limit biomechanical and behavioral control options, not unlike limb design and the tendon anatomy in the hand.^94–96 The fullest flexibility of behavior is achieved by transcending these constraints where it is feasible to do so. The degree of departure from the early infrastructure in an adult individual will determine the relative importance and therapeutic value of the evolutionarily older circuitry. Various groups are now examining how modularity and spinal modularity impact on the motor learning of able bodied individuals.⁶¹ Older tetrapod circuitry could potentially either aid or hinder learning and rehabilitation after some kinds of injury. Depending on the final adult movement compositionality in able bodied individuals, it is conceivable that the older circuitry could re-emerge as pathology.⁸ However, despite this risk, when thoracic and lumbar circuits are isolated from descending controls in complete spinal cord injury, there may be few options in the clinic but to engage the older and now isolated spinal circuits for therapeutic purposes. It is becoming clear that recruiting these isolated spinal circuits in fact often offers great promise.^115–117 Nonetheless, it is important to understand the end state of spinal circuitry after development and motor learning in man in order to best utilize this promise. Taken together, this all suggests an important role for spinal modularity and pattern generator elaboration in the understanding of disease processes and trauma, and in the design of effective clinical rehabilitaton. Newer studies of human clinical outcomes using modularity analyses support this perspective.

Clinical ramifications of modularity

Recently, the modularity perspectives developed in animal models have begun to be tested in clinical settings. These studies have involved both the upper and lower limb. More is known about animal pattern generation In the lower limb, and work from various groups supports modularity and pattern generation contributions in man.^7,54,55 Clark, Neptune, Ting, Zajac and Kautz have shown that, following stroke, the modularity reported by themselves and others in able-bodied individuals can collapse to still lower dimensions.⁷ This collapse looks like a merging of the healthy modules or synergies. The degree of collapse maybe related to the degree of deficit. With rehabilitation, the merged synergies may again separate themselves and the degree of this re-differentiation may relate to the degree of rehabilitation improvement. These data provide a compelling account of the pathology and recovery processes with clear links to the hierarchical pattern generation and synergy literature. Bizzi and colleagues have examined stroke in the upper limb.^5,6 The C3–C4 systems of Alstermark and the overall modularity described by Drew, Krouchev and colleagues in cats⁵⁰ may be relevant. By comparing the unaffected and affected arms, and the muscle pattern structures recorded in reaching movement tasks in each, they have shown that the same modularity or premotor drive structures often exist in both limb. However, drive use is disordered in pattern in the affected limb. Beyond this, they also observed merging, as was seen in the lower limb by Clark and colleagues. This merging process could be directly correlated with the degree of deficit on clinical scales. Such merging is seen in animal models in deafferentation or other manipulations.⁸² The data from both upper and lower limb human studies suggest that the basic synergy circuits are embedded in the spinal cord and brainstem. Taken together, the Cheung/Bizzi and Clark/Neptune/Ting data suggest that loss of cortical controls causes initial failures in the temporally differentiated control of spinal interneuron systems for synergies in man, but that temporally differentiated controls can be re-established. The Cheung/Bizzi work also showed a further process at work in late chronic stroke. This involved the splitting of some synergies in the affected arm from those that were observed in the unaffected arm (i.e., splitting in the affected limb of the modules observed in the healthy and unaffected limb). The splitting process they observed was interpreted as a possible compensatory reorganization of brainstem and spinal controls that was only possible on a timescale of several or more years. The finer subdivision of modules, as opposed to module merging and separation, seems to take very long periods of concerted effort by patients, suggesting a robustness of modules and a need for prolonged practice or difficult identification of latent circuits to create these subdivisions. Stroke recovery also involves changes in kinematic modules or elements, though these take a different form,²³ with kinematic merging indicating increasing function and skill. What spinal mechanisms support such processes? Transient addition, deletion, merging, and switching processes in modular pattern elements are part of the normal operation of spinal cord reflex and pattern generating systems as underscored by work in turtle by Stein,^118,119 Berkowitz,¹²⁰ and the data in frog discussed above.^52,53,82,107 It is likely the pathological merging observed in trauma relates closely to these low level mechanisms and their neural support. Understanding splitting, merging, and control of component synergy drives and bursts may thus form a key to more principled rehabilitation. Animal models of injury and rehabilitation that exhibit similar merging and splitting phenomena through injury and recovery are likely to provide such understanding.

Conclusions : future issues and known unknowns

Current data support a well defined spinal infrastructure in tetrapods that is layered onto earlier trunk locomotor swimming systems, to augment or supplant them.¹¹⁴ This infrastructure seems to have both rhythm generation and separated modular pattern shaping layers. The modular shaping may comprise specific premotor drive systems, and these are likely to participate, albeit in modified fashion, in adult human movements. Activating the isolated lumbar circuits to restore some level of stepping in severe spinal cord injury recruits all of these systems. Our knowledge of the modular drive systems is still very sketchy. Understanding the organization and operations in the pattern shaping part of the CPG hierarchy is likely to have strong clinical significance. In injury, modular mergings or timing collapses of synergies occur. Later, on timescales of several years, splitting of normal synergies may be possible. We do not know in detail how merging, splitting, and rhythm to pattern shaping interactions operate at the circuit level, what neural systems they employ, or how best to support these circuits in a rehabilitative or other intervention. These latter data are likely to arise more quickly in basic animal models, using neural recordings in reduced preparations and fictive and genetic methods. The resulting knowledge of how the building blocks of pattern interact and support one another in the context of descending and other controls is essential to develop principled integrative therapies and interventions for the clinic.