Abstract
High-order cubic Hermite finite elements have been valuable in modeling cardiac geometry, fiber orientations, biomechanics, and electrophysiology, but their use in solving three-dimensional problems has been limited to ventricular models with simple topologies. Here, we utilized a subdivision surface scheme and derived a generalization of the “local-to-global” derivative mapping scheme of cubic Hermite finite elements to construct bicubic and tricubic Hermite models of the human atria with extraordinary vertices from computed tomography images of a patient with atrial fibrillation. To an accuracy of 0.6 millimeters, we were able to capture the left atrial geometry with only 142 bicubic Hermite finite elements, and the right atrial geometry with only 90. The left and right atrial bicubic Hermite meshes were G1 continuous everywhere except in the one-neighborhood of extraordinary vertices, where the mean dot products of normals at adjacent elements were 0.928 and 0.925. We also constructed two biatrial tricubic Hermite models and defined fiber orientation fields in agreement with diagrammatic data from the literature using only 42 angle parameters. The meshes all have good quality metrics, uniform element sizes, and elements with aspect ratios near unity, and are shared with the public. These new methods will allow for more compact and efficient patient-specific models of human atrial and whole heart physiology.
Keywords: Cubic Hermite finite elements, patient-specific cardiac models, atrial anatomy
1. Introduction
Computational models of cardiac biomechanics and electrophysiology have been used to study normal cardiac physiology (Kerckhoffs et al., 2007; Niederer et al., 2011) and pathological conditions such as heart failure (Kerckhoffs et al., 2010) and atrial fibrillation (Ashihara et al., 2012; Comtois and Nattel, 2011; Gong et al., 2007; Haissaguerre et al., 2007; Jacquemet et al., 2003; Tobón et al., 2008). Recent advances in non-invasive imaging technology have made it feasible to generate patient-specific computational models of the atria and the ventricles, and these models show promise for improving the interpretation of clinical data from patients.
High-order cubic Hermite finite element interpolation schemes have been popular in ventricular finite element modeling: they capture smooth geometries with few finite elements, they can be subdivided to have more degrees of freedom while preserving exact shape, and they represent anisotropy compactly and smoothly by means of fiber angle fields referred to local coordinate axes. Furthermore, cubic Hermite and other high-order solution spaces have convergence advantages in finite element simulations of ventricular biomechanics (Costa et al., 1996) and electrophysiology (Arthurs et al., 2012; Rogers et al., 1996) compared with linear solution spaces, and give rise to continuous currents between elements in electrophysiology problems and continuous stresses between elements in biomechanics problems. The continuity of field solutions in these finite element problems necessitated the use of a “local-to-global mapping” proposed by Nielsen (1987) to define a global set of finite element basis functions and to allow for arc-length continuity between finite elements of different sizes.
A limitation of cubic Hermite finite element problems of the ventricles is that the geometries must be described by a single set of parametric coordinates on a regular grid to guarantee smoothness. Each atrium has a smooth shape and thus could be described compactly by cubic Hermite elements, but the irregular atrial shapes require that such a mesh be discretized into a number of sub-regions, each with its own set of parametric coordinates. At the interface between these regions, there will be vertices with an irregular number of neighboring elements, known as extraordinary vertices. In quadrilateral meshes, extraordinary vertices are best placed at critical points of the principal curvature field to prevent element skew (Alliez et al., 2003) and to capture regions of high curvature. Even so, regions of high curvature are often captured poorly by linear elements compared with high-order finite elements. Moreover, placement of extraordinary vertices is adversely affected by the noise in medical imaging, which worsens calculation of the principal curvature field.
Here we describe new methods for constructing high-quality bicubic and tricubic Hermite finite element meshes of the atria with extraordinary vertices derived from segmentation of non-invasive imaging data. In our patient, we accurately capture the endocardial surface of the left atrium with only 142 bicubic Hermite finite elements, and the endocardial surface of the right atrium with only 90. These meshes are then used to construct a tricubic Hermite biatrial model. Our methods can be applied to atria with variations in pulmonary vein anatomy, wall thicknesses, and fiber architecture, as these variations are important components of patient-specific atrial models (Dössel et al., 2012; Hanna et al., 2011; Jacquemet et al., 2008). As geometric models from in vivo imaging studies are often output as fine triangulations, our methods could be utilized to construct coarse, high-quality models of other irregularly shaped structures as well.
The organization of this paper is as follows: First, we show that a coarse, high-quality atrial mesh can be constructed using a minimum set of extraordinary vertices computed by the Euler characteristic number of the atrium, and that finer geometric details can be captured if additional extraordinary vertices are utilized. Second, we show how Hermite derivatives can be calculated from a linear mesh using a subdivision surface scheme. Third, we show how the local-to-global mapping customarily used in cubic Hermite interpolation can be generalized to meshes with extraordinary vertices to preserve smoothness between elements and to define global basis functions for finite element problems. We then use the global basis functions to solve a penalized least-squares finite element problem and capture the atrial geometries to the accuracy of the segmented data. Fourth, we show our models provide a convenient way to approximate atrial fiber architecture compactly and give rise to smooth fiber orientations between elements. Last, we show that our methods extend readily to patients with anomalous pulmonary vein anatomies, and discuss how precise C1 and G1 continuity can be achieved near extraordinary vertices.
All of the atrial models described here are available to the public in a database as part of the Continuity software project (http://www.continuity.ucsd.edu).
2. Methods
2.1. Definitions
Two contours (surfaces) have tangent continuity, or G1 continuity, at their joining point (edge) if their tangent (normal) vectors point in the same direction. If their magnitudes are also equal in their current parameterizations, they have parametric (C1) continuity. Two contours f and g are arc-length continuous if df / ds = dg / ds for the differential of the arc-length function ds; as defined, continuity of arc-length requires G1, but not C1 continuity. Barsky and DeRose (1989) elaborate the differences in more detail. We sometimes call a surface “smooth” to indicate it is nearly, but not precisely G1 continuous; we elaborate this choice of terminology in Results, Section 3.1.
We define an ordinary vertex to be a vertex on a surface having four connected surface edges; otherwise, it is extraordinary, unless on a boundary. The valence of a vertex is the number of connected surface edges; an ordinary vertex not lying on a boundary has valence four. The elements containing an extraordinary vertex constitute its one-neighborhood. Continuity around an extraordinary vertex means continuity along the common edges in its entire one-neighborhood, and continuity at an extraordinary vertex means continuity in the infinitesimal neighborhood around the point.
Derivative parameters of cubic Hermite interpolation with respect to the parametric coordinates ξ are called local derivatives, and their dual basis functions ψ are called local basis functions. Derivative parameters transformed into the arc-length coordinatess are called global derivatives or ensemble derivatives, and their dual basis functions ψ* called global basis functions or ensemble basis functions.
We refer to the interpolating subdivision scheme utilized in this paper as the Li-Kobbelt subdivision scheme (Li et al., 2005). We use Li-Kobbelt subdivision to calculate Hermite derivatives, and also can use it to refine linear meshes. In contrast, we refine cubic Hermite meshes by interpolating the coordinate functions of each element to interior points. We refer to this subdivision as refinement by Hermite interpolation. Both Li-Kobbelt subdivision and refinement by Hermite interpolation add only ordinary vertices to the refined meshes—the number of extraordinary vertices remains unchanged.
2.2. Overview
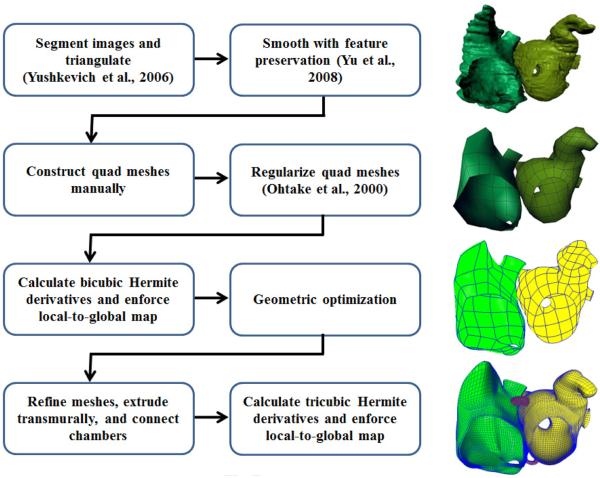
A 68 year-old male was referred to the Veterans Administration Hospital, San Diego for surgical ablation of his persistent atrial fibrillation. He gave informed consent to participate in an Institutional Review Board-approved study and underwent a clinically-indicated computed tomography (CT) study (General Electric 64-slice Lightspeed CT Scanner, 0.5×0.5×0.625 mm) with retrospective electrocardiogram gating. Images were segmented manually with the assistance of an expert cardiac radiologist (P.S.) and structures (left atrium, right atrium, tricuspid valve, and mitral valve) were triangulated using a marching cubes algorithm implemented in ITK-SNAP (www.itksnap.org; Yushkevich et al., 2006). The triangular models were smoothed and coarsened with feature-preservation using GAMer (www.fetk.org/gamer; Yu et al., 2008). The crista terminalis was identified readily in the imaging study as a muscular protrusion in the intercaval region of the right atrium. Owing to insufficient contrast in the imaging study, we were unable to identify Bachmann's bundle or determine atrial wall thicknesses.
Quadrilaterals were overlaid manually onto the endocardial surface triangulations of the left and right atria. Using visual estimation, extraordinary vertices were placed in accordance with principal directions of curvature, and were most often placed at apparent saddle points of the triangular surfaces. The left atrial mesh had 142 elements, and the right atrial mesh had 90. To improve element quality, a regularization step was employed on the left and right endocardial surface meshes using a scheme by Ohtake et al. (2000). The linear quadrilateral meshes were used to calculate bicubic Hermite derivative parameters using the Li-Kobbelt subdivision scheme (Section 2.3). The generalized “local-to-global map” commonly used in cubic Hermite interpolation was used to enforce smoothness at ordinary vertices (Section 2.4) as well as extraordinary vertices (Section 2.5). A geometric optimization scheme (Section 2.6) was used to deform the left and right atrial surface meshes to the vertices of the smoothed triangular meshes obtained above until root-mean squared (RMS) error was 0.62 mm (the largest voxel dimension). We then tested G1 continuity near extraordinary vertices in the geometrically optimized left and right atrial meshes and also in subdivided versions of these meshes (Results, Section 3.1). We calculated the quality metrics of our left atrial mesh and compared them to the quality metrics of a geometrically optimized left atrial mesh constructed from the same patient, but using a different pattern of extraordinary vertices and only 103 elements (Results, Section 3.2).
The left and right atrial surface meshes were refined by Hermite interpolation of coordinates until mean edge length was approximately 2.0 mm. Left and right atrial hexahedral meshes were constructed by extruding the endocardial surface meshes outward in the vertex normal direction 2.0 mm in most regions (Supplemental Data, Table S1). Literature values were used to assign thicknesses to the left atrial roof (Hall et al., 2006), the pulmonary veins (Ho et al., 2001), and the posterior wall of the left atrium (Platonov et al., 2008). Hexahedra representing Bachmann's bundle, the limbus of the fossa ovalis, the coronary sinus, and two inferoposterior bridges were used to connect the two atria. A tricubic Hermite hexahedral mesh having 9,486 elements was constructed using Li-Kobbelt subdivision generalized to volumes, and then the local-to-global map was applied again to enforce smoothness. Using refinement by Hermite interpolation, a second mesh having 75,888 elements was constructed.
Atrial fiber orientations were defined as angles relative to local finite element coordinate axes. One angle at each point defines orientation if atrial fibers are assumed not to lie oblique to endocardial and epicardial surfaces—otherwise, two are required. We captured the principal directions of fiber tracts in our geometric model using consensus fiber orientations described in multiple studies (Cabrera et al., 2008; Ho and Sanchez-Quintana, 2009; Nathan and Eliakim, 1966; Papez, 1920; Wang et al., 1995). We visually compared our results to the description of fiber architecture of Wang and colleagues (Section 3.3). Local angles were represented by a linearly interpolated field with Lagrange basis functions. In most regions (35 of 42 in BiA-75888), the fiber orientation was defined to coincide with the first coordinate axis (i.e., angle zero). In the remaining regions, angles (Supplemental Data, Table S1) were assumed constant with respect to local coordinate axes. Loci of gross discontinuity between fiber tracts (e.g., each lateral border of the septopulmonary bundle) lay at the interface of adjacent mesh regions by construction. Since BiA-9486 was one layer of hexahedra thick, it was unable to capture the abrupt differences in fiber orientation between the subepicardium and the subendocardium known to exist in the posterior left atrial wall and the region of the crista terminalis (Papez, 1920). These transmural differences of fiber orientation were included in BiA-75888 (Figure S1), which has two layers of hexahedra. Fibers in the crista terminalis were defined to course in a superior-inferior direction.
A schematic diagram of the process is displayed in Figure 1.
Figure 1.
A schematic diagram for construction of a biatrial tricubic Hermite hexahedral mesh and intermediate bicubic Hermite surface meshes from a segmented computed tomography study.
2.3. Construction of bicubic and tricubic Hermite meshes using subdivision surfaces
A unitary tricubic Hermite hexahedron is constructed as a mapping from the parametric space (ξ1, ξ2, ξ3) to the coordinate system (Y1, Y2, Y3). Each coordinate function Y is expressed as a linear combination of geometric coefficients yi in a set of basis functions ψi (Eq.1)
| Eq.1 |
The geometric coefficients are coordinate values and coordinate derivatives in the parametric space (e.g., ∂Y/∂ξ1), whereas basis functions ψ are tensor products of cubic Hermite polynomial basis functions Φ. A bicubic Hermite hexahedron constructed similarly, but with only two parametric coordinates (ξ1, ξ2) and only sixteen geometric coefficients and basis functions. More complete descriptions of cubic Hermite splines are given elsewhere (Nielsen et al., 1991; Petera and Pittman, 1991).
Bicubic and tricubic Hermite meshes were constructed from linear quadrilateral and linear hexahedral meshes based on a subdivision surface scheme. A subdivision surface scheme can be used recursively to subdivide a linear surface mesh into more refined instances of itself. Customarily, a sequence of subdivision surfaces will have C1 or C2 continuity properties in a piecewise-linear sense in the infinite limit. Here, we truncate the subdivision surface sequence after two iterations, giving rise to cubic Hermite elements that are nearly but not precisely C1 continuous (see Section 4.2). In contrast to most subdivision schemes, such as that of Catmull and Clark (1978), interpolating subdivision schemes feature vertices in the “parent” surface that remain stationary in each subdivided “daughter” surface. Owing to this constraint, interpolating subdivision captures geometric features that otherwise would be lost, whereas non-interpolating subdivision schemes smooth a surface after comparatively fewer iterations of subdivision.
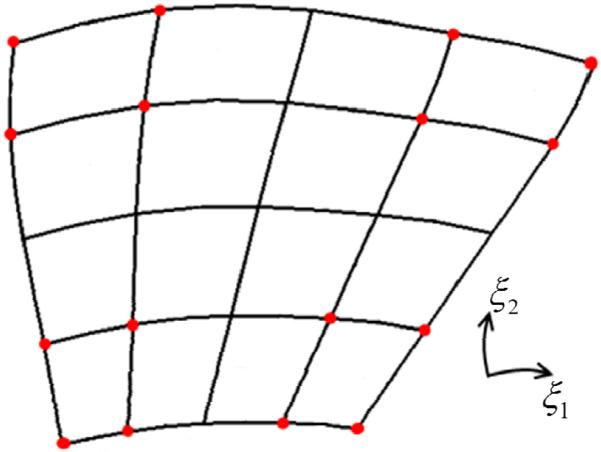
For an interpolating subdivision surface scheme, the natural correspondence between a parent quadrilateral and the sixteen quadrilaterals resulting from two subdivisions provides a means to select derivative parameters for cubic Hermite interpolation. The global and parametric coordinates of 16 of the 25 vertices (21 are newly-added) can be selected to construct a linear system (Eq.2) in the 16 unknown derivative parameters of cubic Hermite interpolation in one quadrilateral from the parent surface. Adjacent vertices lie ξ = 0.25 apart in the parametric coordinates of the parent quadrilateral (Figure 2). In the present work, we used Li-Kobbelt subdivision to select cubic Hermite derivative parameters because it gives rise to C1 continuity and finite Gaussian curvature at ordinary and extraordinary vertices in the infinite limit.
| Eq.2 |
Figure 2.
One linear quadrilateral is subdivided twice by the Li-Kobbelt scheme into 16 linear quadrilaterals containing 25 vertices. The coordinates of 16 of the new vertices (red) are used to solve Eq.2 and calculate the 16 Hermite parameters for the original unsubdivided quadrilateral.
A similar scheme was used to define cubic Hermite derivative parameters for hexahedral meshes: a twice-subdivided hexahedron became 64 hexahedra having 125 vertices, 64 of which were selected to calculate the 64 geometric degrees of freedom of each coordinate function. The interpolating subdivision surface scheme used above was extended to solids by applying the scheme separately to each surface in the model, and using linear interpolation to place new vertices between corresponding surfaces. The use of linear interpolation to place internal vertices (i.e., between surfaces) adversely affected element quality and led to inverted elements in some cases; these problems could be avoided by applying one scheme to minimize element skew (Zhang et al., 2007a) and another to regularize hexahedral element volumes (Vartziotis and Wipper, 2011).
2.4. Interpolation near ordinary vertices: A review
A spatial domain discretized into quadrilaterals or into hexahedra constructed as tensor products of cubic polynomials is guaranteed to be C1 continuous everywhere except at the boundary interfacing neighbor elements. Tangent (G1), parametric (C1), or arc-length continuity may be enforced at element interfaces. Parametric derivatives of equal magnitude may have different arc-length derivatives (speeds), as noted by Nielsen (1987). Arc-length continuity may be preferred to parametric continuity in finite element analysis because the arc-length connects derivatives to physical space—∂u/∂S1 is the directional derivative for an arbitrary scalar-valued function u in the direction tangent to the ξ1 contour—in contrast, the derivative ∂u / ∂ξ1 has only mathematical significance. Consequently, Nielsen proposed arc-length derivatives be used as an “ensemble” coordinate frame at each mesh vertex to define a canonical length of tangent vectors—the collection of ensemble, or global, field parameters and their dual basis functions would then be used as the functional space for a finite element problem, and arc-length derivatives computed would be consistent in neighboring elements. Fernandez et al. (2004) suggested nodal tangent vectors have unit arc-length magnitude (i.e., ∥ df / ds ∥= 1 for ), and local parametric derivatives (i.e., df / dξ) be calculated using non-linear iteration of the arc-length equation, with the approximation that arc-length (speed) of each contour is constant. Using this scheme, an arc-length parameterization of the cubic Hermite splines is unnecessary—only the integrated arc-length function need be considered. Surface derivative terms in the two frames are related by
| Eq.3 |
| Eq.4 |
Where s is the ensemble frame, ξ is the local frame, and the terms ∂s / ∂ξ are the scalar correctors determined by integration of the arc-length equation.
Henceforth, continuity would be imposed among neighboring cubic Hermite elements using a matrix of these scalar correctors, or “scale factors”. The matrix of scale factors is a derivative map (Jacobian) for a change-of-coordinates transformation between “local” parametric coordinate systems of the element, and “global” ensemble coordinate systems of Nielsen. In the present work, we use the scale factors described in Eq.3 and Eq.4 to enforce arc-length continuity at ordinary vertices, and to enforce G1 continuity along the contours joining ordinary vertices (see Discussion, Section 4.2).
2.5. Interpolation near extraordinary vertices
In a mesh with only ordinary vertices, the derivative maps between element and global coordinate systems will only scale vector magnitudes. More generally, the derivative maps may also transform vectors between coordinate systems whose axes are skew to one another. In a mesh with extraordinary vertices, it is necessary to utilize derivative maps this way: if local coordinate vectors and ensemble coordinate vectors are skew to one another, a linear transformation maps the components of a vector in one frame to components in a new frame.
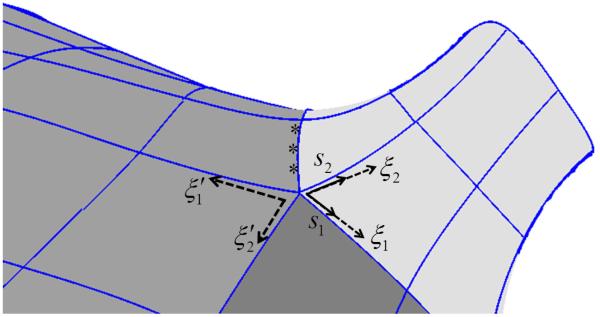
Thence, the normed coordinate axes of one reference element at each extraordinary vertex may be selected as the local ensemble frame (Figure 3), and a linear transformation Γ computed for each element containing that vertex. The matrix values in the linear transformation Γ are obtained by finding the contravariant components of local coordinate vectors of an element in the ensemble frame. First, ensemble tangent vectors of form are arranged in matrix columns ∀i, and the dual basis vectors computed by the matrix inverse (or the matrix pseudoinverse for surfaces). Second, for the local coordinate vector expanded in the reference frame , the ith component of the jth local coordinate vector ∂ / ∂ξj can be computed in ensemble coordinates with the dot product
| Eq.5 |
Where the star indicates the dual basis vector. Thus calculated, the relationship between vectors in local coordinates and ensemble coordinates is
| Eq.6 |
instead of Eq.3, where the term . The indices i, j = {1, 2} for surfaces and i, j = {1, 2,3} for volumetric solids.
Figure 3.
An extraordinary vertex lies at the interface of the right superior pulmonary vein (light grey), posterior left atrial wall (darker grey), and a third region between the right pulmonary veins (darkest grey), at a saddle point. Ensemble coordinates s1 and s2 (solid arrows) coincide with parametric coordinates ξ1 and ξ2 (broken arrows) of one element but have unit magnitude. A neighboring element has parametric coordinates ξ1 and ξ2 relatable to ensemble coordinates by linear transformation. Geometric continuity of adjoining patches in the one-neighborhood of an extraordinary vertex was evaluated along the shared contours at three points per contour (asterisks).
The second and third-order mixed derivatives ∂2Y / ∂ξi∂ξj(i ≠ j) and ∂3Y / ∂ξ1∂ξ2∂ξ3 are selected from the element whose basis vectors are chosen to coincide with the local ensemble frame, and determined in other elements with the chain rule (Appendix).
Cubic splines such as Hermites have degrees of freedom sufficient to enforce C1 continuity at regular vertices, but insufficient to enforce C1 continuity near extraordinary vertices. Continuity for cubic splines is achieved only for special configurations of the vertex “one-neighborhood” (Wang and Zhang, 2010). Using Eq.2 to select Hermite derivative parameters does not guarantee C1 continuity because we truncate the subdivision surface sequence at its second member. If some deviation from C1 continuity can be tolerated, special configurations in the one-neighborhood of the extraordinary vertex need not be utilized, and regions of high curvature can be captured at coarser mesh resolutions (Discussion, Section 4.2). In the present work, we tolerate this deviation from C1 and G1 continuity (Results, Section 3.1).
2.6. Global basis functions are dual to the ensemble frame
In functional analysis and differential geometry, vector coefficients and basis set are mathematically dual to one another. The choice of an ensemble frame at each vertex defines the dual ensemble (i.e., global) set of basis functions required for a finite element problem. As finite element equations are written in “local” element basis functions, they must be transformed to the global frame—this transformation was termed the “element-to-ensemble mapping” by Nielsen (1987). For non-derivative values (and thus for linear finite elements), the transformation is Boolean, but in general is real-valued and linear in the local element degrees of freedom.
Let the matrix Γ encapsulate the chain rule transformation from ensemble (global) coefficients to element (local) coefficients in the functional space spanned by the tensor product Hermite basis functions (Eq.1). As discussed in Section 2.4 and Section 2.5, Γ effects the transformations given by Eq.3, Eq.4, Eq.6, and Eq.A1–Eq.A4. The column vector of global coefficients u* are transformed to local coefficients u by
| Eq.7 |
Where we use u for the coefficient vector to emphasize it may be for any field interpolant, not exclusively a coordinate function, previously represented by y. Defined this way, the matrix transpose ΓT transforms the column vector of local basis functions ψ to the column vector of global basis functions ψ* —again an encapsulation of the chain rule, but for the basis functions, dual to the coefficients
| Eq.8 |
It is worthwhile to emphasize Γ, as defined, maps coefficients from global to local, whereas ΓT maps basis functions from local to global, if both operate on column vectors. An analog in differential geometry might be more familiar: for some change-of-coordinates , the associated Jacobian matrix J transforms tangent vectors from , whereas JT transforms dual vectors from . The matrices J−1 and J−T enact the other transformations.
The product of local basis functions often appears in finite element problems in an integral
| Eq.9 |
Where the domain Ω is one element, and i and j are indices for element basis functions. In matrix form, the product of local basis functions is the Cartesian product ψ ⊗ ψ, which transforms to the global frame as would a second-order tensor
| Eq.10 |
With these basis function transformations applied to the finite element problem, the unknown coefficients are determined in the ensemble (global) frame.
We tested the behavior of our methods in a finite element problem with regularized least-squares optimization (see Results, Section 3.2). The objective function F can be written (Fernandez et al., 2004)
| Eq.11 |
Where u is a vector of field variables, d is an index over data points, ud is the value of the field for data point d, ξd are the parametric coordinates of the dth data point projected onto a surface, u(ξd) are the interpolated field coefficients for data point d, Ω is the finite element domain, and αk is the Sobolev smoothing weight for the kth derivative term. The choice of smoothing weights is arbitrary, but we used αk = 1 for the smoothing weights multiplied with the first derivative terms ∂u / ∂ξ1 and ∂u / ∂ξ2, and αk = 5 for the other three smoothing weights multiplied with second derivative terms, whenever Eq.11 is used in this paper. Detailed guidelines for the choice of smoothing weight values are described elsewhere (Mazhari et al., 1998). The data points fitted were the vertices from the marching cubes surface triangulations of segmented endocardial surfaces after geometric fairing with feature preservation by GAMEr (Yu et al., 2008). The data point parametric coordinates ξd were determined as follows: First, all bicubic Hermite patches were tessellated into fine triangles. Second, the triangles to which each data point projects normally were identified. Last, the triangle with minimum distance to each data point was identified, and its parametric coordinates ξd with respect to its original quadrilateral recorded.
We use the scaled Jacobian and condition number to assess mesh quality at nine interpolated Gauss-Legendre quadrature points for each surface mesh (three points along each parametric coordinate). The scaled Jacobian and condition number are calculated as described by Zhang et al. (2007a). The scaled Jacobian equals one for right-handed orthogonal coordinate axes, equals zero if coordinate axes are coplanar (and thus, do not span ), is negative if coordinate axes are left-handed, and decreases from one towards zero as coordinate axes become skewed. The condition number equals one for orthogonal coordinate axes with equal magnitudes, increases from one as coordinate axes become skewed, increases from one also as tangent vectors to coordinate axes have increasingly different magnitudes, and is unbounded if coordinate axes are coplanar. Further descriptions are given by Knupp (2000).
3. Results
3.1. Geometry is smooth and almost G1 continuous near extraordinary vertices
We constructed one coarse right atrial mesh (90 quads) and one coarse left atrial mesh (142 quads), and used Eq.2 to construct cubic Hermite derivatives (Figure 4)—henceforth, we refer to these meshes as RA-90, and LA-142; other meshes were named by the same scheme. Extraordinary vertices were needed to capture the morphology of the pulmonary veins, atrial appendages, coronary sinus ostium, and venae cavae without producing severe element distortions. The number of extraordinary vertices was consistent with the Euler characteristic number χ of each atrial surface model: for the left atrial model, χ = −3, and for the right atrial model, χ = −2 (see Discussion, Section 4.3). Vertices of valence 5 were placed near orifices to capture their circumferential shape compactly (e.g., coronary sinus ostium, Figure 4A), and at regions of high curvature (e.g., right superior and right inferior pulmonary veins, Figure 4C) to avoid element skewing that otherwise resulted. Vertices of valence 3 typically were placed near vertices of valence 5; this resulted in quadrilaterals with regular angles (i.e., angles were close to 90 degrees) and aspect ratios close to unity throughout the meshes. After geometric optimization (Section 2.6), the bicubic Hermite surfaces LA-142 and RA-90 (Figure 4A and Figure 4C) captured pulmonary veins, venae cavae, and regions of high curvature more compactly than did refined bilinear surfaces (Figure 4B and Figure 4D) with a comparable number of geometric degrees of freedom (LA-568 and RA-360). Whereas the bicubic meshes LA-142 and RA-90 had RMS errors of 0.6 mm, the linear meshes LA-568 and RA-360 had RMS errors of 0.8 mm and 0.7 mm.
Figure 4.
Anterolateral views of bicubic Hermite mesh RA-90 (A) and bilinear mesh RA-360 (B), and septal views of bicubic Hermite mesh LA-142 (C) and bilinear mesh LA-568 (D) after geometric optimization with Eq.11. Valence 5 vertices (teal), valence 3 vertices (red), and one valence 6 vertex (black) were used. The tricuspid and mitral valve rings are shaded dark grey for visual contrast. See Results, Section 3.2 for details. SVC = Superior Vena Cava; IVC = Inferior Vena Cava; RAA = Right atrial appendage; TVO = Tricuspid valve orifice; CS = Coronary sinus ostium; RSPV = Right superior pulmonary vein; RIPV = Right inferior pulmonary vein; LAA = Left atrial appendage; MVO = Mitral valve orifice.
Since we truncate the subdivision surface scheme after two iterations, we tested G1 continuity in the one-neighborhood of extraordinary vertices using the dot product of normal vectors at points where two adjacent quads coincide (asterisks in Figure 3); in other regions, G1 or C1 continuity could be guaranteed (see Discussion, Section 4.2). For RA-90 and LA-142, mean dot products of normal vectors rooted at coincident points were 0.931 and 0.928. The analysis was repeated on two successive Li-Kobbelt subdivisions; the twice-subdivded meshes had mean dot products of 0.990 and 0.992, and additional data are provided in Table 1.
Table 1.
Analysis of normal vectors in the one-neighborhood of extraordinary vertices as a measure of smoothness. Three quadrature points on the contour bounding two quads were selected within the one-neighborhood, and for each point, unit normals were computed in the two adjoining elements. Last, the dot product was computed for each pair of normals.
| RA-90 | RA-360 | RA-1440 | LA-142 | LA-568 | LA-2272 | |
|---|---|---|---|---|---|---|
| Mean dot product | 0.925 | 0.974 | 0.990 | 0.928 | 0.981 | 0.992 |
| Fraction of points with dot product > 0.99 | 0.42 | 0.66 | 0.83 | 0.39 | 0.63 | 0.84 |
| Fraction of points with dot product > 0.95 | 0.74 | 0.86 | 0.96 | 0.66 | 0.89 | 0.96 |
| Fraction of points with dot product > 0.5 | 0.96 | 1.0 | 1.0 | 0.98 | 1.0 | 1.0 |
3.2. Extraordinary vertices capture geometric detail while minimizing element distortion
We were able to capture the left atrial geometry accurately with 142 bicubic Hermite elements (LA-142), but we had considered using a coarser model with 103 bicubic Hermite elements (LA-103). The meshes LA-103 and LA-142 were identical except at the left atrial appendage (LAA), where 10 extraordinary vertices and 29 ordinary vertices were added to LA-103 to capture anatomic detail. The additional extraordinary vertices in LA-142 allowed finer details of the geometry to be captured (i.e., RMS error was lower) and improved mesh quality, at the cost of mesh simplicity (more topological regions were required), as shown in Figure 5. The LAA of LA-103 had three topological regions, whereas the LAA of LA-142 had six, attributable to the additional extraordinary vertices in LA-142 (Figure 5C–D). The mesh LA-103 (LA-142) was refined one iteration by Li-Kobbelt subdivision to produce LA-412 (LA-568). These subdivisions add only ordinary vertices.
Figure 5.
Lateral views of bicubic Hermite meshes LA-142 (A) and LA-412 (B). Compared to LA-142, LA-412 cannot capture the geometric detail of the left atrial appendage (LAA), in spite of more geometric degrees of freedom. The additional extraordinary vertices in LA-142 are needed to capture the geometric shape of the LAA and preserve element quality. Cartographic projections of LA-142 and LA-412 are displayed in (C) and (D). The distorted quadrilaterals in the cartographic projection (C) become regular in LA-142 (A), whereas the regular quadrilaterals in cartographic projection (D) become distorted in LA-412 (B) as they are deformed to capture the irregular shape of the LAA. Colors in (C) and (D) are used to indicate distinct topology regions. Valence 5 vertices are teal in (A) and (B), and are indicated by asterisks (*) in (C) and (D). Valence 3 vertices are red in (A) and (B), and are indicated by the symbol ⊗ in (C) and (D). Four valence 3 vertices at the tip of the LAA are indicated by the symbol ⊕ in (C). In (A) and (B), the mitral valve is shaded dark grey for visual contrast. LAA = Left atrial appendage; MVO = Mitral valve orifice; LSPV = Left superior pulmonary vein; LIPV = Left inferior pulmonary vein.
Geometric optimization using Eq.11 was completed recursively on each mesh until RMS error was less than 0.62 mm. Regional RMS error of the LAA in LA-103 was 1.0 mm, whereas regional RMS error of the LAA in LA-142 was 0.6 mm. The decrease in regional RMS error of the LAA could not be attributed solely to an increase in the number of degrees of freedom; error of the LAA for LA-412 (a refined version of LA-103) was 0.9 mm, yet it had slightly more degrees of freedom per coordinate in the LAA (228) than did LA-142 (224).
A similar pattern was followed for two quality metrics, the scaled Jacobian and condition number: mean and worst values for LA-142 were superior to mean and worst values of LA-103 and LA-412, owing to its additional extraordinary vertices in the LAA. Successive optimizations by Eq.11 could reduce the regional error of the LAA for LA-412 to be lower than 0.9 mm at the expense of the mean and worst values of the quality metrics, which were already worse than the mean and worst values of the quality metrics for the LAA of LA-142 for regional error of 0.6 mm. Mean quality metrics in the refined meshes LA-412 and LA-568 were superior to the values in their non-refined counterparts LA-103 and LA-412, whereas the worst value of quality metrics typically was inferior for the refined meshes, owing to torsion introduced by capture of sharp curvature near the pulmonary veins. Additional mesh statistics, including statistics for RA-90 after geometric optimization, are provided in Table 2.
Table 2.
Statistics for bicubic Hermite left atrial (LA) and right atrial (RA) surface meshes after geometric optimization. Mesh quality metrics were evaluated at 9 quadrature points per element.
| LA-103 | LA-142 | LA-412 | LA-568 | RA-90 | |
|---|---|---|---|---|---|
| Vertices, total | 116 | 155 | 441 | 597 | 103 |
| Geometric d.o.f. per coordinate | 464 | 620 | 1764 | 2388 | 412 |
| Geometric d.o.f. per coordinate, LAA | 68 | 224 | 228 | 852 | - |
| Vertices, valence 3 | 8 | 13 | 8 | 13 | 4 |
| Vertices, valence 5 | 20 | 25 | 20 | 25 | 10 |
| Vertices, valence 6 | 0 | 0 | 0 | 0 | 1 |
| Topology regions | 17 | 20 | 17 | 20 | 11 |
| Mean edge length, mm | 12.9 | 10.8 | 6.4 | 5.3 | 14.3 |
| RMS error, mm | 0.6 | 0.6 | 0.5 | 0.5 | 0.6 |
| RMS error, LAA, mm | 1.0 | 0.6 | 0.9 | 0.5 | - |
| Scaled Jacobian – mean, worst | 0.96, 0.49 | 0.96, 0.49 | 0.96, 0.49 | 0.97, 0.48 | 0.96, 0.43 |
| Condition number – mean, worst | 1.10, 2.62 | 1.08, 2.56 | 1.10, 2.95 | 1.09, 2.79 | 1.11, 2.45 |
| Scaled Jacobian, LAA - mean, worst | 0.94, 0.57 | 0.97, 0.70 | 0.95, 0.61 | 0.97, 0.70 | - |
| Condition number, LAA - mean, worst | 1.15, 1.76 | 1.07, 1.48 | 1.13, 1.69 | 1.07, 1.56 | - |
Meshes were named in accordance with the number of elements (e.g., mesh with 103 elements is named LA-103).
d.o.f. = degrees of freedom.
3.3. Atrial fiber architecture is described compactly in a tricubic Hermite model
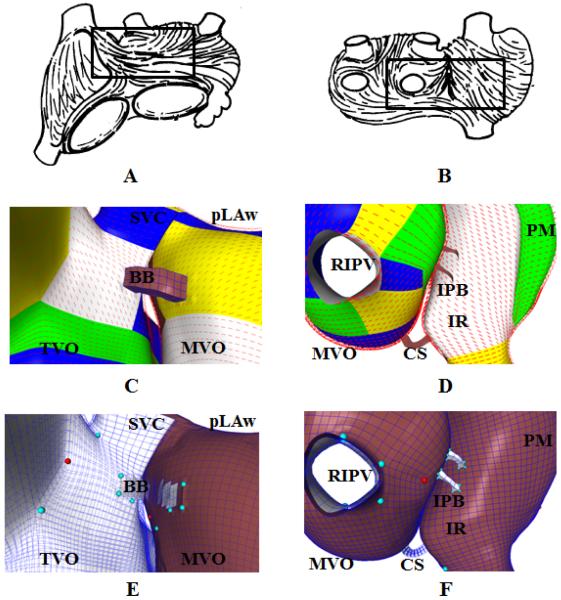
Qualitative fiber patterns from explanted human atria are depicted in Figure 6A–B. Enlarged views of the biatrial model BiA-9486 corresponding to the regions boxed in Figure 6A–B are depicted in Figure 6C–D with the constructed fiber patterns overlaid. In Figure 6C, fiber tracts course from the superior border of the region of the crista terminalis (white region) anteriorally and septally, towards Bachmann's bundle. Fiber tracts on the left atrial roof course posterolaterally, whereas fiber tracts closer to the mitral valve course laterally, towards the left atrial appendage. A fiber tract courses circumferentially around the tricuspid valve. In Figure 6D, fiber tracts of the posterior left atrial wall (upper-left blue region) course inferiorly before blending with fiber tracts of the left atrial floor, which course left-to-right. Fiber tracts of the left atrial septum course from anterior to posterior (green), and encircle the right inferior pulmonary vein. Fiber tracts of the intercaval band originate between the venae cavae (lower-right white region) and course obliquely. The atria are connected inferiorly by the coronary sinus musculature. Views of the hexahedral mesh with prominent coordinate lines are displayed in Figure 6E–F.
Figure 6.
Fiber orientations in a tricubic Hermite model. Images (A) and (B) are depictions of typical fiber orientations from explanted human atria, reprinted from Wang, Br. Heart J., 1995 with permission. The regions indicated by boxes are enlarged in (C) and (D), in which a qualitatively-matching fiber pattern is displayed. Each block of color indicates a region with consistent coordinate axes (a single topological region). See Results, Section 3.3 for details. Images (E) and (F) are equivalent views of the tricubic Hermite hexahedral model. The epicardial surface is colored brown and the endocardial surface is colored white. Valence 3 vertices are colored red, and valence 5 vertices are colored teal. SVC = Superior Vena Cava; BB = Bachmann's bundle; TVO = Tricuspid valve orifice; pLAw = Posterior left atrial wall; MVO = Mitral valve orifice; RIPV = Right inferior pulmonary vein; CS = Coronary sinus; IR = Intercaval region; PM = Pectinate muscles, IPB = Inferoposterior bridge.
The posterior left atrial wall and the crista terminalis each feature separate subepicardial and subendocardial fiber tracts with distinct orientations (in Figure 6B, only the subepicardial fibers superficial to the crista terminalis are visible). We captured the abrupt intramural fiber orientation transitions in these two regions using refinement by Hermite interpolation on BiA-9486 to give BiA-75888, which was two hexahedra thick. A visualization of the resulting fiber pattern near the crista terminalis is displayed in Figure S1. Additional details of the tricubic Hermite hexahedral mesh BiA-9486 and the refined model BiA-75888 are provided in the Supplemental Data section.
4. Discussion
4.1. Related work
Computational meshes of the human atria have been constructed previously (Harrild and Henriquez, 2000; Seemann et al., 2006; Vigmond et al., 2001; Virag et al., 2002)—to our knowledge, ours is the first atrial mesh that is tricubic Hermite. Most previous computational meshes of the atria have been composed of simplices or linear hexahedra. Detailed descriptions of existing human atrial models are described in reviews by Dössel and colleagues (2012) and Jacquemet and colleagues (2008).
Cubic Hermite meshes with some topological complexity have been constructed using “duplicate” vertices with derivative constraints, most typically at the joining points of the right ventricle and the ventricular septum, as in the work of Usyk and colleagues (2002). To our knowledge, no general framework has been proposed to construct more complicated shapes while preserving smoothness between elements. A previous work constructed a tricubic Hermite model of porcine ventricles with topological complexity just sufficient to capture the valve annuli (Stevens et al., 2003). Fernandez and colleagues (2004) constructed cubic Hermite models of more complicated shapes with extraordinary vertices and “hanging” vertices, but did not attempt to preserve smoothness near these points. We previously demonstrated deformable registration of a cubic Hermite four-chamber heart model (Zhang et al., 2012), but as we had not yet defined the local-to-global map in meshes with extraordinary vertices, we could only apply the deformations to the linear hexahedral mesh. In the future, our deformable registration scheme will be used on the higher-quality models created by the methods here, and may also utilize the local-to-global map to deform the cubic Hermite meshes directly.
Zhang and colleagues (2007b) constructed a hexahedral non-uniform rational B-splines (NURBS) model with extraordinary vertices, and simulated elastic deformation of the aorta coupled with incompressible Navier-Stokes equations (Bazilevs et al., 2006). The NURBS meshes can be “k-refined” (Hughes et al., 2005) to increase the order of their basis functions while preserving continuity, but enforcing continuity near extraordinary vertices is difficult, as with cubic Hermite splines. Cubic Hermite splines (and other interpolating splines) connect functional space to underlying geometry directly because coefficients of the solution space include parametric derivatives of the solution field. Approximating splines such as NURBS have other advantages, discussed by Hughes and colleagues (2005).
We use subdivision surfaces to define parameters of spline surfaces; previously, Catmull-Clark subdivision has been used to parameterize bicubic Beziér splines (Loop and Schaefer, 2008), biquadratic B-splines (Zheng et al., 2005), and non-uniform rational B-splines (Peters, 2000). Our approach differs principally in that Eq.2 computes parametric derivatives of cubic Hermite splines rather than control points of approximating splines, and we parameterize the derivatives of tricubic hexahedra as well as bicubic quadrilaterals. Subdivision surfaces have been useful in cardiac modeling for purposes aside from computing cubic Hermite derivatives. Chandrashekara and colleagues (2007) use subdivision surfaces to track cardiac deformation in tagged MRI, using the coarseness of the subdivision surface template to decrease computational burden. Sheehan and colleagues (2008) use subdivision surfaces to analyze right ventricular shape and volume in patients with tetralogy of Fallot, and in so doing are able to include the two right ventricular valve annuli in their geometric models.
4.2. Precise G1 and C1 Continuity
Bicubic splines have degrees of freedom insufficient to enforce C1 continuity near extraordinary vertices; consequently, C1 continuity in these regions is achieved only for special geometric configurations. Wang and Zhang (2010) demonstrated these requirements mathematically in nonuniform rational B-splines (NURBS), but only for vertices with valence five. We selected Hermite derivative parameters using the Li-Kobbelt scheme with limit-surface C1 continuity rather than enforcing the requirements for splines.
In spite of Hermite derivative parameterization with the Li-Kobbelt scheme, our meshes do not achieve precise G1 or C1 continuity in the one-neighborhood of extraordinary vertices. The subdivision scheme utilized demonstrates continuity properties of the limit surface by eigenanalysis, which cannot be applied directly to our meshes because we truncate the subdivision surface sequence at its second member. In general, this will induce normals with different directions at the boundary of adjoining elements, as tabulated in Table 1. In principle, the truncation problem could be eliminated if the one-neighborhood vertices are arranged symmetrically around an extraordinary vertex, and are placed in a common plane—this was called the “natural configu ration” by Ball and Storry (1988). The natural configuration is flat, but configurations with non-zero curvature may also give rise to C1 continuity. Ball, Storry, and Sabin noted the natural configuration could be transformed to all C1 continuous configurations around extraordinary vertices by affine transformation, but did not specify for which affine transformations. Ball and Storry also noted the natural configuration eliminates the Fourier coefficients of high-frequency components in the subdivision matrix for arbitrary valence, while Doo and Sabin (1978) earlier had noted convergence occurs because contributions of high-frequency components diminish. We did not place one-neighborhood vertices of extraordinary vertices symmetrically—this worsened quality metrics of the surrounding elements severely. However, if desired, G1 continuity can be achieved precisely at the extraordinary vertex by projection of the parametric tangent vectors (derivatives) of different elements at the extraordinary vertex into a common plane defined by the span of the ensemble derivatives.
As with extraordinary vertices, calculation of cubic Hermite derivatives by Li-Kobbelt subdivision only approximates C1 continuity at ordinary vertices. Nonetheless, tangent (G1) or parametric (C1) continuity can be enforced by the local-to-global map at ordinary vertices (see Section 2.4). The sufficient conditions were described by Bradley et al. (1997). Bradley and colleagues showed adjacent bicubic Hermite patches are C1 continuous when scale factors of adjoining splines are chosen to be the same, but with this choice, arc-length continuity is satisfied only in special cases. Alternatively, scale factors of bicubic Hermite patches can be constructed as described by Nielsen (1987), in which case the scale factors of adjoining splines may have different values. With the approach of Nielsen, arc-length continuity is enforced at the ordinary vertex, tangent (G1) continuity is satisfied along contours joining ordinary vertices, and in general, C1 continuity is satisfied neither at vertices nor along contours joining vertices. Ensemble derivatives may be transformed to parametric derivatives of adjacent elements with Eq.5, Eq.6 and Eq.A1–Eq.A4 using the scale factor definition of Bradley or of Nielsen. In the present work, we used the scale factor convention of Nielsen: arc-length continuity was enforced at ordinary vertices, and tangent (G1) continuity was satisfied along contours joining ordinary vertices.
4.3. Topology of a human atrial geometric model
A completely unstructured quadrilateral mesh, as may be generated by triangle pairing, has more extraordinary vertices than is necessary for capturing the morphologic features of the atrial geometries. Such meshes can have high-quality elements at the expense of topological structure. As structure is simplified (by use of fewer extraordinary vertices), mesh quality is compromised, especially for coarse meshes. Nonetheless, a topologically simple mesh may be preferred for domain decomposition, fiber field construction, or to match the topologies of other biatrial hexahedral models for comparative studies.
In the future, the pipeline from non-invasive imaging data to high-quality hexahedral finite element model may be automated. Our previous study (Zhang et al., 2012) utilizes a “sweeping” method to construct an atlas of linear hexahedral four-chamber models directly from imaging data—subsequent geometries may be constructed de novo or by deformable registration to atlas models. Owing to limitations of the sweeping method, we used freehand to construct topological patterns in this study, which may be incorporated into the atlas. Automatic triangular mesh generation, followed by conversion to quadrilaterals (Velho and Zorin, 2001), followed by transmural extrusion to a hexahedral mesh was considered, but for the present study, it was advantageous to define the topological patterns manually—this approach enabled fiber fields to be defined easily. In general, a topological pattern can be chosen objectively for a given surface by identification of its critical points of curvature (Campen et al., 2012; Pennec et al., 2000).
Topology choice by freehand does not lead to an endless number of possible topology patterns—extraordinary vertices are placed naturally in some locations (e.g., at saddle points), and extraordinary vertices together must be consistent with the Euler characteristic number χ of the surface. The Euler characteristic number of a surface must satisfy the relation χ = V − E + F, where V is the number of mesh vertices, E is the number of mesh edges, and F is the number of mesh faces. Furthermore, our surface meshes are orientable, and homeomorphic to the sphere if their boundaries (holes) are filled by disks to make them closed surfaces. For such a surface having b boundaries, χ = 2 − b (Kinsey, 1993). If valence 3 vertices are assigned a characteristic index of +1/4, valence 5 vertices assigned an index of −1/4, and valence 6 vertices assigned an index of −1/2, then the sum of characteristic indices for all extraordinary vertices of the surface equals its Euler characteristic number. For example, the left atrium has 5 boundaries (the four pulmonary vein orifices and the mitral valve orifice), so χ = −3. The mesh LA-103 has eight valence 3 vertices, each having index +1/4, and twenty valence 5 vertices, each having index −1/4. The sum of all extraordinary vertex indices is −3. We added extraordinary vertices to LA-142 to capture geometric detail that LA-103 could not capture, but we were required to add the same number of valence 3 and valence 5 vertices (in this case, five) for the left atrial appendage to remain a blind pouch (i.e., have no holes). Further description is given by Koenderink (1990), who describes the Euler characteristic number and its relationship to indices of surface umbilical points.
Our methods are readily extendable to patients with accessory pulmonary veins or pulmonary vein bifurcations. A left atrial model with an accessory (fifth) pulmonary vein will have χ = −4. Accordingly, four additional extraordinary vertices of valence 5 will be placed to decrement the Euler characteristic number by one. The vertices should be placed near the accessory pulmonary vein to minimize element distortions (Figure S2A). A left atrial model with early bifurcation of one pulmonary vein will also have χ = −4. In this case, mesh quality will be highest when two valence 6 vertices—which also decrement the Euler characteristic number by one—are placed near the point of vein bifurcation (Figure S2B).
4.4. Atrial fiber architecture
Finite element simulations of cardiac mechanics and electrophysiology require material anisotropy (defined in part by a vector field representing fiber orientation) to capture essential features of deformation and electrical activation sequence. In this regard, fewer data exist for fiber architecture of the atria compared to ventricles because histology and diffusion tensor magnetic resonance imaging (DT-MRI) of atria are difficult, owing to their thin walls. As a consequence, previous studies (Krueger et al., 2011) and the current work use rule-based methods to define atrial fiber architecture qualitatively based on published diagrams of atrial fiber tracts. Since no detailed human atrial fiber data are available currently, it is unknown if qualitatively-described fiber data compromise computational models of healthy or diseased atria.
Human atrial musculature comprises fiber tracts spanning large areas, and the fiber tract orientations partially follow geometric features. Extraordinary vertices may be placed to align coordinate axes of mesh regions with dominant directions of fiber tracts, and demarcate loci of gross fiber discontinuity or abrupt directional change. Abrupt transmural changes in fiber orientation can also be represented if a model is two or more layers of hexahedra thick, as was demonstrated in BiA-75888 (Figure S1). Moreover, a C1 continuous cubic Hermite mesh features local coordinate frames that vary smoothly between elements. Interpolation of angles referred to these frames gives rise to smooth fiber orientations between elements in each subregion. An alternative approach for fiber modeling uses twenty-two “seed points” to drive fiber orientations throughout the biatrial model without using element coordinate axes (Krueger et al., 2011; Krueger et al., 2013). In both approaches, a limited number of parameters was sufficient to give qualitative agreement with diagrams of fiber architecture.
More detailed fiber field information has been obtained in imaging studies by Zhao and colleagues in sheep (2012) and by Aslanidi and colleagues in canine (2013) using imaging of tissue microstructure. In humans, DT-MRI has been used to construct fiber orientations near the sinoatrial node (Aslanidi et al., 2011), but extracting fiber direction by DT-MRI remains difficult in the atria. As with the approach of Krueger and colleagues, our approach for representing fiber orientations has no loss of generality, and can incorporate more detailed human fiber data when they become available by imaging of tissue microstructure or DT-MRI.
4.5. Potential applications
Cubic Hermite meshes (and other high-order splines) have several well-known advantages in numerical analysis of cardiac function: One, they capture smooth geometries with few finite elements and can be deformed easily from template meshes (Lamata et al., 2011). Two, they have convergence advantages in biomechanics (Costa et al., 1996) and electrophysiology (Arthurs et al., 2012; Rogers et al., 1996). Third, they are useful for modeling electrical mapping studies when data are missing or poor-quality (Bayly et al., 1998). Last, a C1 continuity of geometry allows for continuous stresses across element boundaries for biomechanics problems, continuous currents across element boundaries for electrophysiology problems, and continuous fiber orientation fields across boundaries when fibers are represented as angular fields referred to local coordinate axes. However, the problem of retaining smoothness between cubic Hermite elements with extraordinary vertices has prevented these meshes from being used for atrial modeling. In the present work, we propose a solution to this problem so that these advantages can be utilized in complex geometries such as that of the atria.
Even so, our work has other potential applications. Automatic meshing from in vivo imaging typically creates fine surface triangulations with triangle sizes near the sizes of the image voxels, yet applications such as biomechanics and deformable registration do not require such refined meshes for accurate solutions. Here, we suggest a strategy to coarsen these fine triangulations not only with bicubic Hermite quadrilaterals but also with linear quadrilaterals, both of which capture the smooth shapes of the heart more compactly than do linear simplices. As noted above, automatic methods for placement of extraordinary vertices have been reported previously (Alliez et al., 2003; Kälberer et al., 2007). Nonetheless, manual placement of extraordinary vertices may be preferred when in vivo imaging data have appreciable noise, and also when it is advantageous to define coordinate lines manually—here, for example, we place some of the extraordinary vertices to define discontinuities in the fiber orientation field easily.
4.6. Limitations and future directions
The interpolating subdivision scheme utilized has deficiencies: First, its limit surface is not defined in spline form, unlike Catmull-Clark subdivision. Second, as a hexahedral subdivision, it requires topological consistency between inner and outer surfaces to define tricubic Hermite derivative parameters. Restriction to topological correspondence between inner and outer surfaces may be lifted by using volumetric hexahedral meshing schemes with more general topology (Nieser et al., 2011) and interpolating subdivision schemes for hexahedral meshes (Bajaj et al., 2002; McDonnell et al., 2004), but this approach is not needed for the present work, and descriptions of C1 continuity requirements for hexahedral subdivision schemes are sparse compared to surface schemes. Our models do not include pectinate muscles, patient-specific wall thicknesses, or patient-specific interatrial connections, owing to limitations of imaging technology in vivo. In the future, advances in imaging technology may allow finer details to be captured.
5. Conclusions
We generalized the local-to-global mapping used in cubic Hermite modeling to construct smooth meshes with extraordinary vertices, and solve finite element problems with smooth solutions. We utilized a subdivision surface scheme, adapted for hexahedral meshes, to select cubic Hermite parameters to achieve arc-length continuity at ordinary vertices and near-G1 continuity around extraordinary vertices. Next, we used the topological structure of the mesh to represent fiber fields compactly. Finally, we described how our methods could be applied to patients with different pulmonary vein anatomies.
Supplementary Material
Highlights
Cubic Hermite models of the atria are constructed from non-invasive imaging data.
Only about 100 cubic Hermite elements are needed to capture each atrium accurately.
Extraordinary vertices capture geometric details and improve mesh quality.
Smoothness is maintained between neighboring finite elements.
All of the models are available to the public.
Acknowledgments
We thank Chandrajit Bajaj and Joe Warren for providing advice about subdivision surfaces. This work was supported by NIH grants NHLBI 1 R01 HL96544 (ADM), NHLBI 1 R01 HL083359 (SMN, WJR), NHLBI 1 K24 HL103800 (SMN), NHLBI 1 RO1 HL091036 (WPS), NHLBI 5 T32 HL007089, NHLBI 1 T32 HL105373, NIBIB 1 T32 EB009380 (ADM), NIGMS 8 P41 GM103426 (National Biomedical Computation Resource), and NIGMS P50 GM094503 (Virtual Physiological Center for the Study of Complex Diseases). This work was also supported by NSF Career Award OCI-1149591 (YZ), the San Diego Fellowship (MJG), and the Center of Excellence grant from the Research Council of Norway to the Center for Biomedical Computing at Simula Research Laboratory.
Appendix
The chain rule can be used to determine the relationship between second and third-order mixed derivatives in the local and global frames:
| Eq.A1 |
| Eq.A2 |
| Eq.A3 |
| Eq.A4 |
We note Eq.A1 simplifies to Eq.4, the previous definition for high-order scale factors, for singular topology (i.e., extraordinary vertices are absent) because the terms ∂Si/∂ξj are zero for i ≠ j. Arc-length parameterization of each spline is avoided if second derivatives mapped between the coordinates s and ξ are estimated to be zero (i.e., the speed of the contour is constant).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alliez P, Cohen-Steiner D, Devillers O, Lévy B, Desbrun M. Anisotropic polygonal remeshing, ACM Transactions on Graphics. ACM. 2003:485–493. [Google Scholar]
- Arthurs CJ, Bishop MJ, Kay D. Efficient simulation of cardiac electrical propagation using high order finite elements. Journal of Computational Physics. 2012 doi: 10.1016/j.jcp.2012.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashihara T, Haraguchi R, Nakazawa K, Namba T, Ikeda T, Nakazawa Y, Ozawa T, Ito M, Horie M, Trayanova NA. The Role of Fibroblasts in Complex Fractionated Electrograms During Persistent/Permanent Atrial FibrillationNovelty and Significance Implications for Electrogram-Based Catheter Ablation. Circulation Research. 2012;110:275–284. doi: 10.1161/CIRCRESAHA.111.255026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aslanidi O, Nikolaidou T, Zhao J, Smaill B, Gilbert S, Jarvis J, Stephenson R, Hancox J, Boyett M, Zhang H. Application of Micro-Computed Tomography with Iodine Staining to Cardiac Imaging, Segmentation and Computational Model Development. IEEE Transacations on Medical Imaging. 2013;32:8–17. doi: 10.1109/TMI.2012.2209183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aslanidi OV, Colman MA, Stott J, Dobrzynski H, Boyett MR, Holden AV, Zhang H. 3D virtual human atria: A computational platform for studying clinical atrial fibrillation. Progress in Biophysics and Molecular Biology. 2011;107:156–168. doi: 10.1016/j.pbiomolbio.2011.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajaj C, Schaefer S, Warren J, Xu G. A subdivision scheme for hexahedral meshes. The Visual Computer. 2002;18:343–356. [Google Scholar]
- Ball A, Storry D. Conditions for tangent plane continuity over recursively generated B-spline surfaces. ACM Transactions on Graphics (TOG) 1988;7:83–102. [Google Scholar]
- Barsky BA, DeRose TD. Geometric continuity of parametric curves: three equivalent characterizations. Computer Graphics and Applications, IEEE. 1989;9:60–69. [Google Scholar]
- Bayly PV, KenKnight BH, Rogers JM, Hillsley RE, Ideker RE, Smith WM. Estimation of conduction velocity vector fields from epicardial mapping data. IEEE Transactions on Biomedical Engineering. 1998;45:563–571. doi: 10.1109/10.668746. [DOI] [PubMed] [Google Scholar]
- Bazilevs Y, Calo VM, Zhang Y, Hughes TJR. Isogeometric Fluid–structure Interaction Analysis with Applications to Arterial Blood Flow. Computational Mechanics. 2006;38:310–322. [Google Scholar]
- Bradley C, Pullan A, Hunter P. Geometric modeling of the human torso using cubic Hermite elements. Annals of biomedical engineering. 1997;25:96–111. doi: 10.1007/BF02738542. [DOI] [PubMed] [Google Scholar]
- Cabrera JA, Ho SY, Climent V, Sanchez-Quintana D. The architecture of the left lateral atrial wall: a particular anatomic region with implications for ablation of atrial fibrillation. European heart journal. 2008;29:356–362. doi: 10.1093/eurheartj/ehm606. [DOI] [PubMed] [Google Scholar]
- Campen M, Bommes D, Kobbelt L. Dual loops meshing: quality quad layouts on manifolds. ACM Transactions on Graphics (TOG) 2012;31:110. [Google Scholar]
- Catmull E, Clark J. Recursively generated B-spline surface on arbitrary topological meshes. Computer-Aided Design. 1978;10:350–355. [Google Scholar]
- Chandrashekara R, Mohiaddin R, Razavi R, Rueckert D. Nonrigid image registration with subdivision lattices: Application to cardiac mr image analysis. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2007;2007:335–342. doi: 10.1007/978-3-540-75757-3_41. [DOI] [PubMed] [Google Scholar]
- Chauvin M, Shah DC, Haïssaguerre M, Marcellin L, Brechenmacher C. The anatomic basis of connections between the coronary sinus musculature and the left atrium in humans. Circulation. 2000;101:647–652. doi: 10.1161/01.cir.101.6.647. [DOI] [PubMed] [Google Scholar]
- Comtois P, Nattel S. Impact of tissue geometry on simulated cholinergic atrial fibrillation: A modeling study. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2011;21 doi: 10.1063/1.3544470. 013108-013108-013113. [DOI] [PubMed] [Google Scholar]
- Costa K, Hunter P, Wayne J, Waldman L, Guccione J, McCulloch A. A three-dimensional finite element method for large elastic deformations of ventricular myocardium: II—prolate spheroidal coordinates. Journal of biomechanical engineering. 1996;118:464. doi: 10.1115/1.2796032. [DOI] [PubMed] [Google Scholar]
- Doo D, Sabin M. Behaviour of recursive division surfaces near extraordinary points. Computer-Aided Design. 1978;10:356–360. [Google Scholar]
- Dössel O, Krueger MW, Weber FM, Wilhelms M, Seemann G. Computational modeling of the human atrial anatomy and electrophysiology. Medical and Biological Engineering and Computing. 2012:1–27. doi: 10.1007/s11517-012-0924-6. [DOI] [PubMed] [Google Scholar]
- Fernandez J, Mithraratne P, Thrupp S, Tawhai M, Hunter P. Anatomically based geometric modelling of the musculo-skeletal system and other organs. Biomechanics and modeling in mechanobiology. 2004;2:139–155. doi: 10.1007/s10237-003-0036-1. [DOI] [PubMed] [Google Scholar]
- Gong Y, Xie F, Stein KM, Garfinkel A, Culianu CA, Lerman BB, Christini DJ. Mechanism underlying initiation of paroxysmal atrial flutter/atrial fibrillation by ectopic foci. Circulation. 2007;115:2094–2102. doi: 10.1161/CIRCULATIONAHA.106.656504. [DOI] [PubMed] [Google Scholar]
- Haissaguerre M, Lim KT, Jacquemet V, Rotter M, Dang L, Hocini M, Matsuo S, Knecht S, Jaïs P, Virag N. Atrial fibrillatory cycle length: computer simulation and potential clinical importance. Europace. 2007;9:vi64–vi70. doi: 10.1093/europace/eum208. [DOI] [PubMed] [Google Scholar]
- Hall B, Jeevanantham V, Simon R, Filippone J, Vorobiof G, Daubert J. Variation in left atrial transmural wall thickness at sites commonly targeted for ablation of atrial fibrillation. Journal of Interventional Cardiac Electrophysiology. 2006;17:127–132. doi: 10.1007/s10840-006-9052-2. [DOI] [PubMed] [Google Scholar]
- Hanna R, Barschdorf H, Klinder T, Weber F, Krueger M, Dössel O, Lorenz C. A hybrid method for automatic anatomical variant detection and segmentation. Functional Imaging and Modeling of the Heart. 2011:333–340. [Google Scholar]
- Harrild DM, Henriquez CS. A computer model of normal conduction in the human atria. Circulation Research. 2000;87:e25–e36. doi: 10.1161/01.res.87.7.e25. [DOI] [PubMed] [Google Scholar]
- Ho SY, Cabrera J, Tran V, Farre J, Anderson R, Sanchez-Quintana D. Architecture of the pulmonary veins: relevance to radiofrequency ablation. Heart. 2001;86:265–270. doi: 10.1136/heart.86.3.265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho SY, Sanchez-Quintana D. The importance of atrial structure and fibers. Clinical Anatomy. 2009;22:52–63. doi: 10.1002/ca.20634. [DOI] [PubMed] [Google Scholar]
- Hughes TJR, Cottrell JA, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering. 2005;194:4135–4195. [Google Scholar]
- Jacquemet V, Kappenberger L, Henriquez CS. Modeling atrial arrhythmias: Impact on clinical diagnosis and therapies. Biomedical Engineering, IEEE Reviews in 1. 2008:94–114. doi: 10.1109/RBME.2008.2008242. [DOI] [PubMed] [Google Scholar]
- Jacquemet V, Virag N, Ihara Z, Dang L, Blanc O, Zozor S, Vesin J, Kappenberger L, Henriquez C. Study of unipolar electrogram morphology in a computer model of atrial fibrillation. Journal of cardiovascular electrophysiology. 2003;14:S172–S179. doi: 10.1046/j.1540.8167.90308.x. [DOI] [PubMed] [Google Scholar]
- Kälberer F, Nieser M, Polthier K. QuadCover-Surface Parameterization using Branched Coverings, Computer Graphics Forum. Wiley Online Library. 2007:375–384. [Google Scholar]
- Kerckhoffs RCP, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Annals of biomedical engineering. 2007;35:1–18. doi: 10.1007/s10439-006-9212-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerckhoffs RCP, Omens JH, McCulloch AD, Mulligan LJ. Ventricular Dilation and Electrical Dyssynchrony Synergistically Increase Regional Mechanical Nonuniformity But Not Mechanical DyssynchronyClinical Perspective. Circulation: Heart Failure. 2010;3:528–536. doi: 10.1161/CIRCHEARTFAILURE.109.862144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinsey LC. Topology of surfaces. Springer; New York: 1993. [Google Scholar]
- Knupp PM. Achieving finite element mesh quality via optimization of the Jacobian Matrix norm and associated quantities. Part II—A framework for volume mesh optimization and the condition number of the Jacobian matrix. International Journal for Numerical Methods in Engineering. 2000;48:1165–1185. [Google Scholar]
- Koenderink JJ. Solid shape. The MIT Press; Cambridge: 1990. [Google Scholar]
- Krueger M, Schmidt V, Tobón C, Weber F, Lorenz C, Keller D, Barschdorf H, Burdumy M, Neher P, Plank G. Modeling atrial fiber orientation in patient-specific geometries: a semi-automatic rule-based approach. Functional Imaging and Modeling of the Heart. 2011:223–232. [Google Scholar]
- Krueger M, Seemann G, Rhode K, Keller D, Schilling C, Arujuna A, Gill J, O'Neill M, Razavi R, Doessel O. Personalization of Atrial Anatomy and Elelectophysiology as a Basis for Clinical Modeling of Radio-Frequency-Ablation of Atrial Fibrillation. IEEE Transacations on Medical Imaging. 2013;32:73–84. doi: 10.1109/TMI.2012.2201948. [DOI] [PubMed] [Google Scholar]
- Lamata P, Niederer S, Nordsletten D, Barber DC, Roy I, Hose DR, Smith N. An accurate, fast and robust method to generate patient-specific cubic Hermite meshes. Medical image analysis. 2011;15:801–813. doi: 10.1016/j.media.2011.06.010. [DOI] [PubMed] [Google Scholar]
- Li G, Ma W, Bao H. A new interpolatory subdivision for quadrilateral meshes. Computer Graphics Forum. 2005;24:3–16. [Google Scholar]
- Loop C, Schaefer S. Approximating Catmull-Clark subdivision surfaces with bicubic patches. ACM Transactions on Graphics (TOG) 2008;27:8. [Google Scholar]
- Mazhari R, Omens JH, Waldman LK, McCulloch AD. Regional myocardial perfusion and mechanics: a model-based method of analysis. Annals of biomedical engineering. 1998;26:743–755. doi: 10.1114/1.74. [DOI] [PubMed] [Google Scholar]
- McDonnell KT, Chang Y-S, Qin H. Interpolatory, solid subdivision of unstructured hexahedral meshes. The Visual Computer. 2004;20:418–436. [Google Scholar]
- Nathan H, Eliakim M. The junction between the left atrium and the pulmonary veins: an anatomic study of human hearts. Circulation. 1966;34:412–422. doi: 10.1161/01.cir.34.3.412. [DOI] [PubMed] [Google Scholar]
- Niederer SA, Plank G, Chinchapatnam P, Ginks M, Lamata P, Rhode KS, Rinaldi CA, Razavi R, Smith NP. Length-dependent tension in the failing heart and the efficacy of cardiac resynchronization therapy. Cardiovascular research. 2011;89:336–343. doi: 10.1093/cvr/cvq318. [DOI] [PubMed] [Google Scholar]
- Nielsen P. PhD thesis. The University of Auckland; 1987. The Anatomy of the Heart: A Finite Element Model. [Google Scholar]
- Nielsen P, Le Grice I, Smaill B, Hunter P. Mathematical model of geometry and fibrous structure of the heart. American Journal of Physiology-Heart and Circulatory Physiology. 1991;260:H1365–H1378. doi: 10.1152/ajpheart.1991.260.4.H1365. [DOI] [PubMed] [Google Scholar]
- Nieser M, Reitebuch U, Polthier K. CUBECOVER-Parameterization of 3D Volumes. Computer Graphics Forum. 2011;30:1397–1406. [Google Scholar]
- Ohtake Y, Belyaev AG, Bogaevski IA. Polyhedral surface smoothing with simultaneous mesh regularization. In: Martin R, Wang W, editors. Geometric Modeling and Processing. Hong Kong: 2000. pp. 229–237. [Google Scholar]
- Papez JW. Heart musculature of the atria. American Journal of Anatomy. 1920;27:255–285. [Google Scholar]
- Pennec X, Ayache N, Thirion JP. Landmark-based registration using features identified through differential geometry. Handbook of Medical Imaging-Processing and Analysis. I. 2000:499–513. [Google Scholar]
- Petera J, Pittman JFT. Isoparametric hermite elements. International Journal for Numerical Methods in Engineering. 1991;37:3489–3519. [Google Scholar]
- Peters J. Patching Catmull-Clark Meshes. SIGGRAPH. 2000:255–258. [Google Scholar]
- Platonov PG, Ivanov V, Ho SY, Mitrofanova L. Left atrial posterior wall thickness in patients with and without atrial fibrillation: data from 298 consecutive autopsies. Journal of cardiovascular electrophysiology. 2008;19:689–692. doi: 10.1111/j.1540-8167.2008.01102.x. [DOI] [PubMed] [Google Scholar]
- Reig J, Mirapeix R, Jornet A, Petit M. Morphologic characteristics of the fossa ovalis as an anatomic basis for transseptal catheterization. Surgical and Radiologic Anatomy. 1997;19:279–282. doi: 10.1007/BF01637589. [DOI] [PubMed] [Google Scholar]
- Rogers J, Courtemanche M, McCulloch A. Finite element methods for modelling impulse propagation in the heart. In: Panfilov AV, Holden AV, editors. Computational Biology of the Heart. John Wiley and Sons, Ltd.; Sussex: 1996. [Google Scholar]
- Saremi F, Channual S, Krishnan S, Gurudevan SV, Narula J, Abolhoda A. Bachmann Bundle and Its Arterial Supply: Imaging with Multidetector CT—Implications for Interatrial Conduction Abnormalities and Arrhythmias1. Radiology. 2008;248:447–457. doi: 10.1148/radiol.2482071908. [DOI] [PubMed] [Google Scholar]
- Seemann G, Höper C, Sachse FB, Dössel O, Holden AV, Zhang H. Heterogeneous three-dimensional anatomical and electrophysiological model of human atria. Philosophical Transactions of the Royal Society A: Mathematical. Physical and Engineering Sciences. 2006;364:1465–1481. doi: 10.1098/rsta.2006.1781. [DOI] [PubMed] [Google Scholar]
- Sheehan FH, Ge S, Vick G, III, Urnes K, Kerwin WS, Bolson EL, Chung T, Kovalchin JP, Sahn DJ, Jerosch-Herold M. Three-dimensional shape analysis of right ventricular remodeling in repaired tetralogy of Fallot. The American journal of cardiology. 2008;101:107–113. doi: 10.1016/j.amjcard.2007.07.080. [DOI] [PubMed] [Google Scholar]
- Stevens C, Remme E, LeGrice I, Hunter P. Ventricular mechanics in diastole: material parameter sensitivity. Journal of biomechanics. 2003;36:737–748. doi: 10.1016/s0021-9290(02)00452-9. [DOI] [PubMed] [Google Scholar]
- Tobón C, Ruiz C, Sáiz J, Heidenreich E, Hornero F. Reentrant mechanisms triggered by ectopic activity in a three-dimensional realistic model of human atrium. a computer simulation study. Computers in Cardiology, 2008. IEEE. 2008:629–632. [Google Scholar]
- Usyk TP, LeGrice IJ, McCulloch AD. Computational model of three-dimensional cardiac electromechanics. Computing and visualization in science. 2002;4:249–257. [Google Scholar]
- Vartziotis D, Wipper J. A dual element based geometric element transformation method for all-hexahedral mesh smoothing. Computer Methods in Applied Mechanics and Engineering. 2011;200:1186–1203. [Google Scholar]
- Velho L, Zorin D. 4–8 Subdivision. Computer Aided Geometric Design. 2001;18:397–427. [Google Scholar]
- Vigmond EJ, Ruckdeschel R, Trayanova N. Reentry in a morphologically realistic atrial model. Journal of cardiovascular electrophysiology. 2001;12:1046–1054. doi: 10.1046/j.1540-8167.2001.01046.x. [DOI] [PubMed] [Google Scholar]
- Virag N, Jacquemet V, Henriquez C, Zozor S, Blanc O, Vesin JM, Pruvot E, Kappenberger L. Study of atrial arrhythmias in a computer model based on magnetic resonance images of human atria. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2002;12:754–763. doi: 10.1063/1.1483935. [DOI] [PubMed] [Google Scholar]
- Wang K, Ho SY, Gibson DG, Anderson RH. Architecture of atrial musculature in humans. British heart journal. 1995;73:559–565. doi: 10.1136/hrt.73.6.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W, Zhang Y. Wavelets-based NURBS simplification and fairing. Computer Methods in Applied Mechanics and Engineering. 2010;199:290–300. [Google Scholar]
- Yu Z, Holst MJ, Cheng Y, McCammon JA. Feature-preserving adaptive mesh generation for molecular shape modeling and simulation. Journal of Molecular Graphics and Modelling. 2008;26:1370–1380. doi: 10.1016/j.jmgm.2008.01.007. [DOI] [PubMed] [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31:1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Bajaj C, Xu G. Surface Smoothing and Quality Improvement of Quadrilateral/Hexahedral Meshes with Geometric Flow. Communications in numerical methods in engineering. 2007a;25:1–18. doi: 10.1002/cnm.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Bazilevs Y, Goswami S, Bajaj CL, Hughes TJ. Patient-Specific Vascular NURBS Modeling for Isogeometric Analysis of Blood Flow. Computer Methods in Applied Mechanics and Engineering. 2007b;196:2943–2959. doi: 10.1016/j.cma.2007.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Liang X, Ma J, Jing Y, Gonzales MJ, Villongco C, Krishnamurthy A, Frank LR, Nigam V, Stark P. An atlas-based geometry pipeline for cardiac Hermite model construction and diffusion tensor reorientation. Medical image analysis. 2012;16:1130–1141. doi: 10.1016/j.media.2012.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J, Butters TD, Zhang H, Pullan AJ, LeGrice IJ, Sands GB, Smaill BH. An Image-Based Model of Atrial Muscular ArchitectureClinical Perspective Effects of Structural Anisotropy on Electrical Activation. Circulation: Arrhythmia and Electrophysiology. 2012;5:361–370. doi: 10.1161/CIRCEP.111.967950. [DOI] [PubMed] [Google Scholar]
- Zheng JJ, Zhang JJ, Zhou H, Shen L. Smooth spline surface generation over meshes of irregular topology. The Visual Computer. 2005;21:858–864. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.