Long Lived NMR Signal in Bone

Abstract

Solids and rigid tissues, such as bone, ligaments, and tendons, typically appear dark in MRI, which is due to the extremely short-lived proton nuclear magnetic resonance signals. This short lifetime is due to strong dipolar interactions between immobilized proton spins, which render it challenging to detect these signals with sufficient resolution and sensitivity. Here we show the possibility of exciting long-lived signals in cortical bone tissue with a signature consistent with that of bound water signals. It is further shown that dipolar coupling networks are an integral requirement for the excitation of these long-lived signals. The use of these signals could enhance the ability to visualize rigid tissues and solid samples with high resolution and sensitivity via MRI.

1. Introduction

MRI has become a prime noninvasive diagnostic tool in the medical field [1, 2], and is becoming popular in the materials sciences as well [3–7]. One of its major challenges, particularly in the medical field, is the requirement of relatively long-lived signals (> 1–10 ms) for adequate image reconstruction with sufficient microscopic detail in vivo. Bone and rigid tissues, such as ligaments and tendons, however, have very short-lived signals (< 1ms), and therefore often remain dark in conventional MRI images [8–12]. Although there exist advanced methods for visualizing relatively short-lived signal components, these are generally demanding on hardware, require specialized instrumentation, and are frequently incompatible with in vivo constraints [8–10].

The origin of the short lifetime in rigid tissues (and rigid samples, in general) can be two-fold. First, considerable magnetic field inhomogeneity may be present due to susceptibility gradients, leading to signal dephasing (inhomogeneous broadening) [13]. The second contribution is from homogeneous broadening, with one of its major mechanisms being dipolar coupling between many spins. The inhomogeneous mechanism can, in principle, be refocused. Elaborate schemes, typically based on interleaved pulsing and acquisition, often in combination with sample spinning, have been developed for reducing the homogeneous broadening [14]. These techniques are incompatible however with in vivo MRI constraints [15, 16].

One can excite narrow portions of an inhomogeneously broadened resonance by selective radiofrequency (rf) pulses, while it had been a long-standing dogma that the same cannot be done for dipolar broadening [17] – until it was shown to be possible by Khitrin et al. [18–20]. It was shown that one could excite many narrow signals (up to a thousand), from a dipolar-broadened line in the context of ‘molecular photography’ [21, 22]. Since then, it was shown that narrow (and therefore long-lived) signals could be excited in a number of solid compounds, including adamantane, 5CB liquid crystal, naphthalene, polybutadiene, and glucose, by either a long and weak single rf irradiation, or such irradiation in combination with a strong refocusing π pulse [19, 20]. A complete theory of this puzzling phenomenon is still missing. The proposed mechanism for the appearance of these long-lived signals is based on a symmetry breaking which comes from a small difference of chemical shifts of nuclei directly coupled by much stronger dipole-dipole interactions [19, 20].

In this work, we show that such long-lived signals can be excited in cortical bone tissue samples and used for imaging. Most notably, it is shown here that the intensity of the long-lived signals is related to the dipolar coupling network complexity, further underlining that this intriguing phenomenon may be caused by unusual spin dynamics.

2. Methods

Samples of fresh bovine tibia bone were purchased from a local slaughterhouse. Cortical bone was obtained from the center of the tibia and soaked in phosphate buffered saline (PBS) solution for three hours before experiments. Trabecular bone was cut from the end of the tibia. The bone samples were cut to fit into a 5 mm NMR tube. Dry collagen strips (from bovine Achilles tendon CAS 9007-34-5) and 99.8% D₂O were purchased from Sigma-Aldrich (St. Louis, MO, USA) and used without further modification.

All experiments were performed at 11.7 T (500 MHz ¹H frequency) using a Bruker Avance spectrometer (Billerica, MA, USA) equipped with a BBO probe.

Here, two sequences are used, one with a long and weak single radio-frequency (rf) irradiation, and one with a shorter irradiation followed by a hard π pulse which is phase-shifted by π/2. We call the first one the long-lived response (LLR) experiment, and the second one the LLR echo (LLRE) experiment. The duration and power for LLR were optimized for maximal signal and were 18 ms and at a rf amplitude (γB₁/2π) of 40 Hz. A pre-acquisition delay of 1 ms was used, which improved the baseline in the spectra by dephasing spurious broader components. The LLRE signal was excited first with a 5 ms soft pulse with rf amplitude of 80 Hz, followed by a π pulse with a 25 kHz amplitude. The nutation experiments for LLR in Figs. 1b and S2b were performed with flip angles ranging from ~π/6 to 5π with a pulse amplitude of 40 Hz.

Figure 1.

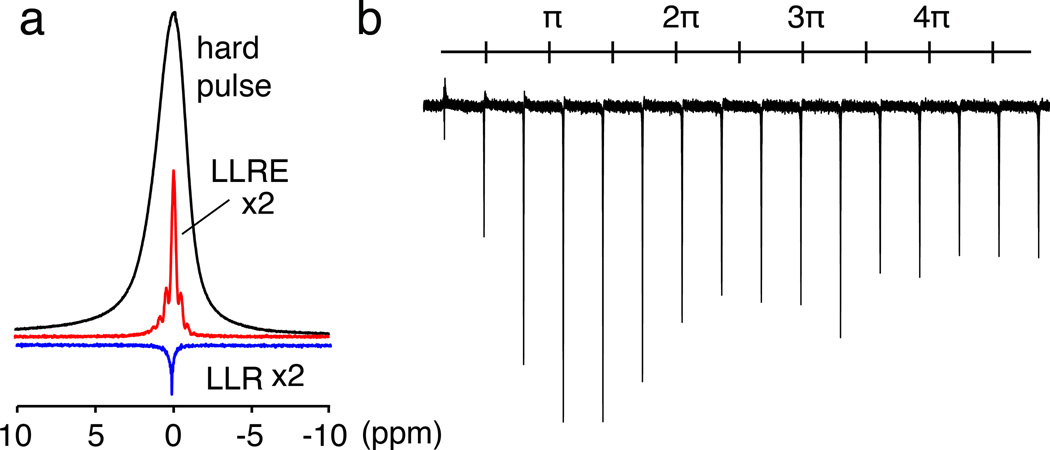
Long-lived signals excited in a cortical bone sample. (a) Conventional ¹H NMR spectrum (black) compared with a LLR spectrum (blue) and a LLRE spectrum (red) of a cortical bone sample. The linewidths are 1150 Hz, 70 Hz, and 165 Hz, respectively. The LLR spectrum was acquired after applying a 18 ms long pulse with rf power of 40 Hz. The LLRE spectrum was acquired with a 5 ms soft pulse with rf power of 80 Hz, followed by a high power π pulse. (b) LLR signals excited with pulses of 40 Hz power with nominal flip angles ranging from ~π/6 to 5π in a cortical bone sample.

The equilibration of bone samples in D₂O/H₂O mixtures (Fig. 2) was conducted following the procedure reported by Techawiboonwong et al. [23]. The bone sample was immersed in D₂O/H₂O mixtures with different isotopic compositions (1%, 3%, 5%, 7%, 10%, 30%, 50% and 90% D₂O volume fraction) for 24 hours at 55°C. To remove the free water in large macroscopic pores on the endosteal surface, the specimen was blow-dried for 1 minute. The sample was then placed inside a 5-mm NMR tube. Fluorinated oil (Fluorinert, FC-77, 3M, St. Paul, MN, USA) was filled into the void spaces for protection and for reduction of susceptibility artifacts.

Figure 2.

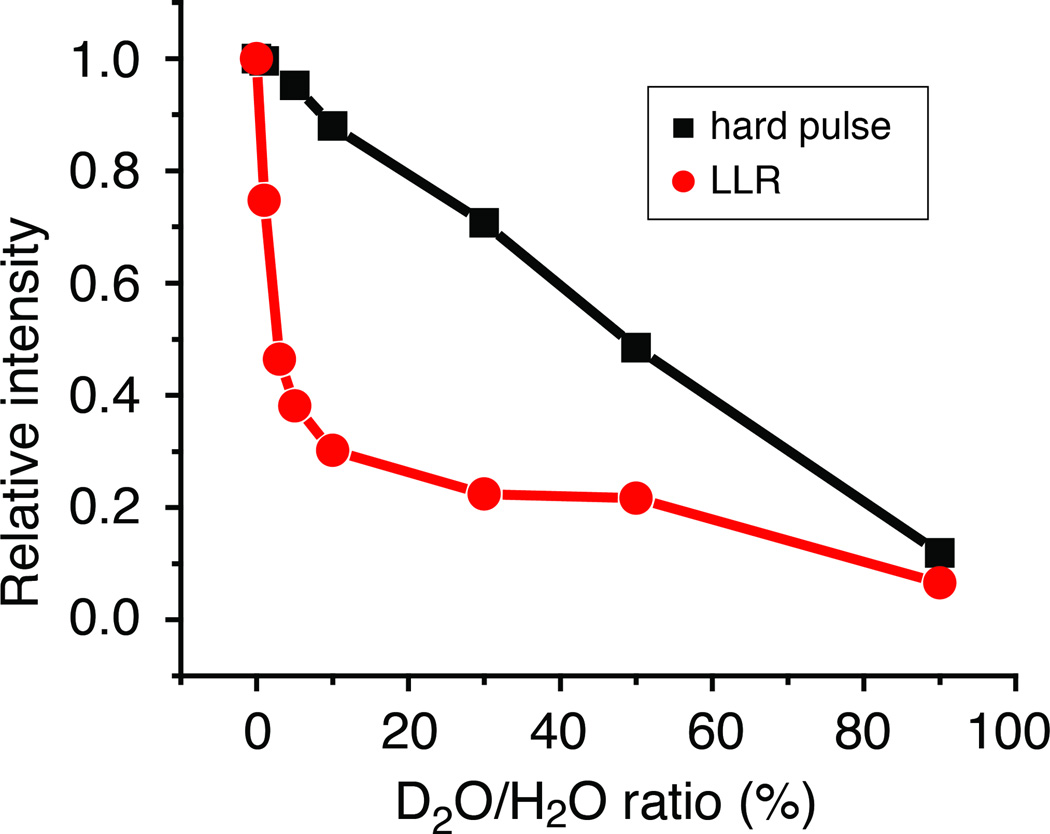
Signal intensity as a function of D₂O/H₂O ratio for a hard pulse response (black squares) and LLR (red circles) in a cortical bone sample. The rapid decrease of the LLR signal with D₂O ratio increase is a testament to the dipolar coupling nature of the effect.

The two-dimensional LLRE images (Figs. 3a, 3b and S4) were acquired with a gradient echo imaging block with a 2 ms echo time and 16 averages. In the 2D images of cortical bone (Figs. 3a and 3b), the data matrix 128×32 had a resolution of 51×151 µm². The applied gradient strengths were 7.8 G/cm for both the read-out and the phase-encoding gradients. In Supplementary Fig. S4, the data matrix was of size 256×32 with a resolution of 77×226 µm²; the applied gradient strengths were 6 G/cm for the read-out gradient and a maximum of 5.2 G/cm for the phase-encoding gradient. The one-dimensional images in Figs. 3c and S3 were obtained along the z-direction, i.e., along the sample tube and with a 2 ms echo time and 2 averages. The gradient strength was 6 G/cm and the spatial resolution 76.5 µm/pt.

Figure 3.

Images of a cortical bone sample. (a) Two-dimensional LLRE and (b) conventional gradient echo (GE) images, both at nominal resolutions of 51×151 µm², with 51 µm as the resolution of the direct imaging dimension. (c) One-dimensional images using a spin-echo (SE), gradient echo (GE), and a LLRE. The SE image is scaled down by a factor of 4 for comparison.

3. Results and Discussion

Fig. 1 shows the LLR and LLRE signals excited in a cortical tissue sample. The excited signal generally appears at the same frequency as the respective weak rf irradiation, and the linewidths are reduced when compared to the single hard pulse excitation (1150, 70, and 165 Hz for the hard pulse, LLR, and LLRE spectra, respectively). The sensitivity ratios are 28:1:7 for the hard pulse, LLR, and LLRE spectra, respectively. Although both LLR and LLRE signals are significantly weaker than the signals excited by a hard pulse, the decreased sensitivity can be compensated for by slower signal decay. Based on the measured linewidths, one can estimate that the LLR signal intensity becomes equal to the one of the hard pulse signal after a delay of 3.1 ms (for the LLRE signal, the delay would be 1.4 ms). Such delays are often significantly shorter than typical phase-encoding periods used in MRI sequences, in particular in vivo. Therefore, LLR and LLRE could lead to enhanced sensitivity in certain applications.

Another important point is also that the LLRE signal can be clearly linked to the bound water pool (see below), and does not respond strongly to the pore water signal which would also be included in the amplitude of the conventional signal. Further examples of LLRE signal excitation in a homogeneously-broadened system are shown as supplementary material, which includes a demonstration with a solid collagen sample (Supplementary Fig. S2).

The LLR signal as a function of nominal flip angle (α = ω₁τ) shows that it does not follow a sine function, and a maximum excitation efficiency is found at a flip angle of 5π/4. Such a behavior is consistent with homogeneous or inhomogeneous broadening, where no sine-oscillation should be seen beyond a regime where the original line width greatly exceeds the bandwidth of the rf irradiation.

Multi-spin quantum simulations are particularly challenging to perform for systems larger than 10–13 densely coupled spins [24]. A limited simulation with 10 dipolar-coupled spins, however, also shows the appearance of a LLR signal (Fig. S1). The rf nutation curve of Fig. S1b also reveals a behavior similar to the experimental results of Fig. 1b, although one should keep in mind the limitations of simulations with relatively small spin systems.

A complete theoretical description of the LLR phenomenon remains elusive at this point due to the complexity of studying a large dipolar coupled spin system. The most plausible explanation so far is based on the use of linear response theory [19, 20]. Experimental evidence on related systems has shown that the LLR signal only arises in the presence of at least small chemical shift differences. This aspect can be confirmed with the linear response treatment [19, 20]. This approach, however, does have the limitation that it can only consider small flip angle pulses, or a small flip angle pulse in combination with a π pulse. Clearly, the phenomenon can be more complex.

In order to provide further insight into the origin of the LLR phenomenon, and to show that dipolar coupling complexity must be involved in the observed phenomenon in bone, the following experiment was performed: a cortical bone sample was equilibrated successively in D₂O/H₂O mixtures for a prolonged period (24h) at 55°C in order to facilitate the equilibration of the solution with pore and bound water pools in the tissue. This procedure has been used to determine the connection between the short-lived NMR signals and the bound bone water fractions [23, 25]. In previous work, it was shown that this signal, when measured in vivo, correlated with cortical bone porosity [23, 25]. In Fig. 3 it is seen that the conventional pulsed NMR signal obeys a linear relationship with D₂O concentration, while the long-lived signal displays a strikingly non-linear relationship. The long-lived signal decreases rapidly when the D₂O content increases over the first 10%, and then decreases more gradually when increasing the D₂O content further.

Such a rapid decrease of the LLR signal in the low D₂O percentage range may qualitatively support an interpretation based on the dipolar coupling network: Dilution with D₂O and subsequent H/D exchange decreases the dipolar network connectivity and the LLR intensity. The exchange dynamics itself may play a further role in destroying the averaged coupling network, and hence also the LLR signal.

This result presents a new, and perhaps the strongest demonstration so far, that the long-lived signals depend on dipolar coupling complexity. With respect to the previously-reported distinction between cortical bone pore water and bound water [26], this experiment also clearly demonstrates that the LLR signals must arise from bound water (in pore water, the major broadening arises from the inhomogeneous mechanism, which is clearly ruled out in the results of Fig. 2).

The line narrowing afforded by this LLR signal excitation could then be used for imaging with enhanced resolution, as illustrated in Fig. 3. The LLRE image (Fig. 3a) of cortical bone appears superior to the conventional gradient echo (GE) image of the same nominal resolution (Fig. 3b). Furthermore, in the GE the image is distorted, likely as a result of the broad linewidth. The reduced linewidth in LLRE places fewer constraints on the minimal gradient strength necessary to achieve a specified resolution. Image readout times can also be made longer, thereby obviating the need for strong and fast-switching gradients. These long-lived signal acquisitions could be combined with radial [27] or other nonuniform [28] readout techniques, where they could also be used to reduce the required gradient strength along the individual k-space trajectories. The one-dimensional imaging projections illustrate this point further (Fig. 3c). While the conventional spin-echo (SE) image shows the strongest signal, its resolution is significantly degraded due to signal overlap. In particular, both the GE and the SE images show their signals extending beyond the physical limits of the sample on the right side. While it appears here that the SE shows the best signal, it should be remembered that the signal is only stronger at the expense of resolution, and that such efficient echoes cannot normally be implemented on an MRI scanner. Additional demonstration of resolution enhancement by LLRE is demonstrated in Supplementary Fig. S3 for a trabecular bone sample. Supplementary Fig. S4 also shows how LLRE allows one to observe cortical bone signals in a sample containing both cortical and trabecular bone.

4. Conclusion

In conclusion, we show herein that long-lived signals can be excited in the homogeneously broadened signal portion of cortical bone. This signal therefore likely originates from bound water (as opposed to pore water), due to the homogeneous nature of the spectrum. Furthermore, deuterium-exchange experiments indicate that the long-lived signals correlate with the dipolar coupling network complexity, which has never been seen directly before. Due to this connection, it is possible that these signals can produce a new type of image contrast. These long-lived signals could become important for imaging rigid tissues and bone, in particular, in vivo, where they may be useful for the diagnosis and the study of osteoporosis and many other bone disorders.

• We show evidence of long-lived signals in cortical bone and collagen.

• The signals can be linked to homogeneously broadened pools.

• The signals are likely due to tightly bound bone water pools.

• The signals can be used for imaging.