Control of Sarcoplasmic Reticulum Ca²⁺ Release by Stochastic RyR Gating within a 3D Model of the Cardiac Dyad and Importance of Induction Decay for CICR Termination

Abstract

The factors responsible for the regulation of regenerative calcium-induced calcium release (CICR) during Ca²⁺ spark evolution remain unclear. Cardiac ryanodine receptor (RyR) gating in rats and sheep was recorded at physiological Ca²⁺, Mg²⁺, and ATP levels and incorporated into a 3D model of the cardiac dyad, which reproduced the time course of Ca²⁺ sparks, Ca²⁺ blinks, and Ca²⁺ spark restitution. The termination of CICR by induction decay in the model principally arose from the steep Ca²⁺ dependence of RyR closed time, with the measured sarcoplasmic reticulum (SR) lumen Ca²⁺ dependence of RyR gating making almost no contribution. The start of CICR termination was strongly dependent on the extent of local depletion of junctional SR Ca²⁺, as well as the time course of local Ca²⁺ gradients within the junctional space. Reducing the dimensions of the dyad junction reduced Ca²⁺ spark amplitude by reducing the strength of regenerative feedback within CICR. A refractory period for Ca²⁺ spark initiation and subsequent Ca²⁺ spark amplitude restitution arose from 1), the extent to which the regenerative phase of CICR can be supported by the partially depleted junctional SR, and 2), the availability of releasable Ca²⁺ in the junctional SR. The physical organization of RyRs within the junctional space had minimal effects on Ca²⁺ spark amplitude when more than nine RyRs were present. Spark amplitude had a nonlinear dependence on RyR single-channel Ca²⁺ flux, and was approximately halved by reducing the flux from 0.6 to 0.2 pA. Although rat and sheep RyRs had quite different Ca²⁺ sensitivities, Ca²⁺ spark amplitude was hardly affected. This suggests that moderate changes in RyR gating by second-messenger systems will principally alter the spatiotemporal properties of SR release, with smaller effects on the amount released.

Introduction

In cardiac muscle, depolarization of the sarcolemma initiates Ca²⁺ release by activating sarcolemmal L-type Ca²⁺ channels, providing a local increase in cytoplasmic calcium concentration in the junctional space of the dyad (for review, see Bers (1)). This initiates [Ca²⁺]-dependent activation of the sarcoplasmic reticulum (SR) Ca²⁺ release channels, which are ryanodine receptors (RyRs) (2,3). The subsequent release of Ca²⁺ from the SR further increases the [Ca²⁺] in the junctional space and leads to regenerative RyR activation in a process known as calcium-induced calcium release (CICR) (4). In such a regenerative process, the larger SR Ca²⁺ flux should prevent subsequent control by the surface membrane (5) and deep-SR Ca²⁺-store depletion. However, the quantity of Ca²⁺ released from the SR has a graded dependence on the magnitude of the Ca²⁺ influx across the sarcolemma (5,6), and the SR releases only ∼50% of its content (see, e.g., Picht et al. (7)). The discovery of Ca²⁺ sparks (1,8) and local control theories (9) provided a solution to this problem by showing that graded responses can result from the spatiotemporal summation of individual Ca²⁺ release sites that are spatially uncoupled to limit regenerative behavior (10,11). However, local regeneration in CICR during Ca²⁺ sparks might still oppose reliable Ca²⁺ spark termination (12,13).

The termination problem in the local control mechanism has been reviewed elsewhere (12,13), and several mechanisms have been proposed to limit local regeneration. For example, it has been suggested that time-, SR-Ca²⁺-, and cytosolic-Ca²⁺-dependent RyR inactivation (4–6,14–16) would dampen regenerative behavior. However, the reported rates of inactivation are much slower than the time to peak of the Ca²⁺ spark (14,16,17). Stochastic RyR gating and the rapid response of local [Ca²⁺] to changing RyR flux may also contribute to spontaneous closure via stochastic attrition (9), although stochastic attrition on the timescale of a Ca²⁺ spark seems unlikely for more than ∼5–10 RyRs in a junctional cluster. The addition of inter-RyR allosteric interactions, which effectively reduces the number of RyRs in the cluster (e.g., very strong coupling will make the cluster gate as a single channel), can allow reliable termination for larger numbers of RyRs (12,18). However, direct observations of such allosteric interactions are few, and to our knowledge, such behavior has only been seen under quite nonphysiological conditions with detergent-solubilized RyRs (19).

Depletion of the SR lumen [Ca²⁺] may reduce the RyR release flux to the point where regenerative CICR is no longer supported (5,6,20–22), but measurements of SR [Ca²⁺] with fluo-5N suggest only moderate SR depletion (e.g., Picht et al. (7) and Shannon et al. (23)). We recently reported that the complex interaction of stochastically gating RyRs within a 3D spatial model could produce reliable spontaneous closure without any form of RyR inactivation (24). This closure was due to induction decay, wherein the increasing RyR closed time associated with declining RyR flux (due to junctional SR depletion) prevented closed RyRs from responding to the nearby open RyRs. Further support for the idea of induction decay comes from recent experiments in which reduced RyR conductance resulted in reduced Ca²⁺ spark amplitude despite the fact that there was no change in RyR gating (21). However, our previous report did not explore the generality of the result for different dyad geometries and used only gating data from rat RyRs, which seemed relatively insensitive to cytosolic Ca²⁺ compared to data reported elsewhere in the literature (i.e., K_d ∼ 10 μM).

Here, we expand on our previous study, examining the robustness of induction decay as a termination mechanism for both rat and sheep RyR gating in the presence of physiological levels of Mg²⁺ and ATP and with different dyad geometries and single-channel currents. It is important to note that the rat RyR model reproduces measured Ca²⁺ spark restitution (25) and that our measured RyR regulation by luminal Ca²⁺ has little effect on Ca²⁺ spark properties. The model also displays a Ca²⁺ spark amplitude dependence on single RyR channel current, which is similar to that recently explored using TRIS as a permeable blocking ion (21). In addition, we discuss the implications of the model for understanding the role(s) played by possible RyR gating changes and dyad restructuring.

Methods

Isolation of hearts

Healthy male adult rats (Harlan Sprague-Dawley, Indianapolis, IN) were heparinized (2000 U heparin injection BP, Weddel Pharmaceuticals, London, United Kingdom) and 15 min later anesthetized with isoflurane (Laser Animal Health, Brisbane, Australia). The hearts were rapidly removed and immediately perfused via the Langendorff method with ice-cold Krebs-Henseleit buffer (in mM, 120 NaCl, 25 NaHCO₃, 10 Glucose, 5 KCl, 2 MgCl₂, 1 NaH₂PO₄, and 2.5 CaCl₂) for 2 min until the blood was washed out. Hearts were then perfused for 5 min with warmed (37°C) and oxygenated (95% O₂, 5% CO₂) Krebs-Henseleit buffer, after which they were snap-frozen. Sheep hearts were excised from anesthetized ewes (5% pentobartitone (IV) followed by oxygen/halothane) and rinsed in ice-cold homogenizing buffer (20 mM imidazole and 300 mM sucrose, pH 7.4 with HCl) before snap-freezing. All hearts were snap-frozen in liquid nitrogen and stored at −80°C until further use.

SR vesicle preparation

Briefly, heart tissue was homogenized in buffer containing 10 mM imidazole, 0.5 mM dithiothreitol (DTT), 3 mM sodium azide, 0.29 M sucrose, 1 μg/ml leupeptin, 1 μg/ml pepstatin A, 1 mM benzamidine, 0.5 mM phenylmethylsulfonyl fluoride, and 20 mM NaF, pH 6.9 (homogenization buffer). SR vesicles were separated by centrifugation as described in the Supporting Methods. The NaF inhibited phosphatases during the SR vesicle preparation. The whole procedure was carried out at 4°C.

Single-channel recordings

Lipid bilayers were formed as described in the Supporting Methods. Lipid bilayers separated cis (cytoplasmic) and trans (luminal) compartments. Both compartments contained 250 mM Cs⁺ (230 mM CsCH₃O₃S, 20 mM CsCl, and 10 mM TES buffer). In the trans bath, [Ca²⁺] was either 0.1 or 1 mM. The cis bath contained 2 mM ATP and 3 mM MgCl₂ (1 mM free Mg²⁺), and Ca²⁺ was titrated between 1 and 500 μM (see Supporting Methods for details of pH and Ca ²⁺ buffering). The composition of the cis solution was altered by local perfusion and the composition of the trans solutions was altered by addition of aliquots of stock solutions. All experiments were performed at room temperature (21–26°C) and membrane potential of −40 mV (lumen at ground). Before analysis, the current signal was low-pass digitally filtered at 1 kHz. Channel 3 software (N. W. Laver, nic@niclaver.com) was used to detect channel events and measure open probability (P_o), mean open time (τ_o), and mean closed time (τ_c).

Model geometry

The geometry of the model dyad is shown in Fig. 1. Electron micrographs suggest a large variation in dyad size and t-tubule radius (see, e.g., Franzini-Armstrong (26), Fawcett and McNutt (27), Forbes and Van Neil (28), and Forssman and Girardier (29)). In the simulations shown here, the t-tubule is a cylinder 250 nm in diameter between computational boundaries. Wrapped around its circumference, at its midpoint, is the terminal or junctional SR (j-SR), which is represented as a pancake 360 nm along the axis, 26 nm radial thickness, and 450 nm tubule circumference. RyR Ca²⁺ release channels were arranged in clusters with a nearest-neighbor separation of 31 nm on the j-SR membrane facing the t-tubule. The j-SR was connected to the network SR (n-SR) at its center. The n-SR was isotropically distributed throughout the computational volume to mimic a labyrinth of tubules occupying a volume fraction of 3.5% of the cytoplasmic volume. Model parameter values for dyad structure are given in the Table S1 in the Supporting Material.

Figure 1.

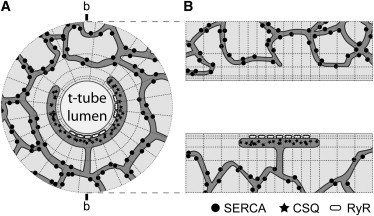
Illustration of the model geometry. (A) Cross section of the cylindrical model with a t-tubule in the center. The j-SR wraps around the t-tubule at a 15-nm radial distance (dyad cleft). RyRs are located in the j-SR membrane and release Ca²⁺ into the dyad cleft. The j-SR contains calsequestrin (CSQ) and is connected to the n-SR by a tubule, which allows for Ca²⁺ diffusion between these two compartments. The SERCA Ca²⁺ uptake transporters are uniformly distributed throughout the n-SR. (B) Side view of the model in the cross section indicated by b-b in A. In this view, the t-tubule lumen runs horizontally and the j-SR can be seen on one side.

Ion movements

Computational details are given in the Supporting Methods. Ca²⁺ diffusion and binding to Ca²⁺ indicators (fluo-4 and fluo-5N) in and around the dyad were calculated using Matlab (Mathworks, Natick, MA). The ion concentrations in each volume element were calculated by solving a discretized form of the electro-diffusion/transport equation that is shown here for the case of Ca²⁺:

$$\frac{\partial \left[C{a}^{2+}\right]}{\partial t}\mathrm{=-}{D}_{Ca}\nabla \left(\nabla \left[C{a}^{2+}\right]+2\left[C{a}^{2+}\right]\nabla \Phi \right)+\sum _{RyR}{J}_{RyR}-J_{SERCA}-\sum _{buffer}{J}_{buffer},$$ (1)

where D_Ca is the diffusion coefficient for Ca²⁺ and Φ is the electrostatic potential arising from charged lipids on the t-tubule membrane. The term involving ∇Φ was assumed to have only radial components. J_RyR represents the flow of Ca²⁺ through each open RyR into the adjacent volume element in the dyad cleft (with volume V_cleft), which was given by

$$J_{RyR}=\frac{i_{RyR}}{2F{V}_{cleft}}\left({\left[C{a}^{2+}\right]}_{j-SR}-{\left[C{a}^{2+}\right]}_{cleft}\right),$$ (2)

where i_RyR is a constant to give a 0.6-pA flux (30,31) for an open RyR with a 1 mM [Ca²⁺] gradient and F is Faraday’s constant. Ca²⁺ uptake was simulated by a simplified model for sarcoendoplasmic reticulum calcium-transport ATPase (SERCA) (32) located in the n-SR, as given by

$$J_{SERCA}=\frac{K_{SR,\max }}{V_{cyto}}\left(\frac{{\left(K_{SERCA}{\left[C{a}^{2+}\right]}_{cyto}\right)}^2}{1+{\left(K_{SERCA}{\left[C{a}^{2+}\right]}_{cyto}\right)}^2}-k_{leak}\right),$$ (3)

where K_SR,max is the maximum rate of SERCA uptake, K_SERCA the cytoplasmic Ca²⁺ binding constant, and V_cyto the element volume. k_leak sets J_SERCA to zero under initial/resting conditions. K_SR,max was set by reproducing the rate of decline of whole-cell [Ca²⁺] after setting cytoplasmic [Ca²⁺] to 1 μM, and the value is given in Table S3.

J_buffer is the contribution to Ca²⁺ fluxes from Ca²⁺ reacting with a buffer, B:

$$J_{Buffer}=k_{on}\left[B\right]\left[C{a}^{2+}\right]-k_{off}\left[CaB\right].$$ (4)

Diffusible buffers included ATP, calmodulin, fluo-4, and fluo-5N, with diffusion coefficients described in Table S2. Troponin buffering was fixed in the cytoplasmic compartment, whereas calsequestrin was fixed in the SR compartments and concentrated mainly in the j-SR. Negatively charged lipids such as phosphatidylserine (PS) and zwitterionic phosphatidylcholine (PC) give rise to a negative net charge on the lipid bilayer and provide binding sites for cations such as Ca.²⁺ and K⁺. In the model, these effects are treated using simplifying approximations, as described previously (32) (also see Supporting Material).

The equations were solved on a cylindrical coordinate system with Neumann reflective boundaries at ±2 μm along the t-tubule and at a radius of 2 μm. Model parameters for ion diffusion and buffering are given in Table S2.

RyR gating

RyR gating was simulated using an empirical two-state (open and closed) stochastic model. The opening and closing rates were derived from two-segment linear fits to experimental transition rates (see Fig. S1), which are limited to Ca²⁺ levels during CICR and are not intended to describe RyR gating behavior at resting Ca²⁺ levels (see below). The transition rates were calculated from the reciprocal of the empirical RyR mean closed and open times, respectively. A Monte Carlo method was used to simulate stochastic transitions of each RyR, and at the computed transition times for each RyR, the integration was restarted using the new values of J_RyR.

Initiation of Ca²⁺ sparks

Simulations were started either by 1- to 3-ms Ca²⁺ injection into a volume element adjacent to an RyR at a rate corresponding to 0.2 pA (to mimic an L-type Ca²⁺ channel opening) or by initializing one RyR in the open state (to mimic the initiation of a spontaneous Ca²⁺ spark). The subsequent evolution of the Ca²⁺ spark showed no difference between simulations triggered in these two ways (not shown).

Microscope blurring

To simulate the Ca²⁺ sparks and blinks as observed by confocal microscopy, the spatial distributions of fluo-4 and fluo-5N generated by the model were convolved with 3D Gaussian point-spread function. The full width at half-maximum of the Gaussian was 0.3 μm in the focal plane of the microscope (x and y directions) and 0.93 μm perpendicular to the focal plane (z direction).

Results

Fig. 2 A shows the typical pattern of RyR gating observed at various cytoplasmic [Ca²⁺] and in the presence of 2 mM ATP and 1 mM free Mg²⁺. Under these conditions, the open probability (P_o) of RyRs from sheep (Fig. 2 B, open triangles) had a much weaker dependence on [Ca²⁺] than that of RyRs from rat at either 0.1 mM (open circles) or 1 mM (solid circles) luminal [Ca²⁺]. The RyR P_o for both species increased to a maximum of ∼0.5 at 0.1 mM [Ca²⁺]. The P_o for rat RyRs showed only a modest dependence on luminal Ca²⁺ levels, consistent with studies on sheep RyRs (33,34). For [Ca²⁺] between 1 and 100 μM, the mean P_o varied as ∼[Ca²⁺]^2.8 for rat (24) and ∼[Ca²⁺]^2.1 for sheep, which was primarily due to changes in closed time (Figs. 2 C and S1). For simplicity, we used the closed-time data at 0.1 mM SR (trans) [Ca²⁺], because the model showed that j-SR levels dropped to about this level during the Ca²⁺ spark, and as shown below, allowing SR Ca²⁺ to influence closed time had only minor effects on Ca²⁺ spark properties. Any extrapolation of the empirical power function(s) describing the RyR gating seen at higher [Ca²⁺] to lower resting [Ca²⁺] predicts a resting Ca²⁺-spark rate that is too low and is therefore problematic. However, if the longest-closed-time data points of Fig. 2 C for rat and sheep RyRs are extrapolated to resting conditions, these data points suggest that (shorter) closed times of ∼1000 s might pertain at 0.1 μM [Ca²⁺]. It has been estimated that a confocal microscope samples ∼1.1 release sites per μm scanned (35). Therefore, a 100-μm scan line would record from ∼110 release sites (junctions), and with ∼20 RyRs in each junction, and assuming that most spontaneous RyR openings trigger a Ca²⁺ spark, the resting Ca²⁺ spark rate would be ∼2 s⁻¹, in reasonable agreement with experimental observations (8,36).

Figure 2.

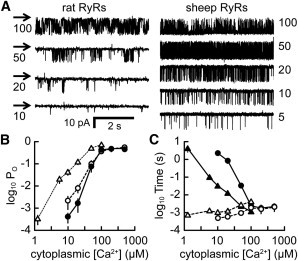
[Ca²⁺]-dependent RyR2 gating in lipid bilayers. Both sides of the bilayer contained (in mM) 230 CsCH₃O₃S and 20 CsCl (pH 7.4), with 2 ATP and 3 MgCl₂ on the cytoplasmic side ([Ca²⁺] as indicated). (A) Channel openings at various [Ca²⁺] are downward deflections from the baseline (arrows). (B) Cytoplasmic [Ca²⁺] dependence of P_o for RyRs from rat (luminal [Ca²⁺], 0.1 mM (solid circles) and 1 mM (open circles)) and sheep heart (luminal [Ca²⁺], 0.1 mM (open triangles)). Data points show the mean ± SE for n = 3–11 (solid circles), n = 4–8 (open circles), and n = 2–14 (open triangles)). Some of the rat data values have been replotted from Laver et al. (24). (C) Cytoplasmic [Ca²⁺] dependence of sheep RyR mean open and closed durations (0.1 mM luminal [Ca²⁺]). Solid symbols represent closed times and open symbols open times. Sheep RyR gating is shown by triangles and rat RyR gating, replotted from Laver et al. (24), by circles.

Morphology of simulated Ca²⁺ sparks and blinks

We could simulate Ca²⁺ sparks and associated SR Ca²⁺ depletion signals (Ca²⁺ blinks (8)) by incorporating fluo-4 and fluo-5N Ca²⁺ indicators into the model. Fig. 3 illustrates the time course and spatial spread of Ca²⁺ sparks (Fig. 3 A) and blinks (Fig. 3 B), derived from simulations of Ca²⁺ release by an array of 21 rat RyRs triggered by a 3 ms dihydropyridine receptor (DHPR) opening after simulated optical blurring. The simulated Ca²⁺ spark is similar to those observed experimentally (see also Laver et al. (24)), with the Ca²⁺ spark having a greater spatial width than the Ca²⁺ blink (Fig. 3 C). It is notable that no triggering sparklet (37) is seen; the trigger signal is essentially lost due to the small volume of the dyad cleft and the rapid activation of the RyR cluster. Although we do not have experimental records for Ca²⁺ blinks in rat RyRs, the simulated blinks were of comparable in amplitude, duration, and spatial extent to those reported for rabbit (minimum F/F_o = 60 ± 8%, full duration at half-maximum (FDHM) = 175 ± 7 ms (38), and 823 ± 476 nm (39). The fluo-5N fluorescence signal significantly underestimated the extent of local depletion of the j-SR due to blurring of the j-SR, t-tubule, and n-SR structures by the microscope (40). The rate of recovery of the fluo-5N fluorescence signal (time constant = 80 ms) was substantially faster than the rate of j-SR replenishment (time constant = 180 ms), which was largely due to the saturation effects in the fluo-5N signal.

Figure 3.

Simulation of Ca²⁺ sparks and blinks. (A) Simulated Ca²⁺ sparks. The simulated Ca²⁺ spark was generated by the array of RyRs shown in Fig. 4. (B) The corresponding simulated Ca²⁺ blink. Scale bars apply to both A and B. (C) Corresponding spatial profiles of spark and blink fluorescence at the times of their peak and minimum intensities, respectively. The noisy line shows the profile of an experimentally recorded Ca²⁺ spark (see also (23, 24) for additional comparison of model behavior to experimental data).

Ca²⁺ dynamics and RyR regulation during Ca²⁺ sparks

Fig. 4 shows an exemplar response of the model, with 21 irregularly arranged RyRs stimulated by the DHPR-trigger opening. The time courses (n = 7) of the computed average Ca²⁺ spark and blink signals are shown in Fig. 4 A. Mean [Ca²⁺] in the dyad cleft and j-SR elements is shown in Fig. 4 B. The initial rise in dyad [Ca²⁺] is due to the Ca²⁺ influx from DHPR triggering (which has no variance). Subsequent changes in [Ca²⁺] due to stochastic RyR gating then lead to variance in both signals. Fig. 4 C shows that shortly after initiation, the number of open RyRs increased to ∼10, which corresponds to P_o ∼ 0.5, and remained at this level for ∼132 ms before the RyRs started to close; closure was complete at 22 ms. This RyR response can be understood in terms of the dyadic and j-SR [Ca²⁺] (Fig. 4 B). Initially, dyad [Ca²⁺] rose to high levels resulting from a regenerative phase of CICR that persisted for ∼15 ms. By that time, j-SR [Ca²⁺] had declined to ∼10% of resting levels, which reduced the Ca²⁺ flux via open RyRs (Fig. 4 C) and consequently reduced local dyad [Ca²⁺] to a point where regeneration decayed and the RyRs started to close. Once RyRs had closed, [Ca²⁺] in the dyad cleft equilibrated with the bulk cytoplasm and Ca²⁺ in the j-SR was replenished by diffusion of Ca²⁺ from the n-SR. The decline in Ca²⁺ spark fluorescence was primarily due to Ca²⁺ diffusion in the cytoplasm and buffering, with SERCA reuptake playing a lesser role, as previously described (41,42). In this simulation, rat RyRs were distributed in a loose cluster, as depicted in Fig. 4 D, which also shows the distribution of open RyRs and local dyad [Ca²⁺] at several time points. The time course of Ca²⁺ flux from the dyad is shown in Fig. 4 E and is in good agreement with that calculated from Ca²⁺ spark flux reconstructions (43). Therefore the model reproduces all of the major features of Ca²⁺ sparks and blinks with reasonable accuracy.

Figure 4.

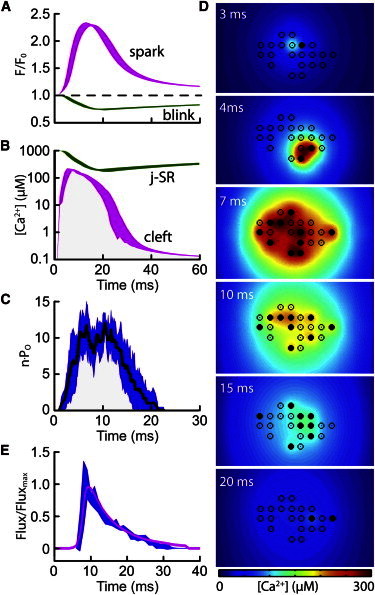
RyR cluster behavior during Ca²⁺ sparks. (A) Ca²⁺ spark and Ca²⁺ blink time courses for a cluster of 21 RyRs with a distribution as shown in D. (B) Spatial mean of [Ca²⁺] in the dyadic cleft and j-SR. (C) Numbers of open RyRs corresponding to the means in B. In A–C, line thickness shows the SD of 10 simulations. (D) Spatial distribution of [Ca²⁺] in the dyad at several time points during a typical simulation. RyRs are located at the circles, with solid and open circles representing open and closed RyRs, respectively. (E) Simulated time course of j-SR Ca²⁺ flux (wide trace) compared to the Ca²⁺ flux calculated from experimental Ca²⁺ spark profiles (line) replotted from Soeller and Cannell (43).

Termination of Ca²⁺ sparks

Termination of RyR activity resulted principally from the steep Ca²⁺ dependence of RyR closed time (Fig. 2 C). If the opening rate of RyRs is sufficiently low, the open RyR(s) that is (are) supporting local dyad [Ca²⁺] may close before the closed RyRs reopen to sustain CICR. We have termed this process induction decay (24), because it reflects the gradual loss of the activating Ca²⁺ induction process in CICR, which is responsible for the initial rapid rise in RyR P_o. Thus, the termination of RyR activity depends on RyR sensitivity to [Ca²⁺] in the dyad cleft, as well as the time course of j-SR depletion. For rat RyRs, the minimum dyad [Ca²⁺] that could sustain CICR was ∼50 μM (Fig. 4 B). RyRs from sheep exhibited P_o and opening rates that were ∼40-fold higher than the corresponding values for rat RyRs at 10 μM Ca²⁺ (Fig. 2, B and C, respectively). Fig. 5 compares the mean response of models incorporating RyRs (organized as a square cluster of 16 RyRs) from rat and sheep to a DHPR trigger. The computed time course of Ca²⁺ sparks (Fig. 5 A) show a similar rate of rise for rat (magenta) and sheep (blue) but a longer decay phase for sheep (Ca²⁺ spark parameters are given in Table 1.). The corresponding computed [Ca²⁺] in the dyad cleft and j-SR and the RyR P_o are shown in Fig. 5, B and C, respectively. Both rat and sheep showed similar initiation of RyR activity and maximal P_o. However, sheep RyR activity was sustained for ∼40 ms compared to ∼18 ms for rat RyR activity. This is because with RyRs from sheep, the minimum dyad Ca²⁺ level that could sustain CICR was ∼10 μM (Fig. 5 B), which was fivefold lower than the corresponding value for rat RyRs, and it took approximately twice as long for the dyad [Ca²⁺] to decline to this lower threshold. This different behavior may reflect physiological adaptation to the very different heart rates seen in these species (i.e., to have a shorter duration of SR release in rat RyRs). Even with more Ca²⁺ sensitive sheep RyRs, the combination of the limited j-SR volume and j-SR Ca²⁺ buffering capacity ensures that closure by induction decay occurs on the timescale of a Ca²⁺ spark.

Figure 5.

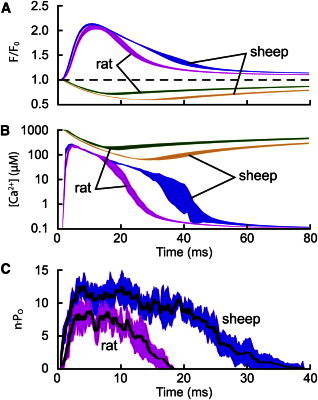
Effect of RyR Ca²⁺ sensitivity on Ca²⁺ spark activation and termination. (A) Mean time courses of Ca²⁺ spark and blink signals generated using a square cluster of 16 RyRs with Ca²⁺-activation kinetics derived from rat (n = 10) and sheep data (n = 3). (B) Corresponding spatial means of [Ca²⁺] in the dyadic cleft and j-SR. (C) Number of open RyRs for rat and sheep Ca²⁺-spark simulations, showing the mean (line) ± SD, (wide trace).

Table 1.

Morphological parameters of simulated sparks

Condition	iRyR (pA/mM)	nRyR	Fmax/Fo	Δt(Fmax) (ms)	ΔF/Δt (ms−1)	FWHM (μm)	FDHM (ms)	n
Fig. 4	0.6	21	1.30 ± 0.03	14.3	0.15 ± 0.04	1.44 ± 0.03	19.6 ± 1.6	6
Square RyR cluster	0.6	16	1.04 ± 0.06	12.2	0.144 ± 0.017	1.40 ± 0.03	18.7 ± 2.0	17
Luminal gating	0.6	16	1.07 ± 0.02	12.9	0.141 ± 0.018	1.41 ± 0.03	19.0 ± 1.4	9
Sheep RyRs	0.6	16	1.07 ± 0.01	11.7	0.161 ± 0.007	1.42 ± 0.02	25.6 ± 2.1	3
Narrower dyad	0.6	16	0.86 ± 0.02	8	0.184 ± 0.022	1.07 ± 0.02	10.6 ± 0.9	4
nRYR varied	0.6	36	1.21 ± 0.01	12	0.175 ± 0.003	1.39 ± 0.02	18.8 ± 0.3	3
	0.6	16	1.04 ± 0.06	12.2	0.144 ± 0.017	1.40 ± 0.03	18.7 ± 2.0	17
	0.6	9	0.95 ± 0.02	13.7	0.113 ± 0.003	1.42 ± 0.03	23.5 ± 1.4	3
	0.6	4	0.68 ± 0.06	14.3	0.071 ± 0.003	1.38 ± 0.04	18.4 ± 2.0	6
	0.6	2	0.47 ± 0.05	9.7	0.069 ± 0.003	1.32 ± 0.03	14.8 ± 1.1	9
iRyR varied	0.6	16	1.04 ± 0.06	12.2	0.144 ± 0.017	1.40 ± 0.03	18.7 ± 2.0	17
	0.4	16	0.89 ± 0.07	13.2	0.108 ± 0.035	1.37 ± 0.05	16.5 ± 1.9	6
	0.35	16	0.87 ± 0.07	12.3	0.107 ± 0.025	1.35 ± 0.03	15.4 ± 1.1	7
	0.3	16	0.83 ± 0.07	13.2	0.098 ± 0.018	1.36 ± 0.02	15.9 ± 2.2	10
	0.25	16	0.74 ± 0.16	13.9	0.079 ± 0.023	1.37 ± 0.05	16.0 ± 2.5	10
	0.2	16	0.52 ± 0.27	10.3	0.067 ± 0.022	1.31 ± 0.07	13.7 ± 3.2	9
	0.15	16	0.38 ± 0.14	9.4	0.057 ± 0.007	1.30 ± 0.07	12.4 ± 3.2	12

First row is for the simulation depicted in Fig. 4. Subsequent rows show how spark properties change as various factors are altered, as indicated in the first column. i_RyR is the RyR single-channel Ca²⁺ current, n_RyR the number of RyRs in the simulated cluster, F_max/F_o the peak Ca²⁺ spark fluorescence change, Δt(F_max) the time to peak of the Ca²⁺ spark, ΔF/Δt the rate of rise of normalized fluorescence, FWHM the width of the spark at half-maximum amplitude, and FDHM the Ca²⁺ spark duration measured at half-maximum amplitude. Table gives mean ± SD of n simulations.

The role of luminal regulation of RyR P_o was examined using gating data derived from Fig. 2. j-SR [Ca²⁺] of 1 mM resulted in the RyR opening rate varying as cytoplasmic [Ca²⁺]^1.9 compared to [Ca²⁺]^2.8. Opening rates at intermediate j-SR [Ca²⁺] were given by linear interpolation. This RyR regulation by j-SR [Ca²⁺] in our model produced almost no change in Ca²⁺ spark and blink morphology (Table 1, rows 2 and 3). From these measurements, we conclude that regulation of RyR gating by Ca²⁺ in the j-SR may not be a major factor in determining the spatiotemporal properties of Ca²⁺ sparks and blinks.

Effects of RyR organization and dyad size

The role of local nanoscopic [Ca²⁺] gradients in maintaining regeneration in CICR is illustrated in Fig. 6 A, which shows two arrangements of 18 RyRs as either two adjacent groups or one large group with every other RyR removed. Wherever there is a gap between adjacent RyRs, CICR terminated slightly earlier, but this had little effect on the amplitude of the Ca²⁺ spark (Fig. 6, A and B). This paradoxical result arises from the consequences of nanoscopic [Ca²⁺] gradients within the dyad for determining both Ca²⁺ fluxes and CICR regeneration. As the RyRs become more separated, local CICR regeneration is weakened due to the spatial gradient of [Ca²⁺] from each open RyR resulting in adjacent RyRs experiencing lower [Ca²⁺] on average (leading to weakened regeneration and earlier termination). However, at the same time, the average flux associated with each RyR opening is increased due to a decreased local Ca²⁺ accumulation increasing the [Ca²⁺] gradient that determines i_RyR (which offsets the former effect). Thus, nanoscopic gradients (illustrated in Figs. 4 D and 6 C) of [Ca²⁺] within the RyR cluster play a key role in all phases of CICR regulation, from initiation to regeneration (which allows the j-SR to release a large fraction of its total Ca²⁺), as well as eventual termination. The dimensions of the dyad itself also have effects on CICR termination (as well as activation probability (44)). Fig. 6 D shows that a dyad with reduced area (but the same number of RyRs) results in a smaller Ca²⁺ spark that is abbreviated in time course.

Figure 6.

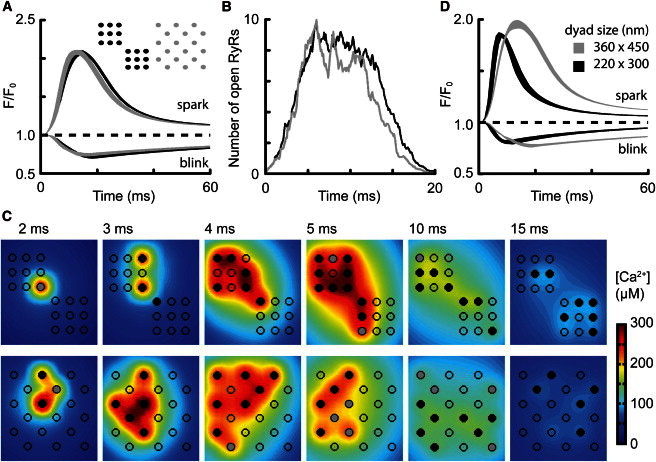
Intradyad geometric effects. (A) Ca²⁺ spark and blink time courses for two geometric arrangements of 18 RyRs. (Inset) Cluster organization with color key. (B) Evolution of mean P_o (shown as nP_o) for the two clusters indicated in A. (C) Spatial distribution of [Ca²⁺] in the dyad at several time points for the clusters shown in A. RyR states are depicted as described in Fig. 4 legend. (D) Effect of dyad dimensions. For a square cluster of 16 RyRs, the dyad space was set to the dimensions shown. Note that the smaller dyad results in faster Ca²⁺ spark termination but with a relatively small effect on amplitude.

Varying RyR cluster size between 2 and 36 RyRs revealed that Ca²⁺ spark properties were relatively insensitive to cluster size in clusters of more than nine RyRs (Table 1, rows 6–10). As noted previously, the shallow dependence of Ca²⁺ spark amplitude on the number of RyRs (24) arose from the effective diffusional resistance of the RyR open channels being less than the series diffusional resistances of the dyad cleft and SR.

Restitution of Ca²⁺ sparks after Ca²⁺ release

The time course of Ca²⁺ spark recovery between spontaneous Ca²⁺ sparks (restitution) has been used to examine SR Ca²⁺ depletion, as well as possible RyR inactivation (20,25,45). Although our model contained no inactivated, adapted, or refractory states, the time course of recovery of Ca²⁺ spark amplitude (Fig. 7 A) and probability of evoking a second Ca²⁺ spark (Fig. 7 B) reproduced experimental observations (25). The explanation for the apparent refractory and restitution behavior lies in the extent to which the inductive regenerative phase of CICR can be supported by the partially depleted j-SR, and this is seen by comparing the time course of restitution of j-SR [Ca²⁺], peak F/F_o, and nP_o (Fig. 7 C).

Figure 7.

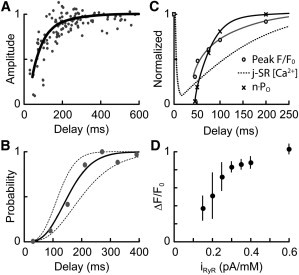
Ca²⁺ spark restitution and i_RyR dependence. (A) Amplitude of the second Ca²⁺ spark (line) compared to experimental data (circles, replotted from Sobie et al. (25)). (B) Probability of triggering a second Ca²⁺ spark after various delays from the first. The trigger was assumed to be spontaneous RyR openings of 1 ms duration that occurred at intervals of 10 ms (left dashed line), 20 ms (solid line) and 40 ms (right dashed line). Data points (gray) are replotted from Sobie et al. (25). (C) Comparison of the time courses of j-SR [Ca²⁺] (dashed line), peak fluorescence (open circles) and nP_o (crosses). (D) Effect of i_RyR on Ca²⁺ spark amplitude. Sparks were simulated in a dyad containing 16 RyRs in a 4 × 4 array. The Ca²⁺ permeability of the RyR was varied and is expressed on the abscissa as Ca²⁺ current through the RyR in the presence of a 1 mM [Ca²⁺] difference across the SR membrane. Data show the mean ± SD for 6–17 simulations.

The close agreement of our model with the reported restitution of Ca²⁺ spark amplitude (Fig. 7 A) was achieved without freely adjustable parameters. Ca²⁺ sparks had an apparent refractory period of ∼70 ms, and the second Ca²⁺ spark amplitude recovered to 80% of the initial Ca²⁺ spark amplitude in 130 ms. The restitution in the probability of triggering a second spark also depended on both the rate of occurrence of a triggering event (a spontaneous opening of either an RyR or a DHPR) and j-SR refilling, as shown by the dotted lines in Fig. 7 B. The Ca²⁺ spark restitution time course was determined by the rate of refilling of the j-SR, which in turn was constrained by the model fitting the rate of recovery of Ca²⁺ blinks (80% in 140 ms). j-SR refilling by diffusion from the n-SR and, to a lesser extent, local Ca²⁺ reuptake via SERCA was transduced via the local i_RyR to produce a more rapid recovery in nP_o than j-SR [Ca²⁺] due to the power dependence of nP_o on dyad [Ca²⁺] (Fig. 7 C). Ca²⁺ spark amplitude restitution also depended on the ability of the local Ca²⁺ flux (i_RyR) to support the regenerative phase of CICR, with induction decay developing more rapidly at low j-SR [Ca²⁺] (see below).

Effect of RyR single-channel Ca²⁺ flux

Recently, the effect of reducing RyR Ca²⁺ conductance and current (iRyR) with impermeant ions on Ca²⁺ spark amplitude and frequency has been reported (21). These data provide an important additional test of the model, and Fig. 7 D shows how Ca²⁺ spark amplitude varied as i_RyR was reduced to <0.6 pA/mM. For i_RyR between 0.3 and 0.6 pA/mM, Ca²⁺ spark amplitude varied by 20%. However, when i_RyR was reduced to <0.3 pA/mM the Ca²⁺ spark amplitude decreased more rapidly, reaching a ΔF/F_o of 0.4 at 0.15 pA/mM, in reasonable agreement with the data of Guo et al. (21). Reducing i_RyR also hastened the onset of induction decay, resulting in a reduced time to peak for the resulting smaller-amplitude Ca²⁺ spark (Table 1, rows 15–17). In this regime, Ca²⁺ spark amplitude became more variable (as seen by the length of the error bars) as stochastic gating effects became relatively more important.

Discussion

The computer simulations presented here are based upon our best synthesis of available data on RyR gating, dyad geometry, and Ca²⁺ buffering. Although future work may lead to refinement of the geometry and parameters used, the model has given useful insight into the (likely) factors that determine the time course of SR Ca²⁺ release during Ca²⁺ sparks. Since the spatiotemporal evolution of Ca²⁺ sparks determines the rise of Ca²⁺ that activates contraction (35), this model can also give new insight into the factors that determine the cell-wide Ca²⁺ transient.

The simulations show that termination of RyR activity results from the spatiotemporal evolution of nanoscopic [Ca²⁺] changes within the dyad, which are not properly captured by treating the junctional space of the dyad as a single compartment (46). As the Ca²⁺ flux via open RyRs starts to decrease, the decline in local dyad [Ca²⁺] causes a decrease in the P_o of neighboring RyRs, which in turn reduces the total Ca²⁺ flux. This decrease in flux then further decreases cluster P_o (mainly via the RyR closed time), forming an inactivating process we called induction decay (24). Induction decay is essentially the reverse of the normal activating regenerative process of CICR and occurs due to the reduction in single-channel flux being unable to support regeneration of closed RyRs within the open time of adjacent RyRs. Our simulations show that the latency for induction decay to develop depends on the sensitivity of RyRs to dyad [Ca²⁺], as well as geometric factors such as the diameter of the dyad junction and number/organization of RyRs in the junction (Table 1 and Figs. 5 and 6).

A given dyad produces stereotyped Ca²⁺ sparks and blinks despite quite large stochastic variations in the number of open RyRs (compare the standard deviations in spark morphology in Fig. 4 A and Table 1 with the standard deviation in the number of open RyRs in Fig. 4 C). The reason for this behavior is that stochastic RyR gating is tempered by other, nonstochastic contributions to Ca²⁺ spark morphology, such as the series diffusion resistances of the dyad junction and the SR (when the RyRs have a Ca²⁺-release flux (i_RyR) >∼0.3 pA/mM). In addition, the Ca²⁺ spark fluorescence is smoothed by diffusion and buffering, which act as a low-pass filter for the stochastic RyR gating. The stereotypical nature of Ca²⁺ sparks in these simulations is less than the Ca²⁺ spark variation that occurs throughout the cell (36,47) but more than that observed at a single cytoplasmic release site (48). When i_RyR was <0.3 pA/mM, the resulting Ca²⁺ sparks showed much greater variability due to increased stochastic noise. However, reports of highly variable or even quantized spark amplitudes (49,50) could be related to peripheral superclusters (51) or multiple dyadic junctions within the recording volume (12), which are uncertain factors not considered in this model. These possibilities could be tested with the 3D stochastic modeling approach presented here, but at this time, it is unknown how variable size groups of RyRs should be combined within a supercluster fed by a single piece of extended j-SR. Nevertheless, our simulations show that the actual organization of a fixed number of closely spaced RyRs sharing a single dyadic cleft (formed by a single SR junction) has quite small effects on Ca²⁺ release during a Ca²⁺spark.

The limited effect on Ca²⁺ spark amplitude illustrates the remarkable resilience of dyad to moderate changes in geometry (although the geometry and RyR distribution have large effects on the ease with which CICR can be triggered (44)). The reduced diffusional resistance associated with reduced j-SR area accelerates CICR termination due to a more rapid collapse of nanoscopic CICR support, and at the same time, increases the rate at which Ca²⁺ leaves the dyad space (32). Reduction in the j-SR area also reduced the width of the Ca²⁺ spark, as the indicator signal principally arises from Ca²⁺ that has left the dyad cleft edges. Varying the arrangement of RyRs from uniform squares of variable numbers of RyRs to looser arrangements (see Figs. 4 and 6) had relatively small effects on the amplitude of Ca²⁺ sparks and did not prevent termination of CICR by induction decay.

The robust nature of CICR activation and termination and the relative constancy of Ca²⁺ spark amplitude demonstrated here is underscored by the relative insensitivity of the release to the number of RyRs incorporated in the dyad at n > ∼9 RyRs (Table 1, rows 6–10, and (24)). Peripheral RyR clusters appear to contain ∼14 RyRs on average (51), and more central dyads should contain a somewhat larger number of RyRs (for review, see Cannell and Kong (12)). Although extensive electron microscopic tomography data are lacking, murine junctions appear to contain ∼8–34 RyRs (52). This suggests that the dyad is not normally in a regime where Ca²⁺ spark amplitude is strongly influenced by the number of RyRs.

The rather limited effect of different RyR gating behavior associated with rat and sheep RyRs on Ca²⁺ spark amplitude might not be expected based on previous models. This result suggests that physiological modulation of RyR gating could have quite limited effects on Ca²⁺ spark amplitude, as the quantity released is mainly controlled by the ability of the local i_RyR to support regeneration. This hypothesis is compatible with the report by Guo et al. who found that RyR phosphorylation by protein kinase A had no effect on Ca²⁺ spark amplitude when SR load changes were controlled (53). Also, CaMKII RyR phosphorylation increases RyR Ca²⁺ sensitivity (54) and prolongs the release phase of Ca²⁺ sparks with little effect on Ca²⁺ spark amplitude (53). This is in general agreement with model behavior, as shown by the Ca²⁺ more Ca²⁺-sensitive sheep RyR simulations (Fig. 5) where the onset of induction decay is delayed but Ca²⁺ sparks were only slightly increased in amplitude.

In connection with the above, it has been previously pointed out that a steady-state change in the amplitude of the Ca²⁺ transient would not be possible without a change in SR Ca²⁺ uptake (since time-averaged release must equal time-averaged uptake) (55). On the other hand, if pathological conditions lead to alterations in dyad geometry as a result of subcellular remodeling (such as the dyad morphing into multiple diffusionally connected subclusters of RyRs), our model shows that quite large effects on excitation-contraction coupling could result (from changes in triggering efficiency and altered Ca²⁺ spark termination). Such changes may help explain the paradoxical report of the development of a subpopulation of big resting Ca²⁺ sparks in a heart failure model without changes in SR Ca²⁺ content or expression levels of RyR, calsequestrin, SERCA2a, phospholamban, triadin, and junctin proteins (56). It should also be noted that there is evidence for the existence of superclusters of RyRs on the cell surface (51), so the idea that RyRs may not always be packed into a single junctional cluster (as modeled here) is not without precedent. Thus, moderate pathological changes in dyad structure or distribution of RyR should not affect the average amplitude of Ca²⁺ sparks in the steady state, but by altering the ability of a trigger to start CICR, they could contribute to a change in Ca²⁺ transient time course and/or the development of spatial nonuniformities in Ca²⁺, as seen in heart failure (see, e.g., Litwin et al. (57).).

Modulation of i_RyR has been used recently to probe the Ca²⁺ spark dependence on local Ca²⁺ flux and SR load (21). In those experiments, chemically skinned cells were exposed to 30 mM and 60 mM Tris, which produced a 20–40% reduction in i_RyR and Ca²⁺ spark amplitude and, importantly, also decreased Ca²⁺ spark time to peak (implying a more rapid onset of CICR termination). In our model, varying i_RyR over the range 0.15–0.35 pA caused similar variations in the amplitude as well as the time to peak of the computed Ca²⁺ sparks (Fig. 7 and Table 1, rows 11–17). This forms an additional independent test of our model (note that no other parameters were changed) and adds to our confidence that this stochastic 3D model captures the fundamental behavior of the dyad and shows that induction decay dominates CICR termination (24). From their experiments, Guo et al. (21) deduced that CICR termination during a Ca²⁺ spark was at least partly due to the loss of ability of i_RyR to support CICR, in accord with our demonstration of induction decay (24). A very recent review (58) describes induction decay as “pernicious attrition” but does not address the sufficiency and/or reliability of the falling RyR Ca²⁺ flux to limit CICR via the growth in RyR closed time that we show here. In any case, we view induction decay in CICR not as pernicious “pernicious,” but rather as a beneficial intrinsic component of CICR within dyads that necessarily limits SR Ca²⁺ release time course. We conclude that our stochastic 3D model captures the fundamental behavior of the dyad and that induction decay is sufficient to explain local termination of CICR without additional regulatory factors.

In summary, we show that a stochastic model that incorporates our current understanding of dyad structure and measurements of RyR gating in lipid bilayers reproduces the major features of Ca²⁺ sparks and blinks with reasonable accuracy and is able to reproduce additional properties such as the effect of changing i_RyR and the time course of restitution. The key to this behavior resides in the development of induction decay, as well as the time course of Ca²⁺ gradients between the dyadic space and j-SR. Changing RyR gating behavior to that of more Ca²⁺-sensitive sheep RyRs had only small effects, suggesting that possible modulation of RyR gating by second messengers should be more effective in smaller couplons where regenerative support is weaker. Overall, the behavior of the model is reminiscent of the cluster-bomb model proposed by Stern, wherein local depletion plus stochastic attrition in a small RyR cluster limits the amount of j-SR Ca²⁺ released (9). However, the problem inherent in stochastic attrition (i.e., a limit to the number of RyRs that can close by this mechanism within the timescale of a Ca²⁺ spark) is overcome by the automatic development of induction decay within the nanoscopic cellular architecture that forms the dyad.