Abstract
Thermo-transient receptor potential channels display outstanding temperature sensitivity and can be directly gated by low or high temperature, giving rise to cold- and heat-activated currents. These constitute the molecular basis for the detection of changes in ambient temperature by sensory neurons in animals. The mechanism that underlies the temperature sensitivity in thermo-transient receptor potential channels remains unknown, but has been associated with large changes in standard-state enthalpy (ΔHo) and entropy (ΔSo) upon channel gating. The magnitude, sign, and temperature dependence of ΔHo and ΔSo, the last given by an associated change in heat capacity (ΔCp), can determine a channel’s temperature sensitivity and whether it is activated by cooling, heating, or both, if ΔCp makes an important contribution. We show that in the presence of allosteric gating, other parameters, besides ΔHo and ΔSo, including the gating equilibrium constant, the strength- and temperature dependence of the coupling between gating and the temperature-sensitive transitions, as well as the ΔHo/ΔSo ratio associated with them, can also determine a channel’s temperature-dependent activity, and even give rise to channels that respond to both cooling and heating in a ΔCp-independent manner.
Introduction
Thermo-transient receptor potential (TRP) channels are nonselective cation channels, structurally related to voltage-gated potassium channels and involved in the detection of ambient temperature changes. These channels are unique in their ability to directly modify their gating as a function of temperature (1), being activated at different temperature ranges from noxious cold to noxious heat, and doing so with very large Q10 values (∼30), which is a phenomenological measure of heat sensitivity.
Most information on temperature sensitivity is available from studies involving the capsaicin- and heat-activated TRPV1 and the menthol- and cold-activated TRPM8 channels (2–7). Temperature-dependent activation is associated with large changes in standard-state enthalpy (ΔHo) and entropy (ΔSo) between states in the activation pathway (2). TRPM8 is thus assigned negative ΔHo and ΔSo values that drive channel opening upon cooling, and TRPV1 positive ΔHo and ΔSo values that increase open probability upon heating (3). These thermodynamic differences have been generally postulated to reflect different molecular processes involving the action of different temperature sensors, which might be localized at a defined structural domain within the channel (6,8). In fact, a number of differing structural regions of the channel have been proposed to act as temperature sensors (8–10). More recently (11), it has been noted that a change in heat capacity (ΔCp) between states in the activation pathway, which could be caused by a change in hydration of ∼20 residues per subunit, would be sufficient to account for the activation of thermo-TRPs by temperature. Moreover, a large heat capacity change, associated with any gating transition, implies that a given channel should be activated by both increasing and decreasing temperatures.
Even though a definitive demonstration is lacking, several lines of evidence suggest that the stimulus sensors in these channels, including the temperature sensor, act as functionally independent modules allosterically coupled to the pore domain to influence gating. This evidence includes single-channel recordings showing that some transitions between open and closed states have negligible temperature sensitivity, indicating that intrinsic gating is not highly temperature-dependent. Consistently, the voltage, ligand, and temperature dependence of several thermo-TRP channels can be accurately described by allosteric mechanisms of varying complexity (4–7).
Here, we explore the predictions of simple allosteric models and postulate that the highly temperature-sensitive transition(s) may be thermodynamically similar among thermo-TRP channels, but differences in allosteric coupling between modules and in the intrinsic gating equilibrium of the pore could account for the variability in temperature responses observed in these channels. Moreover, we find that including in the models a coupling-energy term that is temperature-dependent leads to regimes in which the same channel can be activated by increasing and decreasing temperature, without the need for a change in heat capacity.
Methods
Cell culture, transfection, and electrophysiological recording methods have been described previously in Rosenbaum et al. (12). Temperature was monitored with a thermistor (Warner Instruments, Hamden, CT) placed near the tip of the pipette.
Nonstationary noise analysis was performed as previously described in Rosenbaum et al. (12). Briefly, a train of 30–70 pulses of 200-ms duration to a given depolarizing voltage (60–180 mV) from a holding potential of −90 mV was delivered to TRPV1-expressing inside-out patches and the currents recorded at 20 kHz and low-pass-filtered at 5 kHz. The variance (σ2) was calculated according to Heinemann and Conti (13). Mean current (I) versus σ2 plots were used to obtain the single-channel current i and the number of active channels in the patch, N. Open probability was calculated from Po = I/Ni.
Membrane patches with openings from a few channels were used to verify the magnitude of the single-channel current obtained from noise analysis. At voltages below 60 mV the time course of channel activation cannot be accurately resolved, so the open probability could not be obtained from nonstationary noise analysis, and was calculated as follows: a series of 100-ms voltage pulses from −100 mV to 180 mV in increments of 20 mV were delivered to membrane patches after applying the train of pulses for noise analysis. Leak currents were estimated by blocking channels with a saturating (∼80-μM) concentration of tetrahexyl ammonium (Sigma-Aldrich, St. Louis, MO). The leak-subtracted currents were then divided by N, estimated from noise analysis in the same patch, and by the extrapolated single-channel current assuming a linear I-V behavior.
The model’s parameter space was sampled with programs written in IgorPro (WaveMetrics, Portland, OR) by using the analytical expressions for the open probability for each model, which are presented in the text. Data analysis was also carried out in IgorPro.
Results
Fundamental thermodynamics relate the temperature dependence of the standard-state Gibbs free energy (Go) in a population of states (and the resulting equilibrium constant K, see Eq. 1a) to the difference in standard-state enthalpy and entropy between the states (ΔHo and ΔSo, see Eq. 1b):
| (1a) |
| (1b) |
Enthalpy and entropy may or may not have a temperature dependence of their own, depending on whether there is a significant change in heat capacity (ΔCp) between states:
| (2a) |
| (2b) |
Hence, thermo-TRP channel activation is associated with large changes in Ho and possibly Cp between states along the activation pathway, accompanied by large changes in entropy, which are required to lower the free energy difference between states at physiological temperatures (2). Indeed, this compensation of ΔHo and ΔSo has been experimentally confirmed for several thermo-TRPs (3,7,14–18). On the other hand, contemporary experimental data do not support a large change in ΔCp associated with channel activity (1,3,4,19).
In the simplest models of thermo-TRP gating (e.g., the two-state model), temperature-dependent activity is controlled by few relevant parameters: ΔHo, ΔSo, and Z, the last being the small (∼0.6–0.9 e0) apparent gating charge responsible for the modest voltage dependence observed in TRP channels (3,19). This implies that differences between thermo-TRP channels have to arise from the different values these parameters take. So, in channels that are activated by cooling (e.g., TRPM8), or by heating (e.g., TRPV1), there has to be a complete reversal in sign in both ΔHo and ΔSo to account for their respective temperature sensitivities (1,3).
A shortcoming of these models is that experiments suggest that channel opening might neither be directly responsible for the temperature sensitivity of the channel, nor possess significant voltage sensitivity (2,4–7). As a better approximation, modular allosteric models have been proposed to describe the temperature- and voltage-dependent activity of TRPV1 (5,7), TRPA1 (20), and TRPM8 (4–6) channels. The simplest of these models (Fig. 1) considers the transitions between open and closed states to be stimulus-independent and given by the equilibrium constant L. Temperature-dependent transitions (C0 → C1, C2 → C3, O0 → O1, and O2 → O3) or voltage-dependent transitions (C0 → C2, C1 → C3, O0 → O2, and O1 → O3) are allosterically coupled to the gating equilibrium of the channel. This coupling is described by multiplicative terms (which are also equilibrium constants) given by C for temperature and D for voltage (Eq. 3, a and b). Generally, it is assumed that they are practically temperature-independent, having a ΔHo ≈ 0:
| (3a) |
| (3b) |
| (3c) |
Figure 1.
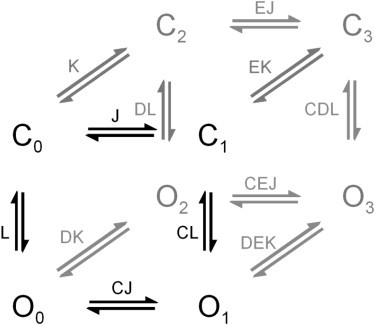
Allosteric model for temperature- and voltage-activation of thermo-TRP channels. (Solid symbols) Channel activity with deactivated voltage sensors; (shaded symbols) voltage-sensor activation and channel transitions with activated voltage sensors. L is the intrinsic gating equilibrium constant. The activation/deactivation equilibrium constants for the temperature- (J) and voltage-sensors (K) are given by and , respectively. C, D, and E are allosteric coupling constants between channel gating and the temperature- or voltage sensors or between the two sensors, respectively.
Although allosteric models of thermo-TRPs provide a better description of experimental measurements of channel function, significant molecular mechanistic insight is still lacking. For example, it has not been possible to obtain a direct measurement of the temperature-driven conformational rearrangements. Hence, the interpretation of data in terms of these allosteric models has followed the same lines as the more restricted ones, considering the same set of parameters, ΔHo, ΔSo, and Z, as the sole determinants of the differences between channels. An example is the requirement for a change in the signs of both ΔHo and ΔSo to represent either TRPV1 or TRPM8 temperature sensitivity (4,5,7).
Arguably, the most dramatic difference among thermo-TRP channels is whether cooling or heating activates them. Even orthologs of a given TRP channel can show this disparity (21–23). Interestingly, a similar phenomenon also occurs among voltage-gated channels: whereas voltage-dependent potassium channels are activated by depolarization, the structurally similar hyperpolarization-activated potassium channels are closed upon depolarization. However, the difference between the two channels lies not in their stimulus-sensing domains, but in the mechanisms by which they are coupled to the channel pore domain (24). We decided to explore some of the implications for temperature sensitivity of an allosteric coupling model and to determine whether mechanisms other than temperature-sensor function, such as the nature of the allosteric coupling, could control temperature-dependent channel function and determine whether a channel is activated by heating, cooling, or both.
Fig. 2 A shows the open probability (Po) versus voltage curves at three temperatures for TRPV1, measured from inside-out patches. The continuous curves are fits of Eq. 4, as derived for the model in Fig. 1 (see parameters in the legend to Fig. 2 A). Both changes in enthalpy and entropy have a positive sign and the allosteric coupling constant between the gate and the temperature sensor is larger than unity (C = 6.04), leading to heat activation:
| (4) |
Figure 2.

Experimental TRPV1 and TRPM8 data can be described by assuming inverse coupling in an allosteric model. (A) TRPV1 open probability versus voltage curves at the indicated temperatures. (Black curves) Fits from the eight-state model with the parameters: ΔHo = 91.13 kcal mol−1, ΔSo = 0.295 kcal mol−1 K−1, L = 2.6 × 10−3, K(0) = 3.17 × 10−2, Z = 0.9, C = 6.04, D = 260, E = 0.92; and T = 298 K (25°C), 305 K (32°C), or 316 K (43°C). Group data are shown as mean ± SE (n = 5–18). (B) TRPM8 open probability versus voltage curves at various temperatures obtained from published data (4). (Black curves) Fits from the eight-state model with the parameters: ΔHo = 91 kcal mol−1, ΔSo = 0.317 kcal mol−1 K−1, L = 18 × 10−3, K(0) = 0.15, Z = 0.6, C = 0.022, E = 1.6, and D = 478. (C) Po-T landscape calculated from the portion of Fig. 1 (highlighted in black), for different values of C (twofold multiplicative increments), L = 3 or 0.2, ΔHo = 90 kcal mol−1, and ΔSo = 0.294 kcal mol−1 K−1. Po-T curves (highlighted with black circles) correspond to C = 2 and C = 1.68 × 104. (D) Po-T curves calculated from the four-state subscheme (Fig. 1, solid characters) with ΔHo = 90 kcal mol−1 and ΔSo values of 0.31 (blue) or 0.28 (red) kcal mol−1 K−1.
To determine whether differences in the values of parameters other than the signs of ΔHo and ΔSo could switch Po-temperature dependence to that of a cooling-activated channel, we fitted TRPM8 channel activation data from Brauchi et al. (4) with the eight-state model, keeping the ΔHo from the fit to our TRPV1 data (Fig. 2 A) fixed. The resulting activation curves now describe the cold-activation of TRPM8 (Fig. 2 B). Notably, the allosteric coupling constant C between temperature sensor activation and channel gating had to be reduced 275-fold, and the gating constant L increased around sevenfold (see parameters in the legend of Fig. 2 B). As expected from the fact that TRPM8 and TRPV1 are considerably different channels, not only L and C had to change to describe TRPM8 data with TRPV1 parameters. For example, the equilibrium constant of the voltage sensor at 0 mV, given by K(0), was shifted fivefold toward the activated state. Yet, the major parameter changes occurred in L and C, more so in C (see the legend to Fig. 2 B). This implies that a thermodynamically similar conformational change, with positive ΔHo and ΔSo values, which in TRPV1 favors channel opening, could promote channel closing in a cooling-activated channel. In other words, the temperature sensors of these channels might be activated by heating but be inversely coupled to channel opening.
To analyze with more detail the role of the coupling constant C in determining temperature sensitivity, we further explored the model with the voltage sensor in the deactivated position (Fig. 1, black characters only), which is a simplified condition. In this case, Po(T) is given by Eq. 5:
| (5) |
Fig. 2 C shows an open probability landscape as a function of temperature for several values of C and two values of L. The switch from a cold- to a heat-activated channel occurs precisely when the value of C changes from smaller to larger than unity, reflecting either a favorable or unfavorable energetic contribution of temperature-sensor activation to channel gating. We also note that for very small (<0.001) or very large (>100) values of C, the effects of changes in L (that could be caused by point mutations, for example) would have a more noticeable effect on either the maximal or the minimal open probabilities, respectively.
The steeper heat-activated Po-T curves in Fig. 2 C are left-shifted in the temperature scale with respect to less steep ones, as can be seen in the curves with highlighted black markers. This is contrary to experimental observations. For example, the heat-activated TRPV2 channel has a greater temperature sensitivity and a right-shifted Po-T curve as compared to TRPV1 (10). This has been interpreted to mean that the enthalpy change associated with TRPV2 activation has to be larger (approximately twofold) than for TRPV1. This may very well be so, but not necessarily. First, the steepness of the Po-T curve (and hence the apparent ΔHo) can be modulated by the value of C (Fig. 2 C). Second, the temperature range over which open probability has larger temperature-dependent changes is most sensitive to the relative magnitude of the enthalpy and entropy values. So, a slight decrease (2.73 kcal/mol) in ΔHo, or a slight increase in ΔSo (0.03 kcal mol−1 K−1), together with a smaller C, could turn the TRPV2 Po-T curve into that of TRPV1 by shifting the temperature for half-activation (T0.5) by −10°C. Consistently, to convert a heat-activated channel with an endothermic temperature sensor and T0.5 of ∼40°C into a cold-activated channel with T0.5 in the range of known cold-activated channels (20°C and 30°C) (4,5,15), we have to not only modify L and C, but also the ΔHo/ΔSo ratio has to be slightly (∼0.96-fold) decreased (Fig. 2 D). This same subtle parameter change was also necessary to fit TRPM8 data with TRPV1’s parameters (Fig. 2, A and B), as seen in the 0.021 kcal mol−1 K−1 increase in ΔSo for TRPM8 as compared to that of TRPV1.
The simulations in Fig. 2 C show that the minimal Po values for heat activation are too high or the maximal Po for cold activation is too low. This is partly due to the fact that the heating- and cooling-activated halves of each surface share the same intrinsic gating constant L. For example, for a large value of L, the cooling-activated half of the Po surface exhibits a large maximal open probability, but the minimal open probability for the heating-activated half of the same surface is equally large. These observations indicate that the intrinsic gating equilibrium constant has to be different for cooling- and heating-activated channels if their temperature sensitivity depends on an inverted coupling. However, other factors affecting gating could compensate for similar values of L in cooling- and heating-activated channels. This may be the case for voltage activation, for example. For TRPV1, the coupling energy between voltage- and temperature sensors is significant, as suggested by the pronounced changes in the channel’s temperature sensitivity when measured at hyperpolarized versus depolarized potentials (7). Consistently, the minimal open probability for heat activation or the maximal Po for cold activation at a given value of C can be modulated by voltage without changes in L, by using the eight-state model that incorporates voltage sensitivity (Fig. 3). The magnitude of this modulation depends largely on the values of K(0) and D, the allosteric coupling factor between the voltage sensor and the gate.
Figure 3.

Switching from heating to cooling-mediated channel activation through inverse allosteric coupling. (A) Open probability landscapes at −60 mV obtained by calculating Po at different temperatures and values for the allosteric coupling constant C using the eight-state model with two sets of parameters (blue and red surfaces). The increments in the varied parameters were additive for T (ΔT = 2°C) and multiplicative for C (factor of 1.3). (Red surface) Parameters obtained from fits of the eight-state model to TRPV1 data; also indicated in the legend in Fig. 1A. (Blue surface) Parameters obtained from fits of the eight-state model to published TRPM8 data; also indicated in Fig. 2B. (B) Same as in panel A with data calculated at +120 mV.
In addition, voltage also changes the slope of the Po-T curves according to the value assigned to E in the simulation (Fig. 3), which reflects coupling between temperature- and voltage-sensors. Furthermore, the data in Fig. 2 A could be equally well fitted with an E value > 10 (as compared to E = 0.92 from the fits in the figure), as long as the enthalpy change is lowered from 91 to ∼20 kcal mol−1 (and the entropy is also proportionally reduced). This indicates that the energetic crosstalk between stimulus-sensing domains could also be a determining factor for thermo-TRP channel function and for the observed differences among these channels. In fact, changes in the magnitude of E can also lead to a switch from cold activation to heat activation independently of C (data not shown), underscoring the prominent role that allosteric coupling can have.
Notably, the surface calculated with the TRPM8 parameters (Fig. 3, blue surface) is left-shifted in the temperature axis as compared to the surface calculated using the TRPV1 parameters (red surface). As pictured in Fig. 2 D for the four-state model, this is a consequence of the 1.07-fold increase in ΔSo for TRPM8 relative to TRPV1, leading to different thresholds for temperature activation.
Allosteric models for thermo-TRP channel function consider a single temperature-dependent transition thought to represent temperature-sensor function. All other transitions are supposed to be temperature-independent (Eqs. 3, a–c). However, all allosteric coupling constants should have an enthalpic contribution ΔHoC,D, usually assumed to be negligible. The enthalpy associated with this constant includes all interactions that form or break as a result of temperature-sensor function. It is entirely possible that ΔHC in thermo-TRP channels makes a greater contribution than in other channels. Thus, we decided to explore the consequences that this may have on channel function.
By only looking at temperature activation (Fig. 1, black symbols), assuming a temperature-dependent coupling term C given by
| (6) |
and varying the value for ΔHoC, we generated Po-T surfaces that exhibit heat- and cold-activation with the same set of parameters and for each value of ΔHoC (Fig. 4 A). This behavior resembles what is predicted by a two-state model that includes a significant change in heat capacity between the open and closed states, a mechanism that was recently proposed to explain the apparent differences in temperature sensitivity between cooling- and heating-activated channels (11).
Figure 4.

A temperature-dependent allosteric coupling constant C is sufficient to enable heating- and cooling-mediated channel activation with the same set of parameters. (A) Po-T landscape calculated from the four-state subscheme (Fig. 1, solid characters) and additive increments in ΔHoC and ΔSoC, keeping a ΔHoC/ΔSoC ratio of 320 K, ΔHo = 80 kcal mol−1, ΔSo = 0.280 kcal mol−1 K−1, and L = 20. C is calculated for each value of ΔHoC, ΔSoC, and T from Eq. 6. (B) Po-T landscape calculated from the eight-state model for different values for the temperature-dependent constant C, obtained by additively incrementing T, ΔHoC, and ΔSoC, with constant ΔHoC/ΔSoC = 340 K. The parameters that were kept unchanged are: ΔHo = 80 kcal mol−1, ΔSo = 0.270 kcal mol−1 K−1, L = 1 × 10−3, K(0) = 0.05, Z = 0.8, E = 10, D = 1 × 105, and V = 150 mV. The increase in ΔHoC/ΔSoC with respect to panel A causes a right-shift in the heat-activated portion of the curve (see Fig. 6). The ΔHo/ΔSo ratio shifts the cold-activation threshold.
From a molecular point of view, a large change in heat capacity or a large value of the ΔHo of C, is associated with different physicochemical processes. However, in terms of the equations that describe a given model, they might result to be equivalent. To determine the degree by which a change in heat capacity or a temperature-dependent allosteric coupling factor differ in terms of the model’s equations, we analyzed each model’s behavior when temperatures are increased or decreased to extreme values. By assuming a voltage-independent two-state model with equilibrium constant K (Eq. 1a), temperature-dependent changes in enthalpy and entropy (Eq. 2, a and b), and , the open probability is given by
| (7) |
For high temperatures (T >> T0), the open probability is near 1. When T << T0, there are two possibilities: if , the first and last exponentials go to + ∞, so that the open probability at low temperatures goes to 0, and the channel is only a heat-activated channel. On the other hand, if , the first exponential goes to 0 and the third to +∞. In this case, by considering the rates of change for the 1/T and ln(T) terms, which are 1/T2 and 1/T, respectively, it can be concluded that the first exponential dominates, so that the open probability goes to 1 at low temperatures, which would result in increased open probability upon heating and cooling.
Now for the four-state model with temperature-dependent allosteric coupling factor C, the open probability is obtained by substituting Eq. 3, b and c, and Eq. 6 into Eq. 5:
| (8) |
The resulting expressions for very large and very low temperatures are
| (9a) |
| (9b) |
If , i.e., L is large, then the open probability at low temperatures goes to 1. On the other hand, if , which is to be expected if the first condition is fulfilled and all changes in entropy are positive, then the open probability also goes to 1 at higher temperatures.
Thus, the low- and high-temperature limits in this model are determined by a set of constant parameters, whereas in the case of a change in heat capacity, the behavior at the temperature extremes is determined by the temperature-dependent terms of the model that result from the change in heat capacity. This analysis indicates that there are different mechanisms, both from a molecular and a mathematical perspective, by which a channel could be activated by both heating and cooling, and that not all of them involve a change in heat capacity.
The previous finding is based on results obtained with the four-state model. To generate channel opening by cooling and heating, unrealistic values for the model parameters are required, such as a very large L (L = 20, Fig. 4 A). However, this may be a consequence of the simplicity of the four-state model, because it does not consider other sources of energy. This extra energy could derive from voltage or from the binding of a ligand, which also drive channel opening and, at sufficient stimulation levels, compensate for a lower value for the intrinsic gating constant L. For completeness, we used the full model in Fig. 1 with a temperature-dependent allosteric coupling constant C, and determined under what conditions this expanded model displays the same behavior as that depicted in Fig. 4 A.
Fig. 4 B shows that Po-T curves that rise upon heating and cooling can be generated with the eight-state model with more realistic parameter values (L = 1 × 10−3) than those necessary for the four-state model (Fig. 2 A and Brauchi et al. (4), Matta and Ahern (5), and Yao et al. (7)). This shows that a putative channel that activates upon heating and cooling as a cause of this mechanism can be described by parameter values that are consistent with experimental results. Notably, activation by both heating and cooling can be achieved by even relatively small values of ΔHoc (e.g., ΔHoc = 11.5 kcal mol−1), which are typical of many molecular processes involving proteins (Fig. 5). Moreover, the temperature sensitivity of the heating-activated branch of the surface is independent from the thermodynamic parameters of the temperature sensor (ΔHo and ΔSo), and is determined solely by ΔHoc.
Figure 5.

Effects of ΔHoc on the change in open probability by both increasing and decreasing temperatures for a given set of parameters. Open probability landscapes calculated at different voltages and temperatures for two sets of values for ΔHoC and ΔSoC using the eight-state model (Fig. 1): ΔHoC = 45 kcal mol−1 and ΔSoC = 0.130 kcal mol−1 K−1 (blue surface) or ΔHoC = 11.5 kcal mol−1 and ΔSoC = 0.029 kcal mol−1 K−1 (black surface). Temperature was additively incremented by 4°C per step, while voltage increments were of 10 mV. The other parameters used are: ΔHo = 90.5 kcal mol−1, ΔSo = 0.313 kcal mol−1 K−1, L = 16 × 10−3, K(0) = 0.16, Z = 0.56, E = 1.42, and D = 476. These parameters were obtained by fitting Eq. 4 with a temperature-dependent allosteric constant C to the TRPM8 data reported in Brauchi et al. (4) and shown in Fig. 2B.
Discussion
It has generally been assumed that separate thermodynamic phenomena mediated by differentially tuned sensors are responsible for thermo-TRP channel activation by either cooling or heating. We show here that activation of cold-activated receptors could be achieved by a heat-activated temperature sensor, characterized by positive ΔHo and ΔSo values, given that the following conditions are met:
-
1.
The coupling energy between temperature sensor function and pore gating (or between temperature- and voltage-sensor function) that is favorable in heat-activated channels has to be unfavorable in a cooling activated channel.
-
2.
The free energy of the open states has to be reduced with respect to its adjacent closed state(s), shifting the gating equilibrium toward the open state.
-
3.
The channel’s temperature-activation threshold (or alternatively the temperature for half-activation) can be fine-tuned by slight modifications of the temperature sensor’s ΔHo/ΔSo ratio.
In support of this inverted coupling hypothesis is the fact that there are thermo-TRP channels of the same type, only from different species, that can be activated either by cooling or by heating. For example, the TRPA1 mouse ortholog is activated by cooling (15), whereas the same channel from snakes, frogs, lizards, and drosophila is activated by heating (21,22,25). Interestingly, experimental evidence suggests that the N-terminal ankyrin repeats of these channels are responsible for their temperature sensitivity (9). Given the considerable amino-acid sequence identity between the heat- and cold-activated TRPA1 channels (57%), it is possible that the observed differences result from changes in the coupling mechanism, and not from differences in the highly temperature-sensitive conformational rearrangements that underlie thermal activation in these channels.
Inverted coupling, if it occurs, might not be the general mechanism that governs whether a TRP channel responds to cooling or heating. For example, TRPM8 and TRPV1 share only 11% amino-acid sequence identity. Although they share gross structural properties, it is expected that they display considerable differences with respect to structural details and interactions at the amino-acid level. Hence, the mechanisms of temperature sensing between these two channels might depend on different structural properties, and could in effect be governed by opposing thermodynamic parameters. However, some degree of similarity with respect to temperature-sensing mechanisms between these two channels is to be expected, because each channel’s temperature sensitivity can be transferred to the other by swapping a C-terminal portion between the two proteins (8). Given that current experimental evidence argues that TRPV1’s temperature-sensing domain might be located at the N-terminal portion of the channel (10), the results with the swapped chimeras would suggest that coupling can indeed determine temperature sensitivity. This also suggests that TRPV1 and TRPM8 channels do have opposing allosteric coupling machineries, localized at their swapped C termini, as has been previously proposed in Yao et al. (10).
Interestingly, thermo-TRP channel activity shares some properties with protein-folding/unfolding processes: activation by elevated temperature in at least the TRPV1, TRPV2 (26), and TRPV3 (27) channels is accompanied by significant hysteresis, which is also a common observation in the protein-folding field. This analogy does not imply that the channel (or a part of it) adopts a random coil configuration when it is activated by temperature, it only suggests that some of the molecular events that accompany a protein unfolding reaction, such as exposure of buried residues to the solvent and the breakage of some intermolecular interactions, might also accompany TRP channel activation by temperature. Moreover, if it is unlikely that channel heat-activation occurs through a (partial) unfolding reaction, it seems even more unlikely that cold activation occurs through a cold-unfolding reaction at temperatures above the freezing point of water, which is a very rare phenomenon among proteins in the first place (28,29).
Also related to the similarities with protein folding/unfolding reactions is the question of the heat capacity. Although protein thermal denaturation is usually associated with large changes in heat capacity, a small conformational change involving no more than 50 residues, as that hypothesized by Clapham and Miller (11), does not have to be accompanied by a large change in heat capacity: the exposure of hydrophobic protein regions to water that results in an increase in heat capacity could very well be balanced by the exposure of polar protein regions to the solvent, which reduces heat capacity (30). Notably, little is known about the changes in heat capacity that occur during normal protein function.
An argument against a significant contribution of heat capacity to thermo-TRP temperature sensitivity is the lack of evidently parabolic van ’t Hoff plots for channel activation (1–7), which are normally observed as a direct consequence of large changes in heat capacity between two conformational states. However, a van ’t Hoff plot might appear to be linear around a protein’s melting temperature Tm (ΔGo(Tm) = 0) and above, even if both changes in enthalpy and entropy are significantly temperature-dependent (31). Then, the apparent linearity in van ’t Hoff plots for thermo-TRP channels is not a good argument against an important contribution from heat capacity. A stronger argument would be the lack of evidence for hot and cold activation of a TRP channel. However, the analysis presented here shows that even if this were found to happen, other mechanisms apart from large changes in heat capacity could explain the behavior.
It has been pointed out that the difficulty in observing cold and hot activation might stem from a large difference between the thresholds for heat- and cold activation within a given channel. Interestingly, a 30 cal mol−1 K−1 increase in ΔSoC is sufficient to separate the activation by heating and cooling to such a degree that one of them would lie in an experimentally inaccessible temperature range (>65°C) (Fig. 6). Our analysis suggests that an important difference between the two mechanisms could possibly be detected at sufficiently low temperatures for TRPV1, or sufficiently high temperatures for TRPM8: whereas the heat-capacity mechanism is symmetric in regards to the steepness of the cold- and heat-activated branches of the Po-T curve, the temperature-dependent coupling mechanism is not, because each branch is determined by different parameters (ΔHoc and ΔHo).
Figure 6.

In the four-state model with temperature-dependent allosteric coupling constant C, a 1.09-fold increase in the ΔHoC/ΔSoC ratio leads to heating-mediated activation in an experimentally inaccessible temperature range. Po-T landscape calculated from the four-state subscheme (Fig. 1, solid characters) and additive increments in ΔHoC and ΔSoC, keeping a ΔHoC/ΔSoC ratio of 350 K (as compared to ΔHoC/ΔSoC = 320 K in Fig. 4A). The model’s parameters were: ΔHo = 80 kcal mol−1, ΔSo = 0.280 kcal mol−1 K−1, and L = 20.
An interesting consequence of the ideas presented here is that temperature gating in thermo-TRPs may be the result of coupling of conformational changes without much intrinsic temperature dependence, by a coupling process with temperature sensitivity. Why would the coupling constant, C in our case, have a significantly higher enthalpy than in other channels? It is entirely possible that the molecular events associated with coupling happen to involve large enthalpy reactions, such as aromatic residue-charge interactions, which might provide large temperature dependence to the coupling process. A possible scenario is as follows. The activation of the temperature sensor could have a direct unfavorable energetic impact on gate opening; for example, activation of the temperature sensor of a single subunit could hamper channel activation. A secondary temperature-dependent transition could follow, possibly in a different part of the channel responsible for the coupling, establishing interactions that favor channel opening. For example, highly cooperative activation of the remaining temperature sensors could lead to a favorable coupling energy for channel opening. This could explain the apparently counterintuitive behavior of the Po-T curves that rise upon heating and cooling through the action of the same temperature sensor. Interestingly, the bundling up of several moderately temperature-sensitive linearly related transitions has been previously proposed as a mechanism for temperature activation in TRPV1 (32,33).
An important final point to consider is the allosteric nature of thermo-TRP channel gating. Even though a comprehensive demonstration of allosterism in TRPV1 and TRPM8 has not been achieved, the available evidence is compelling. Single TRPV1 channel dwell-times are differentially regulated by capsaicin, low pH, or temperature. Additionally, temperature-independent transitions between open and closed states indicate that channel opening is not obligatorily coupled to a high temperature-sensitive conformational transition (2). TRPV1 macroscopic currents measured at saturating concentrations of capsaicin or the more potent agonist resiniferatoxin show that channel conductance at hyperpolarized potentials approaches a minimal voltage-independent value, even when measurements were conducted at voltages as low as −300 mV for capsaicin (7) and −220 mV for resiniferatoxin (5). This behavior appears to hold for voltages down to −150 mV for very high temperatures (52°C) in the absence of ligands (7). This has also been observed in TRPM8 channels when activated by menthol at −220 mV (5). Allosterism is also consistent with the demonstration that membrane depolarization or elevated heat alone are insufficient to fully activate TRPV1, because full activation requires the simultaneous presence of other stimuli such as capsaicin (5,7). The same observations have been made for TRPM8 activation by voltage (4,5). Finally, measurements of the activation delay in TRPM8 after a depolarizing pulse, which report on the voltage-dependent transitions that occur before channel opening, suggest that these are temperature-independent, in line with independent mechanisms for voltage- and temperature-dependent channel activation (6). Notably, several point mutations and other structural perturbations in both TRPV1 and TRPM8 channels disrupt the response to temperature without affecting other mechanisms of channel activation (17,32,34), suggesting that the functional independence between temperature sensing and ligand binding in these channels also involves structural independence.
Although allosterism seems to be a valid assumption in the case of both TRPV1 and TRPM8 channels, the eight-state model employed here suffers from an important shortcoming: if the eight-state model with temperature-dependent coupling constant C applies to the heat activation of the TRPV1 channel, it would predict that at sufficiently high temperature, gating transitions should be mostly temperature-dependent. This is contrary to single-TRPV1 channel measurements obtained at elevated temperatures (2). To account for this discrepancy, additional states should be incorporated into the model. For example, it could be assumed that temperature-sensor activation does not influence the gating transitions directly, but has an effect on a closed state that precedes the open state. As shown by the complexity in the single-channel recordings of this channel, the eight-state model presented here is certainly an oversimplification. However, it is simple enough to allow a detailed analysis of the consequences for channel function derived from the mechanism proposed here, which could be equally applicable to more-complex models.
Acknowledgments
We thank Drs. Tamara Rosenbaum and Ramón Latorre for valuable comments on the manuscript, Itzel Llorente for assistance with cell culture, and Gisela E. Rangel-Yescas for technical assistance.
Work in the L.D.I. lab is supported by grant No. IN212612-3 from Dirección General Assuntos del Personal Académico-Programa de Apoyo a Proyectos de Investigación e Innovación Tecnológica-Universidad Nacional Autónoma de México and grant No. CB-151297 from the Consejo Nacional de Ciencia y Tecnología.
Footnotes
Andrés Jara-Oseguera’s current address is Molecular Physiology and Biophysics Section, Porter Neuroscience Research Center, NINDS, National Institutes of Health, Bethesda, MD 20892.
References
- 1.Voets T. Quantifying and modeling the temperature-dependent gating of TRP channels. Rev. Physiol. Biochem. Pharmacol. 2012;162:91–119. doi: 10.1007/112_2011_5. [DOI] [PubMed] [Google Scholar]
- 2.Liu B., Hui K., Qin F. Thermodynamics of heat activation of single capsaicin ion channels VR1. Biophys. J. 2003;85:2988–3006. doi: 10.1016/S0006-3495(03)74719-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Voets T., Droogmans G., Nilius B. The principle of temperature-dependent gating in cold- and heat-sensitive TRP channels. Nature. 2004;430:748–754. doi: 10.1038/nature02732. [DOI] [PubMed] [Google Scholar]
- 4.Brauchi S., Orio P., Latorre R. Clues to understanding cold sensation: thermodynamics and electrophysiological analysis of the cold receptor TRPM8. Proc. Natl. Acad. Sci. USA. 2004;101:15494–15499. doi: 10.1073/pnas.0406773101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Matta J.A., Ahern G.P. Voltage is a partial activator of thermo-sensitive TRP channels. J. Physiol. 2007;585:469–482. doi: 10.1113/jphysiol.2007.144287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Latorre R., Brauchi S., Vargas G. ThermoTRP channels as modular proteins with allosteric gating. Cell Calcium. 2007;42:427–438. doi: 10.1016/j.ceca.2007.04.004. [DOI] [PubMed] [Google Scholar]
- 7.Yao J., Liu B., Qin F. Kinetic and energetic analysis of thermally activated TRPV1 channels. Biophys. J. 2010;99:1743–1753. doi: 10.1016/j.bpj.2010.07.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brauchi S., Orta G., Latorre R. A hot-sensing cold receptor: C-terminal domain determines thermosensation in transient receptor potential channels. J. Neurosci. 2006;26:4835–4840. doi: 10.1523/JNEUROSCI.5080-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cordero-Morales J.F., Gracheva E.O., Julius D. Cytoplasmic ankyrin repeats of transient receptor potential A1 (TRPA1) dictate sensitivity to thermal and chemical stimuli. Proc. Natl. Acad. Sci. USA. 2011;108:E1184–E1191. doi: 10.1073/pnas.1114124108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yao J., Liu B., Qin F. Modular thermal sensors in temperature-gated transient receptor potential (TRP) channels. Proc. Natl. Acad. Sci. USA. 2011;108:11109–11114. doi: 10.1073/pnas.1105196108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Clapham D.E., Miller C. A thermodynamic framework for understanding temperature sensing by transient receptor potential (TRP) channels. Proc. Natl. Acad. Sci. USA. 2011;108:19492–19497. doi: 10.1073/pnas.1117485108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rosenbaum T., Simon S.A., Islas L.D. Ion channels in analgesia research. Methods Mol. Biol. 2010;617:223–236. doi: 10.1007/978-1-60327-323-7_18. [DOI] [PubMed] [Google Scholar]
- 13.Heinemann S.H., Conti F. Nonstationary noise analysis and application to patch clamp recordings. Methods Enzymol. 1992;207:131–148. doi: 10.1016/0076-6879(92)07009-d. [DOI] [PubMed] [Google Scholar]
- 14.Talavera K., Yasumatsu K., Nilius B. Heat activation of TRPM5 underlies thermal sensitivity of sweet taste. Nature. 2005;438:1022–1025. doi: 10.1038/nature04248. [DOI] [PubMed] [Google Scholar]
- 15.Karashima Y., Talavera K., Voets T. TRPA1 acts as a cold sensor in vitro and in vivo. Proc. Natl. Acad. Sci. USA. 2009;106:1273–1278. doi: 10.1073/pnas.0808487106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vriens J., Owsianik G., Voets T. TRPM3 is a nociceptor channel involved in the detection of noxious heat. Neuron. 2011;70:482–494. doi: 10.1016/j.neuron.2011.02.051. [DOI] [PubMed] [Google Scholar]
- 17.Voets T., Owsianik G., Nilius B. TRPM8 voltage sensor mutants reveal a mechanism for integrating thermal and chemical stimuli. Nat. Chem. Biol. 2007;3:174–182. doi: 10.1038/nchembio862. [DOI] [PubMed] [Google Scholar]
- 18.Yang F., Cui Y., Zheng J. Thermosensitive TRP channel pore turret is part of the temperature activation pathway. Proc. Natl. Acad. Sci. USA. 2010;107:7083–7088. doi: 10.1073/pnas.1000357107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nilius B., Talavera K., Voets T. Gating of TRP channels: a voltage connection? J. Physiol. 2005;567:35–44. doi: 10.1113/jphysiol.2005.088377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Salazar M., Moldenhauer H., Baez-Nieto D. Could an allosteric gating model explain the role of TRPA1 in cold hypersensitivity? J. Neurosci. 2011;31:5554–5556. doi: 10.1523/JNEUROSCI.6775-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Viswanath V., Story G.M., Jegla T. Opposite thermosensor in fruitfly and mouse. Nature. 2003;423:822–823. doi: 10.1038/423822a. [DOI] [PubMed] [Google Scholar]
- 22.Gracheva E.O., Ingolia N.T., Julius D. Molecular basis of infrared detection by snakes. Nature. 2010;464:1006–1011. doi: 10.1038/nature08943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Saito S., Fukuta N., Tominaga M. Evolution of vertebrate transient receptor potential vanilloid 3 channels: opposite temperature sensitivity between mammals and Western clawed frogs. PLoS Genet. 2011;7:e1002041. doi: 10.1371/journal.pgen.1002041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rosenbaum T., Gordon S.E. Quickening the pace: looking into the heart of HCN channels. Neuron. 2004;42:193–196. doi: 10.1016/s0896-6273(04)00199-0. [DOI] [PubMed] [Google Scholar]
- 25.Saito S., Nakatsuka K., Tominaga M. Analysis of transient receptor potential ankyrin 1 (TRPA1) in frogs and lizards illuminates both nociceptive heat and chemical sensitivities and coexpression with TRP vanilloid 1 (TRPV1) in ancestral vertebrates. J. Biol. Chem. 2012;287:30743–30754. doi: 10.1074/jbc.M112.362194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Caterina M.J., Rosen T.A., Julius D. A capsaicin-receptor homologue with a high threshold for noxious heat. Nature. 1999;398:436–441. doi: 10.1038/18906. [DOI] [PubMed] [Google Scholar]
- 27.Liu B., Yao J., Qin F. Hysteresis of gating underlines sensitization of TRPV3 channels. J. Gen. Physiol. 2011;138:509–520. doi: 10.1085/jgp.201110689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Privalov P.L. Cold denaturation of proteins. Crit. Rev. Biochem. Mol. Biol. 1990;25:281–305. doi: 10.3109/10409239009090612. [DOI] [PubMed] [Google Scholar]
- 29.Adrover M., Esposito V., Temussi P.A. Understanding cold denaturation: the case study of Yfh1. J. Am. Chem. Soc. 2010;132:16240–16246. doi: 10.1021/ja1070174. [DOI] [PubMed] [Google Scholar]
- 30.Prabhu N.V., Sharp K.A. Heat capacity in proteins. Annu. Rev. Phys. Chem. 2005;56:521–548. doi: 10.1146/annurev.physchem.56.092503.141202. [DOI] [PubMed] [Google Scholar]
- 31.Nestorovich E.M., Karginov V.A., Bezrukov S.M. Kinetics and thermodynamics of binding reactions as exemplified by anthrax toxin channel blockage with a cationic cyclodextrin derivative. Proc. Natl. Acad. Sci. USA. 2012;109:18453–18458. doi: 10.1073/pnas.1208771109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Grandl J., Kim S.E., Patapoutian A. Temperature-induced opening of TRPV1 ion channel is stabilized by the pore domain. Nat. Neurosci. 2010;13:708–714. doi: 10.1038/nn.2552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Myers B.R., Bohlen C.J., Julius D. A yeast genetic screen reveals a critical role for the pore helix domain in TRP channel gating. Neuron. 2008;58:362–373. doi: 10.1016/j.neuron.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cui Y., Yang F., Zheng J. Selective disruption of high sensitivity heat activation but not capsaicin activation of TRPV1 channels by pore turret mutations. J. Gen. Physiol. 2012;139:273–283. doi: 10.1085/jgp.201110724. [DOI] [PMC free article] [PubMed] [Google Scholar]


