Identification of the Molecular Mechanisms for Cell-Fate Selection in Budding Yeast through Mathematical Modeling

Abstract

The specification and maintenance of cell fates is essential to the development of multicellular organisms. However, the precise molecular mechanisms in cell fate selection are, to our knowledge, poorly understood due to the complexity of multiple interconnected pathways. In this study, model-based quantitative analysis is used to explore how to maintain distinguished cell fates between cell-cycle commitment and mating arrest in budding yeast. We develop a full mathematical model of an interlinked regulatory network based on the available experimental data. By theoretically defining the Start transition point, the model is able to reproduce many experimental observations of the dynamical behaviors in wild-type cells as well as in Ste5-8A and Far1-S87A mutants. Furthermore, we demonstrate that a moderate ratio between Cln1/2→Far1 inhibition and Cln1/2→Ste5 inhibition is required to ensure a successful switch between different cell fates. We also show that the different ratios of the mutual Cln1/2 and Far1 inhibition determine the different cell fates. In addition, based on a new, definition of network entropy, we find that the Start point in wild-type cells coincides with the system’s point of maximum entropy. This result indicates that Start is a transition point in the network entropy. Therefore, we theoretically explain the Start point from a network dynamics standpoint. Moreover, we analyze the biological bistablity of our model through bifurcation analysis. We find that the Cln1/2 and Cln3 production rates and the nonlinearity of SBF regulation on Cln1/2 production are potential determinants for irreversible entry into a new cell fate. Finally, the quantitative computations further reveal that high specificity and fidelity of the cell-cycle and mating pathways can guarantee specific cell-fate selection. These findings show that quantitative analysis and simulations with a mathematical model are useful tools for understanding the molecular mechanisms in cell-fate decisions.

Introduction

The selection of cell fate in response to internal and external stimuli is essential to a cell’s life (1). For example, unicellular organisms make vital decisions to enter various phases of the life cycle to adapt to environmental changes (2). In multicellular organisms, precursor cells mature into specialized cell types, such as muscle cells or blood cells, during development. Therefore, it is important to precisely understand how cell-fate decisions are made. However, due to the complexity of highly interconnected biochemical networks, many related questions require further exploration.

Significant progress has been made in terms of the experimental studies of cell-fate selections (3,4). In theoretical studies, mathematical modeling and dynamical analysis are used to understand and explore the mechanisms of cell-fate decisions. A mathematical model of cell-fate decisions in response to death receptor engagement was proposed to explore the underlying mechanisms used by cytokines to trigger death or survival for various cell lines and cellular conditions (5). An integrated model of the p53 signaling network was developed to study the entire process from the generation of DNA damage to cell-fate decisions (6,7).

Recently, a quantitative, single-cell analysis of the commitment dynamics during the mating-mitosis switch in budding yeast was reported (2). The commitment points are frequently invoked in the explanation of differentiation processes. For the mating-mitosis switch, the purpose of mating is to fuse two haploid cells. This process must be restricted to the G1 phase, before the initiation of DNA replication. The point at which a cell loses its mating competence and commits to the cell cycle is called the “Start” point (8,9). It has been confirmed that Start is accurately predicted by the nuclear Whi5 concentration and is independent of cell size, cell type, and G1 duration (2). This physiology is reflected at the molecular level by inhibitory interactions at the interface between the cell-cycle and mating pathways (see Fig. S1 in the Supporting Material). Hence, upon exposure to the mating pheromones, pre-Start cells arrest directly while post-Start cells complete one more round of division before arresting.

However, several questions about the underlying mechanism in the cell-fate decision between cell-cycle commitment and mating arrest remain unanswered:

• 1.We are interested in the dynamical behaviors of some key components when the cell-fate transition is achieved by the addition of a mating pheromone.
• 2.Despite extensive studies of both the cell-cycle and mitogen-activated protein kinase (MAPK) mating pathways (10–13), Start still remains an abstract concept. The identification of a Start point based on the relationship between an externally added pheromone and cell-fate state remains unclear. Previous researches were primarily focused on studying the Start point in terms of internal proteins without an external stimulus. The Start point was treated as a qualitative concept within cell cycle. Hence, its precise definition is required.
• 3.How the crosstalk between cell-cycle and mating pathways determines the selection of cell fate should be clarified. In particular, the functions of some main regulatory processes, including mutual inhibition among Cln1/2 and Far1, Cln1/2-mediated multisite phosphorylation of Ste5, and the membrane localization of Ste5 at the Start point need to be explored quantitatively.

We developed an integrated model based on recent experimental research (2) that is responsible for selecting between cell-cycle commitment and mating arrest. The model is composed of two subsystems: a Start cell-cycle network and a pheromone-induced MAPK pathway. We begin by clarifying the biochemical mechanisms behind Whi5’s translocation between the cytoplasm and the nucleus to predict the cell fate under pheromone addition. Next, two important quantities, including the Start point and the network entropy, are quantitatively defined. By calculating the Start point and entropy values, the underlying mechanisms that maintain a separation between cell fates, the crucial roles of the crosstalk between the two subsystems, and the mutual inhibition of key proteins in cell-fate decisions, are explored extensively. Finally, investigations of the interlinked network’s specificity and fidelity are used to further elucidate how crosstalk between the two subsystems affects cell-fate selection. This work will create a better understanding of the dynamics and functions of the interaction network that is responsible for selecting cell-cycle commitment and mating arrest.

Models and Methods

Mathematical model

This work aims to clarify the selection mechanism between two cell fates—cell-cycle commitment and mating arrest. The schematic diagram used to build the mathematical model is presented in Fig. 1. Several assumptions are made to simplify the model:

• Assumption 1. The mating pathway is induced by a pheromone signal. The introduction of a stable and sufficient stimulus is required for network investigation. However, the disaggregation of the scaffold protein-MAP kinase complex and the disaggregation of Gαβγ, Ste11, Ste7, and Ste20 are not considered in our model. Consequently, the levels of Gαβγ, Ste11, Ste7, and Ste20 are assumed to be constant.

• Assumption 2. The total amount of Ste5 is assumed to be constant.

• Assumption 3. The reactions associated with the promotion and inhibitions of state transition are represented by Michaelis-Menten kinetics. The reactions related to transcriptional regulations are also written with Michaelis-Menten kinetics. For simplicity, phosphorylation reactions are just described according to mass action laws.

• Assumption 4. The multisite phosphorylation process of Cln1/2 on Ste5 is not shown explicitly in the mating pathway; for details, please refer to Serber and Ferrell (14).

In addition, the transcriptional factor MBF (Mbp1/Swi6) is integrated with SBF, a single variant, in the cell-cycle pathway.

Figure 1.

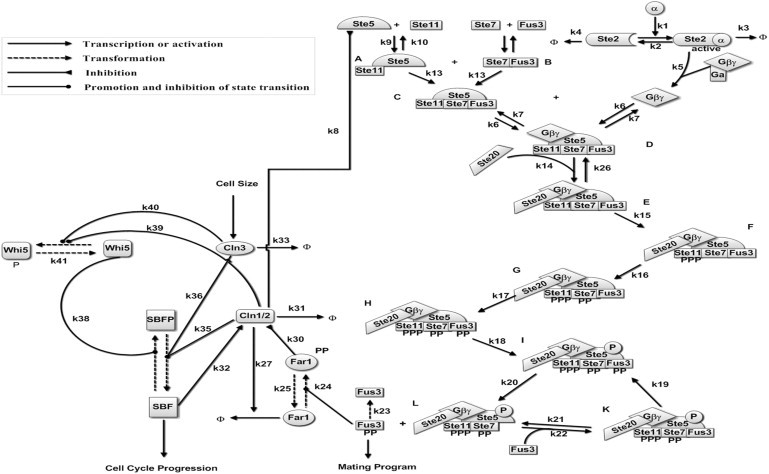
Schematic illustration of the dynamical processes of cell-fate decisions between the cell-cycle commitment and the mating arrest. All components and reactions considered in our mathematical model are included. All arrows for individual reactions are marked with the corresponding number of this reaction in the model (the cell-cycle commitment and pheromone pathway are adapted from Doncic et al. (2) and Kofahl and Klipp (15), respectively).

Detailed network descriptions, which include a subsystem of the Start cell cycle, a subsystem of the pheromone-induced MAPK pathway, and the interactions between the two subsystems, are listed in the Supporting Material. The model dynamics are characterized by ordinary differential equations, which are presented in the Appendix. The equations related to the mating pathway are modified from the base model in Kofahl and Klipp (15). The parameter values and the initial concentrations are listed in Table S1 and Table S2 of the Supporting Material, respectively. The methods and results of sensitivity analysis of the model parameters are described in the Supporting Material (see Table S3 for the results).

Determination of the Start point

In yeast, the G1 checkpoint Start determines whether a cell enters the mitotic cycle or engages in a mating program. The cell must choose between the two programs (i.e., it can never choose both) because their aims are diametrically opposed; the mating process produces one cell from two, while mitosis produces two cells from one. From a system dynamics point of view, Start is a bistable switch (2,16–18). Moreover, Doncic et al. (2) have identified the amount of Whi5 protein exiting the nucleus as the main probe for the status of the Start trigger. The relationship between the activation of Whi5P (i.e., the proportion of Whi5 that has been exported from nucleus after 30 min) and the pheromone addition time is described in this study. Furthermore, the critical point with the largest derivative in the dose-response curve is defined as the Start point.

Defining entropy in our network

To further quantify the network dynamics, we defined the entropy E of the biochemical reaction network based on an extension of the concept of entropy in statistical mechanics,

$$E=-\sum _{i=1}^{n}P\left(i\right)\text{log}\left(P\left(i\right)\right),$$ (1)

where

$$P\left(i\right)=\frac{x\left(i\right)}{\left(\sum _{j=1}^{n}x\left(j\right)\right)}$$

is a distribution function of the protein concentrations, x(i) denotes the concentration of the ith component, and n is the total number of components considered in the model (in this study, n = 42). From the viewpoint of evolutionary biology, a change in entropy implies the evolution of a molecular network’s structure and function due to its adaptive ability.

Calculation of specificity and fidelity

Different cellular signal transduction pathways are often interconnected, so that the potential for undesirable crosstalk between pathways exists. Nevertheless, signaling networks have evolved that maintain specificity from signal to cellular response. We investigate the signal-response characteristics of the network through the quantitative calculation of specificity and fidelity (19–21).We let the corresponding signal-input of the mating pathway be 240 nM pheromone and 0.5e^0.003t for the generation rate of Cln3 and the corresponding signal-input of cell-cycle progress be 1 nM pheromone and 120e^0.003t for the generation rate of Cln3. Fus3PP and SBF stand for the output of the mating pathway and the cell-cycle progress, respectively. Therefore, the specificity S_mating and fidelity F_mating of the mating pathway are defined, respectively, as follows:

$$S_{\text{mating}}=\frac{{{\int }_0^{30}Fus3}_{pp}{\left(t\right)}_{A}dt}{{\int }_0^{30}SBF{\left(t\right)}_{A}dt},$$ (2)

$$F_{\text{mating}}=\frac{{{\int }_0^{30}Fus3}_{pp}{\left(t\right)}_{A}dt}{{{\int }_0^{30}Fus3}_{pp}{\left(t\right)}_{B}dt}.$$ (3)

Just in the same way, we can get the specificity S_cell-cycle and fidelity F_cell-cycle of the cell-cycle progress:

$$S_{\text{cell}\text{-}\text{cycle}}=\frac{{\int }_0^{30}SBF{\left(t\right)}_{B}dt}{{{\int }_0^{30}Fus3}_{pp}{\left(t\right)}_{B}dt},$$ (4)

$$F_{\text{cell}\text{-}\text{cycle}}=\frac{{\int }_0^{30}SBF{\left(t\right)}_{B}dt}{{\int }_0^{30}SBF{\left(t\right)}_{A}dt}.$$ (5)

Results

The consistency between the simulation results and the experimental observations in wild-type and mutation cells

Our theoretical model was validated by simulating the signaling dynamics of two subsystems (see the Supporting Material for a description and Fig. S2, Fig. S3, Fig. S4, Fig. S5, and Fig. S6). Biomarker-like components are chosen to indicate various cell fates in our simplified model. The fate of cell-cycle commitment was represented by high levels of Cln1/2, SBF, and Whi5P (see Fig. S2), while mating arrest was predicted by high levels of Ste5_mem and Fus3_pp (see Fig. S4). In addition, the following assumptions were also considered: The initial states of the yeast cells were simplified because they have already finished at least one cell-cycle and are all at the beginning of the G1 phase. Because pheromone pathway kinetics and media switching (<1 min) are faster than Whi5 kinetics (5 min) and G1 duration (30 min), we treated the pheromone pathway activity as a binary variable that instantaneously changes upon pheromone addition (2). It was reasonable to assume that various cell fates could be inferred from the corresponding protein expression levels after 30 min.

To begin, we studied the propagation of pheromone signals in the fate decision network. Adding the pheromone (240 nM) into the WT cell at various times led to specific cell fates, as shown in Fig. 2. When the addition was quick (Fig. 2, A and B), the proteins Ste5_mem and Fus3_PP, which correspond to the mating pathway, were produced at high levels. This result indicated mating arrest. However, when the addition time was long (Fig. 2, C and D), the proteins Cln1/2, SBF, and Whi5P, which are related to the cell-cycle, were expressed at high levels. This result led to a different fate, namely, cell-cycle commitment. In addition, the competition between the two groups of proteins was clearly indicated by the transient rises of Whi5P levels in the mating fate (Fig. 2 B) and the rise of Ste5_mem levels in the cell-cycle fate (Fig. 2 C). Once one of the cell fates dominated, the proteins related to the other cell fates were suppressed completely. These numerical results in WT cells were in good agreement with experimental data (2).

Figure 2.

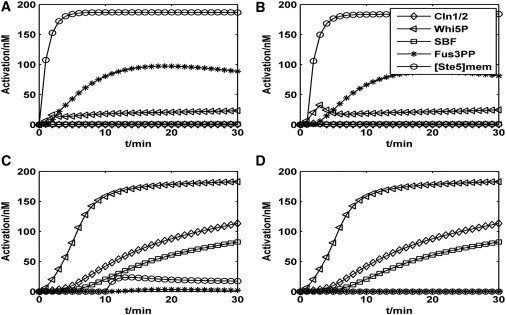
Time courses of the wild-type cells. (A) Pheromone is added at 0 min. (B) Pheromone is added at 1 min. (C) Pheromone is added at 10 min. (D) No pheromone is added.

We also simulated the time courses of Ste5-8A and Far1-S87A mutants (22,23). The detailed explanations for simulation processes are listed in the Supporting Material and numerical results are presented in Fig. S7 and Fig. S8. Our theoretical results qualitatively reproduced the experimental observations in Ste5-8A and Far1-S87A mutants (2,22).

The quantitative determination of the Start point in wild-type cells

According to our definition of the Start point (described in the Models and Methods), the Start point and its relationship between Whi5P activation (i.e., the proportion of Whi5 exported from the nucleus after 30 min) and the time of pheromone addition are shown in Fig. 3. The Start point (i.e., the intersection point of two dashed lines in Fig. 3) is the point at which the two different cell fates were clearly separated. In other words, as the addition time of pheromone increased, the transportation of Whi5P from the nucleus to cytoplasm also increased, leading to a transition from mating arrest to cell-cycle commitment at the Start point (i.e., at the critical addition time). Based on our calculations, the critical ratio of Whi5P at the Start point was ∼51.56% in WT cells. This result was similar to the experimental observation that Start exists at the point in which half of the WT cells arrest, which occurs when approximately half of the Whi5-GFP (52 ± 3%) has been exported (2).

Figure 3.

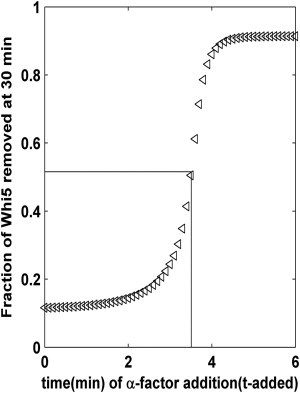
Relationship between the time of pheromone addition and Whi5P activation. At the Start point where the maximum slope is achieved in this response curve, there exists one critical addition time that indentifies the critical ratio of Whi5 required for a successful transition of two distinct cell fates. In WT cells, Start is defined by the export of approximately half of the nuclear Whi5.

The Start point of Ste5-8A and Far1-S87A mutations

Here, we focused our attention on the effects of the Ste5-8A and Far1-S87A mutations on the Start point. As explained by Doncic et al. (2), compared to WT cells, cell-cycle commitment was not altered in Ste5-8A cells, while cell-cycle commitment in the Far1-S87A cells required higher Whi5 export. These experimental observations were reviewed by our model. The dose-responses of the export of nuclear Whi5 after the addition of pheromone in the Ste5-8A and Far1-S87A mutations are plotted in Fig. S9, A and B. According to our theoretical computations, ∼54.33% of Whi5 needed to be exported from the nucleus for the Ste5-8A mutant to commit to the cell cycle, whereas ∼57.50% of Whi5 needed to be exported in the Far1-S87A mutant. Based on the experiment data, the Ste5-8A mutant shows a critical ratio of ∼52% of Whi5 exported from the nucleus, and the Far1-S87A mutant has a larger critical ratio of ∼64%. By comparing these results (summarized in Table S4), it appears that our theoretical model performs well and provided a good explanation for the experimental findings.

Differential rate constants affect the selection of cell fate

The results above indicated that Cln1/2 works in two ways: Cln1/2-mediated inhibition on Far1 (with a rate of k₂₇) and Cln1/2-mediated inhibition on Ste5 (with a rate of k₈). In our model, we assigned a ratio of 4.76 to these corresponding parameters (i.e., k₂₇/k₈ = 4.76). To investigate whether differences in the two inhibition rates could explain the separation of cell fates, we fixed all of the rates except for the inhibition rate of Cln1/2 on Far1 (i.e., k₂₇), varying its ratio with k₈ from 0.01 to 1000.

To begin, we explored the influence of various rate constants on the fate of WT cells that were treated with α-factor at 0 min. The cell was expected to select the mating fate due to the quick addition of a pheromone. Our simulation results are shown in Fig. S10. To guarantee the mating arrest, the ratio of k₂₇/k₈ must be within the range of 0.01–40. When the ratio was large enough, the system committed to the cell-cycle despite its fast treatment with α-factor. For example, in cells with a k₂₇/k₈>100, it is observed that most of the nuclear Whi5 (>80%) was exported, even though α-factor was added at the beginning of the simulation. Clearly, this type of cell was abnormal.

We then explored another question. We knew that the k₂₇/k₈ ratio would change the fate of WT cell, but what influence did it have on the critical ratio represented by the Start point? To answer this question, we calculated the critical ratio of Whi5 (i.e., the Start point) when the k₂₇/k₈ ratio ranged from 0.01 to 1000. The relationship between the Start point and the k₂₇/k₈ ratio is shown in Fig. 4. All data were classified into three categories (Regions I–III). Three typical k27/k8 values in these regions were chosen. In Fig. S11, three dose-response curves of Whi5P activation (i.e., the ratio of Whi5 removed from the nucleus) are presented for various pheromone addition times (1). For cells in Region I (see Fig. S11 A), the critical ratio (<0.5) was smaller than its experimental value. As the addition time of the pheromone increased, the cell could switch from mating arrest (low activation of Whi5P) to cell-cycle commitment (high activation of Whi5P). However, this increase caused large delays in the Start point (2). Most interestingly, the cells in Region II could pass through normal cell-fate transitions.

Figure 4.

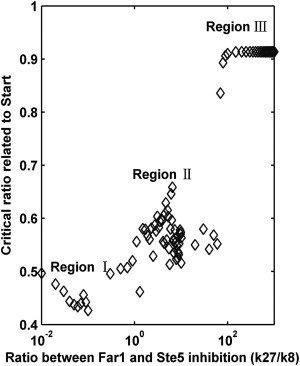
The influence of various k₂₇/k₈ ratios on the critical ratios of Whi5 exported from the nucleus related to the Start point. Only the ratios located in Region II are related to the Start point and can make normal cell-fate transitions (i.e., 52 ± 3%).

First, the critical ratios of Whi5 exported from the nucleus were similar to the experimental values (52 ± 3%) (see Region II in Fig. S11 B). This result showed the robustness of cell-fate decisions.

Second, a successful switch between the mating and cell-cycle fates was realized, i.e., the cell was able to experience two different cell fates for a specific k₂₇/k₈ ratio (see Fig. S11 B). The parameter selected in our theoretical model (k₂₇/k₈ = 4.76) was only found in Region II. Notably, while some cells in Region I could also undergo a similar cell-fate switch, Fig. S11, A and B, shows significant differences in their critical time (3). In comparison, only the cells in Region III could stay in a high Whi5P activation state (see Fig. S11 C), i.e., these cells would always commit to cell cycle. Hence, these parameters are invalid, as the cells would lose fate-selecting ability.

Our analysis suggests that the k₂₇/k₈ ratio could affect the threshold of the stimulus-response curve. Furthermore, Fig. 4 and Fig. S10 indicate that, at an appropriate value, the k₂₇/k₈ ratio could maintain a good separation of the distinct cell-fates. This result indicated that pathway interconnections had to be controlled within a proper range. A Far1 deficiency or excessive inhibition of Far1 by Cln1/2 could destroy the balance between cell cycle and mating, leading to improper cellular outcomes.

Moreover, the parameter pairs associated with crosstalk and mutual inhibition were investigated. We study the impact of the critical ratio of Whi5 exported from the nucleus on k₂₇/k₃₀, k₈ /k₂₇ and k₃₀/k₂₇ in Fig. S12. It is clear that most cells with a critical ratio ranging from 49 to 55% (experimental region) were located in the moderate region. Furthermore, it was notable that change in k₈/k₂₇ had a relatively small influence on the critical ratio (see Fig. S12 B) whereas variations in k₂₇/k₈(or k₂₇/k₃₀) led to diverse cell fates (see Fig. 4 and Fig. S12 A). Our simulation results were verified by the observations that Cln1/2-mediated inhibition on Far1, while not on Ste5, affected the Start point. These results were consistent with cyclins phosphorylating and inhibiting Far1 before Ste5 (2). Thus, Cln1/2→Far1 inhibition was required to ensure a successful switch between different cell fates.

The network entropy determines the Start point

We were interested in studying the relationship between the Start point and the network entropy. For wild-type cells, Fig. 5 A shows that the network entropy nearly achieved its maximum when the curve shown in Fig. 3 has its largest derivative. In other words, the network reached its Start point when the entropy reached its maximum. This observation indicated that the Start point was a state-transformation point when the energy of the system changed. Because it is confirmed that systems suffer a critical transition when their entropy reaches a maximum level (24–26), our definition of the Start point as the largest derivative was quite reasonable. We can obtain the same information from Fig. 5 B. To further investigate the effect of parameter perturbations on the entropy peak position, we conducted sensitivity analysis (methods are provided in the Supporting Material). It was clear from the results (listed in Table S5) that the Start transition point in WT cells near the entropy peak was insensitive to parameter perturbation. Therefore, the evolutionary preference in this interlinked regulatory network to the Start point provided a robust mechanism for cell-fate decisions. However, the Ste5-8A mutants committed to the cell cycle when their entropy reached a minimum (Fig. 5 C), thereby losing the adaptation to the cellular progress. These results further explained the mechanisms behind cell-fate decision from the viewpoint of network dynamics.

Figure 5.

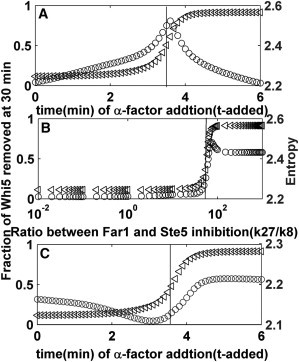
Dependences of network entropy and Whi5P activation on the pheromone addition time (or k₂₇/k₈ ratios). (Rectangles) Whi5P activation. (Circles) Network entropy. (A) WT cells. (B) WT cells treated with pheromone at 0 min. (C) Ste5–8A mutants. (Straight lines) X-coordinate of the critical point (i.e., the Start point in rectangles line).

Biological bistability during one cell-cycle period

The dynamics of our model were based on the mutual inhibition between Cln1/2 and Far1. A potential emergent property of this positive feedback loop was the occurrence of bistability, which was assumed to define the switch between commitment and mating. Therefore, we implemented a steady-state analysis to further investigate the dynamical mechanisms based on the model. The parameter values in our simulations were used to explore two cases:

• 1.Long-term behavior. In traditional bifurcation analysis, the steady-state values are collected after a long time, i.e., the initial transient data are discarded until all of the proteins achieve their stable steady states.
• 2.Short-term behavior. Because the cells select one fate at the Start point, the steady-state values that determine cell fates should be calculated within a biologically reasonable time range, such as one cell cycle.

Initially, the long-term behavior of our system was explored. As shown in Fig. S13, the pheromone was added very quickly (see Fig. S13 A), as a result, the cell was expected to choose mating arrest. However, the system could only sustain a low level of Whi5P (i.e., mating arrest) for a short time. After one cell cycle, the cell jumped to a high level of Whi5P (i.e., cell-cycle commitment), which is contrary to its known biological selection. When the pheromone was added later (see Fig. S13 B), a high level of Whi5P presented (similar to Fig. S13 A). Hence, the cell-cycle commitment was also selected in this scenario. One-parameter bifurcation analysis (Fig. 6 A) illustrated that a single stable steady state (corresponding to cell-cycle commitment) appeared in our theoretical model, verifying the previous result. Mathematically, this long-term dynamic behavior was due to an exponential increase in the Cln1/2 and Cln3 production rates over time (K₄₂ = e^0.06t, K₃₄ = 0.5e^0.003t). Because the G1 duration is ∼30 min, the cell chose its cell fate in the vicinity of 30 min. Any evolutionary processes that occurred after this time were not directly related to the fate-selection mechanisms discussed in our model.

Figure 6.

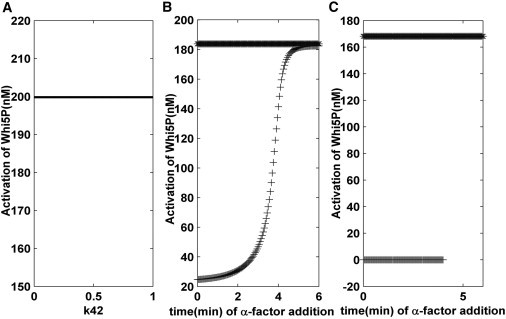
(A) One-parameter bifurcation analysis for the original model. The bifurcation parameter is K₄₂. (B) Dependency of the steady-state value of Whi5P on a given input K₄₂ and K₃₄ (see Table S1 in the Supporting Material) when the value of the steady state is calculated from the average amount of Whi5P at 30–40 min. (C) Dependency of the steady-state value of Whi5P on a given K₄₂ and K₃₄ when the steady-state value is calculated after one cell cycle. Here a reset mechanism for Cln1/2 and Cln3 synthesis is considered in our model.

The system’s short-term behavior was also investigated. Because the cell completed its fate selection at the Start point, a steady-state analysis of short-term behavior near the Start point was important. As shown in Fig. 6 B, different initial conditions led to two different cell fates when the Cln1/2 and Cln3 production rates were both held constant (i.e., a biological bistability). The constant production rates of Cln1/2 and Cln3 were denoted as K₄₂ and K₃₄, respectively. To ensure our model’s bistability when the evolution time exceeded one cell cycle, we accounted for the fact that a yeast cell can stop growing for an extended time. Therefore, a reset mechanism for Cln1/2 and Cln3 synthesis was required and reasonable. When we reset the Cln1/2 and Cln3 synthesis rate to 0 at 80–90 min, bistability was produced. The bistability also occurred in the case of an exponential increase in the Cln3 production rate during this time (Fig. 6 C). The bistability disappeared near the critical addition time (3.6 min), when the entropy reached its peak. These studies clarified the monostability (long-term behavior) and bistability (short-term behavior) of the cell-cycle Start point in our model.

Biological mechanism for irreversible bistability

In our original model, cell size was coupled to the CDK engine by assuming that the synthesis of the upstream cyclins was proportional to cell mass. For simplicity, we assumed that the mass increased exponentially. Hence, the generation rates of Cln1/2 and Cln3 increased exponentially with time. This assumption rendered mating arrest an unstable cell fate even if the pheromone was added quickly, because from the mathematical point of view, the concentration of Cln1/2 and Cln3 were greatly enhanced after 30 min. We performed a one-parameter bifurcation analysis on a modified model with constant Cln1/2 and Cln3 production rates (K₃₄ = 0.5 and K₄₂ = 1, respectively). As shown in Fig. 7 A, we observed a bifurcation into a bistable system, i.e., there was a K₄₂ interval in which Whi5P could take two different values, corresponding to states of low (mating arrest) and high (cell-cycle commitment) Whi5P expression levels. However, this bistability occurred at a negative value of K₄₂, which is biochemically impossible.

Figure 7.

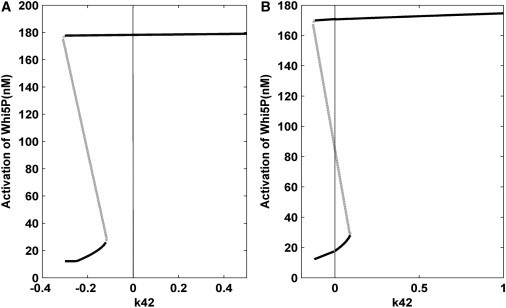
One-parameter bifurcation analysis for our modified model. (A) The Cln1/2 and Cln3 production rates are constants (K₃₄ = 0.5 and K₄₂ = 1). (B) Further, the nonlinearity of the transcriptional regulation of SBF on Cln2 is increased (Hill coefficient is set to 2).

To explore the origins of Start irreversibility in budding yeast, we further hypothesized that the cyclin-dependent Cln2 production rate exhibited high nonlinearity, which has been observed experimentally. Therefore, the nonlinearity of SBF regulation on the production of Cln2 was enhanced in Eq. A29, i.e., the expression k₃₂[SBF]/(Km+[SBF]) was changed to k₃₂[SBF]²/(Km²+[SBF]²). Interestingly, an irreversible bistability was observed, as evident in Fig. 7 B. The switch from a low stable state to a high stable state could occur freely, while the potential for switching from a high state to the low state by decreasing K₄₂ disappeared (it occurred at a negative value of K₄₂). These results revealed the possible biological mechanisms for irreversible bistability.

Maintaining network specificity and fidelity

First, the effects of the pheromone addition time were analyzed, as shown in Fig. 8. The specificity of the mating pathway decreased rapidly with a delay in the addition time (Fig. 8 A), while the specificity of the cell-cycle progress increases dramatically (Fig. 8 B). The fidelity of the mating and cell-cycle pathways were eventually reduced to a low level eventually (Fig. 8, C and D). Especially, the mating pathway lost the specificity while the cell-cycle pathway maintained high specificity when the pheromone addition time exceeded ∼3.50 min, which was consistent with the experimental results that WT cells commit to the cell cycle at 3.51 min.

Figure 8.

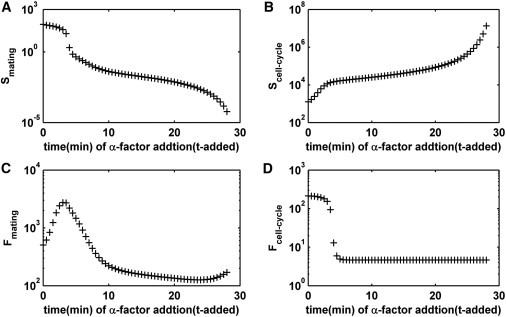
The influences of different pheromone addition time on network specificity and fidelity. (A and C) Mating pathway. (B and D) Cell-cycle progress.

Second, the roles of different ratios of mutual Cln1/2 and Far1 inhibition rates (k₃₀/k₂₇) in the maintenance of network specificity and fidelity were investigated. The specificity of the mating pathway increased with an increase in the k₃₀/k₂₇ ratio (see Fig. S14 A), but the specificity of the cell-cycle progress decreased when the ratio was larger than 40 (see Fig. S14 B). At the same time, the fidelity of both pathways decreased to a low level (see Fig. S14, C and D). As shown in Fig. S14, the two pathways achieved the best specificity and fidelity when the k₃₀/k₂₇ ratio was in the approximate range of 1–40. Additionally, a normal ratio of Whi5 was exported from nucleus in cell-fate decisions when the k₃₀/k₂₇ ratio was within this range (see Fig. S14 C). These results showed that high network specificity and fidelity could guarantee a specific cell fate.

Discussions

Previous studies have shown that bistable switches exist in the cell-cycle system (16–18,23). In terms of traditional bifurcation analysis, mathematical bistability cannot be found in our original model. However, two steady states actually exist during one cell-cycle period. We consider this biologically significant short-term behavior (∼30–40 min) as a biological bistability.

The definition of the maximum entropy point and short-term behavior (the activation of Whi5P at 30 min) were discussed in the Results. A good agreement was found between biological bistability and the maximum entropy point. In terms of its long-term behavior, we revealed the critical biological mechanisms of the system’s irreversible bistability, which include varying the Cln1/2 and Cln3 production rates and increasing the nonlinearity of SBF regulation on Cln2 production. Our research may bridge an important gap between the model’s long-term monostability (short-term biological bistability) and the robust, unidirectional Start transition.

Due to the complexity of interlinked regulatory networks, the pathway that regulates the G1 cell cycle is simplified in this study. Many components involved in the Start transition, such as BCK2, NRM1, YDJ1, MSN5, etc. (27–30), are not included in our model. To further verify the study’s main conclusions, two typical components involved in the Start transition (BCK2 and NRM1) are considered in an extended model (see the Supporting Material). The entropy of the extended network remained at a maximum near the Start transition point (see Fig. S15). This result indicated that the main conclusions from our simplified model are unchanged.

In addition, stochastic noise is not considered in our model. External noise can lead to individual cells with different initial states within a cell population. In this scenario, the addition of a pheromone would cause individual cells to select different cell fates. The number of cells selecting cell-cycle commitment would form a distribution due to different nuclear Whi5 fraction exported in individual cells before pheromone addition. However, for the sake of simplicity, all of the cells in our study have the same initial state, which is similar to the scenario of cell-cycle synchronization in a cell population. Internal noise is also neglected in our theoretical research (31). It will be an important next step to analyze how cells make robust and precise cell-fate decisions in a noisy environment (32,33). Furthermore, the spatial diffusion of biological molecules should not be neglected (34,35). These spatial effects include spatial location of Whi5 in the nucleus or cytoplasm, the membrane recruitment of Ste5, and the binding of MAPK to Ste5. Exploring the spatiotemporal regulations within this biochemical network is a challenge for future research. However, the mathematical model and quantitative analysis tools established in this study can provide a significant foundation for further exploration of the molecular mechanisms in entire signaling networks.

Conclusions

The budding yeast’s decision between cell-cycle commitment and mating arrest involves a complex process, including translocation of Whi5 between the cytoplasm and the nucleus, recruitment of scaffold protein Ste5, multisite phosphorylation of Ste5 by Cln1/2, mutual inhibition between Cln1/2 and Far1, a series of transitions between the active and inactive states of kinase proteins, etc. How these dynamics influence the Start point of cell cycle is critical to understanding cell-fate decisions.

The main contributions of this study include five aspects:

• 1.We propose an integrated mathematical model of a cell-fate decision-making network that links cell-cycle subsystem with the pheromone-induced MAPK signaling subsystem in budding yeast. The model is based on the recent experimental research (2) and other available experimental data (15). The consistency between the simulation results in three cell types (WT cells, Ste5–8A mutations, and Far1–S87A mutations) and the experimental observations indicates that the model is reasonable.
• 2.An important quantity, the Start point, is defined quantitatively. We use the quantitative analysis to characterize the critical ratio of Whi5 removal from nucleus under a critical addition time of pheromone as the Start point in three cell types, which sharply distinguishes between distinct cell fates on a dose-response curve. We also demonstrate that an appropriate ratio between the Cln1/2-mediated phosphorylation of Far1 and that of Ste5 can maintain good separation between distinct cell fates.
• 3.The network entropy is defined. The computational results in all three cell types suggest the Start point is the transition point of the network entropy in WT cells. Therefore, to our knowledge, this is the first time that the Start point has been theoretically explained from a network dynamics perspective.
• 4.Our results from bifurcation analysis suggest that the network has a bistable switch before the Start point. Furthermore, once the system is beyond this switch point, it irreversibly enters into the cell cycle.
• 5.We clarify how the pheromone addition time and the ratio of mutual Cln1/2 and Far1inhibition rates, which represents crosstalk between two pathways, affect network specificity and fidelity. These findings provide apparently new insights into the correlation between the function of specific, stable cell-fate selections and the critical determinants for irreversible entry into new cell fates in budding yeast. This work also contributes to our system-level understanding of molecular mechanisms in interconnected signaling networks.

Appendix: Mathematical Model

$$\frac{d\left[\text{Ste}2\right]}{dt}=-k_1\left[\text{Ste}2\right]\alpha \left(t\right)+k_2{\left[\text{Ste}2\right]}_{\text{act}}-k_4\left[\text{Ste}2\right].$$ (A1)

$$\frac{d{\left[\text{Ste}2\right]}_{\text{act}}}{dt}=k_1\left[\text{Ste}2\right]\alpha \left(t\right)-k_2{\left[\text{Ste}2\right]}_{\text{act}}-k_3{\left[\text{Ste}2\right]}_{\text{act}}.$$ (A2)

$$\frac{d\left[\text{Ste}{5}_{0p}\right]}{dt}=-8k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{0p}\right]+k_{8d}\left[\text{Ste}{5}_{1p}\right]-k_{a0}\left[\text{Ste}{5}_{0p}\right]+k_{d0}{\left[\text{Ste}{5}_{0p}\right]}_{\text{mem}}.$$ (A3)

$$\frac{d\left[\text{Ste}{5}_{1p}\right]}{dt}=8k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{0p}\right]-k_{8d}\left[\text{Ste}{5}_{1p}\right]-7k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{2p}\right]+2k_{8d}\left[\text{Ste}{5}_{2p}\right]-k_{a1}\left[\text{Ste}{5}_{1p}\right]+k_{d1}{\left[\text{Ste}{5}_{1p}\right]}_{\text{mem}}.$$ (A4)

$$\frac{d\left[\text{Ste}{5}_{2p}\right]}{dt}=7k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{1p}\right]-2k_{8d}\left[\text{Ste}{5}_{2p}\right]-6k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{2p}\right]+3k_{8d}\left[\text{Ste}{5}_{3p}\right]-k_{a2}\left[\text{Ste}{5}_{2p}\right]+k_{d2}{\left[\text{Ste}{5}_{2p}\right]}_{\text{mem}}.$$ (A5)

$$\frac{d\left[\text{Ste}{5}_{3p}\right]}{dt}=6k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{2p}\right]-3k_{8d}\left[\text{Ste}{5}_{3p}\right]-5k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{3p}\right]+4k_{8d}\left[\text{Ste}{5}_{4p}\right]-k_{a3}\left[\text{Ste}{5}_{3p}\right]+k_{d3}{\left[\text{Ste}{5}_{3p}\right]}_{\text{mem}}.$$ (A6)

$$\frac{d\left[\text{Ste}{5}_{4p}\right]}{dt}=5k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{3p}\right]-4k_{8d}\left[\text{Ste}{5}_{4p}\right]-4k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{4p}\right]+5k_{8d}\left[\text{Ste}{5}_{5p}\right]-k_{a4}\left[{\text{Ste}5}_{4\text{p}}\right]+k_{d4}{\left[\text{Ste}{5}_{4p}\right]}_{\text{mem}}.$$ (A7)

$$\frac{d\left[\text{Ste}{5}_{5p}\right]}{dt}=4k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{4p}\right]-5k_{8d}\left[\text{Ste}{5}_{5p}\right]-3k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{5p}\right]+6k_{8d}\left[\text{Ste}{5}_{6p}\right]-k_{a5}\left[\text{Ste}{5}_{5p}\right]+k_{d5}{\left[\text{Ste}{5}_{5p}\right]}_{\text{mem}}.$$ (A8)

$$\frac{d\left[\text{Ste}{5}_{6p}\right]}{dt}=3k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{5p}\right]-6k_{8d}\left[\text{Ste}{5}_{6p}\right]-2k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{6p}\right]+7k_{8d}\left[\text{Ste}{5}_{7p}\right]-k_{a6}\left[\text{Ste}{5}_{6p}\right]+k_{d6}{\left[\text{Ste}{5}_{6p}\right]}_{\text{mem}}.$$ (A9)

$$\frac{d\left[\text{Ste}{5}_{7p}\right]}{dt}=2k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[{\text{Ste}5}_{6p}\right]-7k_{8d}\left[\text{Ste}{5}_{7p}\right]-k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{7p}\right]+8k_{8d}\left[\text{Ste}{5}_{8p}\right]-k_{a7}\left[\text{Ste}{5}_{7p}\right]+k_{d7}{\left[\text{Ste}{5}_{7p}\right]}_{\text{mem}}.$$ (A10)

$$\frac{d\left[\text{Ste}{5}_{8p}\right]}{dt}=k_8\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Ste}{5}_{7p}\right]-8k_{8d}\left[\text{Ste}{5}_{8p}\right]-k_{a8}\left[\text{Ste}{5}_{8p}\right]+k_{d8}{\left[\text{Ste}{5}_{8p}\right]}_{\text{mem}}.$$ (A11)

$$\frac{d{\left[\text{Ste}{5}_{ip}\right]}_{\text{mem}}}{dt}=k_{ai}\left[\text{Ste}{5}_{ip}\right]-k_{di}{\left[\text{Ste}{5}_{ip}\right]}_{\text{mem}},i=0,1,\dots ,8.$$ (A12)

$$\frac{d\left[\text{G}\beta \gamma \right]}{dt}=k_5{\left[\text{Ste}2\right]}_{\text{act}}\left[\text{G}\alpha \beta \gamma \right]-k_6\left[\text{G}\beta \gamma \right]\left[\text{C}\right]+k_7\left[\text{D}\right].$$ (A13)

$$\frac{d\left[\text{A}\right]}{dt}=k_9\left[\text{Ste}11\right]{\left[\text{Ste}5\right]}_{\text{total}}-k_{10}\left[\text{A}\right]-k_{13}\left[\text{A}\right]\left[\text{B}\right].$$ (A14)

$$\frac{d\left[\text{B}\right]}{dt}=k_{11}\left[\text{Ste}7\right]\left[\text{Fus}3\right]-k_{12}\left[\text{B}\right]-k_{13}\left[\text{A}\right]\left[\text{B}\right].$$ (A15)

$$\frac{d\left[\text{C}\right]}{dt}=k_{13}\left[\text{A}\right]\left[\text{B}\right]-k_6\left[\text{G}\beta \gamma \right]\left[\text{C}\right]+k_7\left[\text{D}\right].$$ (A16)

$$\frac{d\left[\text{D}\right]}{dt}=k_6\left[\text{G}\beta \gamma \right]\left[C\right]\frac{{\left[\text{Ste}5\right]}_{\text{mem}}}{{\left[\text{Ste}5\right]}_{\text{total}}}-k_{14}\left[\text{D}\right]\left[\text{Ste}20\right]-k_7\left[\text{D}\right]+k_{26}\left[\text{E}\right].$$ (A17)

$$\frac{d\left[\text{E}\right]}{dt}=k_{14}\left[\text{D}\right]\left[\text{Ste}20\right]-k_{15}\left[\text{E}\right]-k_{26}\left[\text{E}\right].$$ (A18)

$$\frac{d\left[\text{F}\right]}{dt}=k_{15}\left[\text{E}\right]-k_{16}\left[\text{F}\right].$$ (A19)

$$\frac{d\left[\text{G}\right]}{dt}=k_{16}\left[\text{F}\right]-k_{17}\left[\text{G}\right].$$ (A20)

$$\frac{d\left[\text{H}\right]}{dt}=k_{17}\left[\text{G}\right]-k_{18}\left[\text{H}\right].$$ (A21)

$$\frac{d\left[\text{I}\right]}{dt}=k_{18}\left[\text{H}\right]+k_{19}\left[\text{K}\right]-k_{20}\left[\text{I}\right].$$ (A22)

$$\frac{d\left[\text{K}\right]}{dt}=-k_{19}\left[\text{K}\right]-k_{21}\left[\text{K}\right]+k_{22}\left[\text{L}\right]\left[\text{Fus}3\right].$$ (A23)

$$\frac{d\left[\text{L}\right]}{dt}=k_{20}\left[\text{I}\right]+k_{21}\left[\text{K}\right]-k_{22}\left[\text{L}\right]\left[\text{Fus}3\right].$$ (A24)

$$\frac{d\left[\text{Fus}3\right]}{dt}=k_{12}\left[\text{B}\right]-k_{11}\left[\text{Ste}7\right]\left[\text{Fus}3\right]+k_{23}\left[\text{Fus}{3}_{pp}\right]-k_{22}\left[\text{L}\right]\left[\text{Fus}3\right].$$ (A25)

$$\frac{d\left[\text{Fus}{3}_{pp}\right]}{dt}=k_{20}\left[I\right]-k_{23}\left[\text{Fus}{3}_{pp}\right].$$ (A26)

$$\frac{d\left[\text{Far}1\right]}{dt}=-k_{24}\left[\text{Far}1\right]\frac{{\left[\text{Fus}{3}_{pp}\right]}^2}{{\left[\text{Fus}{3}_{pp}\right]}^2+k_{37}}+k_{25}\left[\text{Far}{1}_{pp}\right]-k_{27}\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Far}1\right].$$ (A27)

$$\frac{d{\left[\text{Far}1\right]}_{pp}}{dt}=k_{24}\left[\text{Far}1\right]\frac{{\left[\text{Fus}{3}_{pp}\right]}^2}{{\left[\text{Fus}{3}_{pp}\right]}^2+k_{37}}-k_{25}\left[\text{Far}{1}_{pp}\right].$$ (A28)

$$\frac{d\left[\frac{\mathrm{Cln1}}{2}\right]}{dt}={\text{K}}_{42}+\frac{k_{28}{\left[\frac{\mathrm{Cln1}}{2}\right]}^2}{k_{29}+{\left[\frac{\mathrm{Cln1}}{2}\right]}^2}-k_{30}\left[\text{Far}{1}_{pp}\right]-k_{31}\left[\frac{\mathrm{Cln1}}{2}\right]+\frac{k_{32}\left[\text{SBF}\right]}{K_m+\left[\text{SBF}\right]}.$$ (A29)

$$\frac{d\left[\text{Cln}3\right]}{dt}={\text{K}}_{34}-k_{46}\left[\text{Cln}3\right].$$ (A30)

$$\frac{d\left[\text{SBF}\right]}{dt}=k_{35}\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{SBFP}\right]+k_{36}\left[\mathrm{Cln}3\right]\left[\text{SBFP}\right]-k_{38}\left[\text{Whi}5\right]\left[\text{SBF}\right].$$ (A31)

$$\frac{d\left[\text{SBFP}\right]}{dt}=-k_{35}\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{SBFP}\right]-k_{36}\left[\mathrm{Cln}3\right]\left[\text{SBFP}\right]+k_{38}\left[\text{Whi}5\right]\left[\text{SBF}\right].$$ (A32)

$$\frac{d\left[\text{Whi}5\right]}{dt}=-k_{39}\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Whi}5\right]-k_{40}\left[\mathrm{Cln}3\right]\left[\text{Whi}5\right]+k_{41}\left[\text{Whi}5\text{P}\right].$$ (A33)

$$\frac{d\left[\text{Whi}5\text{P}\right]}{dt}=k_{39}\left[\frac{\mathrm{Cln1}}{2}\right]\left[\text{Whi}5\right]+k_{40}\left[\mathrm{Cln}3\right]\left[\text{Whi}5\right]-k_{41}\left[\text{Whi}5\text{P}\right].$$ (A34)

$${\left[\text{Ste}5\right]}_{\text{total}}=\sum _{i=0}^8\left(\left[{\text{Ste}5}_{ip}\right]+{\left[{\text{Ste}5}_{ip}\right]}_{\text{mem}}\right).$$ (A35)

$${\left[\text{Ste}5\right]}_{\text{mem}}={\sum _{i=0}^8\left[{\text{Ste}5}_{ip}\right]}_{\text{mem}}.$$ (A36)