Do Cells Make Decisions Based on Uncertainty in their Biochemical Networks?

New methods of data collection on yeast cells have challenged computational biologists to unravel complex system behavior within cells at different scales. In an article appearing in the Biophysical Journal, Li et al. (1) propose a novel way to analyze competing molecular pathways that determine alternative cell fates, based on classical ideas from statistical physics.

Under favorable conditions, yeast cells grow and divide rapidly by a process called budding, in which a new daughter cell buds off the parent cell. Most new growth goes into the bud, as the mother cell replicates its chromosomes and extrudes a new nucleus into the bud. When this process of DNA synthesis and nuclear division is complete, the bud separates from the mother cell and begins its own separate existence. This series of events that makes one cell into two is called the “cell cycle”. Haploid yeast cells (having only one set of chromosomes), which can grow and divide in this fashion (mitotic cell cycles), have an alternative fate, which is to arrest cell-cycle progression and undergo sexual conjugation with a mating partner. Cell-cycle progression and mating arrest in yeast have been studied extensively during the last few decades by molecular genetics and computational modeling (2–7), making yeast cells an appealing case study of molecular mechanisms of cell-fate determination. Despite being a relatively simple system, yeast cells can help us to unravel the complex decision-making processes that control cell proliferation and differentiation in multicellular organisms and that break down in cancer cells (8,9).

Experimental studies have shown that yeast cells are responsive to mating pheromones only before a certain point in the cell cycle, called “start” (3,4). After passing start, cells are refractory to mating pheromones and are committed to asexual (mitotic) reproduction. Thus, start is a crucial transition point for fate determination in yeast. Computational analysis of cell-cycle and mating pathways by Li et al. (1) has revealed an interesting result. They found that the entropy of the reaction network reaches a peak at start. Inspired by Shannon (10), Li et al. (1) define the entropy of a biochemical reaction network as

$$E=-\sum _i^n{P}_i\text{ln}\left(P_i\right),$$

where

$$P_i=\frac{x_i}{\sum _j^n{x}_j{x}_i},$$

in which x_i is the concentration of ith species in the network, and n is the total number of species in the model. This formula has an easily provable property that E is a maximum when all P_i are equal.

It’s interesting, then, to ask if the fact that E reaches a maximum at start agrees with other findings related to the start transition. Both experimental studies (6,7) and computational modeling (1) show that the concentration difference between two groups of proteins correlates with cell-fate selection. In response to pheromones, yeast cells that are just beginning the cell cycle (i.e., before start) synthesize more mating-related proteins and suppress cell cycle-related proteins. Yeast cells that have already passed start are insensitive to pheromones and synthesize more cell cycle-related proteins, suppressing the synthesis of mating-related proteins. Therefore, at the transition point there is no bias in the concentrations of either group of proteins (cell cycle-related or mating-related), and thus E will be closed to its maximum value. In this sense, indeed, at the start transition point, yeast cells have the largest uncertainty about whether to undergo sexual conjugation or asexual (mitotic) reproduction (Fig. 1). Might this situation in yeast be similar for other competing cell-fate pathways with a critical commitment point?

Figure 1.

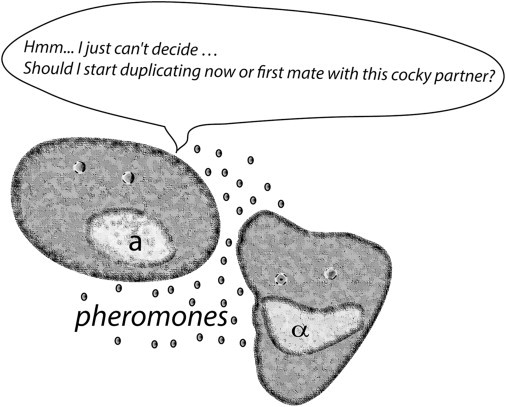
Decision-making for a yeast cell close to the start transition. Yeast cells must decide whether to commit to the cell cycle and divide, producing a genetically identical haploid cell, or to undergo sexual conjugation with a neighboring cell of different mating type. The decision is made based on internal cell stage and the presence of pheromones secreted by the potential mate. When internal phase is close to the start point, decision-making for the cell may not be an obvious task.

In the future, we may expect to see this entropy concept applied to other cell-fate decisions. If entropy turns out to be the locomotive driving cellular decisions, then perhaps we can say that love has its roots not only in biochemistry but also in physics.