Parameterizing the Logistic Model of Tumor Growth by DW-MRI and DCE-MRI Data to Predict Treatment Response and Changes in Breast Cancer Cellularity during Neoadjuvant Chemotherapy

Abstract

Diffusion-weighted and dynamic contrast-enhanced magnetic resonance imaging (MRI) data of 28 patients were obtained pretreatment, after one cycle, and after completion of all cycles of neoadjuvant chemotherapy (NAC). For each patient at each time point, the tumor cell number was estimated using the apparent diffusion coefficient and the extravascular extracellular (v_e) and plasma volume (v_p) fractions. The proliferation/death rate was obtained using the number of tumor cells from the first two time points in conjunction with the logistic model of tumor growth, which was then used to predict tumor cellularity at the conclusion of NAC. The Pearson correlation coefficient between the predicted and the experimental number of tumor cells measured at the end of NAC was 0.81 (P = .0043). The proliferation rate estimated after the first cycle of therapy was able to separate patients who went on to achieve pathologic complete response from those who did not (P = .021) with a sensitivity and specificity of 82.4% and 72.7%, respectively. These data provide preliminary results indicating that incorporating readily available quantitative MRI data into a simple model of tumor growth can lead to potentially clinically relevant information for predicting an individual patient's response to NAC.

Introduction

Neoadjuvant chemotherapy (NAC) is increasingly used in women with locally advanced breast cancer because it can allow downstaging of cancers to render them operable and/or to facilitate breast conservation surgeries [1,2]. Furthermore, early assessment of clinical response to NAC may provide clinicians with the ability to identify patients that are not responding to their current therapy, thereby allowing the ability to explore alternative therapies that could prove to be more effective.

Mathematical models of tumor growth and treatment response have the potential to predict the status of a tumor at a later time point [3–5], but most models require invasive parameters that are extraordinarily difficult to measure for individual patients. This has led to the limited application of mathematical models in clinical care and clinical trials. One way to potentially overcome this limitation is through the use of noninvasive quantitative imaging data to initialize and constrain mathematical models. Since imaging data are specific to each patient and can be obtained at multiple times during the course of therapy, predictions from models incorporating imaging data will be patient specific and can also be readily compared to data obtained at a later time point. In this way, mathematical models initialized by imaging data generate patient-specific hypotheses that can be experimentally tested. Here, we focus on using measurements made with diffusion-weighted magnetic resonance imaging (DW-MRI) and dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) to provide estimates of tumor cellularity to initialize the logistic model of tumor growth.

DW-MRI provides a noninvasive measurement of the degree of random motion of water in tissue. The rate of this diffusion is quantified by the apparent diffusion coefficient (ADC) and largely depends on the presence of barriers to water diffusion within the tissue micro-environment. In well-controlled settings, it has been shown that the ADC inversely correlates with tissue cellularity [6–11]. ADC changes have also been reported after chemotherapy; in particular, several clinical studies in patients with breast cancer have shown an increase in the mean ADC values after NAC [12–15].

DCE-MRI involves the injection of a paramagnetic contrast agent (CA) that can lead to variation of the MR signal intensity with time. By using appropriate pharmacokinetic models, microvascular physiological parameters related to blood flow, vessel permeability, and tissue volume fractions can be extracted from the signal intensity time curves [16]. DCE-MRI changes have also been reported after chemotherapy; in particular, several clinical studies in patients with breast cancer undergoing NAC have shown changes in DCE-MRI after treatment [17–20].

Historically, mathematical models of tumor growth do not include noninvasive parameters obtained from imaging. More recently, however, there have been a number of exciting efforts on this front. For example, Ellingson et al. [21] used ADC data and Szeto et al. [22] used serial gadolinium-enhanced T₁- and T₂-weighted MR images of patients with glioblastoma combined with a reaction-diffusion equation to estimate the proliferation and tumor cell diffusion rates. Konukoglu et al. [23] used diffusion tensor imaging data and T₁- or T₂-weighted MR images in conjunction with the reaction-diffusion equation to estimated the rate of diffusion of tumor cells. These studies, however, do not make explicit use of the biophysical relationships between cellular variations and the ADC values and also the volume fractions that can be obtained from DCE-MRI measurements.

In a previous study of treatment in the 9L rat model of brain cancer, we used serial DW-MRI data obtained before and 1 day after treatment with bis-chloroethylnitrosourea (BCNU; Carmustine) to estimate tumor proliferation rates and cellularity [24]. The prediction of the number of tumor cells 3 days after treatment compared favorably to those measured from experimental imaging data. We were also able to observe a statistically significant difference in the proliferation rates in the treated and control rats after 1 day of treatment. We also reported preliminary results in breast cancer patients undergoing NAC, in which the DW-MRIs for the patients were obtained before, after one cycle, and after completion of NAC [25]. We predicted the number of tumor cells at the conclusion of chemotherapy and compared this to experimental imaging data. The prediction of the number of tumor cells at the end of therapy compared favorably to those measured from experimental imaging data.

In this contribution, we show preliminary results indicating how serial DW- and DCE-MRI data can be used to estimate tumor cellularity and how changes in cellularity observed after one cycle of NAC can allow for an estimate of the tumor proliferation rate. The proliferation rate is then used to predict the tumor cellularity at the conclusion of therapy and is compared to the observed MRI data. Lastly, the proliferation rate is used to separate patients who will achieve pathologic complete response (pCR) from those who will not.

Materials and Methods

Patient Population

DW- and DCE-MRI were acquired from 28 patients with stage II/III breast cancer. The patients provided informed consent, and the study was approved by our Institutional Review Board. Patient age, treatment regimen, receptor status, tumor size, and grade are summarized in Table 1. The patients received 8 to 16 cycles of NAC, which was administered weekly, biweekly, or every 3 weeks depending on the particular regimen. DW- and DCE-MRI of the patients were obtained before any treatment (t₁), after one cycle (t₂), and at the completion (t₃) of NAC. Only 22 DW- and DCE-MRI data sets were available at t₃. At the conclusion of NAC, the patients underwent surgery and pathologic response was determined. The patients were separated into two groups based on the surgical pathologic data: those with no residual invasive cancer in the breast or lymph nodes were classified as achieving pCR (n = 11) and those with any residual disease in either the breast or lymph nodes were classified as nonresponders (NR; n = 17). Of the 17 NR patients, eight were not included in the correlation with experimental imaging data at t₃ due to the following reasons: no DW-MRI coverage of tumor (n = 2), patients did not return for imaging (n =3), problem with the contrast line (n = 1), no enhancing voxels found in DCE-MRI data (n = 1), and no residual breast tumor (disease in lymph nodes; n =1).

Table 1.

Summary of the Patient Data.

Patient	Age (years)	Treatment Regimens	Receptor Status (ER, PR, HER2)	Size Pretreatment (cm)	Tumor Grade	Residual Tumor Size (cm)	Clinical Response
1	50	AC→taxol	+, +, -	10	3	0.52	NR
2	52	Taxotere	+, -, +	5	3	1.5	NR
3	60	AC→taxol + concurrent trastuzumab	+, +, +	5	2	2.9	NR
4	36	Taxol + cisplatin ± everolimus	-, -, -	7	2	2.9	NR
5	48	Dose-dense AC→taxol	+, +, -	3	1	1.3	NR
6	43	Dose-dense AC→taxol	+, +, -	6	2	2.6	NR
7	59	Dose-dense AC→taxol	+, +, -	7	2	4.2	NR
8	53	Taxol + cisplatin ± everolimus	-, -, -	3.5	2	1.3	NR
9	35	Trastuzumab + carboplatin + ixabepilone	+, +, +	4	3	1.4	NR
10	28	Taxol + cisplatin ± everolimus	-, -, -	2	3	0.8	NR
11	33	AC→taxol	+, +, -	5	3	1.2	NR
12	39	AC→taxol	+, +, -	10	1	2.5	NR
13	57	AC→taxol	-, +, +	5.5	3	n/a	NR
14	67	Dose-dense AC→taxol	-, +, +	8	3	1.2	NR
15	45	Taxol + cisplatin ± everolimus	-, -, -	3	3	0.5	NR
16	46	Taxotere + carboplatin + herceptin	+, +, +	7	3	0.3	NR
17	47	Taxotere→AC	+, +, -	6	1	0	NR*
18	53	AC→concurrent taxol + trastuzumab	-, -, +	4	3	0	pCR
19	46	Taxotere→AC	-,+, -	5	3	0	pCR
20	46	AC→concurrent taxol + trastuzumab	-, -, +	12	2	0	pCR
21	33	AC→weekly taxol	-, -, -	10	3	0	pCR
22	39	Trastuzumab and lapatinib	-, -, +	3.5	2	0	pCR
23	46	AC→taxol	+, -, -	2	3	0	pCR
24	42	Taxol + cisplatin ± everolimus	-, -, -	3	3	0	pCR
25	34	Taxotere→AC	-, -, -	3	3	0	pCR
26	44	Trastuzumab + lapatinib	-, -, +	6	3	0	pCR
27	37	Taxol + cisplatin ± everolimus	-, -, -	4.5	3	0	pCR
28	39	AC→taxol	-, -, -	2.5	3	0	pCR

ER indicates estrogen receptor; PR, progesterone receptor; HER2, human epidermal growth factor receptor 2.

^*Tumor found in lymph nodes.

Imaging Protocol

DW- and DCE-MRI were performed using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands) equipped with either a 4- or 16-channel receive double-breast coil (Invivo Inc, Gainesville, FL).

DW-MRIs were acquired with a single-shot spin echo echo planar imaging sequence in three orthogonal diffusion encoding directions (x, y, and z), with two b values [0 and 500 s/mm² for 12 patients (pCR = 6; NR = 6), 0 and 600 s/mm² for 14 patients (pCR = 5; NR = 9), and 50 and 600 s/mm² for 2 patients (NR = 2)], repetition time/echo time (TR/TE) = 3080 ms/43 ms, Δ = 20.7 milliseconds, δ = 11.6 milliseconds, and number of signal acquisitions = 10 for a total scan time of 4 minutes and 40 seconds [signal-to-noise ratio (SNR) in diffusion weighted imaging (DWI) is typically low, relative to standard anatomic sequences, and thus, we acquired multiple measurements to increase the SNR]. The acquisition employed a sensitivity encoding (SENSE) factor of 2 with a 96 x 96 x 12 matrix over a field of view (FOV) of (19.2 cm)² reconstructed to 144 x 144 with a slice thickness of 5 mm with a resulting voxel size of 1.333 x 1.333 x 5 mm³. A spectrally selective adiabatic inversion recovery fat saturation was implemented to reduce image artifacts. DCE-MRI data were acquired with a three-dimensional radio frequency (RF)-spoiled gradient echo sequence with TR/TE/α = 7.9 ms/1.3 ms/20°. The acquisition matrix employed a SENSE factor of 2 with a 192 x 192 x 20 matrix over an FOV of (25.6 cm)², a slice thickness of 5 mm resulting in a voxel size of 1.333 x 1.333 x 5 mm³. Data for the T₁ map were acquired with 10 flip angles from 2° to 20° in 2° increments. The same protocol (with the flip angle fixed at 20°) was used for the dynamic study in which each 20-slice set was collected in 16 seconds at 25 time points. A catheter placed within an antecubital vein delivered 0.1 mmol/kg gadolinium-diethylenetriamine pentaacetic acid (Magnevist; Berlex, Wayne, NJ) at a rate of 2 ml/s (followed by a saline flush) through a power injector after the acquisition of the first three dynamic scans.

The diffusion, T₁, and dynamic image volumes were all acquired with the same center location and with minimal patient motion, thereby making them inherently co-registered.

DW-MRI Analysis

ADC maps were calculated from the DW-MRI data using the following equation:

$$\text{ADC = }\frac{{\displaystyle \sum \text{ ln(}{S}_0/S_i)/b_i}}{3},$$ (1)

where i is the diffusion-weighting direction, b_i is the amount of diffusion-weighting imparted to the sample, S_i and S₀ are the measured signal in each voxel [26]. Voxels with negative ADC values were not used for the analysis.

DCE-MRI Analysis

DCE-MRI data were analyzed by the fast exchange limit formalism [27,28] in which the longitudinal relaxation rate constant, R₁, is assumed to be linearly proportional to the concentration of CA in the tissue, C_t(t). To compute C_t(t), we used the extended Tofts-Kety (ETK) relationship which includes the blood plasma fraction, v_p [29], shown in the following equation:

$$C_{\text{t}}(T)=K^{\text{trans}}{\displaystyle \underset{0}{\overset{T}{\int }}{C}_p(t)\text{exp}(-(K^{\text{trans}}/v_e)(T-t))dt+v_{\text{p}}{C}_{\text{p}}(t),}$$ (2)

where K^trans is the volume transfer constant, v_e is the extravascular extracellular volume fraction, and C_p(t) is the concentration of CA in blood plasma [i.e., the arterial input function (AIF)]. We used a population average AIF that resulted from the averaging of 50 different individual AIFs obtained from scans of patients with breast cancer [30].

Tumor ROI Selection

Region of interests (ROIs) were manually drawn on multiple slices to cover the entire visible tumor as seen at each imaging time point. The voxels within the outlined ROI that showed a postcontrast signal (S_post) intensity ≥80% of the precontrast signal intensity (S_pre) were considered the tumor voxels. This was calculated as follows:

$$\text{Enh = 100 }\cdot \left(\frac{S_{\text{post}}-S_{\text{pre}}}{S_{\text{post}}}\right).$$ (3)

Eighty percent was selected as it is the enhancement threshold that resulted in the greatest agreement between tumor size as measured by MRI at t₃ and the size of the pathology tumor specimen [Pearson and concordance correlation coefficient were 0.84 (P < 10^-6) and 0.74, respectively; data not shown]. Thus, it is reasonable criteria to select voxels for further analyses.

Every voxel in the tumor ROI was fit by the ETK model to return estimates of v_e and v_p. (It is important to note that, in the analyses below, we do not explicitly use the K_trans results.) Voxels that did not converge, converged to unphysical values (v_e or v_p less than 0 or greater than 1), or where the sum of v_e and v_p was greater than 1 were not used for subsequent analysis. Since the DW- and DCE-MRI data were inherently co-registered, the tumor ROIs were drawn very conservatively to encompass all enhancing voxels on the DCE-MRI data and was then transferred to the DW-MRI data. We also visually inspected the registration between the DW- and DCE-MRI data to ensure that they were registered to each other as we expected. The median ADC, v_e, and v_p in the tumor ROI were then calculated for all the patients at all time points and used for the modeling.

Estimation of the Tumor Cells

As several studies have shown a strong negative correlation between ADC and cellularity [6–10], we used Equation 4 to convert ADC values to tumor cell number.

$$N(t)=\text{θ}\left(\frac{{\text{ADC}}_{\text{w}}-\text{ADC(}t)}{{\text{ADC}}_{\text{w}}-{\text{ADC}}_{\text{min}}}\right)v_{\text{TC}}(t).$$ (4)

To calculate the number of tumor cells N(t), we assumed that the voxel with the minimum ADC (ADC_min) will contain the maximum number of cells that can fit into that voxel (i.e., the carrying capacity, θ) [24,25]. Voxels with the ADC of free water (ADC_w = 3 x 10^-3 mm²/s [31]) are taken to have zero tumor cells [24,25].

To calculate θ, we assumed spherical tumor cells with a sphere packing density of 0.7405 [32]. We assumed a nominal tumor cell radius of 10 µm to arrive at a tumor cell volume of 4189 µm²; from this value, and the voxel volume, the tumor cell number can be determined for a given voxel. We then computed the volume of voxel that can be occupied by tumor cells v_TC in two ways: 1) assume the entire voxel was made of tumor cells and 2) incorporate both v_e and v_p from the ETK model into the calculation. The following equation summarizes this approach:

$$v_{\text{TC}}(t)=\{\begin{array}{ll}1\hfill & \text{assume }{v}_{\text{e}}=v_{\text{p}}=0\hfill \\ 1-v_{\text{e}}(t)-v_{\text{p}}(t)\hfill & v_{\text{e}}(t)\text{ and }{v}_{\text{p}}(t)\text{ from the ETK model}\hfill \end{array}$$ (5)

We converted the median ADC in the tumor ROI using Equations 4 and 5 to estimate the median number of tumor cells, N_estimated(t) (from the first relation in Equation 5), and N_{estimated_ETK}(t) (from the second) for all three time points. ADC_min was assigned as the median of the minimum ADC values measured in the tumor ROI at t₁ and t₂ for all the patients.

Logistic Growth Model

The logistic growth model [33] starts out as an exponential growth model but then asymptotically approaches the limiting cellular carrying capacity at later time points:

$$N(t)=\frac{\text{θ}N(t_1)}{N(t_1)+(\text{θ}-N(t_1)){\text{e}}^{-\text{k}t}},$$ (6)

where N(t) is the number of tumor cells at time t, N(t₁) is the initial number of tumor cells, and k is the proliferation rate.

Estimation of Proliferation Rate

We used N_estimated(t) and N_{estimated_ETK}(t) at t₁ and t₂ in conjunction with the logistic model to calculate the proliferation rates (in units of l/day) k and k_ETK, respectively. Note that the proliferation rate can either have a positive value to indicate tumor cell proliferation or a negative value to indicate tumor cell death.

Predicting Cellularity

We used the logistic model of tumor growth to predict the number of tumor cells at the end of NAC for the nine NR patients in which we were able to obtain DW- and DCE-MRI at all three time points. We used the estimated number of tumor cells at t₂ and the proliferation rate in conjunction with Equation 6 to simulate the number of tumor cells at t₃. As the treatment was given in cycles, the logistic model was run in a pulsed fashion. The model was switched “on” for the day of treatment and switched “off” for nontreatment days [31]. At every iteration of the model, which corresponds to a cycle of chemotherapy, a new number of cells for the end of that particular cycle was calculated and used as the initial number of cells for the next cycle [25]. We assumed that the tumor cells proliferated according to the calculated proliferation rate only on the treatment days. We repeated this iteration of the model until the number of cells at the end of all cycles of treatment was calculated. This calculation was performed for each of the two different sets of tumor cell numbers (N_estimated(t) and N_{estimated_ETK}(t)) and proliferation rates (k and k_ETK) to yield N_simulated(t₃) and N_{simulated_ETK}(t₃), respectively.

Statistical Analysis

Three statistical analyses were performed. First, the proliferation rate was used to separate pCR and NR patients using a Wilcoxon test. Second, we calculated the sensitivity, specificity, positive predictive value (PPV), negative predictive value, (NPV) and area under the receiver operating characteristic (ROC) curve of k and k_ETK. To do the calculation, we chose a range of cutoff points; patients with values less than or equal to the cutoff point were classified as achieving pCR, while patients with values greater than the cutoff point were classified as NR patients. The optimal cutoff point was selected on the basis of yielding the largest sum of the sensitivity and specificity values. Lastly, the estimated and the simulated number of tumor cells at t₃ were compared to each other using the Pearson and concordance correlation coefficients.

Results

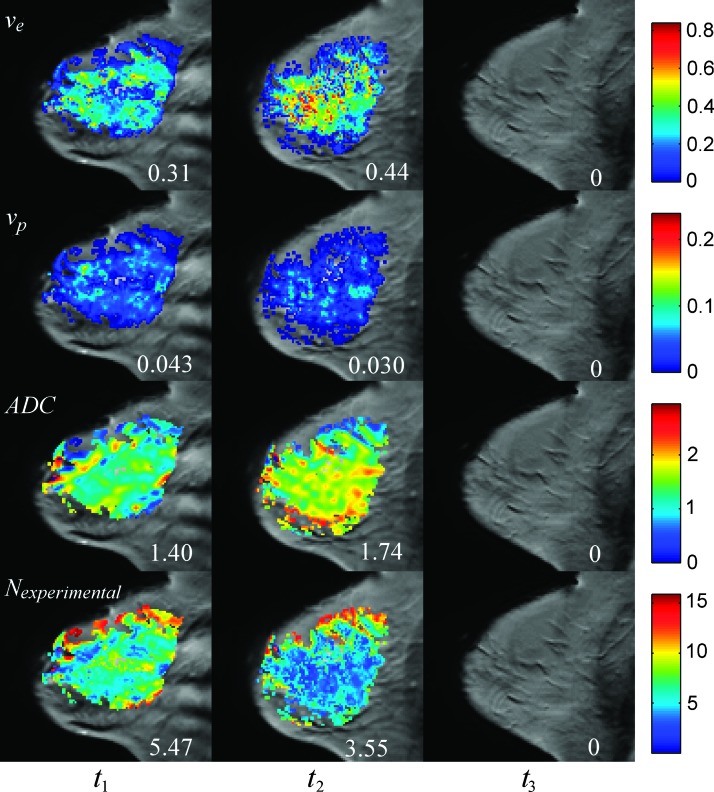
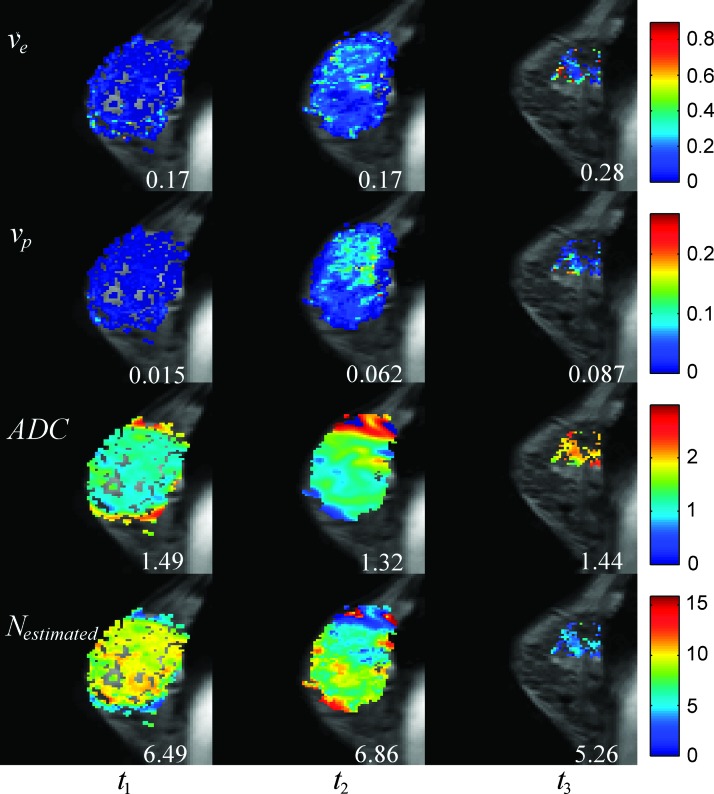
Figures 1 and 2 display representative maps of the parameters used for the modeling overlain on sagittal, T₁-weighted anatomic scans of patients achieving pCR and NR, respectively. Figures 1, panels A to D, and 2, panels A to D, correspond to the v_e, v_p, ADC, and N (t) (computed using the bottom relation in Equation 5) maps, respectively. For the patient achieving pCR in Figure 1, the median v_e for the whole tumor increased from 0.31 to 0.44 from t₁ to t₂, the median v_p decreased from 0.043 to 0.030, the median ADC increased from 1.40 x 10^-3 mm²/s to 1.74 x 10^-3 mm²/s, and the median number of tumor cells decreased from 5.47 x 10⁵ to 3.55 x 10⁵. (Note, as this patient achieved pCR, there was no tumor present at t₃, and thus, there were no parameters calculated for the tumor at that time point.) For the patient achieving NR in Figure 2, the median v_e for the whole tumor remained the same at 0.17 at t₁ and t₂ and increased to 0.28 in t₃. The median v_p increased from 0.015 to 0.062 from t₁ to t₂ and increased to 0.087 at t₃, while the median ADC decreased from 1.49 x10^-3 mm²/s to 1.32 x 10^-3 mm²/s from t₁ to t₂ and increased to 1.44 x 10^-3 mm²/s at t₃. These data were used to find that the median number of tumor cells increased from 6.49 x 10⁵ to 6.86 x 10⁵ from t₁ to t₂ and then decreased to 5.26 x 10⁵ in t₃.

Figure 1.

Parametric maps overlain on sagittal, T₁-weighted anatomic scans for a pCR patient at each time point (one time point per column). The first row shows the v_e obtained before therapy (t₁), after one cycle of therapy (t₂), and at the conclusion of therapy (t₃). Similarly, the second row shows the v_p, the third row shows the ADC maps (x10^-3 mm²/s), and the last row shows the number of tumor cells (calculated using the bottom relation in Equation 5) in each voxel (x10⁵) at these same time points. The numbers in each column represent the median values of each parameter.

Figure 2.

Data for an NR patient that is analogous to the Figure 1 data for a pCR patient. The first row shows the v_e obtained before therapy (t₁), after one cycle of therapy (t₂), and at the conclusion of therapy (t₃). Similarly, the second row shows the v_p, the third row shows the ADC maps (x10^-3 mm²/s), and the last row shows the number of tumor cells (calculated using the bottom relation in Equation 5) in each voxel (x10⁵) at these same time points. The numbers in each column represent the median values of each parameter.

The proliferation rate calculated using the number of tumor cells from pretreatment to after one cycle of chemotherapy was used to separate patients achieving pCR or NR. Figure 3 shows the median k and k_ETK for pCR and NR patients. The 95% confidence intervals are shown as error bars. The median k and k_ETK (-0.0103 and -0.0189, respectively) are negative for patients achieving pCR and very close to zero (-0.0001 and -0.0004, respectively) for NR patients. There was a statistically significant difference (P = .021) between the two groups when k_ETK was used; however, there was no statistically significant difference (P = .22) when k was used.

Figure 3.

The median k and k_ETK for NR and responding patients. (The 95% confidence intervals are shown as error bars.) No DCE corresponds to calculations that employed only the ADC data (i.e., the top relation in Equation 5 was used), while the ETK corresponds to calculations in which the ADC, v_e, and v_p data from the ETK model were used (i.e., the bottom relation in Equation 5). The asterisk denotes a significant (P < .05) difference between patient groups.

The sensitivity was high (88.2%), PPV and NPV were moderately high (71.4%), and the specificity was low (45.5%) when k was used to classify NR patients. When the v_e and v_p data were incorporated into the model and used for the calculation of k_ETK and the classification of NR patients, the sensitivity was decreased modestly (82.4%), but the specificity, PPV, and NPV were all substantially higher (72.7%, 82.4%, and 72.7%). The area under the ROC curve also increased from 0.63 to 0.76 when k_ETK was used to classify NR patients. These data are summarized in Table 2.

Table 2.

Diagnostic Performance of Detecting pCR and NR Patients.

	k	kETK
Sensitivity	88.2%	82.4%
Specificity	45.5%	72.7%
PPV	71.4%	82.4%
NPV	71.4%	72.7%
Area under the ROC curve	0.63	0.76

Table 3 shows the correlation coefficients between the estimated and simulated number of tumor cells at t₃. There was a strong and significant Pearson correlation coefficient (r = 0.92, P = .0004) as well as a strong concordance correlation coefficient (0.74) between the estimated and the simulated number of tumor cells as calculated without the use of the v_e and v_p data. When the v_e and v_p data were used to refine the estimates of N (t), the Pearson correlation coefficient remained strong, though reduced (r = 0.81, P = .0043), while the concordance correlation coefficient increased to 0.81.

Table 3.

Correlation between the Number of Tumor Cells at the End of Therapy.

	No DCE	ETK
Pearson	0.92 (P = .0004)	0.81 (P = .0043)
Concordance	0.74	0.81

Figure 4, A and B, displays the plots of the estimated and the simulated number of tumor cells at t₃ with the 95% confidence interval shown as dotted lines. Figure 4A was calculated without the v_e or v_p data, while Figure 4B incorporates both v_e and v_p data using the ETK model. Note that the incorporation of the v_e and v_p data into the calculation of N (t) results in better agreement with the line of unity.

Figure 4.

Panels A and B are the experimentally estimated number of tumor cells (x10⁵) plotted versus the simulated number of tumor cells (x10⁵) at the conclusion of therapy. The 95% confidence intervals are displayed as dotted lines. Panel A was calculated without the addition of DCE data (i.e., the top relation in Equation 5), and panel B has DCE data incorporated using the ETK model (i.e., the bottom relation in Equation 5).

Discussion

We have presented a methodology for incorporating early DW- and DCE-MRI data into a simple mathematical model of tumor growth to predict the tumor cellularity and treatment response at the conclusion of NAC. We used DW- and DCE-MRI data obtained before and after one cycle of NAC to estimate both the number of tumor cells and their associated proliferation rate. These data were then used to predict the number of tumor cells at the conclusion of NAC. Because the data used to drive the model are obtained noninvasively, the model's prediction could be directly compared to the number of tumor cells estimated from imaging obtained at the conclusion of therapy. We also used the proliferation rate to separate patients who will respond to treatment from those who will not.

The number of tumor cells before treatment and after one cycle of treatment was calculated for each patient. In general, patients achieving pCR had a decrease in the number of tumor cells after one cycle of NAC, while NR patients had an increase or a very minimal decrease in the number of tumor cells after one cycle of NAC. This was shown by the negative median proliferation rate for pCR after one cycle of NAC. Conversely, a very minimally (i.e., very close to zero) median negative proliferation rate was found for NR patients.

The proliferation rate was able to separate patients that are pCR from NR and was also able to identify NR patients with a moderate to high sensitivity, specificity, and PPV. In addition, the specificity and PPV were highest when the volume fractions obtained from the DCE-MRI data were included in the model.

We observed a strong and significant Pearson correlation and a strong concordance correlation between the estimated and the simulated number of tumor cells at the conclusion of NAC. The strong concordance correlation observed indicates that there is a strong agreement along the line of unity between the simulated and the estimated number of tumor cells. Although the Pearson correlation decreased slightly, the concordance correlation increased as the imaging data on tumor volume fractions (i.e., v_e and v_p from the ETK model) was included. While this may seem counterintuitive, recall that the Pearson correlation coefficient is a measure of precision, while the concordance correlation coefficient is a measure of accuracy. Thus, it is quite plausible that incorporating v_e and v_p into the estimation of tumor cell number can increase the accuracy at the cost of precision.

It is important to note that the 1) ability to separate patient groups, 2) prediction of the tumor cell number at the conclusion of therapy, and 3) the concordance correlations between the simulated and the experimental number of tumor cells all improved when v_e and v_p data were all incorporated into the model. This provides some intriguing evidence that integrating quantitative information about tumor properties may provide more robust and accurate information about tumor response and, consequently, increase our predictive ability.

There are a number of important theoretical and experimental limitations in the present effort. One obviously incorrect assumption is that we assumed that all cells within a voxel are tumor cells, thereby ignoring the normal epithelium, stroma, and scattered inflammatory cells in that voxel. This assumption may lead to an overestimation of the number of tumor cells in the voxel; a method that can be used to separate the tumor cells from the other cell types that may be present will reduce this limitation. We also assumed that the change in ADC from the first two time points was entirely due to the reduction in cellularity and that this proliferation rate remains constant throughout the course of treatment. These simplifying assumptions about the proliferation rate may lead to an incorrect prediction of the number of tumor cells at the conclusion of NAC. Another limitation of the model is that it does not explicitly account for therapies that are initially cytostatic (e.g., targeted therapies aimed at disrupting particular pathways in particular tumor subtypes) and is more well suited to therapies that are cytotoxic. Thus, the approach outlined in this manuscript will tend to underestimate the efficacy of cytostatic treatments.

Concerning experimental limitations, we assumed that the regions of tissue showing enhancement in the DCE-MRI data are the only tissue voxels that contain viable tumor cells. This can lead to errors in the calculation of both the number and spatial distribution of tumor cells and, therefore, the calculated proliferation rate. Another limitation is the use of the same model for a heterogeneous patient population receiving different treatment regimens. This heterogeneous population was selected due to practical limitations encountered during most clinical trials, that is, we do not currently have enough patients within any one particular subgroup to perform meaningful statistics on a homogeneous subpopulation. As our patient database increases, we will try to focus on patients with a particular tumor subtype with a more homogenous treatment approach that, we hypothesize, will yield more convincing results. However, the fact that the correlations are still quite strong speaks to the potential power of the approach.

The prediction of cellularity and the separation of the responding and non-responding patients can be further improved by improving the DW-MRI acquisition. This can be accomplished by using a higher minimum b value because the minimum b values of 0 to 50 s/mm² employed in this study are particularly sensitive to perfusion and can possibly lead to the overestimation of ADC that will, in turn, lead to an underestimation of the tumor cell number and an error in the calculation of the proliferation rate. In addition, the use of more than two b values can potentially improve the ADC estimation as there would be more points to fit to Equation 1, thereby increasing the accuracy of the predictive model. We used only two b values because the data used for this study are part of a larger study that includes the acquisition of many MR data types within a limited 30-minute scan session. Additionally, the low resolution of the DW-MRI data can smooth out the estimation of cell number due to the partial volume effect and this can lead to the incorrect estimation of the proliferation rate.

Another possible source of experimental error is related to the temporal resolution (16 seconds) for the DCE-MRI data, which is not optimal for pharmacokinetic analysis; rather, it represents a compromise between the need to image the entire affected breast (requiring a large field of view and reasonable spatial resolution) and the need to image quickly to characterize kinetics. Unfortunately, in extreme cases, this temporal resolution can lead to errors in the estimation of v_e and v_p [34] and, subsequently, incorrect estimation of the number of tumor cells and the proliferation rate. However, it is important to note that some investigators have used temporal resolutions that are not very different from the one employed in this study [19,35,36]. Thus, while the temporal resolution we used is not optimal for kinetic modeling, it represents a (common) practical implementation that might be available from a clinical trial.

In addition to addressing the experimental and theoretical limitations described above, ongoing work is focused on expanding the model to account for tumor-associated vascularity (from DCE-MRI data) and glucose metabolism (from fluorodeoxyglucose positron emission tomography data). We hypothesize that incorporating such data, which would provide a complete description of tumor characteristics, will improve the overall predictive ability of the approach.

Conclusion

ADC, v_e, and v_p data obtained before treatment and after one cycle of chemotherapy can be used to estimate the number of tumor cells and, if validated in a larger patient set, can potentially be used to predict treatment response at the end of chemotherapy. This has the benefit of determining the efficacy of chemotherapy regimen as early as after a single cycle. Knowledge that a particular chemotherapy regimen will ultimately not yield clinical benefit after just one cycle of therapy could prevent a patient from receiving months of toxic and ineffective treatment. To the best of our knowledge, this is the first example of a mathematical model of tumor growth populated by imaging data to predict patient outcome early in the course of NAC.