Comparison of xMAP and ELISA assays for detecting CSF biomarkers of Alzheimer's Disease

Abstract

The best-studied biomarkers of Alzheimer’s disease (AD) are the pathologically linked CSF proteins β-amyloid 42 (Aβ_1–42), total tau (t-tau), and tau phosphorylated on amino acid 181 (p-tau₁₈₁). Many laboratories measure these proteins using Enzyme-Linked ImmunoSorbent Assay (ELISA). Multiplex xMAP Luminex is a semi-automated assay platform with reduced intra-sample variance, which could facilitate its use in CLIA-approved clinical laboratories. CSF concentrations of these three biomarkers reported using xMAP technology differ from those measured by the most commonly used ELISA, confounding attempts to compare results. To develop a model for converting between xMAP and ELISA levels of the three biomarkers, we analyzed CSF samples from 140 subjects (59 AD, 30 controls, 34 with mild cognitive impairment (MCI), and 17 with Parkinson Disease, including 1 with dementia). Log-transformation of ELISA and xMAP levels made the variance constant in all three biomarkers and improved the linear regression: t-tau concentrations were highly correlated (r=0.94); p-tau₁₈₁ concentrations by ELISA can be better predicted using both the t-tau and p-tau₁₈₁ xMAP values (r=0.96) as compared to p-tau₁₈₁ concentrations alone (r=0.82); correlation of Aβ_1–42 concentrations was relatively weaker but still high (r=0.77). Among all six protein/assay combinations, xMAP Aβ_1–42 had the best accuracy for diagnostic classification (88%) between AD and control subjects. In conclusion, our study demonstrates that multiplex xMAP is an appropriate assay platform providing results that can be correlated with research-based ELISA values, facilitating the incorporation of this diagnostic biomarker into routine clinical practice.

Introduction

Late-life dementia is widely recognized as an increasingly urgent worldwide public and personal health problem [1]. Although Alzheimer’s disease (AD) remains the most prevalent cause, there are a variety of pathological processes capable of producing progressive cognitive impairment. Each has been clinically defined by a typical constellation of signs and symptoms. However, there is considerable overlap, both in the cognitive and behavioral impairments and the age of symptom onset associated with each of the dementias such that distinguishing among them solely on clinical features can be a challenge, even for experienced physicians. With more understanding of the molecular pathology associated with AD and many other clinically defined neurodegenerative conditions, it has become possible to incorporate the identification of specific dementia associated pathology into the clinical diagnostic criteria. Currently, this process is furthest along for AD. The validity of a diagnosis based on the NINCDS-ADRDA clinical criteria established in 1984 vary between 65 and 90% and are based on using diagnostic criteria grounded in the recognition of a typical cognitive and behavioral phenotype and the exclusion of any condition other than AD that could account for the progressive late-life dementia [2]. The overlap in signs and symptoms, the co-existence of a variety of neurodegenerative and vascular pathologies, and the need to establish an accurate pathologically based diagnosis as early in the disease process as possible, have driven the need to identify the presence of disease specific pathology during the initial clinical evaluation, moving the diagnosis of AD from one excluding other causes of dementia to one that includes the direct or indirect identification of the presence of AD pathology [3].

Alterations in the CSF levels of Aβ_1–42, t-tau, and p-tau₁₈₁ in patients with progressive late-life cognitive impairment are well established as valid biomarkers associated with the presence of neurofibrillary tangles formed by hyperphosphorylated tau and neuritic plaques composed of Aβ [4][5][6][7]. Most reports on the diagnostic performance characteristics of these biomarkers used traditional ELISA methods. While this methodology is well established, it is labor intensive and associated with high intra- and inter-assay variability [8]. The development of semi-automated methods based on xMAP Luminex technology that include pre-made calibrators to reduce variability partially addresses limitations of the ELISA method. Both xMAP and ELISA use immunologically based methods to identify and quantify the concentrations of target proteins, but the values differ considerably across multiple studies, due to the lack of standard reference materials for each biomarker, and differences in a host of pre-analytical factors as well as differences in antibodies, and the lack of availability of a CSF matrix for use with the calibrators [9]. The movement to this newer, more efficient, and more reliable assay system from a research tool to clinical practice will be facilitated by the ability to compare xMAP values to ELISA values previously reported in the medical literature, and vice versa.

Several prior studies examined the correlation between ELISA and xMAP measurements levels of the three CSF peptides. Reijn et al. compared ELISA and xMAP measurements using 150 CSF samples and concluded a constant factor could not be used to convert between the two technologies accurately, although the authors focused on absolute levels and did not adjust for baseline differences in their analysis [10]. Lewczuk et al. examined a larger cohort (n=223) and found moderate correlations between ELISA and xMAP Aβ_1–42 measurements (r=0.47), and better correlations for measuring tau (r=0.96 for t-tau and r=0.87 for p-tau₁₈₁) [11]. Vanderstichele et al. found similar correlations using CSF samples from 200 subjects [12]. A related study by Fagan et al. focused on the correlation between PiB (Pittsburgh compound B) PET plaque burden and CSF Aβ_1–42, t-tau, and p-tau₁₈₁ peptide levels using a cohort of 103 subjects [13]. They reported moderate correlations between PiB plaque burden and the three CSF peptide levels, and they found no significance difference using either ELISA INNOTEST or xMAP INNO-BIA AlzBio3 measurements. In summary, the four studies reported consistent findings that the three CSF peptide levels measured between xMAP and ELISA are correlated after adjusting for baseline differences.

In this study, we took one step further and focused on how one can interconvert between xMAP and ELISA measurements for the three CSF peptides. We analyzed CSF samples from 140 subjects and examined how to improve the conversion by incorporating log-level transformation and using all three peptides simultaneously.

Materials and Methods

Subjects were participants in a longitudinal study of biomarkers of late-life dementia known as the Center of Excellence for Research on Neurodegenerative Disease (CERND). Written informed consent was obtained using a process approved by the University of Pennsylvania Institutional Review Board. All participants were ≥ 55 years old and met standard clinical criteria for probable AD [2], MCI [14], Parkinson’s disease (PD) [15], or were control subjects with normal cognitive performance [16][17]. Table 1 contains the demographic and clinical characteristics of the study cohort.

Table 1.

	AD	MCI	PD	Control
Number	59	34	17	30
Age*	75±9 yrs	71±8 yrs	71±7 yrs	71±10 yrs
% male	41%	44%	81%	40%
Years symptoms prior to LP*	0.9±1.5y	0.7±1.4y	2.8±2.6y	-
Mini Mental State*	20.8±5.8	26.4±2.9	-	28.6±1.8

^*mean and SD. Years symptoms prior to LP is the year difference between first diagnosis and the LP date; when multiple MMSEs are performed for the same patient, we use the one closest to the first diagnosis.

Spinal fluid was usually (but not exclusively) obtained in the morning after an overnight fast by lumbar puncture using a 25 G Sprotte@ atraumatic needle, following routine clinical procedures. Samples were frozen immediately on dry ice and stored at −80°C until assayed.

ELISA and xMAP

Concentrations of Aβ_1–42, t-tau, and p-tau₁₈₁ in CSF samples were measured using both ELISA and Luminex xMAP assay protocols. All assays were done without knowledge of the subject’s clinical, demographic information, or the values obtained from the alternative assay method.

ELISA assay

CSF t-tau, p-tau₁₈₁, and Aβ_1–42 were determined using INNOTEST tTau Ag, INNOTEST PHOSPHO-TAU(181), and INNOTEST β-AMYLOID(1–42) kits following the manufacture’s assay protocol (Innogenetics Inc., Alpharetta, GA).

xMAP assay

CSF t-tau, p-tau₁₈₁, and Aβ_-42 levels were determined with the INNO-BIA AlzBio3 research-use only assay kit using the multiplex xMAP Luminex platform as described elsewhere [9].

Antibodies and detectors in ELISA and xMAP assays

The ELISA Innotest and xMAP INNO_BIA AlzBio3 immunoassays are produced by Innogenetics-Fujirebio (Ghent, Belgium). INNOTEST reagents included monoclonal capture/detection antibodies 21F12/3D6 for Aβ_1–42, AT120/HT7 and BT2 for total tau, and HT7/AT270 for ptau₁₈₁. INNO-BIA reagents included monoclonal capture/detection antibodies 4D7A3/3D6 for Aβ_1–42, AT120/HT7 for total tau, and AT270/HT7 for p-tau₁₈₁.

Data preprocessing and analysis

All analyses were done using the R software (www.r-project.org). Twenty-four subjects had multiple CSF samples collected with paired xMAP and ELISA measurements performed on separate never before thawed aliquots; for each of these subjects, the most recent CSF sample was chosen. With or without log₁₀ transformations of xMAP and ELISA values, we first ran linear regression analysis using selected combinations of xMAP Aβ_1–42, t-tau, and p-tau₁₈₁ concentration levels as independent variables to predict the corresponding ELISA Aβ_1–42, t-tau, and p-tau₁₈₁ values, then we ran the linear regression analysis using selected combinations of ELISA Aβ_1–42, t-tau, and p-tau₁₈₁ values as independent variables to predict the corresponding xMAP Aβ_1–42, t-tau, and p-tau₁₈₁ values. See Table 2 for the twenty-four combinations we analyzed. For example, model P4 and P8 represent the following regression models:

• P4: log₁₀ ELISA_i(p − tau_181p) = μ + alog₁₀ xMAP_i(t − tau) + blog₁₀ xMAP_i(p − tau_181p) + ε_i,

• P8: log₁₀ xMAP_i(p − tau_181p) = μ + alog₁₀ ELISA_i(t − tau) + blog₁₀ ELISA_i(p − tau_181p) + ε_i

where the index i includes all 140 samples, μ is the regression intercept, a and b are the regression coefficients, and ε_i is the normally-distributed regression residual. To test the robustness of our model, we computed the leave-one-out cross validation (LOOCV) coefficient of variation (COV) as follows. In the LOOCV scheme, each sample was excluded from the regression model estimation process exactly once. We then used the regression model on the data of the excluded sample, and computed the square error between the regression estimate and the actual measurement. We then computed the square root of the average of all square errors, and divided it by the mean of the actual measurements across all samples to obtain an estimate to the coefficient of variation (standard deviation divided by mean). The corresponding regression coefficients, significance, correlation, and LOOCV COV for all regression models are shown in Tables 3 and 4.

Table 2.

Summary of the twenty-four linear regression models.

Model	Dependent Variable	Independent Variable
Predicting ELISA measurements by xMAP measurements
T1	ELISA t-tau	xMAP t-tau
T2	ELISA t-tau	xMAP t-tau, xMAP p-tau181
T3	log10 ELISA t-tau	log10 xMAP t-tau
T4	log10 ELISA t-tau	log10 xMAP t-tau, log10 xMAP p-tau181
P1	ELISA p-tau181	xMAP p-tau181
P2	ELISA p-tau181	xMAP t-tau, xMAP p-tau181
P3	log10 ELISA p-tau181	log10 xMAP p-tau181
P4	log10 ELISA p-tau181	log10 xMAP t-tau, log10 xMAP p-tau181
B1	ELISA Aβ1–42	xMAP Aβ1–42
B2	ELISA Aβ1–42	xMAP Aβ1–42, xMAP t-tau, xMAP p-tau181
B3	log10 ELISA Aβ1–42	log10 xMAP Aβ1–42
B4	log10 ELISA Aβ1–42	log10 xMAP Aβ1–42, log10 xMAP t-tau, log10 xMAP p-tau181
Predicting xMAP measurements by ELISA measurements
T5	xMAP t-tau	ELISA t-tau
T6	xMAP t-tau	ELISA t-tau, ELISA p-tau181
T7	log10 xMAP t-tau	log10 ELISA t-tau
T8	log10 xMAP t-tau	log10 ELISA t-tau, log10 ELISA p-tau181
P5	xMAP p-tau181	ELISA p-tau181
P6	xMAP p-tau181	ELISA t-tau, ELISA p-tau181
P7	log10 xMAP p-tau181	log10 ELISA p-tau181
P8	log10 xMAP p-tau181	log10 ELISA t-tau, log10 ELISA p-tau181
B5	xMAP Aβ1–42	ELISA Aβ1–42
B6	xMAP Aβ1–42	ELISA Aβ1–42, ELISA t-tau, ELISA p-tau181
B7	log10 xMAP Aβ1–42	log10 ELISA Aβ1–42
B8	log10 xMAP Aβ1–42	log10 ELISA Aβ1–42, log10 ELISA t-tau, log10 ELISA p-tau181

Table 3.

Coefficients of linear regression predicting ELISA measurements by xMAP measurements.

Model	Coefficient				Significance				Cor.	LOOCV COV
	Intercept	t-tau	p-tau181	Aβ1–42	Intercept	t-tau	p-tau181	Aβ1–42
T1	−74.68	6.55	-	-	1.71e-03 **	< 2e-16 ***	-	-	0.923	0.0306
T2	−90.72	6.05	1.94	-	2.99e-04 *	<2e-16 ***	4.77e-02	-	0.926	0.0303
T3	0.75	0.99	-	-	<2e-16 ***	<2e-16 ***	-	-	0.942	0.0034
T4	0.78	0.84	0.18	-	<2e-16 ***	<2e-16 ***	2.56e-05 ***	-	0.949	0.0032
P1	29.59	-	1.54	-	1.09e-12 ***	-	<2e-16 ***	-	0.780	0.0297
P2	18.27	0.58	0.32	-	<2e-16 ***	<2e-16 ***	3.05e-06 ***	-	0.964	0.0127
P3	1.08	-	0.55	-	<2e-16 ***	-	<2e-16 ***	-	0.817	0.0056
P4	0.61	0.57	0.14	-	<2e-16 ***	<2e-16 ***	4.27e-7 ***	-	0.957	0.0028
B1	−30.70	-	-	3.62	5.52e-01	-	-	<2e-16 ***	0.749	0.0259
B2	−49.19	0.03	0.38	3.67	5.31e-01	9.32e-01	7.53e-01	<2e-16 ***	0.749	0.0261
B3	0.41	-	-	1.05	1.34e-02 *	-	-	<2e-16 ***	0.771	0.0040
B4	0.21	0.01	0.04	1.10	3.85e-01	8.57e-01	4.63e-01	<2e-16 ***	0.774	0.0040

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Table 4.

Coefficients of linear regression predicting xMAP measurements by ELISA measurements.

Model	Coefficient				Significance				Cor.	LOOCV COV
	Intercept	t-tau	p-tau181	Aβ1–42	Intercept	t-tau	p-tau181	Aβ1–42
T5	21.62	0.13	-	-	5.80e-12 ***	<2e-16 ***	-	-	0.923	0.0243
T6	−18.83	0.01	1.26	-	4.16e-05 ***	2.83e-01	<2e-16 ***	-	0.958	0.0182
T7	−0.47	0.90	-	-	5.26e-10 ***	<2e-16 ***	-	-	0.942	0.0045
T8	−0.57	0.36	0.80	-	2.30e-14 ***	6.20e-04 ***	4.75e-07 ***	-	0.952	0.0042
P5	−0.29	-	0.39	-	9.00e-01	-	<2e-16 ***	-	0.780	0.0385
P6	−3.81	-0.01	0.52	-	2.58e-01	1.55e-01	8.32e-08 ***	-	0.783	0.0384
P7	−0.87	-	1.22	-	1.44e-09***	-	<2e-16 ***	-	0.817	0.0112
P8	−0.87	0.18	0.97	-	2.05e-09 ***	3.94e-01	1.90e-03 ***	-	0.819	0.0112
B5	83.72	-	-	0.15	<2e-16 ***	-	-	<2e-16 ***	0.749	0.0185
B6	136.33	0.05	−0.87	0.14	<2e-16 ***	4.12e-02 *	7.54e-04 ***	<2e-16 ***	0.796	0.0170
B7	0.67	-	-	0.57	9.95e-09 ***	-	-	<2e-16 ***	0.771	0.0036
B8	1.26	−0.08	−0.10	0.49	1.70e-14 ***	4.60e-01	4.99e-01	<2e-16 ***	0.817	0.0033

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

We tested the accuracy of the six xMAP and ELISA measurement levels to correctly identify the diagnostic category of the subjects, i.e. AD vs. control. For each combination of measurements, the optimal accuracy (average of the optimal sensitivity and specificity) and the area under ROC curve (AUC) were computed by the ROCR package for R and are reported in Table 5.

Table 5.

Optimal Error and Area Under ROC Curve (AUC) for disease status classification. Best classifiers are highlighted.

Classification Criterion	Number of subjects	Scoring function	Class with Higher Score	AUC	Error
AD vs. Control	63 AD, 32 Control	ELISA t-tau	AD	0.778	0.225
		ELISA p-tau181	AD	0.737	0.225
		ELISA Aβ1–42	Control	0.868	0.169
		xMAP t-tau	AD	0.728	0.258
		xMAP p-tau	AD	0.744	0.247
		xMAP Aβ1–42	Control	0.921	0.124
		(ELISA p-tau)/(ELISA t-tau)	Control	0.838	0.180
		(ELISA Aβ1–42)/(ELISA t-tau)	Control	0.866	0.135
		(ELISA Aβ1–42)/(ELISA p-tau)	Control	0.855	0.169
		(xMAP p-tau)/(xMAP t-tau)	Control	0.666	0.270
		(xMAP Aβ1–42)/(xMAP t-tau)	Control	0.828	0.169
		(xMAP Aβ1–42)/(xMAP p-tau)	Control	0.840	0.146

Results

Reliable conversions between xMAP and ELISA measurements are possible by linear regressions

We analyzed twelve linear regression models that estimate the ELISA values of the three pathologically linked CSF proteins using xMAP measurements, and another twelve linear regression models that estimate the xMAP values of the three CSF proteins using ELISA levels as described in the Methods section and Table 1. Using data from 140 CERND subjects, we find reliable estimations are possible for both ELISA and xMAP’s t-tau and p-tau values. Regression results are summarized in Figures 1–3 (scatter plots of predicted and observed ELISA concentrations) and 4–6 (scatter plots of predicted and observed xMAP concentrations). Tables 3 and 4 summarize the regression coefficients, significance, correlation, and LOOCV COV for all twenty-four regression models. The data support the following conclusions:

1. Log₁₀ transformation, as is typically done in the analysis of gene expression microarray experiments, improves the accuracy of regression significantly, i.e. correlations of predicted and observed ELISA levels are improved in all models (except P4) when Log₁₀ transformation is used. Except for one model T6, correlations of predicted and observed xMAP levels are improved in all models when Log₁₀ transformation is used. Scatter plot figures (Figures 1–6) show why this is the case. For example, consider the predicted ELISA values: first, the variance of estimated ELISA values is constant regardless of the xMAP concentrations (homoscedastic in statistical terminology), which is a basic assumption of linear regression. Second, outlier values become less extreme using the log-scale, further improving the robustness of the model.

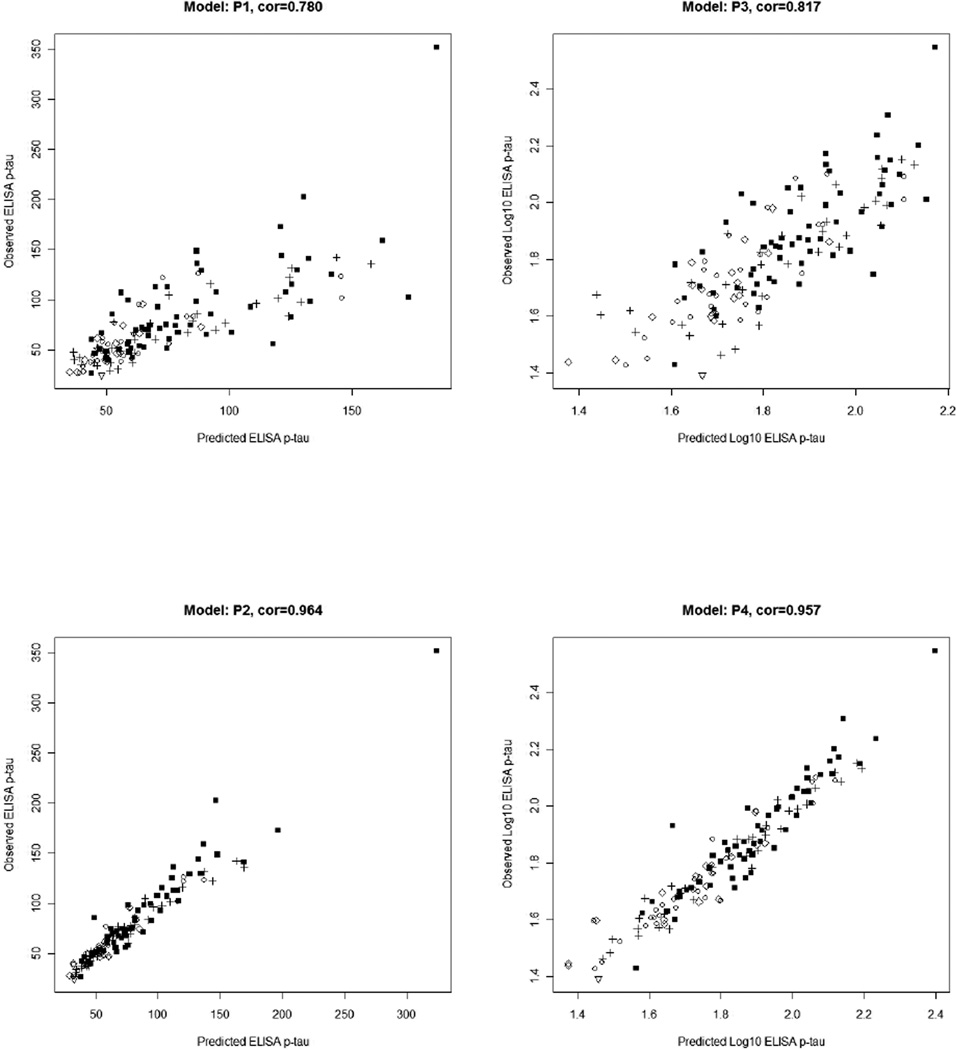
2. Correlation analysis shows that ELISA t-tau levels can be accurately predicted by xMAP t-tau levels alone (r=0.942). For ELISA p-tau₁₈₁ values, using xMAP p-tau₁₈₁ alone in the linear regression model produces accurate predictions (r=0.817), but using a linear combination of xMAP t-tau and p-tau₁₈₁ levels leads to better estimation (r=0.957).

3. Converting xMAP levels of Aβ_1–42 into ELISA Aβ_1–42 levels is less satisfactory. Correlation between the two measurements without Log₁₀ transformation is 0.749. Log₁₀ transformation model produced a similar correlation coefficient of 0.771. The best linear regression model uses Log₁₀ transformation and all three xMAP measurements, leading to the same correlation coefficient of 0.774; moreover the coefficients of xMAP t-tau and p-tau₁₈₁ levels are non-significant, suggesting their contributions in the regression are limited. Similar observations on the low correlation between xMAP and ELISA Aβ_1–42 levels were reported in [10].

4. Correlation analysis shows that xMAP t-tau values can be accurately predicted by ELISA t-tau concentrations alone (r=0.942) or using a linear combination of ELISA t-tau and p-tau₁₈₁ levels (r=0.952). For xMAP p-tau₁₈₁ values, the performance is less satisfactory; using a linear combination of ELISA t-tau and p-tau₁₈₁ levels leads to comparable estimation (r=0.819) to that achieved when using ELISA p-tau₁₈₁ alone (r=0.817). The conversion of ELISA concentrations into xMAP Aβ_1–42 values has similar performance. The best model uses Log₁₀ transformation and all three xMAP measurements, leading to comparable correlation coefficient (r=0.817) when using the Log₁₀ Aβ_1–42 values-only model (r=0.771); moreover the coefficients of ELISA t-tau and p-tau₁₈₁ values are non-significant, suggesting their contributions in the regression are limited.

5. A comparison between Tables 3 and 4 shows that in general, xMAP predicts ELISA levels better than the other way around. In models P3 and P4 of Table 3, ELISA p-tau₁₈₁ values can be predicted best using both xMAP p-tau₁₈₁ and t-tau concentrations, with over 10% improvement in the correlation values (r=0.957 vs. r=0.817). But this degree of improvement cannot be found in the corresponding regression models P7 and P8 in Table 4.

6. Leave-one-out cross validation (LOOCV) shows the coefficient of variation (COV) are low in all models, suggesting the regression models to be robust given our data set. The COV is generally lower when log transformation is applied, although this may also be due to the fact that log transformation decreases the range of the data substantially.

Figure 1.

Scatter plot of ELISA t-tau measurements and corresponding estimated levels by xMAP regression model.

Figure 3.

Scatter plot of ELISA Aβ_1–42 measurements and corresponding estimated levels by xMAP regression model.

Figure 6.

Scatter plot of xMAP Aβ_1–42 measurements and corresponding estimated levels by ELISA regression model.

Accuracy of classification using different biomarkers

We tested the diagnostic accuracy of the ELISA and xMAP measurement values when used in differentiating AD subjects from controls. Using the six measurements individually as well as six ratios as classification scores, the accuracy of the classification for each classification score is summarized as the area under ROC curve and the classification error using an optimal threshold. The results are summarized in Table 5. When used alone, xMAP Aβ_1–42 is the best classifier for AD versus Control (AUC=0.921, Accuracy=87.6%).

Discussion

This assay comparison study demonstrates that xMAP and ELISA values are comparable; for t-tau and p-tau₁₈₁ levels, the regression models can achieve correlations at 0.9 or higher. The xMAP Aβ_1–42 measurements have the best accuracy as an AD diagnostic biomarker in the cross-validation experiment. Together with its advantage as a semi-automated process with pre-prepared calibrators containing bead-linked capture antibodies and fewer manual steps to lower labor and human error, xMAP is a promising technology for developing new AD diagnostics for clinical laboratories.

Although more research is necessary to establish the clinical utilities of our models for conversion, this study has immediate implication for clinical research, namely the possibility to directly compare new studies based on the xMAP technology to the vast collection of literature based on ELISA using the ELISA Innotest and xMAP INNO_BIA AlzBio3 immunoassays examined here. However, this requires applying either a conversion applicable to ELISA or xMAP experiments, or a calibration procedure that a lab can apply, or a combination of both. Our analysis provides an example for constructing the interconversion of ELISA and xMAP measurements made in the same CSF aliquot samples. In addition, the correlation coefficients provide a means to estimate the number of samples needed to reach a reliable estimate of the conversion model, similar to performing a power analysis. Extending our analysis to multi-site xMAP studies will further help elucidate variation within a site or across sites, and it is clear that achievement of the most robust interlaboratory performance requires strict adherence to standard operating proceduresconducting these xMAP experiments. Moreover, it is intriguing that the best conversion model for xMAP p-tau level requires both ELISA p-tau and t-tau levels; in fact ELISA p-tau₁₈₁ is more correlated to xMAP t-tau than xMAP p-tau₁₈₁. Many factors may contribute to this phenomenon, including the difference between the ELISA and xMAP technologies, the difference in the antibodies and detectors being used, or any different affinity/specificity the antibodies possess when used in the two different technologies [12]. However, It should be noted that while the algorithms described here will prove useful in a variety of comparative studies of CSF tau and Aβ using the ELISA Innotest and xMAP INNO_BIA AlzBio3 immunoassays, our data also emphasize the critical importance of further efforts to standardize the use of these assays in order to enable them to become more widely useful in routine clinical practice.

Figure 2.

Scatter plot of ELISA p-tau₁₈₁ measurements and corresponding estimated levels by xMAP regression model.

Figure 4.

Scatter plot of xMAP t-tau measurements and corresponding estimated levels by ELISA regression model.

Figure 5.

Scatter plot of xMAP p-tau₁₈₁ measurements and corresponding estimated levels by ELISA regression model.