Segmentation of retinal OCT images using a random forest classifier

Abstract

Optical coherence tomography (OCT) has become one of the most common tools for diagnosis of retinal abnormalities. Both retinal morphology and layer thickness can provide important information to aid in the differential diagnosis of these abnormalities. Automatic segmentation methods are essential to providing these thickness measurements since the manual delineation of each layer is cumbersome given the sheer amount of data within each OCT scan. In this work, we propose a new method for retinal layer segmentation using a random forest classifier. A total of seven features are extracted from the OCT data and used to simultaneously classify nine layer boundaries. Taking advantage of the probabilistic nature of random forests, probability maps for each boundary are extracted and used to help refine the classification. We are able to accurately segment eight retinal layers with an average Dice coefficient of 0.79 ± 0.13 and a mean absolute error of 1.21 ± 1.45 pixels for the layer boundaries.

1. INTRODUCTION

Optical coherence tomography (OCT) is an emerging technology with many uses in ophthalmology¹, among other fields. One emerging application of OCT is in the evaluation of patients with multiple sclerosis (MS). Subjects with MS have been shown to exhibit significant thinning of various retinal layers.² Automated segmentation methods are becoming especially important to estimate these retinal thicknesses since manual segmentation of each layer is a time consuming task. An assortment of automatic retinal segmentation methods have been proposed in the literature to date. Many authors have proposed automatic retinal layer segmentation methods, utilizing a variety of techniques including active contours³, gradient-based information^{4, 5}, statistical models⁶, graph-based methods^7–9, and pixel classification¹⁰.

There is a growing popularity with graph-based segmentation methods for OCT. The layered structure of the retina lends itself well to such a problem formulation. These methods have also been shown to be efficient, simple and have good optimality properties. Chiu et al.⁸ construct a graph from every 2D OCT image and use a shortest path algorithm to segment multiple layers. Garvin et al.⁷ construct a 4D graph to model a 3D OCT volume and all of the layers together. A solution is found using a novel graph-cut formulation to the problem. One of the problems with these graph-based methods is in finding appropriate cost functions on the graph which differentiate each layer. Antony et al.⁹ build on prior work⁷ by using a k-nearest neighbor classifier to group image features into different regions, which are then used in the graph weights.

Another method which uses pixel classification for segmentation is from Vermeer et al.¹⁰ This work uses a set of 18 gradient and intensity features projected into a higher dimensional space to create a support vector machine classifier for each retinal layer. The independently classified pixels are then regularized using a level set method to create smooth surfaces. Using a single classifier for each layer, as well as a separate regularization for each surface, results in a particularly inefficient method. In addition, results for the segmentation of only five layer interfaces are given.

In this work, we propose to use a random forest classifier¹¹ to automatically learn where the appropriate boundaries are in macular OCT images. In total, nine layer boundaries are detected, resulting in the segmentation of eight layers. This type of classifier has been shown to perform well in different image segmentation tasks^{12, 13} and is popular due to its ease of use, the small number of parameters to tune, and the ability to simultaneously classify multiple labels. One particularly nice feature of random forests is that it provides soft classifications in the form of probabilities for each label. When classifying images, probability maps can be generated and then refined into hard segmentations. In the case of retinal segmentation, we classify on boundaries instead of layers and can then take advantage of the ordered structure of the layers to refine the probabilities into a segmentation by selecting only one pixel per A-scan for each boundary.

2. METHODS

The goal of the proposed work is to segment eight retinal layers in a macular OCT scan (Fig. 1). The layers to be segmented, listed from the top to the bottom of the retina, are: the retinal nerve fiber layer (RNFL), ganglion cell layer and inner plexiform layer (GCL + IPL), inner nuclear layer (INL), outer plexiform layer (OPL), outer nuclear layer (ONL), inner segment (IS), outer segment (OS), and retinal pigment epithelium (RPE). There are nine associated boundaries with these eight layers, noting that the inner limiting membrane (ILM) is used to denote the vitreous-RNFL boundary, the external limiting membrane (ELM) is used for the ONL-IS boundary and Bruch’s membrane (BM) is used for the RPE-choroid boundary. A single 2D OCT image is referred to as a B-scan image, with an A-scan being a single column of pixels from the B-scan. Multiple B-scans are combined in the through-plane direction to form a 3D volume. We also denote the x and y directions as the left-to-right and top-to-bottom directions in a B-scan and the z direction to be the through-plane direction.

Figure 1.

A cropped, manually delineated OCT image. The nine segmented boundaries are, from top to bottom: ILM, RNFL-GCL, IPL-INL, INL-OPL, OPL-ONL, ELM, IS-OS, OS-RPE, and BM.

Before segmentation of the retinal layers, a retinal mask is automatically generated to coarsely define the region-of-interest where we expect to find these layers. Calculation of the retina mask also allows us to flatten each image to the BM. To segment the retinal layers, seven features are extracted from the OCT data and used to train a random forest classifier to find each boundary. The classifier produces the probability of each pixel belonging to each boundary. These probabilities are then refined to estimate the final segmentation for each layer.

2.1 Retina detection and flattening

Before segmentation of the retinal layers, we generate a coarse retina mask, indicating which pixels are inside and outside of the retina. Fig. 2(b) shows an example retina mask for the OCT image in Fig. 2(a), where white and black represent areas inside and outside of the retina, respectively. Calculation of the retina mask requires an estimate of the ILM and BM boundaries. As this is a pre-processing step, fast calculation is desirable. Additionally, since these boundaries will be refined in later stages, they need only to be approximately located.

Figure 2.

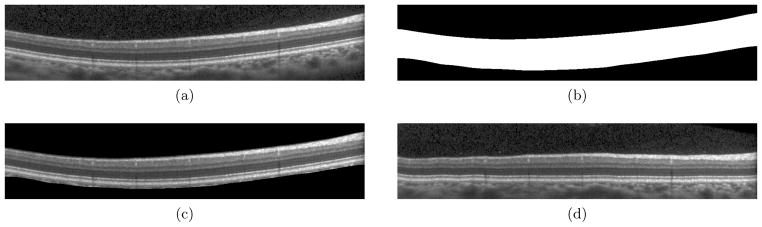
(a,b) An OCT image and the calculated retina mask. (c) The OCT image with the non-retina pixels masked out, showing the coarse accuracy. (d) The OCT image flattened to the bottom boundary.

To calculate the retina mask, every B-scan image in the volume is initially smoothed with a Gaussian filter (σ_x = σ_y = 10). Looking along each A-scan, the pixel with the largest positive gradient value is assumed to be either the ILM or the IS-OS boundary. The pixel with the largest positive gradient value at a minimum of 25 pixels away from the previously found maximum is taken to be the second boundary. Given these two pixels, the one closest to the top of the image is taken as the ILM. The BM is then taken to be the largest negative gradient value below the IS-OS, along each A-scan. Since these estimated ILM and BM surfaces may contain spurious jumps and discontinuities (due to blood vessel artifacts, for example), we remove and fill in outlying boundary points with the nearest point. Outlying points are those which are more than 15 pixels from their respective 10 × 10 median filtered surfaces. Finally, the two surfaces are smoothed with a Gaussian kernel (σ_x,z = {10, 0.75} for the ILM and σ_x,z = {20, 2} for the BM). The retina mask volume then contains all pixels between the estimated ILM and BM surfaces. Figure 2(c) shows a B-scan image with the non-retina area masked out showing that this retina mask only coarsely locates the top and bottom boundaries.

Given the retina mask, the OCT data is then flattened to the BM by the translation of each individual A-scan to make this boundary completely flat. Bilinear interpolation is used for the translation. The flattening process removes much of the curvature in each image, placing all retinal images in a common space across subjects and is a step commonly found in the literature.^{5, 7} An example of an OCT image and its resulting flattened image are in Figs. 2(a) and 2(d).

2.2 Random forest classifier

As an initial step for segmentation, a random forest classifier¹¹ is trained to find boundary pixels for each layer. Only one classifier is used to learn all of the boundaries, with each pixel assigned a label of 0 to 9 depending on the pixel being on one of the nine boundaries (labels 1–9) or not (label 0). Fifty trees are used in the forest and two features are randomly selected at each node. To train the classifier, seven features are used (visualized in Fig. 3). The first two features are positional features while the last five are local image features. These features are calculated at every pixel in a flattened OCT image.

Figure 3.

An OCT image (a) and its associated features: (b) retina mask distance, (c) x-position, (d–g) gradient features at 4 increasing scales, and (h) largest eigenvalue of structure tensor.

The first feature is unique to the retina, utilizing the retina mask calculated in Sec. 2.1. It is the fractional distance of each pixel from the bottom of the retina mask to the top, taking values between 0 and 1. Pixels above or below the retina mask are assigned a value of −1 to help the classifier better distinguish the retina from the background completely. The next feature used is the x-position of each pixel in the image (taking integer values of 1 to 1024 in our data). The purpose of this feature is to help learn the variation of layer thicknesses across the image. It works complementary to the retina mask distance to differentiate the high curvature foveal areas, which, due to the scanning protocol, appear consistently towards the center of the image. The two positional features are shown in Figs. 3(b) and 3(c).

Next, four multi-scale, gradient-like features are calculated by taking the difference of the averages of 3 × 3 neighborhoods above and below each pixel. The neighborhoods are located at 2, 4, 8, and 16 pixels above and below, which helps explain the intensity difference of surrounding layers. Examples of these features are shown in Fig. 3(d–g). This feature was designed to learn which layers are nearby (i.e. a dark layer above and a light layer below). The final feature is the magnitude of the largest eigenvalue of the structure tensor at each pixel.¹⁴ The tensor product was smoothed with a sigma value of 0.5. The first eigenvalue at each pixel is larger in anisotropic areas and is therefore particularly good at finding the thinner layers at the bottom of the retina (Fig. 3(h)).

2.3 Final segmentation

The random forest classifier outputs a probability for each label at each pixel, calculated based on the number of decision trees in the random forest which voted for that label (see Fig. 4). Since we would like each boundary label to be assigned only once per A-scan, taking the label with the largest probability at each pixel does not work well. Instead, for each class’s probability image, we carefully choose only one pixel per A-scan to be on its associated boundary.

Figure 4.

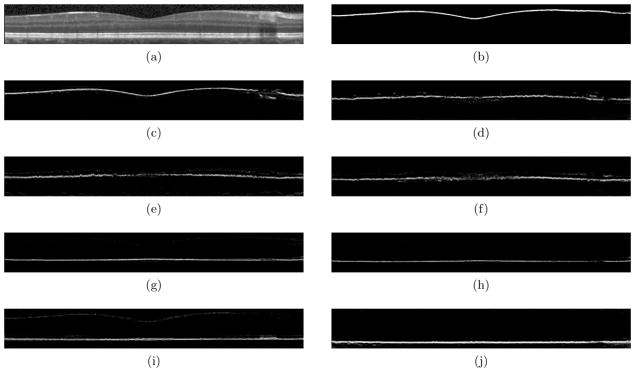
An OCT image (a) and the probability maps (b–j) for all nine layers generated from the random forest classifier on the image in (a). Probabilities range between 0 (black) and 1 (white).

To extract a single boundary from a layer’s probability image, Gaussian smoothing (σ = 15) is first applied to the image. The pixel with the maximum probability along each A-scan is chosen as the initial boundary pixel for that class. Since these boundaries are often noisy, as can be seen in Fig. 4, pixels with a probability below a threshold of 0.05 are removed and the remaining points are then smoothed using a cubic smoothing spline with a large smoothing parameter. This procedure can be repeated for each layer to estimate all boundaries. Layer labels are finally filled in between the appropriate boundaries. To ensure that the ordering of the layers is correct, each layer is filled in one at a time, starting with the top and the bottom layers. As each layer is added, a hard constraint is imposed so that the new layer cannot intersect and cross previously fitted layers. If the surface lies outside of the previously fit surfaces, we adjust those points to lay one pixel above or below the adjacent boundary. A careful selection of how layers are added is important, so layers with higher confidence are added first.

3. RESULTS

Ten manually delineated OCT volumes were used in this study. All manual delineations were done by a single rater using an internally developed software. After providing informed consent, the patients underwent spectral-domain retinal imaging on a Spectralis OCT scanner (Heidelberg Engineering, Heidelberg, Germany). Macular raster scans (20° × 20°) consisting of 49 B-scans were acquired. The scanner utilized automatic real-time (ART) to increase image quality by acquiring and averaging multiple images of the same location for noise reduction. Scans with ART ≥ 12 (number of scans averaged) and with signal quality of at least 20 dB were used in this study. The image volumes had 496 pixels per A-scan, and 1024 A-scans in each B-scan. Also note that the fourth root of the raw Spectralis intensity data was applied before all processing.

A small portion of the data in five OCT volumes were used for training the random forest classifier. Within each training volume, three B-scans were selected as representative scans. One of the three scans included the central fovea area while the other two scans were taken from each side of the fovea. Finally, all points on each boundary (1024 points per layer per B-scan) were used for the training, in addition to an equal number of random background points found between each boundary. The remaining five OCT volumes were used to explore how well the algorithm performed. Two measures were used to analyze the performance of the algorithm. First, we look at the mean absolute error (MAE) between each estimated layer boundary and the ground truth manual segmentation. The second measure used is the Dice coefficient, which is a measure of the overlap between the estimated and true layer segmentation. It is calculated for each layer as,

$$d_k=\frac{2\mid X_k\cap Y_k\mid }{\mid X_k\mid +\mid Y_k\mid },$$ (1)

where X_k and Y_k are the set of points labeled as layer k in the ground truth and estimated layers, respectively.

Tables 1 and 2 show the MAE and Dice coefficient results of our algorithm averaged across all subjects and B-scans. From Table 1, the ILM has the lowest boundary error. This result is expected as this boundary is where the background intersects the retina and has a large gradient. Also, looking at Fig. 2(c), the retina mask localizes the ILM quite closely, making the retina mask feature quite good for this boundary. The ELM, IS-OS, and BM boundaries also show low errors, again due to large, identifiable gradients. The OS-RPE boundary proved to be the most difficult to estimate since this boundary has a tendency to disappear and reappear in some images. Looking at the Dice coefficients, all of the layers show quite good results, with more difficulties in the IS, OS and RPE layers. The layers with the largest Dice coefficients, the RNFL, GCL+IPL, and ONL, are wider than many of the other layers and are also have larger gradients at their boundaries. The IS, OS, and RPE showed the worst performance since these are thinner layers. A one pixel boundary error in these layers translates into a much lower dice coefficient then a similar boundary error would have in larger layers.

Table 1.

Mean absolute error (standard deviation) values for each boundary. Values have units of pixels.

	ILM	RNFL-GCL	IPL-INL	INL-OPL	OPL-ONL
Mean	0.66(0.58)	1.59(2.13)	1.06(1.28)	1.04(1.13)	1.21(1.26)

	ELM	IS-OS	OS-RPE	BM	Overall
Mean	0.69 (0.78)	0.76 (1.07)	2.90 (1.67)	0.99 (1.04)	1.21 (1.45)

Table 2.

Values of the Dice coefficient between the estimated layer segmentations and the true layer segmentations.

	RNFL	GCL+IPL	INL	OPL	ONL
Mean	0.88 (0.05)	0.92 (0.03)	0.83(0.06)	0.81 (0.05)	0.90 (0.03)

	IS	OS	RPE	Overall
Mean	0.66 (0.09)	0.62 (0.10)	0.70 (0.09)	0.79 (0.13)

Fig. 5 shows the results of our segmentation method on three B-scans. The top row shows the input B-scans, the second row shows the manual segmentations and the last row shows the results of our automatic segmentation. One apparent area of difficulty is in regions containing blood vessel artifacts. As Fig. 4 shows, in the probability images, areas with blood vessels either appear as false positives or receive low probability values. False positives result in incorrect boundaries, which are subsequently smoothed in the final segmentation step. This smoothing is not strong enough, however, to eliminate the errors. When the boundary has a low probability, there is usually enough of a response to give a reasonable fit to the boundary. If the response is too small (below the 0.05 threshold), the smoothing is able to interpolate the missing area quite accurately since the surfaces are smoothly varying.

Figure 5.

Segmentation results from three B-scans with each column indicating a different B-scan. The top, middle, and bottom rows are the input OCT image, manual segmentation, and automatic segmentation, respectively.

Finally, we quickly look at the performance of the algorithm. All experiments were run on a computer running Windows 7 with a quad-core processor running at 1.73 GHz using MATLAB R2011b. The random forest implementation is openly available online.¹⁵ This implementation utilizes pre-compiled mex files for efficiency. All other processing uses native MATLAB functions. The performance of different aspects of the algorithm is in Table 3. Training the classifier took about 90 seconds. As shown, the total time to segment a volume is approximately 117 seconds including all steps. This time corresponds to 2.4 seconds per B-scan. Performance could likely be further improved using optimized code. For example, efficient implementations of random forest have been implemented on GPU.¹⁶

Table 3.

Run times for various aspects of the algorithm

	Time (s)
Classifier training	90
Retina detection and flattening	19
Calculating features	12
Random forest classification	75
Final segmentation	11
Complete segmentation	117

4. CONCLUSIONS

We have shown the ability to use random forests to classify retinal layers using only seven features. To generate a final segmentation for each layer, post-processing of the boundary probability images output by the random forest classifier was required. The algorithm proved to be fast and accurate, leading to the successful segmentation of multiple OCT volumes after training on only a small subset of five volumes. There are many aspects of this work which can be improved. The algorithm is inherently 2D, running on individual B-scans instead of using information from the complete 3D volume. Using the full volume may aid in fixing problems with blood vessel artifacts. Further validation must also be performed, comparing inter- and intra-rater variability on the segmentation.