Improved ancestry inference using weights from external reference panels

Abstract

Motivation: Inference of ancestry using genetic data is motivated by applications in genetic association studies, population genetics and personal genomics. Here, we provide methods and software for improved ancestry inference using genome-wide single nucleotide polymorphism (SNP) weights from external reference panels. This approach makes it possible to leverage the rich ancestry information that is available from large external reference panels, without the administrative and computational complexities of re-analyzing the raw genotype data from the reference panel in subsequent studies.

Results: We extensively validate our approach in multiple African American, Latino American and European American datasets, making use of genome-wide SNP weights derived from large reference panels, including HapMap 3 populations and 6546 European Americans from the Framingham Heart Study. We show empirically that our approach provides much greater accuracy than either the prevailing ancestry-informative marker (AIM) approach or the analysis of genome-wide target genotypes without a reference panel. For example, in an independent set of 1636 European American genome-wide association study samples, we attained prediction accuracy (R²) of 1.000 and 0.994 for the first two principal components using our method, compared with 0.418 and 0.407 using 150 published AIMs or 0.955 and 0.003 by applying principal component analysis directly to the target samples. We finally show that the higher accuracy in inferring ancestry using our method leads to more effective correction for population stratification in association studies.

Availability: The SNPweights software is available online at http://www.hsph.harvard.edu/faculty/alkes-price/software/.

Contact: aprice@hsph.harvard.edu or cychen@mail.harvard.edu.

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Applications in genetic association studies, population genetics and personal genomics motivate inference of genetic ancestry using single nucleotide polymorphism (SNP) genotypes. In genetic association studies, ancestry inference can be applied to control population stratification, which can lead to spurious association between the genetic variant and the phenotype under study (Price et al., 2010). In personal genomics, many private companies provide genetic testing on ancestry, which involves inference of ancestry based on information of genetic data from a single individual (Royal et al., 2010).

In genome-wide association studies (GWAS), several methods have been proposed to adjust for population stratification (Price et al., 2010). Methods that explicitly infer genetic ancestry include structured association (Pritchard et al., 2000), principal component analysis (PCA) (Novembre and Stephens, 2008; Novembre et al., 2008; Price et al., 2006) and multidimensional scaling (Purcell et al., 2007). To infer genetic ancestry, these methods can be either applied to the target samples only or applied to the target samples combined with an external reference panel to improve accuracy; when inferring ancestry for a single target individual in a personal genomics setting, it is necessary to include an external reference panel. As an alternative to applying these methods to genome-wide data, they can be applied to a subset of ancestry-informative markers (AIMs). For example, AIM panels have been developed for European Americans (Paschou et al., 2008; Price et al., 2008; Seldin and Price, 2008; Tian et al., 2008) and Latino Americans (Galanter et al., 2012).

The use of raw genotypes from a large reference panel to improve accuracy poses several complexities, including the logistics of obtaining and managing additional raw genotype data, concerns about sharing raw genotype data owing to privacy or other reasons and increased computational cost. Although the AIM approach can ameliorate some of these complexities, restricting to AIMs when genome-wide data are available reduces accuracy (Price et al., 2010). Given that data on genome-wide markers now can be generated through low-coverage sequencing at very low cost, an approach that can fully use the ancestry information of genome-wide markers is needed (Pasaniuc et al., 2012).

Here, we propose methods and software for ancestry inference based on genome-wide SNP weights. This approach requires just the raw genotypes from the target samples and a set of genome-wide SNP weights pre-computed using external reference panels. Notably, the reference panels of genotypes do not need to be shared. Inferring ancestry using the genome-wide SNP weights does not depend on the sample size or diversity of the study samples, and can infer ancestry for related samples, for which direct PCA is often confounded by family structure (Price et al., 2010).

To demonstrate our method, we first built an ancestry inference model for African Americans using genome-wide SNPs and validated our model using independent HapMap 3 samples (Altshuler et al., 2010). This model predicts the first principal component (PC1) for African Americans and can also transform predicted PC1 into % European ancestry. We determined that predicted ancestry using genome-wide SNP weights is more accurate than predicted ancestry using a limited number of AIMs. We extended the model to infer % ancestry from East Asian, European and West African populations using PC1 and PC2 from these populations. Once again, predicted ancestry using genome-wide SNP weights was extremely accurate. Finally, we built an ancestry inference model for European Americans using Northwest European (NW), Southeast European (SE) and Ashkenazi Jewish (AJ) ancestral populations (Price et al., 2008). We used European American reference samples from the Framingham Heart Study (FHS) SHARe data to build the model and validated the model with independent samples from a bipolar disorder (BD) GWAS and a breast cancer (BCa) GWAS (Hunter et al., 2007; Lango Allen et al., 2010; Price et al., 2008; Splansky et al., 2007). For both BD and BCa datasets, the predicted PC1 and PC2 attained higher accuracy than direct application of PCA. In addition, simulations showed that our method outperforms the AIM approach in correcting population stratification in GWAS. Ancestry inference software incorporating SNP weights for all of the populations considered here can be downloaded from http://www.hsph.harvard.edu/faculty/alkes-price/software/.

2 METHODS

2.1 Ancestry inference using genome-wide SNP weights

Our ancestry inference model is based on a set of genome-wide SNP weights. To compute the SNP weights, we first normalize the genotypes of ancestral samples and perform PCA on normalized genotypes. Then, we compute SNP weights using PCs, corresponding eigenvalues and normalized genotypes from ancestral samples. The SNP weights, once obtained, can be applied to target samples to predict PCs and % ancestry. Below, T denotes the transposition of a matrix, and tr(•) denotes the sum of the diagonal elements of a matrix.

Let g_ij be a matrix of SNP genotypes for SNP i and individual j, where i = 1, … , M and j = 1, … , N. The N individuals are samples from the ancestral populations for a given admixed population. We first normalize g_ij by SNP to improve the result of PCA (Patterson et al., 2006). For each entry in row i, we subtract the mean of each row from it and divide it by [p_i(1-p_i)]^0.5, where the mean of each row is μ_i = (∑_j g_ij)/N and p_i = μ_i/2. The normalized g_ij matrix is denoted as X. Then, we perform PCA using EIGENSOFT software on the N × N matrix X^TX. From PCA, we can obtain an N × N matrix V with the k^th column as the k^th PC of X^TX with the k^th largest eigenvalue, and an N × N diagonal matrix S with the k^th largest eigenvalue λ_k at the k^th diagonal element. The SNP weights are computed as W = C × S⁻¹(XV)^T. C is a standardizing constant (N − 1)/tr(X^TX). The standardizing constant is to account for the standardization imposed by EIGENSOFT software on the input genotypes (Patterson et al., 2006). The resulting SNP weights W form an N × M matrix with the SNP weights for predicting the k^th PC in the k^th row.

Once the SNP weights are obtained, we can predict PCs for target samples by applying the SNP weights to their genotypes. Let g_ij,new be an M × P matrix for SNP i and individual j, where i = 1, … , M and j = 1, … , P. The P individuals are our target samples from an admixed population with the ancestral populations corresponding to the SNP weights. We first normalize g_ij,new using the same method described above to obtain the normalized genotype matrix X_new. Note that we use the row means 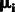calculated with the ancestral population samples to normalize the target samples. We can predict the PCs of X_new^TX_new by computing V_new = (WX_new)^T, where V_new is a P × N matrix with the k^th column as the k^th predicted PCs for the P target samples.

2.2 Application to admixed samples using continental ancestral populations

In general, we can use the predicted PC1 as a continuous axis of ancestry for an admixed population with two ancestral populations, such as African Americans. To build an ancestry inference model for African Americans, we computed genome-wide SNP weights using a pooled sample of 112 individuals with ancestry of Northern and Western Europe (CEU) and 113 individuals with ancestry of Western Africa (YRI) from HapMap 3 (Altshuler et al., 2010). For this model, we aim at predicting PC1 (v_{1, new}), which is the first column of V_new, for the target admixed samples. To test the model with independent samples, we used genotype data collected from 49 African American individuals in the southwestern USA (ASW) from HapMap 3. The HapMap3 samples were genotyped on Affymetrix 6.0 and Illumina 1M arrays. We excluded SNPs on chromosome X, A/T and C/G SNPs (to avoid strand ambiguity issues), and SNPs with any missing genotype in the pooled sample of CEU, YRI and ASW samples. The genotype data used to calculate SNP weights contain 813 976 SNPs.

To assess the prediction ability of the ancestry inference model, we compared the predicted PC1 with the gold standard, which is PC1 obtained by performing PCA on the combined sample of the target samples (ASW) and the ancestral samples (CEU and YRI). We used two metrics: (i) R² between predicted and true PCs and (ii) shrinkage of predicted PCs compared with true PCs, defined as the regression coefficient β from the linear regression model v_{k, new} = βv_{k, true} + ε, where v_{k, new} is the k^th predicted PC of the target samples and v_{k, true} is the k^th PC of the target samples obtained by performing PCA on the combined sample of target samples and ancestral samples. We also calculate the asymptotic shrinkage for each PC with corresponding eigenvalues, number of SNPs and number of ancestral samples used to compute SNP weights (Lee et al., 2010).

We can further perform a linear transformation on the predicted PC1 to obtain the % European ancestry for the target samples. We first perform PCA on a pooled sample of Europeans and West Africans and calculate the average PC1 for the European samples (ē₁) and the West African samples (ē₂) separately. Then we transform the predicted PC1 into % European ancestry by calculating a_{1, new} = (v_{1, new} − ē₂)/(ē₁ − ē₂). The resulting percent European ancestry is a proportion indicating the inferred European ancestry component for the African American individuals. For any value in v_{1, new} that is greater than ē₁ or smaller than ē₂, the corresponding percent European ancestry will be set to 1 or 0, respectively.

The model we described above can be readily extended to infer ancestry for admixed samples with three ancestral populations. In this case, we aim at predicting both PC1 (v_{1, new}) and PC2 (v_{2, new}), which are the first and second columns of V_new, respectively. We built the model with genotypes from 112 CEU samples, 113 YRI samples, 84 samples of Han Chinese in Beijing, China, and 85 samples of Chinese in Metropolitan Denver, Colorado, from HapMap 3, which represent three continental populations. We excluded SNPs on chromosome X, A/T and C/G SNPs, and SNPs with any missing genotype in the pooled sample and used 661 708 SNPs in this analysis. We examined this model by predicting PC1 and PC2 for all HapMap 3 samples that were not used to build the model, including 49 independent ASW samples, 50 independent samples of Mexicans in Los Angeles, California (MXL), and 88 samples of Gujarati Indians in Houston, Texas (GIH). The predicted PCs were compared with the corresponding gold standards, which are the true PC1 and PC2 obtained by performing PCA on the target samples plus the ancestral samples.

To infer the ancestry components, we can perform a linear transformation of the predicted PC1 and PC2 and obtain % ancestry of each continental population. For target samples with three ancestral populations, we first calculate the average of PC1 and PC2 for each of the three ancestral populations separately and denote the average PCs as ē_ij, where i = 1, 2, denotes PCs, and j = 1, 2, 3, denotes three ancestral populations. By assuming that an average sample from ancestral population 1 has 100% ancestry component from population 1, we can formulate a system of equations for linear transformation between PC1 and PC2 and % ancestry of ancestral population 1 (Equation 1). A system of equations for ancestral population 2 transformation can be formulated similarly (Equation 2). We can solve both systems of equations:

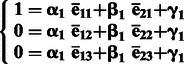(1)

and

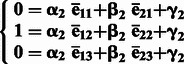(2)

for coefficients α₁, α₂, β₁, β₂, γ₁ and γ₂. With the condition that all % ancestry for a given individual sum to 1, we can infer the ancestry component with

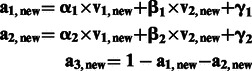where a_{1, new}, a_{2, new} and a_{3, new} are inferred % ancestry with respect to ancestral population 1, 2 and 3. We set the inferred % ancestry to 0 or 1 if the calculated values exceed the range of 0–1 and rescale the inferred percentages of ancestry to make the sum of percentages equal to 1 if needed.

Previously, we implicitly assume that the genotype data of target samples g_{ij, new} contain the same set of SNPs as the SNP weights. In practice, we may encounter the situation where the genotype data of target samples contain fewer SNPs than the SNP weights. In this case, we can still predict PCs with the genotypes available. Assuming that the SNP genotypes are missing at random, we replace the missing genotype data of target samples by 0 and calculate the predicted PCs as V_new = (WX_new)^T × (M/M'), where M' is the number of SNP genotypes used to predict PCs.

To assess our method’s performance under different conditions, we predicted PCs by using different numbers of random SNPs selected across the genome, different numbers of AIMs selected by the largest absolute value of SNP weight and genome-wide SNPs as well as using different numbers of ancestral samples. In addition, we obtained PCs from PCA performed on only the target samples. R² and sample shrinkage were used as accuracy measures.

2.3 Application to European Americans

Ancestry inference poses a greater challenge with more closely related ancestral populations. Thus, we used genome-wide SNP genotypes from FHS SHARe data to build an ancestry inference model for European Americans using NW, SE and AJ ancestral populations. The original SHARe project included 9215 individuals with 549 782 SNPs genotyped with the Affymetrix 500K array and 49 214 SNPs from the Affymetrix 50K array. We selected a subset of 6546 unrelated European American samples to build the model. We examined the model with two sets of independent European American samples, a BD GWAS and a BCa GWAS (Hunter et al., 2007; Price et al., 2008). We analyzed 1636 European American controls from the BD data genotyped on Affymetrix 500K arrays. We analyzed 343 070 SNPs after excluding SNPs on chromosome X and A/T and C/G SNPs. We analyzed 2287 samples from the BCa data genotyped on Illumina HumanHap550 chip, including 1145 BCa cases and 1142 matched controls, retaining 542 944 SNPs. For BCa GWAS samples, we also extracted self-reported ancestry information from questionnaires, which classified samples into Scandinavian, South European, Ashkenazi Jew or European without sub-population ancestry information. We excluded BCa samples without sub-population ancestry information in our analysis.

For BD samples, we first compared predicted PC1 and PC2 using genome-wide SNP weights with the gold standards, which are the PCs obtained by performing PCA on the combined sample of the target samples (BD) and the ancestral samples (FHS). We also compared PC1 and PC2 from direct PCA on BD samples with the gold standard. R² and shrinkage were used as accuracy measures. In addition, we compared the PCA plots of the predicted PCs, PCs from direct PCA and the gold standard for BD samples. The PCA plots are color coded according to the assigned groups as described below. We also compared PCA plots for BCa samples, which are color coded by self-reported ancestry.

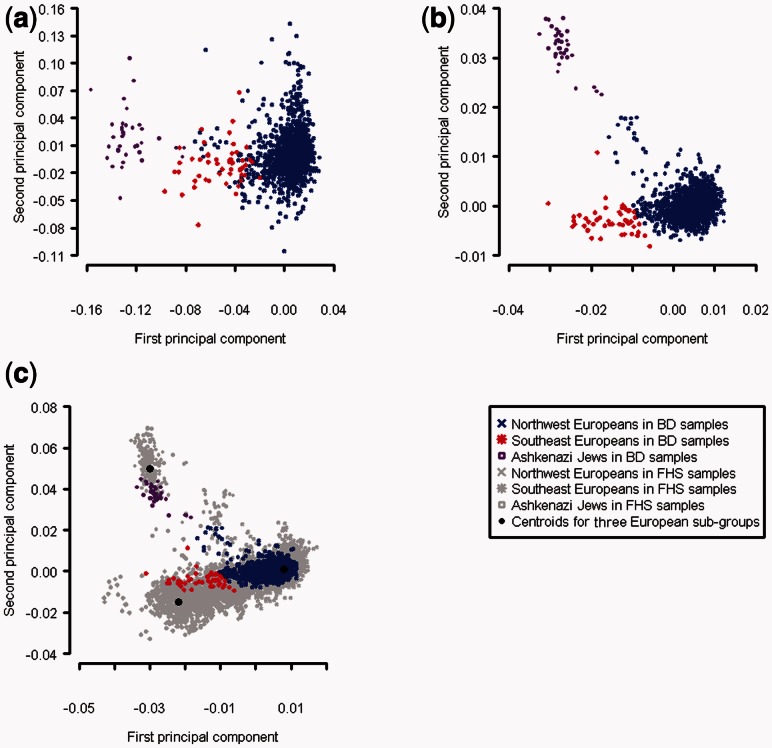
To assign BD samples to distinct ancestry categories, we calculated the distance between each BD samples and three centroids of the three European sub-populations based on the predicted PC1 and PC2 (Fig. 2c). We then assigned BD samples to one of the three groups based on the shortest distance to the centroids. We also assigned BD samples to distinct ancestry categories based on the gold standard and compared the category assignment using predicted PCs versus gold standard. For estimating % ancestry components, we assigned the FHS samples to NW, SE and AJ groups based on the distance to the same centroids mentioned above and calculated average of PC1 and PC2 for each of the three populations separately. We used these average PC1 and PC2 from the three groups in FHS to perform a linear transformation from predicted PC1 and PC2 to % ancestry.

Fig. 2.

Comparison between (a) the first and second PCs by performing PCA on BD data alone, (b) predicted first and second PCs of BD data by using model built with SHARe data and (c) the first and second PCs obtained by performing PCA on combined BD and SHARe data. The BD samples are color coded into three groups based on distance to centroids in panel (c) (see Section 2)

In addition to genome-wide SNP weights, we also used a panel of 300 AIMs specific to European American population to predict the first two PCs for the BD samples and compared predicted PCs with gold standard (Price et al., 2008). A subset of 150 AIMs, which are the intersection between the AIM panel and our SNP genotype panel, was used in our analysis. We also compared R² and sample shrinkage of predicted PCs obtained by using different numbers of random SNPs and AIMs for the BD samples. We selected 100, 200, 500, 1000, 2000, 5000 and 10 000 random SNPs and 10, 20, 50 and 100 AIMs based on SNP weights, and predict the first PC for the BD samples based on selected SNPs.

2.4 Population stratification simulations

We conducted a simulation study to compare the performance of our predicted PCs versus PCs inferred directly from target samples in adjusting for population stratification in GWAS. The simulation framework is similar to that in our previous work (Price et al., 2006). We used BD samples and simulated a phenotype using SNP rs2322659 at the LCT locus on chromosome 2. This SNP has an R² of 0.638 with SNP rs4988235, which is perfectly associated with the lactase persistence phenotype (Enattah et al., 2002). This phenotype is known to be correlated with within-Europe ancestry. We simulated a binary phenotype for the GWAS samples by assigning 1 to individuals carrying one or two reference alleles and 0 to individuals carrying zero reference alleles of rs2322659. We performed association tests on all available genome-wide SNPs except SNPs on chromosome 2. We computed unadjusted χ² statistics and P-values and selected SNPs with genome-wide significance for adjusted analyses. We assume that these SNPs are associated with simulated phenotype owing to population stratification. We computed adjusted association statistics using genomic control (Devlin and Roeder, 1999), predicted PCs based on genome-wide SNPs, PCs obtained by direct PCA and predicted PCs based on AIMs and compared the χ² statistics and P-values from these adjusted analyses.

3 RESULTS

3.1 Application to admixed samples using continental ancestral populations

We first applied the method to African Americans, as a proof of concept. We computed genome-wide SNP weights using 112 CEU and 113 YRI samples and predicted the first PC for 49 ASW samples. We compared predicted PC1 with the gold standard for ASW samples and found that predicted PC1 is accurate, with an R² of 1.000 [95% confidence interval (CI): 1.000–1.000] and a sample shrinkage of 0.978 (SD = 0.0001) (Supplementary Table S1).

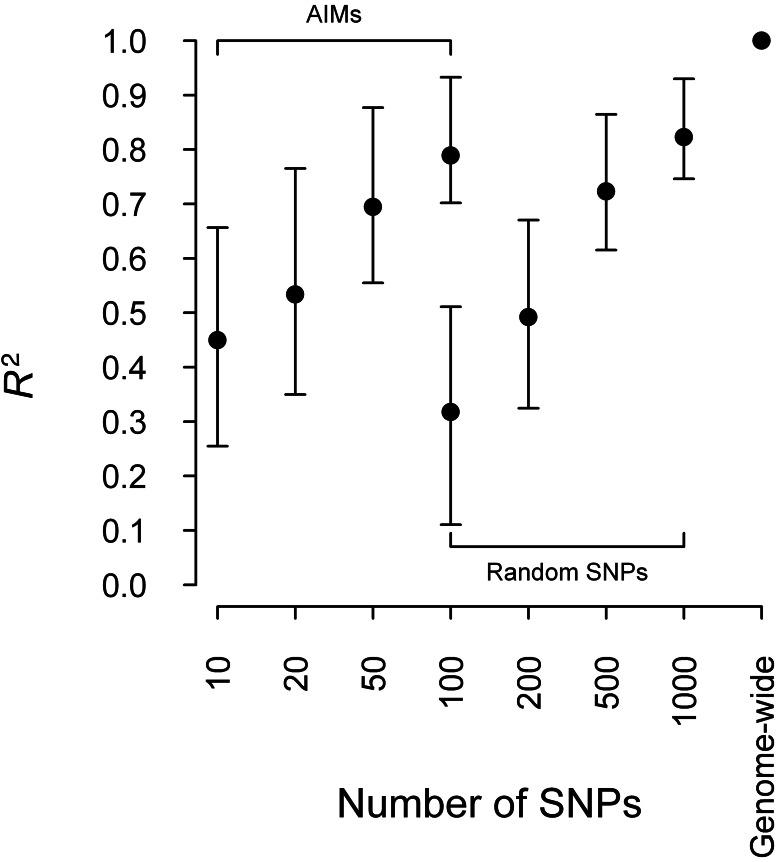
We compared the prediction accuracy by using random SNPs, AIMs and genome-wide SNPs (Fig. 1). The results showed that the R² increased with the number of SNPs included in the model for both random SNPs and AIMs. Notably, AIMs are ∼10-fold more informative than random SNPs for ancestry inference. The R² of the genome-wide SNP model is much higher than that of all models built with a subset of random SNPs or AIMs. This result highlights the advantage of using genome-wide SNPs over using AIMs in ancestry inference. We repeated the analysis by building the model with half of the CEU and YRI samples and testing the model with the other half of the CEU and YRI samples. The results showed a similar trend as the previous analysis but with much higher R² (Supplementary Fig. S2), as expected because ancestry inference for a sample with discrete structure is easier than ancestry inference for admixed samples. We showed that the sample shrinkage did not change substantially with the number of SNPs used for predicting PCs (Supplementary Table S1). In addition, we also built models with different numbers of ancestral samples (Supplementary Table S1) and found that R² remained at 1.000, regardless of the number of ancestral samples used. However, the shrinkage decreased from 0.978 when using 225 ancestral samples to 0.777 (SD = 0.001) when using 20 ancestral samples. In addition to comparisons between predicted PCs, we also evaluated PC1 from directly applying PCA on the ASW samples, as compared with the gold standard. We observed an R² of 0.101 (95% CI: 0–0.201). The poor performance of PC1 from direct PCA is due to family relatedness between some of the ASW samples, which prevents PCA from accurately estimating the population structure for these ASW samples (Supplementary Fig. S3).

Fig. 1.

Comparison between R² for ancestry inference using AIMs, random SNPs and genome-wide SNPs. Models were built with 112 CEU samples and 113 YRI samples and tested with 49 ASW samples. R² was calculated with the predicted first PC and the gold standard, which is the first PC obtained by applying PCA to combined samples of CEU, YRI and ASW with 813 976 SNPs. The vertical bars represent 95% CIs

Finally, we considered a model with three continental populations as ancestral populations and tested the model by predicting PC1 and PC2 for HapMap 3 samples. R² and shrinkage were used to examine the accuracy of the predicted first and second PCs. For ASW and MXL samples, the predicted PC1 and PC2 both had R² of 1.000 (95% CI: 1.000–1.000). The sample shrinkage was 0.992 and 0.968 for predicted PC1 and PC2 in ASW samples, and 0.982 and 0.974 for predicted PC1 and PC2 in MXL samples (Supplementary Table S2), respectively. We also estimated % ancestry for ASW and MXL samples (Supplementary Table S4 and Supplementary Fig. S1).

To investigate the results of applying our model to admixed samples with no good match in the ancestral populations included in the model, we predicted PC1 and PC2 for all HapMap 3 samples and compared these predictions with the top PCs obtained by directly applying PCA to all HapMap 3 samples. We obtain very similar results for predicted PCs and PCs from direct PCA (Supplementary Fig. S4). In particular, results are very similar for GIH samples, which have no good match in the ancestral populations used (Supplementary Table S2). Thus, predicted PCs and top PCs from direct PCA attain similar results, even when the ancestral samples are not a good match for the admixed samples.

3.2 Application to European Americans

Using genotypes from FHS SHARe data, we built a model that predicts the PC1 and PC2 for European Americans. In most European American datasets, PC1 distinguishes NW from SE ancestry, and PC2 distinguishes SE from AJ ancestry (Price et al., 2008). To validate the model, we used samples from a BD GWAS and a BCa GWAS as independent testing datasets (Hunter et al., 2007; Price et al., 2008). We predicted PC1 and PC2 for the BD samples using the model built with SHARe data and compared predicted PCs with the gold standard created by performing PCA on the BD samples and the SHARe samples combined. Using genome-wide SNP weights, the R² for predicted PC1 was 1.000 (95% CI: 1.000–1.000) and the R² for predicted PC2 was 0.994 (95% CI: 0.992–0.994) (Supplementary Table S3). The sample shrinkage was 1.013 (SD = 0.002) for predicted PC1 and 0.844 (SD = 0.002) for predicted PC2. In addition, we performed direct PCA on BD samples and compared PC1 and PC2 from direct PCA with gold standard. The R² for PC1 from direct PCA was 0.994 (95% CI: 0.951–0.960), and the R² for PC2 from direct PCA was 0.003 (95% CI: −0.007–0.006), which suggests that direct PCA cannot distinguish samples with Ashkenazi Jewish ancestry from others. In addition to comparing PCs directly, we also assigned BD samples to one of the three European sub-populations based on predicted PC1 and PC2. We compared the assigned ancestry category with the assigned ancestry category based on the gold standard. The assigned category based on predicted PCs had only 5 out of 1636 samples misclassified (Supplementary Table S5). We also estimated % ancestry from NW, SE and AJ ancestral populations for BD samples (Supplementary Table S4).

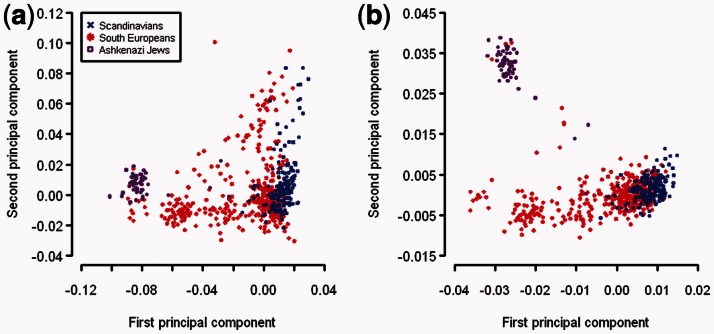
We created three PCA plots and color coded all BD samples into three European sub-populations (Fig. 2). Comparing the PCA plots, the predicted PC1 and PC2 had a very similar pattern to the gold standard. We can visually distinguish the BD samples with Ashkenazi Jewish ancestry from the BD samples with other European ancestry with the predicted PCs. We can also see a gradient of samples with Northwest and Southeast European ancestry. In contrast, the PCs from direct PCA on BD samples alone failed to distinguish the samples with Ashkenazi Jewish ancestry from other samples. We also compared our PCA plots with the PCA plots from Price et al. (2008). The PCA plot we created here with predicted PCs is comparable with Figure 2 from Price et al. (2008) using direct PCA on the same BD samples plus three other additional datasets. This suggests that the predicted PCs by using our model are not only comparable with the gold standard here but also comparable with PCs obtained by using other datasets. The analysis of BCa samples produced similar results, as PCA based on predicted PCs showed better clustering of samples according to self-reported ancestry than direct PCA on BCa samples (Fig. 3). In summary, the results from both BD and BCa samples showed that our method outperformed direct PCA on target samples.

Fig. 3.

Comparison between (a) the first and second PCs by performing PCA on BCa samples directly and (b) the predicted first and second PCs of BCa samples by using ancestry inference model built with SHARe data. These European American samples are color coded according to their self-reported ancestry

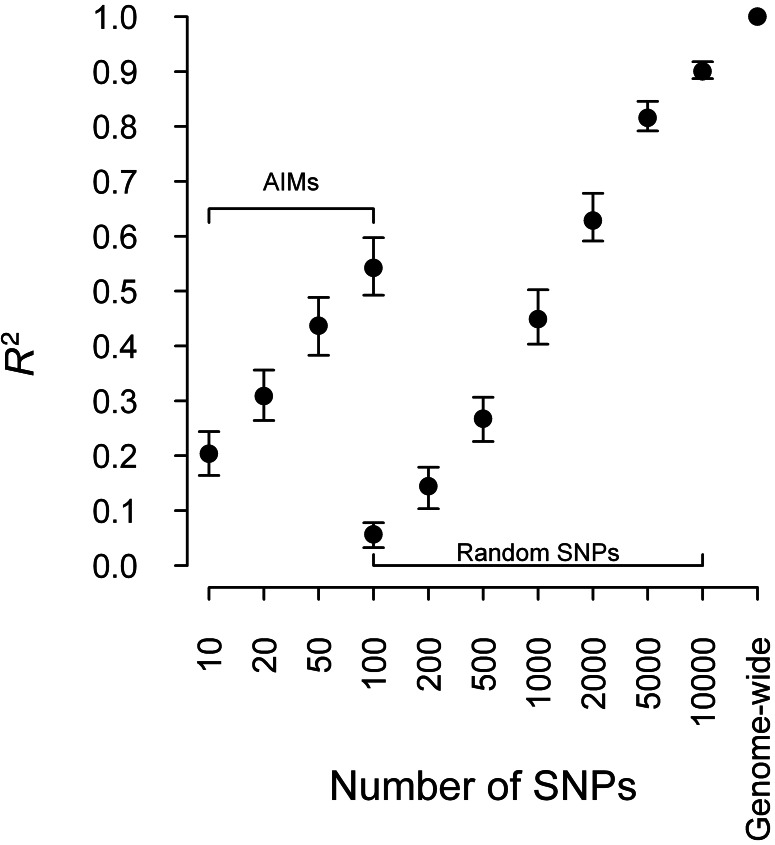
We also used 150 AIMs from a European American AIM panel to predict PC1 and PC2 for BD samples (Price et al., 2008). Using 150 AIMs, the R² was 0.418 (95% CI: 0.354–0.488) for predicted PC1 and 0.407 for PC2 (95% CI: 0.322–0.505). These numbers are limited by the inclusion of only 150 of the 300 AIMs from Price et al. (2008) based on the intersection of SNPs with our data, but it is nonetheless clear that ancestry inference from a limited number of published AIMs substantially underperforms the proposed use of genome-wide SNP weights. In addition to using the AIM panel, we also used different numbers of random SNPs and AIMs that are selected by SNP weights to predict PC1 and PC2 for BD samples. The R² for predicted PC1 using different numbers of random genotypes, AIMs and genome-wide SNPs for BD samples are shown in Figure 4. As expected, the R² increased with the number of random SNPs or AIMs used to predict PCs. However, the R² obtained by using a subset of random SNPs or AIMs were much lower than using the full set of genome-wide SNPs. Results for predicted PC2 were similar to results for predicted PC1 (Supplementary Table S3).

Fig. 4.

Comparison between R² for ancestry inference using AIMs, random SNPs and genome-wide SNPs. Models were built with 6546 FHS SHARe samples and tested with 1636 BD samples. R² was calculated with the predicted first PC and the gold standard, which is the first PC obtained by applying PCA to combined samples of FHS SHARe samples and BD samples with 346 070 SNPs. The vertical bars represent 95% CIs

3.3 Population stratification simulations

We conducted a simulation study of population stratification using BD genotypes and phenotypes simulated from genotypes of an SNP at the LCT locus, similar to the simulation study described in our previous article (Price et al., 2006). We found that five SNPs had spurious association with the simulated phenotype, with genome-wide significant P-values (Table 1). We compared several strategies for correcting for population stratification: genomic control, PC correction using predicted PC1 and PC2 based on genome-wide SNP weights, PC correction using PC1 and PC2 from direct PCA on BD samples only and PC correction using predicted PC1 and PC2 based on 150 AIMs.

Table 1.

SNPs have spurious association with simulated phenotype

SNP	Chr	Unadjusted χ2	Genomic control	Predicted PC1 and PC2 by genome-wide SNPs	PC1 and PC2 by direct PCA	Predicted PC1 and PC2 by 150 AIMs
rs2339390	1	46.90 (7.5 × 10−12)	40.72 (1.8 × 10−10)	7.47 (6.5 × 10−3)	6.37 (1.2 × 10−2)	10.55 (1.2 × 10−3)
rs2339392	1	58.49 (2.0 × 10−14)	50.78 (1.0 × 10−12)	7.81 (4.9 × 10−3)	6.90 (8.6 × 10−3)	11.75 (6.1 × 10−4)
rs9290629	3	54.76 (1.4 × 10−13)	47.54 (5.4 × 10−12)	7.95 (6.1 × 10−3)	8.61 (3.3 × 10−3)	9.67 (1.9 × 10−3)
rs10437421	10	71.46 (2.8 × 10−17)	62.04 (3.3 × 10−15)	8.23 (4.2 × 10−3)	9.35 (2.2 × 10−3)	11.73 (6.1 × 10−4)
rs7091038	10	67.15 (2.5 × 10−16)	58.30 (2.2 × 10−14)	13.23 (7.2 × 10−4)	13.51 (2.4 × 10−4)	16.80 (4.1 × 10−5)

The unadjusted χ² statistics were obtained by Armitage trend test. The χ² statistics adjusted by predicted and observed PCs were obtained by logistic regression models.

Chr, chromosome.

The adjusted χ² statistics and P-values showed that the genomic control failed to correct for the spurious associations, and all five SNPs were still genome-wide significant. In contrast, adjustment by the predicted PC1 and PC2 based on genome-wide SNPs successfully removed the spurious association, yielding non-significant genome-wide P-values. The adjustment by PC1 and PC2 from direct PCA also successfully removed the spurious association and attained similar adjusted P-values as adjustment by predicted PC1 and PC2. This can be explained by the fact that stratification at the LCT locus is predominantly an NW versus SE Europe (i.e. PC1) effect. The P-values after adjustment by predicted PCs based on 150 AIMs were still more significant than those adjusted by two predicted PCs based on genome-wide SNPs or the first two PCs from direct PCA. This result suggests that there is residual confounding after adjustment by predicted PCs based on 150 AIMs and highlights the advantage of using genome-wide SNP weights for PC prediction.

4 DISCUSSION

In this study, we presented methods and software for ancestry inference using genome-wide SNP weights derived from large reference panels. We showed empirically that this approach can accurately predict PCs and % ancestry in populations of admixed continental ancestry and in European Americans, which have more subtle population structure. Our results highlight the advantage of inferring ancestry using genome-wide SNPs obtained from a large external reference panel.

We further compared predicted PCs obtained by using genome-wide SNPs with those obtained by using subsets of random SNPs or AIMs, and showed that predicted PCs using genome-wide SNPs have the highest accuracy. AIM panels have been proposed for ancestry inference in African Americans (Ruiz-Narvaez et al., 2011), Latino Americans (Galanter et al., 2012) and European Americans (Paschou et al., 2008; Price et al., 2008; Tian et al., 2008). For African Americans, it had been suggested that accurate ancestry inference requires only 30 AIMs (Ruiz-Narvaez et al., 2011). However, we observed that genome-wide SNPs provide more accurate ancestry estimates than even 100 AIMs in African Americans. Thus, our approach based on genome-wide SNP weights outperforms the use of AIM panels. Our simulation study of population stratification further confirmed this point by showing that adjustment using our method outperforms adjustment using 150 AIMs. In applications in real data analysis, the AIM approach has the advantage that it requires less genotyping work if genome-wide SNP genotypes are not available. However, as the genome-wide marker data can now be generated at very low cost, genotyping costs are less likely to be a limitation going forward (Pasaniuc et al., 2012). We also stress that our method can be used even when the input genotypes contain an incomplete set of SNPs compared with the genome-wide SNP weights, for example, if they were typed on a different genotyping platform. Our simulations show that 1000 random SNPs or 10 000 random SNPs are sufficient to predict ancestry with high accuracy in African Americans or European Americans, respectively. However, a smaller number of random SNPs genotyped in candidate gene or targeted replication studies would not be sufficient to infer ancestry in these populations.

By constructing SNP weights with a carefully selected unrelated reference panel, our approach can accurately infer ancestry for related target samples, while direct PCA on related target samples may provide inaccurate estimates of population structure. Zhu et al. (2008) proposed a method to correct for population stratification in the presence of family relatedness in the target samples, which uses a subset of unrelated samples to predict PCs for all target samples. Their method can also avoid biased estimation of ancestry due to relatedness, but the ancestry inference is limited to the unrelated target samples, which may have insufficient sample size and diversity. By using a large external reference panel to compute the SNP weights, our method is not limited to the target samples and can attain accurate ancestry inference for related target samples.

Another advantage of our method is that it is based on pre-computed SNP weights. The pre-computed SNP weights can be readily shared with our software release. On the contrary, the existing methods for accurate ancestry estimation usually require raw genotypes from a large external reference sample. Access to raw genotypes entails substantial administrative complexities, which can be time-consuming. The sharing of SNP weights is also more privacy preserving than the sharing of raw genotypes. We note that it may be plausible to detect whether a given individual is in the set of samples used to calculate the SNP weights, analogous to detecting whether a given individual is in the set of samples used to calculate summary statistics (Homer et al., 2008; Sankararaman et al., 2009; Visscher and Hill, 2009). However, because the samples that we used to calculate SNP weights in were ascertained without regard to any phenotype, inferring whether a given individual is in that set of samples reveals less information than inferring whether a given individual is in a set of samples ascertained for a particular phenotype.

Our method also has the advantage of reduced running time. Existing software requires time O(MN²) to compute PCs, where M is the number of SNPs and N is the number of samples (Patterson et al., 2006; Price et al., 2006). In theory, randomized eigenvector approximations can reduce the running time to O(MN) (Rokhlin et al., 2009). However, a colleague of ours reports that efforts to apply this approach to genetic data have not yet been successful, as in large datasets, eigenvalues may be highly significant (reflecting real population structure in the data) but only slightly larger than background noise eigenvalues, and thus sometimes missed by randomized methods (N. Patterson, personal communication). Thus, our simple O(MN) approach offers real practical advantages.

Our method relies on including samples from the appropriate ancestral populations to build the model, to correctly infer % ancestry component for given admixed samples. However, the predicted PCs reflect the PCs obtained by performing PCA on the combined raw genotypes from the admixed population and the ancestral samples, irrespective of which ancestral samples were included in the analysis. In the analyses presented here, we built ancestry inference models using samples from three continental populations or NW, SE and AJ European populations. When applying our method to samples with no good match in the ancestral populations used, we still accurately predicted the top PCs from PCA, although caution is warranted in interpreting the results of either of these analyses with respect to the ancestral populations used.

We can readily extend our method to build models with samples from other ancestral populations. For example, similar models can be built for Indian and Native American populations using appropriate reference panels (Reich et al., 2009, 2012). Extension to more than three ancestral populations is straightforward, but accuracy is contingent on the sample size and diversity of the ancestral samples, as lower PCs may represent more subtle population structure.

In summary, we have developed a method for ancestry inference using genome-wide SNP weights. Our method only requires genotypes from the target samples and publicly available SNP weights, and is highly computationally efficient. The method can be readily applied in genetic association studies for population stratification adjustment and in personal genomics for predicting the ancestry component of an individual. For diseases or health outcomes associated with ancestry, the predicted ancestry values can be used for risk stratification and risk prediction (Alonso-Perez et al., 2011; Hughes et al., 2008; Kumar et al., 2010; Yang et al., 2011).