APP2: automatic tracing of 3D neuron morphology based on hierarchical pruning of a gray-weighted image distance-tree

Abstract

Motivation: Tracing of neuron morphology is an essential technique in computational neuroscience. However, despite a number of existing methods, few open-source techniques are completely or sufficiently automated and at the same time are able to generate robust results for real 3D microscopy images.

Results: We developed all-path-pruning 2.0 (APP2) for 3D neuron tracing. The most important idea is to prune an initial reconstruction tree of a neuron’s morphology using a long-segment-first hierarchical procedure instead of the original termini-first-search process in APP. To further enhance the robustness of APP2, we compute the distance transform of all image voxels directly for a gray-scale image, without the need to binarize the image before invoking the conventional distance transform. We also design a fast-marching algorithm-based method to compute the initial reconstruction trees without pre-computing a large graph. This method allows us to trace large images. We bench-tested APP2 on ∼700 3D microscopic images and found that APP2 can generate more satisfactory results in most cases than several previous methods.

Availability: The software has been implemented as an open-source Vaa3D plugin. The source code is available in the Vaa3D code repository http://vaa3d.org.

Contact: hanchuanp@alleninstitute.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

3D reconstruction of complex neuron morphology from light-microscopic images is an important technique for computational neuroscience. It has received considerable attention in recent years, such as in the DIADEM competition (Brown et al., 2011; Gillette et al., 2011) that involved ∼100 teams worldwide and many related studies (e.g. Al-Kofahi et al., 2002; Choromanska et al., 2012; Cohen et al., 2011; Donohue et al., 2011; Lu et al., 2009; Meijering et al., 2004, 2010; Narayanaswamy et al., 2011; Narro et al., 2007; Peng et al., 2010a, 2010b, 2011; Vallotton et al., 2007; Wang et al., 2011; Xiong et al., 2006; Zhang et al., 2007a,b; Zhao et al., 2011). However, despite a number of developed algorithms of neuron reconstruction (also called ‘neuron tracing’), it remains a significant problem how to trace neurons in a robust and precise way from real 3D microscopic images.

Automation of neuron tracing for complex neuron morphology and low quality image data has been previously discussed in the All-Path-Pruning (APP) method (Peng et al., 2011). The key idea of APP is to generate an initial reconstruction that covers all the potential signal of a neuron in a 3D image, followed by a linear-time pruning of unneeded branches until a least compact representation is produced while the coverage of all neuronal signal is maintained.

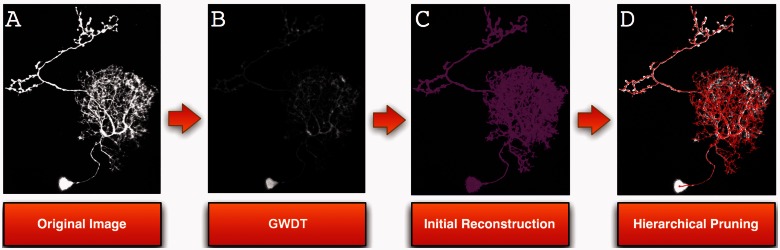
In this study, we present a new version of the APP algorithm, called APP2 (Fig. 1), with the goal to generate a more accurate and robust reconstruction within a shorter amount of time. To attain this goal, we develop new algorithms in three components:

1. A method to generate distance transform of the neuron signal from gray-scale image directly, without thresholding-based binarization (Fig. 1B);

2. A method to generate the initial reconstruction (Fig. 1C);

3. A hierarchical pruning method to produce the final reconstruction (Fig. 1D).

Compared with APP, all three components of APP2 are novel, especially the pruning process for where APP2 is much more efficient than APP. The distance-transform step and the initial reconstruction step of APP2 are useful enhancement and can also be used for APP essentially. Therefore, to evaluate the efficiency of our algorithms, we compared the tracing results with the gray-weighted distance transform (GWDT) or without GWDT. We also compared the result of APP2 and APP methods. To examine the robustness of our algorithm, we used signal deletion tests. We also tested our algorithms on many datasets from different sources, including a DIADEM dataset and many other more challenging datasets of fruit fly and dragonfly neurons that have heavy noise.

Fig. 1.

Schematic illustration of APP2 neuron tracing method. GWDT: gray-weighted distance transform. In (C) and (D), the reconstructions are color rendered and overlaid on top of the image data for better visualization. Raw image: Courtesy of Chiang laboratory

In our experiments, we have found that in most cases, APP2 is able to produce a reasonable tracing result within a short amount of time, usually within seconds for a large 3D image. Our new results are often better than those generated using several other existing competitive methods.

2 METHODS

2.1 Overview of APP2

In this article, we focus on neuron tracing for 3D light-microscopic images (often confocal or multi-photon laser scanning microscopic images). Taking a 3D gray-scale image as the input, a neuron-tracing method produces the digital representation of the morphology of the neuron(s) in this image. Tracing multiple neurons that potentially overlap in an image has been found to be fundamentally ill-posed and might be ultimately tackled using biological tissue labeling methods, such as dBrainbow (Hampel et al., 2011). In the latter case, the problem reduces to tracing of a group of single-channel images, each of which contains a single neuron. Therefore, here we discuss only how to reconstruct a single neuron’s morphology from an image.

In many previous studies, the 3D reconstructed morphology of a neuron is described using a tree graph G. G has a root node that corresponds to the seed location for reconstruction, which in many cases also corresponds to the soma of a neuron. G may also contain many leaf nodes, branching nodes and other inter-nodes.

An important idea in the recent APP method (Peng et al., 2011) is to first generate an over-reconstruction from the image to capture all possible signal/pixels of a neuron and then use an optimal pruning procedure to remove the majority of spurs in this over-reconstruction to produce a final succinct representation of the neuron, with a maximum coverage of all neuron signal. The pruning process starts from leaf nodes of the over-reconstruction. A ‘coverage’ test is iteratively conducted to check whether any of them have been ‘covered’ (i.e. has significant signal overlap) by other nodes. The nodes that are covered by others will be removed; otherwise they will be kept. A similar process is also applied to all internodes. The entire procedure is repeated until a most succinct representation that maximizes the signal coverage has been produced. Although the termini-first-search approach in APP is effective, it needs multiple iterations, which could still be time-consuming, even the algorithm itself has linear-time complexity to the number of reconstruction nodes. In addition, APP does not consider how to best preprocess an input image to optimize the tracing result.

APP2 follows the basic framework of APP. However, it enhances the key components of the original method. In short, APP2 consists of three steps in Figure 1B, C and D: (i) GWDT (Section 2.3); (ii) construction of an initial, over-reconstruction of the traced neuron (Section 2.4); and (iii) pruning of the over-reconstruction in hierarchical order (Section 2.5). The detail of APP2 is described as follows.

2.2 Fast marching method

The fast marching (FM) algorithm (Sethian et al., 1999), which is essentially a region-growing scheme, plays an important role in APP2. Both GWDT and initial neuron reconstruction are implemented in the FM framework.

In FM, we model an image as a graph, where each graph vertex corresponds to an image pixel (voxel). There is an edge between each pair of immediately neighboring pixel vertices. FM grows the image graph from a set of predefined seed vertices to all remaining image pixel vertices in a distance-increasing order. All image pixels are divided into three groups, labeled as ALIVE, TRIAL and FAR.

FM has two main steps: initialization and recursion. First, all the seed vertices are initialized to be ALIVE; the neighbors of seeds are initialized as TRIAL; and the rest are set as FAR. Then, from the set of TRIAL vertices, we will extract one vertex x, which has the minimum distance value to the ALIVE set. The extracted vertex x is then converted from TRIAL to ALIVE. For any non-ALIVE neighbor y of x, we set it to TRIAL if it is FAR. The distance function of y is updated as (also see below for concrete definitions).

where e(x,y) is the distance between vertex x and vertex y [see below for definition of e(x,y)]. FM recursively extracts the vertex that has the minimum distance from the TRIAL set until it becomes empty.

An important implementation trick of FM is to maintain TRIAL vertices in a Fibonacci heap so that the required minima can be obtained efficiently.

2.3 GWDT: gray-weighted image distance transform

To enhance the step of producing an initial neuron reconstruction, in APP2, we apply the distance transform (DT) to the input image. In case of an image region that has relatively ‘flat’ intensity, DT is able to create a gradient of image intensity: close to the center of this region, the image intensity is large, and close to the boundary, the intensity is small. We call this ICDB principle, which stands for ‘increase the intensity in the center and decrease the intensity near boundary’. It would help to build a high quality initial reconstruction by forcing the shortest path to go through the skeleton of the neuron.

However, the conventional distance transform is only applicable to a binary image that is produced by thresholding a gray-scale image. An unsuitable threshold may under or over segment the image. Here, we propose a GWDT method for gray-scale image directly. In the conventional distance transform, the distance value for each image pixel is defined as the minimal Euclidean distance to background pixels. In GWDT, the distance value for each pixel is defined as the sum of image pixels’ intensity along the shortest path to background. GWDT was originally introduced by Rutovitz (1968). However, most of the previous studies of GWDT and the respective implementations (such as the recently released Matlab toolbox function) were limited to 2D cases, whereas our method and implementation are general for N-dimensional data (n = 2, 3, … ). In the following, we describe our fast implementation within FM framework.

The distance value defined in GWDT fits the ICDB principle. To use GWDT, we often use a low threshold value (e.g. the average intensity of an entire image). Any image pixels that have intensity value no greater than this threshold are called ‘background pixels’. We first set all image background pixels as ‘seeds’, then compute the distances from other pixels to these seed pixels. This process is similar to region growing and thus is formulated within the FM framework in Section 2.2. Here, the edge distance between consecutive image pixel vertices is defined as

where x is source vertex, y is target vertex, I(y) is the intensity of image pixel y. Let d(x) denote the distance value of x. In the initialize step, we set

We will set all background pixels as seeds. The neighbor pixels of all seeds will be set as the initial TRIAL vertices and are pushed into the priority queue. In the growing step, we will apply the formula,

to refresh the distance value from background to skeleton center.

Automated Soma detection: We find that GWDT method provides a way to detect the soma position of a neuron. Normally, the soma has the maximum distance-transformed value (e.g. see results in Section 3.5).

2.4 Initial neuron reconstruction

In APP, the initial neuron reconstruction is essentially produced via finding the single-source (often from the soma) shortest path to all remaining foreground image pixels. APP uses Dijkstra’s algorithm, which needs to first build a graph of all foreground pixels and then find the shortest path from each pixel to the seed. For large 3D image stacks, this approach may need a large amount of computer memory to hold the graph. In APP2, we present a new method to use FM to construct the initial reconstruction (Fig. 2), without the need to create such a large graph.

Fig. 2.

Initial reconstruction based on GWDT and comparison results with or without GWDT. (A) The main GWDT-based skeleton (the major mid-curves) of the tracing implies a good tracing. Sphere: the seed location. Also shown is the out-of-center problem, where the left figure is without GWDT preprocessing and the right figure indicates the main structure goes to the neuron center with GWDT preprocessing. (B) top: parallel-path problem without GWDT preprocessing; bottom: parallel paths disappear after GWDT preprocessing

In our implementation, we add a parental map par on the FM as described in Section 2.2 to generate the shortest path tree from a single source s. Initially, the parent of each image pixel x is set to be itself, i.e. . Then, for each neighbor pixel y of s, we set them to have label ‘TRIAL’, and at the same time . In the recursive step, for the minimum pixel x and each of its neighbor y, we set

The edge distance e(x,y) is defined as the geodesic distance,

where the first item is Euclidean distance of the two pixels, and in the second item is defined in the same form of APP (Peng et al., 2011), where λ_I is a coefficient (set as 10 throughout our tests).

When FM has finished, we can build the initial reconstruction from the parental map.

In addition to the small working space needed, another useful property of FM for generating the initial reconstruction is that it can be stopped easily as needed. We consider two methods in APP2. First, the recursive step will stop when any background pixel becomes ALIVE. This method prevents the marching process growing to any irrelevant area. Second, a user can optionally choose to specify some locations in advance (e.g. some special termini of a neuron) as additional priors; when all of these special locations have been labeled as ALIVE, FM stops. The second method forces FM to reach these specified locations. Both methods are used in practice to generate complete initial reconstructions that cover signals as much as possible and thus make it easier to trace broken pieces or gaps in images.

2.5 Hierarchical pruning

Figure 2 displays examples of initial reconstructions of neurons. They are tree graphs, each of which has a number of spurs. The next step is to find the main skeleton of the tree by removing the unnecessary or redundant spurs. Here, we propose a hierarchical pruning method that contains two steps: a hierarchical segments construction step and a recursive pruning step.

2.5.1 Hierarchical segments construction

For simplicity, we call the initial reconstruction a ‘tree’ in this section. We define a segment in the tree as a path connecting two branching nodes in the tree. In the hierarchical segments construction step, we order all segments in the tree from most important to the least important and thus generate a hierarchy of them. The ‘importance’ of a segment is defined based on its length. The longer a segment, the more important it is. Obviously, there is no overlap between any pair of segments. To get the importance scores, we first find the longest path from the most distal leaf node to the source node (seed). We then delete this segment from the tree and find the second longest segment from the remaining parts in the original tree. We iterate this process until all segments have been sorted.

We further improve the efficiency of the algorithm as follows. We observe that in our decomposition of a tree, each hierarchical segment starts from a leaf node. In addition, there is a one-to-one mapping relationship between each hierarchical segment to a leaf node. Therefore, in a refined algorithm, we construct the hierarchical segments in a bottom-up order. First, we detect the segment from each leaf node to its nearest branch node (excluding the branch node). Each branch node connects to at least two such segments. Then, we merge the branch node to the longest segment (called ‘joint-segment’). Next, the other segments originally connects to the branch node are set as child-segments to the joint segment. We iterate this joint segment merging process until the seed node is reached.

2.5.2 Recursive pruning

In the pruning step, from the pool of undeleted hierarchical segments, we choose one segment at a time following the importance-score in decreasing order. Then, we extend the signal-coverage idea in APP to coverage ratio of this segment (see later in the text). If the coverage ratio is larger than a threshold value (normally 75%), we delete this segment and all its child-segments. Otherwise, we keep this chosen segment and mask the coverage area of the segment. We iterate this process until no segment can be removed.

The coverage area of a segment is defined as the merged coverage area of all nodes in the segment. The coverage area of a node is defined as the sphere area centered at the node, with an estimated radius of the node, which is computed using the method described in Peng et al. (2010b, 2011).

The coverage ratio of a segment is defined as the ratio of the number of all masked nodes with respect to the total number of nodes in the segment. Further, we consider image pixels with different intensities should have different weights. Thus, in our scheme, we use the image-pixel-intensity weighted coverage ratio, which is defined as the sum of intensity of all masked nodes divided by that of all nodes in the segment.

3 EXPERIMENTAL RESULTS

3.1 Results between GWDT and non-GWDT

We compared the new GWDT step in APP2 to those generated without GWDT (see Fig. 2). It is clear that when GWDT is not used (left of Fig. 2A), the detected skeleton of the neuron is often skewed to one side of the shape. This is effectively avoided when GWDT is used (right of Fig. 2A); the respective skeleton best covers the neurite signal in a balanced way.

Figure 2B shows that for complex branching patterns, the shortest path algorithm could easily produce ‘parallel paths’ when GWDT is not used (top of Fig. 2B). This problem is also clearly overcome after GWDT is applied to the image (Fig. 2B bottom). For this test image, the overall morphology of the GWDT-based result (Fig. 2B bottom) appears to be more reasonable than the non-GWDT result.

Of course, when GWDT is not invoked, APP2 can run faster (Table 2), although the accuracy might be compromised in a way similar to Figure 2.

Table 2.

Comparison of running time (seconds) of APP2 and APP on a few images

Image	APP	APP2 (with GWDT)	APP2 (w/o GWDT)
Chiang fly	149.7	28.9	12.6
Dragonfly C154	31.6	6.9	1.6
Dragonfly C168	48.8	7.9	1.9
Dragonfly C171	44.2	10.2	2
Dragonfly C190	32.6	7.6	1.3

Testing is based on a MacPro laptop with 2.6 GHz Intel Core i5.

3.2 Comparison with other methods

We examined the robustness of APP2 by tracing images where signal were deleted (Peng et al., 2010b). Three levels of signal deletion, 30, 60 and 90% were tested (Fig. 3). We compared APP2 to several previous automated methods in the public domain, including APP (Peng et al., 2011), NeuronStudio (Rodriguez et al., 2008) and SimpleTracing (a DT-based tracing approach, Yang et al., 2013), as well as the ‘ground truth’ reconstruction, which was obtained by combining semi-automatic tracing and manual editing. To make a fair comparison, the reported results of competing methods correspond to the best possible parameters fine tuned in our testing.

Fig. 3.

Comparison with different neuron tracing methods subject to the deletion noise. The reconstructions are overlaid on top of the original images for better visualization. The fourth row corresponds to 90% signal is deleted. As it is so dark in this case, we set pixel intensity threshold to 1 so that we are able to compare all different methods. Right side subfigures: the three difference-scores compared with the ‘ground truth’ reconstruction. NS, NeuronStudio; ST, SimpleTracing. Images in (A–D) are brightness enhanced by 50% to make them more visible. The color schemes in (E), (F) and (G) are the same

We calculated several difference scores of the reconstructions produced by the automated methods and the ‘ground truth’. These difference scores measure the ‘spatial distance’ between a particular reconstruction and the ground truth, as well as the percentage of reconstruction elements that have significant, i.e. visible, distance to the nearest reconstruction elements in the ‘ground truth’. These scores, as previously defined in Peng et al. (2010a), are called entire structure average, different structure average and percentage of different structure for simplicity in this article.

Figure 3 shows that APP2 is able to achieve the lowest difference-scores among all methods. It actually consistently produced sub-pixel precision compared with other methods, such as NeuronStudio. For the different structure average score, APP2 and APP are close to each other, but APP2 is better than APP in the entire structure average and percentage of different structure scores.

The Supplementary Figures S1–S6, which include additional comparison examples of various 3D images, also show that APP2 is better than the other methods.

3.3 Improvement on APP

Figure 3 indicates that the performance of APP2 is better, but still close to that of APP. Although this observation is anticipated, it raises a natural question that how much APP2 will improve APP. In our design, the biggest difference between these two methods is how they prune the initial over-reconstructions. Therefore, we studied the ability of APP2 in pruning the initial reconstruction. We also compared the running speed of both methods.

We considered using either APP or APP2 to prune an initial reconstruction, followed by using the other method (APP2 or APP) to check whether there is any further redundancy in the reconstruction that can be removed. After applying this test to a number of complicated dragon fly neurons, we found that (Table 1) on average, APP2 is able to prune most redundant segments in an initial reconstruction tree, leaving a small portion of redundancy that can be detected by APP. On the other hand, when we apply APP first, APP2 is still able to remove many tree segments. This shows the advantage of hierarchical pruning. In this sense, APP2 provides a complementary pruning scheme to the APP method.

Table 1.

The numbers of tree-segments pruned by APP2 and APP when sequentially applying APP2 or APP methods in pruning

Neuron image	First APP2 then APP		First APP then APP2
	APP2	APP	APP	APP2
OP1 fly	9421	0	9180	246
Chiang fly	42 069	3	34 185	6529
Dragonfly C147	411	0	252	159
Dragonfly C150	10 082	1	6709	3410
Dragonfly C152	662	0	588	74
Dragonfly C154	969	0	598	368
Dragonfly C157	6084	3	2350	3731
Dragonfly C158	60 331	25	44 216	16 499
Dragonfly C159	395	0	266	129
Dragonfly C160	7787	0	2639	5118
Dragonfly C161	45 409	22	31 098	14 606
Dragonfly C162	328	1	293	38
Dragonfly C165	2854	1	744	2108
Dragonfly C168	2537	0	1777	753
Dragonfly C169	981	0	720	253
Dragonfly C171	2260	0	1509	750
Dragonfly C173	2189	0	1662	518
Dragonfly C175	4830	0	3239	1555
Dragonfly C179	1905	0	1378	518
Dragonfly C180	456	0	350	106
Dragonfly C183	195	0	145	50
Dragonfly C188	2785	0	2401	381
Dragonfly C189	383	0	331	55
Dragonfly C190	39	0	25	14
Dragonfly C192	1048	0	832	215
Dragonfly C193	624	0	464	163
Dragonfly C194	1243	0	815	426

Table 2 summarizes the running speed of APP2 versus APP for several testing images. It can be seen that APP2 is much faster on these images.

3.4 Real applications in tracing different neuron images of different animals and from different laboratories

We tested APP2 on a variety of real neuron datasets, including, for instance, the fruitfly neurons data used in DIADEM competition, the flycircuit.org database and Janelia fly imagery database, as well as some challenging dragonfly neuron datasets (Gonzalez-Bellido et al., 2013) that have heavy noise.

Figure 4 shows a few examples of tracing various datasets:

1. For images that have uneven image pixel intensity (e.g. Fig. 4c), APP2 is able to produce a complete reconstruction.

2. For images that have fine branches (e.g. Fig. 4d), which are easy to get missed by other tracing methods, APP2 is able to detect them reasonably well.

3. For a neuron that may contain a big cell body (e.g. Fig. 4b), APP2 is able to detect the cell body automatically and therefore reconstruct the entire morphology fully automatically.

Fig. 4.

Examples of tracing results on different neuron data sets contributed by different labs. (A–D): tracing results of neurons of different model animals. (E) 3D reconstructed neurons of a large Drosophila neuron image dataset with 678 neurons. Different colors indicate different neurons

3.5 Large-scale reconstruction of single fruitfly neurons

We applied APP2 to 678 3D 40× confocal images contributed by Chiang laboratory. Each image contains a single neuron labeled in a Drosophila brain. We ran both automatic soma detection and automatic neuron tracing in APP2.

After manual proofreading of the tracing results against the original images, we found that for automatic soma detection, we had a success rate 96.6% for this dataset. The failure cases are mainly due to the insufficient pixel resolution in some of the images and thus poor separation in dense arborization areas. For automated neuron tracing, 629 (92.8%) neurons were reconstructed reasonably well. The unacceptable tracing is mainly due to the poor image quality, i.e. broken pieces of neurite in the respective images.

The 629 successfully traced neurons (Fig. 4e) make up one of the largest automatically traced Drosophila single neuron databases to date. These reconstructions will eventually be documented in publicly available neuron morphology databases such as NeuroMorpho.org.

4 CONCLUSION

We present a new neuron-tracing system that contains several novel algorithms based on FM and hierarchical pruning. We use the FM method to compute both the initial neuron reconstruction and the GWDT, and at the same time also improve the robustness of neuron tracing. Hierarchical pruning sorts the individual segments of an initial reconstruction tree in a hierarchical order, thus facilitating efficient removal of redundant segments in the reconstruction. We have compared our new method to various previous methods on a number of datasets and found a better performance of the new method in most cases.