Advancing paternal age and offspring violent offending: A sibling-comparison study

Abstract

Children born to older fathers are at higher risk to develop severe psychopathology (e.g., schizophrenia and bipolar disorder), possibly due to increased de novo mutations during spermatogenesis with older paternal age. Since severe psychopathology is correlated with antisocial behavior, we examined possible associations between advancing paternal age and offspring violent offending.

Interlinked Swedish national registers provided information on fathers’ age at childbirth and violent criminal convictions in all offspring born 1958–1979 (n=2,359,921). We used ever committing a violent crime and number of violent crimes as indices of violent offending. The data included information on multiple levels; we compared differentially exposed siblings in within-family analyses to rigorously test causal influences.

In the entire population, advancing paternal age predicted offspring violent crime according to both indices. Congruent with a causal effect, this association remained for rates of violent crime in within-family analyses. However, in within-analyses, we found no association with ever committing a violent crime, suggesting that factors shared by siblings (genes and environment) confounded this association. Life-course-persistent criminality has been proposed to have a partly biological etiology; our results agree with a stronger biological effect (i.e., de novo mutations) on persistent violent offending.

Background

Advancing paternal age has been identified as a risk factor for (neuro)psychiatric disorders, such as schizophrenia (Malaspina et al., 2001; Miller et al., 2010) bipolar disorder (Frans et al., 2008; Menezes et al., 2010) and autism spectrum disorders (Hultman, Sandin, Levine, Lichtenstein, & Reichenberg, 2010; Lundstrom et al., 2010; Reichenberg et al., 2006). For example, compared to offspring of men aged 25–29, offspring of men aged 50 or older have a relative risk of 1.66 of being diagnosed with schizophrenia (Miller, et al., 2010). Further, advancing paternal age negatively affected general social abilities in a controlled study on mice (Smith et al., 2009). Human studies also suggest that advancing paternal age is associated with poorer social skills (Weiser et al., 2008) and performance in intelligence tests (Malaspina et al., 2005). There is an association between psychiatric disorders and violence (e.g. Arseneault, Moffitt, Caspi, Taylor, & Silva, 2000; Bo, Abu-Akel, Kongerslev, Haahr, & Simonsen 2011). To date, there are no studies on the possible effects of advancing paternal age on offspring criminality.

The main causal hypothesis to explain these associations is mutational errors (point mutations, copy number variations and chromosome breakage) (Crow, 1999) in spermatogenesis that accumulate as males age. In humans most new mutations originates in the male germ line (Crow, 1999). This is because males’ germ cells undergo a greater number of divisions than females’; females’ germ cells undergo 24 divisions while males’ continuously divide during life at approximately 20–30 divisions per year resulting in approximately 600 divisions by the age of 40 (Crow, 1999). At each cell division there is a probability of new mutations, therefore the number of new mutations is likely to increase with age of father at conception. Other biological explanations, such as faulty epigenetic regulation, have also been suggested (Perrin, Brown, & Malaspina, 2007). We use the phrase “de novo mutations” to collectively refer to these effects. Rare copy number variants has been associated with schizophrenia (Sebat, Levy, & McCarthy, 2009), and there is support of de novo mutations’ involvement in sporadic cases of schizophrenia (Xu et al., 2008) as well as in autism (Sebat et al., 2007). An alternative plausible explanation for the association between advancing paternal age and psychosocial functioning is that males who have children at later ages also carry risk factors for mental illness (see e.g. Petersen, Mortensen, & Pedersen, 2011).

Schizophrenia and bipolar disorder have substantial polygenic components where many variants contribute (Purcell et al., 2009); recently similar results have been found for human intelligence (Davies et al., 2011). If the de novo mutations hit the genome relatively randomly it is not implausible that these mutations affect one, or many, of these genes. Thus de novo mutations might negatively affect general cognitive functioning and possibly lead to more severe effects such as mental illnesses and/or violent crime. Further, there is a general genetic susceptibility for so called externalizing syndromes such as conduct disorder, adult antisocial behavior and substance abuse/dependence (Kendler, Prescott, Myers, & Neale, 2003), and common genes and/or shared environment account for some of the associations between schizophrenia, substance abuse and violent criminal convictions (Fazel, Langstrom, Hjern, Grann, & Lichtenstein, 2009) and between bipolar disorder, substance abuse and violent criminal convictions (Fazel et al., 2010; Fazel, Lichtenstein, Grann, Goodwin, & Langstrom, 2010). In sum, since there is an association between mental illnesses and violent crime and this association is at least partly due to common genes; if the de novo mutation hypothesis is correct, there is reason to suspect that there is an association between paternal age and violent criminality.

Early risk factors for antisocial behavior, such as teenage childbearing and adverse fetal environment, have been thoroughly researched, indicating that biological as well as early social factors influence both onset and persistence of antisocial behavior (see e.g. Dodge & Pettit (2003) for an overview). However, most of the evidence for those risk factors relies on studies of non-related individuals (i.e., they are between-family effects). Numerous researchers have noted that strong causal inferences from studies on early risk factors for antisocial behavior requires study designs that investigate if associations are confounded by factors shared within families (D'Onofrio, Rathouz, & Lahey, 2011; Fergusson, 1999; Lahey & Waldman, 2003; Moffitt, 2005; Rutter, 2007; Thapar & Rutter, 2009). This is also consistent with arguments for using rigorous test of causal inferences in the medical and social sciences (Academy of Medical Sciences Working Group, 2007; Shadish, Cook, & Campbell, 2002). Criminality runs in families (Farrington, Coid, & Murray, 2009; Frisell, Lichtenstein, & Langstrom, 2011; Frisell, Pawitan, Langstrom, & Lichtenstein, 2011), indicating that factors shared within families are responsible for at least part of an individual’s criminal propensity. These familial factors might not be measureable (e.g. genetic predisposition) or very impractical to measure for large scale studies (e.g. emotional neglect during toddlerhood), or may not have been identified yet. Thus, informative research on the association between paternal age at childbearing and offspring antisocial behavior needs to use design features that accounts for such unmeasured factors.

One study design that could help rule out genetic and environmental familial confounds when exploring early risk factors, such as advancing paternal age, is the comparison of differentially exposed siblings (Donovan & Susser, 2011; Lahey & D’Onofrio, 2010; Rutter, 2007). This design include multiple levels of analysis information specific to each offspring (e.g., the father's precise age at the conception of each child), as well as information shared by all siblings in the family. The design allows for adequate controlling for unmeasured factors shared by siblings; that is, factors stable across pregnancies. Put differently, this approach diminishes bias due to factors that are highly correlated between siblings, e.g. family socio-economic status at childbirth. However, factors that are only weakly or not correlated between siblings, such as paternal age, are not controlled. To our knowledge, only two studies of advancing paternal age and offspring functioning have attempted to rule out familial confounding; one on schizophrenia (Petersen, et al., 2011) and another on autism spectrum disorder (Hultman, et al., 2010). Both studies found that advancing paternal age was statistically associated with increased offspring risk for illness, but the support specifically for the de novo mutation hypothesis was mixed; Hultman et al. found that advancing paternal age increases risk beyond age at first child whereas Petersen et al. did not.

When studying causal influences on antisocial behavior, it is also critical to examine outcome heterogeneity. Several researchers have proposed different developmental trajectories of antisocial behavior with varying age of onset and severity (e.g., Farrington (1992), Hinshaw, Lahey, & Hart (1993), Loeber (1988), Moffitt (1993), Patterson, DeBaryshe, & Ramsey (1989), Quay (1987)). It is important to note that current developmental trajectory theories assume that each antisocial behavior is differentially influenced by various causal risk factors. For instance, in a seminal paper by Moffitt (1993), she suggested that adolescence-limited and life-course-persistent antisocial behavior might have different etiology: the former being more socially driven (e.g., peer influences during adolescence), while the latter is more biologically determined (e.g., due to neurodevelopmental problems starting at an early age).

We used official records on criminal convictions to study the association between advancing paternal age and offspring violent offending. We used two outcomes; ever committing a violent crime and number of violent crimes. Further, we took advantage of information at multiple levels of analysis to discriminate between different developmental trajectories. We had access to repeated measurements within each individual, as well as multiple assessments within each family, which allowed estimation of a model for both indices of violent offending and sibling comparison analysis to account for familial confounding. Our aims were (1) to study the effects of advancing paternal age on offspring violent crime, and (2) to evaluate if effects were congruent with a causal effect or due to familial confounding.

Methods

Databases

We linked several nationwide, longitudinal registries maintained by Swedish government agencies using the unique personal identification number given to all Swedish citizens. From the National Crime Register (held by the National Council for Crime Prevention) we obtained official data on criminal convictions for 1973–2004, and from the Hospital Discharge Register (National Board of Health and Welfare) we identified diagnoses of mental illness. The Multi-Generation register (Statistics Sweden) was used to link individuals to their parents, we obtained household socio-economic status from the National Censuses 1960, -70 and -80 (Statistics Sweden), the Total Population Register (Statistics Sweden) provided information on gender, birth country and birth date. The birth date information had monthly resolution and was used to assess age for probands and their parents. We used the Cause of Death and Migration registers (Statistics Sweden) to handle attrition and calculate time at risk.

Eligibility

Our cohort consisted of individuals born 1958 through 1979 who were alive and living in Sweden when reaching 15 years of age, the age of criminal responsibility in Sweden. We also required that participants’ parents were identifiable through the Multi-Generation Register. A total of 3,016,637 individuals born 1958–1979 had lived in Sweden according to the Total Population Register, 533,134 (17.7%) of these did not have two identifiable parents in the Multi-Generation Registry (primarily immigrants) and were hence excluded from the study. Another 119,986 individuals (4.0%) were excluded for not living in Sweden when turning 15. Lastly, 3,596 individuals (0.1%) were excluded due to inconsistent data on emigration/immigration and/or death date. A total of 2,359,921 individuals remained in the study.

Measures

The exposure variable, paternal age at childbirth, was defined as the difference between father’s birth date and child’s birth date. Because birth dates were available by the month, the resulting resolution for paternal age was also in months. Paternal age ranged from 13.5 to 80.4 years (mean = 30.0, 98% were within 19.3–48.9 years). The National Crime Register provided data on violent criminality based on all convictions in Swedish lower general courts between 1 January 1973 and 31 December 2004. Each conviction may include one or more crimes, each with its own offence code. We linked all convictions to individuals within our study population and defined each crime as violent or non-violent. Violent crimes included murder, manslaughter, infanticide, assault, kidnapping, illegal confinement, unlawful coercion, gross violation of a person’s/woman’s integrity, unlawful threat, intimidation, robbery, arson and threats and violence against an officer (Frisell, Lichtenstein, et al., 2011). Attempted and aggravated versions of offences were also included whenever applicable. For each individual we considered two outcome measures: (1) ever committed a violent crime and (2) number of violent crimes committed. To elucidate the difference between persistent and less persistent violent offenders we tabulated the prevalence of various violent crime types stratified by different levels of persistence. The distribution between the different levels of recidivism types did not differ substantially (Table 1). We also used non-violent crimes in sensitivity analyses. Non-violent crimes were all crimes not defined as violent crimes.

Table 1.

Percent (%) of types of violent crimes in Sweden 1973–2004 among violent offenders born 1958–1979, by number of violent crimes.

Offense	Number of violent criminal offences
	1	2–3	4–7	8–14	>14
	N=52,900	N=25,257	N=11,353	N=4217	N=1400
Murder	0.30	0.32	0.27	0.33	0.27
Manslaughter	0.15	0.16	0.17	0.18	0.17
Assault	62.12	54.56	49.69	45.62	41.27
Aggravated assault	1.30	2.01	2.61	2.94	3.32
Kidnapping	0.01	0.05	0.04	0.04	0.03
Illegal confinement	0.26	0.43	0.60	0.56	0.48
Unlawful coercion	0.59	0.88	1.01	0.93	1.13
Gross violation of a person’s/woman’s integrity	0.15	0.16	0.47	0.85	0.74
Unlawful threat	6.64	13.45	17.89	21.36	23.76
Intimidation	10.23	7.99	7.24	6.72	5.99
Robbery	2.58	3.45	4.08	4.37	3.52
Aggravated robbery	0.40	0.50	0.61	0.54	0.33
Arson	0.84	0.98	0.93	0.74	0.32
Aggravated arson	0.06	0.08	0.04	0.06	0.02
Threats and violence against an officer	14.36	14.97	14.33	14.74	18.66

Note: Cells represent the percentages of the violent subtype among the total number of offenses. Infanticide was excluded due to too few observations.

We included maternal age at childbirth and child gender as covariates. Based on the Censuses, we also included a measure of family socioeconomic status (SES) when the child was between 5 and 15 years old, derived from parental occupation and coded into three classes; low (skilled and unskilled workers across all fields), medium (low- and intermediate position white collar workers) and high (high-position white collar workers and self-employed professionals and entrepreneurs) (Frisell, Lichtenstein, et al., 2011). For parity we compared firstborn, by mother, to later born. We used official crime statistics to construct a dichotomous variable reflecting any paternal conviction 1973–2004 and included a dichotomous variable indicating if the father was born in Sweden. Finally, we constructed a dichotomous variable on if individuals had a half-sibling. None of the covariates had missing values except for SES (missing rate = 6.6%). However, missing SES data could arise in two different ways: either not answering the census questionnaire or not residing in Sweden at the time of the census. Since answering the censuses was enforced by law, non-answering might indicate a more general pattern of breaking of social norms. Hence, we chose to use missing values for SES in the analyses since we judged them to be informative.

Since previous research has indicated a connection between paternal age and offspring mental illness, we investigated possible mediating effects of offspring psychiatric problems for the association between advancing paternal age and offspring violent convictions. We created two variables; ever diagnosed with bipolar disorder (ICD-8 (International Classification of Diseases 8^th) diagnostic codes 296.1, 296.3 and 296.8; ICD-9 diagnostic codes 296A, 296C, 296D, 296E and 296W; ICD-10 diagnostic codes F30 and F31) or schizophrenia (ICD-8 and ICD-9 diagnostic code 295; ICD-10 diagnostic code F20) as recorded in the Hospital Discharge Register (1973–2004). These discharge diagnoses are assigned by the attending physician only if a person had been hospitalized overnight.

Statistical methods

Dealing with issues of truncation and censoring (i.e. identifying the time at risk for committing a criminal offense) were essential for the current study since all offspring had not lived through the entire risk period for being convicted of a violent crime. Migration and death were both taken into consideration by subtracting time from death/first emigration until end of follow-up from the individual’s time at risk. We disregarded any convictions recorded after emigration. We also accounted for the time when convicted offenders were sentenced to incarceration (we subtracted time as based on the current legislation for the Swedish Prison and Probation service that suggests that any incarceration up to one month is fully served whereas two thirds of longer incarceration sentences is served; see Swedish Penal Code, 26^th Chapter, 6^th §). Another issue when addressing time at risk is that the risk of criminality differs depending on age (see e.g. Moffitt (1993)). More crimes are committed by younger individuals, causing the risk to commit crimes to be associated with age.

We opted for a so-called Poisson hurdle model, described for example by Min and Agresti (2005), which separately analyzes “ever being convicted of a violent crime” as a Bernoulli variable (i.e. 0 or 1) and “total number of violent crimes” (given being convicted at least once) as a truncated Poisson variable (i.e. a count greater than 0). In comparison with ordinary survival analysis (i.e., analyzing time until first violent criminal offense) or ordinary Poisson models (i.e. only analyzing the number of crimes), the Poisson hurdle model has three advantages:

1. It takes care of inflation/deflation of zeros in count data (as compared to if the data came from an ordinary Poisson process).

2. The model allows us to capture information regarding multiple sentences, thereby providing a way to measure the persistence of criminality (as compared to ordinary survival analyses).

3. It fits well with the notion of etiological difference between ever being convicted and being convicted multiple times, as an index of different developmental trajectories of antisocial behavior (Moffitt, 1993).

The Poisson hurdle model

The model consists of two parts: a Bernoulli part modeling the probability of committing at least one crime, i.e. to pass over the hurdle, and a truncated (at zero) Poisson part modeling the number of crimes committed given that at least one has been committed. The first part can be turned around to say that we are modeling the probability to not commit any crimes. The distribution is thus

$$\{\begin{array}{l}Pr(Y_{ij}=0)=1-p_{ij}\hfill \\ Pr(Y_{ij}=k,k\ge 1)=p_{ij}·e^{-{\mu }_{ij}}\frac{{\mu }_{ij}^k}{k!}\frac{1}{1-e^{-{\mu }_{ij}}}\hfill \end{array}$$

Here p_ij is the probability of committing (at least) one crime, μ_ij is the mean parameter in a Poisson distribution indicating the mean number of crimes committed, for the i:th individual within the j:th family (cluster).

One useful property of the Poisson hurdle model is that we can fit each part separately because the likelihood involving p_ij and μ_ij are orthogonal (Min & Agresti, 2005). Both parts of the Poisson hurdle model fits within the Generalized Linear Models (GLM) framework.

We chose to model p_ij using a complementary log-log link (cloglog) and μ_ij using a log link:

$$\begin{array}{l}\text{cloglog}(p_{ij})=log(-log(1-p_{ij}))={\mathbf{x}}_{1ij}^T{\mathbf{\beta }}_1+log({\omega }_{1ij})\\ log({\mu }_{ij})={\mathbf{x}}_{2ij}^T{\mathbf{\beta }}_2+log({\omega }_{2ij})\end{array}$$

Here x_1ij are covariates for the Bernoulli part and x_2ij are covariates for the truncated Poisson part, these must not be the same since the different parts are fitted separately. The ω_1ij and ω_2ij are offset terms which model the risk over time. The reason for using the cloglog link is that one can view the Bernoulli part as modeling the complement of the probability of observing a zero in a Poisson model with a rate parameter, say λ, independent of the rate parameter in the truncated Poisson part, with a log link. Let Y_ij~Poisson(ω_1ijλ_ij), and the log link: log(λ_ij) = x_1ij^Tβ₁, then

$$\begin{array}{l}P(Y_{ij}=0)=exp(-{\lambda }_{ij}{\omega }_{ij})\iff \\ log(P(Y_{ij}=0))=-{\lambda }_{ij}{\omega }_{ij}\iff \\ log(-log(P(Y_{ij}=0)))=log({\lambda }_{ij})+log({\omega }_{ij})={\mathbf{x}}_{1ij}^T{\mathbf{\beta }}_1+log({\omega }_{ij})\iff \\ log(-log(1-p_{ij}))={\mathbf{x}}_{1ij}^T{\mathbf{\beta }}_1+log({\omega }_{ij}),\end{array}$$

where 1-p_ij = P(Y_ij = 0). This is reasonable because we view the number of violent criminal offenses as a type of counting process.

Estimation of risk over time

We chose to model the offset variable as ω_kij = 1 + q_kT_ij, k = 1, 2, where T_ij is the total time at risk for individual i within family j and q_k are parameters estimated from the data (differing between the Bernoulli and truncated Poisson outcomes). By this we capture the elevated risk of being convicted for a violent criminal offence during adolescence (the 1 in the equation), but allows for variability due to differing time at risk (the q_kT_ij in the equation). However, there are alternative ways of parameterizing the offset term; A standard approach within Poisson regression would be to treat the offset term as ω_kij = T_ij which would be appropriate if we considered the risk to be constant over time. Another way is to use an empirical risk estimation from the incidences of criminal offences per individuals’ ages (i.e. 15 years, 16 years, …, 46 years). Yet another way to parameterize the offset would be to set it to 1 for all individuals, this would correspond to assuming that criminals committed their offenses quite early in life, and would not capture variability due to different time at risk. Because we do not know the true shape of the offset term, we performed sensitivity analyses using these different approaches.

Familial confounding

One aim of this study was to take advantage of the multiple levels of the data and account for familial confounding by studying within-cluster/family effects (Begg & Parides, 2003; Donovan & Susser, 2011; Lahey & D’Onofrio, 2010; Rutter, 2007), so we needed to handle clustering of data. We used a Generalized Estimation Equation (GEE) approach to allow for correlation between family members. Since we are using GEE, all inferences are on a population level. We explicitly modeled within-family effects by comparing the deviation of exposure for siblings from the family mean of exposure. This is in agreement with the de novo mutation hypothesis; the associations are due to new mutations, and these happen continuously over time. For the Bernoulli part proc glimmix in SAS software version 9.2 (SAS Institute, 2002–2008) was used (both for GLM and GEE model fitting) and for the truncated Poisson part we wrote an iterative reweighted least squares procedure (Pawitan, 2001, pp. 394–398) in R (R Development Core Team, 2011) for GEE model fitting and we used the hurdle function from pscl package in R (Zeileis, Kleiber, & Jackman, 2008) for fitting the GLM model. We used Wald-type tests for significance in regression parameters, in the GEE models we employed the robust variance estimator (sandwich estimator) for the tests.

Non-violent crimes

We performed additional analyses on non-violent crimes as outcome. As for violent crime we fitted two main models per outcome measure (ever non-violent crime and number of non-violent crimes); a cohort analysis using actual age in categories (GLM) and a within-family analysis using deviation of paternal age from mean paternal age within the family (GEE).

Results

The total number of registered violent crimes in our cohort was 240,699. These were committed by 95,127 (4.0%) individuals (Table 2). The mean number of violent offences for all violent offenders was 2.53. The incidence was 4.95 violent crimes per 1000 person-years in the general population, and 120.70 for the subgroup of offenders.

Table 2.

Descriptive statistics for the study population of 2,359,921 individuals born in Sweden 1958–1979 assessed for violent criminal offending.

	N	Offspring convicted of violent crime		Mean no. violent crimes per offspring	Incidence (violent crimes per 1000 person years)
		N	Prevalence (%)		Overall	Violent offenders
All	2,359,921	95,127	4.0	2.53	4.95	120.70
Paternal age
<20	47,581	3,972	8.4	2.98	11.32	139.25
20–24	477,909	26,796	5.6	2.64	7.09	126.13
25–29	805,540	30,003	3.7	2.46	4.59	119.85
30–34	566,923	18,433	3.3	2.42	3.89	116.42
35–39	278,921	9,297	3.3	2.48	3.82	113.42
40–44	121,105	4,244	3.5	2.57	4.03	116.05
45–49	43,894	1,582	3.6	2.48	3.97	110.69
50–54	13,190	537	4.1	2.25	4.15	99.90
55–59	3,676	182	5.0	2.88	6.64	134.63
>59	1,182	81	6.9	2.84	9.21	129.77
Maternal age
<20	208,269	15,650	7.5	2.83	9.84	133.57
20–24	746,500	35,635	4.8	2.56	5.92	123.12
25–29	781,003	24,865	3.2	2.39	3.81	116.01
30–34	412,974	12,309	3.0	2.41	3.50	113.92
35–39	166,178	5,138	3.1	2.42	3.39	108.60
40–44	42,143	1,435	3.4	2.49	3.64	106.51
> 44	2,854	95	3.3	2.26	3.17	104.70
Gender
Male	1,211,522	85,011	7.0	2.63	8.95	125.63
Female	1,148,399	10,116	0.9	1.68	0.72	79.59
SES
Low	849,063	44,444	5.2	2.55	6.29	120.81
Medium	820,186	24,131	2.9	2.33	3.30	109.39
High	533,552	13,241	2.5	2.24	2.86	110.07
Missing	157,120	13,311	8.5	3.11	12.81	152.25
Parity
Firstborn by mother	1,031,088	39,276	3.8	2.51	4.66	121.15
Not firstborn by mother	1,328,833	55,851	4.2	2.54	5.16	120.40
Father ever convicted of a violent crime
No	2,269,699	83,386	3.7	2.43	4.31	113.78
Yes	90,222	11,741	13.0	3.27	22.87	177.69
Swedish-born father
No	284,766	20,113	7.1	2.83	10.11	144.02
Yes	2,075,155	75,014	3.6	2.45	4.27	114.95
Maternal and/or paternal half sibling
No	1,908,754	62,276	3.3	2.39	3.72	110.32
Yes	451,167	32,851	7.3	2.80	10.60	142.32
Bipolar diagnosis
No	2,354,628	94,465	4.0	2.52	4.91	120.54
Yes	5,293	662	12.5	3.33	18.16	141.17
Schizophrenia diagnosis
No	2,350,925	93,166	4.0	2.50	4.81	119.63
Yes	8,996	1,961	21.8	3.89	36.75	166.23

Note: All covariates plus schizophrenia and bipolar disorder diagnoses were included in cohort analyses.

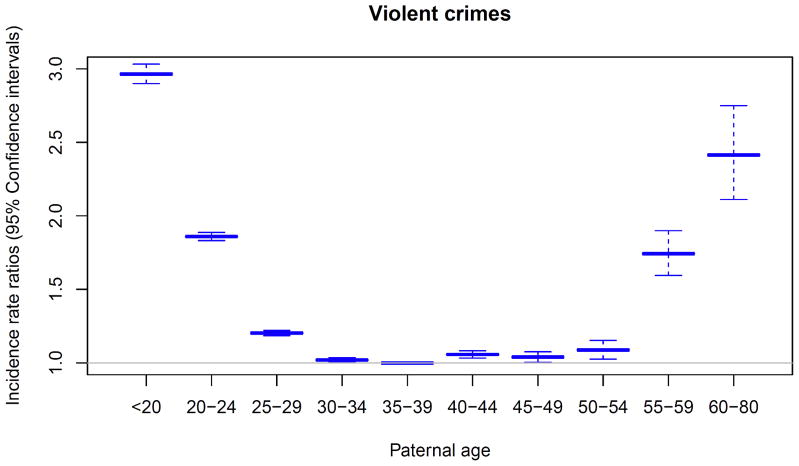
Parental age at childbearing did not have a linear association with the probability of ever committing a crime. The prevalence by paternal age groups went from 8.4% among offspring to fathers below age 20, declining to 3.3% for offspring to fathers aged 30–34 and 35–39, and again increasing to 6.9% among the oldest fathers (Table 2). This U-shaped pattern is also presented in Figure 1, which shows the incidence by paternal age.

Figure 1.

Observed incidence rate ratios of offspring violent criminality as a function of paternal age. Paternal age 35–39 years constituted reference category.

Low maternal age had a similar association to violent crime as low paternal age; however, the prevalence in the older age categories did not increase as dramatically as for paternal age (Table 2). For example; prevalence in age category >44 was only 3.3%, while the lowest prevalence, 3.0%, was found in the maternal age category 30–34. Males were much more likely to have committed a violent crime (7.0%) than females were (0.9%). For the SES variable, the missing category had the highest prevalence of offenders (supporting our decision to treat the category as a fixed effect) and then decreased through the low, medium and high categories. Children who were firstborn (by mother) had a slightly lower prevalence of violent crime (3.8%) than those not firstborn (4.2%). Thirteen percent of children with fathers convicted of a violent criminal offence were themselves convicted, compared to 3.7% of children with fathers not convicted of a violent crime. Having a father not born in Sweden increased the probability of being convicted of a violent crime (7.1% vs. 3.6%) for children of Swedish fathers. Having a half-sibling increased the prevalence of violent criminality to 7.3% vs. 3.3% in families with only full siblings. Being diagnosed with bipolar disorder or schizophrenia also increased the risk for violent offending (12.5% for bipolar disorder and 21.8% for schizophrenia) compared to 4.0% in the total population, indicating relative risks consistent with previous research (systematic reviews in Fazel, Lichtenstein, Grann, et al. (2010) and Fazel, et al. (2009)).

Cohort analyses

Ever committing a violent crime

Table 3 displays the paternal age regression estimates from fitted GLMs, the estimated offset was ω_1ij = 1 + 0.010T_ij. Using 30–34 as reference category, and controlling for all the covariates (except bipolar disorder and schizophrenia) in the Bernoulli model, paternal age still showed an U-shape distribution resembling the observed pattern in Table 2; the risk decreased from fathers age below 20 to fathers aged 30–34, followed by a monotonic increase to the oldest age category. When converting the regression coefficient to risk ratios (i.e., the probability of committing a violent offense in the age category divided by the probability in the reference category using the values for the reference categories of the covariates), the risk for the offspring of the youngest fathers (<20 years) were increased by 30% compared to the offspring born to fathers aged 30–34; the risk among the oldest fathers (>59) was increased by 80%. In the models where the offset was treated differently, and when controlling for birth period, the shape of the association generally persisted (Appendix Table 1).

Table 3.

Parameter estimates for paternal age categories from cohort analyses using the Poisson hurdle model on 2,359,921 (Bernoulli analysis) and 95,127 (truncated Poisson analysis) individuals assessed for violent criminal offending.

	Paternal age	<20	20–24	25–29	30–34	35–39	40–44	45–49	50–54	55–59	>59
Ever committing a violent crime (Bernoulli)	Regression estimate	0.27*	0.15*	0.01	Ref.	0.06*	0.12*	0.15*	0.22*	0.32*	0.59*
	Risk ratio	1.30	1.17	1.01	1	1.07	1.13	1.16	1.24	1.38	1.80
Number of violent crimes (truncated Poisson)	Regression estimate	0.07*	0.02*	−0.01	Ref.	0.03*	0.10*	0.04*	−0.11*	0.21*	0.17*
	Incidence rate ratio	1.07	1.02	0.99	1	1.03	1.10	1.04	0.90	1.23	1.19

Note: GLM-analyses for the two different outcomes adjusted for covariates (treating maternal age as categorical). Offset variable is modeled as 1 + q_k*(time at risk). The estimates for “Ever committing a violent crime” are changes, per unit in offset, for the regression on probability for committing at least one crime using the complementary log-log link. The risk ratio is the probability of committing a violent offense in each age category divided by the probability in the reference category (at the reference categories of the covariates). The estimates for “Number of violent crimes” are changes in the regression on the intensity, per unit in offset, of criminal offenses using the log link. The incidence rate ratio is the incidence rate in each category relative to the incidence rate in the reference category.

^*p < 0.05. Ref = reference category.

Number of violent crimes

We proceeded to fit models for the truncated Poisson outcome variable (again with 30–34 years as reference category; Table 3), the estimated offset was ω_2ij = 1 + 0.093T_ij. After controlling for the covariates, there was a decrease in rate of violent crime from age category <20 to age category 25–29. Also, there seemed to be an increase again after age 25–29, though it was not monotonic and not as clear as for the analyses for ever committing a crime. When converting the regression coefficient to incidence rate ratios (i.e., the incidence rate in each category relative to the incidence rate in the reference category), the risk for the offspring of the youngest fathers (<20 years) was increased by 7% compared to the offspring born to fathers aged 30–34 whereas the risk among children to the oldest fathers (>59) was increased by 19%. These observations were also found in the sensitivity analyses where the offset variable was treated differently and when we controlled for birth period (in 5-year intervals; Appendix Table 2).

Maternal age

Maternal age did not exhibit the U-shape for offspring risk that paternal age did; instead, the effect was higher in younger maternal age categories and lower in older categories (Appendix Table 3). This pattern was found both for ever committing a violent crime as and for number of crimes. In the Bernoulli analysis, the regression estimate went from 0.68 in the youngest age category (mother under 20 years) to −0.21 in the oldest age category (mothers aged over 44 years), corresponding to risk ratios of 1.96 and 0.81, respectively. The figures for the truncated Poisson analysis were 0.14 and −0.18, with corresponding incidence rate ratios of 1.15 and 0.84. These results indicate that the higher risk due to increasing paternal age was not due to correlation between paternal and maternal age; rather, maternal age may counteract advancing paternal age effects.

We conducted additional analyses stratified on schizophrenia or bipolar disorder diagnoses to elucidate if these diagnoses might mediate the association. If there was a strong mediation of the effect, and no strong confounder between mental illness and violent crime, we would expect a substantial change of size of the association between paternal age and violent crime. However, the estimates did not change notably in the non-illness group (Appendix Table 4).

In summary, our analyses show that there are significant associations of both young and old paternal age with criminality, and that the associations are not due to either maternal age or severe psychiatric disorder.

Family-based analyses

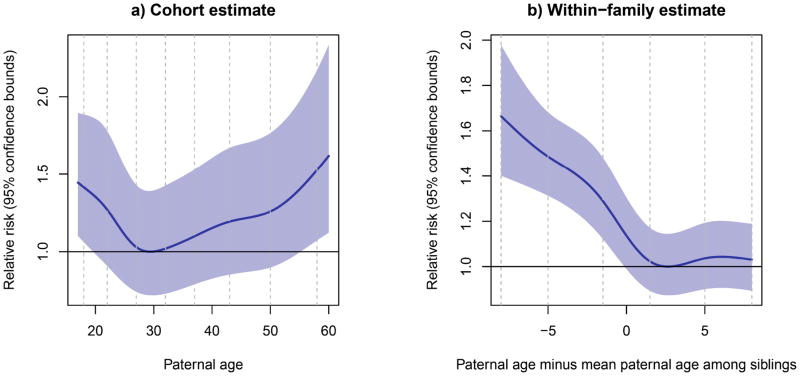
Our second aim was to evaluate whether the effects of advancing paternal age were congruent with a causal effect, or whether the association was due to familial confounding. We therefore continued with within-family analyses to test if observed patterns were present also among offspring of the same father. Here, the deviance in paternal age at child birth for a sibling from the mean paternal age for all births within the paternal family was used in GEE-analyses. Ever committing a violent crime. We restricted the data set to individuals with siblings (1,818,657 individuals). In Figure 2b fitted splines for the within-family effect are plotted, for comparative purposes we included a fitted spline on the cohort effect (i.e. the actual paternal age) in Figure 2a. In the within-family analysis the probability of ever committing a violent crime did not increase with advancing paternal age, but rather decreased (Figure 2b). This is in contrast to the results for the cohort analyses (Table 3; Figure 2a). We therefore conclude that the observed association between advancing paternal age and higher probability of ever committing a violent crime might not be causal. In contrast, the higher probability of committing a violent crime among offspring to younger parents might be causal. As seen in Figure 2b, the within-family effect is almost linear; fitting a linear effect yielded a regression coefficient of −0.039 (p < 0.0001) per year increase in paternal age.

Figure 2.

Analyses for the probability of ever committing a violent crime (Bernoulli outcome). a) Fitted natural spline from the cohort analysis (GLM) with 95% confidence bounds with paternal age as exposure. b) Spline for the within-family effect (GEE) with 95% confidence bounds based on the robust variance estimation. The exposure is deviation of paternal age from mean paternal age within the family. Results were transformed to probabilities and divided by the lowest value in the age span (0.018 for cohort and 0.013 for within-family). The vertical dashed lines are the knots in the splines.

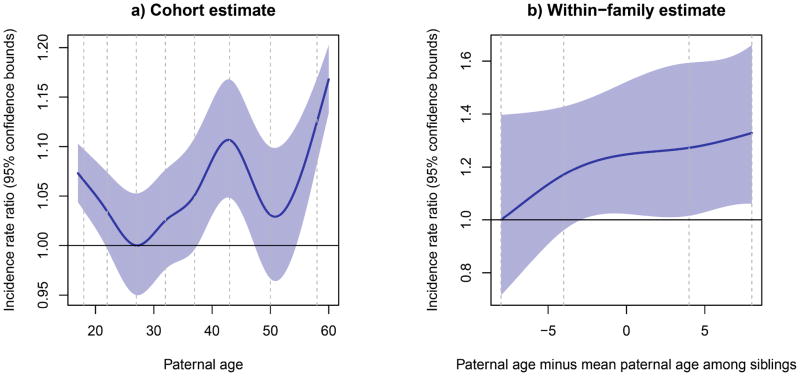
Number of violent crimes

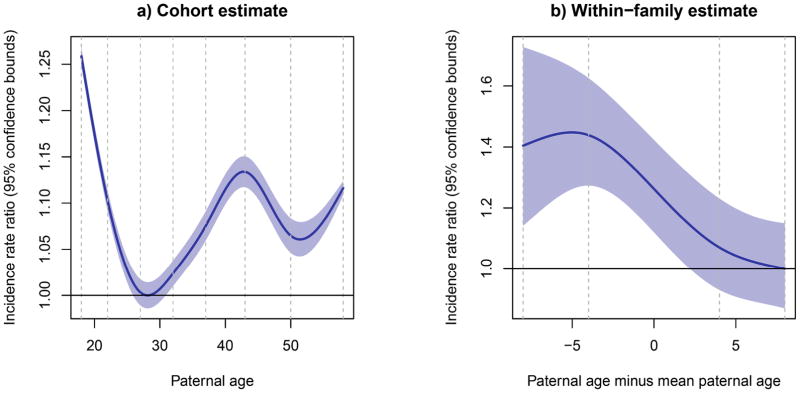
We proceeded to fit a GEE model for the truncated Poisson outcome. We restricted the analysis to individuals with siblings who also committed at least one violent offence (16,709 individuals). We used splines to evaluate the need to fit a non-linear effect for the within-family effect. In Figure 3b, the fitted splines of within-family effect are plotted, for comparative purposes we included a fitted spline on the cohort effect in Figure 3a. The within-family effect is monotonically increasing and we accepted that a linear effect could be fitted. The linear effect was 0.014, corresponding to an incidence rate ratio of 1.014 per year of paternal age that siblings differ, the p-value was 0.0006 (using the robust variance estimator). To exemplify: on a population level, given that two siblings commit violent crimes, at the same number of years at risk for siblings that differ 10 years in age, the younger sibling (i.e. born to older father) have a mean number of committed crimes that is 1.15 of that of the older sibling. Thus, we conclude that there is an effect of advancing paternal age on number of violent crimes committed by an offender that is not accounted for by familial confounding.

Figure 3.

Analyses of number of violent crimes committed by violent offenders (truncated Poisson outcome). a) Fitted natural spline from the cohort analysis (GLM) with 95% confidence bounds with paternal age as exposure. b) Spline for the within-family effect (GEE) with 95% confidence bounds based on the robust variance estimation. The exposure is the deviation of paternal age from mean paternal age within family. Results were transformed to rates and divided by the lowest value in the age-span (2.10 for cohort and 0.37 for within-family). The vertical dashed lines are the knots in the splines.

Sensitivity analyses

We confirmed our result with a subset of siblings where fathers were aged over 30 and recalculated family mean and deviations according to the subsample (529,030 individuals for Bernoulli analysis and 4,025 individuals for truncated Poisson analysis). The within-family regression estimates was −0.044 (p < 0.0001) and 0.020 (p = 0.015) for the Bernoulli- and truncated Poisson analyses, respectively. Similarly, we performed analyses with fathers were aged under 30 (872,962 for Bernoulli and 8,844 for truncated Poisson), the regression estimates were –0.048 (p <0.0001) and 0.019 (p = 0.036), respectively. Further, we performed additional analyses with a variable indicating if a person had any diagnosis of mental illness (schizophrenia or bipolar disorder) and the regression estimates did not change markedly (Bernoulli: −0.038, p < 0.0001; truncated Poisson: 0.015, p = 0.0004).

We also performed a set of analyses where we defined the outcome variable to be non-violent crimes (Appendix Table 5;Appendix Figures 1 and 2). In the cohort analyses, we found a similar U-shaped association for both outcome variables. The within-family analyses of ever committing a non-violent crime gave similar risk estimates compared to the analysis of ever committing a violent crime (Appendix Figure 1b; linear effect regression coefficient = −0.022, p-value < 0.0001). Must notably was that there was no increase with advancing paternal age in the within-family analysis for number of non-violent crimes committed (Appendix Figure 2b; linear effect regression coefficient = −0.032, p-value < 0.0001), indicating a different etiology compared to number of violent crimes.

Discussion

Similar to studies of severe psychopathology (Frans, et al., 2008; Hultman, et al., 2010; Malaspina, et al., 2001), we found that also advancing paternal age at childbirth was associated with increased risk of offspring violent criminality. The association of increasing paternal age and higher probability of ever committing a violent crime seemed to be due to familial confounding. In contrast, the association remained for number of violent crimes when we controlled for familial confounding (i.e., in the within-family analyses) suggesting a causal effect. These results thus suggest a different etiology in ever committing a violent crime compared to persistence of violent offending (number of crimes) and highlights the importance in considering heterogeneity in antisocial behavior. If the de novo mutation hypothesis is correct then the effect of advancing paternal age on violent crime is biological, and if life-course-persistent criminality has a stronger biological etiology as claimed by Moffitt and others (Farrington, 1992; Hinshaw, et al., 1993; Loeber, 1988; Moffitt, 1993; Patterson, et al., 1989; Quay, 1987), we would expect the pattern of larger effect on the number violent crimes than on committing any violent crime as found here.

Advancing paternal age and ever committing a violent crime

We found an association between advancing paternal age and offspring risk of ever being convicted of a violent offense. However, when we looked at within-family estimates of paternal age on the probability of committing at least one violent crime the observed association for older fathers did not persist. We interpret this result as familial factors being responsible for the association. This result highlights the old mantra that association does not mean causation, and shows the importance of conducting studies where familial effects are accounted for to avoid incorrect interpretations of associational observations when predicting antisocial behavior (D'Onofrio, et al., 2011; Moffitt, 2005).

Advancing paternal age and number of violent crimes

We concluded that advancing paternal age was causally associated with persistence; a higher rate of violent crimes among violent offenders. This is in agreement with earlier findings on the effect of advancing paternal age on offspring risk of mental illnesses schizophrenia (Malaspina, et al., 2001) and bipolar disorder (Frans, et al., 2008). Since this result persisted in within-family analysis, it is consistent with a causal effect. Our finding supports the de novo mutation hypothesis; new mutations in male germ cells might explain the increase in number of violent crimes among children of older fathers. The monotonically increasing effect (Figure 3b) also supports that the association may arise from continuous accumulation of mutations in male germ cells with advancing paternal age. However, it should be noted that in this study we did not measure actual new mutations.

Heterogeneity in criminality

Current theories of developmental trajectories postulate that the trajectories of different developmental types of antisocial behavior are differentially influenced by various causal risk factors. Moffitt (1993), as well as others, have distinguished between adolescence-limited and life-course-persistent antisocial behavior, and suggested that the former is more socially driven (e.g., peer influences during adolescence), while the latter is more biological (e.g., due to neurodevelopmental problems starting at an early age). The notion that life-course-persistent antisocial behavior might have a stronger biological etiology are also indicated by longitudinal twin studies, which suggest that genetic effects have early onset and persist over time, whereas environmental effects seem to be adolescent-onset (Silberg, Rutter, Tracy, Maes, & Eaves, 2007). Thus, if de novo mutations are important for antisocial behaviors we would expect them to be more important for life-course-persistent antisocial behavior in general and for our measure of number of violent crimes. We believe that our results of a within-family effect of advancing paternal age on repeated violent criminality, in contrast to ever having committed a violent crime, are congruent with the de novo mutation hypothesis, especially since we did not find a within-family effect in the sensitivity analyses of non-violent crimes.

Maternal age

Our cohort analysis showed no association between advancing maternal age and risk for offspring violent offending; on the contrary, advancing maternal age lowered the risks. Therefore, we believe that the within effect of paternal age is not due to confounding with maternal age.

Younger fathers and violent crime

We examined if advancing paternal age is associated with risk for committing a violent crime. However, our analyses showed non-linear effects with both young and old paternal age as risk factors for violent criminality. For ever committing a violent crime, the increased risk for younger fathers persisted in the within-family analyses, and thus was consistent with a causal effect. Since this was not our original research question we have not investigated the result further in the current manuscript. However, the results are consistent with some research on the effect of maternal teenage childbearing and criminality in offspring (D'Onofrio et al., 2009; Harden et al., 2007), although other studies have suggested the association is not causal (Geronimus, Korenman, & Hillemeier, 1994; Turley, 2003). Future quasi-experimental research is needed to more fully understand the mechanisms through which early maternal and paternal age at childbearing influence offspring antisocial behavior.

Mental illness and violent criminality

We also assessed the possible mediation of the association between advancing paternal age at childbearing and offspring criminal convictions by schizophrenia or bipolar disorder. We are aware that conducting analyses with a true mediator as a covariate will not unanimously inform about if it is a mediator or not (Glymor & Greenland, 2008). Yet, we would expect a big change in our estimates if the association was strongly mediated by mental illness. However, our results for the non-ill group did not differ much from that including the ill group, leading us to believe that our measure of mental illness does not mediate our association to that extent that we need to separate analyses into mentally ill and non-ill groups

Strengths and limitations

One strength of our study is the large population-based sample. We had total coverage of exposure, outcome and covariates because official records were used. Using the Poisson hurdle model gave vital information on possible etiological differences between the two violent outcome measures, and we used information from multiple assessments per individual as well as multiple individuals per family. Importantly, the study took advantage of information at multiple levels of analysis to conduct sibling-comparison analyses, an approach that can rule out many genetic and environmental factors that might confound the association between advancing paternal age at childbearing and offspring antisocial behavior.

One obvious limitation, as already mentioned, is confounding of the different time scales and its effect on the association studied. We have tried to solve this by testing different models for time at risk; while we chose one of the models we also performed sensitivity analyses with the others with similar results. In our choice of model for time at risk, each individual starts off at the same risk level and acquires additional risk with time, the additional risk per time is estimated from the data. We chose not to control for birth period, instead we limited the birth period to a 22 year interval where the incidence per age was approximately similar across different birth years.

Treating missing SES as a category might induce bias. However it was clear that the missing category could not be a mixture of the other categories with regard to outcome, since individuals in this category had a higher risk for violent criminality than in any of the other categories. Therefore we are confident that our use of missing values as its own category is justified.

Although we used within-family estimates, we cannot disregard the possibility that the effect found could result from unmeasured confounding (Donovan & Susser, 2011; Lahey & D’Onofrio, 2010). The within-family estimation correctly controls for unmeasured confounders shared by siblings, however non-shared or partly-shared confounders can still cause non-causal associations. Examples of such confounders are peer influence during adolescence, child rearing regime (which might have changed between siblings) etc. Similarly, we could not investigate unmeasured mediations. For example, it is possible that our index of mental illness (requiring overnight hospitalization) was too crude to capture a possible causal mediation.

Conclusions

We investigated the association between advancing paternal age and offspring violent criminality in a large Swedish total population sample. By using two different outcome measures we could identify distinct differences in how advancing paternal age affected the risk of ever committing a violent crime and the rate of violent crimes among violent offenders. We compared siblings to rigorously test the strength of our causal inferences. We found an association between higher paternal age and risk of being convicted of at least one violent crime; however, this association was due to familial (genetic and environmental) confounds that influence all siblings in the family. Further, we found an association between higher paternal age and the rate of violent criminal convictions among violent offenders. Since this effect persisted when familial confounds were controlled for, it is thus due to factors specific for each offspring in a family and consistent with a causal effect. One hypothesis that tries to explain the effect of paternal age on disadvantageous outcomes is that of de novo mutations in the male germ line. The hypothesis can be investigated by identifying actual de novo mutations. However the mechanism through which this works is unknown. Thus, further research might focus on finding mediators and mapping the mechanism. In addition to previously mentioned possible mediators (i.e. mental illness and general cognitive functioning), perinatal effects might be of importance.

Appendices

Appendix Table 1.

Parameter estimates for paternal age categories from sensitivity analyses using different offset terms for the Bernoulli outcome.

Paternal age Offset	<20	20–24	25–29	30–34	35–39	40–44	45–49	50–54	55–59	>59
1	0.27*	0.16*	0.00	Ref.	0.07*	0.13*	0.16*	0.22*	0.33*	0.59*
Time at risk	0.22*	0.14*	0.02	Ref.	0.03	0.08*	0.10*	0.20*	0.31*	0.59*
Empirical/incidences	0.23*	0.15*	0.01	Ref.	0.04*	0.09*	0.12*	0.20*	0.31*	0.58*
Birth year
1 + q1*(time at risk)	0.26*	0.16*	0.02	Ref.	0.05*	0.11*	0.14*	0.22*	0.33*	0.60*
1	0.26*	0.16*	0.02	Ref.	0.05*	0.11*	0.14*	0.22*	0.33*	0.60*
Time at risk	0.26*	0.16*	0.02	Ref.	0.05*	0.11*	0.14*	0.22*	0.32*	0.60*
Empirical/incidences	0.26*	0.16*	0.02	Ref.	0.05*	0.11*	0.14*	0.22*	0.32*	0.60*

Note: GLM analyses of Bernoulli outcome, adjusted for covariates and using different offsets.

Appendix Table 2.

Parameter estimates for paternal age categories from sensitivity analyses using different offset terms for truncated Poisson outcome.

Paternal age	<20	20–24	25–29	30–34	35–39	40–44	45–49	50–54	55–59	>59
Offset
1	0.10*	0.03*	−0.01	Ref.	0.05*	0.11*	0.06*	−0.09*	0.21*	0.17*
Time at risk	0.05*	0.01	−0.00	Ref.	0.02*	0.09*	0.03	−0.11*	0.21*	0.17*
Empirical/incidences	0.07*	0.01	−0.01	Ref.	0.03*	0.10*	0.04	−0.11*	0.20*	0.17*
Birth periods
1 + q2*(time at risk)	0.08*	0.02*	−0.01	Ref.	0.04*	0.11*	0.04*	−0.10*	0.21*	0.18*
1	0.09*	0.03*	−0.01	Ref.	0.04*	0.11*	0.05*	−0.09*	0.21*	0.18*
Time at risk	0.09*	0.03*	−0.01	Ref.	0.04*	0.11*	0.05*	−0.10*	0.21*	0.18*
Empirical/incidences	0.09*	0.03*	−0.01	Ref.	0.04*	0.11*	0.05*	−0.10*	0.21*	0.17*

Note: GLM analyses on truncated Poisson outcome, adjusted for covariates and using different offsets. The upper three rows were not adjusted for birth year whereas the lower four rows were adjusted for birth year.

^*p < 0.05. Ref. = reference category.

Appendix Table 3.

Parameter estimates for maternal age categories from cohort analyses.

	Maternal age	<20	20–24	25–29	30–34	35–39	40–44	≥45
Ever committing a violent crime	Regression estimate	0.68*	0.40*	0.11*	Ref.	−0.06*	−0.04	−0.21*
	Risk ratio	1.96	1.49	1.12	1	0.95	0.96	0.81
Number of violent crimes	Regression estimate	0.14*	0.07*	0.01	Ref.	−0.04*	−0.05*	−0.18*
	Incidence rate ratio	1.15	1.07	1.01	1	0.97	0.95	0.84

Note: GLM-analyses for maternal age for the two different outcomes adjusted for covariates (treating paternal age as categorical). Offset variable is modeled as 1 + q*(time at risk). The estimates for “Ever committing a violent crime” are changes per unit in offset for the regression on probability for committing at least one crime using the complementary log-log link. The risk ratio is the probability of committing a violent offense in each age category divided by the probability in the reference category (at the reference categories of the covariates). The estimates for “Number of violent crimes” are changes in the regression on the intensity, per unit in offset, of criminal offenses using the log link. The incidence rate ratio is the incidence rate in each category relative to the incidence rate in the reference category.

^*p < 0.05. Ref. = reference category.

Appendix Table 4.

Parameter estimates for paternal age categories from sensitivity analyses excluding individuals diagnosed with mental illness.

	Paternal age	<20	20–24	25–29	30–34	35–39	40–44	45–49	50–54	55–59	>59
Ever committing a violent crime	Regression estimate	0.27*	0.16*	0.01	Ref.	0.06*	0.12*	0.14*	0.21*	0.31*	0.59*
Number of violent crimes	Regression estimate	0.08*	0.02	−0.01	Ref.	0.02*	0.09*	0.02	−0.18*	0.18*	0.21*

Note: Estimates for individuals without any diagnosis of schizophrenia or bipolar disorder. GLM-analyses for the two different outcomes adjusted for covariates (treating maternal age as categorical). Offset variable is modeled as 1 + q*(time at risk). The estimates for “Ever committing a violent crime” are changes, per unit in offset, for the regression on probability for committing at least one crime using the complementary log-log link. The estimates for “Number of violent crimes” are changes in the regression on the intensity, per unit in offset, of criminal offenses using the log link.

^*p < 0.05. Ref. = reference category.

Appendix Table 5.

Parameter estimates for paternal age categories from cohort analyses for non-violent crimes.

	Paternal age	<20	20–24	25–29	30–34	35–39	40–44	45–49	50–54	55–59	>59
Ever committing a non-violent crime	Regression estimate	0.19*	0.11*	0.01*	Ref.	0.03*	0.09*	0.12*	0.18*	0.21*	0.26*
	Risk ratio	1.20	1.11	1.01	1	1.03	1.09	1.12	1.20	1.23	1.28
Number of non-violent crimes	Regression estimate	0.18*	0.05*	−0.02*	Ref.	0.05*	0.11*	0.08*	0.01	0.12*	0.09*
	Incidence rate ratio	1.19	1.05	0.98	1	1.05	1.12	1.08	1.02	1.13	1.10

Note: GLM-analyses for the two different outcomes adjusted for covariates (treating maternal age as categorical). Offset variable is modeled as 1 + q_k*(time at risk). The estimates for “Ever committing a non-violent crime” are changes, per unit in offset, for the regression on probability for committing at least one non-violent crime using the complementary log-log link. The risk ratio is the probability of committing a non-violent offense in each age category divided by the probability in the reference category (at the reference categories of the covariates). The estimates for “Number of non-violent crimes” are changes in the regression on the intensity, per unit in offset, of non-violent criminal offenses using the log link. The incidence rate ratio is the incidence rate in each category relative to the incidence rate in the reference category.

^*p < 0.05. Ref. = reference category.

Appendix Figure 1.

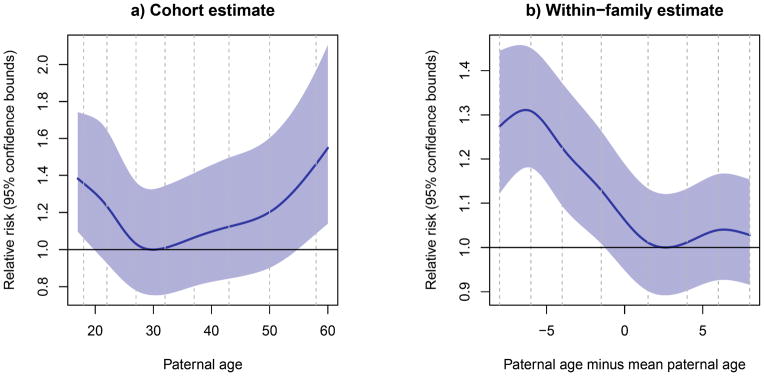
Analyses for the probability of ever committing a non-violent crime (Bernoulli outcome). a) Fitted natural spline from the cohort analysis (GLM) with 95% confidence bounds with paternal age as exposure. b) Spline for the within-family effect (GEE) with 95% confidence bounds based on the robust variance estimation. The exposure is deviation of paternal age from mean paternal age within family. The results are transformed to probabilities and divided by the lowest value in the age span (0.002 for cohort and 0.068 for within-family). The vertical dashed lines are the knots in the splines.

Appendix Figure 2.

Analyses for the number of non-violent crimes committed (truncated Poisson outcome). a) Fitted natural spline from the cohort analysis (GLM) with 95% confidence bounds with paternal age as exposure values. b) Spline for the within-family effect (GEE) with 95% confidence bounds based on the robust variance estimation. The exposure is deviation of paternal age from mean paternal age within family. Results are transformed to rates and divided by the lowest value in the age-span (2.54 for cohort and 1.54 for within family). The vertical dashed lines are the knots in the splines.