Inferential Precision in Single-Case Time-Series Data Streams: How Well Does the EM Procedure Perform When Missing Observations Occur in Autocorrelated Data?

Abstract

The case-based time-series design is a viable methodology for treatment outcome research. However, the literature has not fully addressed the problem of missing observations with such autocorrelated data streams. Mainly, to what extent do missing observations compromise inference when observations are not independent? Do the available missing data replacement procedures preserve inferential integrity? Does the extent of autocorrelation matter? We use Monte Carlo simulation modeling of a single-subject intervention study to address these questions. We find power sensitivity to be within acceptable limits across four proportions of missing observations (10%, 20%, 30%, and 40%) when missing data are replaced using the Expectation-Maximization Algorithm, more commonly known as the EM Procedure (Dempster, Laird, & Rubin, 1977).This applies to data streams with lag-1 autocorrelation estimates under 0.80. As autocorrelation estimates approach 0.80, the replacement procedure yields an unacceptable power profile. The implications of these findings and directions for future research are discussed.

Experts have concluded that maximum likelihood methods are the preferred missing data management approach in group multivariate designs (e.g., Horton & Kleinman, 2007; Ibrahim, Chen, Lipsitz, & Herring, 2005; Ragunathan, 2004). Velicer and Colby (2005a, 2005b) extended this finding to time-series designs by establishing the superiority of maximum likelihood methods to other ad hoc procedures in the estimation of various critical time-series parameters. Velicer and Colby (2005a) applied Monte Carlo simulation to data streams with 100 observations per phase and autoregressive integrated moving averages analysis (ARIMA; Box & Jenkins, 1970) to test the accuracy of parameter estimates. They found the Expectation-Maximization Algorithm (more commonly known as the EM Procedure; Dempster, Laird, & Rubin, 1977) approach to be a good solution with minimal distortion. The EM Procedure is an algorithm derived from maximum likelihood estimation techniques that is available in many common statistical software packages used in the social sciences. However, single-case time-series designs in intervention research rarely satisfy the minimum requirements for autoregressive integrated moving averages analysis used by Velicer and Colby (≈ 30– 50 observations per phase; e.g., Borckardt et al., 2008; Box & Jenkins, 1970). Thus, examination of the relevance of their conclusions in the context of more typical intervention research is warranted.

The time-series design is a longitudinal methodology that requires repeated observations over time (from a single unit or person) across conditions or phases. Among the social sciences, the time-series design occurs most naturally in the fields of physiological psychology, econometrics, and finance where each phase-of-interest has hundreds or thousands of observations that are tightly packed across time (e.g., electroencephalography actuarial data, financial market indices). However, time-series designs are now becoming more common in intervention research conducted in the clinical setting (e.g., Borckardt et al., 2008; Green, Rafaeli, Bolger, Shrout, & Reis, 2006; Kazdin, 2008; Smith, 2011).

Unlike the rich data streams generated by other disciplines, the typical clinical intervention data stream is much shorter, with baseline observation periods most commonly in the range of 8 to 12 measurement points (Center, Skiba, & Casey, 1986; Jones, Vaught, & Weinrott, 1977; Sharpley, 1987; Smith, 2011). Center et al. (1986) suggested 5 as the minimum number of baseline measurements in order to accurately estimate autocorrelation. However, this suggested benchmark doesn't always satisfy the requirements of time-series analytic methods, such as ARIMA. Longer baseline periods also increase the validity of an intervention effect and also reduce the biasing effects of autocorrelation (Huitema & McKean, 1994). Behavioral interventions targeting specific, and often singular, dependent variables are often much shorter, as evidenced by the findings of Huitema's (1985) review of 881 experiments published in the Journal of Applied Behavior Analysis, which resulted in a modal number of 3 to 4 baseline points. A number of recent time-series simulation studies have modeled their data after these very brief interventions (e.g., Manolov & Solanas, 2008; Manolov, Solanas, Sierra, & Evans, 2011; Solanas, Manolov, & Onghena, 2010). However, a recently completed systematic review of 409 recently published single-case experiments by Smith (2011) suggests that baseline periods have increased since the Huitema review of 1985: The Smith review found a mean number of 10.22 observations in the baseline phase. The present study addresses the limitations of these previous simulation studies in which modeling of time-series data streams occurred with either very short or very long baseline periods. This simulation study uses a 10 data-point baseline length, which is more likely to occur in applied clinical intervention research.

There are two real-world implications of conducting intervention research using a time-series design: Longitudinal designs of all types are inherently susceptible to missing observations (Laird, 1988), due in part to the fact that most research designs require observations to occur outside the controlled confines of a laboratory and across an extended period of time (weeks or months compared to seconds or minutes). Since time-series analysis techniques assume complete data, it is imperative that researchers identify a reliable method of substitution that maximizes the precision of our inferences regarding an intervention effect. Second, when we want to test intervention effects in short time-series data streams with single subjects, the paucity of observations compromises our ability to estimate effect above and beyond autocorrelation with few exceptions.

As time-series designs become more common in intervention research, it will be imperative to understand the way in which autocorrelation and missing values affect statistical inferences drawn from this type of data. Numerous statistical methods have been proposed in recent years to analyze single-subject research that accounts for autocorrelation (e.g., Borckardt et al., 2008; Manolov & Solanas, 2009; McKnight, McKean, & Huitema, 2000; Parker & Brossart, 2003; Parker & Vannest, 2009; Parker, Vannest, Davis, & Sauber, 2011; Solanas et al., 2010); yet, there appears to be no consensus regarding the best available method (e.g., Campbell, 2004; Kratochwill et al., 2010;Manolov et al., 2011; Parker & Brossart).

This Monte Carlo simulation study examines the impact of employing the EM Procedure for missing observations on time-series data streams typical of the case-based designs encountered in the clinical outcome literature (e.g., Borckardt et al., 2008; Kazdin, 1992; Lambert & Ogles, 2004; Smith, 2011). In contrast to the studies conducted by Velicer and Colby (2005a, 2005b), Manolov and Solanas (2008), Ferron and Sentovich (2002), and others, we are not necessarily concerned with the accuracy of maximum likelihood estimations (e.g., the EM Procedure) for missing observations in the context of model parameter fit. Instead, we focused on the precision of inferred significance based on time-series level-change (phase-effect) analyses when missing observations have been replaced using the EM Procedure. As the Velicer and Colby (2005a) study demonstrated, the EM Procedure results in relatively accurate estimations of the phase-effect statistics compared to other methods. However, to our knowledge there has yet to be an examination of the way in which these estimates are related to inferential precision. Based on conventional wisdom and previous research findings, we hypothesized that as the proportion of missing data increased, power sensitivity would deteriorate. Similarly, we hypothesized that power sensitivity would deteriorate as autocorrelation increased: Previous single-case time-series simulation studies have established the relationship between higher autocorrelation estimates and distorted effect-size estimations using various analytic techniques (e.g.,Manolov & Solanas, 2008, 2009; Manolov et al., 2011), suggesting that autocorrelation will have an effect on inferential precision as well.

Methods

Outline of Study Procedures

1. Monte Carlo simulation was used to create 5,000 time-series data streams modeled after a typical 8-week study of psychotherapy effectiveness: 10 baseline and 56 intervention data points. Equal proportions of 5 levels of autocorrelation were programmed and were stable across both phases (0.0, 0.2, 0.4, 0.6, 0.8.)

2. Data points were removed completely at random from the data streams in four proportions: 10%, 20%, 30%, and 40%.

3. Missing observations were then replaced using the EM Procedure.

4. A simple effect of phase was calculated for each data stream using Glass's Δ.

5. Power sensitivity was determined across each proportion of missing data and level of autocorrelation.

The Monte Carlo Simulation of Data Streams

In order to mimic the basic A-B design commonly used in treatment outcome research, our simulated data streams are comprised of a 10-day baseline phase and a 56-day (8-week) intervention period, with a daily measurement frequency (i.e., 1 day = 1 measurement). The majority of psychotherapy research is conducted on treatments offered once a week for not more than 14 weeks (Lambert, Bergin, & Garfield, 2003). We chose this simulated intervention period length in order to better simulate a typical psychotherapy treatment and also address the limitations in the literature of modeling simulation studies after very brief behavioral interventions (e.g., Manolov & Solanas, 2008; Manolov et al., 2011; Solanas et al., 2010). The longer data streams also allowed for more accurate estimates of autocorrelation, particularly during the baseline period.

This study used a Monte Carlo simulation to create the time-series data. The simulations were conducted using custom-developed software written using RealBasic (RealSoftware Inc., 2011) by the second author. ¹ The formula used for the simulations is presented as Equation 1.

$$y_i=\alpha \times S{(n_1)}_i+{\epsilon }_i$$ (1)

Where:

εi	ρεi − 1+ei
ρ	autocorrelation
α	step size
ei	indicates each is independently identically standard normally distributed: N(0,1)
n1	Baseline phase length
n	data stream length
i	time

S is a step function being 0 at times i=1, 2, 3…n₁ and 1 at times i=n₁+1, n₁+2, n₁+3…n.

Manolov and Solanas (2008) determined that calculated effect sizes were linearly related to the autocorrelation of the data stream. Thus, 5,000 data streams were created with equal proportions of five different levels of programmed lag-1 autocorrelation that was stable across the two phases (0.0, 0.2, 0.4, 0.6, and 0.8), and a distribution of a mean effect size of 2 (Glass's Δ; [Mean of Phase B – Mean of Phase A] / Standard Deviation of Phase A), programmed to contain a set of random normal deviates with a standard deviation of 1 across each level of autocorrelation. The starting value of the step and the intercept was set to 0. The next 9 values were calculated using Equation 1, with 0 as a constant intercept before the step (i.e., the shift between the baseline and intervention phases). Since the simulated data streams contain a set of random normal deviates, the step size represents the effect size in question, which is the number of standard deviation for each series of simulations. The programmed autocorrelation values are not altered around the step and remain constant between both phases in the data stream. The described characteristics of the 5,000 data streams are prior to the removal of observations and subsequent substitution of missing values described in the remainder of this article.

Removal of Observations

One assumption of maximum likelihood estimation techniques, such as the EM Procedure, is that the data are either missing at random (MAR) or are missing completely at random (MCAR). Ibrahim et al. (2005) discussed these different classifications of missing data.² A third classification of missing values is those that are nonignorable or systematically missing from the data (e.g., the observation that is missing is a function of the value that is not being reported). For example, a suicidal patient may not report the severity of suicidal ideation on days in which these values would be very high. The current study removed data completely at random, satisfying the MCAR assumption. From the original data set of 5,000 data streams, four proportions of observations were randomly removed (10%, 20%, 30%, and 40%). These proportions are identical to those of the Velicer and Colby (2005a) study, which was based on the findings of Rankin and Marsh's (1985) study of the effects of missing data on model fit.

Replacing Missing Observations

In a similar Monte Carlo simulation study, Velicer and Colby (2005a) demonstrated that maximum likelihood methods, such as the EM Procedure, yielded accurate estimates of time-series model parameters, but with significantly longer data streams than this and other time-series simulation studies. Horton and Kleinman (2007) report that for each missing observation, “multiple entries are created in an augmented dataset for each possible value of the missing covariates, and a probability of observing that value is estimated given the observed data and current parameter estimates” (p. 82). Rubin (1976) provides the justification that this is the correct likelihood to be maximized when data are MAR or MCAR. Furthermore, Shumway and Stoffer (1982) discussed the underlying processes of the EM Procedure when applied to time-series data streams. The EM Procedure was applied to all data streams in the data set using PASW Statistics for Windows and Mac. (2010) (Version 18.0.0). Chicago: SPSS Inc.

Calculating an Effect of Phase

Empirical studies (e.g., Ferron, Foster-Johnson, & Kromney, 2003; Ferron & Ware, 1995) suggest that Type II error is the main problem in single-case time-series data streams, since Type I error can usually be controlled using randomization elements in the research design of the study (for examples, see Ferron & Ware; Kratochwill & Levin, 2010). Therefore, power sensitivity is an appropriate statistic for determining precision because it is complementary to Type II error rates. Manolov and Solanas (2008) found that autocorrelation least affected effect sizes using standardized mean differences, such as Glass's Δ, Cohen's d, and Hedge's g, and percentage of nonoverlapping data indices. Similarly, Solanas et al. (2010) concluded that level change effect sizes, calculated using a standardized mean differences approach, were “not affected by the presence of the degree of autocorrelation tested, as the values of its estimators do not change regardless of the values of φ1 for AR(1) processes and θ1 for MA(1) processes” (p. 536). Thus, following the lead of Ferron and Sentovich (2002), Manolov and Solanas (2008), Solanas et al., and others, we calculated an effect of phase using Glass's Δ. ³ Using a standard critical values table, we determined the effect size needed to infer significance (two-tailed) with our data streams, using an alpha (α) of 0.05, was a Glass'sΔof 1.023, based on 17 degrees of freedom (i.e., 16 estimatable lags of autocorrelation+the intercept; see Box & Jenkins, 1970).

Determining Power Sensitivity

Power sensitivity is the ability to detect an effect, if the effect actually exists (See Equation 2; Cohen). The acceptable rate of power sensitivity has been set traditionally at 0.80 (Cohen, 1988). Power sensitivity is influenced by the statistic used (e.g., Glass's Δ, r, d), the N, α, and the size of the effect. In this study, the N is relatively large with 66 observations in each data stream. We chose α = 0.05 because of its commonality, and we chose Glass's Δ based on previous research.

$$\text{Power Sensitivity}=\frac{\text{number of True Positives}}{\text{number of True Positives}+\text{number of False Negatives}}$$ (2)

After Glass's Δ was calculated for each individual data stream across all proportions of missing values, we used a dummy coding scheme to code significant or insignificant effects in the original data streams with no missing observations and those data streams where missing observations were replaced using the EM Procedure. This was done as a means of categorizing results in order to determine the power sensitivity across proportions of missing values and levels of lag 1 autocorrelation.

Results

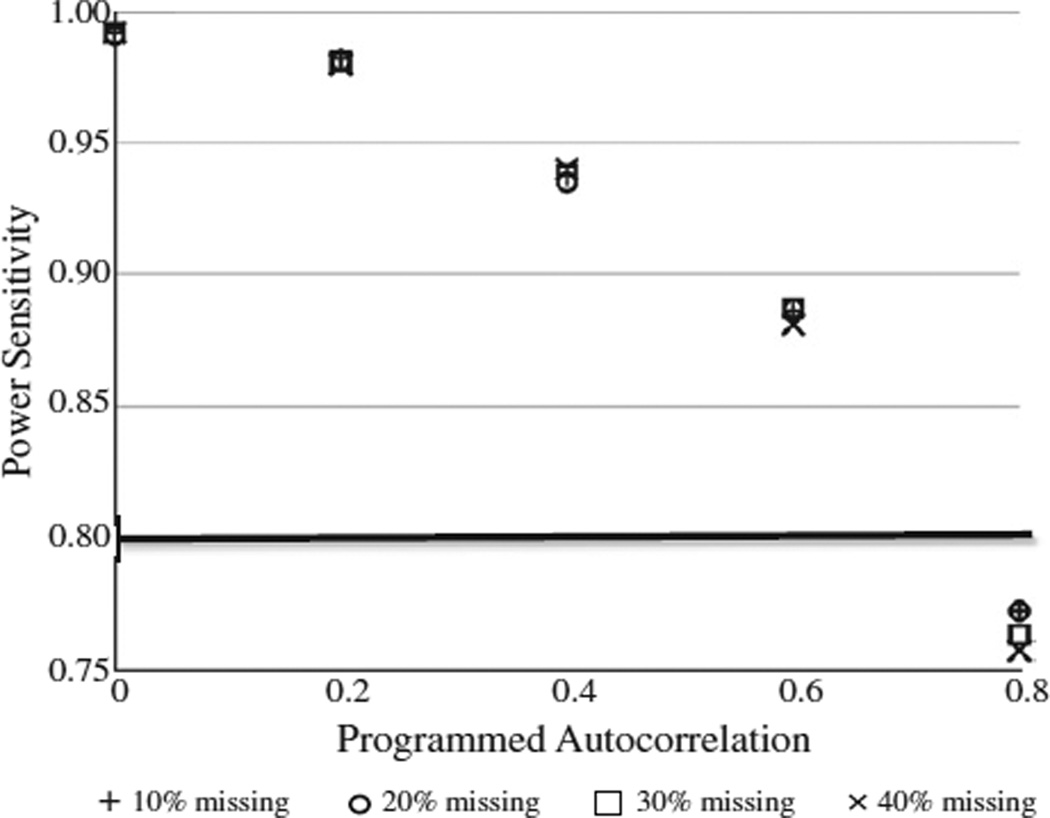
In order to address our first hypothesis, we calculated the power sensitivity for each proportion of missing observations, regardless of autocorrelation. The power sensitivity at each proportion of missing data was: 10%= .914, 20%= .913, 30%=.912, 40%=.910. These results indicate relative consistency across the four proportions of missing values and they are above 0.80, suggesting acceptable power sensitivity. To address our second hypothesis, we calculated the power sensitivity of each level of autocorrelation and proportion of missing observations. Figure 1 illustrates that the pattern of power sensitivity is similar across the four proportions of missing observations and deteriorates as autocorrelation increases, falling just below the acceptable level when autocorrelation reached 0.80.

FIGURE 1.

Power Sensitivity Across Proportions of Missing Observations at Each Level of Programmed Lag 1 Autocorrelation. Note. The bold horizontal line indicates Cohen's (1988) benchmark for power sensitivity (0.80).

Conclusions

This study provides further support for the accuracy of the EM Procedure on the level-change parameter and also extends these findings to inform decision-making in research employing time-series designs. Our results suggest that the proportion of missing observations is not as significant a factor in inferential precision as the level of autocorrelation in the data stream: The EM Procedure seems to be an effective means of replacing missing observations and maintaining power sensitivity, even when 40% of the data stream is missing completely at random. However, when autocorrelation is in the vicinity of 0.80, regardless of the proportion of missing data, power sensitivity falls below the acceptable 0.80 level. Yet, overall power sensitivity remained quite high in our simulated sample, indicating that the EM Procedure is well-suited to managing missing observations in time-series data-streams. It is imperative to appreciate that these results only apply to missing data that is MCAR. Data that is MAR or systematically missing may not perform similarly. Additional research in this area is needed.

Limitations and Future Directions for Research

The findings of this study occurred under nearly optimal conditions, unlike real-world applied research in which the assumption of MCAR is rarely satisfied, and the researcher doesn't have the privilege of “knowing the real effect size” without missing observations. A replication of these studies with naturally occurring data streams is the next logical step in determining the interaction between, and effects of, different time-series parameters on the conclusions drawn from time-series research. Alternatively, employing missing data algorithms with systematically missing observations, which are more likely to occur in applied research, would be useful for researchers conducting single-case time-series studies, as would comparing the accuracy of other available missing-data-estimation techniques, such as multiple imputation and Bayesian.

Second, this study was modeled after an 8-week treatment outcome study with a 10-day pretreatment baseline, which limits generalizability to longer or shorter time periods. Manolov and Solanas (2008) did not find differences due to the length of the data stream, but their streams were rather short compared to the single-subject psychotherapy outcome experiment after which our study was modeled. Given the results of previous simulation studies (e.g., Manolov & Solanas, 2008; Velicer & Colby, 2005a), we believe that our primary findings will hold true in studies of longer and shorter data streams, but this is an area of inquiry that still requires controlled investigation. Future studies with various data stream lengths that might be encountered in applied research settings would improve generalizability.

Last, this study only employed one statistical approach for detecting an effect of phase. However, there are many available options for the analysis of single-case time-series experiments, many of which would arguably be more appropriate in applied research with autocorrelated data. The available statistical methods designed for time-series analysis account for the autocorrelation of the data stream differently, and calculate effect sizes differently as well, which has resulted in a great deal of debate in the field (e.g., Campbell, 2004; Cohen, 1994; Ferron & Sentovich, 2002; Ferron & Ware, 1995; Kirk, 1996; Manolov & Solanas, 2008; Olive & Smith, 2005; Parker & Brossart, 2003; Robey, Schultz, Crawford, & Sinner, 1999; Velicer & Fava, 2003). Future simulation studies might consider comparing inferential precision of multiple statistical analysis methods, preferably those found to be superior in previous research (e.g., Campbell, 2004; Manolov et al., 2011; Parker & Brossart, 2003).