Complex dynamics of defective interfering baculoviruses during serial passage in insect cells

Abstract

Defective interfering (DI) viruses are thought to cause oscillations in virus levels, known as the ‘Von Magnus effect’. Interference by DI viruses has been proposed to underlie these dynamics, although experimental tests of this idea have not been forthcoming. For the baculoviruses, insect viruses commonly used for the expression of heterologous proteins in insect cells, the molecular mechanisms underlying DI generation have been investigated. However, the dynamics of baculovirus populations harboring DIs have not been studied in detail. In order to address this issue, we used quantitative real-time PCR to determine the levels of helper and DI viruses during 50 serial passages of Autographa californica multiple nucleopolyhedrovirus (AcMNPV) in Sf21 cells. Unexpectedly, the helper and DI viruses changed levels largely in phase, and oscillations were highly irregular, suggesting the presence of chaos. We therefore developed a simple mathematical model of baculovirus-DI dynamics. This theoretical model reproduced patterns qualitatively similar to the experimental data. Although we cannot exclude that experimental variation (noise) plays an important role in generating the observed patterns, the presence of chaos in the model dynamics was confirmed with the computation of the maximal Lyapunov exponent, and a Ruelle-Takens-Newhouse route to chaos was identified at decreasing production of DI viruses, using mutation as a control parameter. Our results contribute to a better understanding of the dynamics of DI baculoviruses, and suggest that changes in virus levels over passages may exhibit chaos.

Introduction

Defective interfering (DI) viruses were first reported by Von Magnus [1], who studied their development in Influenza A virus populations passaged in embryonated chicken eggs. Based on these serial passage experiments the existence of ‘incomplete’ virus variants which increase rapidly in frequency and cause drops in overall virus titers was proposed. The existence of virus variants with large genomic deletions has since been confirmed in many virus families [2], including the Alphabaculoviruses [3, 4]. DI viruses are generated almost instantly and accumulate rapidly when baculoviruses are introduced into cultured insect cells [5, 6], leading to problems with sustained expression of heterologous proteins [3] in this widely used expression system [7]. DI viruses are thought to replicate much faster than viruses with a full-length genome, due to their smaller genome sizes. Moreover, DIs can evolve other strategies to better compete with helper viruses, such as the accumulation of origins of DNA replication within a single genome [8–10], a phenomenon that can be cell-line dependent [11]. On the other hand, DI viruses cannot autonomously replicate because they lack essential genes. DI viruses must therefore co-infect a cell with a helper virus in order to replicate, becoming obligate parasites of helper viruses, as they must co-opt gene products and cannot replicate on their own. When the frequency of the DI virus is high, overall virus production is low because essential gene products – which must come from a helper virus – are no longer available (i.e., interference). DI viruses can have implications for virus amplification in cultured cells, protein expression using viral vectors, and vaccination [12].

Co-existence of DI and helper viruses is thought to lead to regular cyclical changes in virus titer: there is a repeated decrease followed by an increase in virus titers over passages. These cyclical changes have been observed in many viral systems [2, 13–16] and have been dubbed the ‘Von Magnus effect’. The following mechanism [2] has been suggested to account for these fluctuations in virus titer: (i) cells are infected with a virus population composed of a helper and a DI virus, or a DI virus is generated spontaneously by mutation, (ii) virus amplification leads to an increase in the cellular multiplicity of infection, the number of virions infecting each cell, (iii) the DI virus will eventually reach a higher frequency of occurrence than the helper virus, as it has a selective advantage over the helper virus during cellular co-infection, and (iv) when the frequency of the DI virus becomes high, interference occurs and the titers of both viruses drop. The process then repeats itself, resulting in cyclical fluctuations in virus titers.

There is some experimental evidence that this mechanism is important for generating cyclical changes in virus titer. Palma and Huang [16] tracked the titer of helper and DI Vesicular stomatitis virus (VSV) variants and found that the two viruses evolved out of phase. Kawai et al. [14] showed that VSV plaque-forming units peak before viral capsid inclusions – an indicator of DI presence – accumulate in cells. On the other hand, Stauffer Thompson and Yin [17] observed irregular fluctuations of VSV over passages in the presence of DI viruses, which were attributed to experimental variation in available cellular resources. The idea that the dynamics of DI viruses could lead to irregular patterns had, however, already been made previously based on theoretical work, albeit for different reasons. Deterministic mathematical models of defective viruses considering discrete dynamics were early studied, and the presence of deterministic chaos was suggested [18]. Later, detailed mathematical models of serial passage predicted irregular fluctuations in virus titer, claimed to be also representative of deterministic chaos [19, 20]. Although these studies suggested the presence of chaos, the confirmation of chaotic dynamics in theoretical models of helper and DI viruses was not thoroughly provided. All these observations suggest that the interactions between helper and DI viruses may in some cases lead to more complex interactions than those postulated by the ‘Von Magnus’ model.

For baculoviruses regular cyclical changes in virus titer have not been observed during passages in insect cells (e.g., [5]), although De Gooijer et al. [21] observed patterns likely caused by the presence of DI viruses in bioreactors [22, 23]. Moreover, few studies have tracked DI baculovirus levels over time [6, 24]. In this study, we therefore first sought to observe experimentally and better understand the dynamics of DI baculoviruses. We employed quantitative real-time PCR (qPCR) to consider how levels of helper and DI baculoviruses change over a high number of passages in insect cells. Given that we observed irregular fluctuations in the titers of both helper and DI viruses, we then explored the characteristics of a simple mechanistic mathematical model that produced patterns qualitatively similar to the data. Our experimental observations and theoretical results help shed light on the question of whether the dynamics of virus populations harboring DIs are chaotic.

Methods

Serial passage in insect cells

For our experiments, bGFP was serially passaged in insect cells. bGFP is a bacmid-derived [25] alphabaculovirus, Autographa californica multiple nucleopolyhedrovirus (AcMNPV), expressing GFP under the polyhedrin promoter [5]. One hundred minimal-dilution (e.g., 1:4 dilution) serial passages were performed in a monolayer of approximately 10⁶ Sf21 cells [26] in 25 ml flasks [5]. For the first passage, 20 median tissue culture infectious dose units per cell were added. The cells were exposed to the virus for 2 h, followed by the refreshing of media and incubation of the cells for 72 h. The media collected at the end of a passage was used for passaging and as samples for analysis.

qPCR

We quantified the concentration of the ie1 and p94 genes in budded virus samples from the serially passaged baculovirus with a SYBR Green I based qPCR assay [24]. DNA was extracted from stored media and analyzed by qPCR as described elsewhere [27]. For ie1, the forward primer 5^′-TCGGAATCCCTTGAGCAGCCTG-3^′ and reverse primer 5^′-TTGCCGATGGTTGGTTCACACC-3^′ were used. For p94, the forward primer 5^′-CCGAGACATACCACAAAGCCG-3^′ and reverse primer 5^′-GCACATAAACGACGCAGAATACAT-3^′ were used. As an internal control, samples were spiked with 10⁹ copies of a plasmid containing luciferase prior to DNA extraction (pGEM-luc; Promega). The forward primer 5^′-TGTTGGGCGCGTTATTTATC-3^′ and reverse primer 5^′-AGGCTGCGAAATGTTCATACT-3^′ were used to amplify luciferase, as previously described [28]. DNA concentrations for all three templates were calculated from fluorescence levels using comparative analysis in RotorGene 6.0 Software (Corbett Research; Sydney, Australia). The ie1 and p94 levels were divided by measured luciferase DNA concentration for normalization. Five time points could not be analyzed for various technical reasons (i.e., sample volume available, low yields of DNA upon extraction).

Statistical analyses were performed with the statistical software package R version 2.14.2 (The R Foundation; Vienna, Austria) or SPSS 20.0 (IBM Corporation, Armonk, NY, USA).

Simple probabilistic model of DI dynamics

In order to model infection dynamics for our system, we assume that during infection of insect cells each virion acts independently, and that the dynamics of infection during serial passaging can be captured by only considering the first round of cellular infection during each passage. Moreover, for simplicity we assume that each virion produced will infect a cell in the next round of passaging. We can make this assumption because we are considering processes within the cell (i.e., replication), and we do not have to consider both virion numbers produced and probabilities of infection in any detail. As virions act independently, the number of infecting virions per cell follows a Poisson distribution for each virus. These distributions will have means ψ_H = n_H/c for the helper virus and ψ_D = n_D/c for the DI virus, where n_H is the number of helper virions, n_D is the number of DI virions and c is the number of cells. We then consider the frequency of cells infected only by the helper virus,α, or co-infected by both viruses, β, since of all cells there will only be virus production in these two fractions. Following [28], the infection probabilities are given by:

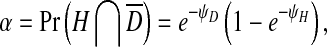1

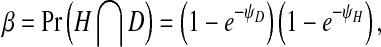2

where 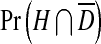is the probability a cell will be infected by the helper virions but not by DI virions, and 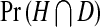is the probability a cell will be infected by both helper and DI virions. Those cells infected by only the helper virus produce v_α virions per cell. However, the helper virus mutates into a DI with a probability μ. In co-infected cells, mainly DIs are produced at a rate of 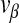virions per cell. However, we allow for the possibility that production of virions in co-infected cells is leaky, allowing a proportion ϕ of virions to be of the helper virus type. Hence the production of helper and DI virions during a passage, t, is:

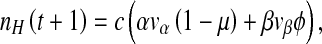3

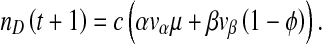4

There are a number of other sources of variation during serial passage experiments besides the distribution of helper and DI viruses over cells. Mutation from helper virus to DI virus is an inherently stochastic process and is therefore an unavoidable source of variation in experiments. We assume these mutations occur in those cells infected only by the helper virus (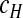 = αc), and that the number of cells in which a mutation occurs follows a binomial distribution with a probability of success χ:

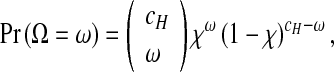5

where Ω is a random variable describing the number of cells in which a mutation occurs, and ω is a realization of Ω. For each passage, one realization of this binomial process ω can then be divided by c_H and substituted for μ in (3) and (4). This addition renders a model incorporating the minimal conceivable stochastic variation due to mutations of helper virus to DI virus.

Stauffer Thompson and Yin [17] considered the effects of various sources of experimental error on the dynamics of helper and DI virus, and concluded the most important source of variation was the number of available cells. To consider what effects plausible sources of variation – other than mutation of helper virus to a DI virus – might have on the dynamics of virus population harboring DI viruses, we therefore allow the number of cells to follow a negative binomial distribution, such that:

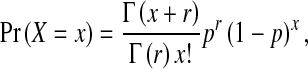6

where X is a random variable describing the number of cells used in each passage, x is a realization of X and for each passage one realization is valid, p is the probability of success for a trial, r is the number of successful trials required and Γ() is the gamma function. The negative binomial distribution was chosen because it is a discrete probability distribution for which we can change the variance without changing the mean [29], and can therefore consider variances higher than those of a Poisson distribution. Note that we attach no significance to particular p and r values or their interpretation here, these were chosen simply to increase the variance of the distribution of the number of cells to levels likely to be seen in experiments, while keeping the mean constant.

Finally, DI baculoviruses are known to accumulate multiple copies of particular loci, such as the non-HR origin of DNA replication in the p94 gene [8–10]. If the detection of DIs is sequence-based, the observed DI virus level, 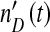, could diverge from the actual number of virions, n_D(t), increasing over passages because multiple copies of the specific sequence used for detection accrue in DI genomes. If the interactions between helper and DI viruses remain otherwise identical, the observed DI virus level at passage t will be:

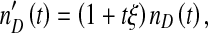7

where ξ is the rate of change in the mean number of DI detection sequences per DI genome per passage. The model was implemented with the statistical software package R 2.14.2.

Computation of the maximal Lyapunov exponent

Here we describe the procedure to compute the maximal Lyapunov exponent (hereafter MLE) for a discrete dynamical system [30, 31] that will be used for our mathematical model. The characteristic Lyapunov exponents are usually introduced to measure the rate of exponential divergence of nearby trajectories in the phase space, i.e., they give us information on the rate of growth of a very small error on the initial state of the system [32–34]. We consider the discrete dynamical system of the following form:

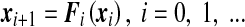8

with a given x₀, 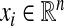and F_i being assumed to be continuously differentiable. Small perturbations to the orbits {x_i} of (8) evolve according to the dynamics of the respective linear variational equations:

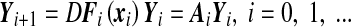with 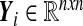and Y₀ = I. The matrix 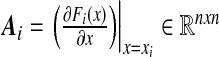is assumed to be full rank in order to obtain the n Lyapunov exponents. Let Y₀ = I and 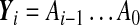; i = 0, 1, ..., be the fundamental solution of (8). Then the following symmetric positive definite matrices exist:

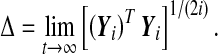The logarithms of their eigenvalues are called Lyapunov exponents of (8), and are denoted as λ₁ > λ₂ > ... > λ_n ; with λ₁ being the MLE.

We emphasize that Lyapunov exponents give us information on the typical behavior along a generic trajectory, followed for infinite time and keeping the initial perturbation infinitesimally small. The rate of separation can be different for different orientations of the initial separation vector. Therefore, there is a spectrum of Lyapunov exponents – which is equal to the dimensionality of the phase space, λ₁ > λ₂ > ... > λ_n . A positive MLE is commonly taken as an indicator of chaotic behavior (provided some conditions are met, e. g., phase space compactness).

Results and discussion

qPCR-determined ie1 and p94 levels indicate complex dynamics

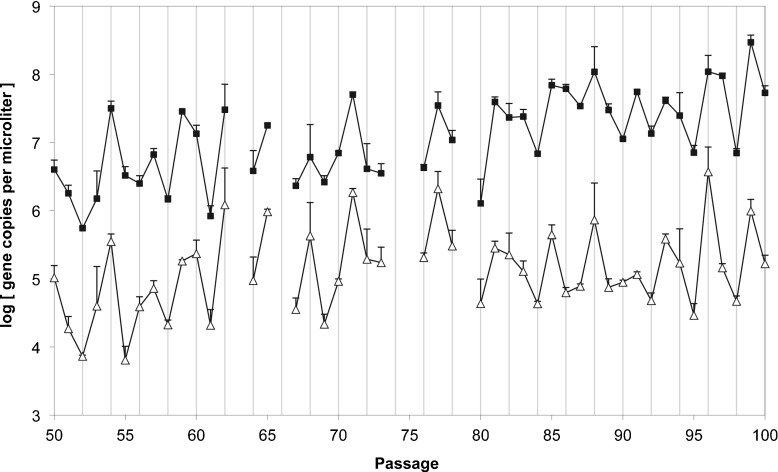
The AcMNPV-derived bGFP was passaged for 100 passages in Sf21 cells, and we then determined the level of the ie1 and p94 genes by qPCR for the ancestral virus and passages 50–100 (Fig. 1). The analysis focused on a virus population with a high number of passages, as we wanted to focus on the dynamics of a population containing DIs rather than their de novo generation, which has already been documented [5, 6, 24, 35]. The concentration of ie1 was used as a proxy for helper virus titers, because this gene encodes an essential transcriptional regulator [36]. All viruses capable of autonomous replication must therefore carry ie1. As a proxy for DI virus titers, we used the concentration of p94 – ie1, which we subsequently refer to as p94^∗. This value gives an approximation of DI levels because p94 contains a non-HR origin of DNA replication that is maintained and selected for in DI viruses [8–10, 24], and by subtracting ie1 we consider only the concentration of those viruses missing this essential gene. However, not all DI viruses need necessarily contain p94, and some DI viruses could in principle contain ie1. Our measurement is therefore a proxy, although previous results suggest it is a good indicator of the frequency of DI viruses [24]. qPCR-measured ie1 levels were significantly lower than both p94 and p94^∗ levels (Wilcoxon signed ranks test: z = −5.905, P < 0.001), in agreement with previous observations [24].

Fig. 1.

Experimental data with the passage number given on the abscissae, and the log concentration of ie1 (open triangles) and p94∗ (filled squares) given on the ordinate (error bars represent the standard error). Consecutive data points are connected by solid lines. Ie1 is used as a proxy for helper virus concentration, and p94∗ as a proxy for DI virus concentration. The concentration of p94∗ is much higher than ie1 for all passages. There are large changes in concentration of both loci over passages, p94∗ concentration increases significantly over passages. Note that the two loci appear to generally change concentration is phase. qPCR was also performed on the ancestral virus rendering similar log concentrations of 6.582 ± 0.044 for ie1 and 6.587 ± 0.038 for p94, the unadjusted level of the p94 gene. The ancestral population therefore has a 1:1 ratio of the two templates, indicating DI viruses are not present

Prima facie there appear to be no regular oscillations in ie1 and p94^∗ levels. Our results therefore contrast with previous findings for other viruses, where helper and DI viruses changed titers out of phase [14, 16] and with evident regular periodicity [14]. There appears to be an increase over passages of p94^∗ levels, whereas ie1 levels, although also showing a great deal of variation, appear to be stationary (Fig. 1). To test if this is indeed the case, we performed a non-parametric Spearman test to look for correlations between ie1 or p94^∗ levels and time. There was no significant trend for ie1 (ρ = 0.277, 44 d.f., P = 0.062), suggesting that minimum helper virus frequencies had already been reached by passage 50. On the other hand, p94^∗ increased significantly over passages (ρ = 0.654, 44 d.f., P < 0.001), suggesting that DI genomes accumulated multiple copies of the non-HR origin of DNA replication in their genomes [8–10]. This trend could, however, also result from an overall increase in the number of DI viruses present per helper virus, indicating the DI virus is optimizing its exploitation of the helper virus.

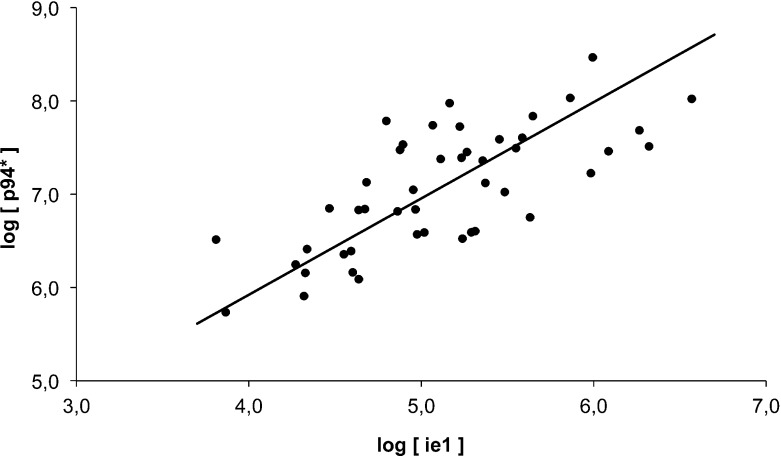
The levels of ie1 and p94^∗ varied greatly between passages, and the two levels of viruses appear to change in phase (Fig. 1). A Model II major-axis linear regression [37] on log-transformed ie1 and p94^∗ concentrations rendered a slope significantly greater than zero (0.965 with a 95% confidence interval 0.713–1.301; P < 0.001), confirming a relationship between the two variables (Fig. 2). This relationship in turn is congruent with the observation that the two viruses change levels in phase: when the level of DI virus increases, the level of helper virus tends to increase, while when the helper virus decreases, levels of DI tend to decrease.

Fig. 2.

Model II major-axis regression on the log ie1 titer (abscissa) vs. log p94^∗ levels (ordinate)

Simple models of DI dynamics

Measurements of ie1 and p94^∗ levels by qPCR gave surprising results, as the helper and DI viruses changed levels in phase and the length of oscillations appeared to be irregular. To better understand these results, we built a simple probabilistic model describing the interactions between helper and DI virus infecting insect cells. The model incorporates stochasticity in the number of cells in which helper viruses will mutate to DI viruses (see Section 2.3).

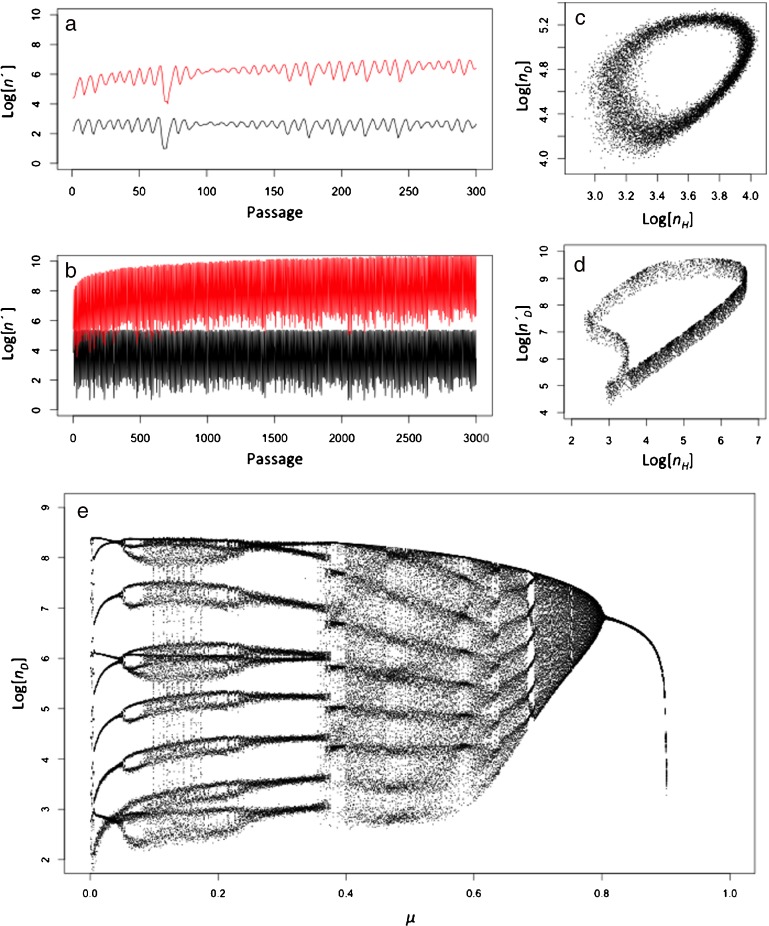
For some parameter sets, the model leads to an equilibrium state or oscillatory dynamics. Moreover, our model can also generate more complex behavior like quasi-periodic or chaotic dynamics (Figs. 3 and 4). This behavior is more similar – in a qualitative sense – to our empirical observations (Fig. 1). In these cases, the oscillatory dynamics are not completely regular and the two viruses can oscillate at different levels (i.e., n_D > > n_H). For instance, the dynamics represented in the (n_H, n_D) phase space shows a ring-like attractor formed by a broad cloud of points due to stochasticity (Fig. 3c). In order for the model to generate behavior qualitatively similar to the data, we required values for the number of insect cells (c) one order of magnitude smaller than the estimated number of cells used in serial passage experiments. As 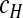depends on c, stochastic effects will become stronger as the number of cells decrease [see (5)]. Hence, this disparity suggests that there are other sources of variation in our experiment, or alternatively that a small number of infected cells actually contribute to the viable virus progeny being passaged.

Fig. 3.

Dynamical behavior of the DI mathematical model. Panel a and b are time series generated by the model, with the lower lines representing the level of the helper virus and the upper line the observed level of the DI virus 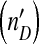. The model can generate a combination of irregular oscillations, much higher levels of DI 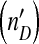than helper virus (n_H), and virus levels which change almost in phase (in the periodic and chaotic behaviors). 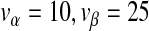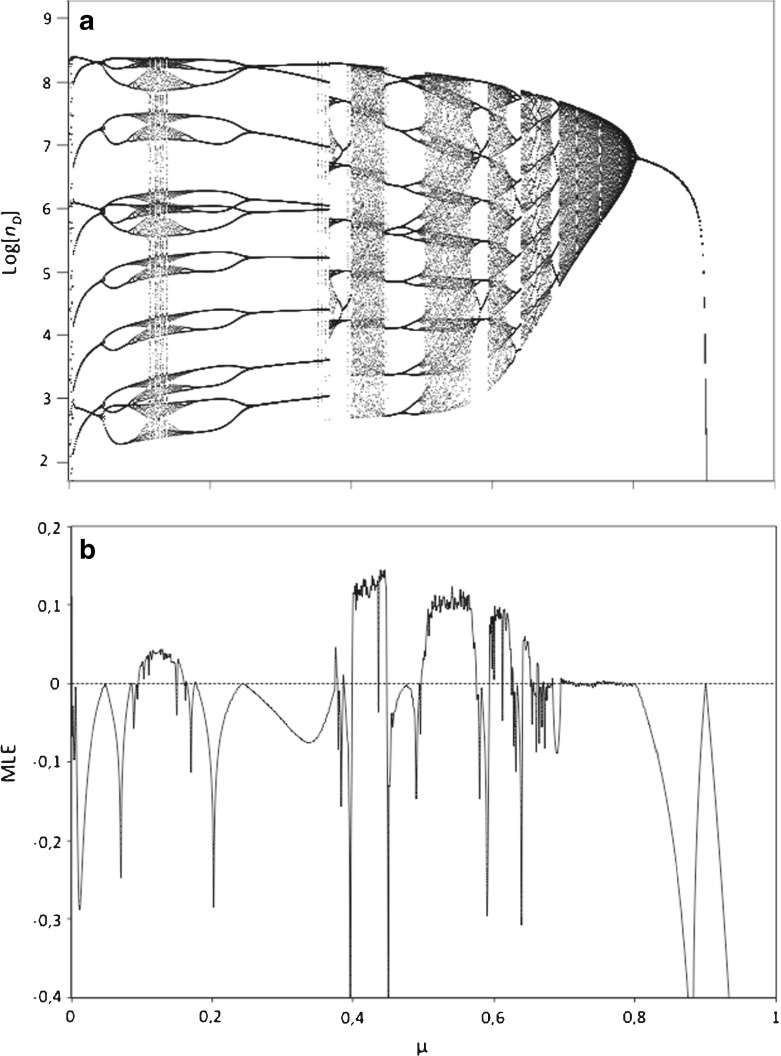In all plots we used and ϕ = 0.0002. For panels a–dξ = 0.01, whereas ξ = 0 for Panel e. In ac = 10⁴ and μ = 0.78, and in bc = 5 × 10⁵ and μ = 0.61. Panel c shows a noisy, ring-like attractor in the phase space obtained by plotting the population numbers of the helper virus on the x-axis and the DI virus on the y-axis for c = 10⁵ and μ = 0.78. Panel e is a bifurcation diagram, for which the model was run for 300 serial passages. We increased μ (the mutation rate) from 0 to 1 by increments of 1 × 10^− 3 (abscissae), and then plotted the log₁₀-transformed DI virus levels (n_D) over the last 100 passages (ordinate). The model was run with a large number of cells (c = 10⁷) to minimize stochasticity and no differences in observed DI numbers [ξ = 0 in (7)] so that virus levels could be compared over passages (i.e., 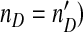. The results suggest a series of bifurcations although there is some variation in the dynamics for all μ values due to the stochasticity of the model. We therefore performed the same analysis without stochastic effects (the mutation rate for each passage is μ, and not a realization of Ω), which makes it possible to observe clearly the structure of the chaotic attractor using c = 10⁷ and μ = 0.61 (Panel d). We also generated a bifurcation diagram without stochastic effects (Fig. 4a)

Fig. 4.

a Bifurcation diagram computed using the same parameter values as in the Fig. 3e. However, here we show the dynamics as mutation is changed without considering stochastic effects (the mutation rate for each passage is μ, and not a realization of Ω). The bifurcation diagram reveals a Ruelle-Takens-Newhouse (i.e., quasi-periodic) route to chaos at decreasing mutation rate, which is confirmed in the plot below. b Maximal Lyapunov exponent (MLE) for the same range of mutation rates shown in the bifurcation diagram above (the MLE is zero when a bifurcation takes place and positive when the dynamics is chaotic). After a first bifurcation (occurring at μ ≈ 0.9), a series of flip bifurcations (within the range 0.7 ≤ μ ≤ 0.8) take place indicating the quasi-periodic route to chaos. Then, some chaotic windows are identified by means of positive MLE (see horizontal dotted line at zero MLE values)

Chaos in the dynamics of helper and DI viruses

The time series in Fig. 3 and the attractor in Fig. 3d suggest the presence of complex dynamics. In order to investigate the possible array of dynamical behaviors arising from our model, we built bifurcation diagrams using mutation rate as control parameter, and identified several parameter regions suggesting chaotic behavior. The bifurcation diagram was first built considering a large population of insect cells to minimize stochastic effects (Fig. 3e). Moreover, similar results were obtained for our model when the rate of mutation (μ) was fixed (Fig. 4a). Therefore, when we remove the stochastic component, our simple probabilistic model appears to exhibit deterministic chaos, in agreement with previous theoretical studies suggesting this type of dynamics among helper and DI viruses [18, 20].

In order to properly identify the presence of chaos in our model we computed the MLE (see Section 2.4). The Lyapunov exponents are used as a convenient indicator of the exponential divergence of close initial conditions, which is characteristic of chaotic dynamics [38, 39]. The results of the MLE computation are shown in Fig. 4. We first show the same bifurcation diagram previously computed (Fig. 3e), but now removing stochasticity (i.e., a variable rate of mutation). The dynamics clearly show a pattern of a series of bifurcations when varying mutation rate. Below the bifurcation diagram we show the MLE computed for the same range of mutation rates used in the bifurcation diagram (Fig. 4b). We notice that the MLE allows us to identify two interesting dynamical properties: (i) chaos and (ii) bifurcations. In this sense, chaotic dynamics arises when the MLE is positive. For example, see the chaotic window in the parameter range 0.5 ≲ μ ≲ 0.57. On the other hand, bifurcations occur when the MLE is zero. At decreasing mutation there is a first bifurcation occurring when μ ≈ 0.9, and then there are a series of flip bifurcations that involve oscillatory (i.e., periodic and quasi-periodic), but not chaotic, dynamics within the range 0.7 ≲ μ ≲ 0.8. Such a series of flip bifurcations suggest the presence of a Ruelle-Takens-Newhouse (or quasiperiodic) route to chaos [38]. The Ruelle-Takens-Newhouse transition to chaos involves that as the control parameter (mutation rate in our system) is changed, the dynamics undergoes a series of flip bifurcations giving place to periodic and toroidal or quasiperiodic attractors that then become unstabilized giving place to a strange attractor (i.e., with positive Lypunov exponents), as we show in Fig. 4. A further decrease of mutation can cause chaotic dynamics (see positive values of the MLE in Fig. 4b). Previous theoretical studies have suggested that DI virus dynamics could exhibit deterministic chaos [18, 20]. However, these studies did not provide dynamical measures (e.g., Lyapunov exponents) confirming the presence of chaos. Finally, we notice that chaotic windows using μ as control parameter and tuning other model parameters were also found (results not shown).

Predicted effects of experimental variation on dynamics of helper and DI viruses

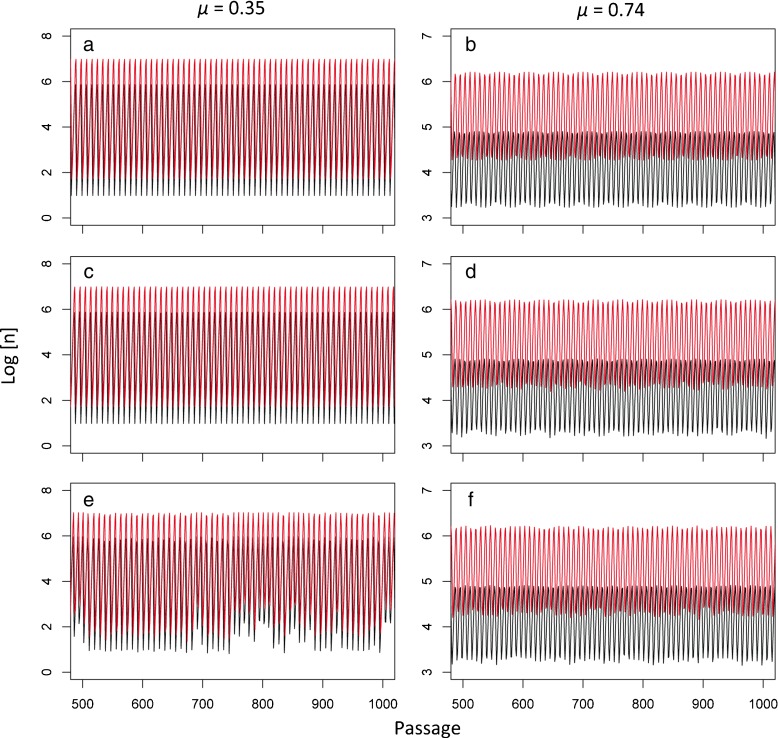
The analysis of MLE was performed on a deterministic model, which does not include the effects of experimental variation. Although this analysis suggests the presence of deterministic chaos in the simple model presented (Fig. 4), the apparently irregular and possibly chaotic patterns in the actual experimental data could conceivably arise because of experimental variation. To assess what the impact of experimental variation may be, we included an important source of experimental variation in our model: variation in the number of cells over passages [17]. Using the same model parameters as in Fig. 3, we considered two μ values: (i) 0.35, for which the MLE is −0.068, and (ii) 0.74, for which the MLE is −0.005. These values were chosen to consider situations in which the deterministic model clearly predicts non-chaotic dynamics (μ = 0.35), and a situation in which the MLE approaches positive values (μ = 0.74). We then ran simulations of the deterministic model (Fig. 5a and b) and simulations incorporating variability in the number of cells (Fig. 5c and d; see Section 2 for details), and stochasticity in the occurrence of mutations (Fig. 5e and f). These simulations show that, for parameter values that the deterministic model predicts non-chaotic dynamics, stochasticity in mutation and variation in the number of cells can both generate time series with irregular fluctuations similar to our experimental observations. However, for the given parameter values the effects of mutation were stronger than the effects of variation in the number of cells.

Fig. 5.

Predicted effects of experimental variation on the dynamics of virus populations. For all panels passage number is given on the abscissae, the log of the virus number is given on the ordinate and the trajectories of helper and DI viruses are given in lower and upper lines, respectively. We considered the effects on model dynamics of two sources of stochasticity: (i) mutation, modeled as a binomially distributed number of cells in which the helper virus mutates to a DI virus, and (ii) variation in the number of cells over passages, modeled as a negative binomial distribution with p = 0.01 and r = 5050.5 resulting in a mean of 5 × 10⁵ and variance 5 × 10⁷. We used the same model parameters as in Fig. 3b (v_α = 10, v_β = 25, ϕ = 0.0002, c = 5 ×10⁵), but set ξ = 0 for clarity. For the left hand panels μ = 0.35, resulting in an MLE well below zero (−0.068; see Fig. 4) and a two point cycle. For the right hand panels μ = 0.74, resulting in an MLE near zero (−0.005) and a regular multipoint cycle. In panels a and b, the results of the deterministic model are given. Here mutation has a fixed rate, and the number of cells is constant over passages. In panels c and d, the number of cells is variable, following a binomial distribution over passages as described above. The effect is negligible when μ = 0.35 c, but much stronger when μ = 0.74 d. In panels e and f, mutation is stochastic. The effects are stronger in panel e than in panel f, because mutation follows a binomial distribution in which the number of trials is the number of cells infected only by the helper virus, and this number reaches lower levels in e. The combined effects of stochastic mutation and a variable frequency of cells rendered similar results to that in panels e and f. These simulations reinforce the idea even if the deterministic model predicts non-chaotic dynamics for a particular set of parameters, experimental variation can generate time series with irregular fluctuations

These results suggest that our analysis of the deterministic model needs to be interpreted cautiously. A simple deterministic model inspired by experimental data displays chaotic dynamics, but even for parameter values for which the model dynamics are not predicted to be chaotic, irregular patterns similar to the data can be observed if sources of variation are included in the model. Moreover, the stochasticity induced by mutation is inherent to the system. In other words, even if a perfect experiment was conducted (there would be no experimental variation whatsoever; i.e., cell number was held constant over passages), mutation would still be a source of stochasticity. We cannot, therefore, unequivocally attribute irregular changes in virus titer over passages to purely deterministic chaotic dynamics. What we can conservatively conclude is that even a simple deterministic model, one that excludes a source of stochasticity inherent to the experimental system, generates chaotic dynamics. Although we cannot exclude that stochastic processes are also responsible for the surprising experimental observations, our work helps bolster the case that deterministic chaos is a plausible hypothesis. Moreover, the consideration of stochasticity is not incompatible with the result that standard-DIs dynamics may behave chaotically, leading to complex fluctuation patterns (see Section 4).

Conclusions

By monitoring the dynamics of helper and DI baculovirus levels over passages in insect cells we observed that the titers of both viruses oscillated irregularly, suggesting the presence of chaos. A simple stochastic model of DI dynamics illustrated how such irregular cyclical dynamics could be generated, a result similar to that obtained by others [17, 18, 20]. Early theoretical studies on helper and DI viruses predicted oscillations [18], and even suggested the possibility of chaotic attractors governing the dynamics of these types of systems [18, 20]. Our results demonstrate that the ‘Von Magnus’ model may be too simple to explain the dynamics of DI baculoviruses in insect cells. The observed dynamics hint that the evolution of virus levels over time may very well be chaotic, as suggested by Szathmáry [18] and Kirkwood and Bangham [20].

Our simple model without stochasticity generated chaos, and both bifurcation diagrams and Lyapunov exponents analyses revealed a quasiperiodic (i.e., Ruelle-Takens-Newhouse) route to chaos at decreasing mutation rates generating defective particles. Although previous studies [18, 20] suggested the presence of chaos underlying the dynamics of helper and DI viruses, these authors did not provide quantitative measures of chaos. By computing the MLE we have numerically shown that for some parameter regions chaos is found in this type of system. Such a finding has important implications for the predictability of DI dynamics in insect cells, making it impossible to accurately predict dynamics in the long term even if the composition of a virus population is known. On the other hand, we cannot discard the notion that experimental variation – especially stochasticity in the helper virus mutating to a DI virus – may play an important role in generating the dynamical patterns we have observed. However, noise may not be incompatible with chaotic behavior: it has been suggested that a system with negative Lyapunov exponent in the absence of noise can have a positive stochastic Lyapunov exponent when noise is introduced [40]. In this sense, possible sources of noise in our experiments such as stochastic mutation or variation in the number of insect cells could increase parameter regions displaying chaos (see Figs. 3e and 5). Previous studies of the geometry of the attractors found in the driven anharmonic oscillator revealed that increased noise levels could induce a transition to chaotic behavior [41]. Hence, rather than destabilizing or eradicating chaotic motions in the phase space, noise can enhance chaos, while destroying periodic orbits. Actually, local instabilities responsible for the deterministic chaos actually increased the observability of chaos in the presence of fluctuations [41, 42].

We have presented a simple model of DI dynamics in order to better elucidate the mechanisms underlying the experimentally observed behavior. The use of simple mathematical models makes it easier to identify mechanisms underlying different dynamics. On the other hand, we could only consider whether particular qualitative aspects of model behavior were supported by the data. Furthermore, it was recently shown that alphabaculovirus populations passaged in insect cells accumulate multiple DI viruses [6], a conclusion supported by the different qPCR-measured levels for 4 different loci in passaged baculovirus populations [24]. Here we only modeled one helper virus and one DI virus, a reasonable approach given that our qPCR-based proxies, ie1 and p94^∗ levels, are also dichotomous.